संदर्भ वायुमंडलीय मॉडल: Difference between revisions
No edit summary |
No edit summary |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 13: | Line 13: | ||
:<math> \rho = \frac{M P}{R T} </math> | :<math> \rho = \frac{M P}{R T} </math> | ||
जहाँ ρ द्रव्यमान घनत्व है, M औसत आणविक भार है, P दबाव है | जहाँ ρ द्रव्यमान घनत्व है, M औसत आणविक भार है, P दबाव है T तापमान है और R आदर्श गैस स्थिरांक है। | ||
गैस तथाकथित [[द्रवस्थैतिक]] बलों द्वारा आयोजित की जाती है। कहने का अर्थ यह है कि कुछ ऊँचाई पर गैस की एक विशेष परत के लिए: इसके भार का नीचे की ओर (ग्रह की ओर) बल इसके ऊपर की परत में दबाव द्वारा लगाया गया नीचे का बल, और नीचे की परत में दबाव द्वारा उर्ध्वगामी बल सभी का योग शून्य है। गणितीय रूप से यह है: | गैस तथाकथित [[द्रवस्थैतिक]] बलों द्वारा आयोजित की जाती है। कहने का अर्थ यह है कि कुछ ऊँचाई पर गैस की एक विशेष परत के लिए: इसके भार का नीचे की ओर (ग्रह की ओर) बल इसके ऊपर की परत में दबाव द्वारा लगाया गया नीचे का बल, और नीचे की परत में दबाव द्वारा उर्ध्वगामी बल सभी का योग शून्य है। गणितीय रूप से यह है: | ||
| Line 34: | Line 34: | ||
=== समतापीय-बारोट्रोपिक सन्निकटन और [[पैमाने की ऊंचाई|मापदंड की ऊंचाई]] === | === समतापीय-बारोट्रोपिक सन्निकटन और [[पैमाने की ऊंचाई|मापदंड की ऊंचाई]] === | ||
यह वायुमंडलीय मॉडल मानता है कि आणविक भार और तापमान दोनों ऊंचाई की एक विस्तृत श्रृंखला पर स्थिर हैं। ऐसे मॉडल को इज़ोटेर्मल (निरंतर तापमान) कहा जा सकता है। [[आदर्श गैस कानून|आदर्श गैस नियम]] | यह वायुमंडलीय मॉडल मानता है कि आणविक भार और तापमान दोनों ऊंचाई की एक विस्तृत श्रृंखला पर स्थिर हैं। ऐसे मॉडल को इज़ोटेर्मल (निरंतर तापमान) कहा जा सकता है। [[आदर्श गैस कानून|आदर्श गैस नियम]] के लिए समीकरण में निरंतर आणविक भार और निरंतर तापमान डालने से परिणाम उत्पन्न होता है कि घनत्व और दबाव दो शेष चर केवल एक दूसरे पर निर्भर करते हैं। इस कारण से इस मॉडल को [[बैरोट्रोपिक]] भी कहा जा सकता है (घनत्व केवल दबाव पर निर्भर करता है)। | ||
इज़ोटेर्मल-बैरोट्रोपिक मॉडल के लिए घनत्व और दबाव ऊंचाई के घातीय कार्य होते हैं। पी या ρ के प्रारंभिक मान के 1/e तक गिरने के लिए आवश्यक ऊंचाई में वृद्धि को मापदंड की ऊंचाई कहा जाता है: | इज़ोटेर्मल-बैरोट्रोपिक मॉडल के लिए घनत्व और दबाव ऊंचाई के घातीय कार्य होते हैं। पी या ρ के प्रारंभिक मान के 1/e तक गिरने के लिए आवश्यक ऊंचाई में वृद्धि को मापदंड की ऊंचाई कहा जाता है: | ||
| Line 41: | Line 41: | ||
जहाँ R आदर्श गैस स्थिरांक है, T तापमान है, M औसत आणविक भार है, और ''g''<sub>0</sub> ग्रह की सतह पर गुरुत्वीय त्वरण है। पृथ्वी के वायुमंडल की विशेषता के रूप में T=273 K और M=29 g/mol मानों का उपयोग करना H = RT/Mg = (8.315*273)/(29*9.8) = 7.99 या लगभग 8 किमी जो संयोग से माउंट एवरेस्ट की अनुमानित ऊंचाई है | जहाँ R आदर्श गैस स्थिरांक है, T तापमान है, M औसत आणविक भार है, और ''g''<sub>0</sub> ग्रह की सतह पर गुरुत्वीय त्वरण है। पृथ्वी के वायुमंडल की विशेषता के रूप में T=273 K और M=29 g/mol मानों का उपयोग करना H = RT/Mg = (8.315*273)/(29*9.8) = 7.99 या लगभग 8 किमी जो संयोग से माउंट एवरेस्ट की अनुमानित ऊंचाई है | ||
एक इज़ोटेर्माल वातावरण के लिए, | एक इज़ोटेर्माल वातावरण के लिए, <math>(1-\frac{1}{e})</math> या वायुमंडल के कुल द्रव्यमान का लगभग 63% ग्रह की सतह और एक मापदंड की ऊँचाई के बीच उपस्थित है। (एक निश्चित ऊंचाई के नीचे कुल वायु द्रव्यमान की गणना घनत्व कार्य को एकीकृत करके की जाती है।) | ||
समुद्र के उदाहरण के लिए समुद्र के शीर्ष या सतह पर घनत्व में तेज संक्रमण था। चूँकि गैस से बने वायुमंडल के लिए कोई समकक्ष तेज संक्रमण या बढ़त नहीं है। गैस के वायुमंडल कम से कम घने होते जाते हैं जब तक कि वे इतने पतले नहीं हो जाते कि वे अंतरिक्ष बन जाते हैं। | समुद्र के उदाहरण के लिए समुद्र के शीर्ष या सतह पर घनत्व में तेज संक्रमण था। चूँकि गैस से बने वायुमंडल के लिए कोई समकक्ष तेज संक्रमण या बढ़त नहीं है। गैस के वायुमंडल कम से कम घने होते जाते हैं जब तक कि वे इतने पतले नहीं हो जाते कि वे अंतरिक्ष बन जाते हैं। | ||
| Line 56: | Line 56: | ||
=== नासा वैश्विक संदर्भ वायुमंडलीय मॉडल === | === नासा वैश्विक संदर्भ वायुमंडलीय मॉडल === | ||
नासा अर्थ ग्लोबल रेफरेंस एटमॉस्फेरिक मॉडल (अर्थ-ग्राम) को [[ मार्शल अंतरिक्ष उड़ान केंद्र ]] द्वारा एक डिजाइन संदर्भ वातावरण प्रदान करने के लिए विकसित किया गया था, जो मानक वायुमंडल के विपरीत, भौगोलिक परिवर्तनशीलता, ऊंचाई की एक विस्तृत श्रृंखला (सतह से कक्षीय ऊंचाई तक) की अनुमति देता है। और दिन के अलग-अलग महीने और समय यह अशांति और अन्य वायुमंडलीय अव्यवस्थाएं की घटनाओं के कारण वायुमंडलीय मापदंडों में स्थानिक और लौकिक अव्यवस्थाएं का अनुकरण भी कर सकता है। उपलब्ध है<ref>{{Citation | title = Software Catalog 2015–2016 | chapter = Earth Global Reference Atmospheric Model (Earth-Gram) 2010 | publisher = NASA – Technology Transfer Program | chapter-url = https://software.nasa.gov/software/MFS-32780-1 | access-date = 16 August 2016 }}</ref> [[फोरट्रान]] में लिखे कंप्यूटर कोड में<ref>{{Citation | last = Leslie | first = F.W. | last2 = Justus | first2 = C.G. | date = June 2011 | title = The NASA Marshall Space Flight Center Earth Global Reference Atmospheric Model—2010 Version | series = NASA/TM—2011–216467 | publisher = National Aeronautics and Space Administration | place = Marshall Space Flight Center, Alabama | url = https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20110012696.pdf | access-date = 15 August 2016 }}</ref> ग्राम श्रृंखला में [[शुक्र]], मंगल और [[ नेपच्यून ]] ग्रहों और [[ शनि ग्रह ]]सैटर्नियन चंद्रमा, [[टाइटन (चंद्रमा)]] के लिए वायुमंडलीय मॉडल भी सम्मिलित हैं।<ref>{{Citation | last = Justh | first = Hilary L. | last2 = Justus | first2 = C. G. | last3 = Keller | first3 = Vernon W. | date = 2006 | title = AIAA/AAS Astrodynamics Specialists Conference; 21–24 Aug. 2006; Keystone, CO; United States | contribution = Global Reference Atmospheric Models, Including Thermospheres, for Mars, Venus and Earth | doi = 10.2514/6.2006-6394 | hdl = 2060/20060048492 | hdl-access = free }}</ref> | नासा अर्थ ग्लोबल रेफरेंस एटमॉस्फेरिक मॉडल (अर्थ-ग्राम) को [[ मार्शल अंतरिक्ष उड़ान केंद्र |मार्शल अंतरिक्ष उड़ान केंद्र]] द्वारा एक डिजाइन संदर्भ वातावरण प्रदान करने के लिए विकसित किया गया था, जो मानक वायुमंडल के विपरीत, भौगोलिक परिवर्तनशीलता, ऊंचाई की एक विस्तृत श्रृंखला (सतह से कक्षीय ऊंचाई तक) की अनुमति देता है। और दिन के अलग-अलग महीने और समय यह अशांति और अन्य वायुमंडलीय अव्यवस्थाएं की घटनाओं के कारण वायुमंडलीय मापदंडों में स्थानिक और लौकिक अव्यवस्थाएं का अनुकरण भी कर सकता है। उपलब्ध है<ref>{{Citation | title = Software Catalog 2015–2016 | chapter = Earth Global Reference Atmospheric Model (Earth-Gram) 2010 | publisher = NASA – Technology Transfer Program | chapter-url = https://software.nasa.gov/software/MFS-32780-1 | access-date = 16 August 2016 }}</ref> [[फोरट्रान]] में लिखे कंप्यूटर कोड में<ref>{{Citation | last = Leslie | first = F.W. | last2 = Justus | first2 = C.G. | date = June 2011 | title = The NASA Marshall Space Flight Center Earth Global Reference Atmospheric Model—2010 Version | series = NASA/TM—2011–216467 | publisher = National Aeronautics and Space Administration | place = Marshall Space Flight Center, Alabama | url = https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20110012696.pdf | access-date = 15 August 2016 }}</ref> ग्राम श्रृंखला में [[शुक्र]], मंगल और [[ नेपच्यून |नेपच्यून]] ग्रहों और [[ शनि ग्रह |शनि ग्रह]] सैटर्नियन चंद्रमा, [[टाइटन (चंद्रमा)]] के लिए वायुमंडलीय मॉडल भी सम्मिलित हैं।<ref>{{Citation | last = Justh | first = Hilary L. | last2 = Justus | first2 = C. G. | last3 = Keller | first3 = Vernon W. | date = 2006 | title = AIAA/AAS Astrodynamics Specialists Conference; 21–24 Aug. 2006; Keystone, CO; United States | contribution = Global Reference Atmospheric Models, Including Thermospheres, for Mars, Venus and Earth | doi = 10.2514/6.2006-6394 | hdl = 2060/20060048492 | hdl-access = free }}</ref> | ||
| Line 65: | Line 65: | ||
:<math>g(z) = \frac{G m_e}{(r_e + z)^2} </math> | :<math>g(z) = \frac{G m_e}{(r_e + z)^2} </math> | ||
''g'' | ''g'' घटने की इस समस्या से निपटने के लिए वास्तविक ज्यामितीय ऊंचाई z से भू-संभावित ऊंचाई h नामक एक अमूर्तता में परिवर्तन को परिभाषित किया जा सकता है, जिसे परिभाषित किया गया है: | ||
:<math>h = \frac{r_e z}{r_e + z} </math> | :<math>h = \frac{r_e z}{r_e + z} </math> | ||
''h'' के पास गुण है | ''h'' के पास गुण है | ||
| Line 72: | Line 72: | ||
हाइड्रोस्टेटिक समीकरणों में ज्यामितीय ऊंचाई z के अतिरिक्त इस भू-स्थैतिक ऊंचाई h का उपयोग किया जाता है। | हाइड्रोस्टेटिक समीकरणों में ज्यामितीय ऊंचाई z के अतिरिक्त इस भू-स्थैतिक ऊंचाई h का उपयोग किया जाता है। | ||
== सामान्य मॉडल == | == सामान्य मॉडल == | ||
* [[COSPAR अंतर्राष्ट्रीय संदर्भ वातावरण|कोस्पार अंतर्राष्ट्रीय संदर्भ वातावरण]] | * [[COSPAR अंतर्राष्ट्रीय संदर्भ वातावरण|कोस्पार अंतर्राष्ट्रीय संदर्भ वातावरण]] | ||
| Line 97: | Line 94: | ||
*[http://www.pdas.com/programs/atmos.f90 FORTRAN code to calculate the US Standard Atmosphere] | *[http://www.pdas.com/programs/atmos.f90 FORTRAN code to calculate the US Standard Atmosphere] | ||
*[https://web.archive.org/web/20060513194659/http://modelweb.gsfc.nasa.gov/atmos/about_atmos.html NASA GSFC Atmospheric Models overview] | *[https://web.archive.org/web/20060513194659/http://modelweb.gsfc.nasa.gov/atmos/about_atmos.html NASA GSFC Atmospheric Models overview] | ||
*[https://web.archive.org/web/20060511235337/http://modelweb.gsfc.nasa.gov/atmos/atmos_index.html Various | *[https://web.archive.org/web/20060511235337/http://modelweb.gsfc.nasa.gov/atmos/atmos_index.html Various models at NASA GSFC ModelWeb] | ||
*[https://web.archive.org/web/20161115075834/https://see.msfc.nasa.gov/model-gram Earth Global Reference Atmospheric Model (Earth-GRAM 2010)] | *[https://web.archive.org/web/20161115075834/https://see.msfc.nasa.gov/model-gram Earth Global Reference Atmospheric Model (Earth-GRAM 2010)] | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Commons category link from Wikidata]] | |||
[[Category:Created On 23/05/2023]] | [[Category:Created On 23/05/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:वायुमंडलीय विज्ञान]] | |||
Latest revision as of 15:23, 15 June 2023
एक संदर्भ वायुमंडलीय मॉडल बताता है कि वायुमंडल के आदर्श गैस गुण (अर्थात्: दबाव, तापमान, घनत्व और आणविक भार) कैसे बदलते हैं, मुख्य रूप से ऊंचाई के कार्य के रूप में और कभी-कभी अक्षांश वर्ष के दिन आदि के कार्य के रूप में भी एक स्थिर वायुमंडलीय मॉडल में समय को छोड़कर अधिक सीमित डोमेन होता है। विश्व मौसम विज्ञान संगठन द्वारा एक मानक वातावरण को वायुमंडलीय तापमान, दबाव और घनत्व के एक काल्पनिक लंबवत वितरण के रूप में परिभाषित किया गया है, जो अंतरराष्ट्रीय समझौते द्वारा सामान्यतः साल भर मध्य अक्षांश स्थितियों का प्रतिनिधि है।
विशिष्ट उपयोग अल्टीमीटर या दबाव अल्टीमीटर अंशांकन विमान प्रदर्शन गणना विमान और रॉकेट डिजाइन बाहरी प्राक्षेपिकी या परिवेश वायु घनत्व तालिकाओं और मौसम संबंधी आरेखों के आधार के रूप में हैं।[1]
उदाहरण के लिए यू.एस. मानक वायुमंडल समुद्र तल से ऊंचाई के एक कार्य के रूप में हवा के तापमान दबाव और द्रव्यमान घनत्व के मानो को प्राप्त करता है।
अन्य स्थिर वायुमंडलीय मॉडल में अन्य आउटपुट हो सकते हैं या ऊंचाई के अतिरिक्त इनपुट पर निर्भर हो सकते हैं।
मूलभूत धारणाएँ
जिस गैस में वातावरण होता है उसे सामान्यतः एक आदर्श गैस माना जाता है जिसका अर्थ है:
जहाँ ρ द्रव्यमान घनत्व है, M औसत आणविक भार है, P दबाव है T तापमान है और R आदर्श गैस स्थिरांक है।
गैस तथाकथित द्रवस्थैतिक बलों द्वारा आयोजित की जाती है। कहने का अर्थ यह है कि कुछ ऊँचाई पर गैस की एक विशेष परत के लिए: इसके भार का नीचे की ओर (ग्रह की ओर) बल इसके ऊपर की परत में दबाव द्वारा लगाया गया नीचे का बल, और नीचे की परत में दबाव द्वारा उर्ध्वगामी बल सभी का योग शून्य है। गणितीय रूप से यह है:
अंत में प्रणाली का वर्णन करने वाले ये चर समय के साथ नहीं बदलते हैं; अर्थात यह एक स्थिर प्रणाली है।
g_0, गुरुत्वाकर्षण त्वरण यहाँ एक स्थिर के रूप में उपयोग किया जाता है मानक गुरुत्वाकर्षण के समान मान के साथ (पृथ्वी या अन्य बड़े पिंड की सतह पर गुरुत्वाकर्षण के कारण औसत त्वरण)। सादगी के आधार पर यह अक्षांश ऊंचाई या स्थान के साथ बदलता नहीं है। इन सभी कारकों के कारण भिन्नता 50 किमी तक लगभग 1% है। अधिक जटिल मॉडल इस विविधताओं के लिए खाते हैं।
कुछ उदाहरण
मॉडल के आधार पर ऊंचाई के संबंध में कुछ गैस गुणों को स्थिर माना जा सकता है।
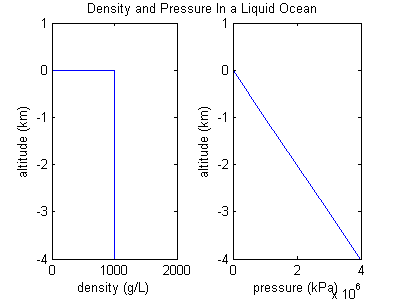
महासागर का उदाहरण
यदि किसी गैस का घनत्व स्थिर है तो वह वास्तव में गैस की तरह व्यवहार नहीं कर रही है। इसके अतिरिक्त यह एक असंपीड्य द्रव या तरल की तरह व्यवहार कर रहा है, और यह स्थिति समुद्र की तरह अधिक दिखती है। मान लिया जाए कि घनत्व स्थिर है तो दबाव बनाम ऊंचाई के ग्राफ में एक ढलान बनी रहेगी क्योंकि सिर के ऊपर समुद्र का वजन सीधे उसकी गहराई के समानुपाती होता है।
समतापीय-बारोट्रोपिक सन्निकटन और मापदंड की ऊंचाई
यह वायुमंडलीय मॉडल मानता है कि आणविक भार और तापमान दोनों ऊंचाई की एक विस्तृत श्रृंखला पर स्थिर हैं। ऐसे मॉडल को इज़ोटेर्मल (निरंतर तापमान) कहा जा सकता है। आदर्श गैस नियम के लिए समीकरण में निरंतर आणविक भार और निरंतर तापमान डालने से परिणाम उत्पन्न होता है कि घनत्व और दबाव दो शेष चर केवल एक दूसरे पर निर्भर करते हैं। इस कारण से इस मॉडल को बैरोट्रोपिक भी कहा जा सकता है (घनत्व केवल दबाव पर निर्भर करता है)।
इज़ोटेर्मल-बैरोट्रोपिक मॉडल के लिए घनत्व और दबाव ऊंचाई के घातीय कार्य होते हैं। पी या ρ के प्रारंभिक मान के 1/e तक गिरने के लिए आवश्यक ऊंचाई में वृद्धि को मापदंड की ऊंचाई कहा जाता है:
जहाँ R आदर्श गैस स्थिरांक है, T तापमान है, M औसत आणविक भार है, और g0 ग्रह की सतह पर गुरुत्वीय त्वरण है। पृथ्वी के वायुमंडल की विशेषता के रूप में T=273 K और M=29 g/mol मानों का उपयोग करना H = RT/Mg = (8.315*273)/(29*9.8) = 7.99 या लगभग 8 किमी जो संयोग से माउंट एवरेस्ट की अनुमानित ऊंचाई है
एक इज़ोटेर्माल वातावरण के लिए, या वायुमंडल के कुल द्रव्यमान का लगभग 63% ग्रह की सतह और एक मापदंड की ऊँचाई के बीच उपस्थित है। (एक निश्चित ऊंचाई के नीचे कुल वायु द्रव्यमान की गणना घनत्व कार्य को एकीकृत करके की जाती है।)
समुद्र के उदाहरण के लिए समुद्र के शीर्ष या सतह पर घनत्व में तेज संक्रमण था। चूँकि गैस से बने वायुमंडल के लिए कोई समकक्ष तेज संक्रमण या बढ़त नहीं है। गैस के वायुमंडल कम से कम घने होते जाते हैं जब तक कि वे इतने पतले नहीं हो जाते कि वे अंतरिक्ष बन जाते हैं।
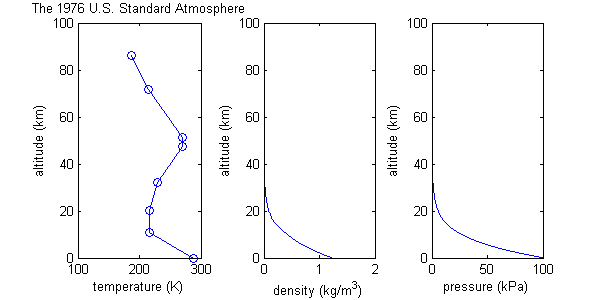
यू.एस. मानक वातावरण
यूएस स्टैंडर्ड एटमॉस्फियर मॉडल इज़ोटेर्मल-बैरोट्रोपिक मॉडल के समान कई मान्यताओं के साथ प्रराम्ह्ब होता है जिसमें आदर्श गैस व्यवहार और निरंतर आणविक भार सम्मिलित है किंतु यह एक अधिक यथार्थवादी तापमान कार्य को परिभाषित करके भिन्न होता है जिसमें सीधी रेखाओं से जुड़े आठ डेटा बिंदु होते हैं; अर्थात निरंतर तापमान प्रवणता वाले क्षेत्र। (ग्राफ़ देखें।) अवश्य ही!वास्तविक वातावरण में इस स्पष्ट आकार के साथ तापमान वितरण नहीं होता है। तापमान कार्य एक सन्निकटन है। दबाव और घनत्व के मानो की गणना इस तापमान कार्य के आधार पर की जाती है और निरंतर तापमान प्रवणता कुछ गणित को आसान बनाने में सहायता करती है।
नासा वैश्विक संदर्भ वायुमंडलीय मॉडल
नासा अर्थ ग्लोबल रेफरेंस एटमॉस्फेरिक मॉडल (अर्थ-ग्राम) को मार्शल अंतरिक्ष उड़ान केंद्र द्वारा एक डिजाइन संदर्भ वातावरण प्रदान करने के लिए विकसित किया गया था, जो मानक वायुमंडल के विपरीत, भौगोलिक परिवर्तनशीलता, ऊंचाई की एक विस्तृत श्रृंखला (सतह से कक्षीय ऊंचाई तक) की अनुमति देता है। और दिन के अलग-अलग महीने और समय यह अशांति और अन्य वायुमंडलीय अव्यवस्थाएं की घटनाओं के कारण वायुमंडलीय मापदंडों में स्थानिक और लौकिक अव्यवस्थाएं का अनुकरण भी कर सकता है। उपलब्ध है[2] फोरट्रान में लिखे कंप्यूटर कोड में[3] ग्राम श्रृंखला में शुक्र, मंगल और नेपच्यून ग्रहों और शनि ग्रह सैटर्नियन चंद्रमा, टाइटन (चंद्रमा) के लिए वायुमंडलीय मॉडल भी सम्मिलित हैं।[4]
भू-संभावित ऊंचाई
गुरुत्वाकर्षण त्वरण, गुरुत्वाकर्षण त्वरण|g(z), ऊंचाई के साथ घटता है क्योंकि ऊपर जाने का अर्थ ग्रह के केंद्र से दूर जाना है।
g घटने की इस समस्या से निपटने के लिए वास्तविक ज्यामितीय ऊंचाई z से भू-संभावित ऊंचाई h नामक एक अमूर्तता में परिवर्तन को परिभाषित किया जा सकता है, जिसे परिभाषित किया गया है:
h के पास गुण है
- कहाँ
जो मूल रूप से कहता है कि एक परीक्षण द्रव्यमान m को ऊंचाई z तक एक वातावरण के माध्यम से उठाने के लिए किए गए कार्य की मात्रा जहां ऊंचाई के साथ गुरुत्वाकर्षण कम हो जाता है, उसी द्रव्यमान को एक ऊंचाई तक उठाने के लिए किए गए कार्य की मात्रा के समान होता है, जहां g जादुई रूप से समान g0, समुद्र तल पर इसका मान रहता है
हाइड्रोस्टेटिक समीकरणों में ज्यामितीय ऊंचाई z के अतिरिक्त इस भू-स्थैतिक ऊंचाई h का उपयोग किया जाता है।
सामान्य मॉडल
- कोस्पार अंतर्राष्ट्रीय संदर्भ वातावरण
- अंतर्राष्ट्रीय मानक वातावरण
- जैकी का संदर्भ आत्मसफेरा से है, एक पुराना मॉडल जो अभी भी सामान्यतः अंतरिक्ष यान की गतिशीलता में उपयोग किया जाता है
- जेट मानक वातावरण
- एनआरएलएमएसआईएसई -00 अमेरिकी नौसेना अनुसंधान प्रयोगशाला का एक वर्तमान मॉडल है जिसका उपयोग अधिकांशतः वायुमंडलीय विज्ञान में किया जाता है
- यूएस मानक वातावरण
यह भी देखें
संदर्भ
- ↑ National Oceanic and Atmospheric Administration; National Aeronautics and Space Administration; United States Air Force (October 1976), U. S. Standard Atmosphere, 1976 (PDF), Washington, D.C.: U. S. Government Printing Office, p. xiv
- ↑ "Earth Global Reference Atmospheric Model (Earth-Gram) 2010", Software Catalog 2015–2016, NASA – Technology Transfer Program, retrieved 16 August 2016
- ↑ Leslie, F.W.; Justus, C.G. (June 2011), The NASA Marshall Space Flight Center Earth Global Reference Atmospheric Model—2010 Version (PDF), NASA/TM—2011–216467, Marshall Space Flight Center, Alabama: National Aeronautics and Space Administration, retrieved 15 August 2016
- ↑ Justh, Hilary L.; Justus, C. G.; Keller, Vernon W. (2006), "Global Reference Atmospheric Models, Including Thermospheres, for Mars, Venus and Earth", AIAA/AAS Astrodynamics Specialists Conference; 21–24 Aug. 2006; Keystone, CO; United States, doi:10.2514/6.2006-6394, hdl:2060/20060048492
बाहरी संबंध
- Public Domain Aeronautical Software – Derivation of hydrostatic equations used in the 1976 US Standard Atmosphere
- FORTRAN code to calculate the US Standard Atmosphere
- NASA GSFC Atmospheric Models overview
- Various models at NASA GSFC ModelWeb
- Earth Global Reference Atmospheric Model (Earth-GRAM 2010)