अधिकतम प्रवाह की समस्या: Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 4: | Line 4: | ||
[[अनुकूलन (गणित)]] में, अधिकतम प्रवाह समस्याओं में [[प्रवाह नेटवर्क]] के माध्यम से व्यवहार्य प्रवाह खोजना सम्मिलित होता है जो अधिकतम संभव प्रवाह दर प्राप्त करता है। | [[अनुकूलन (गणित)]] में, अधिकतम प्रवाह समस्याओं में [[प्रवाह नेटवर्क]] के माध्यम से व्यवहार्य प्रवाह खोजना सम्मिलित होता है जो अधिकतम संभव प्रवाह दर प्राप्त करता है। | ||
'''अधिकतम प्रवाह समस्या''' को संचलन समस्या जैसे अधिक जटिल नेटवर्क प्रवाह समस्याओं के विशेष स्थिति के रूप में देखा जा सकता है। एसटी प्रवाह का अधिकतम मूल्य (अर्थात, ग्राफ सिद्धांत की शब्दावली से प्रवाह दिशा s से ग्राफ़ सिद्धांत की शब्दावली दिशा t) [[कट (ग्राफ सिद्धांत)]] की न्यूनतम क्षमता के समान होती | '''अधिकतम प्रवाह समस्या''' को संचलन समस्या जैसे अधिक जटिल नेटवर्क प्रवाह समस्याओं के विशेष स्थिति के रूप में देखा जा सकता है। एसटी प्रवाह का अधिकतम मूल्य (अर्थात, ग्राफ सिद्धांत की शब्दावली से प्रवाह दिशा s से ग्राफ़ सिद्धांत की शब्दावली दिशा t) [[कट (ग्राफ सिद्धांत)]] की न्यूनतम क्षमता के समान होती है। और एसटी कट (अर्थात, विच्छेदित एस टी से) नेटवर्क में, जैसा कि [[मैक्स-फ्लो मिन-कट प्रमेय]] में कहा गया है। | ||
== इतिहास == | == इतिहास == | ||
अधिकतम प्रवाह समस्या प्रथम | अधिकतम प्रवाह समस्या प्रथम बार 1954 में टेड हैरिस (गणितज्ञ) टी द्वारा तैयार की गई थी। सोवियत रेलवे यातायात प्रवाह के सरलीकृत मॉडल के रूप में ई. हैरिस और एफ.एस. रॉस है।<ref name=":0">{{Cite journal | last1 = Schrijver | first1 = A. | title = परिवहन के इतिहास और अधिकतम प्रवाह की समस्याओं पर| doi = 10.1007/s101070100259 | journal = Mathematical Programming | volume = 91 | issue = 3 | pages = 437–445 | year = 2002 | citeseerx = 10.1.1.23.5134 | s2cid = 10210675 }}</ref><ref>{{Cite book | doi = 10.1007/0-387-25837-X_5 | first1 = Saul I. | last1 = Gass| first2 = Arjang A. | last2 = Assad | chapter = Mathematical, algorithmic and professional developments of operations research from 1951 to 1956 | title = ऑपरेशंस रिसर्च की एन एनोटेटेड टाइमलाइन| series = International Series in Operations Research & Management Science | volume = 75 | pages = 79–110 | year = 2005 | isbn = 978-1-4020-8116-3 }}</ref><ref name=":2">{{cite journal | first1 = T. E. | last1 = Harris | author-link1 = Ted Harris (mathematician) | first2 = F. S. | last2 = Ross | year = 1955 | title = रेल नेट क्षमताओं के मूल्यांकन के लिए एक विधि के मूल सिद्धांत| journal = Research Memorandum| url = http://www.dtic.mil/dtic/tr/fulltext/u2/093458.pdf| archive-url = https://web.archive.org/web/20140108021700/http://www.dtic.mil/dtic/tr/fulltext/u2/093458.pdf| url-status = dead| archive-date = 8 January 2014}}</ref> | ||
1955 में, लेस्टर आर. फोर्ड, जूनियर और डी. आर. फुलकर्सन या डेलबर्ट आर. फुलकर्सन ने पहला ज्ञात एल्गोरिदम, फोर्ड-फुलकर्सन एल्गोरिदम बनाया गया था।<ref name=":1">{{Cite journal | last1 = Ford | first1 = L. R. | author-link1 = L. R. Ford, Jr.| last2 = Fulkerson | first2 = D. R. | author-link2 = D. R. Fulkerson| doi = 10.4153/CJM-1956-045-5 | title = एक नेटवर्क के माध्यम से अधिकतम प्रवाह| journal = [[Canadian Journal of Mathematics]]| volume = 8 | pages = 399–404 | year = 1956 | doi-access = free }}</ref><ref name=":3">Ford, L.R., Jr.; Fulkerson, D.R., ''Flows in Networks'', Princeton University Press (1962).</ref> उनके 1955 के पेपर में,<ref name=":1" /> फोर्ड और फुलकर्सन ने लिखा है कि हैरिस और रॉस की समस्या निम्नानुसार तैयार की गई है (देखें <ref name=":0" /> पी। 5):<blockquote>रेल नेटवर्क पर विचार करें जोकी | 1955 में, लेस्टर आर. फोर्ड, जूनियर और डी. आर. फुलकर्सन या डेलबर्ट आर. फुलकर्सन ने पहला ज्ञात एल्गोरिदम, फोर्ड-फुलकर्सन एल्गोरिदम बनाया गया था।<ref name=":1">{{Cite journal | last1 = Ford | first1 = L. R. | author-link1 = L. R. Ford, Jr.| last2 = Fulkerson | first2 = D. R. | author-link2 = D. R. Fulkerson| doi = 10.4153/CJM-1956-045-5 | title = एक नेटवर्क के माध्यम से अधिकतम प्रवाह| journal = [[Canadian Journal of Mathematics]]| volume = 8 | pages = 399–404 | year = 1956 | doi-access = free }}</ref><ref name=":3">Ford, L.R., Jr.; Fulkerson, D.R., ''Flows in Networks'', Princeton University Press (1962).</ref> उनके 1955 के पेपर में,<ref name=":1" /> फोर्ड और फुलकर्सन ने लिखा है कि हैरिस और रॉस की समस्या निम्नानुसार तैयार की गई है (देखें <ref name=":0" /> पी। 5):<blockquote>रेल नेटवर्क पर विचार करें जोकी दो शहरों को कई मध्यवर्ती शहरों के माध्यम से जोड़ता है, जहां नेटवर्क के प्रत्येक लिंक में नंबर दिया गया है जो इसकी क्षमता का प्रतिनिधित्व करता है। स्थिर स्थिति की स्थिति मानते हुए, दिए गए शहर से दूसरे शहर में अधिकतम प्रवाह खोजते है।</blockquote>1962 में अपनी किताब फ्लोज़ इन नेटवर्क <ref name=":3" /> में फोर्ड और फुलकर्सन ने लिखा:<blockquote>यह लेखकों को 1955 के वसंत में टी. ई. हैरिस द्वारा प्रस्तुत किया गया था, जिन्होंने जनरल एफ.एस. रॉस (सेवानिवृत्त) के साथ मिलकर रेलवे यातायात प्रवाह का सरलीकृत मॉडल तैयार किया था, और इस विशेष समस्या को मॉडल द्वारा सुझाई गई केंद्रीय समस्या के रूप में इंगित किया गया था।</blockquote> जहां हैरिस और रॉस द्वारा रेल नेट क्षमताओं के मूल्यांकन के लिए 1955 की गुप्त प्रतिवेदन फंडामेंटल्स ऑफ ए मेथड को संदर्भित करता है।<ref name=":2" /> (देखना <ref name=":0" /> पी। 5). | ||
इन वर्षों में, अधिकतम प्रवाह समस्या के विभिन्न उन्नत समाधानों की खोज की गई थी, विशेष रूप से एडमंड्स और कार्प और स्वतंत्र रूप से डिनिट्ज़ का सबसे छोटा संवर्द्धन पथ एल्गोरिथम; डिनिट्ज़ का ब्लॉकिंग फ्लो एल्गोरिथम; पुश-रीलेबेल अधिकतम प्रवाह एल्गोरिथम या एंड्रयू वी. गोल्डबर्ग और [[रॉबर्ट टार्जन]] का पुश-रीलेबेल एल्गोरिथम; और गोल्डबर्ग और राव का बाइनरी ब्लॉकिंग फ्लो एल्गोरिथम या शर्मन के एल्गोरिदम <ref>{{Cite book | last = Sherman | first = Jonah | chapter = Nearly Maximum Flows in Nearly Linear Time | doi = 10.1109/FOCS.2013.36 | title = Proceedings of the 54th Annual IEEE Symposium on Foundations of Computer Science | pages = 263–269 | year = 2013 | arxiv = 1304.2077 | isbn = 978-0-7695-5135-7 | s2cid = 14681906 }}</ref> और केलनर, ली, ओरेचिया और सिडफोर्ड,<ref>{{Cite book | last1 = Kelner | first1 = J. A. | last2 = Lee | first2 = Y. T. | last3 = Orecchia | first3 = L. | last4 = Sidford | first4 = A. | chapter = An Almost-Linear-Time Algorithm for Approximate Max Flow in Undirected Graphs, and its Multicommodity Generalizations | doi = 10.1137/1.9781611973402.16 | title = असतत एल्गोरिदम पर पच्चीसवीं वार्षिक एसीएम-सियाम संगोष्ठी की कार्यवाही| pages = 217 | year = 2014 | isbn = 978-1-61197-338-9 | chapter-url = http://math.mit.edu/~kelner/Publications/Docs/klos_maxflow_main.pdf | arxiv = 1304.2338 | s2cid = 10733914 | url-status = dead | archive-url = https://web.archive.org/web/20160303170302/http://math.mit.edu/~kelner/Publications/Docs/klos_maxflow_main.pdf | archive-date =2016-03-03 }}</ref><ref>{{cite web | url = http://web.mit.edu/newsoffice/2013/new-algorithm-can-dramatically-streamline-solutions-to-the-max-flow-problem-0107.html | title = नया एल्गोरिदम नाटकीय रूप से 'अधिकतम प्रवाह' समस्या के समाधान को सुव्यवस्थित कर सकता है| first = Helen | last = Knight | date = 7 January 2014 | access-date = 8 January 2014 | publisher = MIT News}}</ref> क्रमशः, लगभग इष्टतम अधिकतम प्रवाह ज्ञात करें किन्तु केवल अप्रत्यक्ष रेखांकन में काम करें। | इन वर्षों में, अधिकतम प्रवाह समस्या के विभिन्न उन्नत समाधानों की खोज की गई थी, विशेष रूप से एडमंड्स और कार्प और स्वतंत्र रूप से डिनिट्ज़ का सबसे छोटा संवर्द्धन पथ एल्गोरिथम; डिनिट्ज़ का ब्लॉकिंग फ्लो एल्गोरिथम; पुश-रीलेबेल अधिकतम प्रवाह एल्गोरिथम या एंड्रयू वी. गोल्डबर्ग और [[रॉबर्ट टार्जन]] का पुश-रीलेबेल एल्गोरिथम; और गोल्डबर्ग और राव का बाइनरी ब्लॉकिंग फ्लो एल्गोरिथम या शर्मन के एल्गोरिदम <ref>{{Cite book | last = Sherman | first = Jonah | chapter = Nearly Maximum Flows in Nearly Linear Time | doi = 10.1109/FOCS.2013.36 | title = Proceedings of the 54th Annual IEEE Symposium on Foundations of Computer Science | pages = 263–269 | year = 2013 | arxiv = 1304.2077 | isbn = 978-0-7695-5135-7 | s2cid = 14681906 }}</ref> और केलनर, ली, ओरेचिया और सिडफोर्ड,<ref>{{Cite book | last1 = Kelner | first1 = J. A. | last2 = Lee | first2 = Y. T. | last3 = Orecchia | first3 = L. | last4 = Sidford | first4 = A. | chapter = An Almost-Linear-Time Algorithm for Approximate Max Flow in Undirected Graphs, and its Multicommodity Generalizations | doi = 10.1137/1.9781611973402.16 | title = असतत एल्गोरिदम पर पच्चीसवीं वार्षिक एसीएम-सियाम संगोष्ठी की कार्यवाही| pages = 217 | year = 2014 | isbn = 978-1-61197-338-9 | chapter-url = http://math.mit.edu/~kelner/Publications/Docs/klos_maxflow_main.pdf | arxiv = 1304.2338 | s2cid = 10733914 | url-status = dead | archive-url = https://web.archive.org/web/20160303170302/http://math.mit.edu/~kelner/Publications/Docs/klos_maxflow_main.pdf | archive-date =2016-03-03 }}</ref><ref>{{cite web | url = http://web.mit.edu/newsoffice/2013/new-algorithm-can-dramatically-streamline-solutions-to-the-max-flow-problem-0107.html | title = नया एल्गोरिदम नाटकीय रूप से 'अधिकतम प्रवाह' समस्या के समाधान को सुव्यवस्थित कर सकता है| first = Helen | last = Knight | date = 7 January 2014 | access-date = 8 January 2014 | publisher = MIT News}}</ref> क्रमशः, लगभग इष्टतम अधिकतम प्रवाह ज्ञात करें किन्तु केवल अप्रत्यक्ष रेखांकन में काम करें। | ||
| Line 18: | Line 18: | ||
[[File:Simpe_flow_network.svg|thumb|upright=0.8|प्रवाह नेटवर्क, स्रोत एस और सिंक टी के साथ। किनारे के आगे की संख्याएँ क्षमताएँ हैं।]]पहले हम कुछ अंकन स्थापित करते हैं: | [[File:Simpe_flow_network.svg|thumb|upright=0.8|प्रवाह नेटवर्क, स्रोत एस और सिंक टी के साथ। किनारे के आगे की संख्याएँ क्षमताएँ हैं।]]पहले हम कुछ अंकन स्थापित करते हैं: | ||
*माना <math>N = (V, E)</math> वाला नेटवर्क है जो क्रमशः <math>N</math> का <math>s, t \in V</math> स्रोत और सिंक है। | *माना <math>N = (V, E)</math> वाला नेटवर्क है जो क्रमशः <math>N</math> का <math>s, t \in V</math> स्रोत और सिंक है। | ||
*यदि <math>g</math>, <math>N</math> के किनारों पर | *यदि <math>g</math>, <math>N</math> के किनारों पर फलन है, तो इसका मान <math>(u,v) \in E</math> पर <math>g_{uv}</math> या <math>g(u,v).</math> द्वारा दर्शाया जाता है | ||
'''परिभाषा''' किनारे की क्षमता प्रवाह की अधिकतम मात्रा है जो किनारे से निकल सकती है। औपचारिक रूप से यह <math>c: E \to \R^+.</math> रुपरेखा है । | '''परिभाषा''' किनारे की क्षमता प्रवाह की अधिकतम मात्रा है जो किनारे से निकल सकती है। औपचारिक रूप से यह <math>c: E \to \R^+.</math> रुपरेखा है । | ||
| Line 31: | Line 31: | ||
परिभाषा अधिकतम प्रवाह समस्या स्रोत से सिंक तक जितना संभव हो उतना प्रवाह मार्ग है, दूसरे शब्दों में प्रवाह <math>f_\textrm{max}</math> को अधिकतम मूल्य के साथ खोजते है। | परिभाषा अधिकतम प्रवाह समस्या स्रोत से सिंक तक जितना संभव हो उतना प्रवाह मार्ग है, दूसरे शब्दों में प्रवाह <math>f_\textrm{max}</math> को अधिकतम मूल्य के साथ खोजते है। | ||
ध्यान दें कि कई अधिकतम प्रवाह उपस्थित हो सकते हैं | ध्यान दें कि कई अधिकतम प्रवाह उपस्थित हो सकते हैं और यदि इच्छानुसार वास्तविक (या यहां तक कि इच्छानुसार तर्कसंगत) प्रवाह के मूल्यों की अनुमति है (केवल पूर्णांकों के अतिरिक्त), तो या तो अधिकतम प्रवाह होता है, या असीमित रूप से कई होते हैं, क्योंकि असीमित रूप से कई रैखिक संयोजन होते हैं आधार अधिकतम प्रवाह दूसरे शब्दों में, यदि हम भेजते हैं <math>x</math> किनारे पर प्रवाह की इकाइयाँ <math>u</math> अधिकतम प्रवाह में, और <math>y > x</math> प्रवाह की इकाइयाँ <math>u</math> दूसरे अधिकतम प्रवाह में, फिर प्रत्येक के लिए <math>\Delta \in [0, y-x]</math> हम भेज सकते हैं <math>x+\Delta</math> इकाइयों पर <math>u</math> और अधिकतम प्रवाह प्राप्त करने के लिए तदनुसार शेष किनारों पर प्रवाह को रूट करें। यदि प्रवाह मान कोई वास्तविक या परिमेय संख्या हो सकती है, तो ऐसे अपरिमित रूप <math>\Delta</math> से अनेक होते हैं प्रत्येक <math>x, y</math> जोड़ी के लिए मान है। | ||
== एल्गोरिदम == | == एल्गोरिदम == | ||
| Line 67: | Line 67: | ||
| सामान्य पुश-रिलेबल एल्गोरिथम<ref name="goldberg1988"/> | | सामान्य पुश-रिलेबल एल्गोरिथम<ref name="goldberg1988"/> | ||
| <math>O(V^2E)</math> | | <math>O(V^2E)</math> | ||
| पुश रीलेबल एल्गोरिथम प्रीफ्लो बनाए रखता है, अर्थात वर्टिकल में अधिकता की संभावना के साथ फ्लो | | पुश रीलेबल एल्गोरिथम प्रीफ्लो बनाए रखता है, अर्थात वर्टिकल में अधिकता की संभावना के साथ फ्लो फलन या एल्गोरिथम तब चलता है जब धनात्मक आधिक्य वाला शीर्ष होता है, अर्थात ग्राफ़ में सक्रिय शीर्ष। पुश ऑपरेशन अवशिष्ट किनारे पर प्रवाह को बढ़ाता है, और शीर्षों पर ऊंचाई फलन नियंत्रित करता है जिसके माध्यम से अवशिष्ट किनारों को प्रवाहित किया जा सकता है। ऊंचाई फलन को रीलेबल ऑपरेशन द्वारा बदल दिया जाता है। इन परिचालनों की उचित परिभाषाएं आश्वासन देती हैं कि परिणामी प्रवाह फलन अधिकतम प्रवाह है। | ||
|- | |- | ||
| फीफो शीर्ष चयन नियम के साथ पुश-रीलेबल एल्गोरिथम<ref name="goldberg1988"/> | | फीफो शीर्ष चयन नियम के साथ पुश-रीलेबल एल्गोरिथम<ref name="goldberg1988"/> | ||
| Line 90: | Line 90: | ||
}}</ref> | }}</ref> | ||
| <math>O(V^2 \sqrt{E})</math> | | <math>O(V^2 \sqrt{E})</math> | ||
| पुश-रीलेबल एल्गोरिथम वैरिएंट जो सदैव | | पुश-रीलेबल एल्गोरिथम वैरिएंट जो सदैव 𝑠 या 𝑡 (अर्थात उच्चतम लेबल शीर्ष) से सबसे दूर के शीर्ष का चयन करता है, किन्तु अन्यथा फीफो एल्गोरिथ्म के रूप में आगे बढ़ता है। | ||
|- | |- | ||
| डायनेमिक ट्री के साथ पुश-रीलेबल एल्गोरिथम<ref name="goldberg1988">{{Cite journal | | डायनेमिक ट्री के साथ पुश-रीलेबल एल्गोरिथम<ref name="goldberg1988">{{Cite journal | ||
| Line 142: | Line 142: | ||
== इंटीग्रल फ्लो प्रमेय == | == इंटीग्रल फ्लो प्रमेय == | ||
अभिन्न प्रवाह प्रमेय कहता है कि | अभिन्न प्रवाह प्रमेय कहता है कि | ||
: यदि प्रवाह नेटवर्क में प्रत्येक किनारे की अभिन्न क्षमता है, तो अभिन्न अधिकतम प्रवाह उपस्थित होती | : यदि प्रवाह नेटवर्क में प्रत्येक किनारे की अभिन्न क्षमता है, तो अभिन्न अधिकतम प्रवाह उपस्थित होती है। | ||
प्रमाणित न केवल यह है कि प्रवाह का मान पूर्णांक है, जो अधिकतम-प्रवाह न्यूनतम-कट प्रमेय से सीधे अनुसरण करता है, | प्रमाणित न केवल यह है कि प्रवाह का मान पूर्णांक है, जो अधिकतम-प्रवाह न्यूनतम-कट प्रमेय से सीधे अनुसरण करता है, किन्तु यह कि 'हर किनारे' पर प्रवाह अभिन्न है। यह कई असतत गणित अनुप्रयोगों (नीचे देखें) के लिए महत्वपूर्ण है, जहां किनारे पर प्रवाह एन्कोड कर सकता है कि उस किनारे से संबंधित आइटम को समुच्चय में सम्मिलित किया जाना है या नहीं। | ||
== आवेदन == | == आवेदन == | ||
| Line 157: | Line 157: | ||
# <math>c(e) = 1</math> प्रत्येक <math>e \in E'</math> के लिए (चित्र देखें। 4.3.1)। | # <math>c(e) = 1</math> प्रत्येक <math>e \in E'</math> के लिए (चित्र देखें। 4.3.1)। | ||
तब <math>N</math> में अधिकतम प्रवाह का मान <math>G</math> में अधिकतम मिलान के आकार के | तब <math>N</math> में अधिकतम प्रवाह का मान <math>G</math> में अधिकतम मिलान के आकार के समान होता है, और अधिकतम कार्डिनैलिटी मिलान उन किनारों को ले कर पाया जा सकता है जिनके पास अभिन्न अधिकतम-प्रवाह में प्रवाह <math>1</math> है। | ||
निर्देशित चक्रीय ग्राफ में न्यूनतम पथ कवर | निर्देशित चक्रीय ग्राफ में न्यूनतम पथ कवर | ||
| Line 168: | Line 168: | ||
तभी यह दिखाया जा सकता है <math>G'</math> मेल खाता है <math>M</math> आकार का <math>m</math> यदि और केवल यदि <math>G</math> वर्टेक्स-डिसजॉइंट पाथ कवर है <math>C</math> युक्त <math>m</math> किनारों और <math>n-m</math> पथ, जहाँ <math>n</math> में शीर्षों की संख्या है <math>G</math>. इसलिए, अधिकतम कार्डिनैलिटी मैचिंग का पता लगाकर समस्या को हल किया जा सकता है <math>G'</math> अतिरिक्त। | तभी यह दिखाया जा सकता है <math>G'</math> मेल खाता है <math>M</math> आकार का <math>m</math> यदि और केवल यदि <math>G</math> वर्टेक्स-डिसजॉइंट पाथ कवर है <math>C</math> युक्त <math>m</math> किनारों और <math>n-m</math> पथ, जहाँ <math>n</math> में शीर्षों की संख्या है <math>G</math>. इसलिए, अधिकतम कार्डिनैलिटी मैचिंग का पता लगाकर समस्या को हल किया जा सकता है <math>G'</math> अतिरिक्त। | ||
मान लें कि हमें मिलान मिल गया है <math>M</math> का <math>G'</math>, और आवरण का निर्माण किया <math>C</math> यह | मान लें कि हमें मिलान मिल गया है <math>M</math> का <math>G'</math>, और आवरण का निर्माण किया <math>C</math> यह से सहज रूप से, यदि दो कोने <math>u_\mathrm{out}, v_\mathrm{in}</math> में मेल खाते हैं <math>M</math>, फिर किनारा <math>(u, v)</math> में निहित है <math>C</math>. स्पष्ट रूप से किनारों की संख्या <math>C</math> है <math>m</math>. यह देखने के लिए <math>C</math> वर्टेक्स-डिसजॉइंट है, निम्नलिखित पर विचार करें: | ||
# प्रत्येक शीर्ष <math>v_\textrm{out}</math> में <math>G'</math> या तो में बेमेल हो सकता है <math>M</math>, जिस स्थिति में कोई किनारा नहीं बचता है <math>v</math> में <math>C</math>; या इसका मिलान किया जा सकता है, जिस स्थिति में ठीक किनारा बचता है <math>v</math> में <math>C</math>. किसी भी स्थिति में, किनारे से अधिक कोई शीर्ष नहीं छोड़ता है | # प्रत्येक शीर्ष <math>v_\textrm{out}</math> में <math>G'</math> या तो में बेमेल हो सकता है <math>M</math>, जिस स्थिति में कोई किनारा नहीं बचता है <math>v</math> में <math>C</math>; या इसका मिलान किया जा सकता है, जिस स्थिति में ठीक किनारा बचता है <math>v</math> में <math>C</math>. किसी भी स्थिति में, किनारे से अधिक कोई शीर्ष नहीं छोड़ता है | ||
# इसी प्रकार प्रत्येक शीर्ष के लिए <math>v_\textrm{in}</math> में <math>G'</math> - यदि इसका मिलान किया जाता है, तो इसमें आने वाला किनारा होता है <math>v</math> में <math>C</math>; अन्यथा <math>v</math> में कोई आने वाला किनारा | # इसी प्रकार प्रत्येक शीर्ष के लिए <math>v_\textrm{in}</math> में <math>G'</math> - यदि इसका मिलान किया जाता है, तो इसमें आने वाला किनारा होता है <math>v</math> में <math>C</math>; अन्यथा <math>v</math> में कोई आने वाला किनारा <math>C</math> नहीं है . | ||
इस प्रकार किसी भी शीर्ष में दो आने वाले या दो बाहर जाने वाले किनारे | इस प्रकार किसी भी शीर्ष में दो आने वाले या दो बाहर जाने वाले किनारे <math>C</math> नहीं होते हैं , जिसका अर्थ है सभी रास्ते अंदर <math>C</math> वर्टेक्स-डिसजॉइंट हैं। | ||
यह दिखाने के लिए कि कवर <math>C</math> आकार है <math>n-m</math>, हम खाली कवर से | यह दिखाने के लिए कि कवर <math>C</math> आकार है <math>n-m</math>, हम खाली कवर से प्रारंभिक करते हैं और इसे वृद्धिशील रूप से बनाते हैं। शिखर जोड़ने के लिए <math>u</math> कवर में, हम इसे या तो उपस्थिता पथ में जोड़ सकते हैं, या उस शीर्ष पर प्रारंभिक होने वाली लंबाई शून्य का नया पथ बना सकते हैं। पूर्व का स्थिति जब भी प्रयुक्त होता है <math>(u,v) \in E</math> और कवर में कुछ रास्ता प्रारंभिक होता है <math>v</math>, या <math>(v,u) \in E</math> और कुछ पथ पर समाप्त होता है <math>v</math>. बाद वाला स्थिति सदैव प्रयुक्त होता है। पूर्व स्थिति में, कवर में किनारों की कुल संख्या 1 से बढ़ जाती है और पथों की संख्या समान रहती है; बाद वाले स्थिति में रास्तों की संख्या बढ़ जाती है और किनारों की संख्या वही रहती है। अब यह स्पष्ट हो गया है कि सभी को कवर करने के बाद <math>n</math> शिखर, आवरण में पथों और किनारों की संख्या का योग है <math>n</math>. इसलिए, यदि कवर में किनारों की संख्या <math>m</math> है , पथों की संख्या <math>n-m</math> है . | ||
=== शीर्ष क्षमता के साथ अधिकतम प्रवाह === | === शीर्ष क्षमता के साथ अधिकतम प्रवाह === | ||
[[File:Node splitting.svg|thumb|right|चित्र 4.4.1। नोड विभाजन द्वारा मूल अधिकतम प्रवाह समस्या में वर्टेक्स क्षमता बाधा के साथ अधिकतम प्रवाह समस्या का परिवर्तन]]माना <math>N = (V, E)</math> नेटवर्क हो। मान लीजिए कि बढ़त क्षमता के अतिरिक्त | [[File:Node splitting.svg|thumb|right|चित्र 4.4.1। नोड विभाजन द्वारा मूल अधिकतम प्रवाह समस्या में वर्टेक्स क्षमता बाधा के साथ अधिकतम प्रवाह समस्या का परिवर्तन]]माना <math>N = (V, E)</math> नेटवर्क हो। मान लीजिए कि बढ़त क्षमता के अतिरिक्त प्रत्येक नोड पर क्षमता है, अर्थात मैपिंग <math>c: V\to \R^+,</math> ऐसा कि प्रवाह <math>f</math> न केवल क्षमता की कमी और प्रवाह के संरक्षण को पूरा करना है, किन्तु वर्टेक्स क्षमता की कमी को भी पूरा करना है | ||
:<math> \sum_{i\in V} f_{iv} \le c(v) \qquad \forall v \in V \backslash \{s,t\}.</math> | :<math> \sum_{i\in V} f_{iv} \le c(v) \qquad \forall v \in V \backslash \{s,t\}.</math> | ||
दूसरे शब्दों में, शीर्ष से निकलने | दूसरे शब्दों में, शीर्ष से निकलने वाले प्रवाह की मात्रा इसकी क्षमता से अधिक नहीं हो सकती। अधिकतम प्रवाह खोजने के लिए <math>N</math>, हम विस्तार करके समस्या को मूल अर्थ में अधिकतम प्रवाह समस्या <math>N</math> में बदल सकते हैं . सबसे पहले, प्रत्येक <math>v\in V</math> द्वारा प्रतिस्थापित किया जाता है <math>v_{\text{in}}</math> और <math>v_{\text{out}}</math>, जहाँ <math>v_{\text{in}}</math> में जाकर किनारों से जुड़ा है <math>v</math> और <math>v_{\text{out}}</math> से निकलने वाले किनारों से जुड़ा है <math>v</math>, फिर क्षमता असाइन करें <math>c(v)</math> किनारे से जोड़ने के लिए <math>v_{\text{in}}</math> और <math>v_{\text{out}}</math> (चित्र देखें। 4.4.1)। इस विस्तारित नेटवर्क में, वर्टेक्स क्षमता की कमी को हटा दिया जाता है और इसलिए समस्या को मूल अधिकतम प्रवाह समस्या के रूप में माना जा सकता है। | ||
==== s से t तक पथों की अधिकतम संख्या ==== | ==== s से t तक पथों की अधिकतम संख्या ==== | ||
निर्देशित ग्राफ दिया <math>G = (V, E)</math> और दो शिखर <math>s</math> और <math>t</math>, हमें पथों की अधिकतम संख्या ज्ञात करनी है <math>s</math> को <math>t</math>. इस समस्या के कई रूप हैं: | निर्देशित ग्राफ दिया <math>G = (V, E)</math> और दो शिखर <math>s</math> और <math>t</math>, हमें पथों की अधिकतम संख्या ज्ञात करनी है <math>s</math> को <math>t</math>. इस समस्या के कई रूप हैं: | ||
1. पथ एज-डिसजॉइंट होने चाहिए। नेटवर्क बनाकर इस समस्या को अधिकतम प्रवाह समस्या में बदला जा सकता है <math>N = (V, E)</math> से <math>G</math>, साथ <math>s</math> और <math>t</math> स्रोत और सिंक होने के नाते <math>N</math> क्रमशः, और प्रत्येक किनारे की क्षमता निर्दिष्ट करना <math>1</math>. इस नेटवर्क में अधिकतम प्रवाह है <math>k</math> यदि हैं <math>k</math> किनारे-अलग | 1. पथ एज-डिसजॉइंट होने चाहिए। नेटवर्क बनाकर इस समस्या को अधिकतम प्रवाह समस्या में बदला जा सकता है <math>N = (V, E)</math> से <math>G</math>, साथ <math>s</math> और <math>t</math> स्रोत और सिंक होने के नाते <math>N</math> क्रमशः, और प्रत्येक किनारे की क्षमता निर्दिष्ट करना <math>1</math>. इस नेटवर्क में अधिकतम प्रवाह है <math>k</math> यदि हैं <math>k</math> किनारे-अलग रास्ते होते है। | ||
2. पथ स्वतंत्र होने चाहिए, अर्थात, वर्टेक्स-डिसजॉइंट (को छोड़कर) <math>s</math> और <math>t</math>). हम नेटवर्क बना सकते हैं <math>N = (V, E)</math> से <math>G</math> वर्टेक्स योग्यता के साथ, जहां सभी वर्टिकल और सभी एज की योग्यता होती है <math>1</math>. तब अधिकतम प्रवाह का मान स्वतंत्र पथों की अधिकतम संख्या | 2. पथ स्वतंत्र होने चाहिए, अर्थात, वर्टेक्स-डिसजॉइंट (को छोड़कर) <math>s</math> और <math>t</math>). हम नेटवर्क बना सकते हैं इस प्रकार <math>N = (V, E)</math> से <math>G</math> वर्टेक्स योग्यता के साथ, जहां सभी वर्टिकल और सभी एज की योग्यता होती है <math>1</math>. तब अधिकतम प्रवाह का मान स्वतंत्र पथों की अधिकतम संख्या <math>s</math> को <math>t</math>. के समान होता है | ||
3. पथों के किनारे-विच्छेद और/या शीर्ष असंयुक्त होने के अतिरिक्त , पथों में लंबाई की बाधा भी होती है: हम केवल उन पथों की गणना करते हैं जिनकी लंबाई ठीक है <math>k</math>, या अधिक से अधिक <math>k</math>. के छोटे मूल्यों को छोड़कर, इस समस्या | 3. पथों के किनारे-विच्छेद और/या शीर्ष असंयुक्त होने के अतिरिक्त , पथों में लंबाई की बाधा भी होती है: हम केवल उन पथों की गणना करते हैं जिनकी लंबाई ठीक है <math>k</math>, या अधिक से अधिक <math>k</math>. के छोटे मूल्यों को छोड़कर, इस समस्या <math>k</math> के अधिकांश रूप एनपी-पूर्ण हैं .<ref>{{Cite journal|last1=Itai|first1=A.|last2=Perl|first2=Y.|last3=Shiloach|first3=Y.|year=1982|title=लंबाई की कमी के साथ अधिकतम असम्बद्ध पथ खोजने की जटिलता|journal=Networks|language=en|volume=12|issue=3|pages=277–286|doi=10.1002/net.3230120306|issn=1097-0037}}</ref> | ||
=== बंद करने की समस्या === | === बंद करने की समस्या === | ||
मुख्य लेख: बंद करने की समस्या | मुख्य लेख: बंद करने की समस्या | ||
निर्देशित ग्राफ़ का बंद होना 'सी' वर्टिकल का समुच्चय है, जैसे कोई किनारा ''सी'' | निर्देशित ग्राफ़ का बंद होना 'सी' वर्टिकल का समुच्चय है, जैसे कोई किनारा ''सी'' नहीं छोड़ता है। क्लोजर प्रॉब्लम वर्टेक्स-वेटेड डायरेक्टेड ग्राफ में अधिकतम-वेट या न्यूनतम-वेट क्लोजर खोजने का कार्य है। अधिकतम प्रवाह समस्या में कमी का उपयोग करके इसे बहुपद समय में हल किया जा सकता है। | ||
== वास्तविक विश्व अनुप्रयोग == | == वास्तविक विश्व अनुप्रयोग == | ||
=== बेसबॉल उन्मूलन === | === बेसबॉल उन्मूलन === | ||
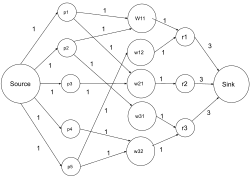
[[File:Baseball Elimination Problem.png|thumb|बेसबॉल उन्मूलन समस्या के लिए नेटवर्क प्रवाह का निर्माण]][[बेसबॉल]] उन्मूलन समस्या में लीग में प्रतिस्पर्धा करने वाली n टीमें हैं। लीग सीज़न के विशिष्ट चरण में, w<sub>''i''</sub> जीत और आर की संख्या है | [[File:Baseball Elimination Problem.png|thumb|बेसबॉल उन्मूलन समस्या के लिए नेटवर्क प्रवाह का निर्माण]][[बेसबॉल]] उन्मूलन समस्या में लीग में प्रतिस्पर्धा करने वाली n टीमें हैं। लीग सीज़न के विशिष्ट चरण में, w<sub>''i''</sub> जीत और आर की संख्या है टीम और ''r''<sub>ij</sub>के लिए खेले जाने वाले खेलों की संख्या है टीम ''r''<sub>ij</sub> के विरुद्ध बचे हुए खेलों की संख्या है। टीम का सफाया कर दिया जाता है यदि उसके पास सीजन को पहले स्थान पर खत्म करने का कोई मौका नहीं है। बेसबॉल उन्मूलन समस्या का कार्य यह निर्धारित करना है कि सीजन के समय प्रत्येक बिंदु पर कौन सी टीम समाप्त हो जाती है। श्वार्ट्ज<ref>{{Cite journal | last1 = Schwartz | first1 = B. L. | title = आंशिक रूप से पूर्ण टूर्नामेंट में संभावित विजेता| doi = 10.1137/1008062 | journal = [[SIAM Review]]| jstor = 2028206| volume = 8 | issue = 3 | pages = 302–308 | year = 1966 | bibcode = 1966SIAMR...8..302S }}</ref> विधि प्रस्तावित किया जो इस समस्या को अधिकतम नेटवर्क प्रवाह तक कम कर देता है। इस पद्धति में यह निर्धारित करने के लिए नेटवर्क बनाया जाता है कि टीम k समाप्त हो गई है या नहीं। | ||
मान लीजिए G = (V, E) एक नेटवर्क है जिसमें s,t ∈ V क्रमशः स्रोत और सिंक है। एक गेम नोडीज जोड़ता है - जो इन दो टीमों के बीच नाटकों की संख्या का प्रतिनिधित्व करता है। हम प्रत्येक टीम के लिए एक टीम नोड भी जोड़ते हैं और प्रत्येक गेम नोड {i, j} को i <j से V तक जोड़ते हैं, और उनमें से प्रत्येक को क्षमता | मान लीजिए G = (V, E) एक नेटवर्क है जिसमें s,t ∈ V क्रमशः स्रोत और सिंक है। एक गेम नोडीज जोड़ता है - जो इन दो टीमों के बीच नाटकों की संख्या का प्रतिनिधित्व करता है। हम प्रत्येक टीम के लिए एक टीम नोड भी जोड़ते हैं और प्रत्येक गेम नोड {i, j} को i <j से V तक जोड़ते हैं, और उनमें से प्रत्येक को क्षमता ''r<sub>ij</sub>'' के साथ किनारे से जोड़ते हैं - जो इन दो टीमों के बीच नाटकों की संख्या का प्रतिनिधित्व करता है . हम प्रत्येक टीम के लिए एक टीम नोड भी जोड़ते हैं और प्रत्येक गेम नोड {i, j} को दो टीम नोड्स i और j से जोड़ते हैं जिससे उनमें से एक जीत सुनिश्चित हो सकता है । इन किनारों पर प्रवाह मान को सीमित करने की आवश्यकता नहीं है। अंत में किनारों को टीम नोड i से सिंक नोड ''t'' तक बनाया जाता है और टीम i को {{math|''w''<sub>''k''</sub> + ''r''<sub>''k''</sub>}} से अधिक जीतने से रोकने के लिए {{math|''w''<sub>''k''</sub> + ''r''<sub>''k''</sub> – ''w''<sub>''i''</sub>}} की क्षमता निर्धारित की जाती है। | ||
मान लीजिए S लीग में भाग लेने वाली सभी टीमों का समुच्चय है और मान लीजिए | मान लीजिए S लीग में भाग लेने वाली सभी टीमों का समुच्चय है और मान लीजिए | ||
:<math>r(S - \{k\}) = \sum_{i,j \in \{S-\{k\}\} \atop i < j} r_{ij}</math>. | :<math>r(S - \{k\}) = \sum_{i,j \in \{S-\{k\}\} \atop i < j} r_{ij}</math>. | ||
इस पद्धति में यह प्रमाणित किया जाता है कि टीम k को समाप्त नहीं किया जाता है यदि और केवल यदि आकार r(S - {k}) का प्रवाह मान नेटवर्क G में उपस्थित है। उल्लिखित लेख में यह सिद्ध किया गया है कि यह प्रवाह मान से अधिकतम प्रवाह मान | इस पद्धति में यह प्रमाणित किया जाता है कि टीम k को समाप्त नहीं किया जाता है यदि और केवल यदि आकार r(S - {k}) का प्रवाह मान नेटवर्क G में उपस्थित है। उल्लिखित लेख में यह सिद्ध किया गया है कि यह प्रवाह मान से अधिकतम प्रवाह मान है। | ||
=== विमान सेवा समय-निर्धारण === | === विमान सेवा समय-निर्धारण === | ||
विमान सेवा उद्योग में बड़ी समस्या उड़ान कर्मचारियों के समय-निर्धारण | विमान सेवा उद्योग में बड़ी समस्या उड़ान कर्मचारियों के समय-निर्धारण किया गया है। और विमान सेवा समय समस्या को विस्तारित अधिकतम नेटवर्क प्रवाह के अनुप्रयोग के रूप में माना जा सकता है। इस समस्या का इनपुट विमान ''F'' का समुच्चय है जिसमें यह जानकारी होती है कि प्रत्येक विमान कहाँ और कब प्रस्थान करती है और कब आती है। विमान सेवा समय के संस्करण में लक्ष्य अधिकतम ''k'' कर्मचारियों के साथ व्यवहार्य समय तैयार करना है। | ||
इस समस्या को हल करने के लिए परिबद्ध संचलन नामक संचलन समस्या की भिन्नता का उपयोग किया जाता है जोकी | इस समस्या को हल करने के लिए परिबद्ध संचलन नामक संचलन समस्या की भिन्नता का उपयोग किया जाता है जोकी प्रवाह नेटवर्क समस्याओं का सामान्यीकरण है, किनारे प्रवाह पर निचली सीमा के अतिरिक्त प्रतिबंध किया है । | ||
''G'' = (''V'', ''E'') | ''G'' = (''V'', ''E'') स्रोत और सिंक नोड्स के रूप में {{math|''s'',''t'' ∈ ''V''}} के साथ एक नेटवर्क बनें। प्रत्येक उड़ान ''i'' के स्रोत और गंतव्य के लिए, ''V'' में दो नोड जोड़े जाते हैं, नोड ''s<sub>i</sub>'' स्रोत के रूप में और नोड ''d<sub>i</sub>'' उड़ान के गंतव्य नोड के रूप में ''i,'' ''E'' में निम्नलिखित किनारों को भी जोड़ा जाता है: | ||
# ''s'' | # ''s'' और प्रत्येक ''s<sub>i</sub>'' के बीच क्षमता [0, 1] वाला किनारा | ||
#E' में G के किनारों को X से a तक निर्देशित किया गया है | |||
# प्रत्येक ''d<sub>i</sub>'' के बीच क्षमता [0, 1] वाला किनारा और ''t''। | # प्रत्येक ''d<sub>i</sub>'' के बीच क्षमता [0, 1] वाला किनारा और ''t''। | ||
#''s<sub>i</sub>'' | #''s<sub>i</sub>'' और ''d<sub>i</sub>'' की प्रत्येक जोड़ी के बीच क्षमता [1, 1] वाला किनारा। | ||
#प्रत्येक ''d<sub>i</sub>'' और ''s<sub>j</sub>'' के बीच क्षमता [0, 1] के साथ एक किनारा, यदि स्रोत ''s<sub>j</sub>'' उड़ान के गंतव्य i से उचित समय और व्यय | #प्रत्येक ''d<sub>i</sub>'' और ''s<sub>j</sub>'' के बीच क्षमता [0, 1] के साथ एक किनारा, यदि स्रोत ''s<sub>j</sub>'' उड़ान के गंतव्य i से उचित समय और व्यय के साथ पहुंच योग्य है। | ||
# ''s'' | # ''s'' और ''t'' के बीच क्षमता [0, ∞] वाला किनारा। | ||
उल्लिखित विधि में, यह प्रमाणित किया गया है और सिद्ध किया गया है कि ''s'' | उल्लिखित विधि में, यह प्रमाणित किया गया है और सिद्ध किया गया है कि ''s'' और ''t'' के बीच G में k के प्रवाह मूल्य का पता लगाना अधिकतम k कर्मचारियों के साथ उड़ान समुच्चय F के लिए व्यवहार्य कार्यक्रम खोजने के समान है।<ref name="ITA">{{cite book | author = [[Thomas H. Cormen]], [[Charles E. Leiserson]], [[Ronald L. Rivest]], and [[Clifford Stein]] | title=एल्गोरिदम का परिचय, दूसरा संस्करण| chapter = 26. Maximum Flow | year = 2001 | publisher = MIT Press and McGraw-Hill | isbn = 978-0-262-03293-3 | pages=643–668| title-link=Introduction to Algorithms }}</ref> | ||
विमान सेवा समय का अन्य संस्करण सभी उड़ानों को निष्पादित करने के लिए न्यूनतम आवश्यक कर्मचारियों की खोज | विमान सेवा समय का अन्य संस्करण सभी उड़ानों को निष्पादित करने के लिए न्यूनतम आवश्यक कर्मचारियों की खोज कर रहा है। इस समस्या का उत्तर खोजने के लिए, द्विदलीय ग्राफ <var>G'</var> = (''A'' ∪ ''B'', ''E'') वहाँ बनाया जाता है। जहाँ प्रत्येक उड़ान की समुच्चय A और समुच्चय B में प्रति होती है। यदि वही विमान उड़ान ''i'' के बाद उड़ान ''j'' निष्पादित कर सकता है, i∈A j∈B से जुड़ा है। G' में मेल खाता है ''F'' के लिए समय को प्रेरित करता है और स्पष्ट रूप से इस ग्राफ में अधिकतम द्विपक्षीय मिलान कर्मचारियों की न्यूनतम संख्या के साथ विमान सेवा समय तैयार करता है।<ref name="ITA" /> जैसा कि इस लेख के अनुप्रयोग भाग में बताया गया है, अधिकतम कार्डिनैलिटी द्विपक्षीय मिलान अधिकतम प्रवाह समस्या का अनुप्रयोग है। | ||
=== परिसंचरण-मांग समस्या === | === परिसंचरण-मांग समस्या === | ||
कुछ कारखाने हैं जो माल का उत्पादन करते हैं और कुछ गाँव जहाँ माल पहुँचाना होता है। वे सड़कों के नेटवर्क से जुड़े हुए हैं जिनमें प्रत्येक सड़क की क्षमता है अधिकतम माल {{mvar|c}} के लिए जो इसके माध्यम से बह सकता है। समस्या यह पता लगाने की है कि क्या कोई संचलन है जो मांग को पूरा करता है। यह समस्या अधिकतम-प्रवाह समस्या में परिवर्तित हो सकती है। | |||
यह समस्या अधिकतम-प्रवाह समस्या में परिवर्तित हो सकती है। | # स्रोत नोड जोड़ें {{mvar|s}} और इसके किनारों को हर फैक्ट्री नोड में जोड़ें {{mvar|f<sub>i</sub>}} क्षमता के साथ {{mvar|p<sub>i</sub>}} जहाँ {{mvar|p<sub>i</sub>}} कारखाने {{mvar|f<sub>i</sub>}} की उत्पादन दर है . | ||
# स्रोत नोड जोड़ें {{mvar|s}} और इसके किनारों को हर फैक्ट्री नोड में जोड़ें {{mvar|f<sub>i</sub>}} क्षमता के साथ {{mvar|p<sub>i</sub>}} जहाँ {{mvar|p<sub>i</sub>}} कारखाने | # सिंक नोड जोड़ें {{mvar|t}} और सभी गांवों से किनारे जोड़ें {{mvar|v<sub>i</sub>}} को {{mvar|t}} क्षमता के साथ {{mvar|d<sub>i</sub>}} जहाँ {{mvar|d<sub>i</sub>}} गांव की मांग {{mvar|v<sub>i</sub>}} दर है . | ||
# सिंक नोड जोड़ें {{mvar|t}} और सभी गांवों से किनारे जोड़ें {{mvar|v<sub>i</sub>}} को {{mvar|t}} क्षमता के साथ {{mvar|d<sub>i</sub>}} जहाँ {{mvar|d<sub>i</sub>}} गांव की मांग | |||
बता दें कि जी = (वी, ई) यह नया नेटवर्क है। संचलन उपस्थित है जो मांग को संतुष्ट करता है यदि और केवल यदि: | बता दें कि जी = (वी, ई) यह नया नेटवर्क है। संचलन उपस्थित है जो मांग को संतुष्ट करता है यदि और केवल यदि: | ||
: {{math|Maximum flow value(''G'')}} <math> = \sum_{i \in v} d_i </math>. | : {{math|Maximum flow value(''G'')}} <math> = \sum_{i \in v} d_i </math>. | ||
यदि कोई संचलन उपस्थित है, | यदि कोई संचलन उपस्थित है, जिससे अधिकतम-प्रवाह समाधान को देखने से यह उत्तर मिलेगा कि मांगों को पूरा करने के लिए किसी विशेष सड़क पर कितना माल भेजा जाना है। | ||
कुछ किनारों पर प्रवाह पर निचली सीमा जोड़कर समस्या को बढ़ाया जा सकता है।<ref>{{Cite web|url=https://www.cs.cmu.edu/~ckingsf/bioinfo-lectures/flowext.pdf|title=Max-flow extensions: circulations with demands|last=Carl Kingsford}}</ref> | कुछ किनारों पर प्रवाह पर निचली सीमा जोड़कर समस्या को बढ़ाया जा सकता है।<ref>{{Cite web|url=https://www.cs.cmu.edu/~ckingsf/bioinfo-lectures/flowext.pdf|title=Max-flow extensions: circulations with demands|last=Carl Kingsford}}</ref> | ||
=== छवि विभाजन === | === छवि विभाजन === | ||
[[File:Maxflow imagesegmentation image.png|thumb|आकार 8x8 की स्रोत छवि।|Alt=|बाएं|110x110px]] | [[File:Maxflow imagesegmentation image.png|thumb|आकार 8x8 की स्रोत छवि।|Alt=|बाएं|110x110px]] | ||
[[File:Maxflow imagesegmentation network.png|thumb|बिटमैप से निर्मित नेटवर्क। स्रोत बाईं ओर है, सिंक दाईं ओर है। किनारा जितना गहरा होता है, उसकी क्षमता उतनी ही बड़ी होती है। ए<sub>i</sub> उच्च होता है जब पिक्सेल हरा होता है, b<sub>i</sub> जब पिक्सेल हरा नहीं होता है। दंड पी<sub>ij</sub> सब समान हैं।<ref>{{Cite web|url=https://gitlab.com/francois.schwarzentruber/imagesegmentationwithmaxflow|title=प्रोजेक्ट इमेजेजमेंटेशनविथमैक्सफ्लो, जिसमें इन दृष्टांतों को बनाने के लिए स्रोत कोड शामिल है।|website=GitLab|language=en|url-status=dead|archive-url=https://web.archive.org/web/20191222173132/https://gitlab.com/francois.schwarzentruber/imagesegmentationwithmaxflow|archive-date=2019-12-22|access-date=2019-12-22}}</ref>]]क्लेनबर्ग और टार्डोस ने अपनी पुस्तक में [[छवि विभाजन]] के लिए छवि के लिए एल्गोरिथ्म प्रस्तुत किया है।<ref>{{Cite web|url=https://www.pearson.com/us/higher-education/program/Kleinberg-Algorithm-Design/PGM319216.html |title=एल्गोरिथम डिजाइन|website=pearson.com|language=en|access-date=2019-12-21}}</ref> वे छवि में पृष्ठभूमि और अग्रभूमि खोजने के लिए एल्गोरिथ्म प्रस्तुत करते हैं। अधिक स्पष्ट | [[File:Maxflow imagesegmentation network.png|thumb|बिटमैप से निर्मित नेटवर्क। स्रोत बाईं ओर है, सिंक दाईं ओर है। किनारा जितना गहरा होता है, उसकी क्षमता उतनी ही बड़ी होती है। ए<sub>i</sub> उच्च होता है जब पिक्सेल हरा होता है, b<sub>i</sub> जब पिक्सेल हरा नहीं होता है। दंड पी<sub>ij</sub> सब समान हैं।<ref>{{Cite web|url=https://gitlab.com/francois.schwarzentruber/imagesegmentationwithmaxflow|title=प्रोजेक्ट इमेजेजमेंटेशनविथमैक्सफ्लो, जिसमें इन दृष्टांतों को बनाने के लिए स्रोत कोड शामिल है।|website=GitLab|language=en|url-status=dead|archive-url=https://web.archive.org/web/20191222173132/https://gitlab.com/francois.schwarzentruber/imagesegmentationwithmaxflow|archive-date=2019-12-22|access-date=2019-12-22}}</ref>]]क्लेनबर्ग और टार्डोस ने अपनी पुस्तक में [[छवि विभाजन]] के लिए छवि के लिए एल्गोरिथ्म प्रस्तुत किया है।<ref>{{Cite web|url=https://www.pearson.com/us/higher-education/program/Kleinberg-Algorithm-Design/PGM319216.html |title=एल्गोरिथम डिजाइन|website=pearson.com|language=en|access-date=2019-12-21}}</ref> वे छवि में पृष्ठभूमि और अग्रभूमि खोजने के लिए एल्गोरिथ्म प्रस्तुत करते हैं। अधिक स्पष्ट रूप से, एल्गोरिथ्म बिटमैप को इनपुट के रूप में निम्नानुसार लेता है: a<sub>i</sub>≥ 0 संभावना है कि पिक्सेल i अग्रभूमि से संबंधित है, b<sub>i</sub>≥ 0 इस संभावना में कि पिक्सेल i पृष्ठभूमि से संबंधित है, और p<sub>ij</sub>यदि दो सन्निकट पिक्सेल i और j को अग्रभूमि में और दूसरे को पृष्ठभूमि में रखा जाता है तो यह जुर्माना है। लक्ष्य निम्नलिखित मात्रा को अधिकतम करने वाले पिक्सेल के समुच्चय के विभाजन (ए, बी) को ढूंढना है | ||
:<math>q(A, B) = \sum_{i \in A} a_i + \sum_{i \in B} b_i - \sum_{\begin{matrix}i, j \text{ adjacent} \\ |A \cap \{i, j\}| = 1 \end{matrix}} p_{ij}</math>, | :<math>q(A, B) = \sum_{i \in A} a_i + \sum_{i \in B} b_i - \sum_{\begin{matrix}i, j \text{ adjacent} \\ |A \cap \{i, j\}| = 1 \end{matrix}} p_{ij}</math>, | ||
दरअसल, | दरअसल, a<sub>i</sub> में पिक्सेल के लिए (अग्रभूमि के रूप में माना जाता है), हम प्राप्त करते हैं; बी में सभी पिक्सल के लिए (पृष्ठभूमि के रूप में माना जाता है), हम b<sub>i</sub> प्राप्त करते हैं. सीमा पर, दो आसन्न पिक्सेल i और j के बीच, हम p<sub>ij</sub> को ढीला करते हैं. यह मात्रा को कम करने के समान है | ||
:<math>q'(A, B) = \sum_{i \in A} b_i + \sum_{i \in B} a_i + \sum_{\begin{matrix}i, j \text{ adjacent} \\ |A \cap \{i, j\}| = 1 \end{matrix}} p_{ij}</math> | :<math>q'(A, B) = \sum_{i \in A} b_i + \sum_{i \in B} a_i + \sum_{\begin{matrix}i, j \text{ adjacent} \\ |A \cap \{i, j\}| = 1 \end{matrix}} p_{ij}</math> | ||
| Line 244: | Line 244: | ||
:<math>q(A, B) = \sum_{i \in A\cup B} a_i + \sum_{i \in A\cup B} b_i - q'(A, B).</math> | :<math>q(A, B) = \sum_{i \in A\cup B} a_i + \sum_{i \in A\cup B} b_i - q'(A, B).</math> | ||
[[File:Maxflow imagesegmentation result.png|thumb|नेटवर्क पर प्रदर्शित न्यूनतम कट (त्रिकोण बनाम वृत्त)।]]अब हम उस नेटवर्क का निर्माण करते हैं जिसके नोड पिक्सेल हैं, साथ ही स्रोत और सिंक, दाईं ओर चित्र देखें। हम स्रोत को पिक्सेल i से वजन a | [[File:Maxflow imagesegmentation result.png|thumb|नेटवर्क पर प्रदर्शित न्यूनतम कट (त्रिकोण बनाम वृत्त)।]]अब हम उस नेटवर्क का निर्माण करते हैं जिसके नोड पिक्सेल हैं, साथ ही स्रोत और सिंक, दाईं ओर चित्र देखें। हम स्रोत को पिक्सेल i से वजन a<sub>i</sub> के किनारे से जोड़ते हैं. हम पिक्सेल i को वज़न b<sub>i</sub> के किनारे से सिंक से जोड़ते हैं. हम पिक्सेल i को पिक्सेल j से वजन p<sub>ij</sub> के साथ जोड़ते हैं. अब, यह उस नेटवर्क में न्यूनतम कटौती (या समकक्ष अधिकतम प्रवाह) की गणना करने के लिए बनी हुई है। अंतिम आंकड़ा न्यूनतम कटौती दिखाता है। | ||
== एक्सटेंशन == | == एक्सटेंशन == | ||
1. न्यूनतम-व्यय प्रवाह समस्या में, प्रत्येक किनारे (''u'',v) का व्यय-गुणांक | 1. न्यूनतम-व्यय प्रवाह समस्या में, प्रत्येक किनारे (''u'',v) का व्यय-गुणांक ''a<sub>uv</sub>'' भी होता है ''इसकी क्षमता के अतिरिक्त यदि किनारे से प्रवाह f<sub>uv</sub> है, तो कुल व्यय f<sub>uv</sub> है. सबसे छोटी व्यय के साथ दिए गए आकार d का प्रवाह खोजना आवश्यक है। अधिकांश प्रकारों में, व्यय-गुणांक सकारात्मक या नकारात्मक हो सकते हैं। इस समस्या के लिए विभिन्न बहुपद-समय एल्गोरिदम हैं।'' | ||
2. अधिकतम-प्रवाह समस्या को 'वियोगात्मक बाधाओं' द्वारा संवर्धित किया जा सकता है: नकारात्मक वियोगात्मक बाधा का कहना है कि किनारों की निश्चित जोड़ी साथ गैर-शून्य प्रवाह नहीं कर सकती है; सकारात्मक वियोगात्मक बाधाएँ कहती हैं कि, किनारों की निश्चित जोड़ी में, कम से कम गैर-शून्य प्रवाह होना चाहिए। नकारात्मक बाधाओं के साथ, सरल नेटवर्क के लिए भी समस्या एनपी-हार्ड हो जाती है। सकारात्मक बाधाओं के साथ, यदि आंशिक प्रवाह की अनुमति दी जाती है, | 2. अधिकतम-प्रवाह समस्या को 'वियोगात्मक बाधाओं' द्वारा संवर्धित किया जा सकता है: नकारात्मक वियोगात्मक बाधा का कहना है कि किनारों की निश्चित जोड़ी साथ गैर-शून्य प्रवाह नहीं कर सकती है; सकारात्मक वियोगात्मक बाधाएँ कहती हैं कि, किनारों की निश्चित जोड़ी में, कम से कम गैर-शून्य प्रवाह होना चाहिए। नकारात्मक बाधाओं के साथ, सरल नेटवर्क के लिए भी समस्या एनपी-हार्ड हो जाती है। सकारात्मक बाधाओं के साथ, यदि आंशिक प्रवाह की अनुमति दी जाती है, जिससे समस्या बहुपद है, किन्तु जब प्रवाह अभिन्न होना चाहिए जिससे यह एनपी-हार्ड हो सकता है।<ref>{{Cite journal|last1=Schauer|first1=Joachim|last2=Pferschy|first2=Ulrich|date=1 July 2013|title=असंबद्ध बाधाओं के साथ अधिकतम प्रवाह समस्या|journal=Journal of Combinatorial Optimization|language=en|volume=26|issue=1|pages=109–119|doi=10.1007/s10878-011-9438-7|issn=1382-6905|citeseerx=10.1.1.414.4496|s2cid=6598669}}</ref> | ||
== संदर्भ == | == संदर्भ == | ||
{{reflist}} | {{reflist}} | ||
| Line 279: | Line 279: | ||
* {{cite book | author = Eugene Lawler | author-link = Eugene Lawler | title = Combinatorial Optimization: Networks and Matroids | chapter = 4. Network Flows | year = 2001 | publisher = Dover | isbn = 978-0-486-41453-9 | pages = 109–177}} | * {{cite book | author = Eugene Lawler | author-link = Eugene Lawler | title = Combinatorial Optimization: Networks and Matroids | chapter = 4. Network Flows | year = 2001 | publisher = Dover | isbn = 978-0-486-41453-9 | pages = 109–177}} | ||
{{DEFAULTSORT:Maximum Flow Problem}} | {{DEFAULTSORT:Maximum Flow Problem}} | ||
[[Category:CS1 British English-language sources (en-gb)]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category: | [[Category:CS1 maint]] | ||
[[Category:Created On 31/05/2023]] | [[Category:Created On 31/05/2023|Maximum Flow Problem]] | ||
[[Category:Lua-based templates|Maximum Flow Problem]] | |||
[[Category:Machine Translated Page|Maximum Flow Problem]] | |||
[[Category:Pages with script errors|Maximum Flow Problem]] | |||
[[Category:Templates Vigyan Ready|Maximum Flow Problem]] | |||
[[Category:Templates that add a tracking category|Maximum Flow Problem]] | |||
[[Category:Templates that generate short descriptions|Maximum Flow Problem]] | |||
[[Category:Templates using TemplateData|Maximum Flow Problem]] | |||
[[Category:ग्राफ सिद्धांत में कम्प्यूटेशनल समस्याएं|Maximum Flow Problem]] | |||
[[Category:नेटवर्क प्रवाह की समस्या|Maximum Flow Problem]] | |||
Latest revision as of 09:24, 28 June 2023
अनुकूलन (गणित) में, अधिकतम प्रवाह समस्याओं में प्रवाह नेटवर्क के माध्यम से व्यवहार्य प्रवाह खोजना सम्मिलित होता है जो अधिकतम संभव प्रवाह दर प्राप्त करता है।
अधिकतम प्रवाह समस्या को संचलन समस्या जैसे अधिक जटिल नेटवर्क प्रवाह समस्याओं के विशेष स्थिति के रूप में देखा जा सकता है। एसटी प्रवाह का अधिकतम मूल्य (अर्थात, ग्राफ सिद्धांत की शब्दावली से प्रवाह दिशा s से ग्राफ़ सिद्धांत की शब्दावली दिशा t) कट (ग्राफ सिद्धांत) की न्यूनतम क्षमता के समान होती है। और एसटी कट (अर्थात, विच्छेदित एस टी से) नेटवर्क में, जैसा कि मैक्स-फ्लो मिन-कट प्रमेय में कहा गया है।
इतिहास
अधिकतम प्रवाह समस्या प्रथम बार 1954 में टेड हैरिस (गणितज्ञ) टी द्वारा तैयार की गई थी। सोवियत रेलवे यातायात प्रवाह के सरलीकृत मॉडल के रूप में ई. हैरिस और एफ.एस. रॉस है।[1][2][3]
1955 में, लेस्टर आर. फोर्ड, जूनियर और डी. आर. फुलकर्सन या डेलबर्ट आर. फुलकर्सन ने पहला ज्ञात एल्गोरिदम, फोर्ड-फुलकर्सन एल्गोरिदम बनाया गया था।[4][5] उनके 1955 के पेपर में,[4] फोर्ड और फुलकर्सन ने लिखा है कि हैरिस और रॉस की समस्या निम्नानुसार तैयार की गई है (देखें [1] पी। 5):
रेल नेटवर्क पर विचार करें जोकी दो शहरों को कई मध्यवर्ती शहरों के माध्यम से जोड़ता है, जहां नेटवर्क के प्रत्येक लिंक में नंबर दिया गया है जो इसकी क्षमता का प्रतिनिधित्व करता है। स्थिर स्थिति की स्थिति मानते हुए, दिए गए शहर से दूसरे शहर में अधिकतम प्रवाह खोजते है।
1962 में अपनी किताब फ्लोज़ इन नेटवर्क [5] में फोर्ड और फुलकर्सन ने लिखा:
यह लेखकों को 1955 के वसंत में टी. ई. हैरिस द्वारा प्रस्तुत किया गया था, जिन्होंने जनरल एफ.एस. रॉस (सेवानिवृत्त) के साथ मिलकर रेलवे यातायात प्रवाह का सरलीकृत मॉडल तैयार किया था, और इस विशेष समस्या को मॉडल द्वारा सुझाई गई केंद्रीय समस्या के रूप में इंगित किया गया था।
जहां हैरिस और रॉस द्वारा रेल नेट क्षमताओं के मूल्यांकन के लिए 1955 की गुप्त प्रतिवेदन फंडामेंटल्स ऑफ ए मेथड को संदर्भित करता है।[3] (देखना [1] पी। 5).
इन वर्षों में, अधिकतम प्रवाह समस्या के विभिन्न उन्नत समाधानों की खोज की गई थी, विशेष रूप से एडमंड्स और कार्प और स्वतंत्र रूप से डिनिट्ज़ का सबसे छोटा संवर्द्धन पथ एल्गोरिथम; डिनिट्ज़ का ब्लॉकिंग फ्लो एल्गोरिथम; पुश-रीलेबेल अधिकतम प्रवाह एल्गोरिथम या एंड्रयू वी. गोल्डबर्ग और रॉबर्ट टार्जन का पुश-रीलेबेल एल्गोरिथम; और गोल्डबर्ग और राव का बाइनरी ब्लॉकिंग फ्लो एल्गोरिथम या शर्मन के एल्गोरिदम [6] और केलनर, ली, ओरेचिया और सिडफोर्ड,[7][8] क्रमशः, लगभग इष्टतम अधिकतम प्रवाह ज्ञात करें किन्तु केवल अप्रत्यक्ष रेखांकन में काम करें।
2013 में जेम्स बी. ओर्लिन ने वर्णन करते हुए पेपर प्रकाशित किया कलन विधि है।[9]
2022 में ली चेन, रासमस किन्ग, यांग पी. लियू, रिचर्ड पेंग, मैक्सिमिलियन प्रोबस्ट गुटेनबर्ग और सुशांत सचदेवा ने लगभग-रैखिक समय एल्गोरिदम प्रकाशित किया जो चल रहा है न्यूनतम-व्यय प्रवाह समस्या के लिए जिसमें से अधिकतम प्रवाह समस्या विशेष स्थिति है।[10][11] एकल स्रोत सबसे छोटी पथ समस्या (एसएसएसपी) समस्या के लिए नकारात्मक भार के साथ न्यूनतम-व्यय प्रवाह समस्या का और विशेष स्थिति लगभग-रैखिक समय में एल्गोरिथ्म भी प्रतिवेदन किया गया है।[12][13] दोनों एल्गोरिदम को कंप्यूटर विज्ञान की नींव पर 2022 संगोष्ठी में सर्वश्रेष्ठ पेपर माना गया।[14][15]
परिभाषा
पहले हम कुछ अंकन स्थापित करते हैं:
- माना वाला नेटवर्क है जो क्रमशः का स्रोत और सिंक है।
- यदि , के किनारों पर फलन है, तो इसका मान पर या द्वारा दर्शाया जाता है
परिभाषा किनारे की क्षमता प्रवाह की अधिकतम मात्रा है जो किनारे से निकल सकती है। औपचारिक रूप से यह रुपरेखा है ।
परिभाषा प्रवाह रुपरेखा है जो निम्नलिखित को संतुष्ट करता है:
- क्षमता प्रतिबंध किनारे का प्रवाह दूसरे शब्दों में इसकी क्षमता से अधिक नहीं हो सकता है:
- प्रवाह का संरक्षण स्रोत और सिंक को छोड़कर, नोड में प्रवेश करने वाले प्रवाहों का योग उस नोड से बाहर निकलने वाले प्रवाहों के योग के समान होना चाहिए। या:
प्रवाह विषम सममित हैं: सभी के लिए
परिभाषा प्रवाह का मान स्रोत से सिंक तक जाने वाले प्रवाह की मात्रा है। औपचारिक रूप से प्रवाह के लिए इसके द्वारा दिया गया है:
परिभाषा अधिकतम प्रवाह समस्या स्रोत से सिंक तक जितना संभव हो उतना प्रवाह मार्ग है, दूसरे शब्दों में प्रवाह को अधिकतम मूल्य के साथ खोजते है।
ध्यान दें कि कई अधिकतम प्रवाह उपस्थित हो सकते हैं और यदि इच्छानुसार वास्तविक (या यहां तक कि इच्छानुसार तर्कसंगत) प्रवाह के मूल्यों की अनुमति है (केवल पूर्णांकों के अतिरिक्त), तो या तो अधिकतम प्रवाह होता है, या असीमित रूप से कई होते हैं, क्योंकि असीमित रूप से कई रैखिक संयोजन होते हैं आधार अधिकतम प्रवाह दूसरे शब्दों में, यदि हम भेजते हैं किनारे पर प्रवाह की इकाइयाँ अधिकतम प्रवाह में, और प्रवाह की इकाइयाँ दूसरे अधिकतम प्रवाह में, फिर प्रत्येक के लिए हम भेज सकते हैं इकाइयों पर और अधिकतम प्रवाह प्राप्त करने के लिए तदनुसार शेष किनारों पर प्रवाह को रूट करें। यदि प्रवाह मान कोई वास्तविक या परिमेय संख्या हो सकती है, तो ऐसे अपरिमित रूप से अनेक होते हैं प्रत्येक जोड़ी के लिए मान है।
एल्गोरिदम
निम्न तालिका अधिकतम प्रवाह समस्या को हल करने के लिए एल्गोरिदम सूचीबद्ध करती है। यहाँ, और नेटवर्क के कोने और किनारों की संख्या को निरूपित करें। मूल्य सभी क्षमताओं को पूर्णांक मानों में बदलने के बाद सबसे बड़ी धार क्षमता को संदर्भित करता है (यदि नेटवर्क में अपरिमेय संख्या क्षमताएं हैं, अनंत हो सकता है)।
| विधि | जटिलता | विवरण |
|---|---|---|
| लीनियर प्रोग्रामिंग | वैधानिक प्रवाह की परिभाषा द्वारा दी गई बाधाएं। यहां रैखिक कार्यक्रम देखें। | |
| फोर्ड-फुलकर्सन एल्गोरिथम | जब तक अवशिष्ट ग्राफ के माध्यम से खुला मार्ग है, उस पथ पर न्यूनतम अवशिष्ट क्षमता भेजें। | |
| एडमंड्स-कार्प एल्गोरिथम | फोर्ड-फुलकर्सन की विशेषज्ञता, चौड़ाई-प्रथम खोज के साथ संवर्द्धित पथ ढूँढना। | |
| डिनिक का एल्गोरिदम | प्रत्येक चरण में एल्गोरिदम अवशिष्ट ग्राफ पर चौड़ाई-पहली खोज के साथ स्तरित ग्राफ बनाता है। स्तरित ग्राफ में अधिकतम प्रवाह की गणना की जा सकती है समय, और चरणों की अधिकतम संख्या है . इकाई क्षमता वाले नेटवर्क में, डिनिक का एल्गोरिदम में समाप्त होता है समय. | |
| एमकेएम (मल्होत्रा, कुमार, माहेश्वरी) एल्गोरिथम[16] | अवरुद्ध प्रवाह के निर्माण के लिए अलग दृष्टिकोण के साथ डिनिक का संदेश का संशोधन। मूल पेपर का संदर्भ लें। | |
| डिनिक का एल्गोरिदम गतिशील वृक्षों के साथ | डायनेमिक ट्री डेटा संरचना स्तरित ग्राफ़ में अधिकतम प्रवाह संगणना को गति देती है . | |
| सामान्य पुश-रिलेबल एल्गोरिथम[17] | पुश रीलेबल एल्गोरिथम प्रीफ्लो बनाए रखता है, अर्थात वर्टिकल में अधिकता की संभावना के साथ फ्लो फलन या एल्गोरिथम तब चलता है जब धनात्मक आधिक्य वाला शीर्ष होता है, अर्थात ग्राफ़ में सक्रिय शीर्ष। पुश ऑपरेशन अवशिष्ट किनारे पर प्रवाह को बढ़ाता है, और शीर्षों पर ऊंचाई फलन नियंत्रित करता है जिसके माध्यम से अवशिष्ट किनारों को प्रवाहित किया जा सकता है। ऊंचाई फलन को रीलेबल ऑपरेशन द्वारा बदल दिया जाता है। इन परिचालनों की उचित परिभाषाएं आश्वासन देती हैं कि परिणामी प्रवाह फलन अधिकतम प्रवाह है। | |
| फीफो शीर्ष चयन नियम के साथ पुश-रीलेबल एल्गोरिथम[17] | पुश-रीलेबल एल्गोरिथम वैरिएंट जो सदैव सबसे वर्तमान में सक्रिय वर्टेक्स का चयन करता है और पुश ऑपरेशंस करता है जबकि अतिरिक्त सकारात्मक होता है और इस वर्टेक्स से स्वीकार्य अवशिष्ट किनारे होते हैं। | |
| अधिकतम दूरी वर्टेक्स चयन नियम के साथ पुश-रीलेबल एल्गोरिथम[18] | पुश-रीलेबल एल्गोरिथम वैरिएंट जो सदैव 𝑠 या 𝑡 (अर्थात उच्चतम लेबल शीर्ष) से सबसे दूर के शीर्ष का चयन करता है, किन्तु अन्यथा फीफो एल्गोरिथ्म के रूप में आगे बढ़ता है। | |
| डायनेमिक ट्री के साथ पुश-रीलेबल एल्गोरिथम[17] | एल्गोरिथ्म ऊंचाई कार्य के संबंध में अवशिष्ट ग्राफ पर सीमित आकार के पेड़ बनाता है। ये पेड़ बहुस्तरीय पुश ऑपरेशंस प्रदान करते हैं, अर्थात किनारे के अतिरिक्त पूरे संतृप्त पथ के साथ धक्का देता है। | |
| केआरटी (राजा, राव, टार्जन) का एल्गोरिदम | ||
| बाइनरी ब्लॉकिंग फ्लो एल्गोरिथम[19] | ||
| जेम्स बी ओरलिन का + केआरटी (राजा, राव, टारजन) का एल्गोरिदम[9] | ओर्लिन का एल्गोरिदम अधिकतम प्रवाह को हल करता है के लिए समय जबकि केआरटी इसे हल करता है के लिए . | |
| कथूरिया-लियू-सिडफोर्ड एल्गोरिथ्म | ℓ 𝑝 - मानक प्रवाह का उपयोग करके आंतरिक बिंदु विधियां और बढ़त वृद्धि। मैड्री के पहले के एल्गोरिथम पर बनाता है, जिसने रनटाइम प्राप्त किया था .[20] | |
| बीएलएनपीएसएसएसडब्ल्यू / बीएलएलएसएसएसडब्ल्यू एल्गोरिदम[21] | विस्तारक अपघटन के साथ विद्युत प्रवाह के आंतरिक बिंदु विधि और गतिशील रखरखाव। | |
| गाओ लियू पेंग एल्गोरिथम[23] | गाओ, लियू, और पेंग का एल्गोरिदम [माद्री जेएसीएम '16] से आंतरिक बिंदु विधि आधारित एल्गोरिदम के मूल में बढ़ते विद्युत प्रवाह को गतिशील रूप से बनाए रखने के आसपास घूमता है। यह डेटा संरचनाओं को डिजाइन करने पर जोर देता है, जो सीमित सेटिंग्स में, प्रतिरोध अद्यतनों के दौर से गुजर रहे ग्राफ में बड़ी विद्युत ऊर्जा के साथ किनारों को लौटाते हैं। | |
| चेन, किंग, लियू, पेंग, गुटेनबर्ग और सचदेवा का एल्गोरिदम[10] | चेन, किंग, लियू, पेंग, गुटेनबर्ग और सचदेवा के एल्गोरिदम प्रवाह के अनुक्रम के माध्यम से प्रवाह का निर्माण करके लगभग रैखिक समय में अधिकतम प्रवाह और न्यूनतम व्यय प्रवाह को हल करते हैं अनुमानित अप्रत्यक्ष न्यूनतम-अनुपात चक्र, जिनमें से प्रत्येक की गणना और परिशोधन में संसाधित की जाती है समय गतिशील डेटा संरचना का उपयोग कर. |
अतिरिक्त एल्गोरिदम के लिए, देखें गोल्डबर्ग & टार्जन (1988).
इंटीग्रल फ्लो प्रमेय
अभिन्न प्रवाह प्रमेय कहता है कि
- यदि प्रवाह नेटवर्क में प्रत्येक किनारे की अभिन्न क्षमता है, तो अभिन्न अधिकतम प्रवाह उपस्थित होती है।
प्रमाणित न केवल यह है कि प्रवाह का मान पूर्णांक है, जो अधिकतम-प्रवाह न्यूनतम-कट प्रमेय से सीधे अनुसरण करता है, किन्तु यह कि 'हर किनारे' पर प्रवाह अभिन्न है। यह कई असतत गणित अनुप्रयोगों (नीचे देखें) के लिए महत्वपूर्ण है, जहां किनारे पर प्रवाह एन्कोड कर सकता है कि उस किनारे से संबंधित आइटम को समुच्चय में सम्मिलित किया जाना है या नहीं।
आवेदन
बहु-स्रोत बहु-सिंक अधिकतम प्रवाह समस्या
नेटवर्क दिया सूत्रों के समुच्चय के साथ और सिंक का समुच्चय केवल स्रोत और सिंक के अतिरिक्त, हमें अधिकतम प्रवाह का पता लगाना है हम बहु-स्रोत बहु-सिंक समस्या को अधिकतम प्रवाह समस्या में प्रत्येक शीर्ष से जोड़ने वाले समेकित स्रोत को जोड़कर बदल सकते हैं और प्रत्येक शीर्ष से जुड़ा समेकित सिंक (सुपरसोर्स और सुपरसिंक के रूप में भी जाना जाता है) प्रत्येक किनारे पर अनंत क्षमता के साथ (चित्र देखें। 4.1.1।)।
अधिकतम कार्डिनैलिटी द्विपक्षीय मिलान
द्विदलीय ग्राफ दिया , हमें मिलान करने वाली अधिकतम कार्डिनैलिटी मिलनी है , वह मिलान है जिसमें किनारों की सबसे बड़ी संभव संख्या होती है। नेटवर्क बनाकर इस समस्या को अधिकतम प्रवाह समस्या में बदला जा सकता है , जहाँ
- में के किनारों को से तक निर्देशित किया गया है
- प्रत्येक के लिए और प्रत्येक के लिए
- प्रत्येक के लिए (चित्र देखें। 4.3.1)।
तब में अधिकतम प्रवाह का मान में अधिकतम मिलान के आकार के समान होता है, और अधिकतम कार्डिनैलिटी मिलान उन किनारों को ले कर पाया जा सकता है जिनके पास अभिन्न अधिकतम-प्रवाह में प्रवाह है।
निर्देशित चक्रीय ग्राफ में न्यूनतम पथ कवर
निर्देशित विश्वकोश ग्राफ दिया , हमें प्रत्येक शीर्ष को कवर करने के लिए पथ (ग्राफ सिद्धांत) | शीर्ष-विच्छेद पथों की न्यूनतम संख्या का पता लगाना है . हम द्विदलीय ग्राफ का निर्माण कर सकते हैं से , जहाँ
- .
तभी यह दिखाया जा सकता है मेल खाता है आकार का यदि और केवल यदि वर्टेक्स-डिसजॉइंट पाथ कवर है युक्त किनारों और पथ, जहाँ में शीर्षों की संख्या है . इसलिए, अधिकतम कार्डिनैलिटी मैचिंग का पता लगाकर समस्या को हल किया जा सकता है अतिरिक्त।
मान लें कि हमें मिलान मिल गया है का , और आवरण का निर्माण किया यह से सहज रूप से, यदि दो कोने में मेल खाते हैं , फिर किनारा में निहित है . स्पष्ट रूप से किनारों की संख्या है . यह देखने के लिए वर्टेक्स-डिसजॉइंट है, निम्नलिखित पर विचार करें:
- प्रत्येक शीर्ष में या तो में बेमेल हो सकता है , जिस स्थिति में कोई किनारा नहीं बचता है में ; या इसका मिलान किया जा सकता है, जिस स्थिति में ठीक किनारा बचता है में . किसी भी स्थिति में, किनारे से अधिक कोई शीर्ष नहीं छोड़ता है
- इसी प्रकार प्रत्येक शीर्ष के लिए में - यदि इसका मिलान किया जाता है, तो इसमें आने वाला किनारा होता है में ; अन्यथा में कोई आने वाला किनारा नहीं है .
इस प्रकार किसी भी शीर्ष में दो आने वाले या दो बाहर जाने वाले किनारे नहीं होते हैं , जिसका अर्थ है सभी रास्ते अंदर वर्टेक्स-डिसजॉइंट हैं।
यह दिखाने के लिए कि कवर आकार है , हम खाली कवर से प्रारंभिक करते हैं और इसे वृद्धिशील रूप से बनाते हैं। शिखर जोड़ने के लिए कवर में, हम इसे या तो उपस्थिता पथ में जोड़ सकते हैं, या उस शीर्ष पर प्रारंभिक होने वाली लंबाई शून्य का नया पथ बना सकते हैं। पूर्व का स्थिति जब भी प्रयुक्त होता है और कवर में कुछ रास्ता प्रारंभिक होता है , या और कुछ पथ पर समाप्त होता है . बाद वाला स्थिति सदैव प्रयुक्त होता है। पूर्व स्थिति में, कवर में किनारों की कुल संख्या 1 से बढ़ जाती है और पथों की संख्या समान रहती है; बाद वाले स्थिति में रास्तों की संख्या बढ़ जाती है और किनारों की संख्या वही रहती है। अब यह स्पष्ट हो गया है कि सभी को कवर करने के बाद शिखर, आवरण में पथों और किनारों की संख्या का योग है . इसलिए, यदि कवर में किनारों की संख्या है , पथों की संख्या है .
शीर्ष क्षमता के साथ अधिकतम प्रवाह
माना नेटवर्क हो। मान लीजिए कि बढ़त क्षमता के अतिरिक्त प्रत्येक नोड पर क्षमता है, अर्थात मैपिंग ऐसा कि प्रवाह न केवल क्षमता की कमी और प्रवाह के संरक्षण को पूरा करना है, किन्तु वर्टेक्स क्षमता की कमी को भी पूरा करना है
दूसरे शब्दों में, शीर्ष से निकलने वाले प्रवाह की मात्रा इसकी क्षमता से अधिक नहीं हो सकती। अधिकतम प्रवाह खोजने के लिए , हम विस्तार करके समस्या को मूल अर्थ में अधिकतम प्रवाह समस्या में बदल सकते हैं . सबसे पहले, प्रत्येक द्वारा प्रतिस्थापित किया जाता है और , जहाँ में जाकर किनारों से जुड़ा है और से निकलने वाले किनारों से जुड़ा है , फिर क्षमता असाइन करें किनारे से जोड़ने के लिए और (चित्र देखें। 4.4.1)। इस विस्तारित नेटवर्क में, वर्टेक्स क्षमता की कमी को हटा दिया जाता है और इसलिए समस्या को मूल अधिकतम प्रवाह समस्या के रूप में माना जा सकता है।
s से t तक पथों की अधिकतम संख्या
निर्देशित ग्राफ दिया और दो शिखर और , हमें पथों की अधिकतम संख्या ज्ञात करनी है को . इस समस्या के कई रूप हैं:
1. पथ एज-डिसजॉइंट होने चाहिए। नेटवर्क बनाकर इस समस्या को अधिकतम प्रवाह समस्या में बदला जा सकता है से , साथ और स्रोत और सिंक होने के नाते क्रमशः, और प्रत्येक किनारे की क्षमता निर्दिष्ट करना . इस नेटवर्क में अधिकतम प्रवाह है यदि हैं किनारे-अलग रास्ते होते है।
2. पथ स्वतंत्र होने चाहिए, अर्थात, वर्टेक्स-डिसजॉइंट (को छोड़कर) और ). हम नेटवर्क बना सकते हैं इस प्रकार से वर्टेक्स योग्यता के साथ, जहां सभी वर्टिकल और सभी एज की योग्यता होती है . तब अधिकतम प्रवाह का मान स्वतंत्र पथों की अधिकतम संख्या को . के समान होता है
3. पथों के किनारे-विच्छेद और/या शीर्ष असंयुक्त होने के अतिरिक्त , पथों में लंबाई की बाधा भी होती है: हम केवल उन पथों की गणना करते हैं जिनकी लंबाई ठीक है , या अधिक से अधिक . के छोटे मूल्यों को छोड़कर, इस समस्या के अधिकांश रूप एनपी-पूर्ण हैं .[24]
बंद करने की समस्या
मुख्य लेख: बंद करने की समस्या
निर्देशित ग्राफ़ का बंद होना 'सी' वर्टिकल का समुच्चय है, जैसे कोई किनारा सी नहीं छोड़ता है। क्लोजर प्रॉब्लम वर्टेक्स-वेटेड डायरेक्टेड ग्राफ में अधिकतम-वेट या न्यूनतम-वेट क्लोजर खोजने का कार्य है। अधिकतम प्रवाह समस्या में कमी का उपयोग करके इसे बहुपद समय में हल किया जा सकता है।
वास्तविक विश्व अनुप्रयोग
बेसबॉल उन्मूलन
बेसबॉल उन्मूलन समस्या में लीग में प्रतिस्पर्धा करने वाली n टीमें हैं। लीग सीज़न के विशिष्ट चरण में, wi जीत और आर की संख्या है टीम और rijके लिए खेले जाने वाले खेलों की संख्या है टीम rij के विरुद्ध बचे हुए खेलों की संख्या है। टीम का सफाया कर दिया जाता है यदि उसके पास सीजन को पहले स्थान पर खत्म करने का कोई मौका नहीं है। बेसबॉल उन्मूलन समस्या का कार्य यह निर्धारित करना है कि सीजन के समय प्रत्येक बिंदु पर कौन सी टीम समाप्त हो जाती है। श्वार्ट्ज[25] विधि प्रस्तावित किया जो इस समस्या को अधिकतम नेटवर्क प्रवाह तक कम कर देता है। इस पद्धति में यह निर्धारित करने के लिए नेटवर्क बनाया जाता है कि टीम k समाप्त हो गई है या नहीं।
मान लीजिए G = (V, E) एक नेटवर्क है जिसमें s,t ∈ V क्रमशः स्रोत और सिंक है। एक गेम नोडीज जोड़ता है - जो इन दो टीमों के बीच नाटकों की संख्या का प्रतिनिधित्व करता है। हम प्रत्येक टीम के लिए एक टीम नोड भी जोड़ते हैं और प्रत्येक गेम नोड {i, j} को i <j से V तक जोड़ते हैं, और उनमें से प्रत्येक को क्षमता rij के साथ किनारे से जोड़ते हैं - जो इन दो टीमों के बीच नाटकों की संख्या का प्रतिनिधित्व करता है . हम प्रत्येक टीम के लिए एक टीम नोड भी जोड़ते हैं और प्रत्येक गेम नोड {i, j} को दो टीम नोड्स i और j से जोड़ते हैं जिससे उनमें से एक जीत सुनिश्चित हो सकता है । इन किनारों पर प्रवाह मान को सीमित करने की आवश्यकता नहीं है। अंत में किनारों को टीम नोड i से सिंक नोड t तक बनाया जाता है और टीम i को wk + rk से अधिक जीतने से रोकने के लिए wk + rk – wi की क्षमता निर्धारित की जाती है।
मान लीजिए S लीग में भाग लेने वाली सभी टीमों का समुच्चय है और मान लीजिए
- .
इस पद्धति में यह प्रमाणित किया जाता है कि टीम k को समाप्त नहीं किया जाता है यदि और केवल यदि आकार r(S - {k}) का प्रवाह मान नेटवर्क G में उपस्थित है। उल्लिखित लेख में यह सिद्ध किया गया है कि यह प्रवाह मान से अधिकतम प्रवाह मान है।
विमान सेवा समय-निर्धारण
विमान सेवा उद्योग में बड़ी समस्या उड़ान कर्मचारियों के समय-निर्धारण किया गया है। और विमान सेवा समय समस्या को विस्तारित अधिकतम नेटवर्क प्रवाह के अनुप्रयोग के रूप में माना जा सकता है। इस समस्या का इनपुट विमान F का समुच्चय है जिसमें यह जानकारी होती है कि प्रत्येक विमान कहाँ और कब प्रस्थान करती है और कब आती है। विमान सेवा समय के संस्करण में लक्ष्य अधिकतम k कर्मचारियों के साथ व्यवहार्य समय तैयार करना है।
इस समस्या को हल करने के लिए परिबद्ध संचलन नामक संचलन समस्या की भिन्नता का उपयोग किया जाता है जोकी प्रवाह नेटवर्क समस्याओं का सामान्यीकरण है, किनारे प्रवाह पर निचली सीमा के अतिरिक्त प्रतिबंध किया है ।
G = (V, E) स्रोत और सिंक नोड्स के रूप में s,t ∈ V के साथ एक नेटवर्क बनें। प्रत्येक उड़ान i के स्रोत और गंतव्य के लिए, V में दो नोड जोड़े जाते हैं, नोड si स्रोत के रूप में और नोड di उड़ान के गंतव्य नोड के रूप में i, E में निम्नलिखित किनारों को भी जोड़ा जाता है:
- s और प्रत्येक si के बीच क्षमता [0, 1] वाला किनारा
- E' में G के किनारों को X से a तक निर्देशित किया गया है
- प्रत्येक di के बीच क्षमता [0, 1] वाला किनारा और t।
- si और di की प्रत्येक जोड़ी के बीच क्षमता [1, 1] वाला किनारा।
- प्रत्येक di और sj के बीच क्षमता [0, 1] के साथ एक किनारा, यदि स्रोत sj उड़ान के गंतव्य i से उचित समय और व्यय के साथ पहुंच योग्य है।
- s और t के बीच क्षमता [0, ∞] वाला किनारा।
उल्लिखित विधि में, यह प्रमाणित किया गया है और सिद्ध किया गया है कि s और t के बीच G में k के प्रवाह मूल्य का पता लगाना अधिकतम k कर्मचारियों के साथ उड़ान समुच्चय F के लिए व्यवहार्य कार्यक्रम खोजने के समान है।[26]
विमान सेवा समय का अन्य संस्करण सभी उड़ानों को निष्पादित करने के लिए न्यूनतम आवश्यक कर्मचारियों की खोज कर रहा है। इस समस्या का उत्तर खोजने के लिए, द्विदलीय ग्राफ G' = (A ∪ B, E) वहाँ बनाया जाता है। जहाँ प्रत्येक उड़ान की समुच्चय A और समुच्चय B में प्रति होती है। यदि वही विमान उड़ान i के बाद उड़ान j निष्पादित कर सकता है, i∈A j∈B से जुड़ा है। G' में मेल खाता है F के लिए समय को प्रेरित करता है और स्पष्ट रूप से इस ग्राफ में अधिकतम द्विपक्षीय मिलान कर्मचारियों की न्यूनतम संख्या के साथ विमान सेवा समय तैयार करता है।[26] जैसा कि इस लेख के अनुप्रयोग भाग में बताया गया है, अधिकतम कार्डिनैलिटी द्विपक्षीय मिलान अधिकतम प्रवाह समस्या का अनुप्रयोग है।
परिसंचरण-मांग समस्या
कुछ कारखाने हैं जो माल का उत्पादन करते हैं और कुछ गाँव जहाँ माल पहुँचाना होता है। वे सड़कों के नेटवर्क से जुड़े हुए हैं जिनमें प्रत्येक सड़क की क्षमता है अधिकतम माल c के लिए जो इसके माध्यम से बह सकता है। समस्या यह पता लगाने की है कि क्या कोई संचलन है जो मांग को पूरा करता है। यह समस्या अधिकतम-प्रवाह समस्या में परिवर्तित हो सकती है।
- स्रोत नोड जोड़ें s और इसके किनारों को हर फैक्ट्री नोड में जोड़ें fi क्षमता के साथ pi जहाँ pi कारखाने fi की उत्पादन दर है .
- सिंक नोड जोड़ें t और सभी गांवों से किनारे जोड़ें vi को t क्षमता के साथ di जहाँ di गांव की मांग vi दर है .
बता दें कि जी = (वी, ई) यह नया नेटवर्क है। संचलन उपस्थित है जो मांग को संतुष्ट करता है यदि और केवल यदि:
- Maximum flow value(G) .
यदि कोई संचलन उपस्थित है, जिससे अधिकतम-प्रवाह समाधान को देखने से यह उत्तर मिलेगा कि मांगों को पूरा करने के लिए किसी विशेष सड़क पर कितना माल भेजा जाना है।
कुछ किनारों पर प्रवाह पर निचली सीमा जोड़कर समस्या को बढ़ाया जा सकता है।[27]
छवि विभाजन

क्लेनबर्ग और टार्डोस ने अपनी पुस्तक में छवि विभाजन के लिए छवि के लिए एल्गोरिथ्म प्रस्तुत किया है।[29] वे छवि में पृष्ठभूमि और अग्रभूमि खोजने के लिए एल्गोरिथ्म प्रस्तुत करते हैं। अधिक स्पष्ट रूप से, एल्गोरिथ्म बिटमैप को इनपुट के रूप में निम्नानुसार लेता है: ai≥ 0 संभावना है कि पिक्सेल i अग्रभूमि से संबंधित है, bi≥ 0 इस संभावना में कि पिक्सेल i पृष्ठभूमि से संबंधित है, और pijयदि दो सन्निकट पिक्सेल i और j को अग्रभूमि में और दूसरे को पृष्ठभूमि में रखा जाता है तो यह जुर्माना है। लक्ष्य निम्नलिखित मात्रा को अधिकतम करने वाले पिक्सेल के समुच्चय के विभाजन (ए, बी) को ढूंढना है
- ,
दरअसल, ai में पिक्सेल के लिए (अग्रभूमि के रूप में माना जाता है), हम प्राप्त करते हैं; बी में सभी पिक्सल के लिए (पृष्ठभूमि के रूप में माना जाता है), हम bi प्राप्त करते हैं. सीमा पर, दो आसन्न पिक्सेल i और j के बीच, हम pij को ढीला करते हैं. यह मात्रा को कम करने के समान है
क्योंकि
अब हम उस नेटवर्क का निर्माण करते हैं जिसके नोड पिक्सेल हैं, साथ ही स्रोत और सिंक, दाईं ओर चित्र देखें। हम स्रोत को पिक्सेल i से वजन ai के किनारे से जोड़ते हैं. हम पिक्सेल i को वज़न bi के किनारे से सिंक से जोड़ते हैं. हम पिक्सेल i को पिक्सेल j से वजन pij के साथ जोड़ते हैं. अब, यह उस नेटवर्क में न्यूनतम कटौती (या समकक्ष अधिकतम प्रवाह) की गणना करने के लिए बनी हुई है। अंतिम आंकड़ा न्यूनतम कटौती दिखाता है।
एक्सटेंशन
1. न्यूनतम-व्यय प्रवाह समस्या में, प्रत्येक किनारे (u,v) का व्यय-गुणांक auv भी होता है इसकी क्षमता के अतिरिक्त यदि किनारे से प्रवाह fuv है, तो कुल व्यय fuv है. सबसे छोटी व्यय के साथ दिए गए आकार d का प्रवाह खोजना आवश्यक है। अधिकांश प्रकारों में, व्यय-गुणांक सकारात्मक या नकारात्मक हो सकते हैं। इस समस्या के लिए विभिन्न बहुपद-समय एल्गोरिदम हैं।
2. अधिकतम-प्रवाह समस्या को 'वियोगात्मक बाधाओं' द्वारा संवर्धित किया जा सकता है: नकारात्मक वियोगात्मक बाधा का कहना है कि किनारों की निश्चित जोड़ी साथ गैर-शून्य प्रवाह नहीं कर सकती है; सकारात्मक वियोगात्मक बाधाएँ कहती हैं कि, किनारों की निश्चित जोड़ी में, कम से कम गैर-शून्य प्रवाह होना चाहिए। नकारात्मक बाधाओं के साथ, सरल नेटवर्क के लिए भी समस्या एनपी-हार्ड हो जाती है। सकारात्मक बाधाओं के साथ, यदि आंशिक प्रवाह की अनुमति दी जाती है, जिससे समस्या बहुपद है, किन्तु जब प्रवाह अभिन्न होना चाहिए जिससे यह एनपी-हार्ड हो सकता है।[30]
संदर्भ
- ↑ 1.0 1.1 1.2 Schrijver, A. (2002). "परिवहन के इतिहास और अधिकतम प्रवाह की समस्याओं पर". Mathematical Programming. 91 (3): 437–445. CiteSeerX 10.1.1.23.5134. doi:10.1007/s101070100259. S2CID 10210675.
- ↑ Gass, Saul I.; Assad, Arjang A. (2005). "Mathematical, algorithmic and professional developments of operations research from 1951 to 1956". ऑपरेशंस रिसर्च की एन एनोटेटेड टाइमलाइन. International Series in Operations Research & Management Science. Vol. 75. pp. 79–110. doi:10.1007/0-387-25837-X_5. ISBN 978-1-4020-8116-3.
- ↑ 3.0 3.1 Harris, T. E.; Ross, F. S. (1955). "रेल नेट क्षमताओं के मूल्यांकन के लिए एक विधि के मूल सिद्धांत" (PDF). Research Memorandum. Archived from the original (PDF) on 8 January 2014.
- ↑ 4.0 4.1 Ford, L. R.; Fulkerson, D. R. (1956). "एक नेटवर्क के माध्यम से अधिकतम प्रवाह". Canadian Journal of Mathematics. 8: 399–404. doi:10.4153/CJM-1956-045-5.
- ↑ 5.0 5.1 Ford, L.R., Jr.; Fulkerson, D.R., Flows in Networks, Princeton University Press (1962).
- ↑ Sherman, Jonah (2013). "Nearly Maximum Flows in Nearly Linear Time". Proceedings of the 54th Annual IEEE Symposium on Foundations of Computer Science. pp. 263–269. arXiv:1304.2077. doi:10.1109/FOCS.2013.36. ISBN 978-0-7695-5135-7. S2CID 14681906.
- ↑ Kelner, J. A.; Lee, Y. T.; Orecchia, L.; Sidford, A. (2014). "An Almost-Linear-Time Algorithm for Approximate Max Flow in Undirected Graphs, and its Multicommodity Generalizations" (PDF). असतत एल्गोरिदम पर पच्चीसवीं वार्षिक एसीएम-सियाम संगोष्ठी की कार्यवाही. p. 217. arXiv:1304.2338. doi:10.1137/1.9781611973402.16. ISBN 978-1-61197-338-9. S2CID 10733914. Archived from the original (PDF) on 2016-03-03.
- ↑ Knight, Helen (7 January 2014). "नया एल्गोरिदम नाटकीय रूप से 'अधिकतम प्रवाह' समस्या के समाधान को सुव्यवस्थित कर सकता है". MIT News. Retrieved 8 January 2014.
- ↑ 9.0 9.1 Orlin, James B. (2013). "Max flows in O(nm) time, or better". Proceedings of the 45th annual ACM symposium on Symposium on theory of computing – STOC '13. pp. 765–774. CiteSeerX 10.1.1.259.5759. doi:10.1145/2488608.2488705. ISBN 9781450320290. S2CID 207205207.
{{cite book}}:|journal=ignored (help) - ↑ 10.0 10.1 Chen, L.; Kyng, R.; Liu, Y.P.; Gutenberg, M.P.; Sachdeva, S. (2022). "Maximum Flow and Minimum-Cost Flow in Almost-Linear Time". arXiv:2203.00671 [cs.DS].
- ↑ Klarreich, Erica (2022-06-08). "शोधकर्ताओं ने नेटवर्क प्रवाह के लिए 'एब्सर्डली फास्ट' एल्गोरिथम हासिल किया". Quanta Magazine (in English). Retrieved 2022-06-08.
- ↑ Bernstein, Aaron; Nanongkai, Danupon; Wulff-Nilsen, Christian (2022-10-30). "नेगेटिव-वेट सिंगल-सोर्स शॉर्टेस्ट पाथ इन नियर-लीनियर टाइम". arXiv:2203.03456 [cs.DS].
- ↑ Brubaker, Ben (2023-01-18). "अंत में, नकारात्मक रेखांकन पर सबसे छोटे रास्तों के लिए एक तेज़ एल्गोरिथम". Quanta Magazine (in English). Retrieved 2023-01-25.
- ↑ "FOCS 2022". focs2022.eecs.berkeley.edu. Retrieved 2023-01-25.
- ↑ Santosh, Nagarakatte. "FOCS 2022 Best Paper Award for Prof. Aaron Bernstein's Paper". www.cs.rutgers.edu (in British English). Retrieved 2023-01-25.
- ↑ Malhotra, V.M.; Kumar, M. Pramodh; Maheshwari, S.N. (1978). "An algorithm for finding maximum flows in networks" (PDF). Information Processing Letters. 7 (6): 277–278. doi:10.1016/0020-0190(78)90016-9.
- ↑ 17.0 17.1 17.2 Goldberg, A. V.; Tarjan, R. E. (1988). "A new approach to the maximum-flow problem". Journal of the ACM. 35 (4): 921. doi:10.1145/48014.61051. S2CID 52152408.
- ↑ Cheriyan, J.; Maheshwari, S. N. (1988). "Analysis of preflow push algorithms for maximum network flow". Foundations of Software Technology and Theoretical Computer Science. Lecture Notes in Computer Science. Vol. 338. pp. 30–48. doi:10.1007/3-540-50517-2_69. ISBN 978-3-540-50517-4. ISSN 0302-9743.
- ↑ Goldberg, A. V.; Rao, S. (1998). "Beyond the flow decomposition barrier". Journal of the ACM. 45 (5): 783. doi:10.1145/290179.290181. S2CID 96030.
- ↑ Madry, Aleksander (9–11 October 2016). Computing Maximum Flow with Augmenting Electrical Flows. New Brunswick, New Jersey: IEEE. pp. 593–602.
{{cite book}}: CS1 maint: date format (link) - ↑ Brand, J. vd; Lee, Y.T.; Nanongkai, D.; Peng, R.; Saranurak, T.; Sidford, A.; Song, Z.; Wang, D. (16–19 November 2020). Bipartite Matching in Nearly-linear Time on Moderately Dense Graphs. Durham, NC, USA: IEEE. pp. 919–930.
- ↑ Brand, J. vd; Lee, Y.T.; Liu, Y.P.; Saranurak, T.; Sidford, A; Song, Z.; Wang, D. (2021). "Minimum Cost Flows, MDPs, and ℓ1-Regression in Nearly Linear Time for Dense Instances". arXiv:2101.05719 [cs.DS].
- ↑ Gao, Y.; Liu, Y.P.; Peng, R. (2021). "Fully Dynamic Electrical Flows: Sparse Maxflow Faster Than Goldberg-Rao". arXiv:2101.07233 [cs.DS].
- ↑ Itai, A.; Perl, Y.; Shiloach, Y. (1982). "लंबाई की कमी के साथ अधिकतम असम्बद्ध पथ खोजने की जटिलता". Networks (in English). 12 (3): 277–286. doi:10.1002/net.3230120306. ISSN 1097-0037.
- ↑ Schwartz, B. L. (1966). "आंशिक रूप से पूर्ण टूर्नामेंट में संभावित विजेता". SIAM Review. 8 (3): 302–308. Bibcode:1966SIAMR...8..302S. doi:10.1137/1008062. JSTOR 2028206.
- ↑ 26.0 26.1 Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein (2001). "26. Maximum Flow". एल्गोरिदम का परिचय, दूसरा संस्करण. MIT Press and McGraw-Hill. pp. 643–668. ISBN 978-0-262-03293-3.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ Carl Kingsford. "Max-flow extensions: circulations with demands" (PDF).
- ↑ "प्रोजेक्ट इमेजेजमेंटेशनविथमैक्सफ्लो, जिसमें इन दृष्टांतों को बनाने के लिए स्रोत कोड शामिल है।". GitLab (in English). Archived from the original on 2019-12-22. Retrieved 2019-12-22.
- ↑ "एल्गोरिथम डिजाइन". pearson.com (in English). Retrieved 2019-12-21.
- ↑ Schauer, Joachim; Pferschy, Ulrich (1 July 2013). "असंबद्ध बाधाओं के साथ अधिकतम प्रवाह समस्या". Journal of Combinatorial Optimization (in English). 26 (1): 109–119. CiteSeerX 10.1.1.414.4496. doi:10.1007/s10878-011-9438-7. ISSN 1382-6905. S2CID 6598669.
अग्रिम पठन
- Joseph Cheriyan and Kurt Mehlhorn (1999). "An analysis of the highest-level selection rule in the preflow-push max-flow algorithm". Information Processing Letters. 69 (5): 239–242. CiteSeerX 10.1.1.42.8563. doi:10.1016/S0020-0190(99)00019-8.
- Daniel D. Sleator and Robert E. Tarjan (1983). "A data structure for dynamic trees" (PDF). Journal of Computer and System Sciences. 26 (3): 362–391. doi:10.1016/0022-0000(83)90006-5. ISSN 0022-0000.
- Eugene Lawler (2001). "4. Network Flows". Combinatorial Optimization: Networks and Matroids. Dover. pp. 109–177. ISBN 978-0-486-41453-9.