क्रासिंग से परहेज किया

रिवर्स एचबीएक्स

क्वांटम भौतिकी और क्वांटम रसायन विज्ञान में, में, एक टाली गई क्रॉसिंग (जिसे कभी-कभी इच्छित क्रॉसिंग भी कहा जाता है, गैर-क्रॉसिंग या एंटीक्रॉसिंग) वह घटना है जहां हर्मिटियन मैट्रिक्स के दो आइगेनवैल्यू ​​​​देखे जाने योग्य क्वांटम का प्रतिनिधित्व करते हैं और N-2 आयामों के कई गुना को छोड़कर N निरंतर वास्तविक मापदंडों के आधार पर मूल्य (क्रॉस) में बराबर नहीं हो सकते हैं। घटना को वॉन न्यूमैन-विग्नर प्रमेय के रूप में भी जाना जाता है। एक द्विपरमाणुक अणु के मामले में (एक पैरामीटर के साथ, अर्थात् बांड की लंबाई), इसका मतलब यह है कि आइगेनवेल्यू बिल्कुल भी पार नहीं कर सकते हैं। एक त्रिपरमाणुक अणु के मामले में, इसका मतलब यह है कि ईगेनवेल्यू केवल एक बिंदु पर मेल खा सकते हैं (शंक्वाकार चौराहे देखें)।

यह क्वांटम रसायन विज्ञान में विशेष रूप से महत्वपूर्ण है। बोर्न-ओपेनहाइमर सन्निकटन में, इलेक्ट्रॉनिक आणविक हैमिल्टनियन अलग-अलग आणविक ज्यामिति के एक सेट पर विकर्णीय मैट्रिक्स है (प्राप्त आइगेनवेल्यूज़ रुद्धोष्म संभावित ऊर्जा सतहों के मान हैं)। ज्यामिति जिसके लिए संभावित ऊर्जा सतहों को पार करने से बचा जा रहा है, वे स्थान (गणित) हैं जहां बोर्न-ओपेनहाइमर सन्निकटन विफल हो जाता है।

अविभाजित यांत्रिक प्रणालियों की अनुनाद आवृत्तियों में भी बचा हुआ क्रॉसिंग होता है, जहां कठोरता और द्रव्यमान मैट्रिक्स वास्तविक सममित होते हैं। वहाँ अनुनाद आवृत्तियाँ सामान्यीकृत eigenvalues ​​​​के वर्गमूल हैं।

दो-राज्य प्रणालियों में

उद्भव

क्वांटम यांत्रिकी में दो-स्तरीय प्रणाली का अध्ययन महत्वपूर्ण महत्व रखता है क्योंकि यह कई भौतिक रूप से वसूली योग्य प्रणालियों के सरलीकरण का प्रतीक है। एक दो-राज्य प्रणाली हैमिल्टनियन (क्वांटम यांत्रिकी) पर गड़बड़ी सिद्धांत (क्वांटम यांत्रिकी) का प्रभाव अलग-अलग ऊर्जा बनाम ईजेनस्टेट्स के ऊर्जा अंतर वक्र की साजिश में क्रॉसिंग से बचने के माध्यम से प्रकट होता है। दो-राज्य हैमिल्टनियन को इस रूप में लिखा जा सकता है

$H={\begin{pmatrix}E_{1}&0\\0&E_{2}\end{pmatrix}}\,\!$

जिसके आइगेनवैल्यू हैं $\textstyle E_{1}$ और $\textstyle E_{2}$ और आइजन्वेक्टर, $\textstyle {\begin{pmatrix}1\\0\end{pmatrix}}$ और $\textstyle {\begin{pmatrix}0\\1\end{pmatrix}}$. ये दो eigenvectors सिस्टम के दो राज्यों को नामित करते हैं। यदि किसी भी राज्य में सिस्टम तैयार किया जाता है तो वह उसी राज्य में बना रहेगा। अगर $\textstyle E_{1}$ के बराबर होता है $E_{2}$ हैमिल्टनियन में एक दुगनी गिरावट (क्वांटम यांत्रिकी) होगी। उस मामले में पतित आइजेनस्टेट्स का कोई भी सुपरपोजिशन हैमिल्टनियन का एक और ईजेनस्टेट है। इसलिए किसी भी राज्य में जो व्यवस्था तैयार की गई है, वह उसमें सदा बनी रहेगी।

दो-राज्य प्रणाली में क्रॉसिंग से बचा गया। पैरामीटर बढ़ाने से एनर्जी लेवल क्रॉसिंग से बचा जाता है $\textstyle w(=|W|)$. बाहरी गड़बड़ी की अनुपस्थिति में, यदि मूल ऊर्जा अवस्थाएँ पतित होती हैं, तो स्तर पार हो जाते हैं, अर्थात $\textstyle \Delta E=0$

हालांकि, जब एक बाहरी गड़बड़ी सिद्धांत (क्वांटम यांत्रिकी) के अधीन, हैमिल्टनियन परिवर्तन के मैट्रिक्स तत्व। सादगी के लिए हम केवल विकर्ण तत्वों के साथ गड़बड़ी पर विचार करते हैं। चूंकि समग्र हैमिल्टनियन हर्मिटियन होना चाहिए, इसलिए हम केवल नया हैमिल्टनियन लिख सकते हैं

$H'=H+P={\begin{pmatrix}E_{1}&0\\0&E_{2}\end{pmatrix}}+{\begin{pmatrix}0&W\\W^{*}&0\end{pmatrix}}={\begin{pmatrix}E_{1}&W\\W^{*}&E_{2}\end{pmatrix}}\,\!$

जहाँ P शून्य विकर्ण शर्तों के साथ गड़बड़ी है। तथ्य यह है कि पी हर्मिटियन है, इसके ऑफ-डायगोनल घटकों को ठीक करता है। संशोधित आइजेनस्टेट्स को संशोधित हैमिल्टनियन को विकर्ण करके पाया जा सकता है। यह पता चला है कि नए eigenvalues ​​​​हैं,

$E_{+}={\frac {1}{2}}(E_{1}+E_{2})+{\frac {1}{2}}{\sqrt {(E_{1}-E_{2})^{2}+4|W|^{2}}}$

$E_{-}={\frac {1}{2}}(E_{1}+E_{2})-{\frac {1}{2}}{\sqrt {(E_{1}-E_{2})^{2}+4|W|^{2}}}$

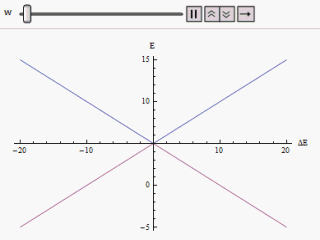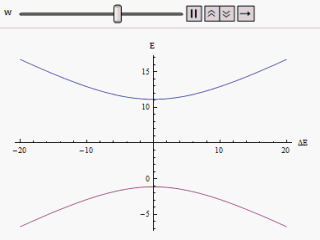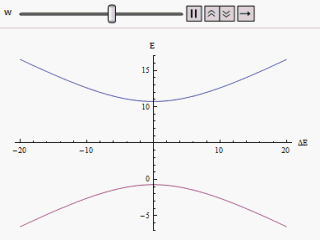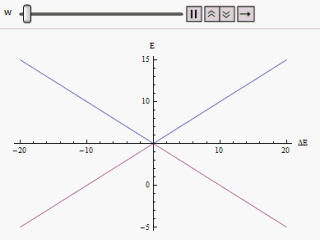
यदि एक ग्राफ अलग-अलग प्लॉट किया जाता है $\textstyle (E_{1}-E_{2})$ क्षैतिज अक्ष के साथ और $\textstyle E_{+}$ या $\textstyle E_{-}$ ऊर्ध्वाधर के साथ, हमें हाइपरबोला की दो शाखाएँ मिलती हैं (जैसा कि चित्र में दिखाया गया है)। वक्र स्पर्शोन्मुख रूप से मूल अविचलित ऊर्जा स्तरों तक पहुंचता है। वक्रों का विश्लेषण करने पर यह स्पष्ट हो जाता है कि भले ही मूल अवस्थाएँ पतित थीं (अर्थात् $\textstyle E_{1}=E_{2}$ ) नई ऊर्जा अवस्थाएँ अब समान नहीं हैं। हालांकि, यदि $\textstyle W$ शून्य पर सेट है हम पर पा सकते हैं $\textstyle (E_{1}-E_{2})=0$, $\textstyle E_{+}=E_{-}$ और स्तर पार हो जाते हैं। इस प्रकार क्षोभ के प्रभाव से इन समपारों से बचा जा सकता है।

क्वांटम प्रतिध्वनि

एक पतित दो राज्य प्रणाली में टाले गए स्तर के क्रॉसिंग का तत्काल प्रभाव एक निम्न ऊर्जा ईजेनस्टेट का उद्भव है। ऊर्जा का प्रभावी रूप से कम होना हमेशा बढ़ती हुई स्थिरता के अनुरूप होता है। इन मामलों का वर्णन करने के लिए हम ध्यान दे सकते हैं कि पूर्ववर्ती विकर्ण हैमिल्टनियन में गैर-विकर्ण तत्व न केवल ऊर्जा ईजेनवैल्यू को संशोधित करते हैं बल्कि पुराने ईजेनस्टेट्स को नए में सुपरपोज भी करते हैं। ये प्रभाव अधिक प्रमुख हैं यदि मूल हेमिल्टनियन में अध:पतन था। अधिक स्थिरता प्राप्त करने के लिए ईजेनस्टेट्स की यह सुपरपोजिशन ठीक रासायनिक बंधन अनुनाद की घटना है।

हमारा पहले का उपचार ईजेनवेक्टरों को निरूपित करके शुरू किया गया था $\textstyle {\begin{pmatrix}1\\0\end{pmatrix}}$ और $\textstyle {\begin{pmatrix}0\\1\end{pmatrix}}$ eigenstates के मैट्रिक्स प्रतिनिधित्व के रूप में $\textstyle |\psi _{1}\rangle$ और $\textstyle |\psi _{2}\rangle$ दो-राज्य प्रणाली का। ब्रा-केट नोटेशन का उपयोग मैट्रिक्स तत्वों का $H'$ वास्तव में शर्तें हैं

$H'_{ij}=\langle \psi _{i}|H'|\psi _{j}\rangle$ साथ $i,j\in \left\{{1,2}\right\}$

कहाँ $H'_{11}=H'_{22}=E$ बेफिक्र हैमिल्टनियन की गिरावट और ऑफ-डायगोनल गड़बड़ी के कारण हैं $H'_{12}=W$ और $H'_{21}=W^{*}$.

द न्यू ईजेनस्टेट्स $\textstyle |\psi _{+}\rangle$ और $\textstyle |\psi _{-}\rangle$ eigenvalue समीकरणों को हल करके पाया जा सकता है $H'|\psi _{+}\rangle =E_{+}|\psi _{+}\rangle$ और $H'|\psi _{-}\rangle =E_{-}|\psi _{-}\rangle$. सरल गणनाओं से यह दिखाया जा सकता है

$|\psi _{+}\rangle ={\frac {1}{\sqrt {2}}}{\begin{pmatrix}e^{i\phi }\\1\end{pmatrix}}={\frac {1}{\sqrt {2}}}(e^{i\phi }|\psi _{1}\rangle +|\psi _{2}\rangle )$ और

$|\psi _{-}\rangle ={\frac {1}{\sqrt {2}}}{\begin{pmatrix}-e^{i\phi }\\1\end{pmatrix}}={\frac {1}{\sqrt {2}}}(-e^{i\phi }|\psi _{1}\rangle +|\psi _{2}\rangle )$ कहाँ $e^{i\phi }=W/|W|$

यह स्पष्ट है कि दोनों नए ईजेनस्टेट्स मूल पतित ईजेनस्टेट्स के सुपरपोजिशन हैं और इनमें से एक आइगेनवेल्यूज (यहाँ $E_{-}$) मूल अविचलित आइजेनर्जी से कम है। तो संबंधित स्थिर प्रणाली स्वाभाविक रूप से अपनी ऊर्जा को कम करने के लिए पूर्व अपरंपरागत eigenstates को मिला देगी। बेंजीन के उदाहरण में संभावित बंधन संरचनाओं के प्रायोगिक साक्ष्य दो अलग-अलग ईजेनस्टेट्स को जन्म देते हैं, $\textstyle |\psi _{1}\rangle$ और $\textstyle |\psi _{2}\rangle$. इन दो संरचनाओं की समरूपता अनिवार्य करती है $\langle \psi _{1}|H|\psi _{1}\rangle =\langle \psi _{2}|H|\psi _{2}\rangle =E$.

हालाँकि यह पता चला है कि दो-राज्य हैमिल्टनियन $H$ बेंजीन का विकर्ण नहीं है। ऑफ-डायगोनल तत्वों के परिणामस्वरूप ऊर्जा कम हो जाती है और बेंजीन अणु एक संरचना में स्थिर हो जाता है जो ऊर्जा के साथ इन सममित लोगों का एक सुपरपोजिशन है $E_{-}<E$. किसी भी सामान्य दो-राज्य प्रणाली के लिए टाल क्रॉसिंग स्वदेशी राज्यों को पीछे हटाता है $|\psi _{+}\rangle$ और $|\psi _{-}\rangle$ जैसे कि सिस्टम को उच्च ऊर्जा विन्यास प्राप्त करने के लिए अधिक ऊर्जा की आवश्यकता होती है।

टाले गए क्रॉसिंग में प्रतिध्वनि

अणुओं में, दो रुद्धोष्म क्षमता के बीच गैर-एडियाबेटिक युग्मन टाले गए क्रॉसिंग (एसी) क्षेत्र का निर्माण करते हैं। दो-युग्मित क्षमता के एसी क्षेत्र में रोविब्रोनिक अनुनाद बहुत खास हैं, क्योंकि वे रुद्धोष्म क्षमता के बाध्य राज्य क्षेत्र में नहीं हैं, और वे आमतौर पर बिखरने पर महत्वपूर्ण भूमिका नहीं निभाते हैं और कम चर्चा की जाती है। यू कुन यांग एट अल ने न्यू जे फिज में इस समस्या का अध्ययन किया। 22 (2020)। कण बिखरने में अनुकरणीय, एसी क्षेत्र में अनुनादों की व्यापक जांच की जाती है। प्रकीर्णन क्रॉस सेक्शन पर एसी क्षेत्र में अनुनादों का प्रभाव सिस्टम के गैर-एडियाबेटिक कपलिंग पर दृढ़ता से निर्भर करता है, यह तेज चोटियों के रूप में बहुत महत्वपूर्ण हो सकता है, या पृष्ठभूमि में अस्पष्ट दफन हो सकता है। इससे भी महत्वपूर्ण बात यह है कि यह ज़ू और नाकामुरा द्वारा प्रस्तावित एक साधारण मात्रा को दर्शाता है जो गैर-एडियाबेटिक इंटरैक्शन की युग्मन शक्ति को वर्गीकृत करता है, जिसे एसी क्षेत्र में अनुनादों के महत्व का मात्रात्मक अनुमान लगाने के लिए अच्छी तरह से लागू किया जा सकता है।

सामान्य परिहार प्रमेय

टाले गए क्रॉसिंग का उपरोक्त उदाहरण हालांकि एक बहुत ही विशिष्ट मामला है। एक सामान्यीकृत दृष्टिकोण से बचने के क्रॉसिंग की घटना वास्तव में परेशानी के पीछे पैरामीटर द्वारा नियंत्रित होती है। सबसे सामान्य गड़बड़ी के लिए $\textstyle P={\begin{pmatrix}W_{1}&W\\W&W_{2}\end{pmatrix}}$ हैमिल्टनियन के द्वि-आयामी रैखिक उप-क्षेत्र को प्रभावित करना $H$, हम उस उप-समष्टि में प्रभावी हैमिल्टनियन मैट्रिक्स लिख सकते हैं

${\begin{pmatrix}E_{1}&0\\0&E_{2}\end{pmatrix}}+{\begin{pmatrix}W_{1}&W\\W&W_{2}\end{pmatrix}}={\begin{pmatrix}E_{1}+W_{1}&W\\W&E_{2}+W_{2}.\end{pmatrix}}.$

यहां राज्य वैक्टर के तत्वों को वास्तविक होने के लिए चुना गया ताकि सभी मैट्रिक्स तत्व वास्तविक हो जाएं। अब इस उपसमष्टि के लिए निकाय के आइगेनमान इस प्रकार दिए गए हैं

$E_{\pm }={\frac {1}{2}}(E_{1}+E_{2}+W_{1}+W_{2})\pm {\frac {1}{2}}{\sqrt {(E_{1}-E_{2}+W_{1}-W_{2})^{2}+4W^{2}}}$

वर्गमूल के अंतर्गत पद वर्ग वास्तविक संख्याएँ हैं। तो इन दो स्तरों को पार करने के लिए हमें एक साथ आवश्यकता होती है

$(E_{1}-E_{2}+W_{1}-W_{2})=0$

$W=0.$ अब अगर गड़बड़ी $P$ है $k$ पैरामीटर ${\alpha _{1},\alpha _{2},\alpha _{3}.....\alpha _{k}}$ हम आम तौर पर इन दो समीकरणों को संतुष्ट करने के लिए इन नंबरों को बदल सकते हैं।

$(E_{1}-E_{2}+W_{1}-W_{2})=F_{1}(\alpha _{1},\alpha _{2},\alpha _{3}.....\alpha _{k})=0$

$W=F_{2}(\alpha _{1},\alpha _{2},\alpha _{3}.....\alpha _{k})=0.$ यदि हम के मान चुनते हैं $\alpha _{1}$ को $\alpha _{k-1}$ तो उपरोक्त दोनों समीकरणों में एक एकल मुक्त पैरामीटर है। सामान्य तौर पर एक को खोजना संभव नहीं है $\alpha _{k}$ जैसे कि दोनों समीकरण संतुष्ट हैं। हालाँकि, यदि हम एक और पैरामीटर मुक्त होने की अनुमति देते हैं, तो ये दोनों समीकरण अब उन्हीं दो मापदंडों द्वारा नियंत्रित होंगे

$F_{1}(\alpha _{k-1},\alpha _{k})|_{\alpha _{1},\alpha _{2},...,\alpha _{k-2}\,fixed}=0$

$F_{2}(\alpha _{k-1},\alpha _{k})|_{\alpha _{1},\alpha _{2},...,\alpha _{k-2}\,fixed}=0.$

और आम तौर पर उनके दो ऐसे मूल्य होंगे जिनके लिए समीकरण एक साथ संतुष्ट होंगे। के साथ $k$ विशिष्ट पैरामीटर $k-2$ मापदंडों को हमेशा मनमाने ढंग से चुना जा सकता है और फिर भी हम दो ऐसे पा सकते हैं $\alpha _{k}$s ऐसा है कि ऊर्जा eigenvalues ​​​​का क्रॉसिंग होगा। दूसरे शब्दों में, के मान $E_{+}$ और $E_{-}$ के लिए समान होगा $k-2$ स्वतंत्र रूप से अलग-अलग निर्देशांक (जबकि बाकी दो निर्देशांक स्थिति समीकरणों से तय होते हैं)। ज्यामितीय रूप से eigenvalue समीकरण एक सतह (गणित) का वर्णन करते हैं $k$ आयामी स्थान।

$E_{\pm }=E_{\pm }(\alpha _{1},\alpha _{2},\alpha _{3}.....\alpha _{k}).$

चूंकि उनका चौराहा Parametrization (ज्यामिति) द्वारा है $k-2$ निर्देशांक, हम औपचारिक रूप से कह सकते हैं कि के लिए $k$ परेशान हेमिल्टनियन को नियंत्रित करने वाले निरंतर वास्तविक पैरामीटर, स्तर (या सतह) केवल आयाम के कई गुना पार कर सकते हैं $k-2$. हालाँकि, हैमिल्टनियन की समरूपता की आयामीता में भूमिका होती है। यदि मूल हैमिल्टन में असममित अवस्थाएँ हैं, $\langle \psi _{1}|P|\psi _{2}\rangle \neq \langle \psi _{2}|P|\psi _{1}\rangle$, अनुप्रस्थता सुनिश्चित करने के लिए ऑफ-डायगोनल शब्द स्वचालित रूप से गायब हो जाते हैं। यह हमें समीकरण से छुटकारा पाने की अनुमति देता है $W=0$. अब ऊपर दिए गए समान तर्कों से, यह सीधा है कि एक विषम हैमिल्टनियन के लिए, ऊर्जा सतहों का प्रतिच्छेदन कई गुना आयाम में होता है $k-1$.

बहुपरमाणुक अणुओं में

एक N-परमाणु बहुपरमाणुक अणु में 3N-6 कंपन होते हैं निर्देशांक (3N-5 एक रैखिक अणु के लिए) जो प्रवेश करता है मापदंडों के रूप में इलेक्ट्रॉनिक हैमिल्टन। एक डायटोमिक के लिए अणु में केवल एक ऐसा समन्वय होता है, बंधन की लंबाई आर। इस प्रकार, द्विपरमाणुक में टाले गए क्रॉसिंग प्रमेय के कारण अणु हम इलेक्ट्रॉनिक के बीच समपार नहीं रख सकते हैं समान समरूपता की अवस्थाएँ। हालांकि, एक बहुपरमाणुक के लिए अणु में एक से अधिक ज्यामिति पैरामीटर होते हैं इलेक्ट्रॉनिक हैमिल्टन और इलेक्ट्रॉनिक के बीच समपार समान समरूपता की अवस्थाओं से बचा नहीं जाता है।

यह भी देखें

• ज्यामितीय चरण
• क्रिस्टोफर लॉन्गेट-हिगिंस
• शंक्वाकार चौराहा
• वाइब्रोनिक कपलिंग
• एडियाबेटिक प्रमेय
• बंधन सख्त
• बंधन नरमी
• लैंडौ-जेनर फॉर्मूला
• स्तर प्रतिकर्षण