ज़ीटा पोटेंशियल: Difference between revisions

Revision as of 20:41, 1 July 2023

एक परिक्षेपण माध्यम में निलंबित कण की आवेशित सतह से दूरी के फलन के रूप में आयनिक सांद्रता और संभावित अंतर को दर्शाने वाला आरेख

जीटा विभवांतर सर्पण समतल में विद्युत विभव है। यह समतल अंतरापृष्ठ है जो सतह से जुड़े रहने वाले द्रव से मोबाइल द्रव को अलग करता है।

इस प्रकार से जीटा विभवांतर कोलॉइडी परिक्षेपण (रसायन विज्ञान) में विद्युत् गतिक घटनाएं विद्युतीय संभाव्यता के लिए वैज्ञानिक शब्द है^[1]^[2]। अतः कोलॉइडी रसायन शास्त्र साहित्य में, इसे सामान्यतः ग्रीक अक्षर ज़ेटा (ζ) का उपयोग करके दर्शाया जाता है, इसलिए ζ-संभावित होता है। सामान्य इकाइयाँ वाल्ट (V) या, अधिक सामान्यतः, मिलीवोल्ट्स (mV) हैं। सैद्धांतिक दृष्टिकोण से, जीटा विभवांतर अंतरापृष्ठ से दूर बल्क तरल में बिंदु के सापेक्ष सर्पण समतल के दोहरी परत (इंटरफेसियल) दोहरी परत (डीएल) में विद्युत विभव है। इस प्रकार से दूसरे शब्दों में, जीटा विभव, परिक्षेपण माध्यम और परिक्षिप्त कण से जुड़ी द्रव की स्थिर परत के बीच का संभावित अंतर है।

इस प्रकार से जीटा विभवांतर सर्पण समतल से घिरे क्षेत्र के भीतर निहित शुद्ध विद्युत के आवेश के कारण होता है, और यह उस समतल (ज्यामिति) के स्थान पर भी निर्भर करता है। इस प्रकार, यह व्यापक रूप से आवेश के परिमाण के परिमाणीकरण के लिए उपयोग किया जाता है। यद्यपि, जीटा विभव दोहरी परत में स्टर्न विभव या विद्युत सतह विभव के बराबर नहीं है,^[3]^[4]^[5]^[6] क्योंकि इन्हें विभिन्न स्थानों पर परिभाषित किया गया है। इस प्रकार से समानता की ऐसी धारणाओं को सावधानी के साथ लागू किया जाना चाहिए। फिर भी, दोहरी परत गुणों के लक्षण वर्णन के लिए जीटा विभव प्रायः एकमात्र उपलब्ध मार्ग है।

इस प्रकार से जीटा विभव कोलॉइडी परिक्षेपण के परिक्षेपण स्थिरता का महत्वपूर्ण और सरलता से मापने योग्य संकेतक है। जीटा विभव का परिमाण परिक्षेपण में आसन्न, समान रूप से आवेशित कणों के बीच स्थिर वैद्युत प्रतिकर्षण की मात्रा को इंगित करता है। अतः अणुओं और कणों के लिए जो अत्यधिक छोटे हैं, उच्च जीटा विभव स्थिरता प्रदान करेगी, अर्थात हल या परिक्षेपण एकत्रीकरण का विरोध करेगा। इस प्रकार से जब विभव कम होती है, तो आकर्षक बल इस प्रतिकर्षण से अधिक हो सकते हैं और परिक्षेपण टूट सकता है और ऊर्णन हो सकता है। अतः इसलिए, उच्च जीटा विभव (ऋणात्मक या धनात्मक) वाले कोलाइड विद्युत रूप से स्थिर होते हैं जबकि कम जीटा विभव वाले कोलाइड स्कंदन या प्रवाहित होते हैं जैसा कि तालिका में बताया गया है।^[7]

[A] दुर्बल अम्ल का पीएच-निर्भर आयनीकरण [HA] और इसके संयुग्मित आधार [A-] हेंडरसन-हैसलबल्च समीकरण का उपयोग करके तैयार किया गया; [B] पीएच के फलन के रूप में पीएच-उत्तरदायी बहुलक की आयनीकरण और घुलनशीलता [C] माध्यम में कण की आवेशित सतह से दूरी के फलन के रूप में संभावित अंतर को दर्शाने वाला योजनाबद्ध है; [D] अनुमति के साथ पुन: उत्पन्न पीएच-उत्तरदायी बहुलक के विघटन तंत्र। [D] में घिरी हुई संख्याएँ दर्शाती हैं (1) जेल परत बनाने के लिए बहुलक आव्यूह में जल और हाइड्रॉक्सिल आयनों का प्रसार, (2) जेल परत में बहुलक श्रृंखलाओं का आयनीकरण, (3) जेल से बहुलक श्रृंखलाओं का विघटन बहुलक-हल अंतरापृष्ठ के लिए परत, (4) बहुलक अंतरापृष्ठ पर बहुलक श्रृंखलाओं का आगे आयनीकरण, (5) अंतरफलक से दूर बल्क हल की ओर विसंक्रमित बहुलक श्रृंखलाओं का प्रसार।^[8]

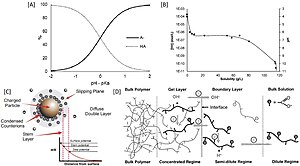
इस प्रकार से जीटा विभव का उपयोग जटिल बहुलक के पीकेए अनुमान के लिए भी किया जा सकता है जो पारंपरिक विधियों का उपयोग करके यथार्थ रूप से मापना जटिल है। अतः यह विभिन्न परिस्थितियों में विभिन्न कृत्रिम और प्राकृतिक बहुलक के आयनीकरण परीक्षण का अध्ययन करने में सहायता कर सकता है और पीएच उत्तरदायी बहुलक के लिए मानकीकृत विघटन-पीएच देहली स्थापित करने में सहायता कर सकता है।^[8]

जीटा विभव के आधार पर कोलाइड का स्थिरता परीक्षण^[9]
जीटा विभव का परिमाण (एमवी)	स्थिरता परीक्षण
0 से 5	तीव्र स्कंदन या उर्णन
10 से 30	आरंभिक अस्थिरता
30 से 40	मध्यम स्थिरता
40 से 60	ठीक स्थिरता
>61	उत्कृष्ट स्थिरता

माप

इस प्रकार से कुछ नवीन उपकरण तकनीकें स्थित हैं जो जीटा विभव को मापने की अनुमति देती हैं। अतः जीटा विभवांतर विश्लेषक ठोस, फाइबर या पाउडर पदार्थ को माप सकता है। उपकरण में पाया जाने वाला मोटर प्रतिदर्श के माध्यम से विद्युत् अपघट्य हल का दोलनशील प्रवाह बनाता है। इस प्रकार से उपकरण में कई संवेदक अन्य कारकों की देख रेख करते हैं, इसलिए संलग्न सॉफ़्टवेयर जीटा विभव को खोजने के लिए गणना करने में सक्षम है। इस कारण से तापमान, पीएच, चालकता, दाब और प्रवाही विभव सभी को उपकरण में मापा जाता है।

अतः जीटा विभव की गणना सैद्धांतिक मॉडल और प्रयोगात्मक रूप से निर्धारित वैद्युतकणसंचलन गतिशीलता या गतिशील वैद्युत कण संचालक गतिशीलता का उपयोग करके भी की जा सकती है।

इस प्रकार से जीटा विभव की गणना के लिए विद्युत् गतिक घटनाएं और वैद्युत् ध्वनिक घटनाएं डेटा के सामान्य स्रोत हैं। (ज़ीटा संभावित अनुमापन देखें।)

विद्युतगतिकी घटना

इस प्रकार से वैद्युतकणसंचलन का उपयोग एयरोसोल की जीटा विभव का अनुमान लगाने के लिए किया जाता है, जबकि प्रवाही विभव/धारा का उपयोग छिद्रित निकायों और समतल सतहों के लिए किया जाता है। अतः परीक्षण में, परिक्षेपण की जीटा विभव को परिक्षेपण पर विद्युत क्षेत्र लागू करके मापा जाता है। इस प्रकार से जीटा विभव वाले परिक्षेपण के भीतर के कण जीटा विभव के परिमाण के समानुपाती वेग से विपरीत आवेश वाले इलेक्ट्रोड की ओर पलायन करेंगे।

इस प्रकार से इस वेग को लेजर डॉपलर प्रभाव एनीमोमीटर की तकनीक से मापा जाता है। अतः इन गतिमान कणों के कारण से घटना लेजर किरण पुंज की आवृत्ति परिवर्तन या चरण परिवर्तन को कण गतिशीलता के रूप में मापा जाता है, और इस गतिशीलता को परिक्षेपक श्यानता और परावैद्युतांक, और स्मोलुचोव्स्की सिद्धांतों के अनुप्रयोग द्वारा जीटा विभव में परिवर्तित किया जाता है।^[10]

वैद्युतकणसंचलन

इस प्रकार से वैद्युत कण संचालक गतिशीलता वैद्युत कण संचालक वेग के समानुपाती होती है, जो मापने योग्य पैरामीटर है। अतः ऐसे कई सिद्धांत हैं जो वैद्युत कण संचालक गतिशीलता को जीटा विभव से जोड़ते हैं। वैद्युतकणसंचलन पर लेख में और कोलाइड और अंतरापृष्ठ विज्ञान पर कई पुस्तकों में विवरण में उनका संक्षेप में वर्णन किया गया है।^[3]^[4]^[5]^[11] इस प्रकार से विद्युत् गतिक घटना पर विश्व के विशेषज्ञों के समूह द्वारा तैयार की गई शुद्ध और व्यावहारिक रसायन के अंतर्राष्ट्रीय संघ तकनीकी रिपोर्ट है।^[12] अतः सहायक दृष्टिकोण से, तीन अलग-अलग प्रायोगिक तकनीकें माइक्रोवैद्युत कण संचलन, वैद्युतकणसंचलन प्रकाश प्रकीर्णन और समस्वरणीय प्रतिरोधक स्पंद संवेदक हैं। माइक्रोवैद्युत कण संचलन में गतिमान कणों की प्रतिबिम्ब प्राप्त करने का लाभ है। दूसरी ओर, यह प्रतिदर्श सेल की दीवारों पर विद्युत असमस द्वारा जटिल है। इस प्रकार से वैद्युत कण संचालक प्रकाश प्रकीर्णन गतिशील प्रकाश परिक्षेपण पर आधारित है। यह विवृत सेल में माप की अनुमति देता है जो केशिका सेल की स्थिति को छोड़कर विद्युत आसमाटिक प्रवाह की समस्या को समाप्त करता है। और, इसका उपयोग बहुत छोटे कणों को चित्रित करने के लिए किया जा सकता है, परन्तु गतिमान कणों की प्रतिबिम्बों को प्रदर्शित करने की लुप्त हुई विभव के मान पर है। इस प्रकार से समस्वरणीय प्रतिरोधक स्पंद संवेदक (टीआरपीएस) प्रतिबाधा-आधारित माप तकनीक है जो प्रतिरोधक स्पंद संकेतन की अवधि के आधार पर व्यक्तिगत कणों की जीटा विभव को मापती है।^[13] अतः सूक्ष्मकण की स्थानान्तरण अवधि को वोल्टता और अनुप्रयुक्त दाब के फलन के रूप में मापा जाता है। व्युत्क्रम स्थानान्तरण समय बनाम वोल्टता-निर्भर वैद्युत कण संचालक गतिशीलता से, और इस प्रकार जीटा विभव की गणना की जाती है। इस प्रकार से टीआरपीएस पद्धति का मुख्य लाभ यह है कि यह कण-दर-कण आधार पर एक साथ आकार और सतह आवेश माप की अनुमति देता है, जिससे कृत्रिम और जैविक नैनो/माइक्रोकणों और उनके मिश्रण के व्यापक स्पेक्ट्रम के विश्लेषण को सक्षम किया जा सकता है।^[14]

इस प्रकार से मापन की इन सभी तकनीकों के लिए प्रतिदर्श को तनूकरण करने की आवश्यकता हो सकती है। अतः कभी-कभी यह दुर्बल पड़ने से प्रतिदर्श के गुण प्रभावित हो सकते हैं और जीटा विभव परिवर्तित कर सकती है। इस तनुकरण को करने का मात्र एक ही न्यायसंगत विधि है - संतुलन अधिप्लवी का उपयोग करके किया जाता है। इस स्थिति में, सतह और बल्क तरल के बीच पारस्परिक संतुलन बनाए रखा जाएगा और निलंबन में कणों के सभी आयतन अंशों के लिए जीटा विभव समान होगी। इस प्रकार से जब तनुकारक ज्ञात हो (जैसा कि रासायनिक सूत्रीकरण की स्थिति में होता है), अतिरिक्त तनुकारक तैयार किए जा सकते है। यदि मंदक अज्ञात है, तो अपकेंद्रीकरण द्वारा संतुलन सतह पर अधिप्लवी सरलता से प्राप्त किया जाता है।

प्रवाही विभव, धाराप्रवाह

इस प्रकार से प्रवाही विभव विद्युत विभव है जो केशिका के माध्यम से तरल के प्रवाह के समय विकसित होती है। प्रकृति में, ज्वालामुखीय गतिविधियों वाले क्षेत्रों में महत्वपूर्ण परिमाण में प्रवाही विभव हो सकती है।^[15] ठोस पदार्थ-जल इंटरफेस पर जीटा विभव के आकलन के लिए प्रवाही विभव भी प्राथमिक विद्युत् गतिक घटना है। इस प्रकार से केशिका प्रवाह चैनल बनाने के लिए संगत ठोस प्रतिदर्श इस प्रकार से व्यवस्थित किया जाता है। अतः समतल सतह वाली पदार्थ को प्रतिरूप प्रतिदर्शों के रूप में माउंट किया जाता है जो समानांतर प्लेटों के रूप में संरेखित होते हैं। इस प्रकार से केशिका प्रवाह चैनल बनाने के लिए प्रतिदर्श सतहों को छोटी दूरी से अलग किया जाता है। अनियमित आकार वाले पदार्थ, जैसे फाइबर या कणिक मीडिया, छिद्र नेटवर्क प्रदान करने के लिए छिद्रित प्लग के रूप में माउंट होते हैं, जो प्रवाह संभावित माप के लिए केशिकाओं के रूप में कार्य करता है। इस प्रकार से परीक्षण हल पर दाब के अनुप्रयोग पर, तरल प्रवाहित होने लगता है और विद्युत विभव उत्पन्न करता है। अतः यह प्रवाही विभव सतह जीटा विभव की गणना करने के लिए या तो एकल प्रवाह चैनल (एक समतल सतह वाले प्रतिदर्शों के लिए) या छिद्रित प्लग (फाइबर और कणिक मीडिया के लिए) के सिरों के बीच दाब प्रवणता से संबंधित है।

इस प्रकार से वैकल्पिक रूप से प्रवाही विभव के लिए, धाराप्रवाह का माप सतह जीटा विभव के लिए और दृष्टिकोण प्रदान करता है। सामान्यतः, मैरियन स्मोलुचोव्स्की द्वारा प्राप्त शास्त्रीय समीकरणों का उपयोग प्रवाही विभव या प्रवाह धारा परिणामों को सतह जीटा विभव में परिवर्तित करने के लिए किया जाता है।^[16]

इस प्रकार से सतह जीटा विभवांतर निर्धारण के लिए प्रवाह विभवांतर और धाराप्रवाह विधि के अनुप्रयोगों में बहुलक झिल्ली,^[17] बायोमैटेरियल्स और चिकित्सा उपकरण,^[18]^[19] और खनिजों के सतह आवेश के लक्षण वर्णन सम्मिलित हैं।^[20]

विद्युत ध्वनिक घटना

इस प्रकार से जीटा विभव के लक्षण वर्णन के लिए दो वैद्युत् ध्वनिक प्रभाव कोलाइड कंपन धारा और विद्युत ध्वनि आयाम व्यापक रूप से उपयोग किए जाते हैं।^[5] व्यावसायिक रूप से उपलब्ध उपकरण हैं जो गतिशील वैद्युत कण संचालक गतिशीलता को मापने के लिए इन प्रभावों का लाभ उठाते हैं, जो जीटा विभव पर निर्भर करता है।

इस प्रकार से विद्युत-ध्वनिक तकनीकों का यह लाभ है कि वे बिना तनुकरण के अक्षुण्ण प्रतिदर्शों में मापन करने में सक्षम हैं। प्रकाशित और ठीक रूप से सत्यापित सिद्धांत इस प्रकार के माप को 50% तक मात्रा अंशों पर अनुमति देते हैं। गतिशील वैद्युत कण संचालक गतिशीलता से जीटा विभव की गणना के लिए कणों और तरल के घनत्व पर सूचना की आवश्यकता होती है। इसके अतिरिक्त, लगभग 300 एनएम आकार से अधिक बड़े कणों के लिए कण आकार की सूचना भी आवश्यक है।

गणना

प्रायोगिक डेटा से जीटा विभव की गणना के लिए सबसे अधिक ज्ञात और व्यापक रूप से उपयोग किया जाने वाला सिद्धांत 1903 में मैरियन स्मोलुचोव्स्की द्वारा विकसित किया गया है।^[21] इस प्रकार से यह सिद्धांत मूल रूप से वैद्युतकणसंचलन के लिए विकसित किया गया था; यद्यपि, अब विद्युत ध्वनिकी का विस्तार भी उपलब्ध है।^[5] अतः स्मोलुचोव्स्की का सिद्धांत शक्तिशाली है क्योंकि यह किसी भी आकार और किसी भी एकाग्रता के प्रकीर्णित कणों के लिए मान्य है। यद्यपि, इसकी सीमाएँ इस प्रकार से हैं:

विस्तृत सैद्धांतिक विश्लेषण ने सिद्ध किया कि स्मोलुचोव्स्की का सिद्धांत मात्र पर्याप्त पतली दोहरी परत के लिए मान्य है, जब डेबी की लंबाई, $1/\kappa$ , कण त्रिज्या, $a$ :

{\kappa }\cdot a\gg 1

से बहुत छोटी है

पतली दोहरी परत का मॉडल न मात्र वैद्युतकणसंचलन सिद्धांत के लिए बल्कि कई अन्य विद्युत् गतिक और वैद्युत् ध्वनिक सिद्धांतों के लिए अतिबृहत सरलीकरण प्रदान करता है। यह मॉडल अधिकांश जलीय प्रणालियों के लिए मान्य है क्योंकि डेबी की लंबाई सामान्यतः जल में मात्र कुछ नैनोमीटर होती है। यह मॉडल मात्र नैनो-कोलाइड के लिए आयनिक शक्ति वाले घोल में शुद्ध जल के निकट आता है।

स्मोलुचोव्स्की का सिद्धांत सतह चालकता के योगदान की उपेक्षा करता है। इसे आधुनिक सिद्धांतों में एक छोटी दुखिन संख्या की स्थिति के रूप में व्यक्त किया गया है:

Du\ll 1

इस प्रकार से 20वीं शताब्दी के समय कई अध्ययनों का उद्देश्य वैधता की विस्तृत श्रृंखला के साथ वैद्युत कण संचालक और वैद्युत् ध्वनिक सिद्धांतों का विकास था। अतः कई विश्लेषणात्मक सिद्धांत हैं जो सतह चालकता को सम्मिलित करते हैं और विद्युत् गतिक और वैद्युत् ध्वनिक दोनों अनुप्रयोगों के लिए छोटे दुखिन संख्या के प्रतिबंध को समाप्त करते हैं।

अतः इस दिशा में प्रारंभिक अग्रणी फलन ओवरबीक^[22] और बूथ के समय से प्रारंभ होता है।^[23]

इस प्रकार से आधुनिक, कठोर विद्युत् गतिक सिद्धांत जो किसी भी जीटा विभव और प्रायः किसी भी $\kappa a$ के लिए मान्य हैं, अधिकांशतः सोवियत यूक्रेनी (दुखिन, शिलोव, और अन्य) और ऑस्ट्रेलियाई (ओ'ब्रायन, व्हाइट, हंटर, और अन्य) विद्यालयों से उपजे हैं। अतः ऐतिहासिक रूप से, पहला दुखिन-सेमेनिखिन सिद्धांत था।^[24] इस प्रकार का सिद्धांत दस वर्ष पश्चात ओ'ब्रायन और हंटर द्वारा बनाया गया था।^[25] पतली दोहरी परत मानते हुए, ये सिद्धांत ऐसे परिणाम देंगे जो ओ'ब्रायन और व्हाइट द्वारा प्रदान किए गए संख्यात्मक हल के बहुत निकट हैं।^[26] इस प्रकार से सामान्य विद्युत ध्वनिक सिद्धांत भी हैं जो डेबी लंबाई और दुखिन संख्या के किसी भी मान के लिए मान्य हैं।^[5]^[11]

हेनरी का समीकरण

इस प्रकार से जब κa बड़े मानों के बीच होता है जहां सरल विश्लेषणात्मक मॉडल उपलब्ध होते हैं, और निम्न मान जहां संख्यात्मक गणना मान्य होती है, हेनरी के समीकरण का उपयोग तब किया जा सकता है जब जीटा विभव कम हो जाता हो। अतः अचालक क्षेत्र के लिए, हेनरी का समीकरण $u_{e}={\frac {2\varepsilon _{rs}\varepsilon _{0}}{3\eta }}\zeta f_{1}(\kappa a)$ है, जहां f₁ हेनरी फलन है, फलनों के संग्रह में से एक है जो 1.0 से 1.5 तक सरलता से भिन्न होता है क्योंकि κa अनंत तक पहुंचता है।^[12]

संदर्भ

↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "electrokinetic potential, ζ". doi:10.1351/goldbook.E01968
↑ "Colloidal systems – Methods for Zeta potential determination". ISO International Standard 13099, Parts 1,2 and 3. International Organization for Standardization (ISO). 2012.
↑ ^3.0 ^3.1 Lyklema J (1995). इंटरफेस और कोलाइड साइंस के फंडामेंटल. Vol. 2. pp. 3–208. ISBN 978-0-12-460529-9.
↑ ^4.0 ^4.1 Russel WB (1991). कोलाइडल फैलाव. Cambridge: Cambridge University Press. ISBN 978-0-521-42600-8.^{[page needed]}
↑ ^5.0 ^5.1 ^5.2 ^5.3 ^5.4 Dukhin AS (2017). अल्ट्रासाउंड का उपयोग करते हुए तरल पदार्थ, फैलाव, पायस और झरझरा सामग्री का लक्षण वर्णन (Third ed.). Amsterdam: Elsevier. ISBN 978-0-444-63908-0.^{[page needed]}
↑ Kirby BJ (2010). Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices. Cambridge University Press. ISBN 978-0-521-11903-0.^{[page needed]}
↑ Hanaor D, Michelazzi M, Leonelli C, Sorrell CC (2012). "The effects of carboxylic acids on the aqueous dispersion and electrophoretic deposition of ZrO₂". Journal of the European Ceramic Society. 32 (1): 235–244. arXiv:1303.2754. doi:10.1016/j.jeurceramsoc.2011.08.015. S2CID 98812224.
↑ ^8.0 ^8.1 Barbosa JA, Abdelsadig MS, Conway BR, Merchant HA (December 2019). "Using zeta potential to study the ionisation behaviour of polymers employed in modified-release dosage forms and estimating their pK_a". International Journal of Pharmaceutics. 1: 100024. doi:10.1016/j.ijpx.2019.100024. PMC 6733289. PMID 31517289.
↑ Kumar A, Dixit CK (2017). "Methods for characterization of nanoparticles". Advances in Nanomedicine for the Delivery of Therapeutic Nucleic Acids. pp. 43–58. doi:10.1016/B978-0-08-100557-6.00003-1. ISBN 978-0-08-100557-6.
↑ "जीटा क्षमता लेजर डॉपलर वैद्युतकणसंचलन का उपयोग". Malvern.com. Archived from the original on 7 April 2012.
↑ ^11.0 ^11.1 Hunter RJ (1989). कोलाइड विज्ञान की नींव. Oxford University Press. ISBN 978-0-19-855189-8.^{[page needed]}
↑ ^12.0 ^12.1 Delgado AV, González-Caballero F, Hunter RJ, Koopal LK, Lyklema J (1 January 2005). "इलेक्ट्रोकाइनेटिक घटना का मापन और व्याख्या (आईयूपीएसी तकनीकी रिपोर्ट)". Pure and Applied Chemistry. 77 (10): 1753–1805. doi:10.1351/pac200577101753. hdl:10481/29099. S2CID 16513957.
↑ जीटा संभावित मापन - इज़ोन साइंस>{{cite web |url=http://izon.com/nanoparticlemeasurement/zeta-potential/ |website=Izon Science | title= टीआरपीएस के साथ जीटा संभावित मापन}
↑ Vogel R, Pal AK, Jambhrunkar S, Patel P, Thakur SS, Reátegui E, et al. (December 2017). "ट्यून करने योग्य प्रतिरोधक पल्स सेंसिंग का उपयोग करके जैविक नैनोकणों का उच्च-रिज़ॉल्यूशन सिंगल पार्टिकल जीटा संभावित लक्षण वर्णन". Scientific Reports. 7 (1): 17479. Bibcode:2017NatSR...717479V. doi:10.1038/s41598-017-14981-x. PMC 5727177. PMID 29234015.
↑ Jouniaux, L.; Ishido, T. (2012). "Electrokinetics in Earth Sciences: A Tutorial". International Journal of Geophysics (in English). 2012: e286107. doi:10.1155/2012/286107. ISSN 1687-885X.
↑ Luxbacher, Thomas (2014). The ZETA Guide: Principles of the streaming potential technique. Anton Paar GmbH. ISBN 978-3-200-03553-9.
↑ Elimelech, Menachem; Chen, William H.; Waypa, John J. (1994). "स्ट्रीमिंग पोटेंशियल एनालाइजर द्वारा रिवर्स ऑस्मोसिस मेम्ब्रेन की जेटा (इलेक्ट्रोकाइनेटिक) क्षमता को मापना". Desalination (in English). 95 (3): 269–286. doi:10.1016/0011-9164(94)00064-6. ISSN 0011-9164.
↑ Werner, Carsten; König, Ulla; Augsburg, Antje; Arnhold, Christine; Körber, Heinz; Zimmermann, Ralf; Jacobasch, Hans-Jörg (1999). "Electrokinetic surface characterization of biomedical polymers — a survey". Colloids and Surfaces A: Physicochemical and Engineering Aspects (in English). 159 (2): 519–529. doi:10.1016/S0927-7757(99)00290-3. ISSN 0927-7757.
↑ Ferraris, Sara; Cazzola, Martina; Peretti, Veronica; Stella, Barbara; Spriano, Silvia (2018). "Zeta Potential Measurements on Solid Surfaces for in Vitro Biomaterials Testing: Surface Charge, Reactivity Upon Contact With Fluids and Protein Absorption". Frontiers in Bioengineering and Biotechnology. 6: 60. doi:10.3389/fbioe.2018.00060. ISSN 2296-4185. PMC 5954101. PMID 29868575.
↑ Fuerstenau, D. W. (1956). "क्वार्ट्ज़-सॉल्यूशन इंटरफ़ेस पर हेमी-मिसेल के गठन के संबंध में अमिनियम एसीटेट के समाधान में क्वार्ट्ज पर संभावित अध्ययन स्ट्रीमिंग". The Journal of Physical Chemistry. 60 (7): 981–985. doi:10.1021/j150541a039. ISSN 0022-3654.
↑ Smoluchowski M (1903). "विद्युत एंडोस्मोसिस के सिद्धांत और कई संबंधित घटनाओं में योगदान" [Contribution to the theory of electro-osmosis and related phenomena] (PDF) (in Polish). Archived from the original (PDF) on August 10, 2017.{{cite web}}: CS1 maint: unrecognized language (link)
↑ Overbeek JT (1943). "Theory of electrophoresis — The relaxation effect". Koll. Bith.: 287.
↑ Booth F (January 1948). "इलेक्ट्रोकाइनेटिक प्रभाव का सिद्धांत". Nature. 161 (4081): 83–86. Bibcode:1948Natur.161...83B. doi:10.1038/161083a0. PMID 18898334.
↑ Semenikhin NM, Dukhin SS (January 1975). "गोलाकार-कणों के आसपास एक मामूली पतली डबल-लेयर का ध्रुवीकरण और वैद्युतकणसंचलन पर इसका प्रभाव।". Colloid Journal of the USSR. 37 (6): 1013–1016.
↑ O'Brien RW, Hunter RJ (July 1981). "बड़े कोलाइडल कणों की इलेक्ट्रोफोरेटिक गतिशीलता". Canadian Journal of Chemistry. 59 (13): 1878–1887. doi:10.1139/v81-280.
↑ O'Brien RW, White LR (1978). "एक गोलाकार कोलाइडल कण की इलेक्ट्रोफोरेटिक गतिशीलता". Journal of the Chemical Society, Faraday Transactions 2. 74: 1607. doi:10.1039/F29787401607.

[1] IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "electrokinetic potential, ζ". doi:10.1351/goldbook.E01968

[2] "Colloidal systems – Methods for Zeta potential determination". ISO International Standard 13099, Parts 1,2 and 3. International Organization for Standardization (ISO). 2012.

[Lyklema1995-3] 3.0 ^3.1 Lyklema J (1995). इंटरफेस और कोलाइड साइंस के फंडामेंटल. Vol. 2. pp. 3–208. ISBN 978-0-12-460529-9.

[russel1992-4] 4.0 ^4.1 Russel WB (1991). कोलाइडल फैलाव. Cambridge: Cambridge University Press. ISBN 978-0-521-42600-8.^{[page needed]}

[Dukhin-5] 5.0 ^5.1 ^5.2 ^5.3 ^5.4 Dukhin AS (2017). अल्ट्रासाउंड का उपयोग करते हुए तरल पदार्थ, फैलाव, पायस और झरझरा सामग्री का लक्षण वर्णन (Third ed.). Amsterdam: Elsevier. ISBN 978-0-444-63908-0.^{[page needed]}

[Kirby-6] Kirby BJ (2010). Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices. Cambridge University Press. ISBN 978-0-521-11903-0.^{[page needed]}

[7] Hanaor D, Michelazzi M, Leonelli C, Sorrell CC (2012). "The effects of carboxylic acids on the aqueous dispersion and electrophoretic deposition of ZrO₂". Journal of the European Ceramic Society. 32 (1): 235–244. arXiv:1303.2754. doi:10.1016/j.jeurceramsoc.2011.08.015. S2CID 98812224.

[:0-8] 8.0 ^8.1 Barbosa JA, Abdelsadig MS, Conway BR, Merchant HA (December 2019). "Using zeta potential to study the ionisation behaviour of polymers employed in modified-release dosage forms and estimating their pK_a". International Journal of Pharmaceutics. 1: 100024. doi:10.1016/j.ijpx.2019.100024. PMC 6733289. PMID 31517289.

[9] Kumar A, Dixit CK (2017). "Methods for characterization of nanoparticles". Advances in Nanomedicine for the Delivery of Therapeutic Nucleic Acids. pp. 43–58. doi:10.1016/B978-0-08-100557-6.00003-1. ISBN 978-0-08-100557-6.

[10] "जीटा क्षमता लेजर डॉपलर वैद्युतकणसंचलन का उपयोग". Malvern.com. Archived from the original on 7 April 2012.

[Hunter-11] 11.0 ^11.1 Hunter RJ (1989). कोलाइड विज्ञान की नींव. Oxford University Press. ISBN 978-0-19-855189-8.^{[page needed]}

[Delgado_2005-12] 12.0 ^12.1 Delgado AV, González-Caballero F, Hunter RJ, Koopal LK, Lyklema J (1 January 2005). "इलेक्ट्रोकाइनेटिक घटना का मापन और व्याख्या (आईयूपीएसी तकनीकी रिपोर्ट)". Pure and Applied Chemistry. 77 (10): 1753–1805. doi:10.1351/pac200577101753. hdl:10481/29099. S2CID 16513957.

[13] जीटा संभावित मापन - इज़ोन साइंस>{{cite web |url=http://izon.com/nanoparticlemeasurement/zeta-potential/ |website=Izon Science | title= टीआरपीएस के साथ जीटा संभावित मापन}

[14] Vogel R, Pal AK, Jambhrunkar S, Patel P, Thakur SS, Reátegui E, et al. (December 2017). "ट्यून करने योग्य प्रतिरोधक पल्स सेंसिंग का उपयोग करके जैविक नैनोकणों का उच्च-रिज़ॉल्यूशन सिंगल पार्टिकल जीटा संभावित लक्षण वर्णन". Scientific Reports. 7 (1): 17479. Bibcode:2017NatSR...717479V. doi:10.1038/s41598-017-14981-x. PMC 5727177. PMID 29234015.

[15] Jouniaux, L.; Ishido, T. (2012). "Electrokinetics in Earth Sciences: A Tutorial". International Journal of Geophysics (in English). 2012: e286107. doi:10.1155/2012/286107. ISSN 1687-885X.

[16] Luxbacher, Thomas (2014). The ZETA Guide: Principles of the streaming potential technique. Anton Paar GmbH. ISBN 978-3-200-03553-9.

[17] Elimelech, Menachem; Chen, William H.; Waypa, John J. (1994). "स्ट्रीमिंग पोटेंशियल एनालाइजर द्वारा रिवर्स ऑस्मोसिस मेम्ब्रेन की जेटा (इलेक्ट्रोकाइनेटिक) क्षमता को मापना". Desalination (in English). 95 (3): 269–286. doi:10.1016/0011-9164(94)00064-6. ISSN 0011-9164.

[18] Werner, Carsten; König, Ulla; Augsburg, Antje; Arnhold, Christine; Körber, Heinz; Zimmermann, Ralf; Jacobasch, Hans-Jörg (1999). "Electrokinetic surface characterization of biomedical polymers — a survey". Colloids and Surfaces A: Physicochemical and Engineering Aspects (in English). 159 (2): 519–529. doi:10.1016/S0927-7757(99)00290-3. ISSN 0927-7757.

[19] Ferraris, Sara; Cazzola, Martina; Peretti, Veronica; Stella, Barbara; Spriano, Silvia (2018). "Zeta Potential Measurements on Solid Surfaces for in Vitro Biomaterials Testing: Surface Charge, Reactivity Upon Contact With Fluids and Protein Absorption". Frontiers in Bioengineering and Biotechnology. 6: 60. doi:10.3389/fbioe.2018.00060. ISSN 2296-4185. PMC 5954101. PMID 29868575.

[20] Fuerstenau, D. W. (1956). "क्वार्ट्ज़-सॉल्यूशन इंटरफ़ेस पर हेमी-मिसेल के गठन के संबंध में अमिनियम एसीटेट के समाधान में क्वार्ट्ज पर संभावित अध्ययन स्ट्रीमिंग". The Journal of Physical Chemistry. 60 (7): 981–985. doi:10.1021/j150541a039. ISSN 0022-3654.

[21] Smoluchowski M (1903). "विद्युत एंडोस्मोसिस के सिद्धांत और कई संबंधित घटनाओं में योगदान" [Contribution to the theory of electro-osmosis and related phenomena] (PDF) (in Polish). Archived from the original (PDF) on August 10, 2017.{{cite web}}: CS1 maint: unrecognized language (link)

[22] Overbeek JT (1943). "Theory of electrophoresis — The relaxation effect". Koll. Bith.: 287.

[23] Booth F (January 1948). "इलेक्ट्रोकाइनेटिक प्रभाव का सिद्धांत". Nature. 161 (4081): 83–86. Bibcode:1948Natur.161...83B. doi:10.1038/161083a0. PMID 18898334.

[24] Semenikhin NM, Dukhin SS (January 1975). "गोलाकार-कणों के आसपास एक मामूली पतली डबल-लेयर का ध्रुवीकरण और वैद्युतकणसंचलन पर इसका प्रभाव।". Colloid Journal of the USSR. 37 (6): 1013–1016.

[25] O'Brien RW, Hunter RJ (July 1981). "बड़े कोलाइडल कणों की इलेक्ट्रोफोरेटिक गतिशीलता". Canadian Journal of Chemistry. 59 (13): 1878–1887. doi:10.1139/v81-280.

[26] O'Brien RW, White LR (1978). "एक गोलाकार कोलाइडल कण की इलेक्ट्रोफोरेटिक गतिशीलता". Journal of the Chemical Society, Faraday Transactions 2. 74: 1607. doi:10.1039/F29787401607.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

Anonymous

Search

ज़ीटा पोटेंशियल: Difference between revisions

Namespaces

More

Page actions

Revision as of 20:41, 1 July 2023

Contents