भूतल चालकता: Difference between revisions
(Created page with "thumb|300pxभूतल चालकता चार्ज किए गए इंटरफेस के आसपास एक अतिर...") |
No edit summary |
||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
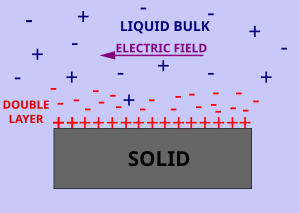
[[File:Surface Conductivity.svg|thumb|300px]]भूतल चालकता | [[File:Surface Conductivity.svg|thumb|300px]]'''भूतल चालकता''' आवेशित किए गए अंतरापृष्ठ के निकट अतिरिक्त विद्युत प्रतिरोधकता और [[इलेक्ट्रोलाइट|विद्युत् अपघट्य]] की चालकता है।<ref name="ISO">[https://www.iso.org/standard/52807.html ISO International Standard 13099, Parts 1,2 and 3, “Colloidal systems – Methods for Zeta potential determination", (2012)]</ref> इस प्रकार से तरल पदार्थ की सतह और [[चालकता (इलेक्ट्रोलाइटिक)|चालकता (विद्युत् अपघटनी)]] [[विद्युत क्षेत्र]] में [[आयनों]] की विद्युत चालित गति के अनुरूप होती है। अतः सतह आवेश के विपरीत ध्रुवता के प्रति आयनों की परत अंतरापृष्ठ के निकट स्थित होती है। यह पृष्ठीय आवेशों द्वारा प्रतिआयनों के आकर्षण के कारण बनता है। इस प्रकार से उच्च आयनिक सांद्रता की [[डबल परत (इंटरफेसियल)|देहरी परत (अंतरापृष्ठीय)]] दोहरी परत (अंतरापृष्ठीय) का भाग है। इस परत में आयनों की सांद्रता तरल बल्क की आयनिक शक्ति की तुलना में अधिक होती है। अतः इससे इस परत की उच्च विद्युत चालकता होती है। | ||
[[मैरियन स्मोलुचोव्स्की]] | इस प्रकार से [[मैरियन स्मोलुचोव्स्की]] 20वीं शताब्दी के प्रारंभ में सतह चालकता के महत्व को पहचानने वाले प्रथम व्यक्ति थे।<ref>M. von Smoluchowski, Physik, Z., 6, 529 (1905)</ref> | ||
इस प्रकार से लिकलेमा द्वारा "अंतरापृष्ठ और कोलाइड विज्ञान के मूल सिद्धांत" में सतह चालकता का विस्तृत विवरण दिया गया है।<ref>Lyklema, J. "Fundamentals of Interface and Colloid Science", vol. 2, Academic Press, 1995</ref> | |||
स्टर्न परत का योगदान कम वर्णित है। इसे | इस प्रकार से ठीक रूप से स्थापित गौई-चैपमैन-स्टर्न मॉडल के अनुसार दोहरी परत (सतह विज्ञान) (डीएल) के दो क्षेत्र हैं।<ref name="ISO" /> अतः ऊपरी स्तर, जो बल्क तरल के संपर्क में है, विसरित परत है। आंतरिक परत जो अंतरापृष्ठ के संपर्क में है वह [[कड़ी परत|स्टर्न परत]] है। | ||
डीएल के विसरित भाग की सतह चालकता का सिद्धांत बाइकमैन द्वारा विकसित किया गया था।<ref>Bikerman, J.J. Z.Physik.Chem. A163, 378, 1933</ref> उन्होंने | |||
इस प्रकार से यह संभव है कि डीएल के दोनों भागों में आयनों की पार्श्व गति सतह चालकता में योगदान करती है। | |||
अतः स्टर्न परत का योगदान कम वर्णित है। इसे प्रायः अतिरिक्त सतह चालकता कहा जाता है।<ref>Dukhin, S.S. and Derjaguin, B.V. "Electrokinetic Phenomena", John Wiley and Sons, New York (1974)</ref> | |||
इस प्रकार से डीएल के विसरित भाग की सतह चालकता का सिद्धांत बाइकमैन द्वारा विकसित किया गया था।<ref>Bikerman, J.J. Z.Physik.Chem. A163, 378, 1933</ref> अतः उन्होंने साधारण समीकरण निकाला जो पूर्ण रूप से सतह चालकता κ<sup>σ</sup> को अंतरापृष्ठ पर आयनों के व्यवहार के साथ जोड़ता है। इस प्रकार से सममित विद्युत् अपघट्य के लिए और समान आयन प्रसार गुणांक D+=D−=D मानने के लिए यह संदर्भ में दिया गया है:<ref name="ISO" /> | |||
:<math> {\kappa}^{\sigma} = \frac{4F^2Cz^2D(1+3m/z^2)}{RT\kappa}\left(\cosh\frac{zF\zeta}{2RT}-1\right)</math> | :<math> {\kappa}^{\sigma} = \frac{4F^2Cz^2D(1+3m/z^2)}{RT\kappa}\left(\cosh\frac{zF\zeta}{2RT}-1\right)</math> | ||
जहां | |||
: | : F [[फैराडे स्थिरांक]] है | ||
: | : T पूर्ण तापमान है | ||
: | : R [[गैस स्थिरांक]] है | ||
:C | :C बल्क द्रव में [[आयन|आयनिक]] सांद्रता है | ||
: z आयन [[वैलेंस (रसायन विज्ञान)]] है | : z आयन [[वैलेंस (रसायन विज्ञान)|संयोजकता(रसायन विज्ञान)]] है | ||
: ζ [[इलेक्ट्रोकाइनेटिक क्षमता]] है | : ζ [[इलेक्ट्रोकाइनेटिक क्षमता|विद्युत् गतिक विभव]] है | ||
पैरामीटर | इस प्रकार से पैरामीटर ''m'' डीएल के भीतर आयनों की गति के लिए [[विद्युत असमस]] के योगदान को दर्शाता है: | ||
:<math> m = \frac{2\varepsilon_0\varepsilon_m R^2T^2}{3\eta F^2 D}</math> | :<math> m = \frac{2\varepsilon_0\varepsilon_m R^2T^2}{3\eta F^2 D}</math> | ||
दुखिन संख्या | अतः दुखिन संख्या आयाम रहित पैरामीटर है जो विभिन्न प्रकार के विद्युत् गतिक विभव घटनाओं, जैसे [[वैद्युतकणसंचलन]] और वैद्युत् ध्वनिक घटनाओं के लिए सतह चालकता के योगदान की विशेषता है।<ref name="dukhin2002">Dukhin, A. S. and Goetz, P. J. ''Characterization of liquids, nano- and micro- particulates and porous bodies using Ultrasound'', Elsevier, 2017 | ||
{{ISBN|978-0-444-63908-0}}</ref> यह पैरामीटर और, फलस्वरूप, सतह चालकता की गणना उपयुक्त सिद्धांत का उपयोग करके | {{ISBN|978-0-444-63908-0}}</ref> इस प्रकार से यह पैरामीटर और, फलस्वरूप, सतह चालकता की गणना उपयुक्त सिद्धांत का उपयोग करके विद्युतकणसंचलन गतिशीलता से की जा सकती है। अतः [[माल्वर्न इंस्ट्रूमेंट्स|माल्वर्न]] द्वारा विद्युतकणसंचलन उपकरण और [[फैलाव प्रौद्योगिकी|प्रकीर्णन तकनीक]] द्वारा वैद्युत् ध्वनिक उपकरण में ऐसी गणना करने के लिए सॉफ्टवेयर होते हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
*[[इंटरफ़ेस और कोलाइड साइंस]] | *[[इंटरफ़ेस और कोलाइड साइंस|अंतरापृष्ठ और कोलाइड विज्ञान]] | ||
== भूतल विज्ञान == | == भूतल विज्ञान == | ||
सतह चालकता सतह जांच द्वारा मापी गई ठोस सतह पर विद्युत चालन को संदर्भित कर सकती है। इस भौतिक | इस प्रकार से सतह चालकता सतह जांच द्वारा मापी गई ठोस सतह पर विद्युत चालन को संदर्भित कर सकती है। अतः इस भौतिक गुण का परीक्षण करने के लिए पी-प्रकार([[बाहरी अर्धचालक|बाह्य अर्धचालक]]) की एन-प्रकार की सतह चालकता के जैसे प्रयोग किए जा सकते हैं।<ref><nowiki>ब्राउन पीपी। 518-527>{{cite journal | last=Brown | first=W. L. | title=एन-टाइप सरफेस कंडक्टिविटी ऑनपी-टाइप जर्मेनियम| journal=Physical Review | publisher=American Physical Society (APS) | volume=91 | issue=3 | date=1 July 1953 | issn=0031-899X | doi=10.1103/physrev.91.518 | pages=518–527| bibcode=1953PhRv...91..518B }</nowiki></ref> इस प्रकार से अतिरिक्त इसके कि यह सतह चालकता को युग्मित घटनाओं में माप सकता है जैसे [[फोटोकंडक्टिविटी|प्रकाशिक चालकता]], उदाहरण के लिए, धातु ऑक्साइड अर्ध चालक [[ ज़िंक ऑक्साइड |ज़िंक ऑक्साइड]] आदि के लिए होते है।<ref name= Shapira Cox Lichtman 1976 pp. 43–59 >{{cite journal | last1=Shapira | first1=Y. | last2=Cox | first2=S.M. | last3=Lichtman | first3=David | title=ZnO सतहों पर रसोवशोषण, प्रकाशविशोषण और चालकता मापन| journal=Surface Science | publisher=Elsevier BV | volume=54 | issue=1 | year=1976 | issn=0039-6028 | doi=10.1016/0039-6028(76)90086-8 | pages=43–59| bibcode=1976SurSc..54...43S }</ref> इस प्रकार से विद्युत् अपघट्य विलयन की स्थिति के समान कारणों से सतह चालकता बल्क चालकता से भिन्न होती है, जहां छिद्रों (+1) और इलेक्ट्रॉनों (-1) के आवेश वाहक विलयन में आयनों की भूमिका निभाते हैं। | ||
==संदर्भ== | ==संदर्भ== | ||
{{reflist}} | {{reflist}} | ||
{{DEFAULTSORT:Surface Conductivity}} | {{DEFAULTSORT:Surface Conductivity}} | ||
[[Category: Machine Translated Page]] | [[Category:Created On 24/05/2023|Surface Conductivity]] | ||
[[Category: | [[Category:Machine Translated Page|Surface Conductivity]] | ||
[[Category:Pages with reference errors]] | |||
[[Category:Pages with script errors|Surface Conductivity]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:कोमल पदार्थ|Surface Conductivity]] | |||
[[Category:कोलाइडल रसायन|Surface Conductivity]] | |||
[[Category:भूतल विज्ञान|Surface Conductivity]] | |||
[[Category:मामला|Surface Conductivity]] | |||
[[Category:रासायनिक मिश्रण|Surface Conductivity]] | |||
Latest revision as of 11:53, 2 July 2023
भूतल चालकता आवेशित किए गए अंतरापृष्ठ के निकट अतिरिक्त विद्युत प्रतिरोधकता और विद्युत् अपघट्य की चालकता है।[1] इस प्रकार से तरल पदार्थ की सतह और चालकता (विद्युत् अपघटनी) विद्युत क्षेत्र में आयनों की विद्युत चालित गति के अनुरूप होती है। अतः सतह आवेश के विपरीत ध्रुवता के प्रति आयनों की परत अंतरापृष्ठ के निकट स्थित होती है। यह पृष्ठीय आवेशों द्वारा प्रतिआयनों के आकर्षण के कारण बनता है। इस प्रकार से उच्च आयनिक सांद्रता की देहरी परत (अंतरापृष्ठीय) दोहरी परत (अंतरापृष्ठीय) का भाग है। इस परत में आयनों की सांद्रता तरल बल्क की आयनिक शक्ति की तुलना में अधिक होती है। अतः इससे इस परत की उच्च विद्युत चालकता होती है।
इस प्रकार से मैरियन स्मोलुचोव्स्की 20वीं शताब्दी के प्रारंभ में सतह चालकता के महत्व को पहचानने वाले प्रथम व्यक्ति थे।[2]
इस प्रकार से लिकलेमा द्वारा "अंतरापृष्ठ और कोलाइड विज्ञान के मूल सिद्धांत" में सतह चालकता का विस्तृत विवरण दिया गया है।[3]
इस प्रकार से ठीक रूप से स्थापित गौई-चैपमैन-स्टर्न मॉडल के अनुसार दोहरी परत (सतह विज्ञान) (डीएल) के दो क्षेत्र हैं।[1] अतः ऊपरी स्तर, जो बल्क तरल के संपर्क में है, विसरित परत है। आंतरिक परत जो अंतरापृष्ठ के संपर्क में है वह स्टर्न परत है।
इस प्रकार से यह संभव है कि डीएल के दोनों भागों में आयनों की पार्श्व गति सतह चालकता में योगदान करती है।
अतः स्टर्न परत का योगदान कम वर्णित है। इसे प्रायः अतिरिक्त सतह चालकता कहा जाता है।[4]
इस प्रकार से डीएल के विसरित भाग की सतह चालकता का सिद्धांत बाइकमैन द्वारा विकसित किया गया था।[5] अतः उन्होंने साधारण समीकरण निकाला जो पूर्ण रूप से सतह चालकता κσ को अंतरापृष्ठ पर आयनों के व्यवहार के साथ जोड़ता है। इस प्रकार से सममित विद्युत् अपघट्य के लिए और समान आयन प्रसार गुणांक D+=D−=D मानने के लिए यह संदर्भ में दिया गया है:[1]
जहां
- F फैराडे स्थिरांक है
- T पूर्ण तापमान है
- R गैस स्थिरांक है
- C बल्क द्रव में आयनिक सांद्रता है
- z आयन संयोजकता(रसायन विज्ञान) है
- ζ विद्युत् गतिक विभव है
इस प्रकार से पैरामीटर m डीएल के भीतर आयनों की गति के लिए विद्युत असमस के योगदान को दर्शाता है:
अतः दुखिन संख्या आयाम रहित पैरामीटर है जो विभिन्न प्रकार के विद्युत् गतिक विभव घटनाओं, जैसे वैद्युतकणसंचलन और वैद्युत् ध्वनिक घटनाओं के लिए सतह चालकता के योगदान की विशेषता है।[6] इस प्रकार से यह पैरामीटर और, फलस्वरूप, सतह चालकता की गणना उपयुक्त सिद्धांत का उपयोग करके विद्युतकणसंचलन गतिशीलता से की जा सकती है। अतः माल्वर्न द्वारा विद्युतकणसंचलन उपकरण और प्रकीर्णन तकनीक द्वारा वैद्युत् ध्वनिक उपकरण में ऐसी गणना करने के लिए सॉफ्टवेयर होते हैं।
यह भी देखें
भूतल विज्ञान
इस प्रकार से सतह चालकता सतह जांच द्वारा मापी गई ठोस सतह पर विद्युत चालन को संदर्भित कर सकती है। अतः इस भौतिक गुण का परीक्षण करने के लिए पी-प्रकार(बाह्य अर्धचालक) की एन-प्रकार की सतह चालकता के जैसे प्रयोग किए जा सकते हैं।[7] इस प्रकार से अतिरिक्त इसके कि यह सतह चालकता को युग्मित घटनाओं में माप सकता है जैसे प्रकाशिक चालकता, उदाहरण के लिए, धातु ऑक्साइड अर्ध चालक ज़िंक ऑक्साइड आदि के लिए होते है।Cite error: Invalid <ref> tag; invalid names, e.g. too many इस प्रकार से विद्युत् अपघट्य विलयन की स्थिति के समान कारणों से सतह चालकता बल्क चालकता से भिन्न होती है, जहां छिद्रों (+1) और इलेक्ट्रॉनों (-1) के आवेश वाहक विलयन में आयनों की भूमिका निभाते हैं।
संदर्भ
- ↑ 1.0 1.1 1.2 ISO International Standard 13099, Parts 1,2 and 3, “Colloidal systems – Methods for Zeta potential determination", (2012)
- ↑ M. von Smoluchowski, Physik, Z., 6, 529 (1905)
- ↑ Lyklema, J. "Fundamentals of Interface and Colloid Science", vol. 2, Academic Press, 1995
- ↑ Dukhin, S.S. and Derjaguin, B.V. "Electrokinetic Phenomena", John Wiley and Sons, New York (1974)
- ↑ Bikerman, J.J. Z.Physik.Chem. A163, 378, 1933
- ↑ Dukhin, A. S. and Goetz, P. J. Characterization of liquids, nano- and micro- particulates and porous bodies using Ultrasound, Elsevier, 2017 ISBN 978-0-444-63908-0
- ↑ ब्राउन पीपी। 518-527>{{cite journal | last=Brown | first=W. L. | title=एन-टाइप सरफेस कंडक्टिविटी ऑनपी-टाइप जर्मेनियम| journal=Physical Review | publisher=American Physical Society (APS) | volume=91 | issue=3 | date=1 July 1953 | issn=0031-899X | doi=10.1103/physrev.91.518 | pages=518–527| bibcode=1953PhRv...91..518B }