तरंगदैर्घ्य: Difference between revisions
No edit summary |
No edit summary |
||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 2: | Line 2: | ||
{{Other uses}} | {{Other uses}} | ||
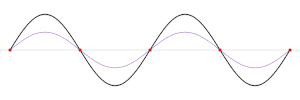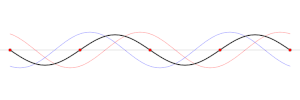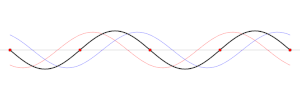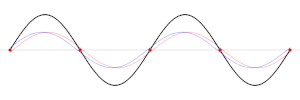
[[File:Sine wavelength.svg|thumb|right|साइन तरंग की तरंग दैर्ध्य, λ, को एक ही चरण के साथ किन्हीं दो बिंदुओं के बीच मापा जा सकता है, जैसे कि शीर्ष (शीर्ष पर), या गर्त (नीचे पर), या दिखाए गए शून्य रेखन के बीच।]] | [[File:Sine wavelength.svg|thumb|right|साइन तरंग की तरंग दैर्ध्य, λ, को एक ही चरण के साथ किन्हीं दो बिंदुओं के बीच मापा जा सकता है, जैसे कि शीर्ष (शीर्ष पर), या गर्त (नीचे पर), या दिखाए गए शून्य रेखन के बीच।]] | ||
भौतिकी में, | भौतिकी में, तरंगदैर्घ्य एक नियत काल में तरंग की आकाशीय अवधि है। वह दूरी जिस पर तरंग की आकृति दोहराई जाती है।<ref name=hecht> | ||
{{cite book | {{cite book | ||
|first=Eugene | |first=Eugene | ||
| Line 23: | Line 23: | ||
|edition=2nd | |edition=2nd | ||
|publisher = Cambridge University Press | |publisher = Cambridge University Press | ||
}}</ref>यह तरंग पर समान | }}</ref>यह तरंग पर समान स्थिति के लगातार संगत बिंदुओं के बीच की दूरी है, जैसे कि दो निकटवर्ती शीर्ष, गर्त, या शून्य रेखन, और यह प्रगामी तरंगों और अप्रगामी तरंगेों के साथ-साथ अन्य आवर्ती तरंग की विशेषता है। .<ref name=Seaway> | ||
{{cite book | {{cite book | ||
|title=Principles of physics | |title=Principles of physics | ||
| Line 40: | Line 40: | ||
| page=17 | | page=17 | ||
}}</ref> तरंग दैर्ध्य के गुणनात्मक व्युत्क्रम को [[ स्थानिक आवृत्ति |आवर्ती]] कहा जाता है। तरंग दैर्ध्य आमतौर पर [[ ग्रीक अक्षर ]] [[ लैम्ब्डा ]] (λ) द्वारा निर्दिष्ट किया जाता है। | }}</ref> तरंग दैर्ध्य के गुणनात्मक व्युत्क्रम को [[ स्थानिक आवृत्ति |आवर्ती]] कहा जाता है। तरंग दैर्ध्य आमतौर पर [[ ग्रीक अक्षर ]] [[ लैम्ब्डा ]] (λ) द्वारा निर्दिष्ट किया जाता है। | ||
तरंगदैर्घ्य शब्द को कभी-कभी [[ मॉडुलन ]] तरंगों पर और कई ज्यावक्रीय तरंग के [[ हस्तक्षेप (लहर प्रसार) | हस्तक्षेप (तरंग प्रसार)]] द्वारा गठित माडुलित | तरंगदैर्घ्य शब्द को कभी-कभी [[ मॉडुलन ]] तरंगों पर और कई ज्यावक्रीय तरंग के [[ हस्तक्षेप (लहर प्रसार) | हस्तक्षेप (तरंग प्रसार)]] द्वारा गठित माडुलित तरंगों या तरंगों के ज्यावक्रीय आवरण पर भी लागू किया जाता है।<ref> | ||
{{cite book | {{cite book | ||
| title = Electromagnetic Theory for Microwaves and Optoelectronics | | title = Electromagnetic Theory for Microwaves and Optoelectronics | ||
| Line 61: | Line 61: | ||
| quote = wavelength lambda light sound frequency wave speed. | | quote = wavelength lambda light sound frequency wave speed. | ||
}}</ref> | }}</ref> | ||
तरंगदैर्घ्य उस माध्यम पर निर्भर करता है | तरंगदैर्घ्य उस माध्यम पर निर्भर करता है, उदाहरण के लिए, निर्वात, वायु, या पानी जिसमें एक तरंग प्रगामी करती है। तरंगों के उदाहरण है[[ ध्वनि ]] तरंगें, प्रकाश, जल तरंगें और विद्युत चालक में आवधिक विद्युत संकेत हैं। एक ध्वनि तरंग वायु ध्वनि दबाव में भिन्नता है, जबकि प्रकाश और अन्य [[ विद्युत चुम्बकीय विकिरण ]] में [[ विद्युत क्षेत्र ]]और [[ चुंबकीय क्षेत्र ]]की ताकत भिन्न होती है। [[ पानी की लहर | पानी की तरंग]] पानी की तरंगें और पानी के शरीर की ऊंचाई में भिन्नता होती हैं। एक क्रिस्टल [[ जाली कंपन |जाली कंपन]] में परमाणु की स्थिति भिन्न होती है। | ||
तरंग परिघटनाओं के लिए तरंग दैर्ध्य या आवृत्तियों की सीमा को [[ स्पेक्ट्रम | वर्णक्रम]] कहा जाता है। नाम की उत्पत्ति दृश्य प्रकाश वर्णक्रम से हुई थी, लेकिन अब इसे पूरे विद्युत चुम्बकीय वर्णक्रम के साथ-साथ [[ दृश्यमान प्रतिबिम्ब |दृश्यमान प्रतिबिम्ब]] या [[ कंपन स्पेक्ट्रम |कंपन वर्णक्रम]] पर भी लागू किया जा सकता है। | तरंग परिघटनाओं के लिए तरंग दैर्ध्य या आवृत्तियों की सीमा को [[ स्पेक्ट्रम | वर्णक्रम]] कहा जाता है। नाम की उत्पत्ति दृश्य प्रकाश वर्णक्रम से हुई थी, लेकिन अब इसे पूरे विद्युत चुम्बकीय वर्णक्रम के साथ-साथ [[ दृश्यमान प्रतिबिम्ब |दृश्यमान प्रतिबिम्ब]] या [[ कंपन स्पेक्ट्रम |कंपन वर्णक्रम]] पर भी लागू किया जा सकता है। | ||
| Line 76: | Line 76: | ||
</ref> | </ref> | ||
:<math>\lambda = \frac{v}{f}\,\,,</math> | :<math>\lambda = \frac{v}{f}\,\,,</math> | ||
कहाँ पे <math>v</math> तरंग की चरण गति [[ चरण वेग ]]का परिमाण कहलाती है और<math>f</math> तरंग की आवृत्ति है। एक[[ फैलाव माध्यम ]] में, चरण की गति स्वयं तरंग की आवृत्ति पर निर्भर करती है, | कहाँ पे <math>v</math> तरंग की चरण गति [[ चरण वेग ]]का परिमाण कहलाती है और <math>f</math> तरंग की आवृत्ति है। एक[[ फैलाव माध्यम ]] में, चरण की गति स्वयं तरंग की आवृत्ति पर निर्भर करती है, जिससे प्रकीर्णन[[ फैलाव संबंध | संबंध]] अरेखीय हो जाता है। | ||
विद्युत चुम्बकीय विकिरण के मामले में जैसे प्रकाश | विद्युत चुम्बकीय विकिरण के मामले में जैसे प्रकाश [[ मुक्त स्थान ]]में, चरण गति प्रकाश की गति है, लगभग 3×10<sup>8</sup> मी/से. इस प्रकार 100 मेगाहर्ट्ज विद्युत चुम्बकीय रेडियो तरंग की तरंग दैर्ध्य लगभग है, 3×10<sup>8</sup> मी/से. को 10<sup>8</sup>[[ हेटर्स | हेटर्स]] = 3 [[ मीटर | मीटर]] से विभाजित किया जाता है। दृश्यमान प्रकाश की तरंग दैर्ध्य गहरे [[ लाल ]], लगभग 700 [[ नैनोमीटर ]] से लेकर बैंगनी (रंग) तक होती है, लगभग 400 एनएम, अन्य उदाहरणों के लिए, विद्युत चुम्बकीय वर्णक्रम देखें। | ||
हवा में ध्वनि तरंगों के लिए, [[ ध्वनि की गति ]] 343 m/s, तापमान और दबाव के लिए मानक परिस्थितियों मे होती है। मानव कान को सुनाई देने वाली ध्वनि आवृत्तियों की तरंग दैर्ध्य | हवा में ध्वनि तरंगों के लिए, [[ ध्वनि की गति ]] 343 m/s, तापमान और दबाव के लिए मानक परिस्थितियों मे होती है। मानव कान को सुनाई देने वाली ध्वनि आवृत्तियों की तरंग दैर्ध्य, 20 हर्ट्ज़ -20 किलोहर्ट्ज़ है, इस प्रकार क्रमशः लगभग 17 मीटर और 17 [[ मिलीमीटर ]] के बीच होती है। चमगादड़ कुछ हद तक उच्च आवृत्तियों का उपयोग करते हैं ताकि वे 17 मिमी से छोटे लक्ष्यों को प्राप्त कर सकें। श्रव्य ध्वनि में तरंगदैर्घ्य दृश्य प्रकाश की तुलना में अधिक लंबा होता है। | ||
[[File:Waves in Box.svg|thumb|एक बॉक्स में ज्यावक्रीय अप्रगामी तरंगे जो अंत बिंदुओं को नोड्स होने से रोकती हैं, बॉक्स में फिट होने वाली आधी तरंग दैर्ध्य की पूर्णांक संख्या होगी।]] | [[File:Waves in Box.svg|thumb|एक बॉक्स में ज्यावक्रीय अप्रगामी तरंगे जो अंत बिंदुओं को नोड्स होने से रोकती हैं, बॉक्स में फिट होने वाली आधी तरंग दैर्ध्य की पूर्णांक संख्या होगी।]] | ||
| Line 87: | Line 87: | ||
=== अप्रगामी तरंगे === | === अप्रगामी तरंगे === | ||
एक अप्रगामी तरंगे एक अविचल गति है जो एक स्थान पर रहती है। एक ज्यावक्रीय अप्रगामी तरंगे | एक अप्रगामी तरंगे एक अविचल गति है जो एक स्थान पर रहती है। एक ज्यावक्रीय अप्रगामी तरंगे बिना गति के स्थिर बिंदु में शामिल होती हैं, जिन्हें [[ नोड (भौतिकी) |( नोड भौतिकी )]] कहा जाता है, और तरंग दैर्ध्य नोड्स के बीच की दूरी से दोगुना होती हैं। | ||
ऊपरी आकृति एक बॉक्स में तीन अप्रगामी | ऊपरी आकृति एक बॉक्स में तीन अप्रगामी तरंगों को दिखाती है। यह माना जाता है कि बॉक्स की दीवारों पर नोड्स रखने के लिए तरंग की आवश्यकता होती है, सीमा स्थितियों का एक उदाहरण, यह निर्धारित करने के लिए कि कौन सी तरंग दैर्ध्य की अनुमति है। उदाहरण के लिए, एक विद्युत चुम्बकीय तरंग के लिए, यदि बॉक्स में आदर्श धातु की दीवारें हैं, तो दीवारों पर नोड्स की स्थिति का परिणाम होता है, क्योंकि धातु की दीवारें एक स्पर्शरेखा विद्युत क्षेत्र का समर्थन नहीं कर सकती हैं, जिससे तरंग को दीवार पर शून्य आयाम के लिए मजबूर किया जाता है। | ||
स्थिर तरंग को विपरीत दिशा में गति करने वाली दो ज्यावक्रीय तरंगों के योग के रूप में देखा जा सकता है।<ref> | स्थिर तरंग को विपरीत दिशा में गति करने वाली दो ज्यावक्रीय तरंगों के योग के रूप में देखा जा सकता है।<ref> | ||
| Line 140: | Line 140: | ||
जब विद्युत चुम्बकीय विकिरण की तरंग दैर्ध्य को उद्धृत किया जाता है, तो निर्वात में तरंग दैर्ध्य आमतौर पर तब तक नियत होता है जब तक कि तरंग दैर्ध्य को विशेष रूप से किसी अन्य माध्यम में तरंग दैर्ध्य के रूप में पहचाना नहीं जाता है। ध्वनि में जहां तरंगों के अस्तित्व के लिए एक माध्यम आवश्यक है,और एक निर्दिष्ट माध्यम के लिए तरंग दैर्ध्य के मान का आंकलन कर लिया जाता है। | जब विद्युत चुम्बकीय विकिरण की तरंग दैर्ध्य को उद्धृत किया जाता है, तो निर्वात में तरंग दैर्ध्य आमतौर पर तब तक नियत होता है जब तक कि तरंग दैर्ध्य को विशेष रूप से किसी अन्य माध्यम में तरंग दैर्ध्य के रूप में पहचाना नहीं जाता है। ध्वनि में जहां तरंगों के अस्तित्व के लिए एक माध्यम आवश्यक है,और एक निर्दिष्ट माध्यम के लिए तरंग दैर्ध्य के मान का आंकलन कर लिया जाता है। | ||
तरंग दैर्ध्य के साथ प्रकाश की गति में भिन्नता को | तरंग दैर्ध्य के साथ प्रकाश की गति में भिन्नता को[[ फैलाव (प्रकाशिकी) | प्रकाशिकी]] प्रकीर्णन के रूप में जाना जाता है, और यह उस परिचित स्थिति के लिए भी जिम्मेदार है जिसमें प्रकाश एक प्रकीर्णन[[ फैलाव प्रिज्म | प्रिज्म]] द्वारा घटक के रंगों में अलग हो जाता है। और तब पृथक्करण होता है जब प्रिज्म के अंदर अपवर्तनांक तरंग दैर्ध्य के साथ बदलता रहता है, इसलिए विभिन्न तरंग दैर्ध्य प्रिज्म के अंदर अलग-अलग गति से फैलते हैं, जिससे वे विभिन्न कोणों पर अपवर्तित हो जाते हैं। एक माध्यम के भीतर प्रकाश की गति तरंग दैर्ध्य के साथ कैसे भिन्न होती है, इसका वर्णन करने वाले गणितीय संबंध को फैलाव संबंध के रूप में जाना जाता है। | ||
==== गैर-वर्दी माध्यम ==== | ==== गैर-वर्दी माध्यम ==== | ||
[[File:Local wavelength.svg|thumb|तट के निकट आने वाली समुद्र की तरंग में शिखा-से-शिखा के आधार पर विभिन्न स्थानीय तरंगदैर्ध्य<ref name=Pinet2/>]] | [[File:Local wavelength.svg|thumb|तट के निकट आने वाली समुद्र की तरंग में शिखा-से-शिखा के आधार पर विभिन्न स्थानीय तरंगदैर्ध्य<ref name=Pinet2/>]] | ||
तरंगदैर्घ्य एक उपयोगी अवधारणा हो सकती है, भले ही तरंग अंतरिक्ष में[[ आवधिक कार्य ]]न हो। उदाहरण के लिए, समुद्र की ओर आने वाली समुद्र की तरंग में, (चित्र में दिखाया गया है) आने वाली तरंग एक अलग स्थानीय तरंग दैर्ध्य के साथ | तरंगदैर्घ्य एक उपयोगी अवधारणा हो सकती है, भले ही तरंग अंतरिक्ष में[[ आवधिक कार्य ]]न हो। उदाहरण के लिए, समुद्र की ओर आने वाली समुद्र की तरंग में, (चित्र में दिखाया गया है) आने वाली तरंग एक अलग स्थानीय तरंग दैर्ध्य के साथ तरंगदार होती है जो तरंग की ऊंचाई की तुलना में समुद्र तल की गहराई पर निर्भर करती है। तरंग का विश्लेषण स्थानीय तरंग दैर्ध्य के स्थानीय पानी की गहराई की तुलना पर आधारित हो सकती है।<ref name=Pinet2> | ||
{{cite book |title=op. cit | {{cite book |title=op. cit | ||
|author = Paul R Pinet | |author = Paul R Pinet | ||
| Line 154: | Line 154: | ||
[[File:Cochlea wave animated.gif|right|thumb|एक गैर-समान माध्यम में प्रगामी करने वाली एक ज्यावक्रीय तरंग, हानि के साथ]] | [[File:Cochlea wave animated.gif|right|thumb|एक गैर-समान माध्यम में प्रगामी करने वाली एक ज्यावक्रीय तरंग, हानि के साथ]] | ||
तरंगें जो समय में ज्यावक्रीय होती हैं लेकिन एक माध्यम से फैलती हैं जिनके गुण स्थिति के साथ भिन्न होते हैं ,एक असमांगी माध्यम एक वेग से फैल सकता है जो स्थिति के साथ बदलता रहता है, और परिणामस्वरूप अंतरिक्ष में | तरंगें जो समय में ज्यावक्रीय होती हैं लेकिन एक माध्यम से फैलती हैं जिनके गुण स्थिति के साथ भिन्न होते हैं ,एक असमांगी माध्यम एक वेग से फैल सकता है जो स्थिति के साथ बदलता रहता है, और परिणामस्वरूप अंतरिक्ष में ज्यावक्रीय नहीं हो सकता है। दाईं ओर की आकृति एक उदाहरण दिखाती है। जैसे-जैसे तरंग धीमी होती जाती है, तरंगदैर्घ्य कम होती जाती है और आयाम बढ़ता जाता है, अधिकतम प्रतिघटनाक्रम के स्थान के बाद, लघु तरंग दैर्ध्य उतकृष्ट क्षति के बाद तरंग खत्म हो जाती है। | ||
ऐसी प्रणालियों के[[ अंतर समीकरण ]]का विश्लेषण अक्सर (WKB)डब्लू के बी सन्निकटन का उपयोग करते हुए लगभग किया जाता है। जिसे लिउविल-ग्रीन विधि के रूप में भी जाना जाता है, विधि स्थानीय तरंग संख्या का उपयोग करके अंतरिक्ष के माध्यम से चरण को एकीकृत करती है, जिसे समय और स्थान के कार्य के रूप में हल के स्थानीय तरंग दैर्ध्य को इंगित करने के रूप में व्याख्या किया जा सकता है।<ref> | ऐसी प्रणालियों के[[ अंतर समीकरण ]]का विश्लेषण अक्सर (WKB) डब्लू के बी सन्निकटन का उपयोग करते हुए लगभग किया जाता है। जिसे लिउविल-ग्रीन विधि के रूप में भी जाना जाता है, विधि स्थानीय तरंग संख्या का उपयोग करके अंतरिक्ष के माध्यम से चरण को एकीकृत करती है, जिसे समय और स्थान के कार्य के रूप में हल के स्थानीय तरंग दैर्ध्य को इंगित करने के रूप में व्याख्या किया जा सकता है।<ref> | ||
{{cite book | {{cite book | ||
| title = Principles of Plasma Mechanics | | title = Principles of Plasma Mechanics | ||
| Line 179: | Line 179: | ||
==== क्रिस्टल ==== | ==== क्रिस्टल ==== | ||
[[File:Wavelength indeterminacy.JPG|thumb|परमाणुओं की एक रेखा पर एक तरंग की व्याख्या विभिन्न तरंग दैर्ध्य के अनुसार की जा सकती है।]] | [[File:Wavelength indeterminacy.JPG|thumb|परमाणुओं की एक रेखा पर एक तरंग की व्याख्या विभिन्न तरंग दैर्ध्य के अनुसार की जा सकती है।]] | ||
क्रिस्टलीय ठोस में तरंगें निरंतर नहीं होती हैं, क्योंकि वे एक नियमित जाली में व्यवस्थित असतत कणों के कंपन से बनी होती हैं। यह [[ अलियासिंग ]] पैदा करता है क्योंकि एक ही कंपन को विभिन्न तरंग दैर्ध्य की एक बहुरूपता माना जा सकता है, जैसा कि चित्र में दिखाया गया है।<ref name=Putnis>See Figure 4.20 in {{cite book|author1-link=Andrew Putnis|author= A. Putnis |title=Introduction to mineral sciences |url=https://archive.org/details/introductiontomi00putn |url-access= registration |page=[https://archive.org/details/introductiontomi00putn/page/97 97] |isbn=0-521-42947-1 |year=1992 |publisher=Cambridge University Press}} and Figure 2.3 in {{cite book |title=Introduction to lattice dynamics |author=Martin T. Dove |url=https://books.google.com/books?id=vM50l2Vf7HgC&pg=PA22 |page=22 |isbn=0-521-39293-4 |edition=4th |year=1993 |publisher=Cambridge University Press}}</ref> इनमें से एक से अधिक तरंग दैर्ध्य का उपयोग करने वाले निरूपण अपेक्षाधिक हैं, घटना के अनुकूल सबसे लंबी तरंग दैर्ध्य चुनना सांकेतिक है। एक क्रिस्टलीय माध्यम में सभी संभावित तरंगों का निरूपण प्रदान करने के लिए पर्याप्त तरंग दैर्ध्य की सीमा ब्रिलौइन क्षेत्र तक सीमित तरंग वैक्टर से सुमेल खाती है।<ref name=Razeghi>{{cite book |title=Fundamentals of solid state engineering | क्रिस्टलीय ठोस में तरंगें निरंतर नहीं होती हैं, क्योंकि वे एक नियमित जाली में व्यवस्थित असतत कणों के कंपन से बनी होती हैं। यह[[ अलियासिंग ]]पैदा करता है, क्योंकि एक ही कंपन को विभिन्न तरंग दैर्ध्य की एक बहुरूपता माना जा सकता है, जैसा कि चित्र में दिखाया गया है।<ref name=Putnis>See Figure 4.20 in {{cite book|author1-link=Andrew Putnis|author= A. Putnis |title=Introduction to mineral sciences |url=https://archive.org/details/introductiontomi00putn |url-access= registration |page=[https://archive.org/details/introductiontomi00putn/page/97 97] |isbn=0-521-42947-1 |year=1992 |publisher=Cambridge University Press}} and Figure 2.3 in {{cite book |title=Introduction to lattice dynamics |author=Martin T. Dove |url=https://books.google.com/books?id=vM50l2Vf7HgC&pg=PA22 |page=22 |isbn=0-521-39293-4 |edition=4th |year=1993 |publisher=Cambridge University Press}}</ref> इनमें से एक से अधिक तरंग दैर्ध्य का उपयोग करने वाले निरूपण अपेक्षाधिक हैं, घटना के अनुकूल सबसे लंबी तरंग दैर्ध्य चुनना सांकेतिक है। एक क्रिस्टलीय माध्यम में सभी संभावित तरंगों का निरूपण प्रदान करने के लिए पर्याप्त तरंग दैर्ध्य की सीमा ब्रिलौइन क्षेत्र तक सीमित तरंग वैक्टर से सुमेल खाती है।<ref name=Razeghi>{{cite book |title=Fundamentals of solid state engineering | ||
|author=Manijeh Razeghi |pages=165 ''ff'' |url=https://books.google.com/books?id=6x07E9PSzr8C&pg=PA165 |isbn=0-387-28152-5 |year=2006 |publisher=Birkhäuser |edition=2nd}}</ref> | |author=Manijeh Razeghi |pages=165 ''ff'' |url=https://books.google.com/books?id=6x07E9PSzr8C&pg=PA165 |isbn=0-387-28152-5 |year=2006 |publisher=Birkhäuser |edition=2nd}}</ref> | ||
ठोस में तरंगदैर्घ्य में यह अनिश्चितता तरंग परिघटनाओं जैसे [[ ऊर्जा बैंड ]]और फोनन के विश्लेषण में महत्वपूर्ण है। यह गणितीय रूप से एक सिग्नल के अलियासिंग के बराबर है जो असतत अंतराल पर सिग्नल प्रोसेसिंग का नमूना है। | ठोस में तरंगदैर्घ्य में यह अनिश्चितता तरंग परिघटनाओं जैसे [[ ऊर्जा बैंड ]]और फोनन के विश्लेषण में महत्वपूर्ण है। यह गणितीय रूप से एक सिग्नल के अलियासिंग के बराबर है जो असतत अंतराल पर सिग्नल प्रोसेसिंग का नमूना है। | ||
| Line 189: | Line 189: | ||
</ref> तरंग दैर्ध्य वैकल्पिक रूप से तरंग संख्या और तरंग सदिश अंतरिक्ष में तरंग का चरित्र चित्रण वर्णित है, जो कार्यात्मक रूप से इसकी आवृत्ति से संबंधित है, जैसा कि प्रणाली के भौतिकी द्वारा सीमित है। और ज्यावक्रीय सबसे सरल तरंग का मान प्राप्त करने का एक उपाय है, और अधिक जटिल सुपरपोजिशन सिद्धांत द्वारा इसका मान प्राप्त किया जा सकता है।। | </ref> तरंग दैर्ध्य वैकल्पिक रूप से तरंग संख्या और तरंग सदिश अंतरिक्ष में तरंग का चरित्र चित्रण वर्णित है, जो कार्यात्मक रूप से इसकी आवृत्ति से संबंधित है, जैसा कि प्रणाली के भौतिकी द्वारा सीमित है। और ज्यावक्रीय सबसे सरल तरंग का मान प्राप्त करने का एक उपाय है, और अधिक जटिल सुपरपोजिशन सिद्धांत द्वारा इसका मान प्राप्त किया जा सकता है।। | ||
फैलाव मुक्त और एकसमान माध्यम के विशेष मामले में, ज्यावक्रीय के अलावा अन्य तरंगें अपरिवर्तित आकार और निरंतर वेग के साथ फैलती हैं। कुछ परिस्थितियों में, अरेखीय माध्यम में अपरिवर्तनीय आकार की तरंगें भी हो सकती हैं | फैलाव मुक्त और एकसमान माध्यम के विशेष मामले में, ज्यावक्रीय के अलावा अन्य तरंगें अपरिवर्तित आकार और निरंतर वेग के साथ फैलती हैं। कुछ परिस्थितियों में, अरेखीय माध्यम में अपरिवर्तनीय आकार की तरंगें भी हो सकती हैं, उदाहरण के लिए यह आंकड़ा उथले पानी में समुद्र की तरंग को दिखाता है जिसमें एक ज्यावक्रीय की तुलना में तेज शीर्ष और गर्त वाले कुंड होते हैं, जो कि एक शंक्वाकार तरंग की विशिष्ट होती है,<ref name=Pilipchuk> | ||
{{cite book | {{cite book | ||
|title=Nonlinear Dynamics: Between Linear and Impact Limits | |title=Nonlinear Dynamics: Between Linear and Impact Limits | ||
| Line 237: | Line 237: | ||
</ref> जैसा कि चित्र में दिखाया गया है, तरंग दैर्ध्य को तरंग पर लगातार संबंधित बिंदुओं के बीच मापा जाता है। | </ref> जैसा कि चित्र में दिखाया गया है, तरंग दैर्ध्य को तरंग पर लगातार संबंधित बिंदुओं के बीच मापा जाता है। | ||
=== | === तरंग पैकेट्स === | ||
[[File:Wave packet (dispersion).gif|thumb|एक प्रसार तरंग बंडल]] | [[File:Wave packet (dispersion).gif|thumb|एक प्रसार तरंग बंडल]] | ||
| Line 294: | Line 294: | ||
[[File:Interferometer path differences.JPG|thumb|दो झिरियों से गुजरने वाले प्रकाश के लिए पर्दे पर प्रकाश की तीव्रता का आकृति। दाईं ओर के लेबल दो स्लिट्स से पथ की लंबाई के अंतर को संदर्भित करते हैं, जिन्हें यहां बिंदु स्रोतों के रूप में प्रदर्शित किया गया है।]] | [[File:Interferometer path differences.JPG|thumb|दो झिरियों से गुजरने वाले प्रकाश के लिए पर्दे पर प्रकाश की तीव्रता का आकृति। दाईं ओर के लेबल दो स्लिट्स से पथ की लंबाई के अंतर को संदर्भित करते हैं, जिन्हें यहां बिंदु स्रोतों के रूप में प्रदर्शित किया गया है।]] | ||
जब ज्यावक्रीय तरंगें जुड़ती हैं | जब ज्यावक्रीय तरंगें जुड़ती हैं तो वे एक दूसरे को मजबूत कर सकती हैं, रचनात्मक हस्तक्षेप या एक दूसरे को रद्द कर सकती हैं। विनाशकारी हस्तक्षेप उनके सापेक्ष चरण के आधार पर। इस घटना का उपयोग [[ इंटरफेरोमेट्री ]] में किया जाता है। एक साधारण उदाहरण [[ थॉमस यंग (वैज्ञानिक) ]] के कारण एक प्रयोग है जहां प्रकाश को [[ डबल-स्लिट प्रयोग ]]के माध्यम से गुजरता है।<ref name=Sluder> | ||
{{cite book | {{cite book | ||
|title=Digital microscopy | |title=Digital microscopy | ||
| Line 348: | Line 348: | ||
स्रोत और स्क्रीन के बीच अलगाव के आधार पर दो प्रकार के विवर्तन को प्रतिष्ठित किया जाता है, बड़े अलगाव पर [[ फ्रौनहोफर विवर्तन ]] या दूर-क्षेत्र विवर्तन और निकट अलगाव पर फ़्रेज़नेल विवर्तन या निकट-क्षेत्र विवर्तन। | स्रोत और स्क्रीन के बीच अलगाव के आधार पर दो प्रकार के विवर्तन को प्रतिष्ठित किया जाता है, बड़े अलगाव पर [[ फ्रौनहोफर विवर्तन ]] या दूर-क्षेत्र विवर्तन और निकट अलगाव पर फ़्रेज़नेल विवर्तन या निकट-क्षेत्र विवर्तन। | ||
सिंगल स्लिट के विश्लेषण में, स्लिट की गैर-शून्य चौड़ाई को ध्यान में रखा जाता है, और एपर्चर में प्रत्येक बिंदु को प्रकाश की किरण (ह्यूजेंस के तरंगिका) में एक योगदान के स्रोत के रूप में लिया जाता है। स्क्रीन पर, झिरी के भीतर प्रत्येक स्थिति से आने वाले प्रकाश की पथ लंबाई भिन्न होती है, यद्यपि संभवतः बहुत छोटा अंतर होता है। नतीजतन | सिंगल स्लिट के विश्लेषण में, स्लिट की गैर-शून्य चौड़ाई को ध्यान में रखा जाता है, और एपर्चर में प्रत्येक बिंदु को प्रकाश की किरण (ह्यूजेंस के तरंगिका) में एक योगदान के स्रोत के रूप में लिया जाता है। स्क्रीन पर, झिरी के भीतर प्रत्येक स्थिति से आने वाले प्रकाश की पथ लंबाई भिन्न होती है, यद्यपि संभवतः बहुत छोटा अंतर होता है। नतीजतन हस्तक्षेप होता है। | ||
फ्रौनहोफर विवर्तन आकृति में, एक छोटे कोण के सन्निकटन के भीतर, एक एकल स्लिट से पर्याप्त रूप से दूर, तीव्रता का फैलाव S एक वर्ग सिंक फ़ंक्शन के माध्यम से स्थिति x से संबंधित है:<ref>{{cite book | फ्रौनहोफर विवर्तन आकृति में, एक छोटे कोण के सन्निकटन के भीतर, एक एकल स्लिट से पर्याप्त रूप से दूर, तीव्रता का फैलाव S एक वर्ग सिंक फ़ंक्शन के माध्यम से स्थिति x से संबंधित है:<ref>{{cite book | ||
| Line 365: | Line 365: | ||
=== विवर्तन-सीमित संकल्प === | === विवर्तन-सीमित संकल्प === | ||
{{main|Angular resolution|Diffraction-limited system}} | {{main|Angular resolution|Diffraction-limited system}} | ||
विवर्तन ऑप्टिकल उपकरणों के[[ कोणीय संकल्प ]] पर मूल सीमा है, जैसे [[ दूरबीन ]] ([[ रेडियो दूरबीन ]] सहित | विवर्तन ऑप्टिकल उपकरणों के[[ कोणीय संकल्प ]] पर मूल सीमा है, जैसे [[ दूरबीन ]] ([[ रेडियो दूरबीन | रेडियो दूरबीन )]] सहित सूक्ष्मदर्शी।<ref name=Saxby> | ||
{{cite book | {{cite book | ||
|author=Graham Saxby | |author=Graham Saxby | ||
| Line 423: | Line 423: | ||
==कोणीय तरंगदैर्घ्य== | ==कोणीय तरंगदैर्घ्य== | ||
[[File:Commutative diagram of harmonic wave properties.svg|thumb|200px|तरंग दैर्ध्य, कोणीय तरंग दैर्ध्य और अन्य तरंग गुणों के बीच संबंध।]] | [[File:Commutative diagram of harmonic wave properties.svg|thumb|200px|तरंग दैर्ध्य, कोणीय तरंग दैर्ध्य और अन्य तरंग गुणों के बीच संबंध।]] | ||
तरंग दैर्ध्य से संबंधित एक मात्रा कोणीय तरंग दैर्ध्य है जिसे समानीत तरंग दैर्ध्य भी कहा जाता है, जिसे आमतौर पर ''ƛ'' (लैम्ब्डा-बार) द्वारा दर्शाया जाता है। यह 2π (''ƛ'' = ''λ''/2π) के कारक द्वारा कम की गई नियमित तरंग दैर्ध्य के बराबर है। यह आमतौर पर क्वांटम यांत्रिकी में पाया जाता है, जहां इसका उपयोग [[ कम प्लैंक स्थिरांक ]] (प्रतीक ''ħ'', एच-बार) और कोणीय आवृत्ति (प्रतीक ''ω'') या [[ कोणीय तरंग संख्या ]] | तरंग दैर्ध्य से संबंधित एक मात्रा कोणीय तरंग दैर्ध्य है जिसे समानीत तरंग दैर्ध्य भी कहा जाता है, जिसे आमतौर पर ''ƛ'' (लैम्ब्डा-बार) द्वारा दर्शाया जाता है। यह 2π (''ƛ'' = ''λ''/2π) के कारक द्वारा कम की गई नियमित तरंग दैर्ध्य के बराबर है। यह आमतौर पर क्वांटम यांत्रिकी में पाया जाता है, जहां इसका उपयोग [[ कम प्लैंक स्थिरांक ]] (प्रतीक ''ħ'', एच-बार) और कोणीय आवृत्ति (प्रतीक ''ω'') या [[ कोणीय तरंग संख्या ]] प्रतीक ''k'' ''के संयोजन में किया जाता है।'' | ||
==यह भी देखें== | ==यह भी देखें== | ||
* [[ उत्सर्जन चित्र ]] | * [[ उत्सर्जन चित्र ]] | ||
* | * लिफ़ाफ़ा (तरंगे) | ||
* फ्रौनहोफर रेखाएं - सौर | * फ्रौनहोफर रेखाएं - सौर स्पेक्ट्रम में काली रेखाएँ, को पारंपरिक रूप से मानक ऑप्टिकल तरंग दैर्ध्य संदर्भ के रूप में उपयोग किया जाता है | ||
* [[ तरंग लेखों का सूचकांक ]] | * [[ तरंग लेखों का सूचकांक ]] | ||
*[[ लंबाई माप ]] | *[[ लंबाई माप ]] | ||
| Line 1,466: | Line 1,466: | ||
{{Authority control}} | {{Authority control}} | ||
[[Category:Machine Translated Page]] | |||
[[Category:AC with 0 elements]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Articles with short description]] | |||
[[Category:CS1 maint]] | |||
[[Category:Collapse templates]] | |||
[[Category:Exclude in print]] | |||
[[Category:Interwiki category linking templates]] | |||
[[Category:Interwiki link templates]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikimedia Commons templates]] | |||
[[Category:Wikipedia metatemplates]] | |||
Latest revision as of 14:49, 28 October 2022
भौतिकी में, तरंगदैर्घ्य एक नियत काल में तरंग की आकाशीय अवधि है। वह दूरी जिस पर तरंग की आकृति दोहराई जाती है।[1][2]यह तरंग पर समान स्थिति के लगातार संगत बिंदुओं के बीच की दूरी है, जैसे कि दो निकटवर्ती शीर्ष, गर्त, या शून्य रेखन, और यह प्रगामी तरंगों और अप्रगामी तरंगेों के साथ-साथ अन्य आवर्ती तरंग की विशेषता है। .[3][4] तरंग दैर्ध्य के गुणनात्मक व्युत्क्रम को आवर्ती कहा जाता है। तरंग दैर्ध्य आमतौर पर ग्रीक अक्षर लैम्ब्डा (λ) द्वारा निर्दिष्ट किया जाता है। तरंगदैर्घ्य शब्द को कभी-कभी मॉडुलन तरंगों पर और कई ज्यावक्रीय तरंग के हस्तक्षेप (तरंग प्रसार) द्वारा गठित माडुलित तरंगों या तरंगों के ज्यावक्रीय आवरण पर भी लागू किया जाता है।[5] एक ज्यावक्रीय तरंग को एक निश्चित तरंग गति से चलते हुए मानते हुए, तरंग दैर्ध्य तरंग की आवृत्ति के व्युत्क्रमानुपाती होता है, उच्च आवृत्तियों वाली तरंगों में तरंग दैर्ध्य कम होते हैं, और कम आवृत्तियों में लंबी तरंग दैर्ध्य होती है।[6] तरंगदैर्घ्य उस माध्यम पर निर्भर करता है, उदाहरण के लिए, निर्वात, वायु, या पानी जिसमें एक तरंग प्रगामी करती है। तरंगों के उदाहरण हैध्वनि तरंगें, प्रकाश, जल तरंगें और विद्युत चालक में आवधिक विद्युत संकेत हैं। एक ध्वनि तरंग वायु ध्वनि दबाव में भिन्नता है, जबकि प्रकाश और अन्य विद्युत चुम्बकीय विकिरण में विद्युत क्षेत्र और चुंबकीय क्षेत्र की ताकत भिन्न होती है। पानी की तरंग पानी की तरंगें और पानी के शरीर की ऊंचाई में भिन्नता होती हैं। एक क्रिस्टल जाली कंपन में परमाणु की स्थिति भिन्न होती है।
तरंग परिघटनाओं के लिए तरंग दैर्ध्य या आवृत्तियों की सीमा को वर्णक्रम कहा जाता है। नाम की उत्पत्ति दृश्य प्रकाश वर्णक्रम से हुई थी, लेकिन अब इसे पूरे विद्युत चुम्बकीय वर्णक्रम के साथ-साथ दृश्यमान प्रतिबिम्ब या कंपन वर्णक्रम पर भी लागू किया जा सकता है।
ज्यावक्रीय तरंगें
रैखिक माध्यम में, किसी भी तरंग आकृति को ज्यावक्रीय घटकों के स्वतंत्र प्रसार के संदर्भ में वर्णित किया जा सकता है। तरंगदैर्घ्य निरंतर गति से प्रगामी कर रहे। एक ज्यावक्रीय तरंग को v द्वारा दर्शाया गया है।[7]
कहाँ पे तरंग की चरण गति चरण वेग का परिमाण कहलाती है और तरंग की आवृत्ति है। एकफैलाव माध्यम में, चरण की गति स्वयं तरंग की आवृत्ति पर निर्भर करती है, जिससे प्रकीर्णन संबंध अरेखीय हो जाता है।
विद्युत चुम्बकीय विकिरण के मामले में जैसे प्रकाश मुक्त स्थान में, चरण गति प्रकाश की गति है, लगभग 3×108 मी/से. इस प्रकार 100 मेगाहर्ट्ज विद्युत चुम्बकीय रेडियो तरंग की तरंग दैर्ध्य लगभग है, 3×108 मी/से. को 108 हेटर्स = 3 मीटर से विभाजित किया जाता है। दृश्यमान प्रकाश की तरंग दैर्ध्य गहरे लाल , लगभग 700 नैनोमीटर से लेकर बैंगनी (रंग) तक होती है, लगभग 400 एनएम, अन्य उदाहरणों के लिए, विद्युत चुम्बकीय वर्णक्रम देखें।
हवा में ध्वनि तरंगों के लिए, ध्वनि की गति 343 m/s, तापमान और दबाव के लिए मानक परिस्थितियों मे होती है। मानव कान को सुनाई देने वाली ध्वनि आवृत्तियों की तरंग दैर्ध्य, 20 हर्ट्ज़ -20 किलोहर्ट्ज़ है, इस प्रकार क्रमशः लगभग 17 मीटर और 17 मिलीमीटर के बीच होती है। चमगादड़ कुछ हद तक उच्च आवृत्तियों का उपयोग करते हैं ताकि वे 17 मिमी से छोटे लक्ष्यों को प्राप्त कर सकें। श्रव्य ध्वनि में तरंगदैर्घ्य दृश्य प्रकाश की तुलना में अधिक लंबा होता है।
अप्रगामी तरंगे
एक अप्रगामी तरंगे एक अविचल गति है जो एक स्थान पर रहती है। एक ज्यावक्रीय अप्रगामी तरंगे बिना गति के स्थिर बिंदु में शामिल होती हैं, जिन्हें ( नोड भौतिकी ) कहा जाता है, और तरंग दैर्ध्य नोड्स के बीच की दूरी से दोगुना होती हैं।
ऊपरी आकृति एक बॉक्स में तीन अप्रगामी तरंगों को दिखाती है। यह माना जाता है कि बॉक्स की दीवारों पर नोड्स रखने के लिए तरंग की आवश्यकता होती है, सीमा स्थितियों का एक उदाहरण, यह निर्धारित करने के लिए कि कौन सी तरंग दैर्ध्य की अनुमति है। उदाहरण के लिए, एक विद्युत चुम्बकीय तरंग के लिए, यदि बॉक्स में आदर्श धातु की दीवारें हैं, तो दीवारों पर नोड्स की स्थिति का परिणाम होता है, क्योंकि धातु की दीवारें एक स्पर्शरेखा विद्युत क्षेत्र का समर्थन नहीं कर सकती हैं, जिससे तरंग को दीवार पर शून्य आयाम के लिए मजबूर किया जाता है।
स्थिर तरंग को विपरीत दिशा में गति करने वाली दो ज्यावक्रीय तरंगों के योग के रूप में देखा जा सकता है।[8] नतीजतन, तरंग दैर्ध्य, अवधि और तरंग वेग एक प्रगामी तरंग के समान ही संबंधित हैं। उदाहरण के लिए, प्रकाश की गति गुहा अनुनाद एक आदर्श निर्वात युक्त धातु के बक्से में अप्रगामी तरंगेों के अवलोकन से निर्धारित किया जा सकता है।
गणितीय निरूपण
प्रगामी ज्यावक्रीय तरंगों को अक्सर उनके वेग v (x दिशा में), आवृत्ति f और तरंग दैर्ध्य के रूप में गणितीय रूप से दर्शाया जाता है:
जहाँ y किसी भी स्थिति x और समय t पर तरंग का मान है, और A तरंग का आयाम है। वे आमतौर पर वेवनंबर k (तरंग दैर्ध्य के 2π बार पारस्परिक) और कोणीय आवृत्ति ω (आवृत्ति के 2π गुना) के रूप में व्यक्त किए जाते हैं:
जिसमें तरंग दैर्ध्य और तरंग संख्या वेग और आवृत्ति से संबंधित हैं:
या
ऊपर दिए गए दूसरे रूप में, चरण (kx − ωt) अक्सर सामान्यीकृत किया जाता है (k•r − ωt), वेवनंबर k को एक तरंग वेक्टर से प्रतिस्थापित करके जो पोजिशन वेक्टर 'r' द्वारा पैरामिट्रीकृत 3-स्पेस में समतल तरंग की दिशा और वेवनंबर को निर्दिष्ट करता है। उस स्थिति में, वेवनंबर k, 'k' का परिमाण, अभी भी तरंग दैर्ध्य के साथ उसी संबंध में है जैसा कि ऊपर दिखाया गया है, v को तरंग वेक्टर की दिशा में अदिश गति के रूप में व्याख्यायित किया जा रहा है। पहला रूप, चरण में पारस्परिक तरंग दैर्ध्य का उपयोग करते हुए, एक स्वच्छंद दिशा में एक तरंग को आसानी से सामान्यीकृत नहीं करता है।
अन्य चरणों के ज्यावक्रीय तरंग और जटिल घातांक के लिए सामान्यीकरण भी आम हैं, विमान की तरंग देखें। एक तरंग का वर्णन करते समय साइन चरण के बजाय कोज्या चरण का उपयोग करने की विशिष्ट परंपरा इस तथ्य पर आधारित है कि कोसाइन तरंग में जटिल घातांक का वास्तविक हिस्सा है।
सामान्य माध्यम
एक तरंग की गति उस माध्यम पर निर्भर करती है जिसमें वह फैलता है। विशेष रूप से, किसी माध्यम में प्रकाश की गति निर्वात की तुलना में कम होती है, विद्युत चुंबकत्व में, जिसका अर्थ है कि समान आवृत्ति निर्वात की तुलना में माध्यम में कम तरंग दैर्ध्य के अनुरूप होगी, जैसा कि दाईं ओर की आकृति में दिखाया गया है।
माध्यम में प्रवेश करने पर गति में यह परिवर्तन अपवर्तन का कारण बनता है, या तरंगों की दिशा में परिवर्तन होता है जो एक कोण पर माध्यम के बीच अंतरपृष्ठ का सामना करते हैं।[9] विद्युत चुम्बकीय तरंगों के लिए, प्रसार के कोण में यह परिवर्तन स्नेल के नियम द्वारा नियंत्रित होता है।
एक माध्यम में तरंग वेग न केवल दूसरे माध्यम से भिन्न हो सकता है, बल्कि वेग आमतौर पर तरंग दैर्ध्य के साथ बदलता रहता है। नतीजतन, एक अलग माध्यम में प्रवेश करने पर दिशा में परिवर्तन तरंग की तरंग दैर्ध्य के साथ बदल जाता है।
विद्युत चुम्बकीय तरंगों के लिए एक माध्यम में गति उसके अपवर्तनांक द्वारा के अनुसार नियंत्रित होती है
जहाँ c निर्वात में प्रकाश की गति है और n(λ0) तरंग दैर्ध्य पर माध्यम का अपवर्तनांक है λ0, को जहां बाद वाले माध्यम के बजाय निर्वात में मापा जाता है। माध्यम में संगत तरंगदैर्घ्य है।
जब विद्युत चुम्बकीय विकिरण की तरंग दैर्ध्य को उद्धृत किया जाता है, तो निर्वात में तरंग दैर्ध्य आमतौर पर तब तक नियत होता है जब तक कि तरंग दैर्ध्य को विशेष रूप से किसी अन्य माध्यम में तरंग दैर्ध्य के रूप में पहचाना नहीं जाता है। ध्वनि में जहां तरंगों के अस्तित्व के लिए एक माध्यम आवश्यक है,और एक निर्दिष्ट माध्यम के लिए तरंग दैर्ध्य के मान का आंकलन कर लिया जाता है।
तरंग दैर्ध्य के साथ प्रकाश की गति में भिन्नता को प्रकाशिकी प्रकीर्णन के रूप में जाना जाता है, और यह उस परिचित स्थिति के लिए भी जिम्मेदार है जिसमें प्रकाश एक प्रकीर्णन प्रिज्म द्वारा घटक के रंगों में अलग हो जाता है। और तब पृथक्करण होता है जब प्रिज्म के अंदर अपवर्तनांक तरंग दैर्ध्य के साथ बदलता रहता है, इसलिए विभिन्न तरंग दैर्ध्य प्रिज्म के अंदर अलग-अलग गति से फैलते हैं, जिससे वे विभिन्न कोणों पर अपवर्तित हो जाते हैं। एक माध्यम के भीतर प्रकाश की गति तरंग दैर्ध्य के साथ कैसे भिन्न होती है, इसका वर्णन करने वाले गणितीय संबंध को फैलाव संबंध के रूप में जाना जाता है।
गैर-वर्दी माध्यम

तरंगदैर्घ्य एक उपयोगी अवधारणा हो सकती है, भले ही तरंग अंतरिक्ष मेंआवधिक कार्य न हो। उदाहरण के लिए, समुद्र की ओर आने वाली समुद्र की तरंग में, (चित्र में दिखाया गया है) आने वाली तरंग एक अलग स्थानीय तरंग दैर्ध्य के साथ तरंगदार होती है जो तरंग की ऊंचाई की तुलना में समुद्र तल की गहराई पर निर्भर करती है। तरंग का विश्लेषण स्थानीय तरंग दैर्ध्य के स्थानीय पानी की गहराई की तुलना पर आधारित हो सकती है।[10]
तरंगें जो समय में ज्यावक्रीय होती हैं लेकिन एक माध्यम से फैलती हैं जिनके गुण स्थिति के साथ भिन्न होते हैं ,एक असमांगी माध्यम एक वेग से फैल सकता है जो स्थिति के साथ बदलता रहता है, और परिणामस्वरूप अंतरिक्ष में ज्यावक्रीय नहीं हो सकता है। दाईं ओर की आकृति एक उदाहरण दिखाती है। जैसे-जैसे तरंग धीमी होती जाती है, तरंगदैर्घ्य कम होती जाती है और आयाम बढ़ता जाता है, अधिकतम प्रतिघटनाक्रम के स्थान के बाद, लघु तरंग दैर्ध्य उतकृष्ट क्षति के बाद तरंग खत्म हो जाती है।
ऐसी प्रणालियों केअंतर समीकरण का विश्लेषण अक्सर (WKB) डब्लू के बी सन्निकटन का उपयोग करते हुए लगभग किया जाता है। जिसे लिउविल-ग्रीन विधि के रूप में भी जाना जाता है, विधि स्थानीय तरंग संख्या का उपयोग करके अंतरिक्ष के माध्यम से चरण को एकीकृत करती है, जिसे समय और स्थान के कार्य के रूप में हल के स्थानीय तरंग दैर्ध्य को इंगित करने के रूप में व्याख्या किया जा सकता है।[11][12] यह विधि स्थानीय रूप से प्रणाली के साथ ऐसा व्यवहार करती है मानो वह स्थानीय गुणों के साथ एक समान हो, विशेष रूप से, आवृत्ति के साथ जुड़े स्थानीय तरंग वेग ही संबंधित स्थानीय तरंग संख्या या तरंग दैर्ध्य का अनुमान लगाने के लिए आवश्यक है। इसके अलावा, विधि समीकरणों या भौतिक प्रणाली की अन्य बाधाओं को संतुष्ट करने के लिए धीरे-धीरे बदलते आयाम की गणना करती है, जैसे तरंग में ऊर्जा के संरक्षण के लिए।
क्रिस्टल
क्रिस्टलीय ठोस में तरंगें निरंतर नहीं होती हैं, क्योंकि वे एक नियमित जाली में व्यवस्थित असतत कणों के कंपन से बनी होती हैं। यहअलियासिंग पैदा करता है, क्योंकि एक ही कंपन को विभिन्न तरंग दैर्ध्य की एक बहुरूपता माना जा सकता है, जैसा कि चित्र में दिखाया गया है।[13] इनमें से एक से अधिक तरंग दैर्ध्य का उपयोग करने वाले निरूपण अपेक्षाधिक हैं, घटना के अनुकूल सबसे लंबी तरंग दैर्ध्य चुनना सांकेतिक है। एक क्रिस्टलीय माध्यम में सभी संभावित तरंगों का निरूपण प्रदान करने के लिए पर्याप्त तरंग दैर्ध्य की सीमा ब्रिलौइन क्षेत्र तक सीमित तरंग वैक्टर से सुमेल खाती है।[14] ठोस में तरंगदैर्घ्य में यह अनिश्चितता तरंग परिघटनाओं जैसे ऊर्जा बैंड और फोनन के विश्लेषण में महत्वपूर्ण है। यह गणितीय रूप से एक सिग्नल के अलियासिंग के बराबर है जो असतत अंतराल पर सिग्नल प्रोसेसिंग का नमूना है।
अधिक सामान्य तरंग
तरंग दैर्ध्य की अवधारणा को अक्सर ज्यावक्रीय, या लगभग ज्यावक्रीय, तरंगों पर लागू किया जाता है, क्योंकि एक रैखिक प्रणाली में ज्यावक्रीय अद्वितीय आकार का होता है जो बिना किसी आकार परिवर्तन के फैलता है, केवल एक चरण परिवर्तन और संभावित रूप से एक आयाम परिवर्तन।[15] तरंग दैर्ध्य वैकल्पिक रूप से तरंग संख्या और तरंग सदिश अंतरिक्ष में तरंग का चरित्र चित्रण वर्णित है, जो कार्यात्मक रूप से इसकी आवृत्ति से संबंधित है, जैसा कि प्रणाली के भौतिकी द्वारा सीमित है। और ज्यावक्रीय सबसे सरल तरंग का मान प्राप्त करने का एक उपाय है, और अधिक जटिल सुपरपोजिशन सिद्धांत द्वारा इसका मान प्राप्त किया जा सकता है।।
फैलाव मुक्त और एकसमान माध्यम के विशेष मामले में, ज्यावक्रीय के अलावा अन्य तरंगें अपरिवर्तित आकार और निरंतर वेग के साथ फैलती हैं। कुछ परिस्थितियों में, अरेखीय माध्यम में अपरिवर्तनीय आकार की तरंगें भी हो सकती हैं, उदाहरण के लिए यह आंकड़ा उथले पानी में समुद्र की तरंग को दिखाता है जिसमें एक ज्यावक्रीय की तुलना में तेज शीर्ष और गर्त वाले कुंड होते हैं, जो कि एक शंक्वाकार तरंग की विशिष्ट होती है,[16] एक प्रगामी तरंग का नाम इसलिए रखा गया क्योंकि इसे (m-th) एम-वें क्रम के जैकोबी अण्डाकार कार्य द्वारा वर्णित किया गया है, जिसे आमतौर पर दर्शाया जाता है cn(x; m).[17] गैर-रेखीय सतह-तरंग माध्यम के गुणों के कारण, कुछ आकार के साथ बड़े-आयाम वाली समुद्री तरंगें अपरिवर्तित में फैल सकती हैं।[18]
यदि एक प्रगामी तरंग का एक निश्चित आकार होता है जो अंतरिक्ष या समय में दोहराता है, तो यह एक आवधिक तरंग है।[19] ऐसी तरंगों को कभी-कभी तरंग दैर्ध्य के रूप में माना जाता है, भले ही वे ज्यावक्रीय न हों।[20] जैसा कि चित्र में दिखाया गया है, तरंग दैर्ध्य को तरंग पर लगातार संबंधित बिंदुओं के बीच मापा जाता है।
तरंग पैकेट्स
स्थानीयकृत तरंग बंडल, तरंग घटनाक्रम का टूटना जहां प्रत्येक तरंग बंडल एक इकाई के रूप में प्रगामी करता है, भौतिकी के कई क्षेत्रों में आवेदन पाते हैं। एक तरंग बंडल में एक आवरण होता है जो तरंग के समग्र आयाम का वर्णन करता है, आवरण के भीतर, निकटवर्ती चोटियों या गर्तों के बीच की दूरी को कभी-कभी स्थानीय तरंगदैर्घ्य कहा जाता है।[21][22] एक उदाहरण चित्र में दिखाया गया है। सामान्य तौर पर, तरंग बंडल का आवरण घटक तरंगों से भिन्न गति से चलता है।[23] फूरियर विश्लेषण का उपयोग करते हुए, तरंग बंडलों का विश्लेषण विभिन्न तरंगों या तरंग दैर्ध्य के ज्यावक्रीय तरंगों के अनंत योग (या इंटीग्रल) में किया जा सकता है।[24] लुई डी ब्रोगली ने माना कि गति के विशिष्ट मूल्य वाले सभी कणों में तरंग दैर्ध्य λ = h/p होता है, जहां एच प्लैंक स्थिरांक होता है। यह परिकल्पना क्वांटम यांत्रिकी के आधार पर थी। आजकल, इस तरंग दैर्ध्य को डी ब्रोगली तरंग दैर्ध्य कहा जाता है। उदाहरण के लिए, कैथोड रे ट्यूब डिस्प्ले में इलेक्ट्रॉन को डी ब्रोगली तरंग दैर्ध्य लगभग 10−13 मी. होता है, इस तरह के सभी कणों के अंतरिक्ष में फैलने से तरंग प्रकार्य को रोकने के लिए, डी ब्रोगली ने अंतरिक्ष में स्थानीयकृत कणों का प्रतिनिधित्व करने के लिए तरंग बंडल का उपयोग करने का प्रस्ताव रखा।[25] तरंग बंडल का आवर्ती प्रसार, और बंडल बनाने वाले ज्यावक्रीय के तरंगों का प्रसार, कण की स्थिति और गति में अनिश्चितताओं के अनुरूप होता है, जिसका उत्पाद हाइजेनबर्ग अनिश्चितता सिद्धांत से घिरा होता है।[24]
हस्तक्षेप और विवर्तन
डबल-स्लिट हस्तक्षेप
जब ज्यावक्रीय तरंगें जुड़ती हैं तो वे एक दूसरे को मजबूत कर सकती हैं, रचनात्मक हस्तक्षेप या एक दूसरे को रद्द कर सकती हैं। विनाशकारी हस्तक्षेप उनके सापेक्ष चरण के आधार पर। इस घटना का उपयोग इंटरफेरोमेट्री में किया जाता है। एक साधारण उदाहरण थॉमस यंग (वैज्ञानिक) के कारण एक प्रयोग है जहां प्रकाश को डबल-स्लिट प्रयोग के माध्यम से गुजरता है।[26] जैसा कि चित्र में दिखाया गया है, प्रकाश दो झिरियों से होकर गुजरता है और एक स्क्रीन पर चमकता है। स्क्रीन पर किसी स्थिति के लिए प्रकाश का पथ दो झिरियों के लिए भिन्न होता है, और कोण पर निर्भर करता है पथ स्क्रीन के साथ बनाता है। यदि हम मानते हैं कि स्क्रीन स्लिट्स से काफी दूर है (अर्थात, स्लिट पृथकत्व डी की तुलना में एस से बड़ा है) तो पथ लगभग समानांतर हैं, और पथ अंतर केवल (d sin θ) डी साइन थीटा है। तदनुसार, रचनात्मक हस्तक्षेप की शर्त है।[27]
जहां एम एक पूर्णांक है, और विनाशकारी हस्तक्षेप के लिए है।
इस प्रकार, यदि प्रकाश की तरंगदैर्घ्य ज्ञात है, तो झिरी पृथक्करण व्यतिकरण आकृति या फ्रिंजों से निर्धारित किया जा सकता है, और इसके विपरीत बहु-स्लिट के लिए, आकृति है [28]
जहाँ q झिल्लियों की संख्या है, और g झंझरी स्थिरांक है। पहला कारक I1, एकल-झिरी परिणाम है, जो अधिक तेजी से भिन्न होने वाले दूसरे कारक को नियंत्रित करता है जो झिरियों की संख्या और उनके अंतर पर निर्भर करता है। चित्र I1 इकाई के लिए निर्धारित किया गया है, यह एक बहुत ही कठिन सन्निकटन।
हस्तक्षेप का प्रभाव प्रकाश को पुनर्वितरित करना है, इसलिए प्रकाश में निहित ऊर्जा को परिवर्तित नहीं किया जाता है, जहां यह दिखाई देता है।[29]
एकल स्लिट विवर्तन

डबल-स्लिट प्रयोग के लिए ऊपर उपयोग किए गए पथ अंतर और रचनात्मक या विनाशकारी हस्तक्षेप की धारणा स्क्रीन पर अवरोधन किए गए प्रकाश के एकल स्लिट के प्रदर्शन पर भी लागू होती है। इस हस्तक्षेप का मुख्य परिणाम स्क्रीन पर संकीर्ण स्लिट से प्रकाश को एक विस्तृत भाग में फैलाना है। तरंग ऊर्जा के इस वितरण को विवर्तन कहते हैं।
स्रोत और स्क्रीन के बीच अलगाव के आधार पर दो प्रकार के विवर्तन को प्रतिष्ठित किया जाता है, बड़े अलगाव पर फ्रौनहोफर विवर्तन या दूर-क्षेत्र विवर्तन और निकट अलगाव पर फ़्रेज़नेल विवर्तन या निकट-क्षेत्र विवर्तन।
सिंगल स्लिट के विश्लेषण में, स्लिट की गैर-शून्य चौड़ाई को ध्यान में रखा जाता है, और एपर्चर में प्रत्येक बिंदु को प्रकाश की किरण (ह्यूजेंस के तरंगिका) में एक योगदान के स्रोत के रूप में लिया जाता है। स्क्रीन पर, झिरी के भीतर प्रत्येक स्थिति से आने वाले प्रकाश की पथ लंबाई भिन्न होती है, यद्यपि संभवतः बहुत छोटा अंतर होता है। नतीजतन हस्तक्षेप होता है।
फ्रौनहोफर विवर्तन आकृति में, एक छोटे कोण के सन्निकटन के भीतर, एक एकल स्लिट से पर्याप्त रूप से दूर, तीव्रता का फैलाव S एक वर्ग सिंक फ़ंक्शन के माध्यम से स्थिति x से संबंधित है:[30]
- साथ
जहाँ L स्लिट की चौड़ाई है, R रेखाछिद्र से आकृति की दूरी है, और प्रयुक्त प्रकाश की तरंगदैर्घ्य है। फलन S में शून्य है जहाँ u एक शून्येतर पूर्णांक है, जहाँ x मानों पर तरंगदैर्घ्य के पृथक्करण अनुपात में हैं।
विवर्तन-सीमित संकल्प
विवर्तन ऑप्टिकल उपकरणों केकोणीय संकल्प पर मूल सीमा है, जैसे दूरबीन ( रेडियो दूरबीन ) सहित सूक्ष्मदर्शी।[31] एक गोलाकार एपर्चर के लिए, विवर्तन-सीमित प्रतिबिम्ब क्षेत्र को हवादार डिस्क के रूप में जाना जाता है, सिंगल-स्लिट विवर्तन सूत्र में दूरी x को रेडियल दूरी r से बदल दिया जाता है और साइन को 2J1 से बदल दिया जाता है, जहां J1 जे वन पहला ऑर्डर बेसेल फंक्शन है।[32] माइक्रोस्कोप के माध्यम से देखी जाने वाली वस्तुओं का हल करने योग्य आवर्ती आकार रेले मानदंड के अनुसार सीमित है, हवादार डिस्क के पहले नल की त्रिज्या, उपयोग किए गए प्रकाश की तरंग दैर्ध्य के आनुपातिक आकार के लिए, और संख्यात्मक एपर्चर के आधार पर:[33]
जहां संख्यात्मक एपर्चर को परिभाषित किया गया है क्योंकि θ सूक्ष्मदर्शी उद्देश्य द्वारा स्वीकृत किरणों के शंकु का आधा कोण है।
एक गोलाकार एपर्चर द्वारा विवर्तित छवि के केंद्रीय उज्ज्वल भाग (हवादार डिस्क के पहले नल की त्रिज्या) का कोणीय आकार, दूरबीन और कैमरों के लिए सबसे अधिक इस्तेमाल किया जाने वाला उपाय है।[34]
जहां λ प्रतिबिंबन के लिए केंद्रित तरंगों की तरंग दैर्ध्य है, डी प्रतिबिंबन प्रणाली प्रवेश छात्र व्यास, की एक इकाइयों में, और कोणीय संकल्प δ रेडियन में है।
अन्य विवर्तन आकृति के साथ, आकृति तरंगदैर्ध्य के अनुपात में पैमाना करता है, इसलिए कम तरंगदैर्ध्य उच्च संकल्प को जन्म दे सकती है।
उप तरंगदैर्ध्य
उप तरंगदैर्ध्य शब्द का प्रयोग किसी वस्तु का वर्णन करने के लिए किया जाता है जिसमें एक या अधिक आयाम तरंग की लंबाई से छोटे होते हैं जिसके साथ वस्तु बातचीत करती है। उदाहरण के लिए उप तरंगदैर्ध्य-व्यास प्रकाशित तंतु शब्द का अर्थ एक ऑप्टिकल फाइबर है जिसका व्यास इसके माध्यम से फैलने वाले प्रकाश की तरंग दैर्ध्य से कम है।
एक उप तरंगदैर्ध्य कण प्रकाश की तरंग दैर्ध्य से छोटा कण होता है जिसके साथ यह बातचीत करता है देखें ( रेले स्कैटरिंग )। उप तरंगदैर्ध्य एपर्चर उनके माध्यम से फैलने वाले प्रकाश की तरंग दैर्ध्य से छोटे छेद होते हैं। इस तरह की संरचनाओं में फोटोनिक्स के अन्य क्षेत्रों में असाधारण ऑप्टिकल ट्रांसमिशन और शून्य-मोड वेवगाइड में अनुप्रयोग होते हैं।
उप तरंगदैर्ध्य एक घटना को भी संदर्भित कर सकता है जिसमें उप तरंगदैर्ध्य ऑब्जेक्ट्स शामिल हैं, उदाहरण के लिए, उप तरंगदैर्ध्य प्रतिबिंबन ।
कोणीय तरंगदैर्घ्य
तरंग दैर्ध्य से संबंधित एक मात्रा कोणीय तरंग दैर्ध्य है जिसे समानीत तरंग दैर्ध्य भी कहा जाता है, जिसे आमतौर पर ƛ (लैम्ब्डा-बार) द्वारा दर्शाया जाता है। यह 2π (ƛ = λ/2π) के कारक द्वारा कम की गई नियमित तरंग दैर्ध्य के बराबर है। यह आमतौर पर क्वांटम यांत्रिकी में पाया जाता है, जहां इसका उपयोग कम प्लैंक स्थिरांक (प्रतीक ħ, एच-बार) और कोणीय आवृत्ति (प्रतीक ω) या कोणीय तरंग संख्या प्रतीक k के संयोजन में किया जाता है।
यह भी देखें
- उत्सर्जन चित्र
- लिफ़ाफ़ा (तरंगे)
- फ्रौनहोफर रेखाएं - सौर स्पेक्ट्रम में काली रेखाएँ, को पारंपरिक रूप से मानक ऑप्टिकल तरंग दैर्ध्य संदर्भ के रूप में उपयोग किया जाता है
- तरंग लेखों का सूचकांक
- लंबाई माप
- वर्णक्रमीय रेखा
- स्पेक्ट्रोस्कोपी
- वर्णक्रम
संदर्भ
- ↑ Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. pp. 15–16. ISBN 0-201-11609-X.
- ↑ Brian Hilton Flowers (2000). "§21.2 Periodic functions". An introduction to numerical methods in C++ (2nd ed.). Cambridge University Press. p. 473. ISBN 0-19-850693-7.
- ↑ Raymond A. Serway; John W. Jewett (2006). Principles of physics (4th ed.). Cengage Learning. pp. 404, 440. ISBN 0-534-49143-X.
- ↑ A. A. Sonin (1995). The surface physics of liquid crystals. Taylor & Francis. p. 17. ISBN 2-88124-995-7.
- ↑ Keqian Zhang & Dejie Li (2007). Electromagnetic Theory for Microwaves and Optoelectronics. Springer. p. 533. ISBN 978-3-540-74295-1.
- ↑
Theo Koupelis & Karl F. Kuhn (2007). In Quest of the Universe. Jones & Bartlett Publishers. p. 102. ISBN 978-0-7637-4387-1.
wavelength lambda light sound frequency wave speed.
- ↑ David C. Cassidy; Gerald James Holton; Floyd James Rutherford (2002). Understanding physics. Birkhäuser. pp. 339 ff. ISBN 0-387-98756-8.
- ↑ John Avison (1999). The World of Physics. Nelson Thornes. p. 460. ISBN 978-0-17-438733-6.
- ↑ To aid imagination, this bending of the wave often is compared to the analogy of a column of marching soldiers crossing from solid ground into mud. See, for example, Raymond T. Pierrehumbert (2010). Principles of Planetary Climate. Cambridge University Press. p. 327. ISBN 978-0-521-86556-2.
- ↑ 10.0 10.1 Paul R Pinet (2009). op. cit. p. 242. ISBN 978-0-7637-5993-3.
- ↑ Bishwanath Chakraborty (2007). Principles of Plasma Mechanics. New Age International. p. 454. ISBN 978-81-224-1446-2.
- ↑ Jeffrey A. Hogan & Joseph D. Lakey (2005). Time-frequency and time-scale methods: adaptive decompositions, uncertainty principles, and sampling. Birkhäuser. p. 348. ISBN 978-0-8176-4276-1.
- ↑ See Figure 4.20 in A. Putnis (1992). Introduction to mineral sciences. Cambridge University Press. p. 97. ISBN 0-521-42947-1. and Figure 2.3 in Martin T. Dove (1993). Introduction to lattice dynamics (4th ed.). Cambridge University Press. p. 22. ISBN 0-521-39293-4.
- ↑ Manijeh Razeghi (2006). Fundamentals of solid state engineering (2nd ed.). Birkhäuser. pp. 165 ff. ISBN 0-387-28152-5.
- ↑ See Lord Rayleigh (1890). "Wave theory". Encyclopædia Britannica (9th ed.). The Henry G Allen Company. p. 422.
- ↑ Valery N. Pilipchuk (2010). "Figure 4.4: Transition from quasi-harmonic to cnoidal wave". Nonlinear Dynamics: Between Linear and Impact Limits. Springer. p. 127. ISBN 978-3642127984.
- ↑ Andrei Ludu (2012). "§18.3 Special functions". Nonlinear Waves and Solitons on Contours and Closed Surfaces (2nd ed.). Springer. pp. 469 ff. ISBN 978-3642228940.
- ↑ Alfred Osborne (2010). "Chapter 1: Brief history and overview of nonlinear water waves". Nonlinear Ocean Waves and the Inverse Scattering Transform. Academic Press. pp. 3 ff. ISBN 978-0-12-528629-9.
- ↑ Alexander McPherson (2009). "Waves and their properties". Introduction to Macromolecular Crystallography (2 ed.). Wiley. p. 77. ISBN 978-0-470-18590-2.
- ↑ Eric Stade (2011). Fourier Analysis. John Wiley & Sons. p. 1. ISBN 978-1-118-16551-5.
- ↑ Peter R. Holland (1995). The Quantum Theory of Motion: An Account of the de Broglie–Bohm Causal Interpretation of Quantum Mechanics. Cambridge University Press. p. 160. ISBN 978-0-521-48543-2.
- ↑
Jeffery Cooper (1998). Introduction to partial differential equations with MATLAB. Springer. p. 272. ISBN 0-8176-3967-5.
The local wavelength λ of a dispersing wave is twice the distance between two successive zeros. ... the local wavelength and the local wave number k are related by k = 2π / λ.
- ↑ A. T. Fromhold (1991). "Wave packet solutions". Quantum Mechanics for Applied Physics and Engineering (Reprint of Academic Press 1981 ed.). Courier Dover Publications. pp. 59 ff. ISBN 0-486-66741-3.
(p. 61) ... the individual waves move more slowly than the packet and therefore pass back through the packet as it advances
- ↑ 24.0 24.1 See, for example, Figs. 2.8–2.10 in Joy Manners (2000). "Heisenberg's uncertainty principle". Quantum Physics: An Introduction. CRC Press. pp. 53–56. ISBN 978-0-7503-0720-8.
- ↑ Ming Chiang Li (1980). "Electron Interference". In L. Marton; Claire Marton (eds.). Advances in Electronics and Electron Physics. Vol. 53. Academic Press. p. 271. ISBN 0-12-014653-3.
- ↑ Greenfield Sluder & David E. Wolf (2007). "IV. Young's Experiment: Two-Slit Interference". Digital microscopy (3rd ed.). Academic Press. p. 15. ISBN 978-0-12-374025-0.
- ↑
Halliday, Resnick, Walker (2008). "§35-4 Young's interference experiment". Fundamentals of Physics (Extended 8th ed.). Wiley-India. p. 965. ISBN 978-81-265-1442-7.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ Kordt Griepenkerl (2002). "§9.8.2 Diffraction by a grating". In John W Harris; Walter Benenson; Horst Stöcker; Holger Lutz (eds.). Handbook of physics. Springer. pp. 307 ff. ISBN 0-387-95269-1.
- ↑ Douglas B. Murphy (2002). Fundamentals of light microscopy and electronic imaging. Wiley/IEEE. p. 64. ISBN 0-471-23429-X.
- ↑ John C. Stover (1995). Optical scattering: measurement and analysis (2nd ed.). SPIE Press. p. 64. ISBN 978-0-8194-1934-7.
- ↑ Graham Saxby (2002). "Diffraction limitation". The science of imaging. CRC Press. p. 57. ISBN 0-7503-0734-X.
- ↑ Grant R. Fowles (1989). Introduction to Modern Optics. Courier Dover Publications. pp. 117–120. ISBN 978-0-486-65957-2.
- ↑ James B. Pawley (1995). Handbook of biological confocal microscopy (2nd ed.). Springer. p. 112. ISBN 978-0-306-44826-3.
- ↑ Ray N. Wilson (2004). Reflecting Telescope Optics I: Basic Design Theory and Its Historical Development. Springer. p. 302. ISBN 978-3-540-40106-3.
इस पृष्ठ में अनुपलब्ध आंतरिक कड़ियों की सूची
- आनंददायकता
- ऑप्टिकल डिस्क रिकॉर्डिंग प्रौद्योगिकियां
- पुरालेख संबंधी
- प्रति मिनट धूर्णन
- निरंतर रैखिक वेग
- डिफ़्रैक्शन ग्रेटिंग
- आप टिके रहेंगे
- Phthalocyanine
- शब्दशः (ब्रांड)
- अज़ो गॉड
- निजी कंप्यूटर
- ऑप्टिकल स्टोरेज टेक्नोलॉजी एसोसिएशन
- भयावह विफलता
- यूएसबी हत्यारा
- वीडियोडिस्क
- एक बार लिखें कई पढ़ें
- संख्यात्मक छिद्र
- हाय एमडी
- आधार - सामग्री संकोचन
- व्यावसायिक डिस्क
- फ्लोरोसेंट बहुपरत डिस्क
- एक बार लिखें कई पढ़ें
- डिस्क रोट
- भविष्य कहनेवाला विफलता विश्लेषण
- फोनोग्राफ रिकॉर्ड का उत्पादन
- तरल वैकल्पिक रूप से स्पष्ट चिपकने वाला
- आठ से चौदह मॉडुलन
- Benq
- सीडी राइटर
- पैसा
- नमूनाकरण दर
- स्थिर कोणीय वेग
- जूलियट (फाइल प्रणाली)
- घूर्णन प्रति मिनट
- आधा ऊंचाई
- यूएसबी पोर्ट
- लेंस (प्रकाशिकी)
- सीरिज़ सर्किट
- स्वत: नियंत्रण प्राप्त करें
- रंग
- प्रति मिनट धूर्णन
- समानांतर एटीए
- घंटे
- उन्नत तकनीकी जोड़
- रुको (कंप्यूटिंग)
- लचीला सर्किट
- हर कोई
- आप टिके रहेंगे
- आठ से चौदह मॉडुलन
- अधिशुल्क भुगतान
- सोना
- प्रीग्रूव में निरपेक्ष समय
- थोड़ा लिखो
- सूचान प्रौद्योगिकी
- जानकारी के प्रणाली
- कंप्यूटिंग हार्डवेयर का इतिहास
- प्रत्येक से अलग पत्राचार
- बूलियन बीजगणित
- फील्ड इफ़ेक्ट ट्रांजिस्टर
- दावों कहंग
- एकीकृत परिपथ
- सेंट्रल प्रोसेसिंग यूनिट
- जानकारी
- समारोह (इंजीनियरिंग)
- दस्तावेज़ फ़ाइल प्रारूप
- लिनक्स गेमिंग
- एंड्रॉइड (ऑपरेटिंग प्रणाली)
- स्थानीय क्षेत्र अंतरजाल
- जानकारी
- सूचना अवसंरचना
- अवधारणा का सबूत
- सी++
- पेशा
- संगणक वैज्ञानिक
- कार्यकारी प्रबंधक
- कंसल्टेंसी
- सॉफ्टवेयर की रखरखाव
- सॉफ्टवेयर डेवलपमेंट
- शैक्षिक अनुशासन
- जटिल प्रणाली
- सर्विस अटैक से इनकार
- बड़ा डेटा
- संगणक तंत्र संस्था
- कंप्यूटर सेवाएं
- एक सेवा के रूप में बुनियादी ढांचा
- एक सेवा के रूप में मंच
- पैमाने की अर्थव्यवस्थाएं
- बहुत नाजुक स्थिति
- सूचना की इकाइयाँ
- मूल्य (कंप्यूटर विज्ञान)
- सूचना की इकाई
- तुलसी कैप
- विद्युत सर्किट
- राज्य (कंप्यूटर विज्ञान)
- बिजली
- सीरियल ट्रांसमिशन
- चुंबकीय बुलबुला स्मृति
- लिफ़्ट
- चरित्र (कंप्यूटिंग)
- योटा-
- शैनन जानकारी
- टॉर्कः
- यह यहाँ जिराफ
- अंधेरे शहर
- दीदी काँग रेसिंग
- शव (बैंड)
- सेंटर ऑफ मास
- परिवर्णी शब्द
- रोशनी
- प्रेरित उत्सर्जन
- कानून स्थापित करने वाली संस्था
- अस्थायी सुसंगतता
- मुक्त अंतरिक्ष ऑप्टिकल संचार
- फाइबर ऑप्टिक संचार
- संगति (भौतिकी)
- सुसंगतता लंबाई
- परमाणु लेजर
- सक्रिय लेजर माध्यम
- प्रकाश किरण
- रसायन विज्ञान
- भौतिक विज्ञान
- उत्साहित राज्य
- अनिश्चित सिद्धांत
- थर्मल उत्सर्जन
- फोनोन
- फोटोन
- स्वत: उत्सर्जन
- वस्तुस्थिति
- कितना राज्य
- जनसंख्या का ह्रास
- फोटान संख्या
- पॉसों वितरण
- गाऊसी समारोह
- टोफाट बीम
- परावर्तन प्रसार
- फोकस (प्रकाशिकी)
- अल्ट्राफास्ट साइंस
- फेमटोसेकंड केमिस्ट्री
- दूसरी हार्मोनिक पीढ़ी
- शारीरिक समीक्षा
- कोलम्बिया विश्वविद्यालय
- पैटेंट आवेदन
- बेल टेलीफोन लेबोरेटरीज
- शक्ति (भौतिकी)
- कोलोराडो विश्वविद्यालय बोल्डर
- आयन लेजर
- व्युत्क्रम के बिना स्थायी
- ऑप्टिकल विकिरण का आवृत्ति जोड़ स्रोत
- राज्यों का घनत्व
- क्वांटम वेल
- ईण्डीयुम (III) फॉस्फाइड
- रमन बिखरना
- के आदेश पर
- निउवेजिन
- परमाणु समावयवी
- मंगल ग्रह
- लेजर दृष्टि (आग्नेयास्त्र)
- मुंहासा
- विकिरण उपचार
- खून बह रहा है
- फेफड़ों की छोटी कोशिकाओं में कोई कैंसर नहीं
- योनि का कैंसर
- लेज़र से बाल हटाना
- परिमाण का क्रम
- युग्मित उपकरण को चार्ज करें
- मनुष्य की आंख
- उस्तरा
- विकिरण के उत्प्रेरित उत्सर्जन द्वारा ध्वनि प्रवर्धन
- सुसंगत पूर्ण अवशोषक
- Intellaser
- बेरहमी
- deprotonates
- कांच पारगमन तापमान
- मॉलिक्यूलर मास्स
- ब्रेक (शीट मेटल बेंडिंग)
- तनाव जंग खुर
- स्पटर डिपोजिशन
- बलवे या उपद्रवियों से निबट्ने के लिए पुलिस को उपलब्ध साज
- रेडियो नियंत्रित हेलीकाप्टर
- दंगा ढाल
- बढ़ाया अपक्षय
- शराब (रसायन विज्ञान)
- जैविक द्रावक
- बेलीज़
- सेमीकंडक्टर
- एलईडी
- वाहक पीढ़ी और पुनर्संयोजन
- ब्लू रे
- प्रत्यक्ष और अप्रत्यक्ष बैंड अंतराल
- प्रभारी वाहक
- रिक्तीकरण क्षेत्र
- चरण (तरंग ें)
- ध्रुवीकरण (तरंग ें)
- लेजर पम्पिंग
- सुसंगतता (भौतिकी)
- रासायनिक वाष्प निक्षेपन
- राज्यों का घनत्व
- तरंग घटनाक्रम
- ट्यून करने योग्य लेजर
- स्थिरता अभियांत्रिकी
- भयावह ऑप्टिकल क्षति
- दरार (क्रिस्टल)
- परावर्तक - विरोधी लेप
- ईण्डीयुम (III) फॉस्फाइड
- गैलियम (द्वितीय) एंटीमोनाइड
- बेलगाम उष्म वायु प्रवाह
- दृश्यमान प्रतिबिम्ब
- हरा
- पृथक करना
- लाह
- कोणीय गति
- मिनी सीडी
- रेखीय वेग
- lacquerware
- तोकुगावा को
- या अवधि
- एलएसी
- चमक (सामग्री उपस्थिति)
- कमज़ोर लाख
- ऐक्रेलिक रेसिन
- फ्रान्सीसी भाषा
- उरुशीओल-प्रेरित संपर्क जिल्द की सूजन
- तोरिहामा शैल टीला
- शांग वंश
- निओलिथिक
- हान साम्राज्य
- टैंग वंश
- गीत राजवंश
- हान साम्राज्य
- मित्र ट्रुडे
- मेलानोरिया सामान्य
- गोद के समान चिपकनेवाला पीला रोगन
- इनेमल रंग
- चीनी मिटटी
- डिजिटल डाटा
- यूएसबी फ्लैश ड्राइव
- विरासती तंत्र
- संशोधित आवृत्ति मॉडुलन
- कॉम्पैक्ट डिस्क
- पश्च संगतता
- परमाणु कमान और नियंत्रण
- आईबीएम पीसी संगत
- अंगूठी बांधने की मशीन
- प्रयोज्य
- A4 कागज का आकार
- चक्रीय अतिरेक की जाँच
- इजेक्ट (डॉस कमांड)
- अमीगाओएस
- तथा
- शुगार्ट बस
- माप की इकाइयां
- बिलियन
- प्राचीन यूनानी
- सेमीकंडक्टर उद्योग
- सीजेके संगतता
- ओसीडी (डीसी)
- लोहा
- आवृति का उतार - चढ़ाव
- प्रतिबिंब (भौतिकी)
- गलन
- पिछेड़ी संगतता
- अमेरिका का संगीत निगम
- तोशिदादा दोई
- डेटा पूर्व
- घातक हस्तक्षेप
- इंटरनेशनल इलेक्ट्रोटेक्नीकल कमीशन
- अंतरराष्ट्रीय मानकीकरण संगठन
- लाल किताब (ऑडियो सीडी मानक)
- एल टोरिटो (मानक सीडी-रोम)
- आईएसओ छवि
- द्विआधारी उपसर्ग
- असर (यांत्रिक)
- इसके रूप में व्यापार
- चिकित्सीय प्रतिबिंबन
- दवाई
- ललित कलाएं
- ऑप्टिकल कोटिंग
- प्रसाधन सामग्री
- 1984 लॉस एंजिल्स ओलंपिक
- कोविड-19 महामारी
- सर्वश्रेष्ठ मेक्सिकन कंपनियां
- ए पी एस सी
- Fujinon
- परमाणु क्रमांक
- संक्रमण के बाद धातु
- भाग प्रति दस लाख
- अलकाली धातु
- जिंक सल्फाइड
- चमक (खनिज)
- मोह कठोरता
- टिन रो
- क्रांतिक तापमान
- चतुष्कोणीय क्रिस्टल प्रणाली
- चेहरा केंद्रित घन
- संरचनात्मक ताकत पर आकार प्रभाव
- निष्क्रिय जोड़ी प्रभाव
- वैलेंस (रसायन विज्ञान)
- अपचायक कारक
- उभयधर्मी
- आइसोटोप
- जन अंक
- हाफ लाइफ
- समावयवी संक्रमण
- ईण्डीयुम (III) हाइड्रॉक्साइड
- ईण्डीयुम (मैं) ब्रोमाइड
- साइक्लोपेंटैडिएनिल इरिडियम (I)
- साइक्लोपेंटैडेनिल कॉम्प्लेक्स
- जिंक क्लोराइड
- रंग अंधा
- सार्वभौमिक प्रदर्शनी (1867)
- उपोत्पाद
- हवाई जहाज
- जंग
- फ्यूसिबल मिश्र धातु
- पारदर्शिता (प्रकाशिकी)
- दोपंत
- सीआईजीएस सौर सेल
- ईण्डीयुम फेफड़े
- यह प्रविष्टि
- प्रमुख
- आग बुझाने की प्रणाली
- क्षारीय बैटरी
- सतह तनाव
- नाभिकीय रिएक्टर्स
- रंग
- नाभिकीय औषधि
- मांसपेशी
- सीडी आरडब्ल्यू
- बेढब
- चरण-परिवर्तन स्मृति
- DVD-RW
- इलेक्ट्रिकल कंडक्टीविटी
- सोना और चांदी दोनों का
- ताँबा
- बुलियन सिक्का
- निस्संक्रामक
- ओलिगोडायनामिक प्रभाव
- पुरातनता की धातु
- विद्युत कंडक्टर
- पट्टी
- कटैलिसीस
- ऋणावेशित सूक्ष्म अणु का विन्यास
- बढ़ने की योग्यता
- सहसंयोजक बंधन
- हीरा
- शरीर केंद्रित घन
- परमाण्विक भार
- परमाण्विक भार इकाई
- भारात्मक विश्लेषण
- लोहे का उल्कापिंड
- इलेक्ट्रान बन्धुता
- कॉपर (आई) ऑक्साइड
- रसायन बनानेवाला
- रक्षा
- अभिवर्तन
- एल्काइल
- क्लोराइड (डाइमिथाइल सल्फाइड) सोना (I)
- बोरान
- परमाणु रिऐक्टर
- ओल्ड नोर्स
- सजाति
- ओल्ड हाई जर्मन
- लिथुअनिअन की भाषा लिथुअनिअन की भाषा
- बाल्टो-स्लाव भाषाएँ
- पैसे
- धातुकर्म
- चौथी सहस्राब्दी ईसा पूर्व
- एजियन समुद्र
- 16वीं से 19वीं शताब्दी तक वैश्विक चांदी व्यापार
- आदमी की उम्र
- परियों का देश
- पुराना वसीयतनामा
- नए करार
- सींग चांदी
- केशिका की कार्रवाई
- लेड (द्वितीय) ऑक्साइड
- कार्षापण
- एकाग्रता
- डिसेलिनेशन
- खून की कमी
- गल जाना
- हैवी मेटल्स
- रक्त चाप
- पारितोषिक
- बीचवाला मिश्र धातु
- ठोस उपाय
- लाल स्वर्ण
- स्टर्लिंग सिल्वर
- बढ़ने की योग्यता
- उष्मा उपचार
- सामग्री की ताकत
- घुलनशीलता
- लोहा
- संतृप्त घोल
- चरण (मामला)
- गलाने
- अलॉय स्टील
- उच्च गति स्टील
- नरम इस्पात
- मैग्निशियम मिश्रधातु
- निष्कर्षण धातु विज्ञान
- प्रवाह (धातु विज्ञान)
- तन्यता ताकत
- ऊष्मीय चालकता
- ठोस (रसायन विज्ञान)
- अल्फा आयरन
- काम सख्त
- प्लास्टिक विकृत करना
- तेजी से सख्त होना
- उल्कापिंड लोहा
- उल्का पिंड
- लोहे का उल्कापिंड
- देशी लोहा
- सोने का पानी
- बुध (तत्व)
- रंगीन सोना
- कारण की उम्र
- राइट ब्रदर्स
- मिश्र धातु पहिया
- विमान की त्वचा
- धातु का कोना
- कलफाद
- भुना हुआ (धातु विज्ञान)
- अर्धचालक युक्ति
- आवंटन
- सुरमा का विस्फोटक रूप
- तिकोना
- नाज़ुक
- परमाणु समावयवी
- धरती
- नाइट्रिक एसिड
- बोलांगेराइट
- लुईस एसिड
- पॉलीमर
- गठन की गर्मी
- ऑर्गेनोएंटिमोनी केमिस्ट्री
- रासायनिक प्रतीक
- पूर्व राजवंश मिस्र
- छद्म एनकोडर
- इलाके का प्रकार (भूविज्ञान)
- एंटोन वॉन स्वाबा
- फूलना
- गिरोह
- परावर्तक भट्टी
- महत्वपूर्ण खनिज कच्चे माल
- कांच का सुदृढ़ प्लास्टिक
- समग्र सामग्री
- उबकाई की
- पशुचिकित्सा
- जुगाली करनेवाला
- चिकित्सकीय सूचकांक
- अमास्टिगोटे
- पालतु जानवर
- कांच का तामचीनी
- प्रकाश विघटन
- ठंडा
- अनुशंसित जोखिम सीमा
- अनुमेय जोखिम सीमा
- सरकारी उद्योग स्वच्छता पर अमेरिका का सेमिनार
- जीवन या स्वास्थ्य के लिए तुरंत खतरनाक
- रासायनिक तत्वों की प्रचुरता
- धातु के रूप-रंग का एक अधातु पदार्थ
- खनिज विद्या
- परमाणु भार
- ब्रह्मांड की आयु
- क्रस्ट (भूविज्ञान)
- पेट्ज़ाइट
- सल्फ्यूरिक एसिड
- मोलिब्डेनाईट
- इंजन दस्तक
- पोर्फिरी कॉपर डिपॉजिट
- जाल (पैमाने)
- वर्ग तलीय आणविक ज्यामिति
- वर्ग प्रतिवाद
- आवेश-घनत्व तरंग
- चीनी मिट्टी
- थाइरोइड
- नीलम लेजर
- कोरिनेबैक्टीरियम डिप्थीरिया
- व्यावसायिक सुरक्षा और स्वास्थ्य प्रसाशन
- लघुरूपण
- आला बाजार
- व्यक्तिगत अंकीय सहायक
- यूनिवर्सल सीरियल बस
- टक्कर मारना
- सहेजा गया खेल
- अस्थिरमति
- मालिकाना प्रारूप
- हाई डेफिनिशन वीडियो
- डीवीडी फोरम
- कीस शॉहामर इमिंक
- इसके लिए
- एक्सबॉक्स (कंसोल)
- birefringence
- गैर प्रकटीकरण समझौता
- मामला रखो
- डेटा बफर
- इकाइयों की अंतर्राष्ट्रीय प्रणाली
- निस्तो
- पुस्तक का प्रकार
- संयुक्त कंप्यूटर सम्मेलन गिरना
- विलंबता (इंजीनियरिंग)
- टार आर्काइव
- फेज चेंजिंग फिल्म
- एज़ो यौगिक
- प्रकाश द्वारा सहज प्रभावित
- प्रकाश रासायनिक प्रतिघटनाक्रम
- एम-डिस्क
- सूचना प्रक्रम
- कागज़
- दिगपक
- सेंचुरी (HiFi)
- दुकानों से सामान चोरी
- लिफ़ाफ़ा
- संयुक्त राज्य अमेरिका पेटेंट और ट्रेडमार्क कार्यालय
- चंद्रमा का अंधेरा पक्ष
- बादलों से छिपा हुआ
- मेरे पास एक मामला है
- श्रिंक रैप पन्नी
- डिजिटल रिफॉर्मेटिंग
- पैदा हुआ डिजिटल
- फंड
- फ़ाइल का नाम
- इंटरोऑपरेबिलिटी
- मनमुटाव
- हिरासत में लेने की कड़ी
- सोर्स कोड
- एम्यूलेटर
- abandonware
- बाइनरी (सॉफ्टवेयर)
- वाणिज्यिक सॉफ्टवेयर
- अनाथ काम
- क्यूआर कोड
- भूचुंबकीय तूफान
- फाइल का प्रारूप
- एमोरी विश्वविद्यालय पुस्तकालय
- संघीय शिक्षा और अनुसंधान मंत्रालय (जर्मनी)
- अनुसंधान और तकनीकी विकास के लिए रूपरेखा कार्यक्रम
- अंतरिक्ष डेटा प्रणाली के लिए सलाहकार समिति
- समुदाय के स्वामित्व वाली डिजिटल संरक्षण उपकरण रजिस्ट्री
- राष्ट्रीय अभिलेखागार और रिकॉर्ड प्रशासन
- ओपन एक्सेस जर्नल्स की निर्देशिका
- दुनहुआंग पांडुलिपियां
- उन्नत कंप्यूटिंग के विकास के लिए केंद्र
- संस्थागत सहयोग समिति
- चिरस्थायी पहुँच
- डिजिटल आर्टिफिशियल वैल्यू
- यूवीसी आधारित संरक्षण
- क्रोमियम (चतुर्थ) ऑक्साइड
- कैसेट सिंगल
- सर्वाधिकार उल्लंघन
- श्रुतलेख (व्यायाम)
- प्रयोगात्मक संगीत
- DIY पंक नैतिकता
- गृह कम्प्यूटर
- अगफा
- अंशांकन स्वर
- गतिशील सीमा
- वीओआईपी
- दृष्टि दोषरहित
- डिजिटल चित्र
- रंगीन स्थान
- गिरना
- ससम्मान पद अवनति
- संभावना
- पीढ़ी हानि
- सौंदर्य संबंधी
- वीडियो की स्ट्रीमिंग
- स्ट्रीमिंग ऑडियो
- हॉर्न (वाद्य यंत्र)
- मानव मनोविज्ञान
- संपीड़न विरूपण साक्ष्य
- फ़्लिप की गई छवि
- फ्लॉप छवि
- वोरबिस कैसे
- एक ताज रखो
- आईट्यून्स स्टोर
- भग्न संपीड़न
- बनावट का मानचित्रण
- तरंगिकाओं
- जीएलटीएफ
- एमपीईजी-1 ऑडियो परत II
- आराम से कोड-उत्तेजित रैखिक भविष्यवाणी
- कम विलंब CELP
- प्राकृतिक भाषा पीढ़ी
- गौस्सियन धुंधलापन
- दशमलव (सिग्नल प्रोसेसिंग)
- सर्वाधिक बिकने वाले गेम कंसोल की सूची
- स्वतंत्र खेल विकास
- प्लेस्टेशन वीटा
- घड़ी की दर
- उन्नत लघु उपकरण
- उच्च गतिशील रेंज
- और में
- एक्सबॉक्स 360 नियंत्रक
- प्लेस्टेशन कैमरा
- प्लेस्टेशन मूव
- भाप (सेवा)
- देखने के क्षेत्र
- 3 डी ऑडियो प्रभाव
- गूगल क्रोम
- प्लेस्टेशन नेटवर्क ट्राफियां
- प्लेस्टेशन स्टोर
- प्लेस्टेशन वीडियो
- चिकोटी (सेवा)
- स्थापना (कंप्यूटर प्रोग्राम)
- बाहर की दुनिया
- खेल प्रदर्शन
- प्लेस्टेशन 4 फ्री-टू-प्ले गेम्स की सूची
- इंडी गेम डेवलपमेंट
- महाकाव्य खेल
- मरो (एकीकृत सर्किट)
- विकेंद्रीकृत प्रणाली
- जलप्रलय (सॉफ्टवेयर)
- गाना
- अंतराजाल सेवा प्रदाता
- बफ़ेलो में विश्वविद्यालय
- द शेपिंग
- फ़ाइल साझा करना
- समुद्री डाकू खाड़ी
- कर्नेल विश्वविद्यालय
- जैसे को तैसा!
- जलप्रलय (बिटटोरेंट क्लाइंट)
- प्रसारण झंडा
- आईपी पता
- क्लियरनेट (नेटवर्किंग)
- तात्कालिक संदेशन
- प्रतिनिधित्ववादी स्थिति में स्थानांतरण
- संयुक्त राज्य अमेरिका में शुद्ध तटस्थता
- यातायात विश्लेषण
- प्रोग्रामिंग की भाषाएँ
- बहादुर (वेब ब्राउज़र)
- रस (पॉडकास्टिंग)
- द लिबर्टीनेस
- वितरित अभिकलन
- न्याय के उच्च न्यायालय
- उड़ान ऊंचाई
- विद्युतीय संभाव्यता
- इलेक्ट्रोमैग्नेटिक इंडक्शन
- सामान्य मोड संकेत
- वृद्धि रक्षक
- क्षणिक (बिजली)
- बिजली चमकना
- हिमस्खलन टूटना
- विद्युत शक्ति वितरण
- अधिष्ठापन
- बिजली का टूटना
- साइबर क्राइम
- शून्य-दिन (कंप्यूटिंग)
- संगणनीयता सिद्धांत (कंप्यूटर विज्ञान)
- मस्तिष्क (कंप्यूटर वायरस)
- एचटीएमएल ईमेल
- सुनोस
- सेवा का वितरित इनकार
- ज़बरदस्ती वसूली
- सहबद्ध विपणन
- धोखाधड़ी पर क्लिक करें
- ड्राइव-बाय डाउनलोड
- एनएसए एएनटी कैटलॉग
- विस्फ़ोटक (कंप्यूटर कीड़ा)
- अस्पष्टता (सॉफ्टवेयर)
- रचनात्मक गलती
- सामान्य भेद्यताएं और जोखिम
- अतिक्रमण संसूचन प्रणाली
- मज़बूत पारण शब्द
- Windows दुर्भावनापूर्ण सॉफ़्टवेयर निष्कासन उपकरण
- खतरा (कंप्यूटर)
- डोमेन जनरेशन एल्गोरिथम
- कनाडा की राष्ट्रीयता कानून
- वाग्मिता
- वंशागति
- ध्वनि-विज्ञान
- मूक बधिर
- विद्युतीय प्रतिरोध
- शपथ पत्र
- कंपोस्टिंग शौचालय
- अलेक्जेंडर ग्राहम बेल सम्मान और श्रद्धांजलि
- कनाडा की सेना
- फ्रेंच फ़्रैंक
- बधिरों के लिए अलेक्जेंडर ग्राहम बेल एसोसिएशन एंड हार्ड ऑफ हियरिंग
- 100 महानतम ब्रितानी
- विदेश महाविद्यालय
- पब्लिक स्कूल (सरकारी वित्त पोषित)
- शुक्र का पारगमन
- अमेरिकी इतिहास का राष्ट्रीय संग्रहालय
- श्रुतलेख (व्यायाम)
- चचेरा भाई
- सापेक्षता का सिद्धांत
- पुराना क्वांटम सिद्धांत
- तथ्य
- ब्रम्हांड
- समोसी के एरिस्टार्चस
- लीनियर अलजेब्रा
- गणना
- क्वांटम जानकारी
- डॉक्टर की डिग्री
- ब्रह्माण्ड विज्ञान
- पदार्थ विज्ञान
- पोस्ट डॉक्टरल शोधकर्ता
- भौतिकी में नोबेल पुरस्कार
- भौतिक समाज (बहुविकल्पी)
- शैक्षणिक सम्मेलन
- सामरिक रक्षा पहल
- नीदरलैंड में अरब
- नीदरलैंड में 2019 यूरोपीय संसद चुनाव
- नीदरलैंड की राजधानी
- नीदरलैंड की कैबिनेट
- एम्स्टर्डम एयरपोर्ट शिफोलो
- यूरोपीय देशों का क्षेत्रफल और जनसंख्या
- निर्यात करना
- नीदरलैंड की दवा नीति
- धनुष और बाण
- मिट्टी के बरतन
- ब्रिटिश द्कदृरप
- हाथी दांत
- बोर्नियो की लड़ाई
- उट्रेच के बिशपरिक
- हैनॉटो का काउंटी
- डची ऑफ गेल्डरलैंड
- निचले देशों में शहर के अधिकार
- गेम्ब्लोक्स की लड़ाई (1578)
- अभियोग का अधिनियम
- इंग्लैंड की एलिजाबेथ प्रथम
- डची ऑफ गेल्डरलैंड
- कंफेडेरशन
- गयाना का डच उपनिवेश
- बसाना
- परिसंपत्ति मूल्य मुद्रास्फीति
- भालू छापे
- बटावियन गणराज्य
- पूर्वी मोर्चा (द्वितीय विश्व युद्ध)
- द्वितीय विश्व युद्ध के दौरान धुरी शक्तियों के साथ सहयोग
- पहला बख़्तरबंद डिवीजन (पोलैंड)
- ड्रीस वैन एगटो
- नीदरलैंड के राज्य के लिए चार्टर
- आम बाज़ार
- पर्यावरण के मुद्दें
- नीदरलैंड्स एंटिलीज़ का विघटन
- औसत समुद्र तल से ऊपर
- बांध (निर्माण)
- मुहाना
- एओलियन प्रघटनाक्रमएं
- विज्ञापन
- ड्यून
- वृत्ताकार क्षेत्र
- ईकोरियोजन
- एबीसी द्वीप समूह (कम एंटिल्स)
- हॉलैंड की भाषा
- संघात्मक अवस्था
- नीदरलैंड का संविधान
- नीदरलैंड की आपराधिक न्याय प्रणाली
- ईसाई संघ (नीदरलैंड)
- 2021 नीदरलैंड आम चुनाव
- अटलांटिसिज्म
- भरती
- दूसरा इन्फैंट्री डिवीजन (संयुक्त राज्य अमेरिका)
- यूरो के सिक्के
- डच बीमारी
- ऊर्जा घनत्व
- नगर-राज्यों
- महानगर
- क्षेत्रीय या अल्पसंख्यक भाषाओं के लिए यूरोपीय चार्टर
- बुद्ध धर्म
- नीदरलैंड के साम्राज्य में इवेंजेलिकल लूथरन चर्च
- नीदरलैंड में बौद्ध धर्म
- 1886 डच सुधार चर्च विभाजन
- 1834 डच सुधार चर्च विभाजन
- कलविनिज़म
- आमर्सफ़ॉर्ट
- कंटेनर पोर्ट
- थोक सामग्री हैंडलिंग
- बेटुवेरूटे
- आइंडहोवन एयरपोर्ट
- आर्ट नूवो
- भांग (दवा)
- ऐनी (गायक)
- मौत
- यूरोविज़न गाना प्रतियोगिता
- संयुक्त राज्य अमेरिका का सिनेमा
- एक मोस्ट वांटेड मैन (फिल्म)
- फ़ीफ़ा वर्ल्ड कप
- 2021 अबू धाबी ग्रांड प्रिक्स
- 2016 स्पेनिश ग्रां प्री
- एडम (करता है)
- पीएसवी आइंडहोवेन
- मकानों
- नाज़ी प्रसारण
- नीदरलैंड की लड़ाई
- राष्ट्रों के बीच धर्मी
- KZ Herzogenbusch . के उप शिविरों की सूची
- श्रुतलेख मशीनें
- मॉस स्टोरेज उपकरण
- आंसरिंग मशीन
- मुनाफे का अंतर
- फिलिप्स हुए
- लुमिलेड्स
- एक्को
- ADAC प्रयोगशालाएँ
- औद्योगिक डिजाइनों के अंतर्राष्ट्रीय जमा के संबंध में हेग समझौता
- एशिया प्रशांत
- गुआंग्डोंग
- एल्सिंटो
- हाइफ़ा
- सिंगापुर के नए शहर
- टीवीई टेस्ट कार्ड
- लोंगविक
- लैमोटे बेउरोन
- स्टॉकपोर्ट का मेट्रोपॉलिटन बरो
- मौखिक हाइजीन
- सॉलिड स्टेट लाइटिंग
- एडीलेड
- Varese . के प्रांत
- विकिरण कैंसर विज्ञान
- चुम्बकीय अनुनाद प्रतिबिंबन
- सी शाखा
- ज्योफ बोडिने
- राक्षस ऊर्जा NASCAR कप श्रृंखला
- परिपत्र अर्थव्यवस्था में तेजी लाने के लिए मंच
- गरमागरम प्रकाश बल्ब
- गैरकानूनी संलेखन
- ग्रीनहाउस गैस का उत्सर्जन
- ब्रोमिनेटेड फ्लेम रिटार्डेंट
- अमरीकी गृह युद्ध
- 1996 ग्रीष्मकालीन ओलंपिक
- चट्टाहूची नदी
- 1956 चीनी का कटोरा
- नागरिक अधिकारों के आंदोलन
- 1996 ग्रीष्मकालीन ओलंपिक खेल
- 1996 के ग्रीष्मकालीन ओलंपिक के लिए बोलियां
- चट्टाहूची नदी राष्ट्रीय मनोरंजन क्षेत्र
- अटलांटा में अफ्रीकी अमेरिकी
- अफ़्रीकी-अमेरिकी अंग्रेज़ी
- आप दो (फिल्म)
- अटलांटा (टीवी श्रृंखला)
- अमेरिकी फुटबॉल का गठबंधन
- 2020 ग्रीष्मकालीन ओलंपिक
- सिटी पार्क
- बिल कैंपबेल (मेयर)
- रोग नियंत्रण और रोकथाम के लिए केंद्र
- अमेरिकी समुदाय सर्वेक्षण
- अनुकूली रूपांतरण ध्वनिक कोडिंग
- अंतरिक्ष में लेजर संचार
- उच्च परिभाषा ऑप्टिकल डिस्क प्रारूप युद्ध
- इलेक्ट्रॉनिक्स विनिर्माण सेवाएं
- निकोनो
- इल्लुमिना (कंपनी)
- मित्सुबिशी इलेक्ट्रिक
- सीएमओएस इमेज सेंसर
- हार हुआ नेता
- एआरसीसीओएस सुरक्षा
- एनिमे
- eVgo
- कार में मनोरंजन
- निवेश मे भरोसा
- भूतापीय उर्जा
- जैविक प्रकाश उत्सर्जक डायोड
- हायपैक
- आम तौर पर स्वीकृत लेखा सिद्धांत (संयुक्त राज्य अमेरिका)
- दक्षिण - पूर्व एशिया
- विशिष्टता (तकनीकी मानक)
- पारदर्शिता और पारदर्शिता
- लेजर डिस्क
- पीसीएम अनुकूलक
- त्रुटि सुधार
- जीवित आंखें (बी गीज़ एल्बम)
- 52 वीं स्ट्रीट (एल्बम)
- पल्स चौड़ाई मॉडुलन
- सीडी रॉम
- पिछड़ा संगत
- हानिपूर्ण संपीड़न
- अंतर्राष्ट्रीय मानक
- परिमाणीकरण (सिग्नल प्रोसेसिंग)
- तेजस्वी
- बेयरुथ महोत्सव
- WHO
- राजकुमार (संगीतकार)
- पूर्णांक (कंप्यूटर विज्ञान)
- C2 त्रुटि
- ऑडियो फ़ाइल प्रारूप
- कार्य (ऑडियो प्रारूप)
- डुअलडिस्क
- सूचान प्रौद्योगिकी
- चिकित्सकीय संसाधन
- पहला चीन-जापानी युद्ध
- घाटबंधी
- आर्थिक अनुमोदन
- हाइड्रोजन ईंधन सेल
- उच्च परिभाषा ऑप्टिकल डिस्क प्रारूप युद्ध
- फुकुशिमा I परमाणु दुर्घटनाएं
- एमएसएक्स टर्बो आर
- संग्रहालय
- बांड (वित्त)
- विदेशी भ्रष्ट व्यवहार अधिनियम
- पूर्वी जकार्ता
- जर्मनी की राष्ट्रीय फ़ुटबॉल टीम
- भारत की राष्ट्रीय फुटबॉल टीम
- 2005 NASCAR Busch Series
- पैनासोनिक कैमकोर्डर की सूची
- जापानी कंपनियों की सूची
- हैरी न्यक्विस्ट
- खास समय
- निरंतर समय संकेत
- प्रतिक दर
- विद्युत तार
- फुरियर रूपांतरण
- नमूना प्रमेय
- हाई डेफिनिशन वीडियो
- नीला लेजर
- एचडीआई (अंतरघटनाक्रमशीलता)
- एक्सबॉक्स 360 एचडी डीवीडी प्लेयर
- द फैंटम ऑफ़ द ओपेरा (2004 फ़िल्म)
- जंगली में (फिल्म)
- सन्निहित संयुक्त राज्य अमेरिका
- विश्वसनीय ग्राहक
- वॉल्ट डिज़्नी कंपनी
- उच्च बैंडविड्थ डिजिटल सामग्री संरक्षण
- जावास्क्रिप्ट
- पश्च संगतता
- सुझाव दिया खुदरा मूल्य
- उन्नत अन्तरघटनाक्रमशीलता कंसोर्टियम
- मानक परिभाषा
- आधार - सामग्री संकोचन
- असतत कोसाइन परिवर्तन
- 1 इंच टाइप बी वीडियो टेप
- रॉबर्ट बॉश GmbH
- डी-2 (वीडियो)
- स्पार्कस्टेशन
- गैर-रैखिक संपादन प्रणाली
- एप्पल कंप्यूटर
- सीधा प्रसारण उपग्रह
- वर्णक्रम पुनः आवंटन
- स्थिर बिट दर
- गैर-रैखिक संपादन
- छवि वियोजन
- हाई स्पीड कैमरा
- डाल (वीडियो)
- 'prohd
- प्रदर्शन पहलू अनुपात
- साफ कमरा
- दोस्त
- कपास क्लब (फिल्म)
- लंबवत रिक्त अंतराल
- शोर अनुपात का संकेत
- मैं नहीं कर सकता
- एकाधिक उप-Nyquist नमूना एन्कोडिंग
- कोरवस (कंपनी)
- स्वतंत्र राष्ट्रों का राष्ट्रमंडल
- बंद शीर्षक
- उड़ान पर
- बैठक कक्ष
- पहाड़ी (अखबार)
- बजने वाली कलाकृतियां
- मच्छर का शोर
- डिजिटल डाटा
- आस्पेक्ट अनुपात
- स्थिर बिट दर
- चित्रों का समूह
- चीन की सरकार
- वीडियोटेप
- टेलीविज़न सीरीज़
- 16 मिमी फिल्म
- 8 मिमी फिल्म
- वीडियोटेप
- कल्ट फिल्म्स
- रेंटल एग्रीमेंट
- सेल थ्रू
- मांग का नियम
- वॉल्ट डिज़्नी एनिमेशन स्टूडियो फ़िल्मों की सूची
- नागरिक केन
- आस्ट्रेलिया के जादूगर (1939 फिल्म)
- सर्वाधिकार उल्लंघन
- रोम (2018 फिल्म)
- सीमित नाट्य विमोचन
- विखंडन (कंप्यूटर)
- गैपलेस प्लेबैक
- UNIX- जैसे
- मिनीडीवीडी
- अब नाओमी
- Triforce (आर्केड प्रणाली बोर्ड)
- आर्केडिया का आसमान
- डबल घनत्व कॉम्पैक्ट डिस्क
- बंद शीर्षक
- मैक ओएस
- जीबरा क्रोससिंग
- साइन तरंग
- अप्रगामी तरंगे
- आवरण (गणित)
- गुणात्मक प्रतिलोम
- ध्वनि का दबाव
- विद्युत चुम्बकीय वर्णक्रम
- ध्वनि की तरंग
- प्रकाश कि गति
- वायलेट (रंग)
- तापमान और दबाव के लिए मानक स्थितियां
- एक
- सीमा की स्थिति
- उन लोगों के
- विद्युतचुम्बकीय तरंगें
- अपवर्तक सूचकांक
- सीधे रास्ते से फेर देना
- डब्ल्यूकेबी सन्निकटन
- ऊर्जा संरक्षण
- ब्रिलॉइन क्षेत्र
- नमूनाकरण (सिग्नल प्रोसेसिंग)
- फोनोन्स
- कोनोइडल वेव
- अध्यारोपण सिद्धांत
- समुद्र की तरंग
- तरंग बंडल
- तरंग घटनाक्रम
- फ्रेस्नेल विवर्तन
- छोटे कोण सन्निकटन
- sinc समारोह
- माइक्रोस्कोप
- फ्रौनहोफर लाइन्स