न्यूनतम स्पैनिंग ट्री (एमएसटी): Difference between revisions

Revision as of 12:32, 6 July 2023

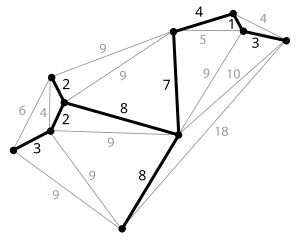
एक समतलीय ग्राफ और उसका न्यूनतम स्पैनिंग ट्री। प्रत्येक किनारे को उसके वजन के साथ लेबल किया गया है, जो यहां लगभग उसकी लंबाई के समानुपाती है।

न्यूनतम स्पैनिंग ट्री (एमएसटी) या न्यूनतम वेट स्पैनिंग ट्री संयोजित ग्राफ के किनारों का उपसमूह है, किनारे-भारित अप्रत्यक्ष ग्राफ जो बिना किसी चक्र (ग्राफ सिद्धांत) के सभी वर्टेक्स (ग्राफ सिद्धांत) को साथ जोड़ता है। ^[1] अर्थात, यह फैला हुआ ट्री है जिसके किनारे के भार का योग यथासंभव छोटा है। ^[2] अधिक सामान्यतः, किसी भी किनारे-भारित अप्रत्यक्ष ग्राफ (आवश्यक रूप से जुड़ा नहीं) में न्यूनतम स्पैनिंग जंगल होते हैं, जो इसके जुड़े घटक (ग्राफ सिद्धांत) के लिए न्यूनतम स्पैनिंग ट्री का संघ है।

न्यूनतम स्पैनिंग ट्री के लिए कई उपयोग के स्थिति हैं। उदाहरण दूरसंचार कंपनी है जो नए पड़ोस में केबल बिछाने की प्रयास कर रही है। यदि केबल को केवल कुछ निश्चित रास्तों (जैसे सड़कों) के किनारे गाड़ने के लिए बाध्य किया जाता है, जिससे उन रास्तों से जुड़े बिंदुओं (जैसे घरों) को सम्मिलित करने वाला ग्राफ होता है। कुछ रास्ते अधिक महंगे हो सकते हैं, क्योंकि वे लंबे हैं, या केबल को अधिक गहराई तक गाड़ने की आवश्यकता होती है; इन पथों को बड़े भार वाले किनारों द्वारा दर्शाया जाता है। मुद्रा किनारे के वजन के लिए स्वीकार्य इकाई है त्रिकोण असमानता जैसे ज्यामिति के सामान्य नियमों का पालन करने के लिए किनारे की लंबाई की कोई आवश्यकता नहीं है। उस ग्राफ़ के लिए स्पैनिंग ट्री उन रास्तों का उपसमूह होगा जिनमें कोई चक्र नहीं है किन्तु फिर भी वे हर घर को जोड़ते हैं; वहाँ अनेक स्पैनिंग ट्री संभव हो सकते हैं। न्यूनतम स्पैनिंग ट्री सबसे कम कुल निवेश वाला होगा, जो केबल बिछाने के लिए सबसे कम खर्चीले पथ का प्रतिनिधित्व करता है।

, जिसके किनारे का वजन शीर्षों के बीच रेक्टिलिनियर दूरी के

गुण

संभावित बहुलता

यदि ग्राफ़ में $n$ शीर्ष हैं तो प्रत्येक स्पैनिंग ट्री में $n - 1$ किनारे हैं।

यह आंकड़ा दर्शाता है कि ग्राफ़ में से अधिक न्यूनतम स्पैनिंग ट्री हो सकते हैं। चित्र में, ग्राफ़ के नीचे के दो ट्री दिए गए ग्राफ़ के न्यूनतम स्पैनिंग ट्री की दो संभावनाएँ हैं।

एक ही वजन के कई न्यूनतम स्पैनिंग ट्री हो सकते हैं; विशेष रूप से, यदि किसी दिए गए ग्राफ़ के सभी किनारों का भार समान है, जिससे उस ग्राफ़ का प्रत्येक फैला हुआ ट्री न्यूनतम है।

अद्वितीयता

यदि प्रत्येक किनारे का अलग वजन है जिससे केवल एक, अद्वितीय न्यूनतम स्पैनिंग ट्री होता है। यह कई यथार्थवादी स्थितियों में सही है, जैसे कि ऊपर दूरसंचार कंपनी का उदाहरण, जहां यह संभव नहीं है कि किन्हीं दो रास्तों की निवेश पूर्ण रूप से समान होता है। यह विस्तृत वनों का भी सामान्यीकरण करता है।

प्रमाण:

विरोधाभास से प्रमाण, कि दो $A$ और $B$ अलग-अलग एमएसटी हैं.
चूंकि $A$ और $B$ समान नोड्स होने के अतिरिक्त भिन्न हैं, इसलिए कम से कम एक किनारा ऐसा है जो एक का है किन्तु दूसरे का नहीं। ऐसे किनारों के बीच मान लीजिए कि $e 1$ सबसे कम वजन वाला है, यह विकल्प अद्वितीय है क्योंकि सभी किनारों का वजन अलग-अलग है। व्यापकता की हानि के बिना मान लें कि $e 1$ , $A$ में है।
चूँकि $B$ एक एमएसटी है ${e 1} \cup B$ में $e 1$ के साथ एक चक्र $C$ होना चाहिए।
चूंकि ट्री A में कोई चक्र नहीं है इसलिए $C$ का एक किनारा $e 2$ होना चाहिए जो $A$ में नहीं है।
चूँकि $e 1$ को $A$ और $B$ में से किसी एक से संबंधित अद्वितीय सबसे कम वजन वाले किनारे के रूप में चुना गया था, इसलिए $e 2$ का वजन $e 1$ के वजन से अधिक होना चाहिए।
चूँकि $e 1$ और $e 2$ चक्र $C$ का भाग हैं, इसलिए $B$ में $e 2$ को $e 1$ से बदलने पर कम वजन वाला एक स्पैनिंग ट्री प्राप्त होता है।
यह इस धारणा का खंडन करता है कि $B$ एमएसटी है.

अधिक सामान्यतः, यदि किनारे के वजन सभी अलग-अलग नहीं होते हैं जिससे न्यूनतम स्पैनिंग ट्री में वजन का केवल बहु सेट अद्वितीय होना निश्चित है; यह सभी न्यूनतम स्पैनिंग ट्री के लिए समान है।^[3]

न्यूनतम-निवेश उपग्राफ

यदि भार सकारात्मक हैं, जिससे न्यूनतम स्पैनिंग ट्री, वास्तव में, ग्राफ सिद्धांत की न्यूनतम-निवेश शब्दावली है सभी शीर्षों को जोड़ने वाले सबग्राफ, क्योंकि यदि सबग्राफ में पथ (ग्राफ सिद्धांत) होता है, तो उस चक्र के साथ किसी भी किनारे को हटाने से कमी आएगी इसकी निवेश और कनेक्टिविटी को सुरक्षित रखें।

साइकिल प्रोपर्टी

ग्राफ़ में किसी भी चक्र $C$ के लिए यदि $C$ के किनारे $e$ का वजन $C$ के अन्य सभी किनारों के किसी भी व्यक्तिगत वजन से बड़ा है तो यह किनारा एमएसटी से संबंधित नहीं हो सकता है।

प्रमाण: इसके विपरीत मान लें कि $e$ एक एमएसटी $T 1$ से संबंधित है। फिर $e$ को हटाने से $T 1$ दो सबट्री में टूट जाएगा और $e$ के दोनों सिरे अलग-अलग सबट्री में होंगे। $C$ का शेष भाग सबट्री को फिर से जोड़ता है इसलिए C का एक किनारा $f$ होता है जिसके सिरे अलग-अलग सबट्री में होते हैं अर्थात यह सबट्री को $T 1$ के भार से कम भार वाले $T 2$ वृक्ष में पुनः जोड़ता है क्योंकि f का भार $e$ के भार से कम है।

प्रोपर्टी कट

यह आंकड़ा एमएसटी की कटी हुई प्रोपर्टी को दर्शाता है।

T

दिए गए ग्राफ़ का एकमात्र एमएसटी है। यदि

S = {A, B, D, E},

इस प्रकार

V - S = {C, F},

तो कट के पार किनारे की 3 संभावनाएँ हैं

(S, V - S)

, वे किनारे हैं

BC

,

EC

,

EF

मूल ग्राफ़ का। फिर, ई कट के लिए न्यूनतम-वजन-किनारे में से है

S \cup {e}

एमएसटी का भाग है

T

.

किसी भी कट के लिए (ग्राफ सिद्धांत) $C$ ग्राफ़ का, यदि किनारे का भार $e$ के कट-सेट में $C$ कट-सेट के अन्य सभी किनारों के वजन से पूर्ण रूप से छोटा है $C$ , तो यह किनारा ग्राफ़ के सभी एमएसटी से संबंधित है।

प्रमाण: यह कहना व्यर्थ है कि एमएसटी $T$ है जिसमें सम्मिलित $e$ नहीं है . जोड़ा जा रहा है $e$ को $T$ चक्र का उत्पादन करेगा, जो एक ही बार में कट को पार कर जाएगा $e$ और दूसरे किनारे पर वापस चला जाता है $e'$ . हटाया जा रहा है $e'$ हमें फैला हुआ ट्री मिलता है $T ∖{e'} \cup {e}$ की तुलना में सख्ती से कम वजन का $T$ . यह इस धारणा का खंडन करता है कि $T$ एमएसटी था.

इसी तरह के तर्क से, यदि कट में से अधिक किनारे न्यूनतम वजन के होते हैं, तो ऐसा प्रत्येक किनारा किसी न्यूनतम स्पैनिंग ट्री में समाहित होता है।

न्यूनतम-निवेश बढ़त

यदि न्यूनतम निवेश बढ़त e किसी ग्राफ़ का अद्वितीय है, जिससे यह किनारा किसी भी एमएसटी में सम्मिलित है।

प्रमाण: यदि $e$ को एमएसटी में सम्मिलित नहीं किया गया था, जोड़ने के बाद बने चक्र में किसी भी (बड़ी निवेश) किनारे को हटा दिया गया था $e$ एमएसटी के लिए, कम वजन का फैला हुआ ट्री प्राप्त होता है।

संकुचन

यदि $T$ एमएसटी किनारों का ट्री है, तो हम अनुबंध कर सकते हैं $T$ अनुबंधित ग्राफ प्लस के एमएसटी को अपरिवर्तनीय बनाए रखते हुए ही शीर्ष पर $T$ संकुचन से पहले ग्राफ़ के लिए एमएसटी देता है।^[4]

एल्गोरिदम

नीचे दिए गए सभी एल्गोरिदम में, $m$ ग्राफ़ में किनारों की संख्या है और $n$ शीर्षों की संख्या है.

क्लासिक एल्गोरिदम

न्यूनतम स्पैनिंग ट्री को खोजने के लिए पहला एल्गोरिदम 1926 में चेक वैज्ञानिक ओटाकर बोरोव्का द्वारा विकसित किया गया था (बोरोव्का का एल्गोरिदम देखें)। इसका उद्देश्य मोराविया का कुशल विद्युत कवरेज था। एल्गोरिदम चरणों के अनुक्रम में आगे बढ़ता है। प्रत्येक चरण में, जिसे बोरुव्का चरण कहा जाता है, यह जंगल की पहचान करता है $F$ ग्राफ़ में प्रत्येक शीर्ष पर न्यूनतम-वजन वाली बढ़त की घटना सम्मिलित है $G$ , फिर ग्राफ बनाता है $G1 = G \ F$ अगले चरण के इनपुट के रूप में। यहाँ $G \ F$ से प्राप्त ग्राफ़ को दर्शाता है $G$ किनारों को अंदर की ओर सिकोड़कर $F$ (कट प्रोपर्टी के अनुसार, ये किनारे एमएसटी से संबंधित हैं)। प्रत्येक बोरुव्का चरण में रैखिक समय लगता है। चूँकि प्रत्येक चरण में शीर्षों की संख्या कम से कम आधी हो जाती है, बोरुव्का का एल्गोरिथ्म $O (m log n)$ समय लेता है।^[4]

दूसरा एल्गोरिथम प्राइम का एल्गोरिथम है, जिसका आविष्कार 1930 में वोजटेक जार्निक द्वारा किया गया था और 1957 में रॉबर्ट सी. प्राइम और 1959 में एडस्गर डब्ल्यू. डिज्क्स्ट्रा द्वारा फिर से खोजा गया था। मूल रूप से, यह एमएसटी को बढ़ाता है ( $T$ ) समय में किनारा प्रारंभ में, $T$ में सही शीर्ष सम्मिलित है। प्रत्येक चरण में, $T$ को कम से कम वजन वाले किनारे के साथ संवर्धित किया गया है $(x, y)$ ऐसा है कि $x$ में है $T$ और $y$ अभी तक अंदर नहीं है $T$ . कट प्रॉपर्टी द्वारा, सभी किनारों को जोड़ा गया $T$ एमएसटी में हैं। इसका रन-टाइम या तो है $O (m log n)$ या $O (m + n log n)$ , प्रयुक्त डेटा-संरचनाओं पर निर्भर करता है।

सामान्यतः उपयोग में आने वाला तीसरा एल्गोरिदम क्रुस्कल का एल्गोरिदम है, जो $O (m log n)$ समय भी लेता है ।

एक चौथा एल्गोरिदम, जो सामान्यतः उपयोग नहीं किया जाता है, रिवर्स-डिलीट एल्गोरिदम है, जो क्रुस्कल के एल्गोरिदम के विपरीत है। इसका रनटाइम है $O(m log n (log log n) 3)$ .

ये चारों ग्रीडी एल्गोरिदम हैं। चूंकि वे बहुपद समय में चलते हैं, ऐसे ट्री को खोजने की समस्या एफपी (जटिलता) में है, और संबंधित निर्णय समस्याएं जैसे कि यह निर्धारित करना कि क्या कोई विशेष किनारा एमएसटी में है या यह निर्धारित करना कि न्यूनतम कुल वजन निश्चित मूल्य से अधिक है या नहीं, पी में हैं।

तेज़ एल्गोरिदम

कई शोधकर्ताओं ने अधिक कम्प्यूटेशनल रूप से कुशल एल्गोरिदम खोजने का प्रयास किया है।

एक तुलना मॉडल में, जिसमें किनारे के वजन पर एकमात्र अनुमत संचालन जोड़ीदार तुलना है, कर्गेर, कलें & टार्जन (1995) बोरोव्का के एल्गोरिदम और रिवर्स-डिलीट एल्गोरिदम के संयोजन के आधार पर अपेक्षित रैखिक समय एमएसटी एल्गोरिदम मिला था।^[5]^[6]

ज्ञात जटिलता के साथ सबसे तेज़ गैर-यादृच्छिक तुलना-आधारित एल्गोरिदम, बर्नार्ड चेज़ेल द्वारा, सॉफ्ट हीप , अनुमानित प्राथमिकता कतार पर आधारित है।^[7]^[8] इसके चलने का समय है $O (m α(m, n))$ , जहाँ $α$ शास्त्रीय कार्यात्मक एकरमैन फ़ंक्शन इनवर्स है। प्रोग्राम $α$ अत्यंत धीमी गति से बढ़ता है, जिससे सभी व्यावहारिक उद्देश्यों के लिए इसे 4 से अधिक नहीं स्थिरांक माना जा सके; इस प्रकार चेज़ेल का एल्गोरिदम रैखिक समय के बहुत निकट ले जाता है।

विशेष स्थितियों में रैखिक-समय एल्गोरिदम

सघन रेखांकन

यदि ग्राफ सघन है (अर्थात्) $m / n \geq log log log n)$ , फिर फ्रेडमैन और टार्जन द्वारा नियतात्मक एल्गोरिदम समय $O(m)$ में एमएसटी का पता लगाता है .^[9] एल्गोरिदम कई चरणों को क्रियान्वित करता है। प्रत्येक चरण प्राइम के एल्गोरिदम को कई बार निष्पादित करता है, प्रत्येक चरण सीमित संख्या में चरणों के लिए। प्रत्येक चरण का रन-टाइम $O(m + n)$ है यदि चरण से पहले शीर्षों की संख्या $n'$ है चरण के बाद शेष शीर्षों की संख्या ${\tfrac {n'}{2^{m/n'}}}$ अधिकतम होती है . इसलिए, अधिक से अधिक $log* n$ चरणों की आवश्यकता होती है, जो घने ग्राफ़ के लिए रैखिक रन-टाइम देता है।^[4]

ऐसे अन्य एल्गोरिदम हैं जो घने ग्राफ़ पर रैखिक समय में काम करते हैं।^[7]^[10]

पूर्णांक भार

यदि किनारे का भार बाइनरी में दर्शाए गए पूर्णांक हैं, जिससे नियतात्मक एल्गोरिदम ज्ञात होते हैं जो $O (m + n)$ पूर्णांक संचालन समस्या को हल करते हैं ।^[11] क्या तुलना-आधारित एल्गोरिदम द्वारा रैखिक समय में सामान्य ग्राफ़ के लिए समस्या को निश्चित रूप से हल किया जा सकता है या नहीं यह खुला प्रश्न बना हुआ है।

निर्णय ट्री

दिया गया ग्राफ $G$ जहां नोड्स और किनारे तय हो गए हैं किन्तु वजन अज्ञात है, वजन के किसी भी क्रमपरिवर्तन के लिए एमएसटी की गणना के लिए बाइनरी निर्णय ट्री (डीटी) का निर्माण करना संभव है। डीटी के प्रत्येक आंतरिक नोड में दो किनारों के बीच तुलना होती है, उदाहरण के लिए के बीच किनारे का वजन है $x$ और $y$ बीच के किनारे के वजन से बड़ा $w$ और $z$ ? . नोड के दो बच्चे हां या ना में दो संभावित उत्तरों के अनुरूप हैं। डीटी के प्रत्येक पत्ते में किनारों की सूची $G$ होती है जो एमएसटी के अनुरूप है। डीटी की रनटाइम जटिलता एमएसटी को खोजने के लिए आवश्यक प्रश्नों की सबसे बड़ी संख्या है, जो डीटी की गहराई है। ग्राफ़ के लिए डीटी $G$ को इष्टतम कहा जाता है यदि इसमें सभी सही डीटी $G$ की तुलना में सबसे छोटी गहराई होटी है .

प्रत्येक पूर्णांक के लिए $r$ , सभी ग्राफ़ के लिए इष्टतम निर्णय ट्री $r$ खोज संभव है पाशविक-बल खोज द्वारा शिखर। यह खोज दो चरणों में आगे बढ़ती है.

A. सभी संभावित डीटी उत्पन्न करना

$r$ शीर्षों पर $2^{r \choose 2}$ अलग-अलग ग्राफ़ हैं।
प्रत्येक ग्राफ़ के लिए एक एमएसटी सदैव $r (r - 1)$ तुलनाओं का उपयोग करके पाया जा सकता है जैसे प्राइम के एल्गोरिदम द्वारा।
इसलिए, $r 2$ इष्टतम डीटी की गहराई से कम है .
इसलिए, इष्टतम डीटी में आंतरिक नोड्स की संख्या $2^{r^{2}}$ कम है .
प्रत्येक आंतरिक नोड दो किनारों की तुलना करता है। किनारों की संख्या $r 2$ अधिकतम है इसलिए तुलनाओं की भिन्न संख्या अधिकतम $r 4$ है .
इसलिए, संभावित डीटी की संख्या से कम है
${(r^{4})}^{(2^{r^{2}})}=r^{2^{(r^{2}+2)}}.$

बी. सही डीटी की पहचान करना यह जांचने के लिए कि क्या डीटी सही है, इसे किनारे के वजन के सभी संभावित क्रमपरिवर्तनों पर जांचा जाना चाहिए।

ऐसे क्रमपरिवर्तनों की संख्या $(r 2)!$ अधिकतम है .
प्रत्येक क्रमपरिवर्तन के लिए, किसी भी वर्तमान एल्गोरिदम का उपयोग करके दिए गए ग्राफ़ पर एमएसटी समस्या को हल करें, और परिणाम की तुलना डीटी द्वारा दिए गए उत्तर से करें।
किसी भी एमएसटी एल्गोरिदम का रनिंग टाइम अधिकतम $r 2$ होता है , इसलिए सभी क्रमपरिवर्तनों की जांच करने के लिए आवश्यक कुल समय $(r 2 + 1)!$ अधिकतम है .

इसलिए, सभी ग्राफ़ के लिए इष्टतम डीटी खोजने के लिए आवश्यक कुल समय $r$ शीर्ष है:^[4]:

$2^{r \choose 2}\cdot r^{2^{(r^{2}+2)}}\cdot (r^{2}+1)!,$

जो कि कम है

2^{2^{r^{2}+o(r)}}.

इष्टतम एल्गोरिदम

सेठ पेटी और विजय रामचन्द्रन ने पाया है सिद्धतः इष्टतम नियतात्मक तुलना-आधारित न्यूनतम स्पैनिंग ट्री एल्गोरिदम है।^[4] निम्नलिखित एल्गोरिथम का सरलीकृत विवरण है।

माना $r = log log log n$ , जहाँ $n$ शीर्षों की संख्या है. सभी इष्टतम निर्णय ट्री खोजें $r$ शिखर. यह $O (n)$ समय रहते किया जा सकता है (ऊपर निर्णय ट्री देखें)।
ग्राफ़ $r$ को अधिकतम घटकों में विभाजित करें प्रत्येक घटक में शीर्ष यह विभाजन सॉफ्ट हीप का उपयोग करता है, जो ग्राफ़ के किनारों की छोटी संख्या को दूषित करता है।
प्रत्येक घटक के अन्दर अदूषित सबग्राफ के लिए एमएसटी खोजने के लिए इष्टतम निर्णय ट्री का उपयोग करें।
एमएसटी द्वारा फैलाए गए प्रत्येक जुड़े हुए घटक को शीर्ष पर अनुबंधित करें, और किसी भी एल्गोरिदम को प्रयुक्त करें जो समय में $O (m)$ घने ग्राफ़ पर काम करता है अभ्रष्ट उपसमूह के संकुचन के लिए
परिणामी फ़ॉरेस्ट में दूषित किनारों को वापस जोड़ें जिससे सबग्राफ़ बनाया जा सके जिसमें न्यूनतम स्पैनिंग ट्री सम्मिलित होने की गारंटी हो, और प्रारंभिक ग्राफ़ की तुलना में स्थिर कारक से छोटा हो। इस ग्राफ़ पर पुनरावर्ती रूप से इष्टतम एल्गोरिदम प्रयुक्त करें।

एल्गोरिथम $O (m)$ में सभी चरणों का रनटाइम है , निर्णय ट्री का उपयोग करने के चरण को छोड़कर। इस चरण का रनटाइम अज्ञात है, किन्तु यह सिद्ध हो चुका है कि यह इष्टतम है - कोई भी एल्गोरिदम इष्टतम निर्णय ट्री से उत्तम नहीं कर सकता है। इस प्रकार, इस एल्गोरिथम में विशिष्ट गुण है सिद्धतः इष्टतम, चूँकि इसकी रनटाइम जटिलता अज्ञात है।

समानांतर और वितरित एल्गोरिदम

अनुसंधान ने न्यूनतम स्पैनिंग ट्री की समस्या के लिए समानांतर एल्गोरिदम पर भी विचार किया है। प्रोसेसर की रैखिक संख्या $O (log n)$ समय के साथ समस्या को हल करना संभव है।^[12]^[13] बदर & कांग (2006) एल्गोरिदम प्रदर्शित करें जो अनुकूलित अनुक्रमिक एल्गोरिदम की तुलना में 8 प्रोसेसर पर 5 गुना तेजी से एमएसटी की गणना कर सकता है।^[14]

अन्य विशिष्ट एल्गोरिदम इतने बड़े ग्राफ़ के न्यूनतम स्पैनिंग ट्री की गणना करने के लिए डिज़ाइन किए गए हैं कि उनमें से अधिकांश को हर समय डिस्क पर संग्रहीत किया जाना चाहिए। ये बाहरी संग्रहण एल्गोरिदम, उदाहरण के लिए, जैसा कि रोमन, डिमेंटिव एट अल द्वारा इंजीनियरिंग ए एक्सटर्नल मेमोरी मिनिमम स्पैनिंग ट्री एल्गोरिदम में वर्णित है।^[15] लेखकों के प्रमाणों के अनुसार, यह पारंपरिक इन-मेमोरी एल्गोरिदम की तुलना में 2 से 5 गुना धीमी गति से काम कर सकता है। वे ग्राफ़ के आकार को कुशलतापूर्वक कम करने के लिए कुशल बाहरी सॉर्टिंग और ग्राफ़ संकुचन तकनीकों पर विश्वास करते हैं।

समस्या का समाधान वितरित कंप्यूटिंग में भी किया जा सकता है। यदि प्रत्येक नोड को कंप्यूटर माना जाता है और कोई भी नोड अपने स्वयं के जुड़े लिंक के अतिरिक्त कुछ भी नहीं जानता है, तब भी कोई वितरित न्यूनतम स्पैनिंग ट्री की गणना कर सकता है।

यादृच्छिक भार के साथ पूर्ण ग्राफ़ पर एमएसटी

एलन एम. फ़्रीज़ ने दिखाया कि n शीर्षों पर पूरा ग्राफ दिया गया है, किनारे के वजन के साथ जो वितरण फ़ंक्शन के साथ स्वतंत्र समान $F$ रूप से वितरित यादृच्छिक चर हैं संतुष्टि देने वाला $F'(0)>0$ , फिर जैसे-जैसे n विस्तारित वास्तविक संख्या रेखा के निकट पहुंचता है | $\zeta (3)/F'(0)$ +∞ एमएसटी का अपेक्षित वजन निकट आता है , जहाँ $\zeta$ रीमैन ज़ेटा फ़ंक्शन है (अधिक विशेष रूप से है)। $\zeta (3)$ एपेरी का स्थिरांक)। फ़्रीज़ और जे. माइकल स्टील ने भी संभाव्यता में अभिसरण सिद्ध किया था। स्वंते जानसन ने एमएसटी के वजन के लिए केंद्रीय सीमा प्रमेय सिद्ध किया था।

एकसमान यादृच्छिक भार के लिए $[0,1]$ , छोटे पूर्ण ग्राफ़ के लिए न्यूनतम स्पैनिंग ट्री के सटीक अपेक्षित आकार की गणना की गई है।^[16]

कार्यक्षेत्र	अपेक्षित आकार	अनुमानित अपेक्षित आकार
2	1/2	0.5
3	3/4	0.75
4	31/35	0.8857143
5	893/924	0.9664502
6	278/273	1.0183151
7	30739/29172	1.053716
8	199462271/184848378	1.0790588
9	126510063932/115228853025	1.0979027

अनुप्रयोग

न्यूनतम स्पैनिंग ट्री का नेटवर्क के डिज़ाइन में प्रत्यक्ष अनुप्रयोग होता है, जिसमें संगणक संजाल , दूरसंचार नेटवर्क, परिवहन नेटवर्क, जल आपूर्ति नेटवर्क और विद्युत ग्रिड सम्मिलित हैं (जैसा कि ऊपर बताया गया है, जिसके लिए उनका पहली बार आविष्कार किया गया था)।^[17] उन्हें अन्य समस्याओं के लिए एल्गोरिदम में सबरूटीन के रूप में प्रयुक्त किया जाता है, जिसमें ट्रैवलिंग सेल्समैन की समस्या का अनुमान लगाने के लिए क्रिस्टोफ़ाइड्स एल्गोरिथ्म भी सम्मिलित है,^[18] बहु-टर्मिनल न्यूनतम कट समस्या का अनुमान लगाना (जो एकल-टर्मिनल स्थिति में अधिकतम प्रवाह समस्या के सामान्य है),^[19] और न्यूनतम-निवेश भारित पूर्ण मिलान (ग्राफ़ सिद्धांत) का अनुमान लगाता है ^[20]

न्यूनतम स्पैनिंग ट्री पर आधारित अन्य व्यावहारिक अनुप्रयोगों में सम्मिलित हैं:

वर्गीकरण (सामान्य)।^[21]
क्लस्टर विश्लेषण: समतल में क्लस्टरिंग बिंदु,^[22] सिंगल-लिंकेज क्लस्टरिंग (पदानुक्रमित क्लस्टरिंग की विधि),^[23] ग्राफ़-सैद्धांतिक क्लस्टरिंग,^[24] और क्लस्टरिंग जीन अभिव्यक्ति डेटा।^[25]
कंप्यूटर नेटवर्क में प्रसारण (नेटवर्किंग) के लिए ट्री का निर्माण।^[26]
छवि पंजीकरण ^[27] और छवि विभाजन^[28] - न्यूनतम स्पैनिंग ट्री-आधारित विभाजन देखें।
कंप्यूटर दृष्टि में वक्ररेखीय सुविधा निष्कर्षण।^[29]
गणितीय अभिव्यक्तियों की लिखावट पहचान।^[30]
सर्किट डिज़ाइन: कुशल एकाधिक निरंतर गुणन को कार्यान्वित करना, जैसा कि परिमित आवेग प्रतिक्रिया फ़िल्टर में उपयोग किया जाता है।^[31]
सामाजिक-भौगोलिक क्षेत्रों का क्षेत्रीयकरण, क्षेत्रों का सजातीय, सन्निहित क्षेत्रों में समूहीकरण।^[32]
ईकोटोकसीकोलौजी डेटा की तुलना करना।^[33]
विद्युत प्रणालियों में टोपोलॉजिकल अवलोकन।^[34]
द्वि-आयामी सामग्रियों की एकरूपता को मापना।^[35]
मिनिमैक्स प्रक्रिया नियंत्रण।^[36]
वित्तीय बाज़ारों का वर्णन करने के लिए न्यूनतम स्पैनिंग ट्री का भी उपयोग किया जा सकता है।^[37]^[38] किन्हीं दो शेयरों के बीच सहसंबंध के गुणांक की गणना करके सहसंबंध मैट्रिक्स बनाया जा सकता है। इस मैट्रिक्स को टोपोलॉजिकल रूप से जटिल नेटवर्क के रूप में दर्शाया जा सकता है और संबंधो की कल्पना करने के लिए न्यूनतम स्पैनिंग ट्री का निर्माण किया जा सकता है।

संदर्भ

↑ "scipy.sparse.csgraph.minimum_spanning_tree - SciPy v1.7.1 मैनुअल". Numpy and Scipy Documentation — Numpy and Scipy documentation. Retrieved 2021-12-10. न्यूनतम स्पैनिंग ट्री एक ग्राफ है जिसमें किनारों का सबसेट होता है जो किनारों पर वजन के कुल योग को कम करते हुए सभी जुड़े हुए नोड्स को एक साथ जोड़ता है।
↑ "नेटवर्कx.algorithms.tree.mst.minimum_spanning_edges". NetworkX 2.6.2 documentation. Retrieved 2021-12-13. एक न्यूनतम स्पैनिंग ट्री ग्राफ़ का एक सबग्राफ (एक ट्री) है जिसमें किनारे के भार का न्यूनतम योग होता है। एक फैला हुआ जंगल ग्राफ़ के प्रत्येक जुड़े घटक के लिए फैले हुए पेड़ों का एक संघ है।
↑ "Do the minimum spanning trees of a weighted graph have the same number of edges with a given weight?". cs.stackexchange.com. Retrieved 4 April 2018.
↑ ^4.0 ^4.1 ^4.2 ^4.3 ^4.4 Pettie, Seth; Ramachandran, Vijaya (2002), "An optimal minimum spanning tree algorithm" (PDF), Journal of the Association for Computing Machinery, 49 (1): 16–34, doi:10.1145/505241.505243, MR 2148431, S2CID 5362916.
↑ Karger, David R.; Klein, Philip N.; Tarjan, Robert E. (1995), "A randomized linear-time algorithm to find minimum spanning trees", Journal of the Association for Computing Machinery, 42 (2): 321–328, doi:10.1145/201019.201022, MR 1409738, S2CID 832583
↑ Pettie, Seth; Ramachandran, Vijaya (2002), "Minimizing randomness in minimum spanning tree, parallel connectivity, and set maxima algorithms", Proc. 13th ACM-SIAM Symposium on Discrete Algorithms (SODA '02), San Francisco, California, pp. 713–722, ISBN 9780898715132{{citation}}: CS1 maint: location missing publisher (link).
↑ ^7.0 ^7.1 Chazelle, Bernard (2000), "A minimum spanning tree algorithm with inverse-Ackermann type complexity", Journal of the Association for Computing Machinery, 47 (6): 1028–1047, doi:10.1145/355541.355562, MR 1866456, S2CID 6276962.
↑ Chazelle, Bernard (2000), "The soft heap: an approximate priority queue with optimal error rate", Journal of the Association for Computing Machinery, 47 (6): 1012–1027, doi:10.1145/355541.355554, MR 1866455, S2CID 12556140.
↑ Fredman, M. L.; Tarjan, R. E. (1987). "फाइबोनैचि हीप्स और बेहतर नेटवर्क अनुकूलन एल्गोरिदम में उनका उपयोग". Journal of the ACM. 34 (3): 596. doi:10.1145/28869.28874. S2CID 7904683.
↑ Gabow, H. N.; Galil, Z.; Spencer, T.; Tarjan, R. E. (1986). "अप्रत्यक्ष और निर्देशित ग्राफ़ में न्यूनतम फैले हुए पेड़ों को खोजने के लिए कुशल एल्गोरिदम". Combinatorica. 6 (2): 109. doi:10.1007/bf02579168. S2CID 35618095.
↑ Fredman, M. L.; Willard, D. E. (1994), "Trans-dichotomous algorithms for minimum spanning trees and shortest paths", Journal of Computer and System Sciences, 48 (3): 533–551, doi:10.1016/S0022-0000(05)80064-9, MR 1279413.
↑ Chong, Ka Wong; Han, Yijie; Lam, Tak Wah (2001), "Concurrent threads and optimal parallel minimum spanning trees algorithm", Journal of the Association for Computing Machinery, 48 (2): 297–323, doi:10.1145/375827.375847, MR 1868718, S2CID 1778676.
↑ Pettie, Seth; Ramachandran, Vijaya (2002), "A randomized time-work optimal parallel algorithm for finding a minimum spanning forest" (PDF), SIAM Journal on Computing, 31 (6): 1879–1895, doi:10.1137/S0097539700371065, MR 1954882.
↑ Bader, David A.; Cong, Guojing (2006), "Fast shared-memory algorithms for computing the minimum spanning forest of sparse graphs", Journal of Parallel and Distributed Computing, 66 (11): 1366–1378, doi:10.1016/j.jpdc.2006.06.001, S2CID 2004627.
↑ Dementiev, Roman; Sanders, Peter; Schultes, Dominik; Sibeyn, Jop F. (2004), "Engineering an external memory minimum spanning tree algorithm", Proc. IFIP 18th World Computer Congress, TC1 3rd International Conference on Theoretical Computer Science (TCS2004) (PDF), pp. 195–208.
↑ Steele, J. Michael (2002), "Minimal spanning trees for graphs with random edge lengths", Mathematics and computer science, II (Versailles, 2002), Trends Math., Basel: Birkhäuser, pp. 223–245, MR 1940139
↑ Graham, R. L.; Hell, Pavol (1985), "On the history of the minimum spanning tree problem", Annals of the History of Computing, 7 (1): 43–57, doi:10.1109/MAHC.1985.10011, MR 0783327, S2CID 10555375
↑ Nicos Christofides, Worst-case analysis of a new heuristic for the travelling salesman problem, Report 388, Graduate School of Industrial Administration, CMU, 1976.
↑ Dahlhaus, E.; Johnson, D. S.; Papadimitriou, C. H.; Seymour, P. D.; Yannakakis, M. (August 1994). "The complexity of multiterminal cuts" (PDF). SIAM Journal on Computing. 23 (4): 864–894. doi:10.1137/S0097539792225297. Archived from the original (PDF) on 24 August 2004. Retrieved 17 December 2012.
↑ Supowit, Kenneth J.; Plaisted, David A.; Reingold, Edward M. (1980). Heuristics for weighted perfect matching. 12th Annual ACM Symposium on Theory of Computing (STOC '80). New York, NY, USA: ACM. pp. 398–419. doi:10.1145/800141.804689.
↑ Sneath, P. H. A. (1 August 1957). "वर्गीकरण विज्ञान में कंप्यूटर का अनुप्रयोग". Journal of General Microbiology. 17 (1): 201–226. doi:10.1099/00221287-17-1-201. PMID 13475686.
↑ Asano, T.; Bhattacharya, B.; Keil, M.; Yao, F. (1988). न्यूनतम और अधिकतम फैले पेड़ों पर आधारित क्लस्टरिंग एल्गोरिदम. Fourth Annual Symposium on Computational Geometry (SCG '88). Vol. 1. pp. 252–257. doi:10.1145/73393.73419.
↑ Gower, J. C.; Ross, G. J. S. (1969). "न्यूनतम फैले हुए पेड़ और एकल लिंकेज क्लस्टर विश्लेषण". Journal of the Royal Statistical Society. C (Applied Statistics). 18 (1): 54–64. doi:10.2307/2346439. JSTOR 2346439.
↑ Päivinen, Niina (1 May 2005). "स्केल-मुक्त-जैसी संरचना के न्यूनतम फैले हुए पेड़ के साथ क्लस्टरिंग". Pattern Recognition Letters. 26 (7): 921–930. Bibcode:2005PaReL..26..921P. doi:10.1016/j.patrec.2004.09.039.
↑ Xu, Y.; Olman, V.; Xu, D. (1 April 2002). "Clustering gene expression data using a graph-theoretic approach: an application of minimum spanning trees". Bioinformatics. 18 (4): 536–545. doi:10.1093/bioinformatics/18.4.536. PMID 12016051.
↑ Dalal, Yogen K.; Metcalfe, Robert M. (1 December 1978). "प्रसारण पैकेटों का रिवर्स पथ अग्रेषण". Communications of the ACM. 21 (12): 1040–1048. doi:10.1145/359657.359665. S2CID 5638057.
↑ Ma, B.; Hero, A.; Gorman, J.; Michel, O. (2000). न्यूनतम स्पैनिंग ट्री एल्गोरिदम के साथ छवि पंजीकरण (PDF). International Conference on Image Processing. Vol. 1. pp. 481–484. doi:10.1109/ICIP.2000.901000. Archived (PDF) from the original on 2022-10-09.
↑ P. Felzenszwalb, D. Huttenlocher: Efficient Graph-Based Image Segmentation. IJCV 59(2) (September 2004)
↑ Suk, Minsoo; Song, Ohyoung (1 June 1984). "न्यूनतम फैले पेड़ों का उपयोग करके वक्ररेखीय सुविधा निष्कर्षण". Computer Vision, Graphics, and Image Processing. 26 (3): 400–411. doi:10.1016/0734-189X(84)90221-4.
↑ Tapia, Ernesto; Rojas, Raúl (2004). "Recognition of On-line Handwritten Mathematical Expressions Using a Minimum Spanning Tree Construction and Symbol Dominance" (PDF). ग्राफ़िक्स पहचान. हाल की प्रगति और परिप्रेक्ष्य. Lecture Notes in Computer Science. Vol. 3088. Berlin Heidelberg: Springer-Verlag. pp. 329–340. ISBN 978-3540224785. Archived (PDF) from the original on 2022-10-09.
↑ Ohlsson, H. (2004). न्यूनतम स्पैनिंग ट्री का उपयोग करके कम जटिलता वाले एफआईआर फिल्टर का कार्यान्वयन. 12th IEEE Mediterranean Electrotechnical Conference (MELECON 2004). Vol. 1. pp. 261–264. doi:10.1109/MELCON.2004.1346826.
↑ Assunção, R. M.; M. C. Neves; G. Câmara; C. Da Costa Freitas (2006). "Efficient regionalization techniques for socio‐economic geographical units using minimum spanning trees". International Journal of Geographical Information Science. 20 (7): 797–811. doi:10.1080/13658810600665111. S2CID 2530748.
↑ Devillers, J.; Dore, J.C. (1 April 1989). "विष विज्ञान में न्यूनतम स्पैनिंग ट्री (एमएसटी) विधि की अनुमानी क्षमता". Ecotoxicology and Environmental Safety. 17 (2): 227–235. doi:10.1016/0147-6513(89)90042-0. PMID 2737116.
↑ Mori, H.; Tsuzuki, S. (1 May 1991). "न्यूनतम स्पैनिंग ट्री तकनीक का उपयोग करके टोपोलॉजिकल अवलोकन विश्लेषण के लिए एक तेज़ विधि". IEEE Transactions on Power Systems. 6 (2): 491–500. Bibcode:1991ITPSy...6..491M. doi:10.1109/59.76691.
↑ Filliben, James J.; Kafadar, Karen; Shier, Douglas R. (1 January 1983). "द्वि-आयामी सतहों की एकरूपता के लिए परीक्षण". Mathematical Modelling. 4 (2): 167–189. doi:10.1016/0270-0255(83)90026-X.
↑ Kalaba, Robert E. (1963), Graph Theory and Automatic Control (PDF), archived from the original (PDF) on February 21, 2016
↑ Mantegna, R. N. (1999). Hierarchical structure in financial markets. The European Physical Journal B-Condensed Matter and Complex Systems, 11(1), 193–197.
↑ Djauhari, M., & Gan, S. (2015). Optimality problem of network topology in stocks market analysis. Physica A: Statistical Mechanics and Its Applications, 419, 108–114.
↑ Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman, ISBN 0-7167-1045-5. ND12
↑ Gabow, Harold N. (1977), "Two algorithms for generating weighted spanning trees in order", SIAM Journal on Computing, 6 (1): 139–150, doi:10.1137/0206011, MR 0441784.
↑ Eppstein, David (1992), "Finding the k smallest spanning trees", BIT, 32 (2): 237–248, doi:10.1007/BF01994879, MR 1172188, S2CID 121160520.
↑ Frederickson, Greg N. (1997), "Ambivalent data structures for dynamic 2-edge-connectivity and k smallest spanning trees", SIAM Journal on Computing, 26 (2): 484–538, doi:10.1137/S0097539792226825, MR 1438526.
↑ Jothi, Raja; Raghavachari, Balaji (2005), "Approximation Algorithms for the Capacitated Minimum Spanning Tree Problem and Its Variants in Network Design", ACM Trans. Algorithms, 1 (2): 265–282, doi:10.1145/1103963.1103967, S2CID 8302085
↑ Hu, T. C. (1961), "The maximum capacity route problem", Operations Research, 9 (6): 898–900, doi:10.1287/opre.9.6.898, JSTOR 167055.
↑ McDonald, Ryan; Pereira, Fernando; Ribarov, Kiril; Hajič, Jan (2005). "Non-projective dependency parsing using spanning tree algorithms" (PDF). Proc. HLT/EMNLP.
↑ Spira, P. M.; Pan, A. (1975), "On finding and updating spanning trees and shortest paths" (PDF), SIAM Journal on Computing, 4 (3): 375–380, doi:10.1137/0204032, MR 0378466.
↑ Holm, Jacob; de Lichtenberg, Kristian; Thorup, Mikkel (2001), "Poly-logarithmic deterministic fully dynamic algorithms for connectivity, minimum spanning tree, 2-edge, and biconnectivity", Journal of the Association for Computing Machinery, 48 (4): 723–760, doi:10.1145/502090.502095, MR 2144928, S2CID 7273552.
↑ Chin, F.; Houck, D. (1978), "Algorithms for updating minimal spanning trees", Journal of Computer and System Sciences, 16 (3): 333–344, doi:10.1016/0022-0000(78)90022-3.
↑ Chang, R.S.; Leu, S.J. (1997), "The minimum labeling spanning trees", Information Processing Letters, 63 (5): 277–282, doi:10.1016/s0020-0190(97)00127-0.
↑ "बॉटलनेक स्पैनिंग ट्री के बारे में सब कुछ". flashing-thoughts.blogspot.ru. 5 June 2010. Retrieved 4 April 2018.
↑ "संग्रहीत प्रति" (PDF). Archived from the original (PDF) on 2013-06-12. Retrieved 2014-07-02.

अग्रिम पठन

Otakar Boruvka on Minimum Spanning Tree Problem (translation of both 1926 papers, Comments, history) (2000) Jaroslav Nešetřil, Eva Milková, Helena Nesetrilová. (SeCtion 7 gives his algorithm, whiCh looks like a Cross between Prim's and Kruskal's.)
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. IntroduCtion to Algorithms, SeCond Edition. MIT Press and MCGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 23: Minimum Spanning Trees, pp. 561–579.
Eisner, Jason (1997). State-of-the-art algorithms for minimum spanning trees: A tutorial disCussion. ManusCript, University of Pennsylvania, April. 78 pp.
Kromkowski, John David. "Still Unmelted after All These Years", in Annual Editions, RaCe and EthniC Relations, 17/e (2009 MCGraw Hill) (Using minimum spanning tree as method of demographiC analysis of ethniC diversity aCross the United States).

बाहरी संबंध

[1] "scipy.sparse.csgraph.minimum_spanning_tree - SciPy v1.7.1 मैनुअल". Numpy and Scipy Documentation — Numpy and Scipy documentation. Retrieved 2021-12-10. न्यूनतम स्पैनिंग ट्री एक ग्राफ है जिसमें किनारों का सबसेट होता है जो किनारों पर वजन के कुल योग को कम करते हुए सभी जुड़े हुए नोड्स को एक साथ जोड़ता है।

[2] "नेटवर्कx.algorithms.tree.mst.minimum_spanning_edges". NetworkX 2.6.2 documentation. Retrieved 2021-12-13. एक न्यूनतम स्पैनिंग ट्री ग्राफ़ का एक सबग्राफ (एक ट्री) है जिसमें किनारे के भार का न्यूनतम योग होता है। एक फैला हुआ जंगल ग्राफ़ के प्रत्येक जुड़े घटक के लिए फैले हुए पेड़ों का एक संघ है।

[3] "Do the minimum spanning trees of a weighted graph have the same number of edges with a given weight?". cs.stackexchange.com. Retrieved 4 April 2018.

[PettieRamachandran2002-4] 4.0 ^4.1 ^4.2 ^4.3 ^4.4 Pettie, Seth; Ramachandran, Vijaya (2002), "An optimal minimum spanning tree algorithm" (PDF), Journal of the Association for Computing Machinery, 49 (1): 16–34, doi:10.1145/505241.505243, MR 2148431, S2CID 5362916.

[5] Karger, David R.; Klein, Philip N.; Tarjan, Robert E. (1995), "A randomized linear-time algorithm to find minimum spanning trees", Journal of the Association for Computing Machinery, 42 (2): 321–328, doi:10.1145/201019.201022, MR 1409738, S2CID 832583

[6] Pettie, Seth; Ramachandran, Vijaya (2002), "Minimizing randomness in minimum spanning tree, parallel connectivity, and set maxima algorithms", Proc. 13th ACM-SIAM Symposium on Discrete Algorithms (SODA '02), San Francisco, California, pp. 713–722, ISBN 9780898715132{{citation}}: CS1 maint: location missing publisher (link).

[Chazelle2000-7] 7.0 ^7.1 Chazelle, Bernard (2000), "A minimum spanning tree algorithm with inverse-Ackermann type complexity", Journal of the Association for Computing Machinery, 47 (6): 1028–1047, doi:10.1145/355541.355562, MR 1866456, S2CID 6276962.

[8] Chazelle, Bernard (2000), "The soft heap: an approximate priority queue with optimal error rate", Journal of the Association for Computing Machinery, 47 (6): 1012–1027, doi:10.1145/355541.355554, MR 1866455, S2CID 12556140.

[9] Fredman, M. L.; Tarjan, R. E. (1987). "फाइबोनैचि हीप्स और बेहतर नेटवर्क अनुकूलन एल्गोरिदम में उनका उपयोग". Journal of the ACM. 34 (3): 596. doi:10.1145/28869.28874. S2CID 7904683.

[10] Gabow, H. N.; Galil, Z.; Spencer, T.; Tarjan, R. E. (1986). "अप्रत्यक्ष और निर्देशित ग्राफ़ में न्यूनतम फैले हुए पेड़ों को खोजने के लिए कुशल एल्गोरिदम". Combinatorica. 6 (2): 109. doi:10.1007/bf02579168. S2CID 35618095.

[11] Fredman, M. L.; Willard, D. E. (1994), "Trans-dichotomous algorithms for minimum spanning trees and shortest paths", Journal of Computer and System Sciences, 48 (3): 533–551, doi:10.1016/S0022-0000(05)80064-9, MR 1279413.

[12] Chong, Ka Wong; Han, Yijie; Lam, Tak Wah (2001), "Concurrent threads and optimal parallel minimum spanning trees algorithm", Journal of the Association for Computing Machinery, 48 (2): 297–323, doi:10.1145/375827.375847, MR 1868718, S2CID 1778676.

[13] Pettie, Seth; Ramachandran, Vijaya (2002), "A randomized time-work optimal parallel algorithm for finding a minimum spanning forest" (PDF), SIAM Journal on Computing, 31 (6): 1879–1895, doi:10.1137/S0097539700371065, MR 1954882.

[14] Bader, David A.; Cong, Guojing (2006), "Fast shared-memory algorithms for computing the minimum spanning forest of sparse graphs", Journal of Parallel and Distributed Computing, 66 (11): 1366–1378, doi:10.1016/j.jpdc.2006.06.001, S2CID 2004627.

[15] Dementiev, Roman; Sanders, Peter; Schultes, Dominik; Sibeyn, Jop F. (2004), "Engineering an external memory minimum spanning tree algorithm", Proc. IFIP 18th World Computer Congress, TC1 3rd International Conference on Theoretical Computer Science (TCS2004) (PDF), pp. 195–208.

[16] Steele, J. Michael (2002), "Minimal spanning trees for graphs with random edge lengths", Mathematics and computer science, II (Versailles, 2002), Trends Math., Basel: Birkhäuser, pp. 223–245, MR 1940139

[17] Graham, R. L.; Hell, Pavol (1985), "On the history of the minimum spanning tree problem", Annals of the History of Computing, 7 (1): 43–57, doi:10.1109/MAHC.1985.10011, MR 0783327, S2CID 10555375

[18] Nicos Christofides, Worst-case analysis of a new heuristic for the travelling salesman problem, Report 388, Graduate School of Industrial Administration, CMU, 1976.

[19] Dahlhaus, E.; Johnson, D. S.; Papadimitriou, C. H.; Seymour, P. D.; Yannakakis, M. (August 1994). "The complexity of multiterminal cuts" (PDF). SIAM Journal on Computing. 23 (4): 864–894. doi:10.1137/S0097539792225297. Archived from the original (PDF) on 24 August 2004. Retrieved 17 December 2012.

[20] Supowit, Kenneth J.; Plaisted, David A.; Reingold, Edward M. (1980). Heuristics for weighted perfect matching. 12th Annual ACM Symposium on Theory of Computing (STOC '80). New York, NY, USA: ACM. pp. 398–419. doi:10.1145/800141.804689.

[21] Sneath, P. H. A. (1 August 1957). "वर्गीकरण विज्ञान में कंप्यूटर का अनुप्रयोग". Journal of General Microbiology. 17 (1): 201–226. doi:10.1099/00221287-17-1-201. PMID 13475686.

[22] Asano, T.; Bhattacharya, B.; Keil, M.; Yao, F. (1988). न्यूनतम और अधिकतम फैले पेड़ों पर आधारित क्लस्टरिंग एल्गोरिदम. Fourth Annual Symposium on Computational Geometry (SCG '88). Vol. 1. pp. 252–257. doi:10.1145/73393.73419.

[23] Gower, J. C.; Ross, G. J. S. (1969). "न्यूनतम फैले हुए पेड़ और एकल लिंकेज क्लस्टर विश्लेषण". Journal of the Royal Statistical Society. C (Applied Statistics). 18 (1): 54–64. doi:10.2307/2346439. JSTOR 2346439.

[24] Päivinen, Niina (1 May 2005). "स्केल-मुक्त-जैसी संरचना के न्यूनतम फैले हुए पेड़ के साथ क्लस्टरिंग". Pattern Recognition Letters. 26 (7): 921–930. Bibcode:2005PaReL..26..921P. doi:10.1016/j.patrec.2004.09.039.

[25] Xu, Y.; Olman, V.; Xu, D. (1 April 2002). "Clustering gene expression data using a graph-theoretic approach: an application of minimum spanning trees". Bioinformatics. 18 (4): 536–545. doi:10.1093/bioinformatics/18.4.536. PMID 12016051.

[26] Dalal, Yogen K.; Metcalfe, Robert M. (1 December 1978). "प्रसारण पैकेटों का रिवर्स पथ अग्रेषण". Communications of the ACM. 21 (12): 1040–1048. doi:10.1145/359657.359665. S2CID 5638057.

[27] Ma, B.; Hero, A.; Gorman, J.; Michel, O. (2000). न्यूनतम स्पैनिंग ट्री एल्गोरिदम के साथ छवि पंजीकरण (PDF). International Conference on Image Processing. Vol. 1. pp. 481–484. doi:10.1109/ICIP.2000.901000. Archived (PDF) from the original on 2022-10-09.

[28] P. Felzenszwalb, D. Huttenlocher: Efficient Graph-Based Image Segmentation. IJCV 59(2) (September 2004)

[29] Suk, Minsoo; Song, Ohyoung (1 June 1984). "न्यूनतम फैले पेड़ों का उपयोग करके वक्ररेखीय सुविधा निष्कर्षण". Computer Vision, Graphics, and Image Processing. 26 (3): 400–411. doi:10.1016/0734-189X(84)90221-4.

[30] Tapia, Ernesto; Rojas, Raúl (2004). "Recognition of On-line Handwritten Mathematical Expressions Using a Minimum Spanning Tree Construction and Symbol Dominance" (PDF). ग्राफ़िक्स पहचान. हाल की प्रगति और परिप्रेक्ष्य. Lecture Notes in Computer Science. Vol. 3088. Berlin Heidelberg: Springer-Verlag. pp. 329–340. ISBN 978-3540224785. Archived (PDF) from the original on 2022-10-09.

[31] Ohlsson, H. (2004). न्यूनतम स्पैनिंग ट्री का उपयोग करके कम जटिलता वाले एफआईआर फिल्टर का कार्यान्वयन. 12th IEEE Mediterranean Electrotechnical Conference (MELECON 2004). Vol. 1. pp. 261–264. doi:10.1109/MELCON.2004.1346826.

[32] Assunção, R. M.; M. C. Neves; G. Câmara; C. Da Costa Freitas (2006). "Efficient regionalization techniques for socio‐economic geographical units using minimum spanning trees". International Journal of Geographical Information Science. 20 (7): 797–811. doi:10.1080/13658810600665111. S2CID 2530748.

[33] Devillers, J.; Dore, J.C. (1 April 1989). "विष विज्ञान में न्यूनतम स्पैनिंग ट्री (एमएसटी) विधि की अनुमानी क्षमता". Ecotoxicology and Environmental Safety. 17 (2): 227–235. doi:10.1016/0147-6513(89)90042-0. PMID 2737116.

[34] Mori, H.; Tsuzuki, S. (1 May 1991). "न्यूनतम स्पैनिंग ट्री तकनीक का उपयोग करके टोपोलॉजिकल अवलोकन विश्लेषण के लिए एक तेज़ विधि". IEEE Transactions on Power Systems. 6 (2): 491–500. Bibcode:1991ITPSy...6..491M. doi:10.1109/59.76691.

[35] Filliben, James J.; Kafadar, Karen; Shier, Douglas R. (1 January 1983). "द्वि-आयामी सतहों की एकरूपता के लिए परीक्षण". Mathematical Modelling. 4 (2): 167–189. doi:10.1016/0270-0255(83)90026-X.

[36] Kalaba, Robert E. (1963), Graph Theory and Automatic Control (PDF), archived from the original (PDF) on February 21, 2016

[37] Mantegna, R. N. (1999). Hierarchical structure in financial markets. The European Physical Journal B-Condensed Matter and Complex Systems, 11(1), 193–197.

[38] Djauhari, M., & Gan, S. (2015). Optimality problem of network topology in stocks market analysis. Physica A: Statistical Mechanics and Its Applications, 419, 108–114.

[39] Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman, ISBN 0-7167-1045-5. ND12

[40] Gabow, Harold N. (1977), "Two algorithms for generating weighted spanning trees in order", SIAM Journal on Computing, 6 (1): 139–150, doi:10.1137/0206011, MR 0441784.

[41] Eppstein, David (1992), "Finding the k smallest spanning trees", BIT, 32 (2): 237–248, doi:10.1007/BF01994879, MR 1172188, S2CID 121160520.

[42] Frederickson, Greg N. (1997), "Ambivalent data structures for dynamic 2-edge-connectivity and k smallest spanning trees", SIAM Journal on Computing, 26 (2): 484–538, doi:10.1137/S0097539792226825, MR 1438526.

[43] Jothi, Raja; Raghavachari, Balaji (2005), "Approximation Algorithms for the Capacitated Minimum Spanning Tree Problem and Its Variants in Network Design", ACM Trans. Algorithms, 1 (2): 265–282, doi:10.1145/1103963.1103967, S2CID 8302085

[44] Hu, T. C. (1961), "The maximum capacity route problem", Operations Research, 9 (6): 898–900, doi:10.1287/opre.9.6.898, JSTOR 167055.

[45] McDonald, Ryan; Pereira, Fernando; Ribarov, Kiril; Hajič, Jan (2005). "Non-projective dependency parsing using spanning tree algorithms" (PDF). Proc. HLT/EMNLP.

[46] Spira, P. M.; Pan, A. (1975), "On finding and updating spanning trees and shortest paths" (PDF), SIAM Journal on Computing, 4 (3): 375–380, doi:10.1137/0204032, MR 0378466.

[47] Holm, Jacob; de Lichtenberg, Kristian; Thorup, Mikkel (2001), "Poly-logarithmic deterministic fully dynamic algorithms for connectivity, minimum spanning tree, 2-edge, and biconnectivity", Journal of the Association for Computing Machinery, 48 (4): 723–760, doi:10.1145/502090.502095, MR 2144928, S2CID 7273552.

[48] Chin, F.; Houck, D. (1978), "Algorithms for updating minimal spanning trees", Journal of Computer and System Sciences, 16 (3): 333–344, doi:10.1016/0022-0000(78)90022-3.

[49] Chang, R.S.; Leu, S.J. (1997), "The minimum labeling spanning trees", Information Processing Letters, 63 (5): 277–282, doi:10.1016/s0020-0190(97)00127-0.

[50] "बॉटलनेक स्पैनिंग ट्री के बारे में सब कुछ". flashing-thoughts.blogspot.ru. 5 June 2010. Retrieved 4 April 2018.

[51] "संग्रहीत प्रति" (PDF). Archived from the original (PDF) on 2013-06-12. Retrieved 2014-07-02.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

Anonymous

Search

न्यूनतम स्पैनिंग ट्री (एमएसटी): Difference between revisions

Namespaces

More

Page actions

Revision as of 12:32, 6 July 2023

Contents

गुण

संभावित बहुलता

अद्वितीयता

न्यूनतम-निवेश उपग्राफ

साइकिल प्रोपर्टी

प्रोपर्टी कट

न्यूनतम-निवेश बढ़त

संकुचन

एल्गोरिदम

क्लासिक एल्गोरिदम

तेज़ एल्गोरिदम

विशेष स्थितियों में रैखिक-समय एल्गोरिदम

सघन रेखांकन

पूर्णांक भार

निर्णय ट्री

इष्टतम एल्गोरिदम

समानांतर और वितरित एल्गोरिदम

यादृच्छिक भार के साथ पूर्ण ग्राफ़ पर एमएसटी

अनुप्रयोग

संबंधित समस्याएँ

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Revision as of 10:49, 4 July 2023 (view source) alpha>Mohd Faishal No edit summary ← Older edit	Revision as of 12:32, 6 July 2023 (view source) alpha>Abhishek m (Abhishek moved page न्यूनतम फैलाव वाला पेड़ to न्यूनतम स्पैनिंग ट्री (एमएसटी) without leaving a redirect) Newer edit →
(No difference)

Anonymous

Search

न्यूनतम स्पैनिंग ट्री (एमएसटी): Difference between revisions

Revision as of 12:32, 6 July 2023

गुण

संभावित बहुलता

अद्वितीयता

न्यूनतम-निवेश उपग्राफ

साइकिल प्रोपर्टी

प्रोपर्टी कट

न्यूनतम-निवेश बढ़त

संकुचन

एल्गोरिदम

क्लासिक एल्गोरिदम

तेज़ एल्गोरिदम

विशेष स्थितियों में रैखिक-समय एल्गोरिदम

सघन रेखांकन

पूर्णांक भार

निर्णय ट्री

इष्टतम एल्गोरिदम

समानांतर और वितरित एल्गोरिदम

यादृच्छिक भार के साथ पूर्ण ग्राफ़ पर एमएसटी

अनुप्रयोग

संबंधित समस्याएँ

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories