तीन चरण विद्युत शक्ति का गणित: Difference between revisions
No edit summary |
No edit summary |
||
| (13 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Mathematics and basic principles of three-phase electric power}} | {{Short description|Mathematics and basic principles of three-phase electric power}} | ||
[[File:3 phase AC waveform.svg|thumb|300px|right|तीन-चरण प्रणाली का | [[File:3 phase AC waveform.svg|thumb|300px|right|तीन-चरण प्रणाली का वोल्टेज चक्र, समय अक्ष के साथ 0 से 360° (2π रेडियन) लेबल किया गया। प्लॉट की गई रेखा समय के संबंध में तात्कालिक वोल्टेज (या धारा ) की भिन्नता को दर्शाती है। यह चक्र [[उपयोगिता आवृत्ति]] के साथ दोहराता है जो विद्युत व्यवस्था पर निर्भर करता है।]][[ विद्युत अभियन्त्रण | विद्युत अभियन्त्रण]] में, [[तीन चरण विद्युत शक्ति]] प्रणाली में कम से कम तीन चालक होते हैं जो बारी-बारी से चालू होते हैं जो कि तिहाई अवधि के समय में बदलाव होते हैं। डेल्टा (∆) या स्टार (वाई) में तीन-चरण प्रणाली की व्यवस्था की जा सकती है (कुछ क्षेत्रों में वाई के रूप में भी निरूपित किया जाता है, क्योंकि प्रतीकात्मक रूप से यह अक्षर 'वाई' के समान है)। वाई प्रणाली तीनों [[एसी चरण]] से दो अलग-अलग वोल्टेज के उपयोग की अनुमति देता है, जैसे कि 230/400 वी प्रणाली जो तटस्थ (सेंटर हब) और किसी चरण के बीच 230 वी प्रदान करता है और किसी भी दो चरणों में 400 वी डेल्टा प्रणाली व्यवस्था केवल वोल्टेज प्रदान करती है किन्तु इसकी अधिक अतिरेक है क्योंकि यह सामान्य रूप से तीन आपूर्ति वाइंडिंग्स में से के साथ ऑफ़लाइन काम करना जारी रख सकती है, यद्यपि कुल क्षमता का 57.7%<ref>{{cite web |url=http://www.ibiblio.org/kuphaldt/socratic/output/deltawye_instructor.pdf |title=Delta and Wye 3-phase circuits |access-date=2012-11-21 |url-status=live |archive-url=https://web.archive.org/web/20130513004710/http://www.ibiblio.org/kuphaldt/socratic/output/deltawye_instructor.pdf |archive-date=2013-05-13 }} public domain</ref> यदि गैर-रैखिक भार जुड़े हुए हैं तो तटस्थ में हार्मोनिक प्रवाह बहुत बड़ा हो सकता है। | ||
== परिभाषाएँ == | == परिभाषाएँ == | ||
घूर्णन अनुक्रम L1 - L2 - L3 के साथ स्टार (डब्ल्यू वाई ई) कनेक्टेड टोपोलॉजी में, समय-भिन्न तात्कालिक वोल्टेज की गणना क्रमशः प्रत्येक चरण ए, सी, बी के लिए की जा सकती है: | |||
: <math>V_{L1-N} = V_P \sin\left(\theta\right)\,\!</math> | : <math>V_{L1-N} = V_P \sin\left(\theta\right)\,\!</math> | ||
: <math>V_{L2-N} = V_P \sin\left(\theta - \frac{2}{3}\pi\right) = V_P \sin\left(\theta + \frac{4}{3}\pi\right)</math> | : <math>V_{L2-N} = V_P \sin\left(\theta - \frac{2}{3}\pi\right) = V_P \sin\left(\theta + \frac{4}{3}\pi\right)</math> | ||
: <math>V_{L3-N} = V_P \sin\left(\theta - \frac{4}{3}\pi\right) = V_P \sin\left(\theta + \frac{2}{3}\pi\right)</math> | : <math>V_{L3-N} = V_P \sin\left(\theta - \frac{4}{3}\pi\right) = V_P \sin\left(\theta + \frac{2}{3}\pi\right)</math> | ||
जहाँ: | |||
:<math>V_P</math> पीक वोल्टेज है, | :<math>V_P</math> पीक वोल्टेज है, | ||
| Line 14: | Line 14: | ||
::<math>t</math> सेकंड में समय है | ::<math>t</math> सेकंड में समय है | ||
::<math>f</math> प्रति सेकंड चक्रों में आवृत्ति है और | ::<math>f</math> प्रति सेकंड चक्रों में आवृत्ति है और | ||
: वोल्टेज L1-N, L2-N और L3-N को स्टार | : वोल्टेज L1-N, L2-N और L3-N को स्टार संबंध बिंदु से संदर्भित किया जाता है। | ||
== | == रेखा-चित्र == | ||
नीचे दी गई छवियां प्रदर्शित करती हैं कि कैसे | नीचे दी गई छवियां प्रदर्शित करती हैं कि कैसे अल्टरनेटर से तीन चरणों को वितरित करने वाले छह तारों की प्रणाली को केवल तीन से बदला जा सकता है। तीन चरण का ट्रांसफार्मर भी दिखाया गया है। | ||
<gallery heights="210px" mode="packed"> | <gallery heights="210px" mode="packed"> | ||
| Line 24: | Line 24: | ||
Transformator-3-fas.png|तीन-चरण ट्रांसफार्मर के प्रत्येक चरण में एक साझा कोर के साथ वाइंडिंग की अपनी जोड़ी होती है। | Transformator-3-fas.png|तीन-चरण ट्रांसफार्मर के प्रत्येक चरण में एक साझा कोर के साथ वाइंडिंग की अपनी जोड़ी होती है। | ||
</gallery> | </gallery> | ||
== संतुलित भार == | == संतुलित भार == | ||
सामान्यतः विद्युत शक्ति प्रणालियों में भार चरणों के बीच व्यावहारिक रूप से समान रूप से वितरित किए जाते हैं। पहले संतुलित प्रणाली पर चर्चा करना और फिर असंतुलित प्रणालियों के प्रभावों का प्राथमिक स्थितियों से विचलन के रूप में वर्णन करना सामान्य अभ्यास है। | |||
=== | === निरन्तर विद्युत हस्तांतरण === | ||
तीन-चरण शक्ति की | तीन-चरण शक्ति की महत्वपूर्ण गुण यह है कि प्रतिरोधक भार के लिए तात्कालिक शक्ति उपलब्ध है, <math>\scriptstyle P \,=\, V I \,=\, \frac{V^2}{R}</math>, हर समय स्थिर रहता है। वास्तव में माना | ||
: <math>\begin{align} | : <math>\begin{align} | ||
| Line 36: | Line 35: | ||
P_{TOT} &= \sum_i P_{Li} | P_{TOT} &= \sum_i P_{Li} | ||
\end{align}</math> | \end{align}</math> | ||
गणित को सरल बनाने के लिए | गणित को सरल बनाने के लिए हम मध्यवर्ती गणनाओं के लिए आयामहीन मात्रा शक्ति को <math>\scriptstyle p \,=\, \frac{1}{V_P^2}P_{TOT} R</math> परिभाषित करते हैं, | ||
: <math>p=\sin^{2} \theta+\sin^{2} \left(\theta-\frac{2}{3} \pi\right)+\sin^{2} \left(\theta-\frac{4}{3} \pi\right)=\frac{3}{2}</math> | : <math>p=\sin^{2} \theta+\sin^{2} \left(\theta-\frac{2}{3} \pi\right)+\sin^{2} \left(\theta-\frac{4}{3} \pi\right)=\frac{3}{2}</math> | ||
इसलिए (वापस प्रतिस्थापन): | इसलिए (वापस प्रतिस्थापन): | ||
: <math>P_{TOT}=\frac{3 V_P^2}{2R}.</math> | : <math>P_{TOT}=\frac{3 V_P^2}{2R}.</math> | ||
चूंकि हमने | चूंकि हमने <math>\theta</math> को हटा दिया है और हम देख सकते हैं कि कुल शक्ति समय के साथ बदलती नहीं है। बड़े जनरेटर और मोटरों को सुचारू रूप से चलाने के लिए यह आवश्यक है। | ||
यह भी ध्यान दें कि रूट माध्य वर्ग वोल्टेज का उपयोग करना <math>V = \frac{V_p}{\sqrt{2}}</math>, उपरोक्त <math>P_{TOT}</math> के लिए अभिव्यक्ति निम्नलिखित अधिक | यह भी ध्यान दें कि रूट माध्य वर्ग वोल्टेज का उपयोग करना <math>V = \frac{V_p}{\sqrt{2}}</math>, उपरोक्त <math>P_{TOT}</math> के लिए अभिव्यक्ति निम्नलिखित अधिक उत्कृष्ट रूप लेती है: | ||
:<math>P_{TOT} = \frac{3V^2}{R}</math>. | :<math>P_{TOT} = \frac{3V^2}{R}</math>. | ||
| Line 49: | Line 48: | ||
: <math>Z=|Z|e^{j\varphi}</math> | : <math>Z=|Z|e^{j\varphi}</math> | ||
जिससे पीक धारा हो | |||
: <math>I_P=\frac{V_P}{|Z|}</math> | : <math>I_P=\frac{V_P}{|Z|}</math> | ||
| Line 62: | Line 61: | ||
: <math>P_{L2}=V_{L2}I_{L2}=V_P I_P\sin\left(\theta-\frac{2}{3}\pi\right)\sin\left(\theta-\frac{2}{3}\pi-\varphi\right)</math> | : <math>P_{L2}=V_{L2}I_{L2}=V_P I_P\sin\left(\theta-\frac{2}{3}\pi\right)\sin\left(\theta-\frac{2}{3}\pi-\varphi\right)</math> | ||
: <math>P_{L3}=V_{L3}I_{L3}=V_P I_P\sin\left(\theta-\frac{4}{3}\pi\right)\sin\left(\theta-\frac{4}{3}\pi-\varphi\right)</math> | : <math>P_{L3}=V_{L3}I_{L3}=V_P I_P\sin\left(\theta-\frac{4}{3}\pi\right)\sin\left(\theta-\frac{4}{3}\pi-\varphi\right)</math> | ||
त्रिकोणमितीय पहचान का उपयोग | त्रिकोणमितीय पहचान का उपयोग कोण योग और अंतर पहचान: | ||
: <math>P_{L1}=\frac{V_P I_P}{2}\left[\cos\left(\varphi\right)-\cos\left(2\theta-\varphi\right)\right]</math> | : <math>P_{L1}=\frac{V_P I_P}{2}\left[\cos\left(\varphi\right)-\cos\left(2\theta-\varphi\right)\right]</math> | ||
| Line 70: | Line 69: | ||
: <math>P_{TOT}=\frac{V_P I_P}{2}\left\{3\cos\varphi-\left[\cos\left(2\theta-\varphi\right)+\cos\left(2\theta-\frac{4}{3}\pi-\varphi\right)+\cos\left(2\theta-\frac{8}{3}\pi-\varphi\right)\right]\right\}</math> | : <math>P_{TOT}=\frac{V_P I_P}{2}\left\{3\cos\varphi-\left[\cos\left(2\theta-\varphi\right)+\cos\left(2\theta-\frac{4}{3}\pi-\varphi\right)+\cos\left(2\theta-\frac{8}{3}\pi-\varphi\right)\right]\right\}</math> | ||
चूँकि वर्ग कोष्ठक में संलग्न तीन पद तीन-चरण प्रणाली हैं | चूँकि वर्ग कोष्ठक में संलग्न तीन पद तीन-चरण प्रणाली हैं वे शून्य तक जुड़ते हैं और कुल शक्ति बन जाती है | ||
: <math>P_{TOT}=\frac{3V_P I_P}{2}\cos\varphi</math> | : <math>P_{TOT}=\frac{3V_P I_P}{2}\cos\varphi</math> | ||
| Line 77: | Line 76: | ||
उपरोक्त विवाद दिखा रहा है। | उपरोक्त विवाद दिखा रहा है। | ||
फिर से | फिर से मूल माध्य वर्ग वोल्टेज <math>V = \frac{V_p}{\sqrt{2}}</math> का उपयोग करके <math>P_{TOT}</math> को सामान्य रूप में लिखा जा सकता है | ||
:<math>P_{TOT}=\frac{3V^2}{Z}\cos\varphi</math>. | :<math>P_{TOT}=\frac{3V^2}{Z}\cos\varphi</math>. | ||
'''कोई तटस्थ धारा नहीं''' | '''कोई तटस्थ धारा नहीं''' | ||
तीन चरणों में से प्रत्येक पर समान भार के | तीन चरणों में से प्रत्येक पर समान भार के स्थितियों में तटस्थ में कोई शुद्ध धारा प्रवाहित नहीं होती है। तटस्थ धारा रेखा धाराओं का विपरीत सदिश योग है। किरचॉफ के परिपथ नियम देखें। | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 88: | Line 87: | ||
-I_{N} &= I_{L1} + I_{L2} + I_{L3} | -I_{N} &= I_{L1} + I_{L2} + I_{L3} | ||
\end{align}</math> | \end{align}</math> | ||
हम | हम गैर-आयामी वर्तमान <math>i=\frac{I_{N}R}{V_P}</math> को परिभाषित करते हैं, | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 96: | Line 95: | ||
&= 0 | &= 0 | ||
\end{align}</math> | \end{align}</math> | ||
चूंकि हमने दिखाया है कि तटस्थ धारा शून्य है | चूंकि हमने दिखाया है कि तटस्थ धारा शून्य है हम देख सकते हैं कि तटस्थ कोर को हटाने से परिपथ पर कोई प्रभाव नहीं पड़ेगा परंतु प्रणाली संतुलित होता है। इस तरह के संबंध सामान्यतः केवल तभी उपयोग किए जाते हैं जब तीन चरणों पर लोड उपकरण के ही टुकड़े का भाग होता है (उदाहरण के लिए तीन-चरण मोटर) अन्यथा स्विचिंग लोड और सामान्य असंतुलन बड़े वोल्टेज में उतार-चढ़ाव का कारण होगा। | ||
== असंतुलित | == असंतुलित प्रणाली == | ||
अभ्यास में प्रणाली में तीनों चरणों में संभवतः ही कभी पूरी तरह से संतुलित भार धाराएं, वोल्टेज और प्रतिबाधा होती है। [[सममित घटक]] की विधि से असंतुलित स्थितियों का विश्लेषण बहुत सरल है। एक असंतुलित प्रणाली का विश्लेषण संतुलित वोल्टेज के सकारात्मक, नकारात्मक या शून्य अनुक्रम के साथ तीन संतुलित प्रणालियों के सुपरपोजिशन के रूप में किया जाता है। | |||
तीन-चरण प्रणाली में तारों के आकार को निर्दिष्ट करते समय | तीन-चरण प्रणाली में तारों के आकार को निर्दिष्ट करते समय हमें केवल चरण और तटस्थ धाराओं के परिमाण को जानने की आवश्यकता होती है। तटस्थ धारा को तीन चरण धाराओं को साथ जटिल संख्याओं के रूप में जोड़कर और फिर आयताकार से ध्रुवीय निर्देशांक में परिवर्तित करके निर्धारित किया जा सकता है। यदि तीन-चरण रूट माध्य वर्ग (आरएमएस) धाराएँ <math>I_{L1}</math>, <math>I_{L2}</math>, और <math>I_{L3}</math>, तटस्थ आरएमएस धारा है: | ||
: <math>I_{L1} + I_{L2} \cos\left(\frac{2}{3}\pi\right) + j I_{L2} \sin\left(\frac{2}{3}\pi\right) + I_{L3} \cos\left(\frac{4}{3}\pi\right) + j I_{L3} \sin\left(\frac{4}{3}\pi\right)</math> | : <math>I_{L1} + I_{L2} \cos\left(\frac{2}{3}\pi\right) + j I_{L2} \sin\left(\frac{2}{3}\pi\right) + I_{L3} \cos\left(\frac{4}{3}\pi\right) + j I_{L3} \sin\left(\frac{4}{3}\pi\right)</math> | ||
जो हल करता है | जो हल करता है | ||
: <math>I_{L1} - I_{L2} \frac{1}{2} - I_{L3} \frac{1}{2} + j \frac{\sqrt{3}}{2} \left(I_{L2} - I_{L3}\right)</math> | : <math>I_{L1} - I_{L2} \frac{1}{2} - I_{L3} \frac{1}{2} + j \frac{\sqrt{3}}{2} \left(I_{L2} - I_{L3}\right)</math> | ||
इसका ध्रुवीय परिमाण वास्तविक और काल्पनिक भागों के वर्गों के योग का वर्गमूल है | इसका ध्रुवीय परिमाण वास्तविक और काल्पनिक भागों के वर्गों के योग का वर्गमूल है जो कम हो जाता है <ref name=Kelijik>{{cite book|last=Keljik|first=Jeffrey|title=Electricity 3: Power Generation and Delivery|year=2008|publisher=Cengage Learning/Delmar|location=Clifton Park, NY|isbn=978-1435400290|pages=49}}</ref> | ||
: <math>\sqrt{I_{L1}^2 + I_{L2}^2 + I_{L3}^2 - I_{L1} I_{L2} - I_{L1} I_{L3} - I_{L2} I_{L3}}</math> | : <math>\sqrt{I_{L1}^2 + I_{L2}^2 + I_{L3}^2 - I_{L1} I_{L2} - I_{L1} I_{L3} - I_{L2} I_{L3}}</math> | ||
=== गैर रेखीय भार === | === गैर रेखीय भार === | ||
रैखिक भार के साथ | रैखिक भार के साथ तटस्थ केवल चरणों के बीच असंतुलन के कारण वर्तमान को वहन करता है। डिवाइस जो रेक्टीफायर-कैपेसिटर फ्रंट एंड (जैसे कंप्यूटर प्रणाली उपकरण और इसी तरह के लिए स्विच-मोड पावर सप्लाई) का उपयोग करते हैं, तीसरे क्रमित हार्मोनिक्स प्रस्तुत करते हैं। तीसरे हार्मोनिक धाराएं आपूर्ति के प्रत्येक चरण में इन-फेज हैं और इसलिए तटस्थ में साथ जुड़ जाएंगी जो वाय प्रणाली में तटस्थ धारा को चरण धाराओं से अधिक कर सकती हैं।<ref>{{cite web|last=Lowenstein|first=Michael|title=The 3rd Harmonic Blocking Filter: A Well Established Approach to Harmonic Current Mitigation|url=http://www.iaei.org/magazine/2003/01/the-3rd-harmonic-blocking-filter-a-well-established-approach-to-harmonic-current-mitigation/|publisher=IAEI Magazine|access-date=24 November 2012|url-status=dead|archive-url=https://web.archive.org/web/20110327130618/http://www.iaei.org/magazine/2003/01/the-3rd-harmonic-blocking-filter-a-well-established-approach-to-harmonic-current-mitigation/|archive-date=27 March 2011}}</ref><ref>{{cite web|last=Enjeti|first=Prasad|title=लो वोल्टेज थ्री-फेज फोर-वायर इलेक्ट्रिक डिस्ट्रीब्यूशन सिस्टम और फ़िल्टरिंग सॉल्यूशंस में हार्मोनिक्स|url=http://www.pserc.wisc.edu/documents/general_information/presentations/pserc_seminars/pserc_seminars0/enjeti_slides.pdf|publisher=Texas A&M University Power Electronics and Power Quality Laboratory|access-date=24 November 2012|url-status=live|archive-url=https://web.archive.org/web/20100613051835/http://www.pserc.wisc.edu/documents/general_information/presentations/pserc_seminars/pserc_seminars0/enjeti_slides.pdf|archive-date=13 June 2010}}</ref> | ||
== परिक्रामी चुंबकीय क्षेत्र == | == परिक्रामी चुंबकीय क्षेत्र == | ||
कोई भी पॉलीपेज़ प्रणाली | कोई भी पॉलीपेज़ प्रणाली चरणों में धाराओं के समय विस्थापन के आधार पर चुंबकीय क्षेत्र को आसानी से उत्पन्न करना संभव बनाता है जो रेखा आवृत्ति पर घूमता है। ऐसा घूमने वाला चुंबकीय क्षेत्र पॉलीफ़ेज़ [[इंडक्शन मोटर]] को संभव बनाता है। वास्तव में जहाँ प्रेरण मोटरों को एकल-चरण शक्ति पर चलना चाहिए (जैसे कि सामान्यतः घरों में वितरित किया जाता है) मोटर में घूमने वाले क्षेत्र का उत्पादन करने के लिए कुछ तंत्र होना चाहिए, अन्यथा मोटर कोई स्टैंड-स्टिल [[ टॉर्कः |टॉर्कः]] उत्पन्न नहीं कर सकती है और प्रारंभ नहीं होगी। एकल-चरण वाइंडिंग द्वारा उत्पन्न क्षेत्र पहले से ही घूम रही मोटर को ऊर्जा प्रदान कर सकता है, किन्तु सहायक तंत्र के बिना मोटर स्टॉप से त्वरित नहीं होगी। | ||
स्थिर आयाम के | स्थिर आयाम के घूर्णन चुंबकीय क्षेत्र के लिए आवश्यक है कि सभी तीन चरण धाराएँ परिमाण में समान हों और चरण में चक्र के तिहाई भाग को स्पष्ट रूप से विस्थापित कर सकता है। असंतुलित संचालन के परिणामस्वरूप मोटरों और जनरेटर पर अवांछनीय प्रभाव पड़ता है। | ||
== अन्य चरण प्रणालियों में रूपांतरण == | == अन्य चरण प्रणालियों में रूपांतरण == | ||
परंतु दो वोल्टेज तरंगों में समय अक्ष पर कम से कम कुछ सापेक्ष विस्थापन हो आधे-चक्र के से अधिक के अतिरिक्त वोल्टेज के किसी भी अन्य [[पॉलीफ़ेज़ सिस्टम|पॉलीफ़ेज़ प्रणाली]] समुच्चय को निष्क्रिय [[ट्रांसफार्मर]] की सरणी द्वारा प्राप्त किया जा सकता है। इस तरह की सरणियाँ समान रूप से स्रोत प्रणाली के चरणों के बीच पॉलीफ़ेज़ लोड को संतुलित करेंगी। उदाहरण के लिए दो विशेष रूप से निर्मित ट्रांसफार्मर का उपयोग करके तीन-चरण नेटवर्क से संतुलित दो-चरण शक्ति प्राप्त की जा सकती है जिसमें प्राथमिक वोल्टेज का 50% और 86.6% है। यह स्कॉट-टी ट्रांसफॉर्मर चरणों के बीच 90 डिग्री समय के अंतर के साथ वास्तविक दो-चरण प्रणाली का उत्पादन करता है। अन्य उदाहरण बड़े [[सही करनेवाला]] प्रणाली के लिए उच्च चरण-क्रमित प्रणाली की पीढ़ी है जो चिकनी प्रत्यक्ष वर्तमान उत्पादन का उत्पादन करने और आपूर्ति में [[ लयबद्ध |लयबद्ध]] धाराओं को कम करने के लिए है। | |||
जब तीन चरण की आवश्यकता होती है किन्तु विद्युत आपूर्तिकर्ता से केवल एकल चरण आसानी से उपलब्ध होता है, तो [[चरण कनवर्टर]] का उपयोग एकल चरण आपूर्ति से तीन चरण की विद्युत उत्पन्न करने के लिए किया जा सकता है। कारखाने के औद्योगिक अनुप्रयोगों में अधिकांशतः मोटर-जनरेटर का उपयोग किया जाता है। | |||
== प्रणाली माप == | |||
तीन-चरण प्रणाली में तटस्थ होने पर कम से कम दो ट्रांसड्यूसर या तटस्थ होने पर तीन ट्रांसड्यूसर की आवश्यकता होती है।<ref>{{cite web|title=Measurement of three-phase power with the 2-wattmeter method.|url=http://eelinux.ee.usm.maine.edu/courses/ele323/2-Wattmeters%20method.pdf}}{{dead link|date=December 2017 |bot=InternetArchiveBot |fix-attempted=yes }}</ref> ब्लोंडेल के प्रमेय में कहा गया है कि आवश्यक माप तत्वों की संख्या वर्तमान-वाहक चालकों की संख्या से कम है।<ref>{{cite web |title=दो मीटर वाटमीटर विधि|url=http://www-ee.uta.edu/online/camacho/ee2446/Fall2009/Notes/Two-wattmeter-method(E).pdf |archive-url=https://web.archive.org/web/20140221162212/http://www-ee.uta.edu/online/camacho/ee2446/Fall2009/Notes/Two-wattmeter-method(E).pdf |archive-date=2014-02-21}}</ref> | |||
== यह भी देखें == | == यह भी देखें == | ||
{{div col|colwidth=23em}} | {{div col|colwidth=23em}} | ||
| Line 143: | Line 135: | ||
*{{cite book|last=Stevenson|first=William D. Jr.|year=1975|title=Elements of Power Systems Analysis|series=McGraw-Hill Electrical and Electronic Engineering Series|edition=3rd|location=New York|publisher=McGraw-Hill|isbn=0-07-061285-4}} | *{{cite book|last=Stevenson|first=William D. Jr.|year=1975|title=Elements of Power Systems Analysis|series=McGraw-Hill Electrical and Electronic Engineering Series|edition=3rd|location=New York|publisher=McGraw-Hill|isbn=0-07-061285-4}} | ||
{{DEFAULTSORT:Three-Phase}} | {{DEFAULTSORT:Three-Phase}} | ||
[[Category: | [[Category:All articles with dead external links]] | ||
[[Category:Created On 08/06/2023]] | [[Category:Articles with dead external links from December 2017]] | ||
[[Category:Articles with permanently dead external links]] | |||
[[Category:Created On 08/06/2023|Three-Phase]] | |||
[[Category:Lua-based templates|Three-Phase]] | |||
[[Category:Machine Translated Page|Three-Phase]] | |||
[[Category:Multi-column templates|Three-Phase]] | |||
[[Category:Pages using div col with small parameter|Three-Phase]] | |||
[[Category:Pages with script errors|Three-Phase]] | |||
[[Category:Templates Vigyan Ready|Three-Phase]] | |||
[[Category:Templates that add a tracking category|Three-Phase]] | |||
[[Category:Templates that generate short descriptions|Three-Phase]] | |||
[[Category:Templates using TemplateData|Three-Phase]] | |||
[[Category:Templates using under-protected Lua modules|Three-Phase]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:थ्री-फेज एसी पावर| थ्री-फेज एसी पावर ]] | |||
[[Category:निकोला टेस्ला|Three-Phase]] | |||
[[Category:विद्युत शक्ति|Three-Phase]] | |||
Latest revision as of 21:38, 11 July 2023

विद्युत अभियन्त्रण में, तीन चरण विद्युत शक्ति प्रणाली में कम से कम तीन चालक होते हैं जो बारी-बारी से चालू होते हैं जो कि तिहाई अवधि के समय में बदलाव होते हैं। डेल्टा (∆) या स्टार (वाई) में तीन-चरण प्रणाली की व्यवस्था की जा सकती है (कुछ क्षेत्रों में वाई के रूप में भी निरूपित किया जाता है, क्योंकि प्रतीकात्मक रूप से यह अक्षर 'वाई' के समान है)। वाई प्रणाली तीनों एसी चरण से दो अलग-अलग वोल्टेज के उपयोग की अनुमति देता है, जैसे कि 230/400 वी प्रणाली जो तटस्थ (सेंटर हब) और किसी चरण के बीच 230 वी प्रदान करता है और किसी भी दो चरणों में 400 वी डेल्टा प्रणाली व्यवस्था केवल वोल्टेज प्रदान करती है किन्तु इसकी अधिक अतिरेक है क्योंकि यह सामान्य रूप से तीन आपूर्ति वाइंडिंग्स में से के साथ ऑफ़लाइन काम करना जारी रख सकती है, यद्यपि कुल क्षमता का 57.7%[1] यदि गैर-रैखिक भार जुड़े हुए हैं तो तटस्थ में हार्मोनिक प्रवाह बहुत बड़ा हो सकता है।
परिभाषाएँ
घूर्णन अनुक्रम L1 - L2 - L3 के साथ स्टार (डब्ल्यू वाई ई) कनेक्टेड टोपोलॉजी में, समय-भिन्न तात्कालिक वोल्टेज की गणना क्रमशः प्रत्येक चरण ए, सी, बी के लिए की जा सकती है:
जहाँ:
- पीक वोल्टेज है,
- रेडियंस में चरण कोण है
- सेकंड में समय है
- प्रति सेकंड चक्रों में आवृत्ति है और
- वोल्टेज L1-N, L2-N और L3-N को स्टार संबंध बिंदु से संदर्भित किया जाता है।
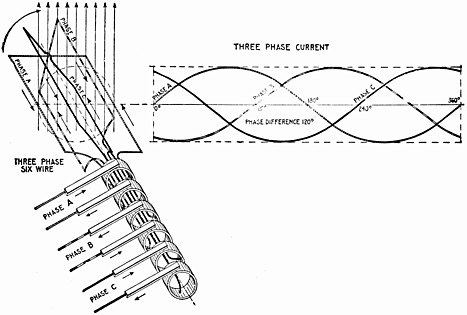
रेखा-चित्र
नीचे दी गई छवियां प्रदर्शित करती हैं कि कैसे अल्टरनेटर से तीन चरणों को वितरित करने वाले छह तारों की प्रणाली को केवल तीन से बदला जा सकता है। तीन चरण का ट्रांसफार्मर भी दिखाया गया है।
संतुलित भार
सामान्यतः विद्युत शक्ति प्रणालियों में भार चरणों के बीच व्यावहारिक रूप से समान रूप से वितरित किए जाते हैं। पहले संतुलित प्रणाली पर चर्चा करना और फिर असंतुलित प्रणालियों के प्रभावों का प्राथमिक स्थितियों से विचलन के रूप में वर्णन करना सामान्य अभ्यास है।
निरन्तर विद्युत हस्तांतरण
तीन-चरण शक्ति की महत्वपूर्ण गुण यह है कि प्रतिरोधक भार के लिए तात्कालिक शक्ति उपलब्ध है, , हर समय स्थिर रहता है। वास्तव में माना
गणित को सरल बनाने के लिए हम मध्यवर्ती गणनाओं के लिए आयामहीन मात्रा शक्ति को परिभाषित करते हैं,
इसलिए (वापस प्रतिस्थापन):
चूंकि हमने को हटा दिया है और हम देख सकते हैं कि कुल शक्ति समय के साथ बदलती नहीं है। बड़े जनरेटर और मोटरों को सुचारू रूप से चलाने के लिए यह आवश्यक है।
यह भी ध्यान दें कि रूट माध्य वर्ग वोल्टेज का उपयोग करना , उपरोक्त के लिए अभिव्यक्ति निम्नलिखित अधिक उत्कृष्ट रूप लेती है:
- .
निरंतर तात्कालिक शक्ति प्राप्त करने के लिए लोड को प्रतिरोधी होने की आवश्यकता नहीं है, जब तक यह संतुलित है या सभी चरणों के लिए समान है, इसे लिखा जा सकता है
जिससे पीक धारा हो
सभी चरणों के लिए और तात्कालिक धाराएँ हैं
अब चरणों में तात्कालिक शक्तियाँ हैं
त्रिकोणमितीय पहचान का उपयोग कोण योग और अंतर पहचान:
जो कुल तात्कालिक शक्ति के लिए जोड़ते हैं
चूँकि वर्ग कोष्ठक में संलग्न तीन पद तीन-चरण प्रणाली हैं वे शून्य तक जुड़ते हैं और कुल शक्ति बन जाती है
या
उपरोक्त विवाद दिखा रहा है।
फिर से मूल माध्य वर्ग वोल्टेज का उपयोग करके को सामान्य रूप में लिखा जा सकता है
- .
कोई तटस्थ धारा नहीं
तीन चरणों में से प्रत्येक पर समान भार के स्थितियों में तटस्थ में कोई शुद्ध धारा प्रवाहित नहीं होती है। तटस्थ धारा रेखा धाराओं का विपरीत सदिश योग है। किरचॉफ के परिपथ नियम देखें।
हम गैर-आयामी वर्तमान को परिभाषित करते हैं,
चूंकि हमने दिखाया है कि तटस्थ धारा शून्य है हम देख सकते हैं कि तटस्थ कोर को हटाने से परिपथ पर कोई प्रभाव नहीं पड़ेगा परंतु प्रणाली संतुलित होता है। इस तरह के संबंध सामान्यतः केवल तभी उपयोग किए जाते हैं जब तीन चरणों पर लोड उपकरण के ही टुकड़े का भाग होता है (उदाहरण के लिए तीन-चरण मोटर) अन्यथा स्विचिंग लोड और सामान्य असंतुलन बड़े वोल्टेज में उतार-चढ़ाव का कारण होगा।
असंतुलित प्रणाली
अभ्यास में प्रणाली में तीनों चरणों में संभवतः ही कभी पूरी तरह से संतुलित भार धाराएं, वोल्टेज और प्रतिबाधा होती है। सममित घटक की विधि से असंतुलित स्थितियों का विश्लेषण बहुत सरल है। एक असंतुलित प्रणाली का विश्लेषण संतुलित वोल्टेज के सकारात्मक, नकारात्मक या शून्य अनुक्रम के साथ तीन संतुलित प्रणालियों के सुपरपोजिशन के रूप में किया जाता है।
तीन-चरण प्रणाली में तारों के आकार को निर्दिष्ट करते समय हमें केवल चरण और तटस्थ धाराओं के परिमाण को जानने की आवश्यकता होती है। तटस्थ धारा को तीन चरण धाराओं को साथ जटिल संख्याओं के रूप में जोड़कर और फिर आयताकार से ध्रुवीय निर्देशांक में परिवर्तित करके निर्धारित किया जा सकता है। यदि तीन-चरण रूट माध्य वर्ग (आरएमएस) धाराएँ , , और , तटस्थ आरएमएस धारा है:
जो हल करता है
इसका ध्रुवीय परिमाण वास्तविक और काल्पनिक भागों के वर्गों के योग का वर्गमूल है जो कम हो जाता है [2]
गैर रेखीय भार
रैखिक भार के साथ तटस्थ केवल चरणों के बीच असंतुलन के कारण वर्तमान को वहन करता है। डिवाइस जो रेक्टीफायर-कैपेसिटर फ्रंट एंड (जैसे कंप्यूटर प्रणाली उपकरण और इसी तरह के लिए स्विच-मोड पावर सप्लाई) का उपयोग करते हैं, तीसरे क्रमित हार्मोनिक्स प्रस्तुत करते हैं। तीसरे हार्मोनिक धाराएं आपूर्ति के प्रत्येक चरण में इन-फेज हैं और इसलिए तटस्थ में साथ जुड़ जाएंगी जो वाय प्रणाली में तटस्थ धारा को चरण धाराओं से अधिक कर सकती हैं।[3][4]
परिक्रामी चुंबकीय क्षेत्र
कोई भी पॉलीपेज़ प्रणाली चरणों में धाराओं के समय विस्थापन के आधार पर चुंबकीय क्षेत्र को आसानी से उत्पन्न करना संभव बनाता है जो रेखा आवृत्ति पर घूमता है। ऐसा घूमने वाला चुंबकीय क्षेत्र पॉलीफ़ेज़ इंडक्शन मोटर को संभव बनाता है। वास्तव में जहाँ प्रेरण मोटरों को एकल-चरण शक्ति पर चलना चाहिए (जैसे कि सामान्यतः घरों में वितरित किया जाता है) मोटर में घूमने वाले क्षेत्र का उत्पादन करने के लिए कुछ तंत्र होना चाहिए, अन्यथा मोटर कोई स्टैंड-स्टिल टॉर्कः उत्पन्न नहीं कर सकती है और प्रारंभ नहीं होगी। एकल-चरण वाइंडिंग द्वारा उत्पन्न क्षेत्र पहले से ही घूम रही मोटर को ऊर्जा प्रदान कर सकता है, किन्तु सहायक तंत्र के बिना मोटर स्टॉप से त्वरित नहीं होगी।
स्थिर आयाम के घूर्णन चुंबकीय क्षेत्र के लिए आवश्यक है कि सभी तीन चरण धाराएँ परिमाण में समान हों और चरण में चक्र के तिहाई भाग को स्पष्ट रूप से विस्थापित कर सकता है। असंतुलित संचालन के परिणामस्वरूप मोटरों और जनरेटर पर अवांछनीय प्रभाव पड़ता है।
अन्य चरण प्रणालियों में रूपांतरण
परंतु दो वोल्टेज तरंगों में समय अक्ष पर कम से कम कुछ सापेक्ष विस्थापन हो आधे-चक्र के से अधिक के अतिरिक्त वोल्टेज के किसी भी अन्य पॉलीफ़ेज़ प्रणाली समुच्चय को निष्क्रिय ट्रांसफार्मर की सरणी द्वारा प्राप्त किया जा सकता है। इस तरह की सरणियाँ समान रूप से स्रोत प्रणाली के चरणों के बीच पॉलीफ़ेज़ लोड को संतुलित करेंगी। उदाहरण के लिए दो विशेष रूप से निर्मित ट्रांसफार्मर का उपयोग करके तीन-चरण नेटवर्क से संतुलित दो-चरण शक्ति प्राप्त की जा सकती है जिसमें प्राथमिक वोल्टेज का 50% और 86.6% है। यह स्कॉट-टी ट्रांसफॉर्मर चरणों के बीच 90 डिग्री समय के अंतर के साथ वास्तविक दो-चरण प्रणाली का उत्पादन करता है। अन्य उदाहरण बड़े सही करनेवाला प्रणाली के लिए उच्च चरण-क्रमित प्रणाली की पीढ़ी है जो चिकनी प्रत्यक्ष वर्तमान उत्पादन का उत्पादन करने और आपूर्ति में लयबद्ध धाराओं को कम करने के लिए है।
जब तीन चरण की आवश्यकता होती है किन्तु विद्युत आपूर्तिकर्ता से केवल एकल चरण आसानी से उपलब्ध होता है, तो चरण कनवर्टर का उपयोग एकल चरण आपूर्ति से तीन चरण की विद्युत उत्पन्न करने के लिए किया जा सकता है। कारखाने के औद्योगिक अनुप्रयोगों में अधिकांशतः मोटर-जनरेटर का उपयोग किया जाता है।
प्रणाली माप
तीन-चरण प्रणाली में तटस्थ होने पर कम से कम दो ट्रांसड्यूसर या तटस्थ होने पर तीन ट्रांसड्यूसर की आवश्यकता होती है।[5] ब्लोंडेल के प्रमेय में कहा गया है कि आवश्यक माप तत्वों की संख्या वर्तमान-वाहक चालकों की संख्या से कम है।[6]
यह भी देखें
- चार्ल्स प्रोटियस स्टेनमेट्ज़
- गैलीलियो फेरारिस
- जॉन हॉपकिंसन
- मिखाइल डोलिवो-डोब्रोवल्स्की
- निकोला टेस्ला
- पॉलीपेज़ सिस्टम
- तीन चरण विद्युत शक्ति
- Y-Δ रूपांतरण
संदर्भ
- ↑ "Delta and Wye 3-phase circuits" (PDF). Archived (PDF) from the original on 2013-05-13. Retrieved 2012-11-21. public domain
- ↑ Keljik, Jeffrey (2008). Electricity 3: Power Generation and Delivery. Clifton Park, NY: Cengage Learning/Delmar. p. 49. ISBN 978-1435400290.
- ↑ Lowenstein, Michael. "The 3rd Harmonic Blocking Filter: A Well Established Approach to Harmonic Current Mitigation". IAEI Magazine. Archived from the original on 27 March 2011. Retrieved 24 November 2012.
- ↑ Enjeti, Prasad. "लो वोल्टेज थ्री-फेज फोर-वायर इलेक्ट्रिक डिस्ट्रीब्यूशन सिस्टम और फ़िल्टरिंग सॉल्यूशंस में हार्मोनिक्स" (PDF). Texas A&M University Power Electronics and Power Quality Laboratory. Archived (PDF) from the original on 13 June 2010. Retrieved 24 November 2012.
- ↑ "Measurement of three-phase power with the 2-wattmeter method" (PDF).[permanent dead link]
- ↑ "दो मीटर वाटमीटर विधि" (PDF). Archived from the original (PDF) on 2014-02-21.
- Stevenson, William D. Jr. (1975). Elements of Power Systems Analysis. McGraw-Hill Electrical and Electronic Engineering Series (3rd ed.). New York: McGraw-Hill. ISBN 0-07-061285-4.