समतुल्य मानचित्र: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{short description|Maps whose domain and codomain are acted on by the same group, and the map commutes}} | {{short description|Maps whose domain and codomain are acted on by the same group, and the map commutes}} | ||
गणित में, समतुल्यता [[फ़ंक्शन (गणित)]] के लिए स्थान से दूसरे स्थान पर [[समरूपता]] के | गणित में, समतुल्यता [[फ़ंक्शन (गणित)|फलन (गणित)]] के लिए एक स्थान से दूसरे स्थान पर [[समरूपता]] के प्रदर्शित होता है, जैसे [[सममित स्थान]] कहते हैं। इस प्रकार उक्त फलन को '''समतुल्य मानचित्र''' कहा जाता है, इस प्रकार जब इसका डोमेन और कोडोमेन ही [[समरूपता समूह]] द्वारा [[समूह क्रिया (गणित)]] होते हैं, और इस प्रकार जब समूह की इस प्रक्रिया के साथ फलन क्रमविनिमेय मान को प्रकट करता है। अर्थात् समरूपता परिवर्तन को लागू करना और पुनः फलन की गणना करना आवश्यक होता हैं, इस प्रकार फलन की इस गणना को करने और इस प्रकार पुनः परिवर्तन को लागू करने के समान परिणाम उत्पन्न करता है। | ||
समतुल्य मानचित्र [[अपरिवर्तनीय (गणित)]] की अवधारणा को सामान्यीकृत | इस समतुल्य मानचित्र की [[अपरिवर्तनीय (गणित)]] की अवधारणा को सामान्यीकृत किया जाता हैं, इस प्रकार ऐसा कार्य जिसका मान उनके तर्क के समरूपता परिवर्तन से अपरिवर्तित होता है। समतुल्य मानचित्र के मान को अधिकांशतः अस्पष्ट रूप से अपरिवर्तनीय कहा जाता है। | ||
सांख्यिकीय | सांख्यिकीय मे अनुमानतः डेटा के सांख्यिकीय परिवर्तनों के अनुसार समतुल्यता विभिन्न अनुमान विधियों की महत्वपूर्ण मान प्राप्त होता है, इस प्रकार उक्त विवरण के लिए [[अपरिवर्तनीय अनुमानक]] देखें। इसकी शुद्ध गणित में समतुल्यता समवर्ती टोपोलॉजी और इसके उप-विषयों समवर्ती कोहोलॉजी और समवर्ती स्थिर होमोटॉपी सिद्धांत में अध्ययन का केंद्रीय उद्देश्य व्याप्त हो जाता है। | ||
==उदाहरण== | ==उदाहरण== | ||
===प्राथमिक ज्यामिति=== | ===प्राथमिक ज्यामिति=== | ||
[[File:Triangle.Centroid.svg|thumb|एक त्रिभुज का केन्द्रक (जहाँ तीन लाल खंड मिलते हैं) [[एफ़िन परिवर्तन]] | [[File:Triangle.Centroid.svg|thumb|एक त्रिभुज का केन्द्रक (जहाँ तीन लाल खंड मिलते हैं) [[एफ़िन परिवर्तन]] के अनुसार समतुल्य होता है: परिवर्तित त्रिभुज का केन्द्रक त्रिभुज के केन्द्रक के परिवर्तन के समान बिंदु होता है।]]त्रिभुजों की ज्यामिति में, त्रिभुज का [[क्षेत्र|क्षेत्रफल]] और परिधि अपरिवर्तनीय होती है: इसके आधार पर किसी त्रिभुज का अनुवाद करने या घुमाने से उसका क्षेत्रफल या परिधि परिवर्तित नहीं होती है। चूंकि, त्रिभुज केंद्र जैसे कि [[केन्द्रक]], परिकेंद्र, अंतकेंद्र और लंबकेंद्र अपरिवर्तनीय नहीं हैं, क्योंकि त्रिभुज के हिलने से उसके केंद्र भी हिल जाएंगे। इसके अतिरिक्त, ये केंद्र समतुल्य हैं: इस प्रकार किसी भी यूक्लिडियन [[सर्वांगसमता (ज्यामिति)]] अनुवाद और घूर्णन का संयोजन हैं, जिसको त्रिभुज में लागू करना आवश्यक होता हैं, और पुनः उसके केंद्र का निर्माण करना पहले केंद्र के निर्माण के समान बिंदु उत्पन्न करता है, और फिर उसी सर्वांगसमता को लागू करना बीच में इसके लिए अधिक सामान्य रूप से सभी त्रिभुज केंद्र [[समानता (ज्यामिति)]] अनुवाद, घूर्णन और स्केलिंग के संयोजन के अंतर्गत भी समतुल्य होते हैं।<ref>{{citation | ||
| last = Kimberling | first = Clark | authorlink = Clark Kimberling | | last = Kimberling | first = Clark | authorlink = Clark Kimberling | ||
| issue = 3 | | issue = 3 | ||
| Line 20: | Line 20: | ||
| year = 1994 | | year = 1994 | ||
| doi=10.2307/2690608}}. "Similar triangles have similarly situated centers", p. 164.</ref> | | doi=10.2307/2690608}}. "Similar triangles have similarly situated centers", p. 164.</ref> | ||
इस प्रकार केन्द्रक एफ़िन ट्रांसफ़ॉर्मेशन के अनुसार समतुल्य है।<ref>The centroid is the only affine equivariant center of a triangle, but more general convex bodies can have other affine equivariant centers; see e.g. {{citation | |||
| last = Neumann | first = B. H. | | last = Neumann | first = B. H. | ||
| journal = Journal of the London Mathematical Society | | journal = Journal of the London Mathematical Society | ||
| Line 30: | Line 30: | ||
| year = 1939 | | year = 1939 | ||
| issue = 4 | | issue = 4 | ||
| doi = 10.1112/jlms/s1-14.4.262 }}.</ref> | | doi = 10.1112/jlms/s1-14.4.262 }}.</ref> इसके उक्त फलन की समरूपता के समूह के लिए अपरिवर्तनीय और समरूपता के अलग समूह के लिए समतुल्य हो सकता है। उदाहरण के लिए इस प्रकार सर्वांगसमताओं के अतिरिक्त समानता परिवर्तनों के अनुसार क्षेत्र और परिधि अब अपरिवर्तनीय नहीं हैं: त्रिभुज को स्केल करने से इसका क्षेत्र और परिधि भी परिवर्तित हो जाती है। चूंकि इस प्रकार ये परिवर्तन पूर्वानुमेय तरीके से होते हैं: यदि त्रिभुज को {{mvar|s}} कारक द्वारा मापा जाता है, इस प्रकार परिधि {{mvar|s}} भी मापी जाती है, और {{math|''s''<sup>2</sup>}} क्षेत्र की माप भी की जाती है, इस प्रकार प्रत्येक त्रिभुज को उसके क्षेत्रफल या परिधि पर मैप करने वाले फलन को धनात्मक वास्तविक संख्याओं पर स्केलिंग परिवर्तनों की गुणक समूह से जुड़ी प्रक्रिया के लिए समतुल्य के रूप में देखा जा सकता है। | ||
===सांख्यिकी=== | ===सांख्यिकी=== | ||
सरल उदाहरणों का अन्य वर्ग [[सांख्यिकीय अनुमान]] से आता है। किसी | सरल उदाहरणों का अन्य वर्ग [[सांख्यिकीय अनुमान]] से आता है। किसी प्रमाण का माध्य इसकी वास्तविक संख्याओं के समुच्चय को सामान्यतः उक्त प्रमाणों की [[केंद्रीय प्रवृत्ति]] के रूप में उपयोग किया जाता है। यह इस प्रकार वास्तविक संख्याओं के रैखिक फलन को कैलकुलस के अनुसार समतुल्य है, उदाहरण के लिए, यह संख्याओं का प्रतिनिधित्व करने के लिए उपयोग की जाने वाली इकाइयों की पसंद से अप्रभावित है। इसके विपरीत, घातांक जैसे अरैखिक परिवर्तनों के संबंध में माध्य समतुल्य नहीं है। | ||
एक | एक प्रमाणों का माध्यिका परिवर्तनों के बहुत बड़े समूह, वास्तविक संख्याओं के लिए मोनोटोनिक कार्यों के लिए समतुल्य है। यह विश्लेषण इंगित करता है कि डेटा समुच्चय में कुछ प्रकार के परिवर्तनों के विरुद्ध माध्यिका अधिक [[मजबूत आँकड़े|शक्तिशाली आँकड़े]] में प्रकट होते हैं, और इस माध्य के विपरीत यह [[क्रमिक डेटा]] के लिए सार्थक है।<ref>{{citation|title=Measurement theory: Frequently asked questions (Version 3)|date=September 14, 1997|publisher=SAS Institute Inc.|url=http://www.medicine.mcgill.ca/epidemiology/courses/EPIB654/Summer2010/EF/measurement%20scales.pdf|first=Warren S.|last=Sarle}}. Revision of a chapter in ''Disseminations of the International Statistical Applications Institute'' (4th ed.), vol. 1, 1995, Wichita: ACG Press, pp. 61–66.</ref> इसके विश्लेषण की इस शैली को औपचारिक बनाने के लिए अपरिवर्तनीय अनुमानक और समतुल्य अनुमानक की अवधारणाओं का उपयोग किया गया है। | ||
विश्लेषण की इस शैली को औपचारिक बनाने के लिए अपरिवर्तनीय अनुमानक और समतुल्य अनुमानक की अवधारणाओं का उपयोग किया गया है। | |||
===प्रतिनिधित्व सिद्धांत=== | ===प्रतिनिधित्व सिद्धांत=== | ||
{{See also| | {{See also|प्रतिनिधित्व सिद्धांत#समतुल्य मानचित्र और समरूपताएँ}} | ||
परिमित समूहों के प्रतिनिधित्व सिद्धांत में, समूह से सुसज्जित सदिश स्थान जो अंतरिक्ष के रैखिक परिवर्तनों द्वारा कार्य करता है, समूह का [[रैखिक प्रतिनिधित्व]] कहलाता है। | परिमित समूहों के '''प्रतिनिधित्व सिद्धांत''' में, समूह से सुसज्जित सदिश स्थान जो अंतरिक्ष के रैखिक परिवर्तनों द्वारा कार्य करता है, यह इस समूह का [[रैखिक प्रतिनिधित्व]] कहलाता है। इस प्रकार [[रेखीय मानचित्र]] जो क्रिया के साथ चलता है उसे इंटरट्विनर कहा जाता है। अर्थात् इंटरट्विनर दो अभ्यावेदन के बीच समतुल्य रेखीय मानचित्र मात्र है। इसे वैकल्पिक रूप से इस समूह के प्रतिनिधित्व के लिए इंटरट्विनर {{mvar|G}} क्षेत्र पर (गणित) {{mvar|K}} [[मॉड्यूल (गणित)]] के समान ही है, यहाँ पर {{math|''K''[''G'']}}-मॉड्यूल (गणित), जहां {{math|''K''[''G'']}} G का समूह वलय है।<ref>{{citation | ||
| last1 = Fuchs | first1 = Jürgen | | last1 = Fuchs | first1 = Jürgen | ||
| last2 = Schweigert | first2 = Christoph | | last2 = Schweigert | first2 = Christoph | ||
| Line 53: | Line 50: | ||
| title = Symmetries, Lie algebras and representations: A graduate course for physicists | | title = Symmetries, Lie algebras and representations: A graduate course for physicists | ||
| url = https://books.google.com/books?id=B_JQryjNYyAC&pg=PA70 | | url = https://books.google.com/books?id=B_JQryjNYyAC&pg=PA70 | ||
| year = 1997}}.</ref> | | year = 1997}}.</ref> इस प्रकार इसकी कुछ शर्तों के अनुसार, यदि वह अंतर्संबंध तब गुणक कारक को गैर-शून्य [[अदिश (गणित)]] [[तक]] अद्वितीय होता है, दो इस गुण को तब धारण करते हैं जब की प्रतिबिंब {{math|''K''[''G'']}} केंद्र सहित सरल बीजगणित है, इसके लिए {{mvar|K}} जिसे शूर्स लेम्मा कहा जाता है, इसके लिए [[सरल मॉड्यूल]] देखें। इसके परिणामस्वरूप महत्वपूर्ण स्थितियों में इंटरट्विनर का निर्माण यह दिखाने के लिए पर्याप्त है कि प्रतिनिधित्व प्रभावी रूप से समान हैं।<ref>{{citation | ||
कुछ शर्तों के | |||
| last1 = Sexl | first1 = Roman U. | | last1 = Sexl | first1 = Roman U. | ||
| last2 = Urbantke | first2 = Helmuth K. | | last2 = Urbantke | first2 = Helmuth K. | ||
| Line 68: | Line 64: | ||
| year = 2001}}.</ref> | | year = 2001}}.</ref> | ||
==औपचारिकीकरण== | ==औपचारिकीकरण== | ||
समूह क्रिया (गणित) की अवधारणा का उपयोग करके समतुल्यता को औपचारिक रूप दिया जा सकता है{{mvar|G}}-एक समूह के लिए | समूह क्रिया (गणित) की अवधारणा का उपयोग करके समतुल्यता को औपचारिक रूप दिया जा सकता है, इस प्रकार {{mvar|G}}-एक समूह के लिए समुच्चय (गणित) {{mvar|G}} द्वारा प्रदर्शित किया जाता हैं। यह गणितीय मान है जिसमें [[सेट (गणित)|समुच्चय (गणित)]] उपस्थित है, यहाँ पर {{mvar|S}} और समूह क्रिया बाईं ओर होती हैं। इस प्रकार {{mvar|G}} पर {{mvar|S}} को यदि {{mvar|X}} और {{mvar|Y}} दोनों {{mvar|G}}-एक ही समूह के लिए समुच्चय {{mvar|G}}, के लिए पुनः फलन {{math|''f'' : ''X'' → ''Y''}} को समतुल्य कहा जाता है यदि | ||
:{{math|1=''f''(''g''·''x'') = ''g''·''f''(''x'')}} | :{{math|1=''f''(''g''·''x'') = ''g''·''f''(''x'')}} | ||
सभी के लिए {{math|''g'' ∈ ''G''}} और सभी {{math|''x'' in ''X''}} | सभी के लिए {{math|''g'' ∈ ''G''}} और सभी {{math|''x'' in ''X''}}<ref>{{citation|title=Nominal Sets: Names and Symmetry in Computer Science|volume=57|series=Cambridge Tracts in Theoretical Computer Science|first=Andrew M.|last=Pitts|publisher=Cambridge University Press|year=2013|isbn=9781107244689|url=https://books.google.com/books?id=VVehscCSPh8C&pg=PA14|at=Definition 1.2, p. 14}}.</ref>हैं, यदि या दोनों क्रियाएं सही क्रियाएं हैं, तो समतुल्य स्थिति को उपयुक्त रूप से संशोधित किया जा सकता है: | ||
यदि या दोनों क्रियाएं सही क्रियाएं हैं तो समतुल्य स्थिति को उपयुक्त रूप से संशोधित किया जा सकता है: | :{{math|1=''f''(''x''·''g'') = ''f''(''x'')·''g''}}, (सत्य मान, सत्य मान) | ||
:{{math|1=''f''(''x''·''g'') = ''f''(''x'')·''g''}} | :{{math|1=''f''(''x''·''g'') = ''g''<sup>−1</sup>·''f''(''x'')}}, (दाएं से बाएं) | ||
:{{math|1=''f''(''x''·''g'') = ''g''<sup>−1</sup>·''f''(''x'')}} | :{{math|1=''f''(''g''·''x'') = ''f''(''x'')·''g''<sup>−1</sup>}}, (बाएँ से दांए) | ||
:{{math|1=''f''(''g''·''x'') = ''f''(''x'')·''g''<sup>−1</sup>}} | |||
समतुल्य मानचित्र | समतुल्य मानचित्र G-समुच्चय (निश्चित G के लिए) इसकी [[श्रेणी (गणित)]] में [[समरूपता]]एं हैं।<ref name="grm">{{citation|title=Groups, Rings, Modules|series=Dover Books on Mathematics|first1=Maurice|last1=Auslander|first2=David|last2=Buchsbaum|publisher=Dover Publications|year=2014|isbn=9780486490823|url=https://books.google.com/books?id=VW2TAwAAQBAJ&pg=PA86|pages=86–87}}.</ref> इसलिए इस प्रकार उन्हें ''G''-रूपवाद के रूप में भी जाना जाता है,<ref name="grm"/>''G''-मानचित्र,<ref>{{citation | ||
| last = Segal | first = G. B. | | last = Segal | first = G. B. | ||
| contribution = Equivariant stable homotopy theory | | contribution = Equivariant stable homotopy theory | ||
| Line 84: | Line 78: | ||
| publisher = Gauthier-Villars, Paris | | publisher = Gauthier-Villars, Paris | ||
| title = Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 2 | | title = Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 2 | ||
| year = 1971}}.</ref> या '' | | year = 1971}}.</ref> या ''G''-समरूपता को प्रकट करता हैं।<ref>{{citation | ||
| last1 = Adhikari | first1 = Mahima Ranjan | | last1 = Adhikari | first1 = Mahima Ranjan | ||
| last2 = Adhikari | first2 = Avishek | | last2 = Adhikari | first2 = Avishek | ||
| Line 95: | Line 89: | ||
| title = Basic modern algebra with applications | | title = Basic modern algebra with applications | ||
| url = https://books.google.com/books?id=lBO7BAAAQBAJ&pg=PA142 | | url = https://books.google.com/books?id=lBO7BAAAQBAJ&pg=PA142 | ||
| year = 2014}}.</ref> | | year = 2014}}.</ref> इसके लिए G-समुच्चय की समरूपताएं केवल विशेषण समतुल्य मानचित्र हैं।<ref name="grm"/> | ||
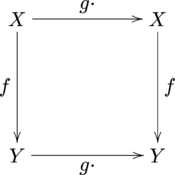
समतुल्य स्थिति को निम्नलिखित [[क्रमविनिमेय आरेख]] के रूप में भी समझा जा सकता है। ध्यान दें कि <math>g\cdot</math> उस मानचित्र को दर्शाता है जो तत्व लेता है <math>z</math> और | समतुल्य स्थिति को निम्नलिखित [[क्रमविनिमेय आरेख]] के रूप में भी समझा जा सकता है। ध्यान दें कि <math>g\cdot</math> उस मानचित्र को दर्शाता है जो तत्व लेता है <math>z</math> और <math>g\cdot z</math> लौट आता है। | ||
[[Image:equivariant commutative diagram.png|center|175px]] | [[Image:equivariant commutative diagram.png|center|175px]] | ||
==सामान्यीकरण== | ==सामान्यीकरण== | ||
{{See also| | {{See also|प्रतिनिधित्व सिद्धांत#सामान्यीकरण|अभ्यावेदन की श्रेणी#श्रेणी-सैद्धांतिक परिभाषा}} | ||
समतुल्य मानचित्रों को सीधे तरीके से मनमानी श्रेणी (गणित) में सामान्यीकृत किया जा सकता है। इस प्रकार प्रत्येक समूह G को ही वस्तु वाली श्रेणी के रूप में देखा जा सकता है, इसके लिए इस श्रेणी में संरचना केवल G के तत्व हैं। इस श्रेणी C को देखते हुए इस श्रेणी C में G का प्रतिनिधित्व G से C तक प्रसारित होता है। ऐसा प्रसार C के मान और उस मान की [[आकारिता|संरचना]] के [[उपसमूह]] का चयन करता है। उदाहरण के लिए, G-समुच्चय, G से [[सेट की श्रेणी|समुच्चय की श्रेणी]], 'समुच्चय' के लिए [[ऑपरेटर]] के समान है, और रैखिक प्रतिनिधित्व क्षेत्र, 'वेक्ट' पर वेक्टर रिक्त स्थान की श्रेणी के लिए फ़ैक्टर K के बराबर है। | |||
दूसरे उदाहरण के लिए, [[टोपोलॉजिकल स्पेस]] की श्रेणी | C में G के दो अभ्यावेदन, ρ और σ को देखते हुए उन अभ्यावेदन के बीच समतुल्य मानचित्र ρ से σ तक [[प्राकृतिक परिवर्तन]] है। इसके प्राकृतिक परिवर्तनों को इस प्रकार रूपवाद के रूप में उपयोग करके, कोई C में G के सभी अभ्यावेदन की श्रेणी बना सकता है। इस प्रकार यह केवल G फ़ंक्टर के लिए श्रेणी C में प्रदर्शित होता है। | ||
दूसरे उदाहरण के लिए, [[टोपोलॉजिकल स्पेस]] की श्रेणी C = 'टॉप' लेते हैं। इस 'टॉप' में G का प्रतिनिधित्व टोपोलॉजिकल स्पेस है जिस पर G निरंतर कार्य करता है। इसके समतुल्य मानचित्र तब अभ्यावेदन के बीच सतत मानचित्र f : X → Y होता है, जो G की क्रिया के साथ परिवर्तित होता है। | |||
==यह भी देखें== | ==यह भी देखें== | ||
*कर्टिस-हेडलंड-लिंडन प्रमेय, समतुल्य मानचित्रों के संदर्भ में [[सेल्यूलर आटोमेटा]] का लक्षण | *कर्टिस-हेडलंड-लिंडन प्रमेय, समतुल्य मानचित्रों के संदर्भ में [[सेल्यूलर आटोमेटा]] का लक्षण वर्णित किया जाता हैं। | ||
==संदर्भ== | ==संदर्भ== | ||
Revision as of 21:53, 9 July 2023
गणित में, समतुल्यता फलन (गणित) के लिए एक स्थान से दूसरे स्थान पर समरूपता के प्रदर्शित होता है, जैसे सममित स्थान कहते हैं। इस प्रकार उक्त फलन को समतुल्य मानचित्र कहा जाता है, इस प्रकार जब इसका डोमेन और कोडोमेन ही समरूपता समूह द्वारा समूह क्रिया (गणित) होते हैं, और इस प्रकार जब समूह की इस प्रक्रिया के साथ फलन क्रमविनिमेय मान को प्रकट करता है। अर्थात् समरूपता परिवर्तन को लागू करना और पुनः फलन की गणना करना आवश्यक होता हैं, इस प्रकार फलन की इस गणना को करने और इस प्रकार पुनः परिवर्तन को लागू करने के समान परिणाम उत्पन्न करता है।
इस समतुल्य मानचित्र की अपरिवर्तनीय (गणित) की अवधारणा को सामान्यीकृत किया जाता हैं, इस प्रकार ऐसा कार्य जिसका मान उनके तर्क के समरूपता परिवर्तन से अपरिवर्तित होता है। समतुल्य मानचित्र के मान को अधिकांशतः अस्पष्ट रूप से अपरिवर्तनीय कहा जाता है।
सांख्यिकीय मे अनुमानतः डेटा के सांख्यिकीय परिवर्तनों के अनुसार समतुल्यता विभिन्न अनुमान विधियों की महत्वपूर्ण मान प्राप्त होता है, इस प्रकार उक्त विवरण के लिए अपरिवर्तनीय अनुमानक देखें। इसकी शुद्ध गणित में समतुल्यता समवर्ती टोपोलॉजी और इसके उप-विषयों समवर्ती कोहोलॉजी और समवर्ती स्थिर होमोटॉपी सिद्धांत में अध्ययन का केंद्रीय उद्देश्य व्याप्त हो जाता है।
उदाहरण
प्राथमिक ज्यामिति

त्रिभुजों की ज्यामिति में, त्रिभुज का क्षेत्रफल और परिधि अपरिवर्तनीय होती है: इसके आधार पर किसी त्रिभुज का अनुवाद करने या घुमाने से उसका क्षेत्रफल या परिधि परिवर्तित नहीं होती है। चूंकि, त्रिभुज केंद्र जैसे कि केन्द्रक, परिकेंद्र, अंतकेंद्र और लंबकेंद्र अपरिवर्तनीय नहीं हैं, क्योंकि त्रिभुज के हिलने से उसके केंद्र भी हिल जाएंगे। इसके अतिरिक्त, ये केंद्र समतुल्य हैं: इस प्रकार किसी भी यूक्लिडियन सर्वांगसमता (ज्यामिति) अनुवाद और घूर्णन का संयोजन हैं, जिसको त्रिभुज में लागू करना आवश्यक होता हैं, और पुनः उसके केंद्र का निर्माण करना पहले केंद्र के निर्माण के समान बिंदु उत्पन्न करता है, और फिर उसी सर्वांगसमता को लागू करना बीच में इसके लिए अधिक सामान्य रूप से सभी त्रिभुज केंद्र समानता (ज्यामिति) अनुवाद, घूर्णन और स्केलिंग के संयोजन के अंतर्गत भी समतुल्य होते हैं।[1]
इस प्रकार केन्द्रक एफ़िन ट्रांसफ़ॉर्मेशन के अनुसार समतुल्य है।[2] इसके उक्त फलन की समरूपता के समूह के लिए अपरिवर्तनीय और समरूपता के अलग समूह के लिए समतुल्य हो सकता है। उदाहरण के लिए इस प्रकार सर्वांगसमताओं के अतिरिक्त समानता परिवर्तनों के अनुसार क्षेत्र और परिधि अब अपरिवर्तनीय नहीं हैं: त्रिभुज को स्केल करने से इसका क्षेत्र और परिधि भी परिवर्तित हो जाती है। चूंकि इस प्रकार ये परिवर्तन पूर्वानुमेय तरीके से होते हैं: यदि त्रिभुज को s कारक द्वारा मापा जाता है, इस प्रकार परिधि s भी मापी जाती है, और s2 क्षेत्र की माप भी की जाती है, इस प्रकार प्रत्येक त्रिभुज को उसके क्षेत्रफल या परिधि पर मैप करने वाले फलन को धनात्मक वास्तविक संख्याओं पर स्केलिंग परिवर्तनों की गुणक समूह से जुड़ी प्रक्रिया के लिए समतुल्य के रूप में देखा जा सकता है।
सांख्यिकी
सरल उदाहरणों का अन्य वर्ग सांख्यिकीय अनुमान से आता है। किसी प्रमाण का माध्य इसकी वास्तविक संख्याओं के समुच्चय को सामान्यतः उक्त प्रमाणों की केंद्रीय प्रवृत्ति के रूप में उपयोग किया जाता है। यह इस प्रकार वास्तविक संख्याओं के रैखिक फलन को कैलकुलस के अनुसार समतुल्य है, उदाहरण के लिए, यह संख्याओं का प्रतिनिधित्व करने के लिए उपयोग की जाने वाली इकाइयों की पसंद से अप्रभावित है। इसके विपरीत, घातांक जैसे अरैखिक परिवर्तनों के संबंध में माध्य समतुल्य नहीं है।
एक प्रमाणों का माध्यिका परिवर्तनों के बहुत बड़े समूह, वास्तविक संख्याओं के लिए मोनोटोनिक कार्यों के लिए समतुल्य है। यह विश्लेषण इंगित करता है कि डेटा समुच्चय में कुछ प्रकार के परिवर्तनों के विरुद्ध माध्यिका अधिक शक्तिशाली आँकड़े में प्रकट होते हैं, और इस माध्य के विपरीत यह क्रमिक डेटा के लिए सार्थक है।[3] इसके विश्लेषण की इस शैली को औपचारिक बनाने के लिए अपरिवर्तनीय अनुमानक और समतुल्य अनुमानक की अवधारणाओं का उपयोग किया गया है।
प्रतिनिधित्व सिद्धांत
परिमित समूहों के प्रतिनिधित्व सिद्धांत में, समूह से सुसज्जित सदिश स्थान जो अंतरिक्ष के रैखिक परिवर्तनों द्वारा कार्य करता है, यह इस समूह का रैखिक प्रतिनिधित्व कहलाता है। इस प्रकार रेखीय मानचित्र जो क्रिया के साथ चलता है उसे इंटरट्विनर कहा जाता है। अर्थात् इंटरट्विनर दो अभ्यावेदन के बीच समतुल्य रेखीय मानचित्र मात्र है। इसे वैकल्पिक रूप से इस समूह के प्रतिनिधित्व के लिए इंटरट्विनर G क्षेत्र पर (गणित) K मॉड्यूल (गणित) के समान ही है, यहाँ पर K[G]-मॉड्यूल (गणित), जहां K[G] G का समूह वलय है।[4] इस प्रकार इसकी कुछ शर्तों के अनुसार, यदि वह अंतर्संबंध तब गुणक कारक को गैर-शून्य अदिश (गणित) तक अद्वितीय होता है, दो इस गुण को तब धारण करते हैं जब की प्रतिबिंब K[G] केंद्र सहित सरल बीजगणित है, इसके लिए K जिसे शूर्स लेम्मा कहा जाता है, इसके लिए सरल मॉड्यूल देखें। इसके परिणामस्वरूप महत्वपूर्ण स्थितियों में इंटरट्विनर का निर्माण यह दिखाने के लिए पर्याप्त है कि प्रतिनिधित्व प्रभावी रूप से समान हैं।[5]
औपचारिकीकरण
समूह क्रिया (गणित) की अवधारणा का उपयोग करके समतुल्यता को औपचारिक रूप दिया जा सकता है, इस प्रकार G-एक समूह के लिए समुच्चय (गणित) G द्वारा प्रदर्शित किया जाता हैं। यह गणितीय मान है जिसमें समुच्चय (गणित) उपस्थित है, यहाँ पर S और समूह क्रिया बाईं ओर होती हैं। इस प्रकार G पर S को यदि X और Y दोनों G-एक ही समूह के लिए समुच्चय G, के लिए पुनः फलन f : X → Y को समतुल्य कहा जाता है यदि
- f(g·x) = g·f(x)
सभी के लिए g ∈ G और सभी x in X[6]हैं, यदि या दोनों क्रियाएं सही क्रियाएं हैं, तो समतुल्य स्थिति को उपयुक्त रूप से संशोधित किया जा सकता है:
- f(x·g) = f(x)·g, (सत्य मान, सत्य मान)
- f(x·g) = g−1·f(x), (दाएं से बाएं)
- f(g·x) = f(x)·g−1, (बाएँ से दांए)
समतुल्य मानचित्र G-समुच्चय (निश्चित G के लिए) इसकी श्रेणी (गणित) में समरूपताएं हैं।[7] इसलिए इस प्रकार उन्हें G-रूपवाद के रूप में भी जाना जाता है,[7]G-मानचित्र,[8] या G-समरूपता को प्रकट करता हैं।[9] इसके लिए G-समुच्चय की समरूपताएं केवल विशेषण समतुल्य मानचित्र हैं।[7]
समतुल्य स्थिति को निम्नलिखित क्रमविनिमेय आरेख के रूप में भी समझा जा सकता है। ध्यान दें कि उस मानचित्र को दर्शाता है जो तत्व लेता है और लौट आता है।
सामान्यीकरण
समतुल्य मानचित्रों को सीधे तरीके से मनमानी श्रेणी (गणित) में सामान्यीकृत किया जा सकता है। इस प्रकार प्रत्येक समूह G को ही वस्तु वाली श्रेणी के रूप में देखा जा सकता है, इसके लिए इस श्रेणी में संरचना केवल G के तत्व हैं। इस श्रेणी C को देखते हुए इस श्रेणी C में G का प्रतिनिधित्व G से C तक प्रसारित होता है। ऐसा प्रसार C के मान और उस मान की संरचना के उपसमूह का चयन करता है। उदाहरण के लिए, G-समुच्चय, G से समुच्चय की श्रेणी, 'समुच्चय' के लिए ऑपरेटर के समान है, और रैखिक प्रतिनिधित्व क्षेत्र, 'वेक्ट' पर वेक्टर रिक्त स्थान की श्रेणी के लिए फ़ैक्टर K के बराबर है।
C में G के दो अभ्यावेदन, ρ और σ को देखते हुए उन अभ्यावेदन के बीच समतुल्य मानचित्र ρ से σ तक प्राकृतिक परिवर्तन है। इसके प्राकृतिक परिवर्तनों को इस प्रकार रूपवाद के रूप में उपयोग करके, कोई C में G के सभी अभ्यावेदन की श्रेणी बना सकता है। इस प्रकार यह केवल G फ़ंक्टर के लिए श्रेणी C में प्रदर्शित होता है।
दूसरे उदाहरण के लिए, टोपोलॉजिकल स्पेस की श्रेणी C = 'टॉप' लेते हैं। इस 'टॉप' में G का प्रतिनिधित्व टोपोलॉजिकल स्पेस है जिस पर G निरंतर कार्य करता है। इसके समतुल्य मानचित्र तब अभ्यावेदन के बीच सतत मानचित्र f : X → Y होता है, जो G की क्रिया के साथ परिवर्तित होता है।
यह भी देखें
- कर्टिस-हेडलंड-लिंडन प्रमेय, समतुल्य मानचित्रों के संदर्भ में सेल्यूलर आटोमेटा का लक्षण वर्णित किया जाता हैं।
संदर्भ
- ↑ Kimberling, Clark (1994), "Central Points and Central Lines in the Plane of a Triangle", Mathematics Magazine, 67 (3): 163–187, doi:10.2307/2690608, JSTOR 2690608, MR 1573021. "Similar triangles have similarly situated centers", p. 164.
- ↑ The centroid is the only affine equivariant center of a triangle, but more general convex bodies can have other affine equivariant centers; see e.g. Neumann, B. H. (1939), "On some affine invariants of closed convex regions", Journal of the London Mathematical Society, Second Series, 14 (4): 262–272, doi:10.1112/jlms/s1-14.4.262, MR 0000978.
- ↑ Sarle, Warren S. (September 14, 1997), Measurement theory: Frequently asked questions (Version 3) (PDF), SAS Institute Inc.. Revision of a chapter in Disseminations of the International Statistical Applications Institute (4th ed.), vol. 1, 1995, Wichita: ACG Press, pp. 61–66.
- ↑ Fuchs, Jürgen; Schweigert, Christoph (1997), Symmetries, Lie algebras and representations: A graduate course for physicists, Cambridge Monographs on Mathematical Physics, Cambridge University Press, Cambridge, p. 70, ISBN 0-521-56001-2, MR 1473220.
- ↑ Sexl, Roman U.; Urbantke, Helmuth K. (2001), Relativity, groups, particles: Special relativity and relativistic symmetry in field and particle physics, Springer Physics, Vienna: Springer-Verlag, p. 165, doi:10.1007/978-3-7091-6234-7, ISBN 3-211-83443-5, MR 1798479.
- ↑ Pitts, Andrew M. (2013), Nominal Sets: Names and Symmetry in Computer Science, Cambridge Tracts in Theoretical Computer Science, vol. 57, Cambridge University Press, Definition 1.2, p. 14, ISBN 9781107244689.
- ↑ 7.0 7.1 7.2 Auslander, Maurice; Buchsbaum, David (2014), Groups, Rings, Modules, Dover Books on Mathematics, Dover Publications, pp. 86–87, ISBN 9780486490823.
- ↑ Segal, G. B. (1971), "Equivariant stable homotopy theory", Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 2, Gauthier-Villars, Paris, pp. 59–63, MR 0423340.
- ↑ Adhikari, Mahima Ranjan; Adhikari, Avishek (2014), Basic modern algebra with applications, New Delhi: Springer, p. 142, doi:10.1007/978-81-322-1599-8, ISBN 978-81-322-1598-1, MR 3155599.