संकेन्द्रित वस्तुएँ: Difference between revisions
No edit summary |
No edit summary |
||
| Line 10: | Line 10: | ||
यदि ज्यामितीय वस्तुएं समान निर्देशांक अक्ष (समरूपता की रेखा) साझा करती हैं तो वे [[समाक्षीय]] होती हैं। उत्तम प्रकार से परिभाषित अक्ष वाली ज्यामितीय वस्तुओं में वृत्त (केंद्र के माध्यम से कोई भी रेखा), गोले, [[सिलेंडर (ज्यामिति)]], सम्मिलित होते हैं।<ref>{{citation|title=Fluid Mechanics|first1=Joseph|last1=Spurk|first2=Nuri|last2=Aksel|publisher=Springer|year=2008|isbn=9783540735366|page=174|url=https://books.google.com/books?id=7_FrhazRTgsC&pg=PA174}}.</ref> शंकुधारी खंड, और क्रांति की सतहें आदि I | यदि ज्यामितीय वस्तुएं समान निर्देशांक अक्ष (समरूपता की रेखा) साझा करती हैं तो वे [[समाक्षीय]] होती हैं। उत्तम प्रकार से परिभाषित अक्ष वाली ज्यामितीय वस्तुओं में वृत्त (केंद्र के माध्यम से कोई भी रेखा), गोले, [[सिलेंडर (ज्यामिति)]], सम्मिलित होते हैं।<ref>{{citation|title=Fluid Mechanics|first1=Joseph|last1=Spurk|first2=Nuri|last2=Aksel|publisher=Springer|year=2008|isbn=9783540735366|page=174|url=https://books.google.com/books?id=7_FrhazRTgsC&pg=PA174}}.</ref> शंकुधारी खंड, और क्रांति की सतहें आदि I | ||
संकेंद्रित वस्तुएं प्रायः घुमावदार स्वरूप की व्यापक श्रेणी का भाग होती हैं, जिसमें सर्पिल (वक्र जो बिंदु से निकलता है, बिंदु के चारों ओर घूमते हुए दूर तक जाता है) भी | संकेंद्रित वस्तुएं प्रायः घुमावदार स्वरूप की व्यापक श्रेणी का भाग होती हैं, जिसमें सर्पिल (वक्र जो बिंदु से निकलता है, बिंदु के चारों ओर घूमते हुए दूर तक जाता है) भी सम्मिलित होते है। | ||
==ज्यामितीय गुण== | ==ज्यामितीय गुण== | ||
| Line 21: | Line 21: | ||
दो संकेंद्रित वृत्तों के बीच के तल का क्षेत्र वलय (गणित) है, और अनुरूप रूप से दो संकेंद्रित क्षेत्रों के बीच के स्थान का क्षेत्र [[गोलाकार खोल]] है।<ref name="apostol">{{citation|title=New Horizons in Geometry|volume=47|series=Dolciani Mathematical Expositions|first=Tom|last=Apostol|author-link=Tom Apostol|publisher=Mathematical Association of America|year=2013|isbn=9780883853542|page=140|url=https://books.google.com/books?id=PUVvwfjhjvMC&pg=PA140}}.</ref> | दो संकेंद्रित वृत्तों के बीच के तल का क्षेत्र वलय (गणित) है, और अनुरूप रूप से दो संकेंद्रित क्षेत्रों के बीच के स्थान का क्षेत्र [[गोलाकार खोल]] है।<ref name="apostol">{{citation|title=New Horizons in Geometry|volume=47|series=Dolciani Mathematical Expositions|first=Tom|last=Apostol|author-link=Tom Apostol|publisher=Mathematical Association of America|year=2013|isbn=9780883853542|page=140|url=https://books.google.com/books?id=PUVvwfjhjvMC&pg=PA140}}.</ref> | ||
समतल में दिए गए बिंदु c के लिए, c को केंद्र मानकर सभी वृत्तों का समुच्चय [[अपोलोनियन वृत्त]] बनाता है। पेंसिल में प्रत्येक दो वृत्त संकेंद्रित हैं, और उनकी त्रिज्याएँ अलग-अलग हैं। साझा केंद्र को छोड़कर, समतल का प्रत्येक बिंदु, पेंसिल के वृत्तों में से से संबंधित है। प्रत्येक दो असंयुक्त वृत्त, और वृत्तों की प्रत्येक अतिशयोक्तिपूर्ण पेंसिल, मोबियस परिवर्तन द्वारा संकेंद्रित वृत्तों के समूह में परिवर्तित हो सकती है।<ref>{{citation|title=Complex Numbers and Geometry|series=MAA Spectrum|first=Liang-shin|last=Hahn|publisher=Cambridge University Press|year=1994|isbn=9780883855102|page=142|url=https://books.google.com/books?id=s3nMMkPEvqoC&pg=PA142}}.</ref><ref>{{citation|title=Geometry|first1=David A.|last1=Brannan|first2=Matthew F.|last2=Esplen|first3=Jeremy J.|last3=Gray|publisher=Cambridge University Press|year=2011|isbn=9781139503709|pages=320–321|url=https://books.google.com/books?id=UlrmKjIjrzQC&pg=PA320}}.</ref> | समतल में दिए गए बिंदु c के लिए, c को केंद्र मानकर सभी वृत्तों का समुच्चय [[अपोलोनियन वृत्त]] बनाता है। पेंसिल में प्रत्येक दो वृत्त संकेंद्रित हैं, और उनकी त्रिज्याएँ अलग-अलग हैं। साझा केंद्र को छोड़कर, समतल का प्रत्येक बिंदु, पेंसिल के वृत्तों में से से संबंधित है। प्रत्येक दो असंयुक्त वृत्त, और वृत्तों की प्रत्येक अतिशयोक्तिपूर्ण पेंसिल, मोबियस परिवर्तन द्वारा संकेंद्रित वृत्तों के समूह में परिवर्तित हो सकती है।<ref>{{citation|title=Complex Numbers and Geometry|series=MAA Spectrum|first=Liang-shin|last=Hahn|publisher=Cambridge University Press|year=1994|isbn=9780883855102|page=142|url=https://books.google.com/books?id=s3nMMkPEvqoC&pg=PA142}}.</ref><ref>{{citation|title=Geometry|first1=David A.|last1=Brannan|first2=Matthew F.|last2=Esplen|first3=Jeremy J.|last3=Gray|publisher=Cambridge University Press|year=2011|isbn=9781139503709|pages=320–321|url=https://books.google.com/books?id=UlrmKjIjrzQC&pg=PA320}}.</ref> | ||
== अनुप्रयोग और उदाहरण == | == अनुप्रयोग और उदाहरण == | ||
किसी छोटी वस्तु को शांत पानी में गिराने से बनने वाली [[केशिका तरंग]]ें स्वाभाविक रूप से संकेंद्रित वृत्तों की विस्तारित प्रणाली बनाती हैं।<ref>{{citation|title=Waves and Ripples in Water, Air, and Æther: Being a Course of Christmas Lectures Delivered at the Royal Institution of Great Britain|first=Sir John Ambrose|last=Fleming|author-link=John Ambrose Fleming|publisher=Society for Promoting Christian Knowledge|year=1902|page=20|url=https://books.google.com/books?id=BiRJAAAAIAAJ&pg=PA20}}.</ref> [[लक्ष्य तीरंदाजी]] में उपयोग किए जाने वाले लक्ष्यों पर समान रूप से दूरी वाले वृत्त<ref>{{citation|title=Archery: Steps to Success|first1=Kathleen|last1=Haywood|first2=Catherine|last2=Lewis|publisher=Human Kinetics|year=2006|isbn=9780736055420|page=xxiii|url=https://books.google.com/books?id=-EFySHOgGmIC&pg=PR23}}.</ref> या इसी तरह के खेल संकेंद्रित वृत्तों का और परिचित उदाहरण प्रदान करते हैं। | किसी छोटी वस्तु को शांत पानी में गिराने से बनने वाली [[केशिका तरंग]]ें स्वाभाविक रूप से संकेंद्रित वृत्तों की विस्तारित प्रणाली बनाती हैं।<ref>{{citation|title=Waves and Ripples in Water, Air, and Æther: Being a Course of Christmas Lectures Delivered at the Royal Institution of Great Britain|first=Sir John Ambrose|last=Fleming|author-link=John Ambrose Fleming|publisher=Society for Promoting Christian Knowledge|year=1902|page=20|url=https://books.google.com/books?id=BiRJAAAAIAAJ&pg=PA20}}.</ref> [[लक्ष्य तीरंदाजी]] में उपयोग किए जाने वाले लक्ष्यों पर समान रूप से दूरी वाले वृत्त<ref>{{citation|title=Archery: Steps to Success|first1=Kathleen|last1=Haywood|first2=Catherine|last2=Lewis|publisher=Human Kinetics|year=2006|isbn=9780736055420|page=xxiii|url=https://books.google.com/books?id=-EFySHOgGmIC&pg=PR23}}.</ref> या इसी तरह के खेल संकेंद्रित वृत्तों का और परिचित उदाहरण प्रदान करते हैं। | ||
Revision as of 10:17, 10 July 2023
ज्यामिति में, दो या दो से अधिक गणितीय वस्तुओं को संकेंद्रित तब कहा जाता है जब उनका केंद्र (ज्यामिति) सामान होता है। उत्तम प्रकार से परिभाषित केंद्रों के साथ (संभवतः असमान) वस्तुओं की कोई भी जोड़ी संकेंद्रित हो सकती है, जिसमें वृत्त, गोले, नियमित बहुभुज, नियमित बहुफलक, समांतर चतुर्भुज, शंकु, शंकु खंड और चतुर्भुज सम्मिलित होते हैं।[1]
यदि ज्यामितीय वस्तुएं समान निर्देशांक अक्ष (समरूपता की रेखा) साझा करती हैं तो वे समाक्षीय होती हैं। उत्तम प्रकार से परिभाषित अक्ष वाली ज्यामितीय वस्तुओं में वृत्त (केंद्र के माध्यम से कोई भी रेखा), गोले, सिलेंडर (ज्यामिति), सम्मिलित होते हैं।[2] शंकुधारी खंड, और क्रांति की सतहें आदि I
संकेंद्रित वस्तुएं प्रायः घुमावदार स्वरूप की व्यापक श्रेणी का भाग होती हैं, जिसमें सर्पिल (वक्र जो बिंदु से निकलता है, बिंदु के चारों ओर घूमते हुए दूर तक जाता है) भी सम्मिलित होते है।
ज्यामितीय गुण
यूक्लिडियन विमान में, संकेंद्रित दो वृत्तों की त्रिज्याएँ आवश्यक रूप से दूसरे से भिन्न होती हैं।[3] हालाँकि, त्रि-आयामी अंतरिक्ष में वृत्त संकेंद्रित हो सकते हैं, और उनकी त्रिज्या दूसरे के समान हो सकती है, लेकिन फिर भी वे अलग-अलग वृत्त हो सकते हैं। उदाहरण के लिए, स्थलीय ग्लोब के दो अलग-अलग मेरिडियन (खगोल विज्ञान) दूसरे के साथ और पृथ्वी के ग्लोब (गोले के रूप में अनुमानित) के साथ संकेंद्रित होते हैं। अधिक सामान्यतः, गोले पर प्रत्येक दो बड़े वृत्त दूसरे के साथ और गोले के साथ संकेंद्रित होते हैं।[4] ज्यामिति में यूलर के प्रमेय के अनुसार त्रिभुज के परिकेन्द्र और अन्तकेन्द्र के बीच की दूरी पर, दो संकेंद्रित वृत्त (जिसकी दूरी शून्य हो) त्रिभुज के परिवृत्त और अंतःवृत्त होते हैं यदि और केवल यदि की त्रिज्या दूसरे की त्रिज्या से दोगुनी हो , जिस स्थिति में त्रिभुज समबाहु त्रिभुज है।[5]: p. 198
नियमित बहुभुज|नियमित एन-गॉन का परिवृत्त और अंतवृत्त, और नियमित एन-गॉन स्वयं, संकेंद्रित होते हैं। विभिन्न n के लिए परित्रिज्या-से-अंतत्रिज्या अनुपात के लिए, द्विकेंद्रीय बहुभुज#नियमित बहुभुज देखें। नियमित बहुफलक के अंतःक्षेत्र, मध्यक्षेत्र और परिक्षेत्र के बारे में भी यही कहा जा सकता है।
दो संकेंद्रित वृत्तों के बीच के तल का क्षेत्र वलय (गणित) है, और अनुरूप रूप से दो संकेंद्रित क्षेत्रों के बीच के स्थान का क्षेत्र गोलाकार खोल है।[6] समतल में दिए गए बिंदु c के लिए, c को केंद्र मानकर सभी वृत्तों का समुच्चय अपोलोनियन वृत्त बनाता है। पेंसिल में प्रत्येक दो वृत्त संकेंद्रित हैं, और उनकी त्रिज्याएँ अलग-अलग हैं। साझा केंद्र को छोड़कर, समतल का प्रत्येक बिंदु, पेंसिल के वृत्तों में से से संबंधित है। प्रत्येक दो असंयुक्त वृत्त, और वृत्तों की प्रत्येक अतिशयोक्तिपूर्ण पेंसिल, मोबियस परिवर्तन द्वारा संकेंद्रित वृत्तों के समूह में परिवर्तित हो सकती है।[7][8]
अनुप्रयोग और उदाहरण
किसी छोटी वस्तु को शांत पानी में गिराने से बनने वाली केशिका तरंगें स्वाभाविक रूप से संकेंद्रित वृत्तों की विस्तारित प्रणाली बनाती हैं।[9] लक्ष्य तीरंदाजी में उपयोग किए जाने वाले लक्ष्यों पर समान रूप से दूरी वाले वृत्त[10] या इसी तरह के खेल संकेंद्रित वृत्तों का और परिचित उदाहरण प्रदान करते हैं।
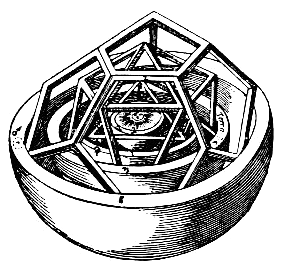
समाक्षीय केबल प्रकार की विद्युत केबल है जिसमें संयुक्त तटस्थ और पृथ्वी कोर संकेंद्रित बेलनाकार आवरणों की प्रणाली में जीवित कोर को पूरी तरह से घेर लेते हैं।[11] जोहान्स केपलर के ब्रह्माण्ड संबंधी रहस्य ने संकेंद्रित नियमित पॉलीहेड्रा और गोले द्वारा गठित ब्रह्माण्ड संबंधी प्रणाली की कल्पना की।[12] डायोप्टर दृष्टि में संकेंद्रित वृत्त भी पाए जाते हैं, प्रकार की मैकेनिक दृष्टि जो आमतौर पर लक्ष्य राइफलों पर पाई जाती है। इनमें आमतौर पर शूटर की आंख के पास छोटे-व्यास वाले छेद वाली बड़ी डिस्क और सामने ग्लोब दृष्टि (दूसरे सर्कल के अंदर समाहित सर्कल, जिसे सुरंग कहा जाता है) की सुविधा होती है। जब ये दृश्य सही ढंग से संरेखित होते हैं, तो प्रभाव का बिंदु सामने के दृश्य चक्र के मध्य में होगा।
यह भी देखें
- केन्द्रित घन संख्या
- होमियोइड
- फ़ोकलॉइड
- [[वृत्ताकार समरूपता]]
- मैजिक सर्कल (गणित)
- ऑस्कुलेटिंग सर्कल
- सर्पिल
संदर्भ
- ↑
Circles: Alexander, Daniel C.; Koeberlein, Geralyn M. (2009), Elementary Geometry for College Students, Cengage Learning, p. 279, ISBN 9781111788599
Spheres: Apostol (2013)
Regular polygons: Hardy, Godfrey Harold (1908), A Course of Pure Mathematics, The University Press, p. 107
Regular polyhedra: Gillard, Robert D. (1987), Comprehensive Coordination Chemistry: Theory & background, Pergamon Press, pp. 137, 139, ISBN 9780080262321.
- ↑ Spurk, Joseph; Aksel, Nuri (2008), Fluid Mechanics, Springer, p. 174, ISBN 9783540735366.
- ↑ Cole, George M.; Harbin, Andrew L. (2009), Surveyor Reference Manual, www.ppi2pass.com, §2, p. 6, ISBN 9781591261742.
- ↑ Morse, Jedidiah (1812), The American universal geography;: or, A view of the present state of all the kingdoms, states, and colonies in the known world, Volume 1 (6th ed.), Thomas & Andrews, p. 19.
- ↑ Dragutin Svrtan and Darko Veljan (2012), "Non-Euclidean versions of some classical triangle inequalities", forumgeom.fau.edu, Forum Geometricorum, pp. 197–209
- ↑ Apostol, Tom (2013), New Horizons in Geometry, Dolciani Mathematical Expositions, vol. 47, Mathematical Association of America, p. 140, ISBN 9780883853542.
- ↑ Hahn, Liang-shin (1994), Complex Numbers and Geometry, MAA Spectrum, Cambridge University Press, p. 142, ISBN 9780883855102.
- ↑ Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (2011), Geometry, Cambridge University Press, pp. 320–321, ISBN 9781139503709.
- ↑ Fleming, Sir John Ambrose (1902), Waves and Ripples in Water, Air, and Æther: Being a Course of Christmas Lectures Delivered at the Royal Institution of Great Britain, Society for Promoting Christian Knowledge, p. 20.
- ↑ Haywood, Kathleen; Lewis, Catherine (2006), Archery: Steps to Success, Human Kinetics, p. xxiii, ISBN 9780736055420.
- ↑ Weik, Martin (1997), Fiber Optics Standard Dictionary, Springer, p. 124, ISBN 9780412122415.
- ↑ Meyer, Walter A. (2006), Geometry and Its Applications (2nd ed.), Academic Press, p. 436, ISBN 9780080478036.
बाहरी संबंध
- Geometry: Concentric circles demonstration With interactive animation