बोल्ट्ज़मान मशीन: Difference between revisions
No edit summary |
No edit summary |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Type of stochastic recurrent neural network}} | {{short description|Type of stochastic recurrent neural network}} | ||
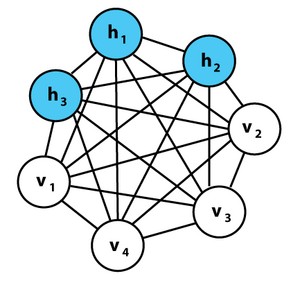
[[File:Boltzmannexamplev1.png|thumb|alt=A graphical representation of an example Boltzmann machine.| बोल्ट्ज़मैन मशीन के एक उदाहरण का चित्रमय प्रतिनिधित्व। प्रत्येक अप्रत्यक्ष किनारा निर्भरता का प्रतिनिधित्व करता है। इस उदाहरण में 3 | [[File:Boltzmannexamplev1.png|thumb|alt=A graphical representation of an example Boltzmann machine.| बोल्ट्ज़मैन मशीन के एक उदाहरण का चित्रमय प्रतिनिधित्व। प्रत्येक अप्रत्यक्ष किनारा निर्भरता का प्रतिनिधित्व करता है। इस उदाहरण में 3 प्रच्छन्न हुई इकाइयाँ और 4 दृश्यमान इकाइयाँ हैं। यह कोई प्रतिबंधित बोल्ट्ज़मैन मशीन नहीं है।]][[लुडविग बोल्ट्ज़मान|'''लुडविग बोल्ट्ज़मान''']] मशीन (जिसे बाहरी क्षेत्र के साथ '''शेरिंगटन-किर्कपैट्रिक मॉडल या प्रसंभाव्य आइसिंग-लेनज़-लिटिल मॉडल''' भी कहा जाता है) एक बाहरी क्षेत्र के साथ प्रसंभाव्य स्पिन-ग्लास मॉडल है, अर्थात, एक प्रचक्रण ग्लास#शेरिंगटन-किर्कपैट्रिक मॉडल ,<ref>{{citation|title=Solvable Model of a Spin-Glass|number=35|year=1975|author1= Sherrington, David|author2=Kirkpatrick, Scott|journal=Physical Review Letters|volume=35|pages=1792–1796|doi=10.1103/PhysRevLett.35.1792|bibcode=1975PhRvL..35.1792S}}</ref> यह एक प्रसंभाव्य [[आइसिंग मॉडल]] है। यह एक [[सांख्यिकीय भौतिकी]] तकनीक है जिसका उपयोग संज्ञानात्मक विज्ञान के संदर्भ में किया जाता है।<ref>{{citation|title=A learning algorithm for Boltzmann machines|number=1|year=1985|author1=Ackley, David H|author2=Hinton Geoffrey E|author3=Sejnowski, Terrence J|journal=Cognitive Science|volume=9|pages=147–169|doi=10.1207/s15516709cog0901_7|url=http://www.cs.toronto.edu/~hinton/absps/cogscibm.pdf|doi-access=free}}</ref> इसे [[मार्कोव यादृच्छिक क्षेत्र]] के रूप में भी वर्गीकृत किया गया है।<ref>{{Cite journal|last=Hinton|first=Geoffrey E.|date=2007-05-24|title=बोल्ट्ज़मान मशीन|journal=Scholarpedia|language=en|volume=2|issue=5|pages=1668|doi=10.4249/scholarpedia.1668|bibcode=2007SchpJ...2.1668H|issn=1941-6016|doi-access=free}}</ref> | ||
बोल्ट्ज़मैन मशीनें अपने प्रशिक्षण कलनविधि की स्थानीयता और [[हेब्बियन]] प्रकृति (हेब्ब के नियम द्वारा प्रशिक्षित होने) और उनके समानांतरवाद (अभिकलन) और सरल [[भौतिक प्रक्रिया]]ओं के साथ उनकी गतिशीलता की समानता के कारण सैद्धांतिक रूप से दिलचस्प हैं। अप्रतिबंधित संयोजकता वाली बोल्ट्ज़मैन मशीनें सीखने या अनुमान में व्यावहारिक समस्याओं के लिए उपयोगी | बोल्ट्ज़मैन मशीनें अपने प्रशिक्षण कलनविधि की स्थानीयता और [[हेब्बियन]] प्रकृति (हेब्ब के नियम द्वारा प्रशिक्षित होने) और उनके समानांतरवाद (अभिकलन) और सरल [[भौतिक प्रक्रिया]]ओं के साथ उनकी गतिशीलता की समानता के कारण सैद्धांतिक रूप से दिलचस्प हैं। अप्रतिबंधित संयोजकता वाली बोल्ट्ज़मैन मशीनें सीखने या अनुमान में व्यावहारिक समस्याओं के लिए उपयोगी सिद्ध नहीं हुई हैं, लेकिन यदि संयोजकता ठीक से बाधित है, तो सीखने को व्यावहारिक समस्याओं के लिए उपयोगी होने के लिए पर्याप्त कुशल बनाया जा सकता है।<ref>{{cite book|title=अंतर्राष्ट्रीय तंत्रिका नेटवर्क सम्मेलन|first=Thomas R.|last=Osborn|date=1 January 1990|publisher=Springer Netherlands|pages=[https://archive.org/details/innc90parisinter0001inte/page/785 785]|doi=10.1007/978-94-009-0643-3_76|chapter=Fast Teaching of Boltzmann Machines with Local Inhibition|isbn=978-0-7923-0831-7|chapter-url=https://archive.org/details/innc90parisinter0001inte/page/785}}</ref> | ||
उनका नाम [[सांख्यिकीय यांत्रिकी]] में [[Index.php?title=बोल्ट्ज़मान बंटन|बोल्ट्ज़मान बंटन]] के नाम पर रखा गया है, जिसका उपयोग उनके नमूनाकरण फलन में किया जाता है। उन्हें संज्ञानात्मक विज्ञान समुदायों और [[ यंत्र अधिगम ]] में [[जेफ्री हिंटन]], [[टेरी सेजनोवस्की]] और [[ वाई एन एल ईसीयू के अंदर ]] द्वारा काफी लोकप्रिय और प्रचारित किया गया था।<ref>{{citation|title=A learning algorithm for Boltzmann machines|number=1|year=1985|author1=Ackley, David H|author2=Hinton Geoffrey E|author3=Sejnowski, Terrence J|journal=Cognitive Science|volume=9|pages=147–169|doi=10.1207/s15516709cog0901_7|url=http://www.cs.toronto.edu/~hinton/absps/cogscibm.pdf|doi-access=free}}</ref> यंत्र अधिगम के भीतर एक अधिक सामान्य वर्ग के रूप में इन मॉडलों को [[ऊर्जा आधारित मॉडल]] (ईबीएम) कहा जाता है, क्योंकि [[Index.php?title=प्रचक्रण ग्लास|प्रचक्रण ग्लास]] के [[हैमिल्टनियन यांत्रिकी]] का उपयोग सीखने के कार्य को परिभाषित करने के लिए | उनका नाम [[सांख्यिकीय यांत्रिकी]] में [[Index.php?title=बोल्ट्ज़मान बंटन|बोल्ट्ज़मान बंटन]] के नाम पर रखा गया है, जिसका उपयोग उनके नमूनाकरण फलन में किया जाता है। उन्हें संज्ञानात्मक विज्ञान समुदायों और [[ यंत्र अधिगम ]] में [[जेफ्री हिंटन]], [[टेरी सेजनोवस्की]] और [[ वाई एन एल ईसीयू के अंदर ]] द्वारा काफी लोकप्रिय और प्रचारित किया गया था।<ref>{{citation|title=A learning algorithm for Boltzmann machines|number=1|year=1985|author1=Ackley, David H|author2=Hinton Geoffrey E|author3=Sejnowski, Terrence J|journal=Cognitive Science|volume=9|pages=147–169|doi=10.1207/s15516709cog0901_7|url=http://www.cs.toronto.edu/~hinton/absps/cogscibm.pdf|doi-access=free}}</ref> यंत्र अधिगम के भीतर एक अधिक सामान्य वर्ग के रूप में इन मॉडलों को [[ऊर्जा आधारित मॉडल]] (ईबीएम) कहा जाता है, क्योंकि [[Index.php?title=प्रचक्रण ग्लास|प्रचक्रण ग्लास]] के [[हैमिल्टनियन यांत्रिकी]] का उपयोग सीखने के कार्य को परिभाषित करने के लिए प्रारंभिकी बिंदु के रूप में किया जाता है।<ref>{{citation|title =On the Anatomy of MCMC-Based Maximum Likelihood Learning of Energy-Based Models|number=34|year=2020|author1=Nijkamp, E. |author2=Hill, M. E|author3= Han, T. |journal=Proceedings of the AAAI Conference on Artificial Intelligence|volume=4|pages=5272–5280|doi=10.1609/aaai.v34i04.5973|url=https://ojs.aaai.org/index.php/AAAI/article/view/5973|doi-access=free}}</ref> | ||
==संरचना== | ==संरचना== | ||
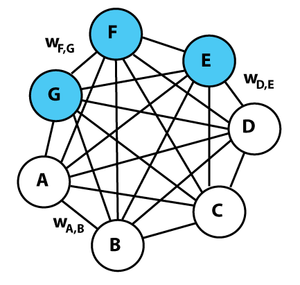
[[File:Boltzmannexamplev2.png|thumb|right|alt=A graphical representation of an example Boltzmann machine with weight labels.| कुछ वजन लेबल के साथ बोल्ट्ज़मैन मशीन का एक चित्रमय प्रतिनिधित्व। प्रत्येक अप्रत्यक्ष किनारा निर्भरता का प्रतिनिधित्व करता है और वजन के साथ भारित होता है <math>w_{ij}</math>. इस उदाहरण में 3 | [[File:Boltzmannexamplev2.png|thumb|right|alt=A graphical representation of an example Boltzmann machine with weight labels.| कुछ वजन लेबल के साथ बोल्ट्ज़मैन मशीन का एक चित्रमय प्रतिनिधित्व। प्रत्येक अप्रत्यक्ष किनारा निर्भरता का प्रतिनिधित्व करता है और वजन के साथ भारित होता है <math>w_{ij}</math>. इस उदाहरण में 3 प्रच्छन्न हुई इकाइयाँ (नीली) और 4 दृश्यमान इकाइयाँ (सफ़ेद) हैं। यह कोई प्रतिबंधित बोल्ट्ज़मैन मशीन नहीं है।]]बोल्ट्ज़मैन मशीन, प्रचक्रण ग्लास#शेरिंगटन-किर्कपैट्रिक मॉडल की तरह, समग्र संजाल के लिए परिभाषित कुल ऊर्जा (हैमिल्टनियन यांत्रिकी) वाली इकाइयों का एक संजाल है। इसकी इकाइयाँ [[बाइनरी संख्या|द्विआधारी संख्या]] परिणाम उत्पन्न करती हैं। बोल्ट्ज़मैन मशीन का वज़न [[स्टोकेस्टिक|प्रसंभाव्य]] है। वैश्विक ऊर्जा <math>E</math> बोल्ट्ज़मैन मशीन [[हॉपफील्ड नेटवर्क|हॉपफील्ड संजाल]] और [[आइसिंग मॉडल]] के समान है: | ||
:<math>E = -\left(\sum_{i<j} w_{ij} \, s_i \, s_j + \sum_i \theta_i \, s_i \right)</math> | :<math>E = -\left(\sum_{i<j} w_{ij} \, s_i \, s_j + \sum_i \theta_i \, s_i \right)</math> | ||
| Line 14: | Line 14: | ||
* <math>\theta_i</math> इकाई का पूर्वाग्रह है <math>i</math> वैश्विक ऊर्जा समारोह में. (<math>-\theta_i</math> इकाई के लिए सक्रियण सीमा है।) | * <math>\theta_i</math> इकाई का पूर्वाग्रह है <math>i</math> वैश्विक ऊर्जा समारोह में. (<math>-\theta_i</math> इकाई के लिए सक्रियण सीमा है।) | ||
अधिकांशत: वजन <math>w_{ij}</math> एक सममित आव्युह के रूप में दर्शाया गया है <math>W=[w_{ij}]</math> विकर्ण के साथ शून्य के साथ है। | |||
== इकाई अवस्था संभाव्यता == | == इकाई अवस्था संभाव्यता == | ||
| Line 40: | Line 40: | ||
जहां [[अदिश (भौतिकी)]] <math>T</math> इसे सिस्टम का [[तापमान]] कहा जाता है। यह संबंध बोल्ट्ज़मैन मशीन के वेरिएंट में संभाव्यता अभिव्यक्तियों में पाए जाने वाले [[लॉजिस्टिक फ़ंक्शन|लॉजिस्टिक फलन]] का स्रोत है। | जहां [[अदिश (भौतिकी)]] <math>T</math> इसे सिस्टम का [[तापमान]] कहा जाता है। यह संबंध बोल्ट्ज़मैन मशीन के वेरिएंट में संभाव्यता अभिव्यक्तियों में पाए जाने वाले [[लॉजिस्टिक फ़ंक्शन|लॉजिस्टिक फलन]] का स्रोत है। | ||
== | == साम्यावस्था == | ||
संजाल बार-बार एक इकाई को चुनने और उसकी स्थिति को पुनर्स्थापन करने से चलता है। एक निश्चित तापमान पर लंबे समय तक चलने के बाद, बोल्ट्ज़मैन बंटन के अनुसार, संजाल की वैश्विक स्थिति की संभावना केवल उस वैश्विक स्थिति की ऊर्जा पर निर्भर करती है, न कि उस प्रारंभिक स्थिति पर जहां से प्रक्रिया शुरू की गई थी। इसका मतलब यह है कि वैश्विक स्थिति की लॉग-संभावनाएं उनकी ऊर्जा में रैखिक हो जाती हैं। यह संबंध तब सत्य होता है जब मशीन [[Index.php?title=ऊष्मीय साम्य|ऊष्मीय साम्य]] पर होती है, जिसका अर्थ है कि वैश्विक स्थिति का संभाव्यता बंटन अभिसरण हो गया है। उच्च तापमान से शुरू होने वाले संजाल को चलाने पर, कम तापमान पर थर्मल संतुलन तक पहुंचने तक इसका तापमान धीरे-धीरे कम हो जाता है। इसके बाद यह एक ऐसे बंटन में परिवर्तित हो सकता है जहां ऊर्जा स्तर वैश्विक न्यूनतम के आसपास उतार-चढ़ाव करता है। इस प्रक्रिया को [[Index.php?title=अनुकारितअनीलन|अनुकारितअनीलन]] कहा जाता है। | |||
संजाल को प्रशिक्षित करने के लिए जिससे कि इन स्थितियों पर बाहरी बंटन के अनुसार वैश्विक स्थिति में परिवर्तित होने का मौका मिले, वजन निर्धारित किया जाना चाहिए जिससे कि उच्चतम संभावनाओं वाले वैश्विक स्थितियों को सबसे कम ऊर्जा मिल सके। यह प्रशिक्षण द्वारा किया जाता है। | |||
==प्रशिक्षण== | ==प्रशिक्षण== | ||
बोल्ट्ज़मान मशीन में इकाइयों को 'दृश्यमान' इकाइयों, | बोल्ट्ज़मान मशीन में इकाइयों को 'दृश्यमान' इकाइयों, V, और 'प्रच्छन्न' इकाइयों, H में विभाजित किया गया है। दृश्यमान इकाइयां वे हैं जो 'पर्यावरण' से जानकारी प्राप्त करती हैं, अर्थात प्रशिक्षण सेट द्विआधारी सदिश का एक सेट है, सेट V। प्रशिक्षण सेट पर बंटन दर्शाया गया है <math>P^{+}(V)</math>। | ||
जैसे ही बोल्ट्ज़मैन मशीन थर्मल संतुलन तक पहुँचती है, वैश्विक | जैसे ही बोल्ट्ज़मैन मशीन थर्मल संतुलन तक पहुँचती है, वैश्विक स्थितियों पर बंटन परिवर्तित हो जाता है। हम इस बंटन को छुपी हुई इकाइयों पर [[सीमांत वितरण|सीमांत बंटन]] के बाद निरूपित करते हैं <math>P^{-}(V)</math>. | ||
हमारा लक्ष्य वास्तविक बंटन का अनुमान लगाना है <math>P^{+}(V)</math> का उपयोग <math>P^{-}(V)</math> मशीन द्वारा उत्पादित. दो बंटनों की समानता कुल्बैक-लीब्लर विचलन द्वारा मापी जाती है, <math>G</math>: | हमारा लक्ष्य वास्तविक बंटन का अनुमान लगाना है <math>P^{+}(V)</math> का उपयोग <math>P^{-}(V)</math> मशीन द्वारा उत्पादित. दो बंटनों की समानता कुल्बैक-लीब्लर विचलन द्वारा मापी जाती है, <math>G</math>: | ||
:<math>G = \sum_{v}{P^{+}(v)\ln\left({\frac{P^{+}(v)}{P^{-}(v)}}\right)}</math> | :<math>G = \sum_{v}{P^{+}(v)\ln\left({\frac{P^{+}(v)}{P^{-}(v)}}\right)}</math> | ||
जहां योग सभी संभावित स्थितियों से अधिक है <math>V</math>. <math>G</math> भार का एक कार्य है, क्योंकि वे एक स्थिति की ऊर्जा निर्धारित करते हैं, और ऊर्जा निर्धारित करती है <math>P^{-}(v)</math>, जैसा कि बोल्ट्ज़मैन बंटन द्वारा वादा किया गया था। एक [[ | जहां योग सभी संभावित स्थितियों से अधिक है <math>V</math>. <math>G</math> भार का एक कार्य है, क्योंकि वे एक स्थिति की ऊर्जा निर्धारित करते हैं, और ऊर्जा निर्धारित करती है <math>P^{-}(v)</math>, जैसा कि बोल्ट्ज़मैन बंटन द्वारा वादा किया गया था। एक [[Index.php?title=प्रवणता अवरोह|प्रवणता अवरोह]] कलनविधि पर <math>G</math>, दिए गए वजन को बदलता है, <math>w_{ij}</math> के [[आंशिक व्युत्पन्न]] को घटाकर वजन के संबंध में <math>G</math> । | ||
बोल्ट्ज़मैन मशीन प्रशिक्षण में दो वैकल्पिक चरण | बोल्ट्ज़मैन मशीन प्रशिक्षण में दो वैकल्पिक चरण सम्मलित हैं। एक सकारात्मक चरण है जहां दृश्यमान इकाइयों की स्थिति को प्रशिक्षण सेट से नमूना किए गए एक विशेष द्विआधारी अवस्था सदिश से जोड़ा जाता है (के अनुसार <math>P^{+}</math>). दूसरा नकारात्मक चरण है जहां संजाल को स्वतंत्र रूप से चलने की अनुमति है, अर्थात केवल निविष्ट नोड्स की स्थिति बाहरी आंकड़ो द्वारा निर्धारित होती है, लेकिन निर्गम नोड्स को प्लव करने की अनुमति होती है। किसी दिए गए वजन के संबंध में ढाल, <math>w_{ij}</math>, समीकरण द्वारा दिया गया है:<ref>{{cite journal|last=Ackley|first=David H.|author2=Hinton, Geoffrey E. |author3=Sejnowski, Terrence J. |title=बोल्ट्ज़मैन मशीनों के लिए एक लर्निंग एल्गोरिदम|journal=[[Cognitive Science (journal)|Cognitive Science]]|year=1985|volume=9|issue=1|pages=147–169|doi=10.1207/s15516709cog0901_7|url=http://learning.cs.toronto.edu/~hinton/absps/cogscibm.pdf|archive-url=https://web.archive.org/web/20110718022336/http://learning.cs.toronto.edu/~hinton/absps/cogscibm.pdf|archive-date=18 July 2011|doi-access=free}}</ref> | ||
:<math>\frac{\partial{G}}{\partial{w_{ij}}} = -\frac{1}{R}[p_{ij}^{+}-p_{ij}^{-}]</math> | :<math>\frac{\partial{G}}{\partial{w_{ij}}} = -\frac{1}{R}[p_{ij}^{+}-p_{ij}^{-}]</math> | ||
जहाँ: | |||
* <math>p_{ij}^{+}</math> यह संभावना है कि जब मशीन सकारात्मक चरण पर संतुलन पर होती है तो इकाइयाँ i और j दोनों चालू होती हैं। | * <math>p_{ij}^{+}</math> यह संभावना है कि जब मशीन सकारात्मक चरण पर संतुलन पर होती है तो इकाइयाँ i और j दोनों चालू होती हैं। | ||
* <math>p_{ij}^{-}</math> यह संभावना है कि जब मशीन नकारात्मक चरण पर संतुलन पर होती है तो इकाइयाँ i और j दोनों चालू होती हैं। | * <math>p_{ij}^{-}</math> यह संभावना है कि जब मशीन नकारात्मक चरण पर संतुलन पर होती है तो इकाइयाँ i और j दोनों चालू होती हैं। | ||
* <math>R</math> सीखने की दर को दर्शाता है | * <math>R</math> सीखने की दर को दर्शाता है | ||
यह परिणाम इस तथ्य से निकलता है कि तापीय संतुलन पर संभाव्यता <math>P^{-}(s)</math> किसी भी वैश्विक स्थिति का <math>s</math> जब | यह परिणाम इस तथ्य से निकलता है कि तापीय संतुलन पर संभाव्यता <math>P^{-}(s)</math> किसी भी वैश्विक स्थिति का <math>s</math> जब संजाल मुक्तधावी होता है तो बोल्ट्ज़मैन बंटन द्वारा दिया जाता है। | ||
यह सीखने का नियम जैविक रूप से प्रशंसनीय है क्योंकि वज़न बदलने के लिए आवश्यक एकमात्र जानकारी स्थानीय जानकारी द्वारा प्रदान की जाती है। अर्थात्, | यह सीखने का नियम जैविक रूप से प्रशंसनीय है क्योंकि वज़न बदलने के लिए आवश्यक एकमात्र जानकारी स्थानीय जानकारी द्वारा प्रदान की जाती है। अर्थात्, संश्रय ([[निष्कर्ष]], जैविक रूप से) को इससे जुड़ने वाले दो न्यूरॉन्स के अतिरिक्त किसी अन्य चीज़ के बारे में जानकारी की आवश्यकता नहीं है। यह [[पश्चप्रचार]] जैसे कई अन्य तंत्रिका संजाल प्रशिक्षण कलनविधि में संश्रय के लिए आवश्यक जानकारी की तुलना में अधिक जैविक रूप से यथार्थवादी है। | ||
बोल्ट्ज़मैन मशीन का प्रशिक्षण [[ईएम एल्गोरिदम|ईएम कलनविधि]] का उपयोग नहीं करता है, जिसका यंत्र अधिगम में भारी उपयोग किया जाता है। कुल्बैक-लीबलर | बोल्ट्ज़मैन मशीन का प्रशिक्षण [[ईएम एल्गोरिदम|ईएम कलनविधि]] का उपयोग नहीं करता है, जिसका यंत्र अधिगम में भारी उपयोग किया जाता है। कुल्बैक-लीबलर डाइवर्जेंस को कम करके, यह आंकड़ो की लॉग-संभावना को अधिकतम करने के बराबर है। इसलिए, प्रशिक्षण प्रक्रिया प्रेक्षित आंकड़ो की लॉग-संभावना पर क्रमिक आरोहण करती है। यह ईएम कलनविधि के विपरीत है, जहां एम-चरण के दौरान पूर्ण आंकड़ा संभावना के अपेक्षित मान को अधिकतम करने से पहले प्रच्छन्न हुए नोड्स के पीछे के बंटन की गणना की जानी चाहिए। | ||
पूर्वाग्रहों का प्रशिक्षण समान है, लेकिन केवल एकल नोड गतिविधि का उपयोग करता है: | पूर्वाग्रहों का प्रशिक्षण समान है, लेकिन केवल एकल नोड गतिविधि का उपयोग करता है: | ||
| Line 76: | Line 76: | ||
==समस्याएँ== | ==समस्याएँ== | ||
सैद्धांतिक रूप से बोल्ट्ज़मान मशीन एक सामान्य | सैद्धांतिक रूप से बोल्ट्ज़मान मशीन एक सामान्य अभिकलनी माध्यम है। उदाहरण के लिए, यदि तस्वीरों पर प्रशिक्षित किया जाता है, तो मशीन सैद्धांतिक रूप से तस्वीरों के बंटन का मॉडल तैयार करेगी, और उदाहरण के लिए, आंशिक तस्वीर को पूरा करने के लिए उस मॉडल का उपयोग कर सकती है। | ||
दुर्भाग्य से, बोल्ट्ज़मैन मशीनें एक गंभीर व्यावहारिक समस्या का अनुभव करती हैं, अर्थात् जब मशीन को एक | दुर्भाग्य से, बोल्ट्ज़मैन मशीनें एक गंभीर व्यावहारिक समस्या का अनुभव करती हैं, अर्थात् जब मशीन को एक क्षुद्र आकार से अधिक बड़े आकार में ले जाया जाता है तो यह सही ढंग से सीखना बंद कर देती है।{{Citation needed|date=January 2013}} यह महत्वपूर्ण प्रभावों के कारण है, विशेष रूप से: | ||
* संतुलन आँकड़े एकत्र करने के लिए आवश्यक समय क्रम मशीन के आकार और | * संतुलन आँकड़े एकत्र करने के लिए आवश्यक समय क्रम मशीन के आकार और संश्रय शक्तियों के परिमाण के साथ तेजी से बढ़ता है{{Citation needed|date=August 2015}} | ||
* | * संश्रय की ताकत अधिक नम्य होती है जब संसक्त इकाइयों में सक्रियण संभावनाएं शून्य और एक के बीच मध्यवर्ती होती हैं, जिससे एक तथाकथित विचरण जाल होता है। निवल प्रभाव यह है कि जब तक गतिविधियां संतृप्त नहीं हो जातीं, तब तक रव के कारण संश्रय की ताकत यादृच्छिक रूप से चलने लगती है। | ||
==प्रकार== | ==प्रकार== | ||
===प्रतिबंधित बोल्ट्ज़मैन मशीन=== | ===प्रतिबंधित बोल्ट्ज़मैन मशीन=== | ||
[[File:Restricted Boltzmann machine.svg|thumb|right|alt=Graphical representation of an example restricted Boltzmann machine |प्रतिबंधित बोल्ट्ज़मैन मशीन का चित्रमय प्रतिनिधित्व। चार नीली इकाइयाँ | [[File:Restricted Boltzmann machine.svg|thumb|right|alt=Graphical representation of an example restricted Boltzmann machine |प्रतिबंधित बोल्ट्ज़मैन मशीन का चित्रमय प्रतिनिधित्व। चार नीली इकाइयाँ प्रच्छन्न हुई इकाइयों का प्रतिनिधित्व करती हैं, और तीन लाल इकाइयाँ दृश्य स्थितियों का प्रतिनिधित्व करती हैं। प्रतिबंधित बोल्ट्ज़मैन मशीनों में प्रच्छन्न और दृश्य इकाइयों के बीच केवल संश्रय (निर्भरताएं) होते हैं, और एक ही प्रकार की इकाइयों के बीच कोई भी नहीं (कोई छिपा-छिपा नहीं, न ही दृश्य-दृश्य संश्रय)।]] | ||
{{main| | {{main|प्रतिबंधित बोल्ट्ज़मैन मशीन}} | ||
प्रतिबंधित बोल्ट्ज़मैन मशीन का विस्तार | चूंकि सामान्य बोल्ट्ज़मैन मशीनों में सीखना अव्यावहारिक है, इसे प्रतिबंधित बोल्ट्ज़मैन मशीन (आरबीएम) में काफी कुशल बनाया जा सकता है जो प्रच्छन्न हुई इकाइयों और दृश्यमान इकाइयों के बीच अंतःस्तर संश्रय की अनुमति नहीं देता है, अर्थात दृश्यमान से दृश्यमान और प्रच्छन्न हुई इकाइयों के बीच कोई संबंध नहीं है। एक आरबीएम को प्रशिक्षित करने के बाद, इसकी प्रच्छन्न हुई इकाइयों की गतिविधियों को उच्च-स्तरीय आरबीएम के प्रशिक्षण के लिए आंकड़ो के रूप में माना जा सकता है। आरबीएम को स्टैक करने की यह विधि प्रच्छन्न हुई इकाइयों की कई परतों को कुशलतापूर्वक प्रशिक्षित करना संभव बनाती है और यह सबसे आम गहन शिक्षण रणनीतियों में से एक है। जैसे-जैसे प्रत्येक नई परत जोड़ी जाती है, जेनरेटिव मॉडल में सुधार होता है। | ||
प्रतिबंधित बोल्ट्ज़मैन मशीन का विस्तार द्विआधारी आंकड़ो के अतिरिक्त वास्तविक मान आंकड़ो का उपयोग करने की अनुमति देता है।<ref>{{Citation|title=Recent Developments in Deep Learning|url=https://www.youtube.com/watch?v=VdIURAu1-aU |archive-url=https://ghostarchive.org/varchive/youtube/20211222/VdIURAu1-aU |archive-date=2021-12-22 |url-status=live|language=en|access-date=2020-02-17}}{{cbignore}}</ref> | |||
व्यावहारिक आरबीएम अनुप्रयोग का एक उदाहरण वाक् पहचान में है।<ref>{{cite journal |url=http://research.microsoft.com/pubs/144412/DBN4LVCSR-TransASLP.pdf |title=बड़ी शब्दावली वाक् पहचान के लिए संदर्भ-निर्भर पूर्व-प्रशिक्षित डीप न्यूरल नेटवर्क|journal=Microsoft Research |volume=20 |year=2011|last1=Yu |first1=Dong |last2=Dahl |first2=George |last3=Acero |first3=Alex |last4=Deng |first4=Li }}</ref> | व्यावहारिक आरबीएम अनुप्रयोग का एक उदाहरण वाक् पहचान में है।<ref>{{cite journal |url=http://research.microsoft.com/pubs/144412/DBN4LVCSR-TransASLP.pdf |title=बड़ी शब्दावली वाक् पहचान के लिए संदर्भ-निर्भर पूर्व-प्रशिक्षित डीप न्यूरल नेटवर्क|journal=Microsoft Research |volume=20 |year=2011|last1=Yu |first1=Dong |last2=Dahl |first2=George |last3=Acero |first3=Alex |last4=Deng |first4=Li }}</ref> | ||
=== डीप बोल्ट्ज़मैन मशीन === | === डीप बोल्ट्ज़मैन मशीन === | ||
एक डीप बोल्ट्ज़मैन मशीन (डीबीएम) एक प्रकार का | एक डीप बोल्ट्ज़मैन मशीन (डीबीएम) एक प्रकार का द्विआधारी युग्मानूसार [[ मार्कोव यादृच्छिक क्षेत्र ]] (ग्राफ (असतत गणित)#अनडायरेक्टेड ग्राफ प्रोबेबिलिस्टिक [[ चित्रमय मॉडल ]]) है जिसमें [[अव्यक्त चर]] [[यादृच्छिक चर]] की कई परतें होती हैं। यह सममित रूप से युग्मित प्रसंभाव्य [[बाइनरी वैरिएबल|द्विआधारी वैरिएबल]] का एक संजाल है। इसमें दृश्य इकाइयों का एक सेट सम्मलित है <math>\boldsymbol{\nu} \in \{0,1\}^D</math> और प्रच्छन्न हुई इकाइयों की परतें हैं।<math>\boldsymbol{h}^{(1)} \in \{0,1\}^{F_1}, \boldsymbol{h}^{(2)} \in \{0,1\}^{F_2}, \ldots, \boldsymbol{h}^{(L)} \in \{0,1\}^{F_L}</math>. कोई भी संश्रय एक ही परत की इकाइयों को नहीं जोड़ता (जैसे कि [[प्रतिबंधित बोल्ट्ज़मैन मशीन]])। के लिए {{tooltip|2=डीप बोल्ट्ज़मैन मशीन|डीबीएम}}, सदिश को सौंपी गई संभाव्यता {{mvar|'''ν'''}} है | ||
: <math>p(\boldsymbol{\nu}) = \frac{1}{Z}\sum_h e^{\sum_{ij}W_{ij}^{(1)}\nu_i h_j^{(1)} + \sum_{jl}W_{jl}^{(2)}h_j^{(1)}h_l^{(2)}+\sum_{lm}W_{lm}^{(3)}h_l^{(2)}h_m^{(3)}},</math> | : <math>p(\boldsymbol{\nu}) = \frac{1}{Z}\sum_h e^{\sum_{ij}W_{ij}^{(1)}\nu_i h_j^{(1)} + \sum_{jl}W_{jl}^{(2)}h_j^{(1)}h_l^{(2)}+\sum_{lm}W_{lm}^{(3)}h_l^{(2)}h_m^{(3)}},</math> | ||
जहाँ <math>\boldsymbol{h} = \{\boldsymbol{h}^{(1)}, \boldsymbol{h}^{(2)}, \boldsymbol{h}^{(3)} \}</math> प्रच्छन्न हुई इकाइयों का समूह हैं, और <math>\theta = \{\boldsymbol{W}^{(1)}, \boldsymbol{W}^{(2)}, \boldsymbol{W}^{(3)} \} </math> मॉडल मापदंड हैं, जो दृश्य-दृश्य, दृश्य-प्रच्छन्न और प्रच्छन्न-प्रच्छन्न अन्योन्यक्रिया का प्रतिनिधित्व करते हैं।<ref name="ref12">{{cite journal|last1=Hinton|first1=Geoffrey|last2=Salakhutdinov|first2=Ruslan|date=2012|title=गहरी बोल्ट्ज़मैन मशीनों को पूर्व-प्रशिक्षित करने का एक बेहतर तरीका|url=http://machinelearning.wustl.edu/mlpapers/paper_files/NIPS2012_1178.pdf|journal=Advances in Neural|volume=3|pages=1–9|access-date=2017-08-18|archive-url=https://web.archive.org/web/20170813152400/http://machinelearning.wustl.edu/mlpapers/paper_files/NIPS2012_1178.pdf|archive-date=2017-08-13|url-status=dead}}</ref> डीबीएन में केवल शीर्ष दो परतें एक प्रतिबंधित बोल्ट्ज़मैन मशीन (जो एक अप्रत्यक्ष ग्राफिकल मॉडल है) बनाती हैं, जबकि निचली परतें एक निर्देशित जेनरेटर मॉडल बनाती हैं। डीबीएम में सभी परतें सममित और अप्रत्यक्ष होती हैं। | |||
डीबीएन की तरह, डीबीएम बिना लेबल वाले संवेदी निविष्ट आंकड़ो के एक बड़े सेट का उपयोग करके बनाए गए अभ्यावेदन को ठीक करने के लिए सीमित, लेबल वाले आंकड़ो का उपयोग करके ऑब्जेक्ट पहचान या [[वाक् पहचान]] जैसे कार्यों में निविष्ट के जटिल और अमूर्त आंतरिक प्रतिनिधित्व सीख सकते हैं। चूंकि, डीबीएन और गहरे [[दृढ़ तंत्रिका नेटवर्क|दृढ़ तंत्रिका संजाल]] के विपरीत, वे नीचे-ऊपर और ऊपर-नीचे दोनों दिशाओं में अनुमान और प्रशिक्षण प्रक्रिया अपनाते हैं, जो डीबीएम को निविष्ट संरचनाओं के प्रतिनिधित्व को बेहतर ढंग से प्रकट करने की अनुमति देता है।<ref name="ref32">{{cite journal|last1=Hinton|first1=Geoffrey|last2=Salakhutdinov|first2=Ruslan|date=2009|title=डीप बोल्ट्ज़मैन मशीनों की कुशल शिक्षा|url=http://machinelearning.wustl.edu/mlpapers/paper_files/AISTATS09_SalakhutdinovH.pdf|volume=3|pages=448–455|access-date=2017-08-18|archive-url=https://web.archive.org/web/20151106235714/http://machinelearning.wustl.edu/mlpapers/paper_files/AISTATS09_SalakhutdinovH.pdf|archive-date=2015-11-06|url-status=dead}}</ref><ref name="ref42">{{cite journal|last1=Bengio|first1=Yoshua|last2=LeCun|first2=Yann|date=2007|title=एआई की ओर लर्निंग एल्गोरिदम को स्केल करना|url=http://www.iro.umontreal.ca/~lisa/bib/pub_subject/language/pointeurs/bengio+lecun-chapter2007.pdf|volume=1|pages=1–41}}</ref><ref name="ref22">{{cite journal|last1=Larochelle|first1=Hugo|last2=Salakhutdinov|first2=Ruslan|date=2010|title=डीप बोल्ट्ज़मैन मशीनों की कुशल शिक्षा|url=http://machinelearning.wustl.edu/mlpapers/paper_files/AISTATS2010_SalakhutdinovL10.pdf|pages=693–700|access-date=2017-08-18|archive-url=https://web.archive.org/web/20170814001329/http://machinelearning.wustl.edu/mlpapers/paper_files/AISTATS2010_SalakhutdinovL10.pdf|archive-date=2017-08-14|url-status=dead}}</ref> | |||
चूंकि, डीबीएम की धीमी गति उनके प्रदर्शन और कार्यक्षमता को सीमित करती है। क्योंकि सटीक अधिकतम संभावना सीखना डीबीएम के लिए कठिन है, केवल अनुमानित अधिकतम संभावना सीखना संभव है। एक अन्य विकल्प आंकड़ो-निर्भर अपेक्षाओं का अनुमान लगाने के लिए माध्य-क्षेत्र अनुमान का उपयोग करना और [[मार्कोव श्रृंखला मोंटे कार्लो]] (एमसीएमसी) का उपयोग करके अपेक्षित पर्याप्त आंकड़ों का अनुमान लगाना है।<ref name="ref12" />यह अनुमानित अनुमान, जो प्रत्येक परीक्षण निविष्ट के लिए किया जाना चाहिए, डीबीएम में एकल बॉटम-अप पास की तुलना में लगभग 25 से 50 गुना धीमा है। यह बड़े आंकड़े सेट के लिए संयुक्त अनुकूलन को अव्यवहारिक बनाता है, और फीचर प्रतिनिधित्व जैसे कार्यों के लिए डीबीएम के उपयोग को प्रतिबंधित करता है। | |||
=== स्पाइक-एंड-स्लैब आरबीएम === | === स्पाइक-एंड-स्लैब आरबीएम === | ||
[[ गाऊसी ]] आरबीएम की तरह, [[वास्तविक संख्या]] | वास्तविक- | [[ गाऊसी ]] आरबीएम की तरह, [[वास्तविक संख्या]] | वास्तविक-मान निविष्ट के साथ गहन सीखने की आवश्यकता ने स्पाइक-एंड-स्लैब प्रतिबंधित बोल्टज़मैन मशीन (एसएस प्रतिबंधित बोल्टज़मैन मशीन) को जन्म दिया, जो द्विआधारी वैरिएबल अव्यक्त चर के साथ निरंतर-मान मॉडल को निविष्ट करता है।<ref name="ref30">{{cite journal|last1=Courville|first1=Aaron|last2=Bergstra|first2=James|last3=Bengio|first3=Yoshua|date=2011|title=एक स्पाइक और स्लैब प्रतिबंधित बोल्ट्ज़मैन मशीन|url=http://machinelearning.wustl.edu/mlpapers/paper_files/AISTATS2011_CourvilleBB11.pdf|journal=JMLR: Workshop and Conference Proceeding|volume=15|pages=233–241|access-date=2019-08-25|archive-url=https://web.archive.org/web/20160304112418/http://machinelearning.wustl.edu/mlpapers/paper_files/AISTATS2011_CourvilleBB11.pdf|archive-date=2016-03-04|url-status=dead}}</ref> बुनियादी प्रतिबंधित बोल्ट्ज़मैन मशीन और उसके वेरिएंट के समान, स्पाइक-एंड-स्लैब आरबीएम एक [[द्विदलीय ग्राफ]] है, जबकि प्रतिबंधित बोल्ट्ज़मैन मशीन की तरह, दृश्य इकाइयाँ (निविष्ट) वास्तविक-मान हैं। अंतर प्रच्छन्न हुई परत में है, जहां प्रत्येक प्रच्छन्न हुई इकाई में एक द्विआधारी स्पाइक वैरिएबल और एक वास्तविक-मान स्लैब वैरिएबल होता है। एक स्पाइक शून्य पर एक असतत [[संभाव्यता द्रव्यमान]] है, जबकि एक स्लैब निरंतर डोमेन पर एक संभाव्यता घनत्व है;<ref name="ref322">{{cite conference|last1=Courville|first1=Aaron|last2=Bergstra|first2=James|last3=Bengio|first3=Yoshua|date=2011|title=Proceedings of the 28th International Conference on Machine Learning|volume=10|pages=1–8|chapter=Unsupervised Models of Images by Spike-and-Slab RBMs|chapter-url=http://machinelearning.wustl.edu/mlpapers/paper_files/ICML2011Courville_591.pdf|conference=|access-date=2019-08-25|archive-date=2016-03-04|archive-url=https://web.archive.org/web/20160304054551/http://machinelearning.wustl.edu/mlpapers/paper_files/ICML2011Courville_591.pdf|url-status=dead}}</ref> उनका मिश्रण एक पूर्व संभाव्यता बनाता है।<ref name="ref31">{{cite journal|last1=Mitchell|first1=T|last2=Beauchamp|first2=J|date=1988|title=रेखीय प्रतिगमन में बायेसियन चर चयन|journal=Journal of the American Statistical Association|volume=83|issue=404|pages=1023–1032|doi=10.1080/01621459.1988.10478694}}</ref> | ||
एसएसप्रतिबंधित बोल्ट्ज़मैन मशीन का एक विस्तार जिसे µ-एसएसप्रतिबंधित बोल्ट्ज़मैन मशीन कहा जाता है, [[Index.php?title=ऊर्जा फलन|ऊर्जा फलन]] में अतिरिक्त शब्दों का उपयोग करके अतिरिक्त मॉडलिंग क्षमता प्रदान करता है। इनमें से एक शब्द मॉडल को एक अवलोकन दिए गए स्लैब चर को हाशिए पर रखकर स्पाइक चर का एक [[सशर्त संभाव्यता वितरण|सशर्त संभाव्यता बंटन]] बनाने में सक्षम बनाता है। | |||
=== गणित में === | |||
''मुख्य लेख: [[गिब्स माप]] और [[लॉग-रैखिक मॉडल]]'' | ''मुख्य लेख: [[गिब्स माप]] और [[लॉग-रैखिक मॉडल]]'' | ||
अधिक सामान्य गणितीय सेटिंग में, बोल्ट्ज़मैन बंटन को गिब्स माप के रूप में भी जाना जाता है। सांख्यिकी और यंत्र अधिगम में इसे लॉग- | अधिक सामान्य गणितीय सेटिंग में, बोल्ट्ज़मैन बंटन को गिब्स माप के रूप में भी जाना जाता है। सांख्यिकी और यंत्र अधिगम में इसे लॉग-रैखिक मॉडल कहा जाता है। गहन शिक्षण में बोल्ट्ज़मैन बंटन का उपयोग बोल्ट्ज़मैन मशीन जैसे [[स्टोकेस्टिक तंत्रिका नेटवर्क|प्रसंभाव्य तंत्रिका संजाल]] के नमूना बंटन में किया जाता है। | ||
== इतिहास == | == इतिहास == | ||
बोल्ट्ज़मैन मशीन शेरिंगटन-किर्कपैट्रिक के प्रसंभाव्य आइसिंग मॉडल के [[ | बोल्ट्ज़मैन मशीन शेरिंगटन-किर्कपैट्रिक के प्रसंभाव्य आइसिंग मॉडल के [[Index.php?title=प्रचक्रण ग्लास|प्रचक्रण ग्लास]] मॉडल पर आधारित है।<ref>{{Cite journal|last1=Sherrington|first1=David|last2=Kirkpatrick|first2=Scott|date=1975-12-29|title=स्पिन-ग्लास का सॉल्व करने योग्य मॉडल|journal=Physical Review Letters|volume=35|issue=26|pages=1792–1796|doi=10.1103/physrevlett.35.1792|bibcode=1975PhRvL..35.1792S|issn=0031-9007}}</ref> | ||
संज्ञानात्मक विज्ञान में ऐसे ऊर्जा आधारित मॉडल को लागू करने में मूल योगदान हिंटन और सेजनोव्स्की के पत्रों में दिखाई दिया।<ref>{{Cite conference|url=http://digitalcollections.library.cmu.edu/awweb/awarchive?type=file&item=360445|title=सहकारी संगणना का विश्लेषण|last1=Hinton|first1=Geoffery|date=May 1983|access-date=17 February 2020 |first2=Terrence J. |last2=Sejnowski|conference= 5th Annual Congress of the Cognitive Science Society|location= Rochester, New York }}</ref><ref>{{cite conference|first1= Geoffrey E. |last1=Hinton |first2= Terrence J. |last2=Sejnowski|title=इष्टतम अवधारणात्मक अनुमान|conference=IEEE Conference on Computer Vision and Pattern Recognition (CVPR)|pages= 448–453|publisher= IEEE Computer Society|location= Washington, D.C.|date=June 1983}}</ref> | संज्ञानात्मक विज्ञान में ऐसे ऊर्जा आधारित मॉडल को लागू करने में मूल योगदान हिंटन और सेजनोव्स्की के पत्रों में दिखाई दिया।<ref>{{Cite conference|url=http://digitalcollections.library.cmu.edu/awweb/awarchive?type=file&item=360445|title=सहकारी संगणना का विश्लेषण|last1=Hinton|first1=Geoffery|date=May 1983|access-date=17 February 2020 |first2=Terrence J. |last2=Sejnowski|conference= 5th Annual Congress of the Cognitive Science Society|location= Rochester, New York }}</ref><ref>{{cite conference|first1= Geoffrey E. |last1=Hinton |first2= Terrence J. |last2=Sejnowski|title=इष्टतम अवधारणात्मक अनुमान|conference=IEEE Conference on Computer Vision and Pattern Recognition (CVPR)|pages= 448–453|publisher= IEEE Computer Society|location= Washington, D.C.|date=June 1983}}</ref> | ||
जॉन हॉपफ़ील्ड के मौलिक प्रकाशन में प्रचक्रण ग्लास का उल्लेख करते हुए भौतिकी और सांख्यिकीय यांत्रिकी को जोड़ा | जॉन हॉपफ़ील्ड के मौलिक प्रकाशन में प्रचक्रण ग्लास का उल्लेख करते हुए भौतिकी और सांख्यिकीय यांत्रिकी को जोड़ा गया है।<ref>{{Cite journal|last=Hopfield, J. J.|title=उभरती हुई सामूहिक कम्प्यूटेशनल क्षमताओं के साथ तंत्रिका नेटवर्क और भौतिक प्रणालियाँ|journal=Proceedings of the National Academy of Sciences of the United States of America|volume=79|issue=8|pages=2554–8|publisher=[s.n.]|oclc=848771572|pmid=6953413|pmc=346238|year=1982|doi=10.1073/pnas.79.8.2554|bibcode=1982PNAS...79.2554H|doi-access=free}}</ref> | ||
एनील्ड [[ गिब्स नमूनाकरण ]] के साथ आइसिंग मॉडल को लागू करने का विचार [[डगलस हॉफ़स्टैटर]] के [[ | एनील्ड [[ गिब्स नमूनाकरण ]] के साथ आइसिंग मॉडल को लागू करने का विचार [[डगलस हॉफ़स्टैटर]] के [[Index.php?title=कॉपीकैट प्रोजेक्ट|कॉपीकैट प्रोजेक्ट]] में सम्मलित है।<ref>{{Cite book|last=Hofstadter, D. R.|title=The Copycat Project: An Experiment in Nondeterminism and Creative Analogies.|date=January 1984|publisher=Defense Technical Information Center|oclc=227617764}}</ref><ref>{{Cite book|editor-last=Caianiello|editor-first=Eduardo R.|title=संज्ञानात्मक प्रक्रियाओं का भौतिकी|date=1988|publisher=World Scientific|isbn=9971-5-0255-0|oclc=750950619|last=Hofstadter |first=Douglas R. |chapter=A Non-Deterministic Approach to Analogy, Involving the Ising Model of Ferromagnetism|location=Teaneck, New Jersey}}</ref> | ||
इसी तरह के विचार (ऊर्जा फलन में संकेत के परिवर्तन के साथ) [[पॉल स्मोलेंस्की]] के हार्मनी | इसी तरह के विचार (ऊर्जा फलन में संकेत के परिवर्तन के साथ) [[पॉल स्मोलेंस्की]] के हार्मनी सिद्धांत में पाए जाते हैं। | ||
बोल्ट्ज़मैन मशीन | बोल्ट्ज़मैन मशीन संरूपण में सांख्यिकीय यांत्रिकी के साथ खींची गई स्पष्ट सादृश्यता ने भौतिकी से उधार ली गई पारिभाषिक (उदाहरण के लिए, सद्भाव के अतिरिक्त ऊर्जा) का उपयोग किया, जो क्षेत्र में मानक बन गया है। इस पारिभाषिक को व्यापक रूप से अपनाने को इस तथ्य से प्रोत्साहित किया गया होगा कि इसके उपयोग से सांख्यिकीय यांत्रिकी से विभिन्न अवधारणाओं और विधियों को अपनाया गया है। अनुमान के लिए अनुकारितअनीलन का उपयोग करने के विभिन्न प्रस्ताव स्पष्ट रूप से स्वतंत्र थे। | ||
आइसिंग मॉडल को मार्कोव यादृच्छिक क्षेत्रों का एक विशेष | आइसिंग मॉडल को मार्कोव यादृच्छिक क्षेत्रों का एक विशेष स्थितिा माना जाता है, जिसका [[भाषा विज्ञान]], [[Index.php?title=रोबोटिक्स|रोबोटिक्स]], [[Index.php?title=अभिकलित्र दृष्टि|अभिकलित्र दृष्टि]] और कृत्रिम बुद्धिमत्ता में व्यापक अनुप्रयोग मिलता है। | ||
==यह भी देखें== | ==यह भी देखें== | ||
| Line 129: | Line 129: | ||
*मार्कोव रैंडम फील्ड | *मार्कोव रैंडम फील्ड | ||
*आइज़िंग मॉडल | *आइज़िंग मॉडल | ||
*हॉपफील्ड | *हॉपफील्ड संजाल | ||
*सीखने का नियम<ref>{{cite conference | *सीखने का नियम<ref>{{cite conference | ||
| first = C.-Y. | | first = C.-Y. | ||
| Line 200: | Line 200: | ||
{{Statistical mechanics topics}} | {{Statistical mechanics topics}} | ||
{{Authority control}} | {{Authority control}} | ||
[[Category: | [[Category:All articles with unsourced statements]] | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Articles with unsourced statements from August 2015]] | |||
[[Category:Articles with unsourced statements from January 2013]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 errors]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 27/06/2023]] | [[Category:Created On 27/06/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:तंत्रिका नेटवर्क आर्किटेक्चर]] | |||
[[Category:लुडविग बोल्ट्ज़मैन|मशीन]] | |||
Latest revision as of 11:49, 14 July 2023
लुडविग बोल्ट्ज़मान मशीन (जिसे बाहरी क्षेत्र के साथ शेरिंगटन-किर्कपैट्रिक मॉडल या प्रसंभाव्य आइसिंग-लेनज़-लिटिल मॉडल भी कहा जाता है) एक बाहरी क्षेत्र के साथ प्रसंभाव्य स्पिन-ग्लास मॉडल है, अर्थात, एक प्रचक्रण ग्लास#शेरिंगटन-किर्कपैट्रिक मॉडल ,[1] यह एक प्रसंभाव्य आइसिंग मॉडल है। यह एक सांख्यिकीय भौतिकी तकनीक है जिसका उपयोग संज्ञानात्मक विज्ञान के संदर्भ में किया जाता है।[2] इसे मार्कोव यादृच्छिक क्षेत्र के रूप में भी वर्गीकृत किया गया है।[3]
बोल्ट्ज़मैन मशीनें अपने प्रशिक्षण कलनविधि की स्थानीयता और हेब्बियन प्रकृति (हेब्ब के नियम द्वारा प्रशिक्षित होने) और उनके समानांतरवाद (अभिकलन) और सरल भौतिक प्रक्रियाओं के साथ उनकी गतिशीलता की समानता के कारण सैद्धांतिक रूप से दिलचस्प हैं। अप्रतिबंधित संयोजकता वाली बोल्ट्ज़मैन मशीनें सीखने या अनुमान में व्यावहारिक समस्याओं के लिए उपयोगी सिद्ध नहीं हुई हैं, लेकिन यदि संयोजकता ठीक से बाधित है, तो सीखने को व्यावहारिक समस्याओं के लिए उपयोगी होने के लिए पर्याप्त कुशल बनाया जा सकता है।[4] उनका नाम सांख्यिकीय यांत्रिकी में बोल्ट्ज़मान बंटन के नाम पर रखा गया है, जिसका उपयोग उनके नमूनाकरण फलन में किया जाता है। उन्हें संज्ञानात्मक विज्ञान समुदायों और यंत्र अधिगम में जेफ्री हिंटन, टेरी सेजनोवस्की और वाई एन एल ईसीयू के अंदर द्वारा काफी लोकप्रिय और प्रचारित किया गया था।[5] यंत्र अधिगम के भीतर एक अधिक सामान्य वर्ग के रूप में इन मॉडलों को ऊर्जा आधारित मॉडल (ईबीएम) कहा जाता है, क्योंकि प्रचक्रण ग्लास के हैमिल्टनियन यांत्रिकी का उपयोग सीखने के कार्य को परिभाषित करने के लिए प्रारंभिकी बिंदु के रूप में किया जाता है।[6]
संरचना
बोल्ट्ज़मैन मशीन, प्रचक्रण ग्लास#शेरिंगटन-किर्कपैट्रिक मॉडल की तरह, समग्र संजाल के लिए परिभाषित कुल ऊर्जा (हैमिल्टनियन यांत्रिकी) वाली इकाइयों का एक संजाल है। इसकी इकाइयाँ द्विआधारी संख्या परिणाम उत्पन्न करती हैं। बोल्ट्ज़मैन मशीन का वज़न प्रसंभाव्य है। वैश्विक ऊर्जा बोल्ट्ज़मैन मशीन हॉपफील्ड संजाल और आइसिंग मॉडल के समान है:
जहाँ:
- इकाई के बीच संबंध शक्ति है और इकाई .
- स्थिति है, , इकाई का .
- इकाई का पूर्वाग्रह है वैश्विक ऊर्जा समारोह में. ( इकाई के लिए सक्रियण सीमा है।)
अधिकांशत: वजन एक सममित आव्युह के रूप में दर्शाया गया है विकर्ण के साथ शून्य के साथ है।
इकाई अवस्था संभाव्यता
वैश्विक ऊर्जा में अंतर जो एक इकाई से उत्पन्न होता है 0 (बंद) बनाम 1 (चालू) के बराबर, लिखा हुआ , वज़न का एक सममित आव्युह मानते हुए, इस प्रकार दिया गया है:
इसे दो स्थितियों की ऊर्जाओं के अंतर के रूप में व्यक्त किया जा सकता है:
प्रत्येक स्थिति की ऊर्जा को उसकी सापेक्ष संभाव्यता के साथ बोल्ट्ज़मान कारक (बोल्ट्ज़मैन बंटन का गुण जो किसी स्थिति की ऊर्जा उस स्थिति की नकारात्मक लॉग संभावना के समानुपाती होती है) के अनुसार प्रतिस्थापित करने पर मिलती है:
जहाँ बोल्ट्ज़मैन स्थिरांक है और तापमान की कृत्रिम धारणा में अवशोषित हो जाता है . फिर हम शर्तों को पुनर्व्यवस्थित करते हैं और विचार करते हैं कि इकाई के चालू और बंद होने की संभावनाओं का योग एक होना चाहिए:
के लिए समाधान , संभावना है कि -वीं इकाई चालू है:
जहां अदिश (भौतिकी) इसे सिस्टम का तापमान कहा जाता है। यह संबंध बोल्ट्ज़मैन मशीन के वेरिएंट में संभाव्यता अभिव्यक्तियों में पाए जाने वाले लॉजिस्टिक फलन का स्रोत है।
साम्यावस्था
संजाल बार-बार एक इकाई को चुनने और उसकी स्थिति को पुनर्स्थापन करने से चलता है। एक निश्चित तापमान पर लंबे समय तक चलने के बाद, बोल्ट्ज़मैन बंटन के अनुसार, संजाल की वैश्विक स्थिति की संभावना केवल उस वैश्विक स्थिति की ऊर्जा पर निर्भर करती है, न कि उस प्रारंभिक स्थिति पर जहां से प्रक्रिया शुरू की गई थी। इसका मतलब यह है कि वैश्विक स्थिति की लॉग-संभावनाएं उनकी ऊर्जा में रैखिक हो जाती हैं। यह संबंध तब सत्य होता है जब मशीन ऊष्मीय साम्य पर होती है, जिसका अर्थ है कि वैश्विक स्थिति का संभाव्यता बंटन अभिसरण हो गया है। उच्च तापमान से शुरू होने वाले संजाल को चलाने पर, कम तापमान पर थर्मल संतुलन तक पहुंचने तक इसका तापमान धीरे-धीरे कम हो जाता है। इसके बाद यह एक ऐसे बंटन में परिवर्तित हो सकता है जहां ऊर्जा स्तर वैश्विक न्यूनतम के आसपास उतार-चढ़ाव करता है। इस प्रक्रिया को अनुकारितअनीलन कहा जाता है।
संजाल को प्रशिक्षित करने के लिए जिससे कि इन स्थितियों पर बाहरी बंटन के अनुसार वैश्विक स्थिति में परिवर्तित होने का मौका मिले, वजन निर्धारित किया जाना चाहिए जिससे कि उच्चतम संभावनाओं वाले वैश्विक स्थितियों को सबसे कम ऊर्जा मिल सके। यह प्रशिक्षण द्वारा किया जाता है।
प्रशिक्षण
बोल्ट्ज़मान मशीन में इकाइयों को 'दृश्यमान' इकाइयों, V, और 'प्रच्छन्न' इकाइयों, H में विभाजित किया गया है। दृश्यमान इकाइयां वे हैं जो 'पर्यावरण' से जानकारी प्राप्त करती हैं, अर्थात प्रशिक्षण सेट द्विआधारी सदिश का एक सेट है, सेट V। प्रशिक्षण सेट पर बंटन दर्शाया गया है ।
जैसे ही बोल्ट्ज़मैन मशीन थर्मल संतुलन तक पहुँचती है, वैश्विक स्थितियों पर बंटन परिवर्तित हो जाता है। हम इस बंटन को छुपी हुई इकाइयों पर सीमांत बंटन के बाद निरूपित करते हैं .
हमारा लक्ष्य वास्तविक बंटन का अनुमान लगाना है का उपयोग मशीन द्वारा उत्पादित. दो बंटनों की समानता कुल्बैक-लीब्लर विचलन द्वारा मापी जाती है, :
जहां योग सभी संभावित स्थितियों से अधिक है . भार का एक कार्य है, क्योंकि वे एक स्थिति की ऊर्जा निर्धारित करते हैं, और ऊर्जा निर्धारित करती है , जैसा कि बोल्ट्ज़मैन बंटन द्वारा वादा किया गया था। एक प्रवणता अवरोह कलनविधि पर , दिए गए वजन को बदलता है, के आंशिक व्युत्पन्न को घटाकर वजन के संबंध में ।
बोल्ट्ज़मैन मशीन प्रशिक्षण में दो वैकल्पिक चरण सम्मलित हैं। एक सकारात्मक चरण है जहां दृश्यमान इकाइयों की स्थिति को प्रशिक्षण सेट से नमूना किए गए एक विशेष द्विआधारी अवस्था सदिश से जोड़ा जाता है (के अनुसार ). दूसरा नकारात्मक चरण है जहां संजाल को स्वतंत्र रूप से चलने की अनुमति है, अर्थात केवल निविष्ट नोड्स की स्थिति बाहरी आंकड़ो द्वारा निर्धारित होती है, लेकिन निर्गम नोड्स को प्लव करने की अनुमति होती है। किसी दिए गए वजन के संबंध में ढाल, , समीकरण द्वारा दिया गया है:[7]
जहाँ:
- यह संभावना है कि जब मशीन सकारात्मक चरण पर संतुलन पर होती है तो इकाइयाँ i और j दोनों चालू होती हैं।
- यह संभावना है कि जब मशीन नकारात्मक चरण पर संतुलन पर होती है तो इकाइयाँ i और j दोनों चालू होती हैं।
- सीखने की दर को दर्शाता है
यह परिणाम इस तथ्य से निकलता है कि तापीय संतुलन पर संभाव्यता किसी भी वैश्विक स्थिति का जब संजाल मुक्तधावी होता है तो बोल्ट्ज़मैन बंटन द्वारा दिया जाता है।
यह सीखने का नियम जैविक रूप से प्रशंसनीय है क्योंकि वज़न बदलने के लिए आवश्यक एकमात्र जानकारी स्थानीय जानकारी द्वारा प्रदान की जाती है। अर्थात्, संश्रय (निष्कर्ष, जैविक रूप से) को इससे जुड़ने वाले दो न्यूरॉन्स के अतिरिक्त किसी अन्य चीज़ के बारे में जानकारी की आवश्यकता नहीं है। यह पश्चप्रचार जैसे कई अन्य तंत्रिका संजाल प्रशिक्षण कलनविधि में संश्रय के लिए आवश्यक जानकारी की तुलना में अधिक जैविक रूप से यथार्थवादी है।
बोल्ट्ज़मैन मशीन का प्रशिक्षण ईएम कलनविधि का उपयोग नहीं करता है, जिसका यंत्र अधिगम में भारी उपयोग किया जाता है। कुल्बैक-लीबलर डाइवर्जेंस को कम करके, यह आंकड़ो की लॉग-संभावना को अधिकतम करने के बराबर है। इसलिए, प्रशिक्षण प्रक्रिया प्रेक्षित आंकड़ो की लॉग-संभावना पर क्रमिक आरोहण करती है। यह ईएम कलनविधि के विपरीत है, जहां एम-चरण के दौरान पूर्ण आंकड़ा संभावना के अपेक्षित मान को अधिकतम करने से पहले प्रच्छन्न हुए नोड्स के पीछे के बंटन की गणना की जानी चाहिए।
पूर्वाग्रहों का प्रशिक्षण समान है, लेकिन केवल एकल नोड गतिविधि का उपयोग करता है:
समस्याएँ
सैद्धांतिक रूप से बोल्ट्ज़मान मशीन एक सामान्य अभिकलनी माध्यम है। उदाहरण के लिए, यदि तस्वीरों पर प्रशिक्षित किया जाता है, तो मशीन सैद्धांतिक रूप से तस्वीरों के बंटन का मॉडल तैयार करेगी, और उदाहरण के लिए, आंशिक तस्वीर को पूरा करने के लिए उस मॉडल का उपयोग कर सकती है।
दुर्भाग्य से, बोल्ट्ज़मैन मशीनें एक गंभीर व्यावहारिक समस्या का अनुभव करती हैं, अर्थात् जब मशीन को एक क्षुद्र आकार से अधिक बड़े आकार में ले जाया जाता है तो यह सही ढंग से सीखना बंद कर देती है।[citation needed] यह महत्वपूर्ण प्रभावों के कारण है, विशेष रूप से:
- संतुलन आँकड़े एकत्र करने के लिए आवश्यक समय क्रम मशीन के आकार और संश्रय शक्तियों के परिमाण के साथ तेजी से बढ़ता है[citation needed]
- संश्रय की ताकत अधिक नम्य होती है जब संसक्त इकाइयों में सक्रियण संभावनाएं शून्य और एक के बीच मध्यवर्ती होती हैं, जिससे एक तथाकथित विचरण जाल होता है। निवल प्रभाव यह है कि जब तक गतिविधियां संतृप्त नहीं हो जातीं, तब तक रव के कारण संश्रय की ताकत यादृच्छिक रूप से चलने लगती है।
प्रकार
प्रतिबंधित बोल्ट्ज़मैन मशीन

चूंकि सामान्य बोल्ट्ज़मैन मशीनों में सीखना अव्यावहारिक है, इसे प्रतिबंधित बोल्ट्ज़मैन मशीन (आरबीएम) में काफी कुशल बनाया जा सकता है जो प्रच्छन्न हुई इकाइयों और दृश्यमान इकाइयों के बीच अंतःस्तर संश्रय की अनुमति नहीं देता है, अर्थात दृश्यमान से दृश्यमान और प्रच्छन्न हुई इकाइयों के बीच कोई संबंध नहीं है। एक आरबीएम को प्रशिक्षित करने के बाद, इसकी प्रच्छन्न हुई इकाइयों की गतिविधियों को उच्च-स्तरीय आरबीएम के प्रशिक्षण के लिए आंकड़ो के रूप में माना जा सकता है। आरबीएम को स्टैक करने की यह विधि प्रच्छन्न हुई इकाइयों की कई परतों को कुशलतापूर्वक प्रशिक्षित करना संभव बनाती है और यह सबसे आम गहन शिक्षण रणनीतियों में से एक है। जैसे-जैसे प्रत्येक नई परत जोड़ी जाती है, जेनरेटिव मॉडल में सुधार होता है।
प्रतिबंधित बोल्ट्ज़मैन मशीन का विस्तार द्विआधारी आंकड़ो के अतिरिक्त वास्तविक मान आंकड़ो का उपयोग करने की अनुमति देता है।[8] व्यावहारिक आरबीएम अनुप्रयोग का एक उदाहरण वाक् पहचान में है।[9]
डीप बोल्ट्ज़मैन मशीन
एक डीप बोल्ट्ज़मैन मशीन (डीबीएम) एक प्रकार का द्विआधारी युग्मानूसार मार्कोव यादृच्छिक क्षेत्र (ग्राफ (असतत गणित)#अनडायरेक्टेड ग्राफ प्रोबेबिलिस्टिक चित्रमय मॉडल ) है जिसमें अव्यक्त चर यादृच्छिक चर की कई परतें होती हैं। यह सममित रूप से युग्मित प्रसंभाव्य द्विआधारी वैरिएबल का एक संजाल है। इसमें दृश्य इकाइयों का एक सेट सम्मलित है और प्रच्छन्न हुई इकाइयों की परतें हैं।. कोई भी संश्रय एक ही परत की इकाइयों को नहीं जोड़ता (जैसे कि प्रतिबंधित बोल्ट्ज़मैन मशीन)। के लिए डीबीएम, सदिश को सौंपी गई संभाव्यता ν है
जहाँ प्रच्छन्न हुई इकाइयों का समूह हैं, और मॉडल मापदंड हैं, जो दृश्य-दृश्य, दृश्य-प्रच्छन्न और प्रच्छन्न-प्रच्छन्न अन्योन्यक्रिया का प्रतिनिधित्व करते हैं।[10] डीबीएन में केवल शीर्ष दो परतें एक प्रतिबंधित बोल्ट्ज़मैन मशीन (जो एक अप्रत्यक्ष ग्राफिकल मॉडल है) बनाती हैं, जबकि निचली परतें एक निर्देशित जेनरेटर मॉडल बनाती हैं। डीबीएम में सभी परतें सममित और अप्रत्यक्ष होती हैं।
डीबीएन की तरह, डीबीएम बिना लेबल वाले संवेदी निविष्ट आंकड़ो के एक बड़े सेट का उपयोग करके बनाए गए अभ्यावेदन को ठीक करने के लिए सीमित, लेबल वाले आंकड़ो का उपयोग करके ऑब्जेक्ट पहचान या वाक् पहचान जैसे कार्यों में निविष्ट के जटिल और अमूर्त आंतरिक प्रतिनिधित्व सीख सकते हैं। चूंकि, डीबीएन और गहरे दृढ़ तंत्रिका संजाल के विपरीत, वे नीचे-ऊपर और ऊपर-नीचे दोनों दिशाओं में अनुमान और प्रशिक्षण प्रक्रिया अपनाते हैं, जो डीबीएम को निविष्ट संरचनाओं के प्रतिनिधित्व को बेहतर ढंग से प्रकट करने की अनुमति देता है।[11][12][13] चूंकि, डीबीएम की धीमी गति उनके प्रदर्शन और कार्यक्षमता को सीमित करती है। क्योंकि सटीक अधिकतम संभावना सीखना डीबीएम के लिए कठिन है, केवल अनुमानित अधिकतम संभावना सीखना संभव है। एक अन्य विकल्प आंकड़ो-निर्भर अपेक्षाओं का अनुमान लगाने के लिए माध्य-क्षेत्र अनुमान का उपयोग करना और मार्कोव श्रृंखला मोंटे कार्लो (एमसीएमसी) का उपयोग करके अपेक्षित पर्याप्त आंकड़ों का अनुमान लगाना है।[10]यह अनुमानित अनुमान, जो प्रत्येक परीक्षण निविष्ट के लिए किया जाना चाहिए, डीबीएम में एकल बॉटम-अप पास की तुलना में लगभग 25 से 50 गुना धीमा है। यह बड़े आंकड़े सेट के लिए संयुक्त अनुकूलन को अव्यवहारिक बनाता है, और फीचर प्रतिनिधित्व जैसे कार्यों के लिए डीबीएम के उपयोग को प्रतिबंधित करता है।
स्पाइक-एंड-स्लैब आरबीएम
गाऊसी आरबीएम की तरह, वास्तविक संख्या | वास्तविक-मान निविष्ट के साथ गहन सीखने की आवश्यकता ने स्पाइक-एंड-स्लैब प्रतिबंधित बोल्टज़मैन मशीन (एसएस प्रतिबंधित बोल्टज़मैन मशीन) को जन्म दिया, जो द्विआधारी वैरिएबल अव्यक्त चर के साथ निरंतर-मान मॉडल को निविष्ट करता है।[14] बुनियादी प्रतिबंधित बोल्ट्ज़मैन मशीन और उसके वेरिएंट के समान, स्पाइक-एंड-स्लैब आरबीएम एक द्विदलीय ग्राफ है, जबकि प्रतिबंधित बोल्ट्ज़मैन मशीन की तरह, दृश्य इकाइयाँ (निविष्ट) वास्तविक-मान हैं। अंतर प्रच्छन्न हुई परत में है, जहां प्रत्येक प्रच्छन्न हुई इकाई में एक द्विआधारी स्पाइक वैरिएबल और एक वास्तविक-मान स्लैब वैरिएबल होता है। एक स्पाइक शून्य पर एक असतत संभाव्यता द्रव्यमान है, जबकि एक स्लैब निरंतर डोमेन पर एक संभाव्यता घनत्व है;[15] उनका मिश्रण एक पूर्व संभाव्यता बनाता है।[16] एसएसप्रतिबंधित बोल्ट्ज़मैन मशीन का एक विस्तार जिसे µ-एसएसप्रतिबंधित बोल्ट्ज़मैन मशीन कहा जाता है, ऊर्जा फलन में अतिरिक्त शब्दों का उपयोग करके अतिरिक्त मॉडलिंग क्षमता प्रदान करता है। इनमें से एक शब्द मॉडल को एक अवलोकन दिए गए स्लैब चर को हाशिए पर रखकर स्पाइक चर का एक सशर्त संभाव्यता बंटन बनाने में सक्षम बनाता है।
गणित में
मुख्य लेख: गिब्स माप और लॉग-रैखिक मॉडल
अधिक सामान्य गणितीय सेटिंग में, बोल्ट्ज़मैन बंटन को गिब्स माप के रूप में भी जाना जाता है। सांख्यिकी और यंत्र अधिगम में इसे लॉग-रैखिक मॉडल कहा जाता है। गहन शिक्षण में बोल्ट्ज़मैन बंटन का उपयोग बोल्ट्ज़मैन मशीन जैसे प्रसंभाव्य तंत्रिका संजाल के नमूना बंटन में किया जाता है।
इतिहास
बोल्ट्ज़मैन मशीन शेरिंगटन-किर्कपैट्रिक के प्रसंभाव्य आइसिंग मॉडल के प्रचक्रण ग्लास मॉडल पर आधारित है।[17] संज्ञानात्मक विज्ञान में ऐसे ऊर्जा आधारित मॉडल को लागू करने में मूल योगदान हिंटन और सेजनोव्स्की के पत्रों में दिखाई दिया।[18][19] जॉन हॉपफ़ील्ड के मौलिक प्रकाशन में प्रचक्रण ग्लास का उल्लेख करते हुए भौतिकी और सांख्यिकीय यांत्रिकी को जोड़ा गया है।[20] एनील्ड गिब्स नमूनाकरण के साथ आइसिंग मॉडल को लागू करने का विचार डगलस हॉफ़स्टैटर के कॉपीकैट प्रोजेक्ट में सम्मलित है।[21][22] इसी तरह के विचार (ऊर्जा फलन में संकेत के परिवर्तन के साथ) पॉल स्मोलेंस्की के हार्मनी सिद्धांत में पाए जाते हैं।
बोल्ट्ज़मैन मशीन संरूपण में सांख्यिकीय यांत्रिकी के साथ खींची गई स्पष्ट सादृश्यता ने भौतिकी से उधार ली गई पारिभाषिक (उदाहरण के लिए, सद्भाव के अतिरिक्त ऊर्जा) का उपयोग किया, जो क्षेत्र में मानक बन गया है। इस पारिभाषिक को व्यापक रूप से अपनाने को इस तथ्य से प्रोत्साहित किया गया होगा कि इसके उपयोग से सांख्यिकीय यांत्रिकी से विभिन्न अवधारणाओं और विधियों को अपनाया गया है। अनुमान के लिए अनुकारितअनीलन का उपयोग करने के विभिन्न प्रस्ताव स्पष्ट रूप से स्वतंत्र थे।
आइसिंग मॉडल को मार्कोव यादृच्छिक क्षेत्रों का एक विशेष स्थितिा माना जाता है, जिसका भाषा विज्ञान, रोबोटिक्स, अभिकलित्र दृष्टि और कृत्रिम बुद्धिमत्ता में व्यापक अनुप्रयोग मिलता है।
यह भी देखें
- प्रतिबंधित बोल्ट्ज़मैन मशीन
- हेल्महोल्त्ज़ मशीन
- मार्कोव रैंडम फील्ड
- आइज़िंग मॉडल
- हॉपफील्ड संजाल
- सीखने का नियम[23] जो सशर्त स्थानीय जानकारी का उपयोग करता है उसे उल्टे रूप से प्राप्त किया जा सकता है ,
- .
संदर्भ
- ↑ Sherrington, David; Kirkpatrick, Scott (1975), "Solvable Model of a Spin-Glass", Physical Review Letters, 35 (35): 1792–1796, Bibcode:1975PhRvL..35.1792S, doi:10.1103/PhysRevLett.35.1792
- ↑ Ackley, David H; Hinton Geoffrey E; Sejnowski, Terrence J (1985), "A learning algorithm for Boltzmann machines" (PDF), Cognitive Science, 9 (1): 147–169, doi:10.1207/s15516709cog0901_7
- ↑ Hinton, Geoffrey E. (2007-05-24). "बोल्ट्ज़मान मशीन". Scholarpedia (in English). 2 (5): 1668. Bibcode:2007SchpJ...2.1668H. doi:10.4249/scholarpedia.1668. ISSN 1941-6016.
- ↑ Osborn, Thomas R. (1 January 1990). "Fast Teaching of Boltzmann Machines with Local Inhibition". अंतर्राष्ट्रीय तंत्रिका नेटवर्क सम्मेलन. Springer Netherlands. pp. 785. doi:10.1007/978-94-009-0643-3_76. ISBN 978-0-7923-0831-7.
- ↑ Ackley, David H; Hinton Geoffrey E; Sejnowski, Terrence J (1985), "A learning algorithm for Boltzmann machines" (PDF), Cognitive Science, 9 (1): 147–169, doi:10.1207/s15516709cog0901_7
- ↑ Nijkamp, E.; Hill, M. E; Han, T. (2020), "On the Anatomy of MCMC-Based Maximum Likelihood Learning of Energy-Based Models", Proceedings of the AAAI Conference on Artificial Intelligence, 4 (34): 5272–5280, doi:10.1609/aaai.v34i04.5973
- ↑ Ackley, David H.; Hinton, Geoffrey E.; Sejnowski, Terrence J. (1985). "बोल्ट्ज़मैन मशीनों के लिए एक लर्निंग एल्गोरिदम" (PDF). Cognitive Science. 9 (1): 147–169. doi:10.1207/s15516709cog0901_7. Archived from the original (PDF) on 18 July 2011.
- ↑ Recent Developments in Deep Learning (in English), archived from the original on 2021-12-22, retrieved 2020-02-17
- ↑ Yu, Dong; Dahl, George; Acero, Alex; Deng, Li (2011). "बड़ी शब्दावली वाक् पहचान के लिए संदर्भ-निर्भर पूर्व-प्रशिक्षित डीप न्यूरल नेटवर्क" (PDF). Microsoft Research. 20.
- ↑ 10.0 10.1 Hinton, Geoffrey; Salakhutdinov, Ruslan (2012). "गहरी बोल्ट्ज़मैन मशीनों को पूर्व-प्रशिक्षित करने का एक बेहतर तरीका" (PDF). Advances in Neural. 3: 1–9. Archived from the original (PDF) on 2017-08-13. Retrieved 2017-08-18.
- ↑ Hinton, Geoffrey; Salakhutdinov, Ruslan (2009). "डीप बोल्ट्ज़मैन मशीनों की कुशल शिक्षा" (PDF). 3: 448–455. Archived from the original (PDF) on 2015-11-06. Retrieved 2017-08-18.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Bengio, Yoshua; LeCun, Yann (2007). "एआई की ओर लर्निंग एल्गोरिदम को स्केल करना" (PDF). 1: 1–41.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Larochelle, Hugo; Salakhutdinov, Ruslan (2010). "डीप बोल्ट्ज़मैन मशीनों की कुशल शिक्षा" (PDF): 693–700. Archived from the original (PDF) on 2017-08-14. Retrieved 2017-08-18.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Courville, Aaron; Bergstra, James; Bengio, Yoshua (2011). "एक स्पाइक और स्लैब प्रतिबंधित बोल्ट्ज़मैन मशीन" (PDF). JMLR: Workshop and Conference Proceeding. 15: 233–241. Archived from the original (PDF) on 2016-03-04. Retrieved 2019-08-25.
- ↑ Courville, Aaron; Bergstra, James; Bengio, Yoshua (2011). "Unsupervised Models of Images by Spike-and-Slab RBMs" (PDF). Proceedings of the 28th International Conference on Machine Learning. Vol. 10. pp. 1–8. Archived from the original (PDF) on 2016-03-04. Retrieved 2019-08-25.
- ↑ Mitchell, T; Beauchamp, J (1988). "रेखीय प्रतिगमन में बायेसियन चर चयन". Journal of the American Statistical Association. 83 (404): 1023–1032. doi:10.1080/01621459.1988.10478694.
- ↑ Sherrington, David; Kirkpatrick, Scott (1975-12-29). "स्पिन-ग्लास का सॉल्व करने योग्य मॉडल". Physical Review Letters. 35 (26): 1792–1796. Bibcode:1975PhRvL..35.1792S. doi:10.1103/physrevlett.35.1792. ISSN 0031-9007.
- ↑ Hinton, Geoffery; Sejnowski, Terrence J. (May 1983). सहकारी संगणना का विश्लेषण. 5th Annual Congress of the Cognitive Science Society. Rochester, New York. Retrieved 17 February 2020.
- ↑ Hinton, Geoffrey E.; Sejnowski, Terrence J. (June 1983). इष्टतम अवधारणात्मक अनुमान. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Washington, D.C.: IEEE Computer Society. pp. 448–453.
- ↑ Hopfield, J. J. (1982). "उभरती हुई सामूहिक कम्प्यूटेशनल क्षमताओं के साथ तंत्रिका नेटवर्क और भौतिक प्रणालियाँ". Proceedings of the National Academy of Sciences of the United States of America. [s.n.] 79 (8): 2554–8. Bibcode:1982PNAS...79.2554H. doi:10.1073/pnas.79.8.2554. OCLC 848771572. PMC 346238. PMID 6953413.
- ↑ Hofstadter, D. R. (January 1984). The Copycat Project: An Experiment in Nondeterminism and Creative Analogies. Defense Technical Information Center. OCLC 227617764.
- ↑ Hofstadter, Douglas R. (1988). "A Non-Deterministic Approach to Analogy, Involving the Ising Model of Ferromagnetism". In Caianiello, Eduardo R. (ed.). संज्ञानात्मक प्रक्रियाओं का भौतिकी. Teaneck, New Jersey: World Scientific. ISBN 9971-5-0255-0. OCLC 750950619.
- ↑ Liou, C.-Y.; Lin, S.-L. (1989). "The other variant Boltzmann machine". International Joint Conference on Neural Networks. Washington, D.C., USA: IEEE. pp. 449–454. doi:10.1109/IJCNN.1989.118618.
अग्रिम पठन
- Hinton, G. E.; Sejnowski, T. J. (1986). D. E. Rumelhart; J. L. McClelland (eds.). "Learning and Relearning in Boltzmann Machines" (PDF). Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Volume 1: Foundations: 282–317. Archived from the original (PDF) on 2010-07-05.
- Hinton, G. E. (2002). "Training Products of Experts by Minimizing Contrastive Divergence" (PDF). Neural Computation. 14 (8): 1771–1800. CiteSeerX 10.1.1.35.8613. doi:10.1162/089976602760128018. PMID 12180402. S2CID 207596505.
- Hinton, G. E.; Osindero, S.; Teh, Y. (2006). "A fast learning algorithm for deep belief nets" (PDF). Neural Computation. 18 (7): 1527–1554. CiteSeerX 10.1.1.76.1541. doi:10.1162/neco.2006.18.7.1527. PMID 16764513. S2CID 2309950.
- Kothari P (2020): https://www.forbes.com/sites/tomtaulli/2020/02/02/coronavirus-can-ai-artificial-intelligence-make-a-difference/?sh=1eca51e55817