द्विअनुकरण: Difference between revisions
(Created page with "{{Short description|Relation between transition systems in computer science}} {{More citations needed|date=February 2017}} सैद्धांतिक कंप्यू...") |
No edit summary |
||
| Line 1: | Line 1: | ||
[[सैद्धांतिक कंप्यूटर विज्ञान]] में '''द्विसिमुलेशन''' संक्रमण प्रणालियों के बीच एक [[द्विआधारी संबंध]] होता है, इसके विपरीत सहयोगी प्रणालियाँ उसी तरह से व्यवहार करती है जिस तरह एक प्रणाली दूसरे का अनुकरण करती है। | |||
[[सैद्धांतिक कंप्यूटर विज्ञान]] में द्विसिमुलेशन | |||
सहज रूप से दो प्रणालियाँ | सहज रूप से दो प्रणालियाँ द्विसमान होती है। इस अर्थ में, पर्यवेक्षक द्वारा प्रत्येक प्रणाली को दूसरे से अलग नहीं किया जा सकता है।ka | ||
== औपचारिक परिभाषा == | == औपचारिक परिभाषा == | ||
एक [[राज्य संक्रमण प्रणाली]] को देखते हुए (<math>S</math>, <math>\Lambda</math>, →), | एक [[राज्य संक्रमण प्रणाली|संक्रमण प्रणाली]] को देखते हुए (<math>S</math>, <math>\Lambda</math>, →), जहाँ <math>S</math> का एक समूह है, <math>\Lambda</math> का एक समूह है और → अंकित किए गए संक्रमण का एक समूह है (अर्थात, एक उपसमूह) <math>S \times \Lambda \times S</math>), द्विसिमुलेशन एक द्विआधारी संबंध है <math>R \subseteq S \times S</math>, ऐसे कि दोनों <math>R</math> और इसका [[विपरीत संबंध]] <math>R^T</math> [[अनुकरण पूर्वआदेश|अनुकरण अनुक्रम]] है। इससे यह पता चलता है कि सममित सिमुलेशन एक द्विसिमुलेशन है। इस प्रकार कुछ लेखक द्विसिमुलेशन को सममित अनुकरण के रूप में परिभाषित करते है।<ref>{{Cite journal |last=Jančar, Petr and Srba, Jiří |year=2008 |title=डिफेंडर के दबाव से द्विसमानता की अनिश्चितता|url=https://doi.org/10.1145/1326554.1326559 |journal=J. ACM |location=New York, NY, USA |publisher=Association for Computing Machinery |volume=55 |pages=26 |doi=10.1145/1326554.1326559 |issn=0004-5411 |url-access=subscription |number=1 |s2cid=14878621}}</ref> | ||
द्विसिमुलेशन एक द्विआधारी संबंध है <math>R \subseteq S \times S</math>, | |||
ऐसे कि दोनों <math>R</math> और इसका [[विपरीत संबंध]] <math>R^T</math> [[अनुकरण पूर्वआदेश]] | |||
समान रूप से, <math>R</math> के लिए यदि एक द्विसिमुलेशन है <math>(p,q)</math> में <math>R</math> और सभी अंकित है α में <math>\Lambda</math>: | |||
* यदि <math>p \mathrel{\overset{\alpha}{\rightarrow}} p'</math>, फिर वहाँ है <math>q \mathrel{\overset{\alpha}{\rightarrow}} q'</math> ऐसा है कि <math>(p',q') \in R</math>, | |||
* यदि <math>q \mathrel{\overset{\alpha}{\rightarrow}} q'</math>, फिर वहाँ है <math>p \mathrel{\overset{\alpha}{\rightarrow}} p'</math> ऐसा है कि <math>(p',q') \in R</math>. | |||
दो संखयाए दिए गए <math>p</math> और <math>q</math> में <math>S</math>, <math>p</math> के समान है <math>q</math>, लिखा हुआ <math>p \, \sim \, q</math>, यदि कोई द्विसिमुलेशन है <math>R</math> ऐसा है कि <math>(p, q) \in R</math>. इसका मतलब है कि द्विसमानता संबंध <math> \, \sim \, </math> सभी द्विअनुकरणों का मिलन है: <math>(p,q) \in\,\sim\,</math> जब <math>(p, q) \in R</math> द्विसिमुलेशन के लिए है <math>R</math>. | |||
द्विसिमुलेशन का समूह संघ के अंतर्गत बंद होता है,<ref group="Note">Meaning the union of two bisimulations is a bisimulation.</ref> इसलिए, द्विसमानता संबंध स्वयं एक द्विसिमुलेशन होता है। चूँकि यह सभी द्विसिमुलेशन का मिलन होता है, यह अद्वितीय सबसे बड़ा द्विसिमुलेशन होता है। द्विसिमुलेशन को पूर्व संबंधी, सममित और सकर्मक समापन के अनुसार भी बंद किया जाता है, इसलिए, सबसे बड़ा द्विसिमुलेशन प्रतिवर्ती, सममित और संक्रमणीय होती है। इससे यह निष्कर्ष निकलता है कि सबसे बड़ा द्विसिमुलेशन - द्विसमानता - एक तुल्यता संबंध है।<ref>{{Cite book |last=Milner |first=Robin |title=संचार और समवर्ती|publisher=Prentice-Hall, Inc. |year=1989 |isbn=0131149849 |location=USA |authorlink=Robin Milner}}</ref> | |||
== वैकल्पिक परिभाषाएँ == | == वैकल्पिक परिभाषाएँ == | ||
=== संबंधपरक परिभाषा === | === संबंधपरक परिभाषा === | ||
द्विसिमुलेशन को [[संबंधों की संरचना]] के संदर्भ में निम्नानुसार परिभाषित किया जा सकता है। | |||
एक | एक संक्रमण प्रणाली दी गई <math>(S, \Lambda, \rightarrow)</math>, एक द्विसिमुलेशन [[संबंध (गणित)]] एक द्विआधारी संबंध है <math>R</math> और <math>S</math> (अर्थात, <math>R</math> ⊆ <math>S</math> × <math>S</math>) ऐसा है कि <math>\forall\alpha\in\Lambda</math> | ||
<math display="block">R\ ;\ \overset{\alpha}{\rightarrow}\quad {\subseteq}\quad \overset{\alpha}{\rightarrow}\ ;\ R</math> | <math display="block">R\ ;\ \overset{\alpha}{\rightarrow}\quad {\subseteq}\quad \overset{\alpha}{\rightarrow}\ ;\ R</math> | ||
और | और | ||
<math display="block">R^{-1}\ ;\ \overset{\alpha}{\rightarrow}\quad {\subseteq}\quad \overset{\alpha}{\rightarrow}\ ;\ R^{-1}</math> | <math display="block">R^{-1}\ ;\ \overset{\alpha}{\rightarrow}\quad {\subseteq}\quad \overset{\alpha}{\rightarrow}\ ;\ R^{-1}</math> | ||
संबंध संरचना की एकरसता और निरंतरता से, यह तुरंत पता चलता है कि द्विसिमुलेशन का | संबंध संरचना की एकरसता और निरंतरता से, यह तुरंत पता चलता है कि द्विसिमुलेशन का समूह संघों (संबंधों की स्थिति में जुड़ता है) के अनुसार बंद होता है, और एक सरल बीजगणितीय गणना से पता चलता है कि द्विसमानता का संबंध - सभी द्विसिमुलेशन का जुड़ाव होता है। इस परिभाषा और द्विसमानता के संबंधित उपचार की व्याख्या किसी भी समावेशी मात्रा में की जा सकती है। | ||
=== | === निश्चित बिंदु परिभाषा === | ||
द्विसमानता को [[ आदेश सिद्धांत |अनुक्रम सिद्धांत]] में भी परिभाषित किया जा सकता है, नास्टर-टार्स्की सिद्धांत के संदर्भ में, अधिक त्रुटिहीन रूप से नीचे परिभाषित सबसे बड़े निश्चित बिंदु के रूप में एक निश्चित फलन होता है। | |||
एक | एक संक्रमण प्रणाली को देखते हुए (<math>S</math>, Λ, →), परिभाषित करता है <math>F:\mathcal{P}(S \times S) \to \mathcal{P}(S \times S)</math> द्विआधारी संबंधों से एक फलन बनता है <math>S</math> द्विआधारी संबंधों को समाप्त करने के लिए होता है <math>S</math>, निम्नलिखित नुसार: | ||
<math>R</math> द्विआधारी संबंध को समाप्त करता है <math>S</math>. <math>F(R)</math> सभी जोड़ियों के समुच्चय के रूप में परिभाषित किया जाता है <math>(p,q)</math> में <math>S</math> × <math>S</math> ऐसा है कि: | |||
<math display="block"> | <math display="block"> | ||
| Line 53: | Line 47: | ||
तब द्विसमानता को सबसे बड़े निश्चित बिंदु के रूप में परिभाषित किया जाता है <math>F</math>. | तब द्विसमानता को सबसे बड़े निश्चित बिंदु के रूप में परिभाषित किया जाता है <math>F</math>. | ||
=== एहरनफ्यूच्ट- | === एहरनफ्यूच्ट-फ्रैस्से खेल परिभाषा === | ||
द्विसिम्यूलेशन को दो खिलाड़ियों के बीच खेल के संदर्भ में भी विचार किया जा सकता है: हमलावर और बचावकर्ता। | |||
हमलावर पहले जाता है और कोई भी वैध संक्रमण चुन सकता है, <math>\alpha</math>, से <math>(p,q)</math>. वह है, | हमलावर पहले जाता है और कोई भी वैध संक्रमण चुन सकता है, <math>\alpha</math>, से <math>(p,q)</math>. वह है, | ||
| Line 64: | Line 58: | ||
(p,q) \overset{\alpha}{\rightarrow} (p,q') | (p,q) \overset{\alpha}{\rightarrow} (p,q') | ||
</math> | </math> | ||
फिर | फिर बचावकर्ता उस परिवर्तन से मेल खाने का प्रयास करता है, <math>\alpha</math> दोनों से <math>(p',q)</math> या <math>(p,q')</math> अर्थात, उन्हें प्राप्त होता है <math>\alpha</math> ऐसा है कि: | ||
<math display="block"> | <math display="block"> | ||
(p',q) \overset{\alpha}{\rightarrow} (p',q') | (p',q) \overset{\alpha}{\rightarrow} (p',q') | ||
| Line 73: | Line 66: | ||
(p,q') \overset{\alpha}{\rightarrow} (p',q') | (p,q') \overset{\alpha}{\rightarrow} (p',q') | ||
</math> | </math> | ||
हमलावर और बचावकर्ता तब तक बारी-बारी से | हमलावर और बचावकर्ता तब तक बारी-बारी से प्रयास करते रहते है: | ||
* | * बचावकर्ता हमलावर की गतिविधियाँ मेल खाने के लिए कोई वैध बदलाव प्राप्त करने में असमर्थ होती है। इस स्थिति में हमलावर जीत जाता है. | ||
* | * खेल तक पहुंचते है <math>(p,q)</math> वे दोनों 'मृत' होते है (अर्थात, किसी भी राज्य से कोई परिवर्तन नहीं हुआ है) इस स्थिति में बचावकर्ता जीतता है | ||
* खेल हमेशा चलता रहता है, ऐसी स्थिति में | * खेल हमेशा चलता रहता है, ऐसी स्थिति में बचावकर्ता जीतता है। | ||
* | * खेल तक पहुंचते है <math>(p,q)</math>, जिसको पहले ही जाना जा चुका होता है। यह एक अनंत खेल के बराबर होता है और बचावकर्ता के लिए जीत के रूप में अंकित किया जाता है। | ||
उपरोक्त परिभाषा के अनुसार | उपरोक्त परिभाषा के अनुसार प्रणाली एक द्विसिमुलेशन तभी होती है यदि जब बचावकर्ता के लिए जीतने की रणनीति उपस्थित होती है। | ||
===कोलगेब्रिक परिभाषा === | ===कोलगेब्रिक परिभाषा === | ||
संक्रमण प्रणालियों के लिए एक द्विसिमुलेशन सहसंयोजक ऊर्जा समूह [[ऑपरेटर|प्रचालक]] के प्रकार के लिए [[ कोलजेब्रा में |कोलजेब्रा में]] द्विसिमुलेशन की एक विशेष स्थिति होती है। ध्यान दें कि प्रत्येक संक्रमण प्रणाली <math>(S, \Lambda, \rightarrow)</math> [[द्विभाजन]] फलन है <math>\xi_{\rightarrow} </math> से <math>S</math> के लिए <math>S</math> द्वारा अनुक्रमित <math>\Lambda</math> के रूप में लिखा गया है <math>\mathcal{P}(\Lambda \times S)</math>, द्वारा परिभाषित है | |||
ध्यान दें कि प्रत्येक | |||
<math display="block"> p \mapsto \{ (\alpha, q) \in \Lambda \times S : p \overset{\alpha}{\rightarrow} q \}.</math> | <math display="block"> p \mapsto \{ (\alpha, q) \in \Lambda \times S : p \overset{\alpha}{\rightarrow} q \}.</math> | ||
मान लेते है <math>\pi_i \colon S \times S \to S</math> और <math>i</math>- [[उत्पाद (श्रेणी सिद्धांत)]] मानचित्रण <math>(p, q)</math> को <math>p</math> और <math>q</math> क्रमशः के लिए <math>i = 1, 2</math>, और <math>\mathcal{P}(\Lambda \times \pi_1)</math> की आगे की छवि <math>\pi_1</math> के तीसरे घटक को हटाकर परिभाषित किया जा सकता है | |||
<math>(p, q)</math> को <math>p</math> और <math>q</math> क्रमशः के लिए <math>i = 1, 2</math> | |||
<math>\mathcal{P}(\Lambda \times \pi_1)</math> की आगे की छवि <math>\pi_1</math> तीसरे घटक को हटाकर परिभाषित किया | |||
<math display="block"> P \mapsto \{ (\alpha, p) \in \Lambda \times S : \exists q . (\alpha, p, q) \in P \}</math> | <math display="block"> P \mapsto \{ (\alpha, p) \in \Lambda \times S : \exists q . (\alpha, p, q) \in P \}</math> | ||
जहाँ <math>P</math> का एक उपसमुच्चय है <math>\Lambda \times S \times S</math>. इसी प्रकार के लिए <math>\mathcal{P}(\Lambda \times \pi_2)</math>. | |||
उपरोक्त | उपरोक्त अंकन का उपयोग करते हुए, एक संबंध <math>R \subseteq S \times S </math> एक संक्रमण प्रणाली पर एक द्विसिमुलेशन होता है <math>(S, \Lambda, \rightarrow)</math> यदि कोई संक्रमण प्रणाली उपस्थित है <math>\gamma \colon R \to \mathcal{P}(\Lambda \times R)</math> और <math>R</math> जैसे कि यह [[क्रमविनिमेय आरेख]] है | ||
[[Image:Coalgebraic bisimulation.svg|frameकम|सीधा=1.5]]आवागमन, अर्थात् के लिए <math>i = 1, 2</math>, समीकरण | [[Image:Coalgebraic bisimulation.svg|frameकम|सीधा=1.5]]आवागमन, अर्थात् के लिए <math>i = 1, 2</math>, समीकरण | ||
<math display="block"> \xi_\rightarrow \circ \pi_i = \mathcal{P}(\Lambda \times \pi_i) \circ \gamma </math> | <math display="block"> \xi_\rightarrow \circ \pi_i = \mathcal{P}(\Lambda \times \pi_i) \circ \gamma </math> | ||
जहाँ <math>\xi_{\rightarrow}</math> का कार्यात्मक प्रतिनिधित्व है <math>(S, \Lambda, \rightarrow)</math>. | |||
== द्विसिमुलेशन के प्रकार == | == द्विसिमुलेशन के प्रकार == | ||
विशेष संदर्भों में द्विसिमुलेशन की धारणा को कभी-कभी अतिरिक्त आवश्यकताओं या बाधाओं को जोड़कर परिष्कृत किया जाता है। एक उदाहरण | विशेष संदर्भों में द्विसिमुलेशन की धारणा को कभी-कभी अतिरिक्त आवश्यकताओं या बाधाओं को जोड़कर परिष्कृत किया जाता है। एक उदाहरण द्विसिमुलेशन का हकलाना होता है, जिसमें एक प्रणाली के एक संक्रमण को दूसरे के कई संक्रमणों के साथ मिलान किया जा सकता है, यदि मध्यवर्ती प्रारंभिक स्थिति (हकलाना) के बराबर होता है।<ref>{{cite book |last1=Baier |first1=Christel|author1-link= Christel Baier |last2=Katoen |first2=Joost-Pieter|author2-link=Joost-Pieter Katoen |title=[[Principles of Model Checking]] |date=2008 |publisher=MIT Press |isbn=978-0-262-02649-9 |page=527}}</ref> | ||
यदि | |||
यदि संक्रमण प्रणाली एक अलग प्रकार लागू होता है, जिसे अधिकांशतः इसके साथ दर्शाया जाता है <math>\tau</math>, अर्थात ऐसी क्रियाएं जो बाहरी पर्यवेक्षकों द्वारा दिखाई नहीं देती है, तो द्विसिमुलेशन को कमजोर द्विसिमुलेशन में शिथिल किया जा सकता है, जिसमें दो अवस्थाएं होती है <math>p</math> और <math>q</math> द्विसमान होते है और कुछ संख्या में आंतरिक क्रियाएं होती है <math>p</math> के लिए <math>p'</math> और <math>q'</math> जैसे कि आंतरिक क्रियाओं की कुछ संख्या संभवतः शून्य होती है <math>q</math> को <math>q'</math>. एक संबंध <math>\mathcal{R}</math> प्रक्रियाओं पर एक कमजोर द्विसिमुलेशन होता है यदि निम्नलिखित के साथ स्थित रहता है <math>\mathcal{S} \in \{ \mathcal{R}, \mathcal{R}^{-1} \}</math>, और <math>a,\tau</math> क्रमशः एक अवलोकनीय और मूक संक्रमण होता है: | |||
<math display="block">\forall p, q. \quad (p,q) \in \mathcal{S} \Rightarrow p \stackrel{\tau}{\rightarrow} p' \Rightarrow \exists q' . \quad q \stackrel{\tau^\ast}{\rightarrow} q' \wedge (p',q') \in \mathcal{S} </math> | <math display="block">\forall p, q. \quad (p,q) \in \mathcal{S} \Rightarrow p \stackrel{\tau}{\rightarrow} p' \Rightarrow \exists q' . \quad q \stackrel{\tau^\ast}{\rightarrow} q' \wedge (p',q') \in \mathcal{S} </math><math display="block">\forall p, q. \quad (p,q) \in \mathcal{S} \Rightarrow p \stackrel{a}{\rightarrow} p' \Rightarrow \exists q' . \quad q \stackrel{\tau^\ast a \tau^\ast}{\rightarrow} q' \wedge (p',q') \in \mathcal{S} </math> | ||
<math display="block">\forall p, q. \quad (p,q) \in \mathcal{S} \Rightarrow p \stackrel{a}{\rightarrow} p' \Rightarrow \exists q' . \quad q \stackrel{\tau^\ast a \tau^\ast}{\rightarrow} q' \wedge (p',q') \in \mathcal{S} </math> | यह द्विसिमुलेशन से लेकर कंप्यूटर विज्ञान तक के संबंध तक निकटता से संबंधित होता है। | ||
यह द्विसिमुलेशन से लेकर | |||
सामान्यतः, यदि संक्रमण प्रणाली एक [[प्रोग्रामिंग भाषा]] का [[परिचालन शब्दार्थ|परिगतिविधिन शब्दार्थ]] होता है, तो द्विसिमुलेशन की त्रुटिहीन परिभाषा प्रोग्रामिंग भाषा के प्रतिबंधों के लिए विशिष्ट होती है। इसलिए, सामान्यतः, संदर्भ के आधार पर एक से अधिक प्रकार के द्विसिमुलेशन, (द्विसमानता) संबंध हो सकते है। | |||
== | == द्विसिमुलेशन और [[मोडल तर्क|प्रतिरूप तर्क]] == | ||
चूंकि [[क्रिपके शब्दार्थ]] | चूंकि [[क्रिपके शब्दार्थ]] संक्रमण प्रणालियों की एक विशेष स्थिति होती है, इसलिए द्विसिमुलेशन भी प्रतिरूप तर्क का एक विषय होता है। वास्तव में, प्रतिरूप तर्क द्विसिमुलेशन (जोहान के सिद्धांत) के अनुसार [[प्रथम-क्रम तर्क]] अपरिवर्तनीय होता है। | ||
== | == कलन विधि == | ||
कलन विधि दो परिमित संक्रमण प्रणालियाँ को द्विसमान बहुपद समय में किया जा सकता है।{{sfnp|Baier|Katoen|2008|loc=Cor. 7.45, p. 486}} कलन विधि से [[विभाजन परिशोधन]] का उपयोग करते हुए [[चतुर्रेखीय समय]] में विभाजन की समस्या को कम किया जा सकता है। | |||
== यह भी देखें == | == यह भी देखें == | ||
| Line 165: | Line 154: | ||
* [[सीएडीपी]]: [http://cadp.inria.fr विभिन्न द्विसिमुलेशन के अनुसार परिमित-राज्य प्रणालियों को कम करने और तुलना करने के लिए उपकरण] | * [[सीएडीपी]]: [http://cadp.inria.fr विभिन्न द्विसिमुलेशन के अनुसार परिमित-राज्य प्रणालियों को कम करने और तुलना करने के लिए उपकरण] | ||
* [[mCRL2]]: विभिन्न द्विसिमुलेशन के अनुसार परिमित-अवस्था प्रणालियों को छोटा करने और तुलना करने के लिए उपकरण | * [[mCRL2]]: विभिन्न द्विसिमुलेशन के अनुसार परिमित-अवस्था प्रणालियों को छोटा करने और तुलना करने के लिए उपकरण | ||
* [http://www.brics.dk/bisim/ द | * [http://www.brics.dk/bisim/ द द्विसिमुलेशन गेम गेम] | ||
{{Authority control}} | {{Authority control}} | ||
Revision as of 03:15, 9 July 2023
सैद्धांतिक कंप्यूटर विज्ञान में द्विसिमुलेशन संक्रमण प्रणालियों के बीच एक द्विआधारी संबंध होता है, इसके विपरीत सहयोगी प्रणालियाँ उसी तरह से व्यवहार करती है जिस तरह एक प्रणाली दूसरे का अनुकरण करती है।
सहज रूप से दो प्रणालियाँ द्विसमान होती है। इस अर्थ में, पर्यवेक्षक द्वारा प्रत्येक प्रणाली को दूसरे से अलग नहीं किया जा सकता है।ka
औपचारिक परिभाषा
एक संक्रमण प्रणाली को देखते हुए (, , →), जहाँ का एक समूह है, का एक समूह है और → अंकित किए गए संक्रमण का एक समूह है (अर्थात, एक उपसमूह) ), द्विसिमुलेशन एक द्विआधारी संबंध है , ऐसे कि दोनों और इसका विपरीत संबंध अनुकरण अनुक्रम है। इससे यह पता चलता है कि सममित सिमुलेशन एक द्विसिमुलेशन है। इस प्रकार कुछ लेखक द्विसिमुलेशन को सममित अनुकरण के रूप में परिभाषित करते है।[1]
समान रूप से, के लिए यदि एक द्विसिमुलेशन है में और सभी अंकित है α में :
- यदि , फिर वहाँ है ऐसा है कि ,
- यदि , फिर वहाँ है ऐसा है कि .
दो संखयाए दिए गए और में , के समान है , लिखा हुआ , यदि कोई द्विसिमुलेशन है ऐसा है कि . इसका मतलब है कि द्विसमानता संबंध सभी द्विअनुकरणों का मिलन है: जब द्विसिमुलेशन के लिए है .
द्विसिमुलेशन का समूह संघ के अंतर्गत बंद होता है,[Note 1] इसलिए, द्विसमानता संबंध स्वयं एक द्विसिमुलेशन होता है। चूँकि यह सभी द्विसिमुलेशन का मिलन होता है, यह अद्वितीय सबसे बड़ा द्विसिमुलेशन होता है। द्विसिमुलेशन को पूर्व संबंधी, सममित और सकर्मक समापन के अनुसार भी बंद किया जाता है, इसलिए, सबसे बड़ा द्विसिमुलेशन प्रतिवर्ती, सममित और संक्रमणीय होती है। इससे यह निष्कर्ष निकलता है कि सबसे बड़ा द्विसिमुलेशन - द्विसमानता - एक तुल्यता संबंध है।[2]
वैकल्पिक परिभाषाएँ
संबंधपरक परिभाषा
द्विसिमुलेशन को संबंधों की संरचना के संदर्भ में निम्नानुसार परिभाषित किया जा सकता है।
एक संक्रमण प्रणाली दी गई , एक द्विसिमुलेशन संबंध (गणित) एक द्विआधारी संबंध है और (अर्थात, ⊆ × ) ऐसा है कि
निश्चित बिंदु परिभाषा
द्विसमानता को अनुक्रम सिद्धांत में भी परिभाषित किया जा सकता है, नास्टर-टार्स्की सिद्धांत के संदर्भ में, अधिक त्रुटिहीन रूप से नीचे परिभाषित सबसे बड़े निश्चित बिंदु के रूप में एक निश्चित फलन होता है।
एक संक्रमण प्रणाली को देखते हुए (, Λ, →), परिभाषित करता है द्विआधारी संबंधों से एक फलन बनता है द्विआधारी संबंधों को समाप्त करने के लिए होता है , निम्नलिखित नुसार:
द्विआधारी संबंध को समाप्त करता है . सभी जोड़ियों के समुच्चय के रूप में परिभाषित किया जाता है में × ऐसा है कि:
एहरनफ्यूच्ट-फ्रैस्से खेल परिभाषा
द्विसिम्यूलेशन को दो खिलाड़ियों के बीच खेल के संदर्भ में भी विचार किया जा सकता है: हमलावर और बचावकर्ता।
हमलावर पहले जाता है और कोई भी वैध संक्रमण चुन सकता है, , से . वह है,
फिर बचावकर्ता उस परिवर्तन से मेल खाने का प्रयास करता है, दोनों से या अर्थात, उन्हें प्राप्त होता है ऐसा है कि:
हमलावर और बचावकर्ता तब तक बारी-बारी से प्रयास करते रहते है:
- बचावकर्ता हमलावर की गतिविधियाँ मेल खाने के लिए कोई वैध बदलाव प्राप्त करने में असमर्थ होती है। इस स्थिति में हमलावर जीत जाता है.
- खेल तक पहुंचते है वे दोनों 'मृत' होते है (अर्थात, किसी भी राज्य से कोई परिवर्तन नहीं हुआ है) इस स्थिति में बचावकर्ता जीतता है
- खेल हमेशा चलता रहता है, ऐसी स्थिति में बचावकर्ता जीतता है।
- खेल तक पहुंचते है , जिसको पहले ही जाना जा चुका होता है। यह एक अनंत खेल के बराबर होता है और बचावकर्ता के लिए जीत के रूप में अंकित किया जाता है।
उपरोक्त परिभाषा के अनुसार प्रणाली एक द्विसिमुलेशन तभी होती है यदि जब बचावकर्ता के लिए जीतने की रणनीति उपस्थित होती है।
कोलगेब्रिक परिभाषा
संक्रमण प्रणालियों के लिए एक द्विसिमुलेशन सहसंयोजक ऊर्जा समूह प्रचालक के प्रकार के लिए कोलजेब्रा में द्विसिमुलेशन की एक विशेष स्थिति होती है। ध्यान दें कि प्रत्येक संक्रमण प्रणाली द्विभाजन फलन है से के लिए द्वारा अनुक्रमित के रूप में लिखा गया है , द्वारा परिभाषित है
उपरोक्त अंकन का उपयोग करते हुए, एक संबंध एक संक्रमण प्रणाली पर एक द्विसिमुलेशन होता है यदि कोई संक्रमण प्रणाली उपस्थित है और जैसे कि यह क्रमविनिमेय आरेख है
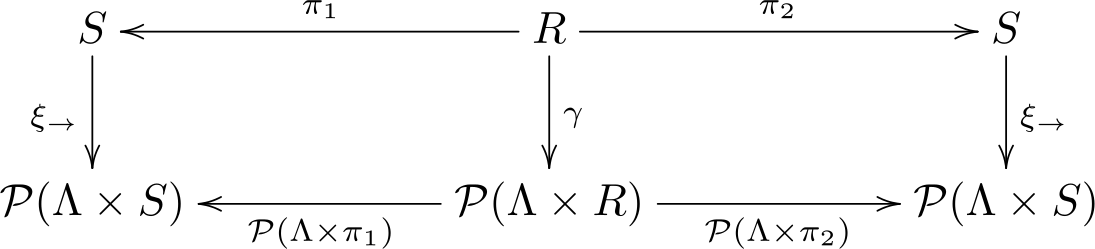 आवागमन, अर्थात् के लिए , समीकरण
आवागमन, अर्थात् के लिए , समीकरण
द्विसिमुलेशन के प्रकार
विशेष संदर्भों में द्विसिमुलेशन की धारणा को कभी-कभी अतिरिक्त आवश्यकताओं या बाधाओं को जोड़कर परिष्कृत किया जाता है। एक उदाहरण द्विसिमुलेशन का हकलाना होता है, जिसमें एक प्रणाली के एक संक्रमण को दूसरे के कई संक्रमणों के साथ मिलान किया जा सकता है, यदि मध्यवर्ती प्रारंभिक स्थिति (हकलाना) के बराबर होता है।[3]
यदि संक्रमण प्रणाली एक अलग प्रकार लागू होता है, जिसे अधिकांशतः इसके साथ दर्शाया जाता है , अर्थात ऐसी क्रियाएं जो बाहरी पर्यवेक्षकों द्वारा दिखाई नहीं देती है, तो द्विसिमुलेशन को कमजोर द्विसिमुलेशन में शिथिल किया जा सकता है, जिसमें दो अवस्थाएं होती है और द्विसमान होते है और कुछ संख्या में आंतरिक क्रियाएं होती है के लिए और जैसे कि आंतरिक क्रियाओं की कुछ संख्या संभवतः शून्य होती है को . एक संबंध प्रक्रियाओं पर एक कमजोर द्विसिमुलेशन होता है यदि निम्नलिखित के साथ स्थित रहता है , और क्रमशः एक अवलोकनीय और मूक संक्रमण होता है:
सामान्यतः, यदि संक्रमण प्रणाली एक प्रोग्रामिंग भाषा का परिगतिविधिन शब्दार्थ होता है, तो द्विसिमुलेशन की त्रुटिहीन परिभाषा प्रोग्रामिंग भाषा के प्रतिबंधों के लिए विशिष्ट होती है। इसलिए, सामान्यतः, संदर्भ के आधार पर एक से अधिक प्रकार के द्विसिमुलेशन, (द्विसमानता) संबंध हो सकते है।
द्विसिमुलेशन और प्रतिरूप तर्क
चूंकि क्रिपके शब्दार्थ संक्रमण प्रणालियों की एक विशेष स्थिति होती है, इसलिए द्विसिमुलेशन भी प्रतिरूप तर्क का एक विषय होता है। वास्तव में, प्रतिरूप तर्क द्विसिमुलेशन (जोहान के सिद्धांत) के अनुसार प्रथम-क्रम तर्क अपरिवर्तनीय होता है।
कलन विधि
कलन विधि दो परिमित संक्रमण प्रणालियाँ को द्विसमान बहुपद समय में किया जा सकता है।[4] कलन विधि से विभाजन परिशोधन का उपयोग करते हुए चतुर्रेखीय समय में विभाजन की समस्या को कम किया जा सकता है।
यह भी देखें
- सिमुलेशन प्रीऑर्डर
- सर्वांगसम संबंध
- संभाव्य द्विसिमुलेशन
टिप्पणियाँ
- ↑ Meaning the union of two bisimulations is a bisimulation.
संदर्भ
- ↑ Jančar, Petr and Srba, Jiří (2008). "डिफेंडर के दबाव से द्विसमानता की अनिश्चितता". J. ACM. New York, NY, USA: Association for Computing Machinery. 55 (1): 26. doi:10.1145/1326554.1326559. ISSN 0004-5411. S2CID 14878621.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Milner, Robin (1989). संचार और समवर्ती. USA: Prentice-Hall, Inc. ISBN 0131149849.
- ↑ Baier, Christel; Katoen, Joost-Pieter (2008). Principles of Model Checking. MIT Press. p. 527. ISBN 978-0-262-02649-9.
- ↑ Baier & Katoen (2008), Cor. 7.45, p. 486.
अग्रिम पठन
- Park, David (1981). "Concurrency and Automata on Infinite Sequences". In Deussen, Peter (ed.). Theoretical Computer Science. Proceedings of the 5th GI-Conference, Karlsruhe. Lecture Notes in Computer Science. Vol. 104. Springer-Verlag. pp. 167–183. doi:10.1007/BFb0017309. ISBN 978-3-540-10576-3.
- Milner, Robin (1989). Communication and Concurrency. Prentice Hall. ISBN 0-13-114984-9.
- Sangiorgi, Davide (2011). An introduction to Bisimulation and Coinduction. Cambridge, UK: Cambridge University Press. ISBN 9781107003637. OCLC 773040572.
बाहरी संबंध
सॉफ्टवेयर उपकरण
- सीएडीपी: विभिन्न द्विसिमुलेशन के अनुसार परिमित-राज्य प्रणालियों को कम करने और तुलना करने के लिए उपकरण
- mCRL2: विभिन्न द्विसिमुलेशन के अनुसार परिमित-अवस्था प्रणालियों को छोटा करने और तुलना करने के लिए उपकरण
- द द्विसिमुलेशन गेम गेम
श्रेणी:सैद्धांतिक कंप्यूटर विज्ञान श्रेणी:औपचारिक तरीके श्रेणी:कंप्यूटर विज्ञान में तर्क श्रेणी:संक्रमण प्रणालियाँ