न्यूनतम-कोण प्रतिगमन: Difference between revisions
(Created page with "{{technical|date=April 2018}} {{Regression bar}} Image:Larsdiabetes.png|thumb|मानकीकृत गुणांक को सिकुड़न के अनुपा...") |
No edit summary |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{technical|date=April 2018}} | {{technical|date=April 2018}} | ||
{{Regression bar}} | {{Regression bar}} | ||
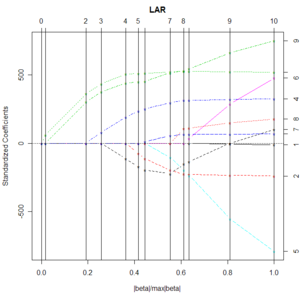
[[Image:Larsdiabetes.png|thumb|मानकीकृत गुणांक को सिकुड़न के अनुपात के एक | [[Image:Larsdiabetes.png|thumb|मानकीकृत गुणांक को सिकुड़न के अनुपात के एक फलन के रूप में दिखाया गया है।]]आंकड़ों में, '''न्यूनतम-कोण प्रतिगमन''' (एलएआरएस) उच्च-आयामी डेटा के लिए रैखिक प्रतिगमन प्रतिरूप को अनुरूप करने के लिए एक कलन विधि है, जिसे [[ब्रैडली एफ्रॉन]], [[ट्रेवर हेस्टी]], [[इयान जॉनस्टोन (गणितज्ञ)]] और [[रॉबर्ट तिबशिरानी]] द्वारा विकसित किया गया है। <ref>{{cite journal | ||
| author = [[Bradley Efron|Efron, Bradley]] |author2=Hastie, Trevor |author3=Johnstone, Iain |author4=Tibshirani, Robert | | author = [[Bradley Efron|Efron, Bradley]] |author2=Hastie, Trevor |author3=Johnstone, Iain |author4=Tibshirani, Robert | ||
| title = Least Angle Regression | | title = Least Angle Regression | ||
| Line 13: | Line 13: | ||
| mr = 2060166 | | mr = 2060166 | ||
| arxiv= math/0406456|s2cid=204004121 }}</ref> | | arxiv= math/0406456|s2cid=204004121 }}</ref> | ||
मान लीजिए कि हम | मान लीजिए कि हम अपेक्षा करते हैं कि एक प्रतिक्रिया चर संभावित सहसंयोजकों के उपवर्ग के रैखिक संयोजन द्वारा निर्धारित किया जाएगा। फिर एलएआरएस कलन विधि अनुमान लगाने का एक साधन प्रदान करता है कि किन चरों को सम्मिलित किया जाए, साथ ही उनके गुणांक भी। | ||
एक | एक परिणाम देने के स्थान पर, एलएआरएस समाधान में पैरामीटर सदिश के L1 मानदंड के प्रत्येक मान के लिए समाधान को दर्शाने वाला एक वक्र होता है। कलन विधि फॉरवर्ड स्टेप [[चरणबद्ध प्रतिगमन]] के समान है, लेकिन प्रत्येक चरण में चर को सम्मिलित करने के स्थान पर, अनुमानित मापदंडों को अवशिष्ट के साथ प्रत्येक के सहसंबंध के समकोणीय दिशा में बढ़ाया जाता है। | ||
== | ==लाभ और हानि == | ||
एलएआरएस पद्धति के लाभ हैं: | |||
# यह कम्प्यूटेशनल रूप से फॉरवर्ड चयन जितना ही | # यह कम्प्यूटेशनल रूप से फॉरवर्ड चयन जितना ही तीव्र है। | ||
# यह एक पूर्ण टुकड़ा-वार रैखिक समाधान पथ तैयार करता है, जो क्रॉस-वैलिडेशन (सांख्यिकी) | # यह एक पूर्ण टुकड़ा-वार रैखिक समाधान पथ तैयार करता है, जो क्रॉस-वैलिडेशन (सांख्यिकी) क्रॉस-वैलिडेशन या प्रतिरूप को ट्यून करने के समान प्रयासों में उपयोगी है। | ||
# यदि दो चर प्रतिक्रिया के साथ लगभग समान रूप से सहसंबद्ध हैं, तो उनके गुणांक लगभग समान दर से बढ़ने चाहिए। इस प्रकार | # यदि दो चर प्रतिक्रिया के साथ लगभग समान रूप से सहसंबद्ध हैं, तो उनके गुणांक लगभग समान दर से बढ़ने चाहिए। इस प्रकार कलन विधि अंतर्ज्ञान की अपेक्षा के अनुरूप व्यवहार करता है, और अधिक स्थिर भी है। | ||
# समान परिणाम देने वाली अन्य विधियों, जैसे [[लैस्सो (सांख्यिकी)]] और फॉरवर्ड स्टेजवाइज रिग्रेशन के लिए कुशल | # समान परिणाम देने वाली अन्य विधियों, जैसे [[लैस्सो (सांख्यिकी)]] और फॉरवर्ड स्टेजवाइज रिग्रेशन के लिए कुशल कलन विधि तैयार करने के लिए इसे आसानी से संशोधित किया जाता है। | ||
# यह उन संदर्भों में प्रभावी है जहां पी ≫ एन (यानी, जब भविष्यवक्ताओं की संख्या पी अंक की संख्या से काफी अधिक है)<ref>{{cite book | # यह उन संदर्भों में प्रभावी है जहां पी ≫ एन (यानी, जब भविष्यवक्ताओं की संख्या पी अंक की संख्या से काफी अधिक है)<ref>{{cite book | ||
|last1= Hastie | |last1= Hastie | ||
| Line 40: | Line 40: | ||
}} | }} | ||
</ref> | </ref> | ||
एलएआरएस पद्धति के नुकसानों में सम्मिलित हैं: | |||
# आश्रित चर में किसी भी मात्रा में | # आश्रित चर में किसी भी मात्रा में लड़ाई और उच्च आयामी बहुसंरेखता स्वतंत्र चर के साथ, यह स्तिथि का कोई कारण नहीं है कि चयनित चर में वास्तविक अंतर्निहित कारण चर होने की उच्च संभावना होगी। यह समस्या एलएआरएस के लिए अद्वितीय नहीं है, क्योंकि यह परिवर्तनीय चयन दृष्टिकोण के साथ एक सामान्य समस्या है जो अंतर्निहित नियतात्मक घटकों को ढूंढना चाहती है। फिर भी, क्योंकि एलएआरएस अवशेषों की पुनरावृत्तीय साजोसामान पर आधारित है, यह लड़ाई के प्रभावों के प्रति विशेष रूप से संवेदनशील प्रतीत होता है। इस समस्या पर वीज़बर्ग द्वारा एफ्रॉन एट अल के चर्चा अनुभाग (2004) एनल्स ऑफ स्टैटिस्टिक्स लेख में विस्तार से चर्चा की गई है। <ref>See Discussion by Weisberg following {{cite journal | ||
| author = [[Bradley Efron|Efron, Bradley]] |author2=Hastie, Trevor |author3=Johnstone, Iain |author4=Tibshirani, Robert | | author = [[Bradley Efron|Efron, Bradley]] |author2=Hastie, Trevor |author3=Johnstone, Iain |author4=Tibshirani, Robert | ||
| title = Least Angle Regression | | title = Least Angle Regression | ||
| Line 53: | Line 53: | ||
| mr = 2060166 | | mr = 2060166 | ||
| arxiv= math/0406456|s2cid=204004121 }}</ref> वीज़बर्ग मूल रूप से एलएआरएस को मान्य करने के लिए उपयोग किए गए डेटा के पुन: विश्लेषण के आधार पर एक अनुभवजन्य उदाहरण प्रदान करता है कि चर चयन में अत्यधिक सहसंबद्ध चर के साथ समस्याएं प्रतीत होती हैं। | | arxiv= math/0406456|s2cid=204004121 }}</ref> वीज़बर्ग मूल रूप से एलएआरएस को मान्य करने के लिए उपयोग किए गए डेटा के पुन: विश्लेषण के आधार पर एक अनुभवजन्य उदाहरण प्रदान करता है कि चर चयन में अत्यधिक सहसंबद्ध चर के साथ समस्याएं प्रतीत होती हैं। | ||
# चूंकि वास्तविक दुनिया में लगभग सभी [[उच्च आयामी डेटा]] संयोग से कम से कम कुछ चर में कुछ हद तक संरेखता प्रदर्शित करेंगे, | # चूंकि वास्तविक दुनिया में लगभग सभी [[उच्च आयामी डेटा]] संयोग से कम से कम कुछ चर में कुछ हद तक संरेखता प्रदर्शित करेंगे, एलएआरएस में सहसंबद्ध चर के साथ जो समस्या है, वह इसके अनुप्रयोग को उच्च आयामी डेटा तक सीमित कर सकती है। | ||
== | == कलन विधि == | ||
न्यूनतम-कोण प्रतिगमन | न्यूनतम-कोण प्रतिगमन कलन विधि के मूल चरण हैं: | ||
* सभी | * सभी गुणांक <math>\beta</math> शून्य के बराबर से प्रारंभ करें | ||
* भविष्यवक्ता | * भविष्यवक्ता <math>x_j</math> को <math>y</math> के साथ सबसे अधिक सहसंबद्ध खोजें। | ||
* गुणांक | * गुणांक <math>\beta_j</math> को <math>y</math> के साथ इसके सहसंबंध के चिह्न की दिशा में बढ़ाएँ। रास्ते में अवशिष्ट <math>r = y - \hat{y}</math> लें। रुकें जब किसी अन्य भविष्यवक्ता <math>x_k</math> का <math>r</math> के साथ उतना ही सहसंबंध हो जितना <math>x_{j}</math> का है। | ||
* | * (<math>\beta_j</math>, <math>\beta_k</math>) को उनके संयुक्त न्यूनतम वर्ग दिशा में बढ़ाएं, जब तक कि किसी अन्य भविष्यवक्ता <math>x_m</math> का अवशिष्ट <math>r</math> के साथ उतना सहसंबंध न हो। | ||
* | * (<math>\beta_j</math>, <math>\beta_k</math>, <math>\beta_m</math>) को उनके संयुक्त न्यूनतम वर्ग दिशा में बढ़ाएं, जब तक कि किसी अन्य भविष्यवक्ता <math>x_n</math> का अवशिष्ट <math>r</math> के साथ उतना सहसंबंध न हो । | ||
* तब तक जारी रखें जब तक: सभी भविष्यवक्ता | * तब तक जारी रखें जब तक: सभी भविष्यवक्ता प्रतिरूप में न आ जाएं। <ref>{{Cite web|url=http://statweb.stanford.edu/~tibs/lasso/simple.html|title=लैस्सो और न्यूनतम कोण प्रतिगमन की एक सरल व्याख्या|archive-url=https://web.archive.org/web/20150621032059/http://statweb.stanford.edu/~tibs/lasso/simple.html |archive-date=2015-06-21 }}</ref> | ||
== सॉफ्टवेयर कार्यान्वयन == | == सॉफ्टवेयर कार्यान्वयन == | ||
कम से कम कोण प्रतिगमन आर (भाषा) में [https://cran.r-project.org/web/packages/lars/index.html | कम से कम कोण प्रतिगमन आर (भाषा) में [https://cran.r-project.org/web/packages/lars/index.html एलएआरएस] पैकेज के माध्यम से, पायथन (भाषा) में प्रक्रिया के साथ कार्यान्वित किया जाता है। पैकेज, और एसएएस (सॉफ्टवेयर) में [https://support.sas.com/documentation/cdl/en के माध्यम से गलमसेलेक्ट है] | ||
==यह भी देखें== | ==यह भी देखें== | ||
| Line 72: | Line 72: | ||
* लैस्सो (सांख्यिकी) | * लैस्सो (सांख्यिकी) | ||
* [[प्रतिगमन विश्लेषण]] | * [[प्रतिगमन विश्लेषण]] | ||
* [[मॉडल चयन]] | * [[मॉडल चयन|प्रतिरूप चयन]] | ||
==संदर्भ== | ==संदर्भ== | ||
{{reflist}} | {{reflist}} | ||
{{DEFAULTSORT:Least-Angle Regression}} | {{DEFAULTSORT:Least-Angle Regression}} | ||
[[Category:All articles that are too technical|Least-Angle Regression]] | |||
[[Category:Articles with invalid date parameter in template|Least-Angle Regression]] | |||
[[Category: | [[Category:Created On 07/07/2023|Least-Angle Regression]] | ||
[[Category:Created On 07/07/2023]] | [[Category:Machine Translated Page|Least-Angle Regression]] | ||
[[Category:Pages with empty portal template|Least-Angle Regression]] | |||
[[Category:Pages with script errors|Least-Angle Regression]] | |||
[[Category:Portal-inline template with redlinked portals|Least-Angle Regression]] | |||
[[Category:Templates Vigyan Ready|Least-Angle Regression]] | |||
[[Category:Wikipedia articles that are too technical from April 2018|Least-Angle Regression]] | |||
[[Category:अनुमान सिद्धांत|Least-Angle Regression]] | |||
[[Category:एकल-समीकरण विधियाँ (अर्थमिति)|Least-Angle Regression]] | |||
[[Category:पैरामीट्रिक आँकड़े|Least-Angle Regression]] | |||
[[Category:प्रतिगमन चर चयन|Least-Angle Regression]] | |||
Latest revision as of 21:04, 15 July 2023
This article may be too technical for most readers to understand. (April 2018) (Learn how and when to remove this template message) |
| एक श्रृंखला का हिस्सा |
| प्रतिगमन विश्लेषण |
|---|
| मॉडल |
| अनुमान |
| पार्श्वभूमि |
|
|
आंकड़ों में, न्यूनतम-कोण प्रतिगमन (एलएआरएस) उच्च-आयामी डेटा के लिए रैखिक प्रतिगमन प्रतिरूप को अनुरूप करने के लिए एक कलन विधि है, जिसे ब्रैडली एफ्रॉन, ट्रेवर हेस्टी, इयान जॉनस्टोन (गणितज्ञ) और रॉबर्ट तिबशिरानी द्वारा विकसित किया गया है। [1]
मान लीजिए कि हम अपेक्षा करते हैं कि एक प्रतिक्रिया चर संभावित सहसंयोजकों के उपवर्ग के रैखिक संयोजन द्वारा निर्धारित किया जाएगा। फिर एलएआरएस कलन विधि अनुमान लगाने का एक साधन प्रदान करता है कि किन चरों को सम्मिलित किया जाए, साथ ही उनके गुणांक भी।
एक परिणाम देने के स्थान पर, एलएआरएस समाधान में पैरामीटर सदिश के L1 मानदंड के प्रत्येक मान के लिए समाधान को दर्शाने वाला एक वक्र होता है। कलन विधि फॉरवर्ड स्टेप चरणबद्ध प्रतिगमन के समान है, लेकिन प्रत्येक चरण में चर को सम्मिलित करने के स्थान पर, अनुमानित मापदंडों को अवशिष्ट के साथ प्रत्येक के सहसंबंध के समकोणीय दिशा में बढ़ाया जाता है।
लाभ और हानि
एलएआरएस पद्धति के लाभ हैं:
- यह कम्प्यूटेशनल रूप से फॉरवर्ड चयन जितना ही तीव्र है।
- यह एक पूर्ण टुकड़ा-वार रैखिक समाधान पथ तैयार करता है, जो क्रॉस-वैलिडेशन (सांख्यिकी) क्रॉस-वैलिडेशन या प्रतिरूप को ट्यून करने के समान प्रयासों में उपयोगी है।
- यदि दो चर प्रतिक्रिया के साथ लगभग समान रूप से सहसंबद्ध हैं, तो उनके गुणांक लगभग समान दर से बढ़ने चाहिए। इस प्रकार कलन विधि अंतर्ज्ञान की अपेक्षा के अनुरूप व्यवहार करता है, और अधिक स्थिर भी है।
- समान परिणाम देने वाली अन्य विधियों, जैसे लैस्सो (सांख्यिकी) और फॉरवर्ड स्टेजवाइज रिग्रेशन के लिए कुशल कलन विधि तैयार करने के लिए इसे आसानी से संशोधित किया जाता है।
- यह उन संदर्भों में प्रभावी है जहां पी ≫ एन (यानी, जब भविष्यवक्ताओं की संख्या पी अंक की संख्या से काफी अधिक है)[2]
एलएआरएस पद्धति के नुकसानों में सम्मिलित हैं:
- आश्रित चर में किसी भी मात्रा में लड़ाई और उच्च आयामी बहुसंरेखता स्वतंत्र चर के साथ, यह स्तिथि का कोई कारण नहीं है कि चयनित चर में वास्तविक अंतर्निहित कारण चर होने की उच्च संभावना होगी। यह समस्या एलएआरएस के लिए अद्वितीय नहीं है, क्योंकि यह परिवर्तनीय चयन दृष्टिकोण के साथ एक सामान्य समस्या है जो अंतर्निहित नियतात्मक घटकों को ढूंढना चाहती है। फिर भी, क्योंकि एलएआरएस अवशेषों की पुनरावृत्तीय साजोसामान पर आधारित है, यह लड़ाई के प्रभावों के प्रति विशेष रूप से संवेदनशील प्रतीत होता है। इस समस्या पर वीज़बर्ग द्वारा एफ्रॉन एट अल के चर्चा अनुभाग (2004) एनल्स ऑफ स्टैटिस्टिक्स लेख में विस्तार से चर्चा की गई है। [3] वीज़बर्ग मूल रूप से एलएआरएस को मान्य करने के लिए उपयोग किए गए डेटा के पुन: विश्लेषण के आधार पर एक अनुभवजन्य उदाहरण प्रदान करता है कि चर चयन में अत्यधिक सहसंबद्ध चर के साथ समस्याएं प्रतीत होती हैं।
- चूंकि वास्तविक दुनिया में लगभग सभी उच्च आयामी डेटा संयोग से कम से कम कुछ चर में कुछ हद तक संरेखता प्रदर्शित करेंगे, एलएआरएस में सहसंबद्ध चर के साथ जो समस्या है, वह इसके अनुप्रयोग को उच्च आयामी डेटा तक सीमित कर सकती है।
कलन विधि
न्यूनतम-कोण प्रतिगमन कलन विधि के मूल चरण हैं:
- सभी गुणांक शून्य के बराबर से प्रारंभ करें
- भविष्यवक्ता को के साथ सबसे अधिक सहसंबद्ध खोजें।
- गुणांक को के साथ इसके सहसंबंध के चिह्न की दिशा में बढ़ाएँ। रास्ते में अवशिष्ट लें। रुकें जब किसी अन्य भविष्यवक्ता का के साथ उतना ही सहसंबंध हो जितना का है।
- (, ) को उनके संयुक्त न्यूनतम वर्ग दिशा में बढ़ाएं, जब तक कि किसी अन्य भविष्यवक्ता का अवशिष्ट के साथ उतना सहसंबंध न हो।
- (, , ) को उनके संयुक्त न्यूनतम वर्ग दिशा में बढ़ाएं, जब तक कि किसी अन्य भविष्यवक्ता का अवशिष्ट के साथ उतना सहसंबंध न हो ।
- तब तक जारी रखें जब तक: सभी भविष्यवक्ता प्रतिरूप में न आ जाएं। [4]
सॉफ्टवेयर कार्यान्वयन
कम से कम कोण प्रतिगमन आर (भाषा) में एलएआरएस पैकेज के माध्यम से, पायथन (भाषा) में प्रक्रिया के साथ कार्यान्वित किया जाता है। पैकेज, और एसएएस (सॉफ्टवेयर) में के माध्यम से गलमसेलेक्ट है
यह भी देखें
- उच्च-आयामी आँकड़े
- लैस्सो (सांख्यिकी)
- प्रतिगमन विश्लेषण
- प्रतिरूप चयन
संदर्भ
- ↑ Efron, Bradley; Hastie, Trevor; Johnstone, Iain; Tibshirani, Robert (2004). "Least Angle Regression" (PDF). Annals of Statistics. 32 (2): pp. 407–499. arXiv:math/0406456. doi:10.1214/009053604000000067. MR 2060166. S2CID 204004121.
- ↑ Hastie, Trevor; Robert, Tibshirani; Jerome, Friedman (2009). The Elements of Statistical Learning Data Mining, Inference, and Prediction (2nd ed. 2009.) (PDF). Springer Series in Statistics. Springer New York. p. 76. doi:10.1007/978-0-387-84858-7. ISBN 978-0-387-84857-0.
- ↑ See Discussion by Weisberg following Efron, Bradley; Hastie, Trevor; Johnstone, Iain; Tibshirani, Robert (2004). "Least Angle Regression" (PDF). Annals of Statistics. 32 (2): pp. 407–499. arXiv:math/0406456. doi:10.1214/009053604000000067. MR 2060166. S2CID 204004121.
- ↑ "लैस्सो और न्यूनतम कोण प्रतिगमन की एक सरल व्याख्या". Archived from the original on 2015-06-21.