सामान्यीकृत सामान्य वितरण: Difference between revisions
No edit summary |
No edit summary |
||
| (4 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Probability distribution}} | {{Short description|Probability distribution}} | ||
'''सामान्यीकृत [[सामान्य वितरण|सामान्य बंटन]]''' या '''सामान्यीकृत गॉसियन बंटन (जीजीडी)''' वास्तविक रेखा पर पैरामीट्रिक निरंतर संभाव्यता बंटन के दो कुलों में से एक है। दोनों कुल सामान्य बंटन में एक आकृति | '''सामान्यीकृत [[सामान्य वितरण|सामान्य बंटन]]''' या '''सामान्यीकृत गॉसियन बंटन (जीजीडी)''' वास्तविक रेखा पर पैरामीट्रिक निरंतर संभाव्यता बंटन के दो कुलों में से एक है। दोनों कुल सामान्य बंटन में एक आकृति प्राचल जोड़ते हैं। दोनों कुलों को अलग करने के लिए, उन्हें नीचे "सममित" और "असममित" कहा गया है; हालाँकि, यह मानक नामकरण नहीं है। | ||
==सममित संस्करण | ==सममित संस्करण== | ||
{{Probability distribution | | {{Probability distribution | | ||
| Line 30: | Line 30: | ||
}} | }} | ||
'''सममित सामान्यीकृत सामान्य बंटन''', जिसे '''चरघातांकी घातीय बंटन''' या सामान्यीकृत त्रुटि बंटन के रूप में भी जाना जाता है, सममित बंटन का पैरामीट्रिक कुल है। इसमें सभी सामान्य और [[लाप्लास वितरण|लाप्लास बंटन]] सम्मिलित हैं, और सीमित | '''सममित सामान्यीकृत सामान्य बंटन''', जिसे '''चरघातांकी घातीय बंटन''' या सामान्यीकृत त्रुटि बंटन के रूप में भी जाना जाता है, सममित बंटन का पैरामीट्रिक कुल है। इसमें सभी सामान्य और [[लाप्लास वितरण|लाप्लास बंटन]] सम्मिलित हैं, और सीमित स्तिथि के रूप में, इसमें वास्तविक रेखा के सीमित अंतराल पर सभी [[निरंतर समान वितरण|निरंतर समान बंटन]] सम्मिलित हैं। | ||
इस कुल में सामान्य बंटन सम्मिलित है जब <math>\textstyle\beta=2</math> (माध्य <math>\textstyle\mu</math> और भिन्नता <math>\textstyle \frac{\alpha^2}{2}</math>} के साथ) और इसमें लाप्लास बंटन सम्मिलित है जब <math>\textstyle\beta=1</math>। <math>\textstyle\beta\rightarrow\infty</math> के रूप में, घनत्व <math>\textstyle (\mu-\alpha,\mu+\alpha)</math> पर बिंदुवार एक समान घनत्व में परिवर्तित हो जाता है। | इस कुल में सामान्य बंटन सम्मिलित है जब <math>\textstyle\beta=2</math> (माध्य <math>\textstyle\mu</math> और भिन्नता <math>\textstyle \frac{\alpha^2}{2}</math>} के साथ) और इसमें लाप्लास बंटन सम्मिलित है जब <math>\textstyle\beta=1</math>। <math>\textstyle\beta\rightarrow\infty</math> के रूप में, घनत्व <math>\textstyle (\mu-\alpha,\mu+\alpha)</math> पर बिंदुवार एक समान घनत्व में परिवर्तित हो जाता है। | ||
यह कुल ऐसी पट की अनुमति देता है जो या तो सामान्य से अधिक भारी होती हैं (जब <math>\beta<2</math>) या सामान्य से हल्की होती हैं (जब <math>\beta>2</math>)। यह सामान्य (<math>\textstyle\beta=2</math>) से एकसमान घनत्व तक फैले सममित, प्लैटीकर्टिक घनत्वों की सातत्यता को पैरामीट्रिज करने का एक उपयोगी तरीका है। (<math>\textstyle\beta=\infty</math>), और लाप्लास (<math>\textstyle\beta=1</math>) से सामान्य घनत्व ( <math>\textstyle\beta=2</math>) तक फैले सममित, लेप्टोकर्टिक घनत्वों की एक निरंतरता। आकार | यह कुल ऐसी पट की अनुमति देता है जो या तो सामान्य से अधिक भारी होती हैं (जब <math>\beta<2</math>) या सामान्य से हल्की होती हैं (जब <math>\beta>2</math>)। यह सामान्य (<math>\textstyle\beta=2</math>) से एकसमान घनत्व तक फैले सममित, प्लैटीकर्टिक घनत्वों की सातत्यता को पैरामीट्रिज करने का एक उपयोगी तरीका है। (<math>\textstyle\beta=\infty</math>), और लाप्लास (<math>\textstyle\beta=1</math>) से सामान्य घनत्व ( <math>\textstyle\beta=2</math>) तक फैले सममित, लेप्टोकर्टिक घनत्वों की एक निरंतरता। आकार प्राचल <math>\beta</math> पट के अतिरिक्त शिखरता को भी नियंत्रित करता है। | ||
=== | ===प्राचल अनुमान=== | ||
अधिकतम संभावना और क्षणों की विधि के माध्यम से | अधिकतम संभावना और क्षणों की विधि के माध्यम से प्राचल अनुमान का अध्ययन किया गया है।<ref>{{cite journal |last= Varanasi |first= M.K. |author2=Aazhang, B. |date=October 1989|title= पैरामीट्रिक सामान्यीकृत गाऊसी घनत्व अनुमान|journal= Journal of the Acoustical Society of America|volume= 86|issue= 4|pages= 1404–1415|doi= 10.1121/1.398700|bibcode= 1989ASAJ...86.1404V }}</ref> अनुमानों का कोई बंद रूप नहीं है और उन्हें संख्यात्मक रूप से प्राप्त किया जाना चाहिए। ऐसे अनुमानकर्ता भी प्रस्तावित किए गए हैं जिन्हें संख्यात्मक गणना की आवश्यकता नहीं है।<ref> | ||
{{cite journal |last= Domínguez-Molina |first= J. Armando|author2=González-Farías, Graciela|author2-link=Graciela González Farías |author3=Rodríguez-Dagnino, Ramón M. | title= A practical procedure to estimate the shape parameter in the generalized Gaussian distribution | url= http://www.cimat.mx/reportes/enlinea/I-01-18_eng.pdf |access-date=2009-03-03 }}</ref> | {{cite journal |last= Domínguez-Molina |first= J. Armando|author2=González-Farías, Graciela|author2-link=Graciela González Farías |author3=Rodríguez-Dagnino, Ramón M. | title= A practical procedure to estimate the shape parameter in the generalized Gaussian distribution | url= http://www.cimat.mx/reportes/enlinea/I-01-18_eng.pdf |access-date=2009-03-03 }}</ref> | ||
सामान्यीकृत सामान्य लॉग-संभावना फलन में अनंत रूप से कई निरंतर व्युत्पन्न होते हैं (यानी यह सुचारू कार्यों के वर्ग C∞ से संबंधित होता है) केवल तभी जब β एक धनात्मक, सम पूर्णांक है। अन्यथा, फलन में <math>\textstyle\lfloor \beta \rfloor</math>निरंतर डेरिवेटिव हैं। परिणामस्वरूप, <math>\beta</math> की अधिकतम संभावना अनुमानों की स्थिरता और स्पर्शोन्मुख सामान्यता के लिए मानक परिणाम केवल तभी | सामान्यीकृत सामान्य लॉग-संभावना फलन में अनंत रूप से कई निरंतर व्युत्पन्न होते हैं (यानी यह सुचारू कार्यों के वर्ग C∞ से संबंधित होता है) केवल तभी जब β एक धनात्मक, सम पूर्णांक है। अन्यथा, फलन में <math>\textstyle\lfloor \beta \rfloor</math>निरंतर डेरिवेटिव हैं। परिणामस्वरूप, <math>\beta</math> की अधिकतम संभावना अनुमानों की स्थिरता और स्पर्शोन्मुख सामान्यता के लिए मानक परिणाम केवल तभी प्रयुक्त होते जब <math>\textstyle\beta\ge 2</math> हैं । | ||
==== अधिकतम संभावना अनुमानक ==== | ==== अधिकतम संभावना अनुमानक ==== | ||
| Line 98: | Line 98: | ||
==== क्षण ==== | ==== क्षण ==== | ||
मान लीजिए कि <math> X_\beta </math> आकृति <math> \beta </math> और स्केलिंग | मान लीजिए कि <math> X_\beta </math> आकृति <math> \beta </math> और स्केलिंग प्राचल <math> \alpha </math> का शून्य माध्य सामान्यीकृत गाऊसी बंटन है। <math> X_\beta </math> के परिमित उपस्थित हैं और −1 से बड़े किसी भी k के लिए सीमित हैं। किसी भी गैर-ऋणात्मक पूर्णांक k के लिए, सादे केंद्रीय क्षण हैं<ref name="Nadarajah" /> | ||
: <math> | : <math> | ||
| Line 109: | Line 109: | ||
==== स्थैतिक गणना बंटन से संपर्क ==== | ==== स्थैतिक गणना बंटन से संपर्क ==== | ||
स्थिर गिनती बंटन के दृष्टिकोण से, <math> \beta </math> को लेवी की स्थिरता | स्थिर गिनती बंटन के दृष्टिकोण से, <math> \beta </math> को लेवी की स्थिरता प्राचल के रूप में माना जा सकता है। इस बंटन को कर्नेल घनत्व के अभिन्न अंग में विघटित किया जा सकता है जहां कर्नेल या तो लाप्लास बंटन या गॉसियन [[गाऊसी वितरण|बंटन]] है: | ||
: <math> | : <math> | ||
| Line 172: | Line 172: | ||
}}</ref> | }}</ref> | ||
===सामान्यीकरण === | ===सामान्यीकरण === | ||
बहुभिन्नरूपी सामान्यीकृत सामान्य बंटन, यानी का उत्पाद <math>n</math> उसी के साथ घातीय घात बंटन <math>\beta</math> और <math>\alpha</math> | बहुभिन्नरूपी सामान्यीकृत सामान्य बंटन, यानी का उत्पाद <math>n</math> उसी के साथ घातीय घात बंटन <math>\beta</math> और <math>\alpha</math> प्राचल, एकमात्र संभाव्यता घनत्व है जिसे फॉर्म में लिखा जा सकता है <math>p(\mathbf x)=g(\|\mathbf x\|_\beta)</math> और स्वतंत्र सीमांत हैं।<ref>{{cite journal |last= Sinz|first= Fabian|author2=Gerwinn, Sebastian |author3=Bethge, Matthias | ||
|date=May 2009|title=पी-सामान्यीकृत सामान्य वितरण की विशेषता।|journal=Journal of Multivariate Analysis|volume= 100|issue= 5|pages= 817–820|doi=10.1016/j.jmva.2008.07.006|doi-access=free}}</ref> [[बहुभिन्नरूपी सामान्य वितरण|बहुभिन्नरूपी सामान्य बंटन]] के विशेष स्तिथि के परिणामों का श्रेय मूल रूप से [[जेम्स क्लर्क मैक्सवेल]] को दिया जाता है।<ref>{{cite journal |last= Kac|first= M.|year= 1939|title=सामान्य वितरण के लक्षण वर्णन पर|journal=American Journal of Mathematics|volume= 61|issue= 3|pages= 726–728|doi= 10.2307/2371328 |jstor= 2371328}}</ref> | |date=May 2009|title=पी-सामान्यीकृत सामान्य वितरण की विशेषता।|journal=Journal of Multivariate Analysis|volume= 100|issue= 5|pages= 817–820|doi=10.1016/j.jmva.2008.07.006|doi-access=free}}</ref> [[बहुभिन्नरूपी सामान्य वितरण|बहुभिन्नरूपी सामान्य बंटन]] के विशेष स्तिथि के परिणामों का श्रेय मूल रूप से [[जेम्स क्लर्क मैक्सवेल]] को दिया जाता है।<ref>{{cite journal |last= Kac|first= M.|year= 1939|title=सामान्य वितरण के लक्षण वर्णन पर|journal=American Journal of Mathematics|volume= 61|issue= 3|pages= 726–728|doi= 10.2307/2371328 |jstor= 2371328}}</ref> | ||
==असममित संस्करण== | ==असममित संस्करण== | ||
| Line 197: | Line 197: | ||
{{distinguish|सामान्य बंटन विषमता}} | {{distinguish|सामान्य बंटन विषमता}} | ||
असममित सामान्यीकृत सामान्य बंटन निरंतर संभाव्यता बंटन का एक कुल है जिसमें आकार | असममित सामान्यीकृत सामान्य बंटन निरंतर संभाव्यता बंटन का एक कुल है जिसमें आकार प्राचल का उपयोग विषमता या स्क्यूपन पेश करने के लिए किया जा सकता है।<ref>Hosking, J.R.M., Wallis, J.R. (1997) ''Regional frequency analysis: an approach based on L-moments'', Cambridge University Press. {{ISBN|0-521-43045-3}}. Section A.8</ref><ref>[http://www.cran.r-project.org/web/packages/lmomco/lmomco.pdf Documentation for the lmomco R package]</ref> जब आकार प्राचल शून्य होता है, तो सामान्य बंटन परिणाम होता है। आकार प्राचल के धनात्मक मान दाईं ओर बंधे बाएं-तिरछे बंटन उत्पन्न करते हैं, और आकार प्राचल के ऋणात्मक मान बाईं ओर बंधे दाएं- सम्मिश्र बंटन उत्पन्न करते हैं। केवल जब आकार प्राचल शून्य होता है, तो इस बंटन के लिए घनत्व फलन पूरी वास्तविक रेखा पर धनात्मक होता है: इस स्तिथि में बंटन एक सामान्य बंटन है, अन्यथा बंटन स्थानांतरित हो जाते हैं और संभवतः [[लॉग-सामान्य वितरण|लॉग-सामान्य बंटन]] उलट जाते हैं। | ||
=== | ===प्राचल अनुमान=== | ||
पैरामीटर्स का अनुमान अधिकतम संभावना अनुमान या क्षणों की विधि के माध्यम से लगाया जा सकता है। | पैरामीटर्स का अनुमान अधिकतम संभावना अनुमान या क्षणों की विधि के माध्यम से लगाया जा सकता है। प्राचल अनुमानों का कोई बंद रूप नहीं होता है, इसलिए अनुमानों की गणना के लिए संख्यात्मक गणना का उपयोग किया जाना चाहिए। चूंकि नमूना स्थान (वास्तविक संख्याओं का सेट जहां घनत्व गैर-शून्य है) प्राचल के वास्तविक मूल्य पर निर्भर करता है, इस कुल के साथ काम करते समय प्राचल अनुमानों के प्रदर्शन के बारे में कुछ मानक परिणाम स्वचालित रूप से प्रयुक्त नहीं होंगे। | ||
===अनुप्रयोग=== | ===अनुप्रयोग=== | ||
असममित सामान्यीकृत सामान्य बंटन का उपयोग उन मानों को मॉडल करने के लिए किया जा सकता है जिन्हें सामान्य रूप से वितरित किया जा सकता है, या जो सामान्य बंटन के सापेक्ष दाएं- | असममित सामान्यीकृत सामान्य बंटन का उपयोग उन मानों को मॉडल करने के लिए किया जा सकता है जिन्हें सामान्य रूप से वितरित किया जा सकता है, या जो सामान्य बंटन के सापेक्ष दाएं-स्क्यू या बाएं-स्क्यू हो सकता है। स्क्यू सामान्य बंटन एक और बंटन है जो स्क्यू होने के कारण सामान्यता से विचलन के मॉडलिंग के लिए उपयोगी है। विषम डेटा को मॉडल करने के लिए उपयोग किए जाने वाले अन्य वितरणों में [[गामा वितरण|गामा बंटन]], [[लॉगनॉर्मल वितरण|लॉगनॉर्मल बंटन]] और वेइबुल बंटन सम्मिलित हैं, लेकिन इनमें विशेष स्तिथि के रूप में सामान्य बंटन सम्मिलित नहीं हैं। | ||
==सामान्य से संबंधित अन्य बंटन== | ==सामान्य से संबंधित अन्य बंटन== | ||
यहां वर्णित दो सामान्यीकृत सामान्य परिवार, | यहां वर्णित दो सामान्यीकृत सामान्य परिवार, स्क्यू सामान्य परिवार की तरह, पैरामीट्रिक परिवार हैं जो आकार प्राचल जोड़कर सामान्य बंटन का विस्तार करते हैं। संभाव्यता और आंकड़ों में सामान्य बंटन की केंद्रीय भूमिका के कारण, कई वितरणों को सामान्य बंटन से उनके संबंध के संदर्भ में चित्रित किया जा सकता है। उदाहरण के लिए, लॉग-सामान्य, मुड़े हुए सामान्य और व्युत्क्रम सामान्य बंटन को सामान्य रूप से वितरित मूल्य के परिवर्तनों के रूप में परिभाषित किया जाता है, लेकिन सामान्यीकृत सामान्य और स्क्यू-सामान्य परिवारों के विपरीत, इनमें विशेष स्तिथि के रूप में सामान्य बंटन सम्मिलित नहीं होते हैं। | ||
वास्तव में, परिमित विचरण वाले सभी बंटन सामान्य बंटन से अत्यधिक संबंधित सीमा में होते हैं। छात्र-टी बंटन, इरविन-हॉल बंटन और बेट्स बंटन भी सामान्य बंटन का विस्तार करते हैं और सामान्य बंटन की सीमा में सम्मिलित होते हैं। इसलिए प्रकार 1 के "सामान्यीकृत" सामान्य बंटन को प्राथमिकता देने का कोई मजबूत कारण नहीं है, उदाहरण के लिए। स्टूडेंट-टी और सामान्यीकृत विस्तारित इरविन-हॉल के संयोजन पर - इसमें उदाहरण सम्मिलित होगा। त्रिकोणीय बंटन (जिसे सामान्यीकृत गाऊसी प्रकार 1 द्वारा प्रतिरूपित नहीं किया जा सकता)। | वास्तव में, परिमित विचरण वाले सभी बंटन सामान्य बंटन से अत्यधिक संबंधित सीमा में होते हैं। छात्र-टी बंटन, इरविन-हॉल बंटन और बेट्स बंटन भी सामान्य बंटन का विस्तार करते हैं और सामान्य बंटन की सीमा में सम्मिलित होते हैं। इसलिए प्रकार 1 के "सामान्यीकृत" सामान्य बंटन को प्राथमिकता देने का कोई मजबूत कारण नहीं है, उदाहरण के लिए। स्टूडेंट-टी और सामान्यीकृत विस्तारित इरविन-हॉल के संयोजन पर - इसमें उदाहरण सम्मिलित होगा। त्रिकोणीय बंटन (जिसे सामान्यीकृत गाऊसी प्रकार 1 द्वारा प्रतिरूपित नहीं किया जा सकता)। | ||
| Line 216: | Line 216: | ||
==यह भी देखें== | ==यह भी देखें== | ||
* [[जटिल सामान्य वितरण| | * [[जटिल सामान्य वितरण|सम्मिश्र सामान्य बंटन]] | ||
* | * विषम (स्क्यू) सामान्य बंटन | ||
==संदर्भ== | ==संदर्भ== | ||
{{Reflist}} | {{Reflist}} | ||
{{ | {{DEFAULTSORT:Generalized Normal Distribution}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page|Generalized Normal Distribution]] | |||
[[Category:CS1 errors]] | |||
[[Category:Created On 07/07/2023|Generalized Normal Distribution]] | |||
[[Category:Lua-based templates|Generalized Normal Distribution]] | |||
[[Category: Machine Translated Page]] | [[Category:Machine Translated Page|Generalized Normal Distribution]] | ||
[[Category: | [[Category:Pages with script errors|Generalized Normal Distribution]] | ||
[[Category:Templates Vigyan Ready|Generalized Normal Distribution]] | |||
[[Category:Templates that add a tracking category|Generalized Normal Distribution]] | |||
[[Category:Templates that generate short descriptions|Generalized Normal Distribution]] | |||
[[Category:Templates using TemplateData|Generalized Normal Distribution]] | |||
[[Category:निरंतर वितरण|Generalized Normal Distribution]] | |||
[[Category:सामान्य वितरण| सामान्य वितरण]] | |||
Latest revision as of 19:25, 21 July 2023
सामान्यीकृत सामान्य बंटन या सामान्यीकृत गॉसियन बंटन (जीजीडी) वास्तविक रेखा पर पैरामीट्रिक निरंतर संभाव्यता बंटन के दो कुलों में से एक है। दोनों कुल सामान्य बंटन में एक आकृति प्राचल जोड़ते हैं। दोनों कुलों को अलग करने के लिए, उन्हें नीचे "सममित" और "असममित" कहा गया है; हालाँकि, यह मानक नामकरण नहीं है।
सममित संस्करण
|
Probability density function 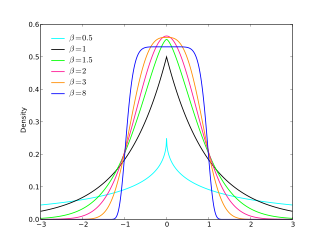 | |||
|
Cumulative distribution function  | |||
| Parameters |
location (real) scale (positive, real) shape (positive, real) | ||
|---|---|---|---|
| Support | |||
|
| |||
| CDF |
where is a shape parameter, is a scale parameter and is the unnormalized incomplete lower gamma function. | ||
| Quantile |
| ||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | 0 | ||
| Ex. kurtosis | |||
| Entropy | [2] | ||
सममित सामान्यीकृत सामान्य बंटन, जिसे चरघातांकी घातीय बंटन या सामान्यीकृत त्रुटि बंटन के रूप में भी जाना जाता है, सममित बंटन का पैरामीट्रिक कुल है। इसमें सभी सामान्य और लाप्लास बंटन सम्मिलित हैं, और सीमित स्तिथि के रूप में, इसमें वास्तविक रेखा के सीमित अंतराल पर सभी निरंतर समान बंटन सम्मिलित हैं।
इस कुल में सामान्य बंटन सम्मिलित है जब (माध्य और भिन्नता } के साथ) और इसमें लाप्लास बंटन सम्मिलित है जब । के रूप में, घनत्व पर बिंदुवार एक समान घनत्व में परिवर्तित हो जाता है।
यह कुल ऐसी पट की अनुमति देता है जो या तो सामान्य से अधिक भारी होती हैं (जब ) या सामान्य से हल्की होती हैं (जब )। यह सामान्य () से एकसमान घनत्व तक फैले सममित, प्लैटीकर्टिक घनत्वों की सातत्यता को पैरामीट्रिज करने का एक उपयोगी तरीका है। (), और लाप्लास () से सामान्य घनत्व ( ) तक फैले सममित, लेप्टोकर्टिक घनत्वों की एक निरंतरता। आकार प्राचल पट के अतिरिक्त शिखरता को भी नियंत्रित करता है।
प्राचल अनुमान
अधिकतम संभावना और क्षणों की विधि के माध्यम से प्राचल अनुमान का अध्ययन किया गया है।[3] अनुमानों का कोई बंद रूप नहीं है और उन्हें संख्यात्मक रूप से प्राप्त किया जाना चाहिए। ऐसे अनुमानकर्ता भी प्रस्तावित किए गए हैं जिन्हें संख्यात्मक गणना की आवश्यकता नहीं है।[4]
सामान्यीकृत सामान्य लॉग-संभावना फलन में अनंत रूप से कई निरंतर व्युत्पन्न होते हैं (यानी यह सुचारू कार्यों के वर्ग C∞ से संबंधित होता है) केवल तभी जब β एक धनात्मक, सम पूर्णांक है। अन्यथा, फलन में निरंतर डेरिवेटिव हैं। परिणामस्वरूप, की अधिकतम संभावना अनुमानों की स्थिरता और स्पर्शोन्मुख सामान्यता के लिए मानक परिणाम केवल तभी प्रयुक्त होते जब हैं ।
अधिकतम संभावना अनुमानक
अनुमानित अधिकतम संभावना पद्धति को अपनाकर सामान्यीकृत सामान्य बंटन को फिट करना संभव है।[5][6] को आरंभ में नमूना प्रथम क्षण पर सेट करने के साथ, का अनुमान न्यूटन-रेफसन पुनरावृत्त प्रक्रिया का उपयोग करके किया जाता है, जो के प्रारंभिक अनुमान से प्रारम्भ होता है,
जहाँ
निरपेक्ष मूल्यों का पहला सांख्यिकीय क्षण (गणित) है और दूसरा सांख्यिकीय क्षण (गणित) है। पुनरावृत्ति है
जहाँ
और
और जहाँ और डिगामा फलन और ट्राइगामा फलन हैं।
के लिए एक मान दिया गया है , अनुमान लगाना संभव है न्यूनतम ज्ञात करके:
आखिरकार के रूप में मूल्यांकन किया जाता है
के लिए, माध्यिका का अधिक उपयुक्त अनुमानक है। एक बार जब का अनुमान लगाया जाता है, तो और का अनुमान लगाया जा सकता है जैसा कि ऊपर वर्णित है।[7]
अनुप्रयोग
सममित सामान्यीकृत सामान्य बंटन का उपयोग मॉडलिंग में किया गया है जब माध्य और पट व्यवहार के आसपास मूल्यों की एकाग्रता विशेष रुचि रखती है।[8][9] यदि सामान्यता से अन्य विचलनों पर ध्यान केंद्रित किया जाता है तो बंटन के अन्य कुलों का उपयोग किया जा सकता है। यदि बंटन की समरूपता मुख्य रुचि है, तो नीचे चर्चा की गई सामान्यीकृत सामान्य कुल के विषम सामान्य कुल या असममित संस्करण का उपयोग किया जा सकता है। यदि पट का व्यवहार मुख्य रुचि है, तो छात्र t कुल का उपयोग किया जा सकता है, जो स्वतंत्रता की डिग्री अनंत तक बढ़ने पर सामान्य बंटन का अनुमान लगाता है। t बंटन, इस सामान्यीकृत सामान्य बंटन के विपरीत, मूल पर पुच्छ प्राप्त किए बिना सामान्य पट की तुलना में भारी हो जाता है।
गुण
क्षण
मान लीजिए कि आकृति और स्केलिंग प्राचल का शून्य माध्य सामान्यीकृत गाऊसी बंटन है। के परिमित उपस्थित हैं और −1 से बड़े किसी भी k के लिए सीमित हैं। किसी भी गैर-ऋणात्मक पूर्णांक k के लिए, सादे केंद्रीय क्षण हैं[2]
स्थैतिक गणना बंटन से संपर्क
स्थिर गिनती बंटन के दृष्टिकोण से, को लेवी की स्थिरता प्राचल के रूप में माना जा सकता है। इस बंटन को कर्नेल घनत्व के अभिन्न अंग में विघटित किया जा सकता है जहां कर्नेल या तो लाप्लास बंटन या गॉसियन बंटन है:
जहां स्थिर गणना बंटन है और स्थिर वोल बंटन है।
धनात्मक-निश्चित फलनों से संबंध
सममित सामान्यीकृत सामान्य बंटन का संभाव्यता घनत्व फलन धनात्मक-निश्चित फलन है .[10][11]
अनंत विभाज्यता
सममित सामान्यीकृत गॉसियन बंटन असीम रूप से विभाज्य बंटन है यदि और केवल यदि .[12]
सामान्यीकरण
बहुभिन्नरूपी सामान्यीकृत सामान्य बंटन, यानी का उत्पाद उसी के साथ घातीय घात बंटन और प्राचल, एकमात्र संभाव्यता घनत्व है जिसे फॉर्म में लिखा जा सकता है और स्वतंत्र सीमांत हैं।[13] बहुभिन्नरूपी सामान्य बंटन के विशेष स्तिथि के परिणामों का श्रेय मूल रूप से जेम्स क्लर्क मैक्सवेल को दिया जाता है।[14]
असममित संस्करण
 | |||
|
Cumulative distribution function  | |||
| Parameters |
location (real) scale (positive, real) shape (real) | ||
|---|---|---|---|
| Support |
| ||
| Unknown type |
, where is the standard normal pdf | ||
| CDF |
, where is the standard normal CDF | ||
| Mean | |||
| Median | |||
| Unknown type | |||
| Skewness | |||
| Ex. kurtosis | |||
असममित सामान्यीकृत सामान्य बंटन निरंतर संभाव्यता बंटन का एक कुल है जिसमें आकार प्राचल का उपयोग विषमता या स्क्यूपन पेश करने के लिए किया जा सकता है।[15][16] जब आकार प्राचल शून्य होता है, तो सामान्य बंटन परिणाम होता है। आकार प्राचल के धनात्मक मान दाईं ओर बंधे बाएं-तिरछे बंटन उत्पन्न करते हैं, और आकार प्राचल के ऋणात्मक मान बाईं ओर बंधे दाएं- सम्मिश्र बंटन उत्पन्न करते हैं। केवल जब आकार प्राचल शून्य होता है, तो इस बंटन के लिए घनत्व फलन पूरी वास्तविक रेखा पर धनात्मक होता है: इस स्तिथि में बंटन एक सामान्य बंटन है, अन्यथा बंटन स्थानांतरित हो जाते हैं और संभवतः लॉग-सामान्य बंटन उलट जाते हैं।
प्राचल अनुमान
पैरामीटर्स का अनुमान अधिकतम संभावना अनुमान या क्षणों की विधि के माध्यम से लगाया जा सकता है। प्राचल अनुमानों का कोई बंद रूप नहीं होता है, इसलिए अनुमानों की गणना के लिए संख्यात्मक गणना का उपयोग किया जाना चाहिए। चूंकि नमूना स्थान (वास्तविक संख्याओं का सेट जहां घनत्व गैर-शून्य है) प्राचल के वास्तविक मूल्य पर निर्भर करता है, इस कुल के साथ काम करते समय प्राचल अनुमानों के प्रदर्शन के बारे में कुछ मानक परिणाम स्वचालित रूप से प्रयुक्त नहीं होंगे।
अनुप्रयोग
असममित सामान्यीकृत सामान्य बंटन का उपयोग उन मानों को मॉडल करने के लिए किया जा सकता है जिन्हें सामान्य रूप से वितरित किया जा सकता है, या जो सामान्य बंटन के सापेक्ष दाएं-स्क्यू या बाएं-स्क्यू हो सकता है। स्क्यू सामान्य बंटन एक और बंटन है जो स्क्यू होने के कारण सामान्यता से विचलन के मॉडलिंग के लिए उपयोगी है। विषम डेटा को मॉडल करने के लिए उपयोग किए जाने वाले अन्य वितरणों में गामा बंटन, लॉगनॉर्मल बंटन और वेइबुल बंटन सम्मिलित हैं, लेकिन इनमें विशेष स्तिथि के रूप में सामान्य बंटन सम्मिलित नहीं हैं।
सामान्य से संबंधित अन्य बंटन
यहां वर्णित दो सामान्यीकृत सामान्य परिवार, स्क्यू सामान्य परिवार की तरह, पैरामीट्रिक परिवार हैं जो आकार प्राचल जोड़कर सामान्य बंटन का विस्तार करते हैं। संभाव्यता और आंकड़ों में सामान्य बंटन की केंद्रीय भूमिका के कारण, कई वितरणों को सामान्य बंटन से उनके संबंध के संदर्भ में चित्रित किया जा सकता है। उदाहरण के लिए, लॉग-सामान्य, मुड़े हुए सामान्य और व्युत्क्रम सामान्य बंटन को सामान्य रूप से वितरित मूल्य के परिवर्तनों के रूप में परिभाषित किया जाता है, लेकिन सामान्यीकृत सामान्य और स्क्यू-सामान्य परिवारों के विपरीत, इनमें विशेष स्तिथि के रूप में सामान्य बंटन सम्मिलित नहीं होते हैं।
वास्तव में, परिमित विचरण वाले सभी बंटन सामान्य बंटन से अत्यधिक संबंधित सीमा में होते हैं। छात्र-टी बंटन, इरविन-हॉल बंटन और बेट्स बंटन भी सामान्य बंटन का विस्तार करते हैं और सामान्य बंटन की सीमा में सम्मिलित होते हैं। इसलिए प्रकार 1 के "सामान्यीकृत" सामान्य बंटन को प्राथमिकता देने का कोई मजबूत कारण नहीं है, उदाहरण के लिए। स्टूडेंट-टी और सामान्यीकृत विस्तारित इरविन-हॉल के संयोजन पर - इसमें उदाहरण सम्मिलित होगा। त्रिकोणीय बंटन (जिसे सामान्यीकृत गाऊसी प्रकार 1 द्वारा प्रतिरूपित नहीं किया जा सकता)।
एक सममित बंटन जो पट (छोटा और लंबा) और केंद्र व्यवहार (जैसे फ्लैट, त्रिकोणीय या गाऊसी) दोनों को पूरी तरह से स्वतंत्र रूप से मॉडल कर सकता है, उदाहरण के लिए X = IH/chi का उपयोग करके प्राप्त किया जा सकता है।
यह भी देखें
- सम्मिश्र सामान्य बंटन
- विषम (स्क्यू) सामान्य बंटन
संदर्भ
- ↑ Griffin, Maryclare. "Working with the Exponential Power Distribution Using gnorm". Github, gnorm package. Retrieved 26 June 2020.
- ↑ 2.0 2.1 Nadarajah, Saralees (September 2005). "A generalized normal distribution". Journal of Applied Statistics. 32 (7): 685–694. doi:10.1080/02664760500079464. S2CID 121914682.
- ↑ Varanasi, M.K.; Aazhang, B. (October 1989). "पैरामीट्रिक सामान्यीकृत गाऊसी घनत्व अनुमान". Journal of the Acoustical Society of America. 86 (4): 1404–1415. Bibcode:1989ASAJ...86.1404V. doi:10.1121/1.398700.
- ↑
Domínguez-Molina, J. Armando; González-Farías, Graciela; Rodríguez-Dagnino, Ramón M. "A practical procedure to estimate the shape parameter in the generalized Gaussian distribution" (PDF). Retrieved 2009-03-03.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Varanasi, M.K.; Aazhang B. (1989). "पैरामीट्रिक सामान्यीकृत गाऊसी घनत्व अनुमान". J. Acoust. Soc. Am. 86 (4): 1404–1415. Bibcode:1989ASAJ...86.1404V. doi:10.1121/1.398700.
- ↑ Do, M.N.; Vetterli, M. (February 2002). "सामान्यीकृत गाऊसी घनत्व और कुल्बैक-लीबलर दूरी का उपयोग करके वेवलेट-आधारित बनावट पुनर्प्राप्ति". Transaction on Image Processing. 11 (2): 146–158. Bibcode:2002ITIP...11..146D. doi:10.1109/83.982822. PMID 18244620.
- ↑ Varanasi, Mahesh K.; Aazhang, Behnaam (1989-10-01). "पैरामीट्रिक सामान्यीकृत गाऊसी घनत्व अनुमान". The Journal of the Acoustical Society of America. 86 (4): 1404–1415. Bibcode:1989ASAJ...86.1404V. doi:10.1121/1.398700. ISSN 0001-4966.
- ↑ Liang, Faming; Liu, Chuanhai; Wang, Naisyin (April 2007). "A robust sequential Bayesian method for identification of differentially expressed genes". Statistica Sinica. 17 (2): 571–597. Archived from the original on 2007-10-09. Retrieved 2009-03-03.
- ↑ Box, George E. P.; Tiao, George C. (1992). Bayesian Inference in Statistical Analysis. New York: Wiley. ISBN 978-0-471-57428-6.
- ↑ Dytso, Alex; Bustin, Ronit; Poor, H. Vincent; Shamai, Shlomo (2018). "Analytical properties of generalized Gaussian distributions". Journal of Statistical Distributions and Applications. 5 (1): 6. doi:10.1186/s40488-018-0088-5.
- ↑ Bochner, Salomon (1937). "Stable laws of probability and completely monotone functions". Duke Mathematical Journal. 3 (4): 726–728. doi:10.1215/s0012-7094-37-00360-0.
- ↑ Dytso, Alex; Bustin, Ronit; Poor, H. Vincent; Shamai, Shlomo (2018). "Analytical properties of generalized Gaussian distributions". Journal of Statistical Distributions and Applications. 5 (1): 6. doi:10.1186/s40488-018-0088-5.
- ↑ Sinz, Fabian; Gerwinn, Sebastian; Bethge, Matthias (May 2009). "पी-सामान्यीकृत सामान्य वितरण की विशेषता।". Journal of Multivariate Analysis. 100 (5): 817–820. doi:10.1016/j.jmva.2008.07.006.
- ↑ Kac, M. (1939). "सामान्य वितरण के लक्षण वर्णन पर". American Journal of Mathematics. 61 (3): 726–728. doi:10.2307/2371328. JSTOR 2371328.
- ↑ Hosking, J.R.M., Wallis, J.R. (1997) Regional frequency analysis: an approach based on L-moments, Cambridge University Press. ISBN 0-521-43045-3. Section A.8
- ↑ Documentation for the lmomco R package