कांस्टेंट शीफ: Difference between revisions
m (Abhishek moved page लगातार पुलिंदा to कांस्टेंट शीफ without leaving a redirect) |
No edit summary |
||
| Line 1: | Line 1: | ||
गणित में, [[टोपोलॉजिकल स्पेस|प्रायोगिकीय समिष्ट]] <math>X</math> पर ''' | गणित में, [[टोपोलॉजिकल स्पेस|प्रायोगिकीय समिष्ट]] <math>X</math> पर '''कांस्टेंट शीफ''' (गणित) संबंधित समुच्चय <math>A</math> की शीफ (गणित) होती है, जिसके डंठल (शेफ) समान <math>A</math> होती हैं। इसे <math>A_X</math>या आंतरवृत्ति <math>\underline{A}</math> के रूप में चिह्नित किया जाता है। इस प्रकार <math>A</math> के संबंधित स्थायी पूर्वशीफ उस पूर्वशीफ को कहते हैं जो <math>X</math> के प्रत्येक गैर-रिक्त खुले उपसमूह को <math>A</math> का मान आवंटित करती है, और जिसके सभी सीमांकन मान अभिन्नता मान <math>A</math> होते हैं। <math>A\to A</math> से संबंधित स्थायी शीफ़ <math>A</math> से जुड़े स्थायी प्रीशीफ़ का [[शीफ़ीकरण]] कहा जाता है। यह शीफ <math>X</math> पर स्थानीय स्थिरांक <math>A</math> -मान्य (स्थानीय रूप से स्थिर <math>A</math>-मान) फ़ंक्शनों के शीफ के समान होती है।<ref>{{Cite web |title=Does the extension by zero sheaf of the constant sheaf have some nice description? |url=https://math.stackexchange.com/questions/4488075/does-the-extension-by-zero-sheaf-of-the-constant-sheaf-have-some-nice-descriptio |access-date=2022-07-08 |website=Mathematics Stack Exchange |language=en}}</ref> | ||
कुछ स्थितियों में, | कुछ स्थितियों में, समुच्चय <math>A</math> किसी (श्रेणी सिद्धांत) <math>\textbf{C}</math> (उदाहरण के लिए जब <math>\textbf{C}</math> [[एबेलियन समूह|एबेलियन समूहों]] की श्रेणी है, या [[क्रमविनिमेय वलय की श्रेणी]] हो) में वस्तु <math>A</math> से प्रतिस्थापित किया जा सकता है। | ||
एबेलियन समूहों के स्थायी शीफ विशेष रूप से [[शीफ़ कोहोमोलोजी|शीफ़ सहयोगिता]] में गणकों के रूप में प्रदर्शित होते हैं। | एबेलियन समूहों के स्थायी शीफ विशेष रूप से [[शीफ़ कोहोमोलोजी|शीफ़ सहयोगिता]] में गणकों के रूप में प्रदर्शित होते हैं। | ||
==बुनियादी बातें== | ==बुनियादी बातें== | ||
यदि <math>X</math> प्रायोगिकीय समिष्ट है और <math>A</math> | यदि <math>X</math> प्रायोगिकीय समिष्ट है और <math>A</math> समुच्चय है,तो स्थायी शीफ के अनुभाग <math>\underline{A}</math> खुले समुच्चय पर <math>U</math> स्थायी फ़ंक्शनों <math>U\to A</math> के रूप में व्याख्या की जा सकती है , जहाँ <math>A</math> को [[असतत टोपोलॉजी]] के साथ दिया गया है। यदि <math>U</math> समिष्ट जुड़ा हुआ है, तो ये स्थानीय रूप से स्थायी फ़ंक्शन स्थायी होते हैं। यदि <math>f:X\to\{\text{pt}\}</math> एकमात्र [[मानचित्र (गणित)]] है जो एक-बिंदु समिष्ट के लिए होता है और <math>A</math> को <math>\{\text{pt}\}</math> पर शीफ के रूप में मान दिया जाता है , तो [[उलटा छवि शीफ]] <math>f^{-1}A</math> स्थायी पूल है <math>\underline{A}</math> पर <math>X</math>. का [[शीफ़ स्थान|शीफ़]] समिष्ट <math>\underline{A}</math> प्रक्षेपण मानचित्र है <math>A</math> (कहाँ <math>X\times A\to X</math> असतत टोपोलॉजी दी गई है)। | ||
==विस्तृत उदाहरण== | ==विस्तृत उदाहरण== | ||
[[File:Constantpresheaf.png|right|thumb|300px|दो-बिंदु असतत समिष्ट पर | [[File:Constantpresheaf.png|right|thumb|300px|दो-बिंदु असतत समिष्ट पर कांस्टेंट प्रीशेफ़ का एक चित्र इस प्रकार है। ]] | ||
[[File:2 point discrete space.png|left|thumb|100px|दो-बिंदु असतत प्रायोगिकीय समिष्ट का एक चित्र इस प्रकार है। ]]यहां <math>X</math> दो बिंदुओं से युक्त प्रायोगिकीय समिष्ट बनें <math>p</math> और <math>q</math> असतत टोपोलॉजी के साथ. <math>X</math> चार खुले | [[File:2 point discrete space.png|left|thumb|100px|दो-बिंदु असतत प्रायोगिकीय समिष्ट का एक चित्र इस प्रकार है। ]]यहां <math>X</math> दो बिंदुओं से युक्त प्रायोगिकीय समिष्ट बनें <math>p</math> और <math>q</math> असतत टोपोलॉजी के साथ. <math>X</math> चार खुले समुच्चय हैं: <math>\varnothing, \{p\}, \{q\}, \{p,q\}</math>. के खुले समुच्चय के पांच गैर-तुच्छ समावेशन <math>X</math> चार्ट में दिखाया गया है. | ||
पूर्वशीफ <math>X</math> के चार खुले | पूर्वशीफ <math>X</math> के चार खुले समुच्चयों में से प्रत्येक के लिए समुच्चय चुनता है इस प्रकार <math>X</math> और नौ [[समावेशन मानचित्र]]ों में से प्रत्येक के लिए प्रतिबंध मानचित्र (पांच गैर-तुच्छ समावेशन और चार तुच्छ समावेशन)। मान के साथ स्थायी पूर्वशीफ <math>\textbf{Z}</math>, जिसे हम निरूपित करेंगे <math>F</math>, वह प्रीशीफ़ है जो सभी चार समुच्चयों को चुनता है <math>\textbf{Z}</math>, पूर्णांक, और सभी प्रतिबंध मानचित्र पहचान होंगे। <math>F</math> फ़नकार है, इसलिए प्रीशीफ़ है, क्योंकि यह स्थायी है। <math>F</math> ग्लूइंग सिद्धांत को संतुष्ट करता है, किन्तु यह शीफ नहीं है क्योंकि यह खाली समुच्चय पर स्थानीय पहचान सिद्धांत को विफल करता है। ऐसा इसलिए है क्योंकि खाली समुच्चय समुच्चय के खाली परिवार द्वारा कवर किया जाता है: रिक्त रूप से, कोई भी दो खंड <math>F</math> खाली परिवार में किसी भी समुच्चय तक सीमित होने पर खाली समुच्चय पर समान होते हैं। इसलिए स्थानीय पहचान स्वयं सिद्ध का तात्पर्य यह होगा कि कोई भी दो खंड <math>F</math> खाली समुच्चय पर समान हैं, किन्तु यह सच नहीं है। | ||
समान पूर्वशीफ <math>G</math> जो खाली | समान पूर्वशीफ <math>G</math> जो खाली समुच्चय पर स्थानीय पहचान सिद्धांत को संतुष्ट करता है उसका निर्माण निम्नानुसार किया जाता है। यहां <math>G(\varnothing)=0</math> दिया जाता है, जहां 0 एक-तत्व समुच्चय है। सभी गैर-रिक्त समुच्चयों पर, <math>G</math> को मान <math>\textbf{Z}</math> दिया जाता है। खुले समुच्चयों के प्रत्येक समावेशन के लिए, <math>G</math> उन्हें या तो 0 को एकमात्र मानचित्र लौटाता है, अगर छोटा समुच्चय खाली है, या <math>\textbf{Z}</math> पर पहचान मानचित्र लौटाता है। | ||
[[File:Constantsheaf intermediate step.png|left|thumb|300px|स्थायी शीफ़ के लिए मध्यवर्ती चरण का एक चित्र इस प्रकार है। ]]ध्यान दें कि खाली | [[File:Constantsheaf intermediate step.png|left|thumb|300px|स्थायी शीफ़ के लिए मध्यवर्ती चरण का एक चित्र इस प्रकार है। ]]ध्यान दें कि खाली समुच्चय के लिए स्थानीय पहचान सिद्धांत के परिणामस्वरूप, खाली समुच्चय से जुड़े सभी प्रतिबंध मानचित्र उबाऊ होते हैं। यह खाली समुच्चय के लिए स्थानीय पहचान स्वयंसिद्ध को संतुष्ट करने वाले किसी भी पूर्वशीफ के लिए और विशेष रूप से किसी भी शीफ के लिए सच है। | ||
इस प्रकार <math>G</math> अलग होने वाली पूर्वशीफ है (अर्थात, स्थानीय पहचान सिद्धांत को संतुष्ट करता है), किन्तु <math>F</math> के विपरीत इसमें ग्लूइंग अधिमान असफल होता है। <math>\{p,q\}</math> द्वारा ढँके जाने वाले दो खुले | इस प्रकार <math>G</math> अलग होने वाली पूर्वशीफ है (अर्थात, स्थानीय पहचान सिद्धांत को संतुष्ट करता है), किन्तु <math>F</math> के विपरीत इसमें ग्लूइंग अधिमान असफल होता है। <math>\{p,q\}</math> द्वारा ढँके जाने वाले दो खुले समुच्चय <math>\{p\}</math> और <math>\{q\}</math>, हैं, और इन समुच्चय्स का रिक्त प्रांसगिक है। <math>\{p\}</math> या <math>\{q\}</math> पर अनुभाग <math>\textbf{Z}</math> का तत्व होता है, अर्थात्, यह संख्या होती है। <math>\{p\}</math> पर अनुभाग <math>m</math> ऊपर और <math>\{q\}</math> पर अनुभाग <math>n</math> का चयन करें, और मान रखें कि <math>m\neq n</math> है, क्योंकि <math>m</math> और <math>n</math> ही तत्व को 0 को रेखांकित करते हैं जब <math>\varnothing</math> पर, ग्लूइंग स्वयंसिद्ध को अद्वितीय अनुभाग के अस्तित्व की आवश्यकता होती है जो <math>s</math> पर <math>G(\{p,q\})</math> जो कि प्रतिबंधित है <math>m</math> पर <math>\{p\}</math> और <math>n</math> पर <math>\{q\}</math>. किन्तु क्योंकि प्रतिबंध मानचित्र से <math>\{p,q\}</math> को <math>\{p\}</math> पहचान है, <math>s=m</math>, और इसी प्रकार <math>s=n</math>, इसलिए <math>m=n</math>, विरोधाभास. | ||
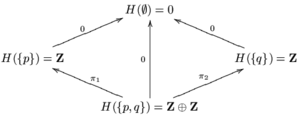
[[File:Constantsheaf.png|right|thumb|300px|दो-बिंदु प्रायोगिकीय समिष्ट पर | [[File:Constantsheaf.png|right|thumb|300px|दो-बिंदु प्रायोगिकीय समिष्ट पर कांस्टेंट शीफ जो इस प्रकार है। ]] | ||
<math>G(\{p,q\})</math> दोनों <math>\{p\}</math> और <math>\{q\}</math> के बारे में जानकारी रखने के लिए बहुत छोटा है। इसे ऐसे विस्तृत किया जा सकता है कि यह ग्लूइंग अधिकार को पूरा करता है। इसके लिए,<math>H(\{p,q\})=\mathbf{Z}\oplus\mathbf{Z}</math>. को परिभाषित करें। यहां, <math>\pi_1</math> और <math>\pi_2</math> दो प्रक्षेपण चित्र हैं: <math>\mathbf{Z}\oplus\mathbf{Z}\to\mathbf{Z}</math>। परिभाषित करें <math>H(\{p\})=\text{im}(\pi_1)=\mathbf{Z}</math> और <math>H(\{q\})=\text{im}(\pi_2)=\mathbf{Z}</math>। शेष खुले | <math>G(\{p,q\})</math> दोनों <math>\{p\}</math> और <math>\{q\}</math> के बारे में जानकारी रखने के लिए बहुत छोटा है। इसे ऐसे विस्तृत किया जा सकता है कि यह ग्लूइंग अधिकार को पूरा करता है। इसके लिए,<math>H(\{p,q\})=\mathbf{Z}\oplus\mathbf{Z}</math>. को परिभाषित करें। यहां, <math>\pi_1</math> और <math>\pi_2</math> दो प्रक्षेपण चित्र हैं: <math>\mathbf{Z}\oplus\mathbf{Z}\to\mathbf{Z}</math>। परिभाषित करें <math>H(\{p\})=\text{im}(\pi_1)=\mathbf{Z}</math> और <math>H(\{q\})=\text{im}(\pi_2)=\mathbf{Z}</math>। शेष खुले समुच्चय और समावेशन के लिए, <math>H</math> को<math>G</math> के समान ठहराया जाए। <math>H</math> ऐसी शीफ है जिसे <math>X</math> पर स्थायी शीफ कहा जाता है मूल्य <math>\textbf{Z}</math> होता है। क्योंकि <math>\textbf{Z}</math> वलय है और सभी प्रतिबंध मानचित्र वलय समरूपताएँ होते हैं, <math>H</math> क्रमविनिमेय छल्लों का शीफ होती है। | ||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 14:53, 14 July 2023
गणित में, प्रायोगिकीय समिष्ट पर कांस्टेंट शीफ (गणित) संबंधित समुच्चय की शीफ (गणित) होती है, जिसके डंठल (शेफ) समान होती हैं। इसे या आंतरवृत्ति के रूप में चिह्नित किया जाता है। इस प्रकार के संबंधित स्थायी पूर्वशीफ उस पूर्वशीफ को कहते हैं जो के प्रत्येक गैर-रिक्त खुले उपसमूह को का मान आवंटित करती है, और जिसके सभी सीमांकन मान अभिन्नता मान होते हैं। से संबंधित स्थायी शीफ़ से जुड़े स्थायी प्रीशीफ़ का शीफ़ीकरण कहा जाता है। यह शीफ पर स्थानीय स्थिरांक -मान्य (स्थानीय रूप से स्थिर -मान) फ़ंक्शनों के शीफ के समान होती है।[1]
कुछ स्थितियों में, समुच्चय किसी (श्रेणी सिद्धांत) (उदाहरण के लिए जब एबेलियन समूहों की श्रेणी है, या क्रमविनिमेय वलय की श्रेणी हो) में वस्तु से प्रतिस्थापित किया जा सकता है।
एबेलियन समूहों के स्थायी शीफ विशेष रूप से शीफ़ सहयोगिता में गणकों के रूप में प्रदर्शित होते हैं।
बुनियादी बातें
यदि प्रायोगिकीय समिष्ट है और समुच्चय है,तो स्थायी शीफ के अनुभाग खुले समुच्चय पर स्थायी फ़ंक्शनों के रूप में व्याख्या की जा सकती है , जहाँ को असतत टोपोलॉजी के साथ दिया गया है। यदि समिष्ट जुड़ा हुआ है, तो ये स्थानीय रूप से स्थायी फ़ंक्शन स्थायी होते हैं। यदि एकमात्र मानचित्र (गणित) है जो एक-बिंदु समिष्ट के लिए होता है और को पर शीफ के रूप में मान दिया जाता है , तो उलटा छवि शीफ स्थायी पूल है पर . का शीफ़ समिष्ट प्रक्षेपण मानचित्र है (कहाँ असतत टोपोलॉजी दी गई है)।
विस्तृत उदाहरण
यहां दो बिंदुओं से युक्त प्रायोगिकीय समिष्ट बनें और असतत टोपोलॉजी के साथ. चार खुले समुच्चय हैं: . के खुले समुच्चय के पांच गैर-तुच्छ समावेशन चार्ट में दिखाया गया है.
पूर्वशीफ के चार खुले समुच्चयों में से प्रत्येक के लिए समुच्चय चुनता है इस प्रकार और नौ समावेशन मानचित्रों में से प्रत्येक के लिए प्रतिबंध मानचित्र (पांच गैर-तुच्छ समावेशन और चार तुच्छ समावेशन)। मान के साथ स्थायी पूर्वशीफ , जिसे हम निरूपित करेंगे , वह प्रीशीफ़ है जो सभी चार समुच्चयों को चुनता है , पूर्णांक, और सभी प्रतिबंध मानचित्र पहचान होंगे। फ़नकार है, इसलिए प्रीशीफ़ है, क्योंकि यह स्थायी है। ग्लूइंग सिद्धांत को संतुष्ट करता है, किन्तु यह शीफ नहीं है क्योंकि यह खाली समुच्चय पर स्थानीय पहचान सिद्धांत को विफल करता है। ऐसा इसलिए है क्योंकि खाली समुच्चय समुच्चय के खाली परिवार द्वारा कवर किया जाता है: रिक्त रूप से, कोई भी दो खंड खाली परिवार में किसी भी समुच्चय तक सीमित होने पर खाली समुच्चय पर समान होते हैं। इसलिए स्थानीय पहचान स्वयं सिद्ध का तात्पर्य यह होगा कि कोई भी दो खंड खाली समुच्चय पर समान हैं, किन्तु यह सच नहीं है।
समान पूर्वशीफ जो खाली समुच्चय पर स्थानीय पहचान सिद्धांत को संतुष्ट करता है उसका निर्माण निम्नानुसार किया जाता है। यहां दिया जाता है, जहां 0 एक-तत्व समुच्चय है। सभी गैर-रिक्त समुच्चयों पर, को मान दिया जाता है। खुले समुच्चयों के प्रत्येक समावेशन के लिए, उन्हें या तो 0 को एकमात्र मानचित्र लौटाता है, अगर छोटा समुच्चय खाली है, या पर पहचान मानचित्र लौटाता है।
ध्यान दें कि खाली समुच्चय के लिए स्थानीय पहचान सिद्धांत के परिणामस्वरूप, खाली समुच्चय से जुड़े सभी प्रतिबंध मानचित्र उबाऊ होते हैं। यह खाली समुच्चय के लिए स्थानीय पहचान स्वयंसिद्ध को संतुष्ट करने वाले किसी भी पूर्वशीफ के लिए और विशेष रूप से किसी भी शीफ के लिए सच है।
इस प्रकार अलग होने वाली पूर्वशीफ है (अर्थात, स्थानीय पहचान सिद्धांत को संतुष्ट करता है), किन्तु के विपरीत इसमें ग्लूइंग अधिमान असफल होता है। द्वारा ढँके जाने वाले दो खुले समुच्चय और , हैं, और इन समुच्चय्स का रिक्त प्रांसगिक है। या पर अनुभाग का तत्व होता है, अर्थात्, यह संख्या होती है। पर अनुभाग ऊपर और पर अनुभाग का चयन करें, और मान रखें कि है, क्योंकि और ही तत्व को 0 को रेखांकित करते हैं जब पर, ग्लूइंग स्वयंसिद्ध को अद्वितीय अनुभाग के अस्तित्व की आवश्यकता होती है जो पर जो कि प्रतिबंधित है पर और पर . किन्तु क्योंकि प्रतिबंध मानचित्र से को पहचान है, , और इसी प्रकार , इसलिए , विरोधाभास.
दोनों और के बारे में जानकारी रखने के लिए बहुत छोटा है। इसे ऐसे विस्तृत किया जा सकता है कि यह ग्लूइंग अधिकार को पूरा करता है। इसके लिए,. को परिभाषित करें। यहां, और दो प्रक्षेपण चित्र हैं: । परिभाषित करें और । शेष खुले समुच्चय और समावेशन के लिए, को के समान ठहराया जाए। ऐसी शीफ है जिसे पर स्थायी शीफ कहा जाता है मूल्य होता है। क्योंकि वलय है और सभी प्रतिबंध मानचित्र वलय समरूपताएँ होते हैं, क्रमविनिमेय छल्लों का शीफ होती है।
यह भी देखें
- स्थानीय रूप से स्थायी शीफ
संदर्भ
- ↑ "Does the extension by zero sheaf of the constant sheaf have some nice description?". Mathematics Stack Exchange (in English). Retrieved 2022-07-08.
- Section II.1 of Hartshorne, Robin (1977), Algebraic Geometry, Graduate Texts in Mathematics, vol. 52, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157
- Section 2.4.6 of Tennison, B.R. (1975), Sheaf theory, ISBN 978-0-521-20784-3