इंटरेक्शन नेट

इंटरेक्शन नेट 1990 में यवेस लाफोंट द्वारा तैयार किये गए गणना का ग्राफिकल मॉडल है रैखिक तर्क की प्रमाण संरचनाओं के सामान्यीकरण के रूप में। इंटरैक्शन नेट प्रणाली प्रतिनिधि प्रकारों के सेट और इंटरैक्शन नियमों के सेट द्वारा निर्दिष्ट किया जाता है। इंटरेक्शन नेट इस अर्थ में गणना का स्वाभाविक रूप से वितरित मॉडल है कि गणना इंटरेक्शन नेट के कई भागो में साथ हो सकती है, और किसी तादात्म्य की आवश्यकता नहीं है। इसलिए गणना के इस मॉडल में कमी की मजबूत संगम संपत्ति द्वारा उत्तरार्द्ध की गारंटी दी जाती है। इस प्रकार इंटरेक्शन नेट बड़े पैमाने पर समानता के लिए प्राकृतिक भाषा प्रदान करते हैं। इंटरेक्शन नेट लैम्ब्डा गणना के कई कार्यान्वयनों के केंद्र में हैं, जैसे कि कुशल बंद कटौती और इष्टतम, लेवी के अर्थ में, लैम्बडास्कोप होता है।

परिभाषा

इंटरेक्शन नेट ग्राफ़ जैसी संरचना होती है जिसमें प्रतिनिधि और किनारे होते हैं।

इस प्रकार का प्रतिनिधि $\alpha$ और समृद्धि के साथ ${\text{ar}}(\alpha )=n\geq 0$ प्रमुख बंदरगाह है और $n$ सहायक बंदरगाह होता है किसी भी पत्तन को अधिकतम किनारे से जोड़ा जा सकता है।इसलिए जो पत्तन किसी किनारे से नहीं जुड़े होते हैं उन्हें मुक्त पत्तन कहा जाता है। मुक्त पत्तन मिलकर इंटरेक्शन नेट का इंटरफ़ेस बनाते हैं। सभी प्रतिनिधि प्रकार सेट से संबंधित हैं $\Sigma$ हस्ताक्षर कहा जाता है.

इंटरेक्शन नेट जिसमें केवल किनारे होते हैं उसे तारों कहा जाता है और सामान्यतः इसे इस रूप में दर्शाया जाता है $\omega$. वृक्ष $t$ इसकी जड़ के साथ $x$ आगमनात्मक रूप से या तो किनारे के रूप में परिभाषित किया गया है $x$, या प्रतिनिधि के रूप में $\alpha$ इसके मुफ़्त मूलधन पत्तन के साथ $x$ और इसके सहायक बंदरगाह $x_{i}$ अन्य पेड़ों की जड़ों से जुड़ा हुआ $t_{i}$.होता है|

रेखांकन रूप से, इंटरेक्शन नेट की आदिम संरचनाओं को निम्नानुसार दर्शाया जा सकता है:

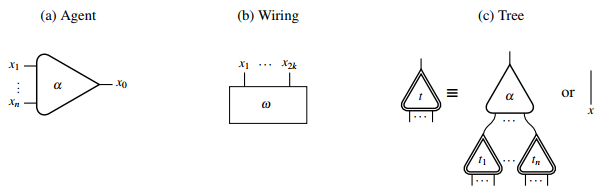जब दो प्रतिनिधि अपने प्रमुख पोर्ट से दूसरे से जुड़े होते हैं, तो वे सक्रिय जोड़ी बनाते हैं।

सक्रिय जोड़े में कोई भी इंटरैक्शन नियम पेश कर सकता है जो बताता है कि सक्रिय जोड़ी किसी अन्य इंटरैक्शन को कैसे फिर से लिखती है

जिससे बिना जाल किसी सक्रिय जोड़े वाले इंटरेक्शन नेट को सामान्य रूप में कहा जाता है। हस्ताक्षर $\Sigma$ (साथ ${\text{ar}}:\Sigma \rightarrow \mathbb {N}$ इस पर परिभाषित) प्रतिनिधि के लिए परिभाषित इंटरैक्शन नियमों के सेट के साथ $\alpha \in \Sigma$ मिलकर अंतःक्रिया प्रणाली का निर्माण करते हैं।

इंटरेक्शन गणना

इंटरेक्शन नेट के पाठ्य प्रतिनिधित्व को इंटरेक्शन गणना कहा जाता है और इसे कार्यक्रमों भाषा के रूप में देखा जा सकता है।

जिससे आगमनात्मक रूप से परिभाषित पेड़ शब्दों के अनुरूप होते हैं $t::=\alpha (t_{1},\dots ,t_{n})\ |\ x$ इंटरेक्शन गणना में, कहां $x$ नाम कहा जाता है.

कोई भी इंटरैक्शन नेट $N$ पहले से परिभाषित तारों और वृक्ष आदिम का उपयोग करके निम्नानुसार फिर से तैयार किया जा सकता है:

जो इंटरेक्शन गणना में विन्यास से मेल खाता है

$c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$,

कहाँ $t_{i}$, $v_{i}$, और $w_{i}$ मनमानी शर्तें हैं. क्रमबद्ध क्रम $t_{1},...,t_{m}$ बाईं ओर को इंटरफ़ेस कहा जाता है, चूँकि दाईं ओर समीकरणों का अव्यवस्थित मल्टीसेट होता है $v_{i}=w_{i}$. तारों $\omega$ नामों का अनुवाद करता है, और प्रत्येक नाम को विन्यास में ठीक दो बार आना पड़ता है।

बिल्कुल वैसे ही जैसे $\lambda$- गणना इंटरेक्शन गणना की धारणाएं हैं; $\alpha$-परिवर्तन और प्रतिस्थापन स्वाभाविक रूप से विन्यास पर परिभाषित होते हैं। विशेष रूप से, किसी भी नाम की दोनों घटनाओं को a से बदला जा सकता है यदि किसी दिए गए विन्यास में उत्तरार्द्ध नहीं होता है तो नया नाम। तक के विन्यास को समतुल्य माना जाता है $\alpha$- रूपांतरण. बदले में, प्रतिस्थापन $t[x:=u]$ नाम बदलने का परिणाम है $x$ शब्द में $t$ दूसरे शब्द के साथ $u$ अगर $x$ पद में बिल्कुल घटना है $t$.

किसी भी इंटरैक्शन नियम को ग्राफ़िक रूप से निम्नानुसार दर्शाया जा सकता है:

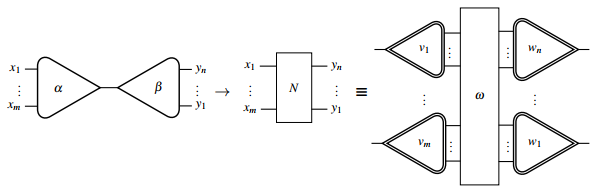कहाँ $\alpha ,\beta \in \Sigma$, और इंटरेक्शन नेट $N$ दाहिनी ओर को इंटरेक्शन गणना में अनुवाद करने के लिए तारों और वृक्ष आदिम का उपयोग करके फिर से तैयार किया गया है $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ लाफोंट के संकेतन का उपयोग करना।

जिससे इंटरेक्शन गणना ग्राफ़ से देखने की तुलना में अधिक विवरण में विन्यास पर कमी को परिभाषित करता है

इंटरेक्शन नेट पर परिभाषित पुनर्लेखन। अर्थात्, यदि $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$, निम्नलिखित कमी:

$\langle {\vec {t}}\ |\ \alpha (t_{1},\dots ,t_{m})=\beta (u_{1},\dots ,u_{n}),\Delta \rangle \rightarrow \langle {\vec {t}}\ |\ t_{1}=v_{1},\dots ,t_{m}=v_{m},u_{1}=w_{1},\dots ,u_{n}=w_{n},\Delta \rangle$

अंतःक्रिया कहलाती है. जब समीकरणों में से का रूप होता है $x=u$, अप्रत्यक्ष परिणाम लागू किया जा सकता है

नाम की अन्य घटना के स्थान पर $x$ किसी अवधि में $t$:

$\langle \dots t\dots \ |\ x=u,\Delta \rangle \rightarrow \langle \dots t[x:=u]\dots \ |\ \Delta \rangle$ या $\langle {\vec {t}}\ |\ x=u,t=w,\Delta \rangle \rightarrow \langle {\vec {t}}\ |\ t[x:=u]=w,\Delta \rangle$.

समीकरण $x=t$ यदि गतिरोध कहा जाता है $x$ अवधि में घटित होता है $t$. सामान्यतः केवल गतिरोध-मुक्त इंटरेक्शन नेट पर ही विचार किया जाता है। साथ में, अंतःक्रिया और अप्रत्यक्षता विन्यास पर कमी संबंध को परिभाषित करते हैं। तथ्य यह है कि विन्यास $c$ अपने सामान्य स्वरूप में कम हो जाता है $c'$ कोई समीकरण न बचे होने को इस रूप में दर्शाया जाता है $c\downarrow c'$.

गुण

इंटरेक्शन नेट निम्नलिखित गुणों से लाभान्वित होते हैं:

• स्थानीयता (केवल सक्रिय जोड़े को फिर से लिखा जा सकता है);
• रैखिकता (प्रत्येक इंटरैक्शन नियम को निरंतर समय में लागू किया जा सकता है);
• मजबूत संगम को एक कदम हीरे की संपत्ति (यदि) के रूप में भी जाना जाता है $c\rightarrow c_{1}$ और $c\rightarrow c_{2}$, तब $c_{1}\rightarrow c'$ और $c_{2}\rightarrow c'$ कुछ के लिए $c'$).

ये गुण मिलकर बड़े पैमाने पर समानता की अनुमति देते हैं।

इंटरेक्शन कॉम्बिनेटर

सबसे सरल इंटरेक्शन सिस्टम में से जो किसी अन्य इंटरेक्शन सिस्टम का अनुकरण कर सकता है वह इंटरेक्शन संयोजक है। इसके हस्ताक्षर हैं $\Sigma =\{\epsilon ,\delta ,\gamma \}$ साथ ${\text{ar}}(\epsilon )=0$ और ${\text{ar}}(\delta )={\text{ar}}(\gamma )=2$. इन प्रतिनिधि के लिए इंटरैक्शन नियम हैं:

• $\epsilon \bowtie \alpha [\epsilon ,\dots ,\epsilon ]$ मिटाना कहते हैं;
• $\delta [\alpha (x_{1},\dots ,x_{n}),\alpha (y_{1},\dots ,y_{n})]\bowtie \alpha [\delta (x_{1},y_{1}),\dots ,\delta (x_{n},y_{n})]$ दुरुक्ति कहा जाता है;
• $\delta [x,y]\bowtie \delta [x,y]$ और $\gamma [x,y]\bowtie \gamma [y,x]$ विनाश कहा जाता है.

ग्राफ़िक रूप से, मिटाने और दोहराव के नियमों को निम्नानुसार दर्शाया जा सकता है:

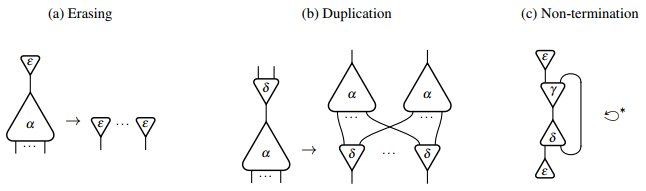गैर-समाप्ति अंतःक्रिया नेट के उदाहरण के साथ जो अपने आप में प्रणाली मट जाता है। इंटरेक्शन गणना में संबंधित विन्यास से प्रारंभ होने वाला इसका अनंत कमी क्रम इस प्रकार है:

${\begin{aligned}&\langle \varnothing \ |\ \delta (\epsilon ,x)=\gamma (x,\epsilon )\rangle \rightarrow \\&\langle \varnothing \ |\ \epsilon =\gamma (x_{1},x_{2}),\ x=\gamma (y_{1},y_{2}),\ x=\delta (x_{1},y_{1}),\ \epsilon =\delta (x_{2},y_{2})\rangle \rightarrow ^{*}\\&\langle \varnothing \ |\ x_{1}=\epsilon ,\ x_{2}=\epsilon ,\ x=\gamma (y_{1},y_{2}),\ x=\delta (x_{1},y_{1}),\ x_{2}=\epsilon ,\ y_{2}=\epsilon \rangle \rightarrow ^{*}\\&\langle \varnothing \ |\ \delta (\epsilon ,x)=\gamma (x,\epsilon )\rangle \rightarrow \dots \end{aligned}}$

गैर-नियतात्मक विस्तार

जिससे इंटरेक्शन नेट अनिवार्य रूप से नियतात्मक हैं और गैर-नियतात्मक संगणनाओं को सीधे मॉडल नहीं कर सकते हैं। गैर-नियतात्मक विकल्प को व्यक्त करने के लिए, इंटरैक्शन नेट को विस्तारित करने की आवश्यकता है। वास्तव में, केवल प्रतिनिधि का परिचय देना ही पर्याप्त है ${\text{amb}}$ दो प्रमुख पोर्ट और निम्नलिखित इंटरैक्शन नियमों के साथ किया गया था|

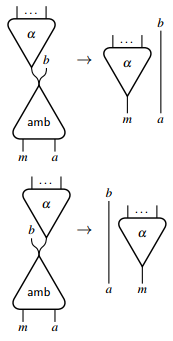यह विशिष्ट प्रतिनिधि अस्पष्ट विकल्प का प्रतिनिधित्व करता है और इसका उपयोग किसी भी अन्य प्रतिनिधि को प्रमुख पोर्ट की मनमानी संख्या के साथ अनुकरण करने के लिए किया जा सकता है। उदाहरण के लिए, यह a को परिभाषित करने की अनुमति देता है ${\text{ParallelOr}}$ बूलियन ऑपरेशन जो अन्य तर्कों में होने वाली गणना से स्वतंत्र होकर, यदि इसका कोई भी तर्क सत्य है, तो सत्य लौटाता है।

यह भी देखें

• इंटरेक्शन की ज्यामिति
• ग्राफ पुनर्लेखन
• लैम्ब्डा गणना
• रेखीय ग्राफ व्याकरण
• रेखीय तर्क
• प्रमाण जाल

अग्रिम पठन

• Asperti, Andrea; Guerrini, Stefano (1998). The Optimal Implementation of Functional Programming Languages. Cambridge Tracts in Theoretical Computer Science. Vol. 45. Cambridge University Press. ISBN 9780521621120.
• Fernández, Maribel (2009). "Interaction-Based Models of Computation". Models of Computation: An Introduction to Computability Theory. Springer Science & Business Media. pp. 107–130. ISBN 9781848824348.

बाहरी संबंध

• de Falco, Marc. "tikz-inet. A set of tikz-based macros for drawing interaction nets".
• de Falco, Marc. "INL. Interaction Nets Laboratory".
• Vilaça, Miguel. "INblobs. An editor and interpreter for Interaction Nets".
• Asperti, Andrea. "The Bologna Optimal Higher-Order Machine". GitHub.
• Salikhmetov, Anton. "JavaScript Engine for Interaction Nets".
• Salikhmetov, Anton. "Macro Lambda Calculus".