के-वे मर्ज एल्गोरिदम: Difference between revisions

From Vigyanwiki
No edit summary
No edit summary
 
(7 intermediate revisions by 3 users not shown)
Line 1: Line 1:
{{DISPLAYTITLE:''k''-way merge algorithm}}
{{DISPLAYTITLE:''k''-way merge algorithm}}
[[कंप्यूटर विज्ञान]] में, ''के''-वे [[एल्गोरिदम मर्ज करें]] या मल्टीवे मर्ज एक विशिष्ट प्रकार के मर्ज एल्गोरिदम हैं जो के क्रमबद्ध सूचियों को लेने और उन्हें एक एकल क्रमबद्ध सूची में विलय करने में विशेषज्ञ हैं। यह मर्ज एल्गोरिदम सामान्यतः मर्ज एल्गोरिदम को संदर्भित करते हैं जो दो से अधिक क्रमबद्ध सूचियों को लेते हैं। दो-तरफा मर्ज को बाइनरी मर्ज भी कहा जाता है। के-वे मर्ज बाहरी सॉर्टिंग एल्गोरिदम भी है।
[[कंप्यूटर विज्ञान]] में, '''के-वे [[एल्गोरिदम मर्ज करें|मर्ज एल्गोरिदम]]''' या मल्टीवे मर्ज एक विशिष्ट प्रकार k अनुक्रम मर्ज एल्गोरिदम हैं जो k क्रमबद्ध सूचियों को लेने और उन्हें एक एकल क्रमबद्ध सूची में विलय करने में विशेषज्ञ हैं। यह मर्ज एल्गोरिदम सामान्यतः मर्ज एल्गोरिदम को संदर्भित करते हैं जो दो से अधिक क्रमबद्ध सूचियों को लेते हैं। इस प्रकार दो-तरफा मर्ज को बाइनरी मर्ज भी कहा जाता है। के-वे मर्ज बाहरी सॉर्टिंग एल्गोरिदम भी है।


== दोतरफा विलय ==
== दोतरफा विलय ==
[[ मर्ज़ सॉर्ट ]] में इसकी महत्वपूर्ण भूमिका के कारण 2-तरफ़ा मर्ज, या बाइनरी मर्ज का बड़े पैमाने पर अध्ययन किया गया है। इसका एक उदाहरण क्लासिक मर्ज है जो मर्ज सॉर्ट उदाहरणों में अधिकांशतः दिखाई देता है। क्लासिक मर्ज प्रत्येक चरण में सबसे कम कुंजी के साथ डेटा आइटम को आउटपुट करता है; कुछ क्रमबद्ध सूचियों को देखते हुए, यह एक क्रमबद्ध सूची तैयार करता है जिसमें किसी भी इनपुट सूची में सभी तत्व सम्मिलित होते हैं, और यह इनपुट सूचियों की लंबाई के योग के अनुपात में समय पर ऐसा करता है।
[[ मर्ज़ सॉर्ट | मर्ज़ सॉर्ट]] में इसकी महत्वपूर्ण भूमिका के कारण 2-तरफ़ा मर्ज, या बाइनरी मर्ज का बड़े पैमाने पर अध्ययन किया गया है। इस प्रकार इसका एक उदाहरण क्लासिक मर्ज है जो मर्ज सॉर्ट उदाहरणों में अधिकांशतः दिखाई देता है। क्लासिक मर्ज प्रत्येक चरण में सबसे कम कुंजी के साथ डेटा आइटम को आउटपुट करता है; कुछ क्रमबद्ध सूचियों को देखते हुए, यह एक क्रमबद्ध सूची तैयार करता है जिसमें किसी भी इनपुट सूची में सभी तत्व सम्मिलित होते हैं, और यह इनपुट सूचियों की लंबाई के योग के अनुपात में समय पर ऐसा करता है।


बढ़ते क्रम में क्रमबद्ध दो सरणियों को A[1..p] और B[1..q] द्वारा निरूपित करें।
बढ़ते क्रम में क्रमबद्ध दो सरणियों को A[1..p] और B[1..q] द्वारा निरूपित करें।
इसके अतिरिक्त, आउटपुट ऐरे को C[1..n] से निरूपित करें।
इसके अतिरिक्त, आउटपुट ऐरे को C[1..n] से निरूपित करें।


Line 16: Line 17:
अन्यथा, एल्गोरिदम B[j] को C[k] में कॉपी करता है और j और k को बढ़ाता है।
अन्यथा, एल्गोरिदम B[j] को C[k] में कॉपी करता है और j और k को बढ़ाता है।


एक विशेष मामला उत्पन्न होता है यदि i या j में से कोई भी A या B के अंत तक पहुँच गया हो।
एक विशेष मामला उत्पन्न होता है यदि i या j में से कोई भी A या B के अंत तक पहुँच गया है।


इस स्थितियों में एल्गोरिदम बी या ए के शेष तत्वों को सी में कॉपी करता है और समाप्त करता है।
इस स्थितियों में एल्गोरिदम B या A के शेष तत्वों को C में कॉपी करता है और समाप्त करता है।


== के-वे मर्ज ==
== '''के-वे मर्ज''' ==
के-वे मर्ज समस्या में समान तत्वों के साथ एकल क्रमबद्ध सरणी बनाने के लिए k क्रमबद्ध सरणियों को मर्ज करना सम्मिलित है।
के-वे मर्ज समस्या में समान तत्वों के साथ एकल क्रमबद्ध सरणी बनाने के लिए k क्रमबद्ध सरणियों को मर्ज करना सम्मिलित है।


तत्वों की कुल संख्या को n से निरूपित करें।
तत्वों की कुल संख्या को n से निरूपित करें।


n आउटपुट ऐरे के आकार और k इनपुट ऐरे के आकार के योग के सामान्तर है।
इस प्रकार n आउटपुट ऐरे k आकार और k इनपुट ऐरे k आकार के योग के सामान्तर है।


सरलता के लिए, हम मानते हैं कि कोई भी इनपुट ऐरे खाली नहीं है।
सरलता के लिए, हम मानते हैं कि कोई भी इनपुट ऐरे खाली नहीं है।
Line 31: Line 32:
एक परिणाम के रूप में <math>k \le n</math>, जो सूची किए गए चलने के समय को सरल बनाता है।
एक परिणाम के रूप में <math>k \le n</math>, जो सूची किए गए चलने के समय को सरल बनाता है।


में समस्या का समाधान किया जा सकता है <math>\mathcal{O}(n \cdot \log(k))</math> के साथ समय चल रहा है <math>\mathcal{O}(n)</math> अंतरिक्ष।
उसमें समस्या का समाधान किया जा सकता है <math>\mathcal{O}(n \cdot \log(k))</math> के साथ समय चल रहा है <math>\mathcal{O}(n)</math> अंतरिक्ष।


इस रनिंग टाइम को प्राप्त करने वाले अनेक एल्गोरिदम उपस्तिथ हैं।
इस रनिंग टाइम को प्राप्त करने वाले अनेक एल्गोरिदम उपस्तिथ हैं।
Line 37: Line 38:
=== पुनरावृत्तीय 2-तरफा विलय ===
=== पुनरावृत्तीय 2-तरफा विलय ===


समस्या को 2-तरफा मर्ज का उपयोग करके दो k सरणियों को पुनरावृत्त रूप से मर्ज करके हल किया जा सकता है जब तक कि केवल एक ही ऐरे न रह जाए। यदि सरणियों को मनमाने क्रम में मर्ज किया जाता है, तब परिणामी रनिंग समय केवल O(kn) होता है। यह उप-इष्टतम है.
समस्या को 2-तरफा मर्ज का उपयोग करके दो k सरणियों को पुनरावृत्त रूप से मर्ज करके हल किया जा सकता है जब तक कि केवल एक ही ऐरे न रह जाए। इस प्रकार यदि सरणियों को मनमाने क्रम में मर्ज किया जाता है, तब परिणामी रनिंग समय केवल O(kn) होता है। यह उप-इष्टतम है.


पहले को दूसरे के साथ, तीसरे को चौथे के साथ, इत्यादि को पुनरावृत्त रूप से विलय करके चलने के समय में सुधार किया जा सकता है। चूँकि प्रत्येक पुनरावृत्ति में सरणियों की संख्या आधी हो जाती है, केवल Θ(लॉग k) पुनरावृत्तियाँ होती हैं। प्रत्येक पुनरावृत्ति में प्रत्येक तत्व को ठीक एक बार स्थानांतरित किया जाता है। इसलिए प्रति पुनरावृत्ति चलने का समय Θ(n) में है क्योंकि n तत्वों की संख्या है। इसलिए कुल चलने का समय Θ(n log k) में है।
पहले को दूसरे के साथ, तीसरे को चौथे के साथ, इत्यादि को पुनरावृत्त रूप से विलय करके चलने के समय में सुधार किया जा सकता है। चूँकि प्रत्येक पुनरावृत्ति में सरणियों की संख्या आधी हो जाती है, केवल Θ(लॉग k) पुनरावृत्तियाँ होती हैं। इस प्रकार प्रत्येक पुनरावृत्ति में प्रत्येक तत्व को ठीक एक बार स्थानांतरित किया जाता है। इसलिए प्रति पुनरावृत्ति चलने का समय Θ(n) में है क्योंकि n तत्वों की संख्या है। इसलिए कुल चलने का समय Θ(n log k) में है।


हम दो सबसे छोटी सरणियों को पुनरावृत्त रूप से मर्ज करके, इस एल्गोरिदम में और सुधार कर सकते हैं। यह स्पष्ट है कि यह चलने के समय को कम करता है और इसलिए पिछले पैराग्राफ में वर्णित रणनीति से बदतर नहीं हो सकता है। इसलिए चलने का समय O(n log k) में है। सौभाग्य से, सीमावर्ती स्थितियों में चलने का समय उत्तम हो सकता है। उदाहरण के लिए पतित स्थितियों पर विचार करें, जहां एक सरणी को छोड़कर सभी में केवल एक तत्व होता है। पिछले पैराग्राफ में बताई गई रणनीति के लिए Θ(n log k) रनिंग टाइम की आवश्यकता होती है, जबकि उत्तम रणनीति के लिए केवल Θ(n + k log k) रनिंग टाइम की आवश्यकता होती है।
हम दो सबसे छोटी सरणियों को पुनरावृत्त रूप से मर्ज करके, इस एल्गोरिदम में और सुधार कर सकते हैं। इस प्रकार यह स्पष्ट है कि यह चलने के समय को कम करता है और इसलिए पिछले पैराग्राफ में वर्णित रणनीति से बदतर नहीं हो सकता है। इसलिए चलने का समय O(n log k) में है। सौभाग्य से, सीमावर्ती स्थितियों में चलने का समय उत्तम हो सकता है। उदाहरण के लिए पतित स्थितियों पर विचार करें, जहां एक सरणी को छोड़कर सभी में केवल एक तत्व होता है। इस प्रकार पिछले पैराग्राफ में बताई गई रणनीति के लिए Θ(n log k) रनिंग टाइम की आवश्यकता होती है, जबकि उत्तम रणनीति के लिए केवल Θ(n + k log k) रनिंग टाइम की आवश्यकता होती है।


=== डायरेक्ट के-वे मर्ज ===
=== '''डायरेक्ट के-वे मर्ज''' ===


इस स्थितियों में, हम एक साथ k-रन को एक साथ मर्ज कर देंगे।
इस स्थितियों में, हम एक साथ k-रन को एक साथ मर्ज कर देंगे।
Line 55: Line 56:
हम सबसे छोटे तत्व की तेजी से गणना करके इसमें सुधार कर सकते हैं।
हम सबसे छोटे तत्व की तेजी से गणना करके इसमें सुधार कर सकते हैं।


हीप (डेटा संरचना), टूर्नामेंट ट्री, या [[ बिखरा हुआ पेड़ | बिखरा हुआ पेड़]] का उपयोग करके, सबसे छोटा तत्व O(लॉग k) समय में निर्धारित किया जा सकता है।
हीप (डेटा संरचना), टूर्नामेंट ट्री, या [[ बिखरा हुआ पेड़ |बिखरा हुआ ट्री]] का उपयोग करके, सबसे छोटा तत्व O(लॉग k) समय में निर्धारित किया जा सकता है।


इसलिए परिणामी चलने का समय O(n log k) में है।
इसलिए परिणामी चलने का समय O(n log k) में है।


ढेर का उपयोग सामान्यतः अधिक किया जाता है, चूंकि टूर्नामेंट ट्री व्यवहार में तेज़ होता है। एक ढेर प्रत्येक चरण में लगभग 2*लॉग(k) तुलनाओं का उपयोग करता है क्योंकि यह पेड़ को जड़ से नीचे तक संभालता है और प्रत्येक नोड के दोनों बच्चों की तुलना करने की आवश्यकता होती है। इस मध्य, एक टूर्नामेंट ट्री को केवल लॉग (के) तुलना की आवश्यकता होती है क्योंकि यह पेड़ के नीचे से प्रारंभ होता है और जड़ तक काम करता है, प्रत्येक परत में केवल एक ही तुलना करता है। इसलिए टूर्नामेंट ट्री को पसंदीदा कार्यान्वयन होना चाहिए।
ढेर का उपयोग सामान्यतः अधिक किया जाता है, चूंकि टूर्नामेंट ट्री व्यवहार में तेज़ होता है। एक ढेर प्रत्येक चरण में लगभग 2*लॉग(k) तुलनाओं का उपयोग करता है क्योंकि यह ट्री को जड़ से नीचे तक संभालता है और प्रत्येक नोड के दोनों बच्चों की तुलना करने की आवश्यकता होती है। इस प्रकार इस मध्य, एक टूर्नामेंट ट्री को केवल लॉग (के) तुलना की आवश्यकता होती है क्योंकि यह ट्री के नीचे से प्रारंभ होता है और जड़ तक काम करता है, प्रत्येक परत में केवल एक ही तुलना करता है। इसलिए टूर्नामेंट ट्री को पसंदीदा कार्यान्वयन होना चाहिए।


==== ढेर ====
==== '''ढेर''' ====


विचार यह है कि k सूचियों का न्यूनतम-ढेर बनाए रखा जाए, प्रत्येक को उनके सबसे छोटे वर्तमान तत्व द्वारा कुंजीबद्ध किया जाए। एक सरल एल्गोरिदम ढेर से नोड्स के साथ एक आउटपुट बफर बनाता है। नोड्स का एक न्यूनतम-ढेर बनाकर प्रारंभ करें, जहां प्रत्येक नोड में सूची का एक प्रमुख तत्व और सूची का शेष (या पूंछ) होता है। चूँकि सूचियाँ प्रारंभ में क्रमबद्ध होती हैं, शीर्ष प्रत्येक सूची का सबसे छोटा तत्व होता है; हीप प्रॉपर्टी गारंटी देती है कि रूट में सभी सूचियों में न्यूनतम तत्व सम्मिलित हैं। हीप से रूट नोड निकालें, हेड एलिमेंट को आउटपुट बफर में जोड़ें, टेल से एक नया नोड बनाएं और इसे हीप में डालें। तब तक दोहराएं जब तक कि ढेर में केवल एक नोड न रह जाए, उस बिंदु पर बस उस शेष सूची (हेड और टेल) को आउटपुट बफर में जोड़ दें।
विचार यह है कि k सूचियों का न्यूनतम-ढेर बनाए रखा जाए, प्रत्येक को उनके सबसे छोटे वर्तमान तत्व द्वारा कुंजीबद्ध किया जाए। इस प्रकार एक सरल एल्गोरिदम ढेर से नोड्स के साथ एक आउटपुट बफर बनाता है। इस प्रकार नोड्स का एक न्यूनतम-ढेर बनाकर प्रारंभ करें, जहां प्रत्येक नोड में सूची का एक प्रमुख तत्व और सूची का शेष (या पूंछ) होता है। चूँकि सूचियाँ प्रारंभ में क्रमबद्ध होती हैं, शीर्ष प्रत्येक सूची का सबसे छोटा तत्व होता है; हीप प्रॉपर्टी गारंटी देती है कि रूट में सभी सूचियों में न्यूनतम तत्व सम्मिलित हैं। हीप से रूट नोड निकालें, हेड एलिमेंट को आउटपुट बफर में जोड़ें, टेल से एक नया नोड बनाएं और इसे हीप में डालें। इस प्रकार तब तक दोहराएं जब तक कि ढेर में केवल एक नोड न रह जाए, उस बिंदु पर बस उस शेष सूची (हेड और टेल) को आउटपुट बफर में जोड़ दें।


पॉइंटर्स का उपयोग करना, एक इन-प्लेस हीप एल्गोरिदम
पॉइंटर्स का उपयोग करना, एक इन-प्लेस हीप एल्गोरिदम<ref>{{cite book
<ref>{{cite book
|last1=Bentley
|last1=Bentley
|first1=Jon Louis
|first1=Jon Louis
Line 75: Line 75:
|isbn=0201657880
|isbn=0201657880
|pages=147–162
|pages=147–162
|edition=2nd}}</ref>
|edition=2nd}}</ref> इनपुट सरणियों में पॉइंटर्स का एक न्यूनतम-ढेर आवंटित करता है।
इनपुट सरणियों में पॉइंटर्स का एक न्यूनतम-ढेर आवंटित करता है।
 
प्रारंभ में यह पॉइंटर्स इनपुट ऐरे के सबसे छोटे तत्वों की ओर संकेत करते हैं।
प्रारंभ में यह पॉइंटर्स इनपुट ऐरे के सबसे छोटे तत्वों की ओर संकेत करते हैं।
सूचकों को उस मान के आधार पर क्रमबद्ध किया जाता है जिस पर वे इंगित करते हैं।
सूचकों को उस मान के आधार पर क्रमबद्ध किया जाता है जिस पर वे इंगित करते हैं।


Line 92: Line 93:
==== टूर्नामेंट ट्री ====
==== टूर्नामेंट ट्री ====


[[File:Tournament tree.png|thumb|टूर्नामेंट वृक्ष]]टूर्नामेंट ट्री <ref name="knuth98">
[[File:Tournament tree.png|thumb|टूर्नामेंट ट्री ]]टूर्नामेंट ट्री <ref name="knuth98">
{{cite book| last = Knuth| first = Donald| author-link = Donald Knuth| series = [[The Art of Computer Programming]]| volume= 3| title= Sorting and Searching| edition = 2nd| publisher = Addison-Wesley| year=  1998| chapter = Chapter 5.4.1. Multiway Merging and Replacement Selection| pages = 252–255| isbn = 0-201-89685-0}}</ref> खेल प्रतियोगिताओं की तरह, एक एलिमिनेशन टूर्नामेंट पर आधारित है। प्रत्येक गेम में, दो इनपुट तत्व प्रतिस्पर्धा करते हैं। विजेता को अगले दौर में पदोन्नत किया जाता है। इसलिए, हमें खेलों का एक [[द्विआधारी वृक्ष]] मिलता है। सूची को आरोही क्रम में क्रमबद्ध किया गया है, इसलिए गेम का विजेता दोनों तत्वों में से छोटा होता है।
{{cite book| last = Knuth| first = Donald| author-link = Donald Knuth| series = [[The Art of Computer Programming]]| volume= 3| title= Sorting and Searching| edition = 2nd| publisher = Addison-Wesley| year=  1998| chapter = Chapter 5.4.1. Multiway Merging and Replacement Selection| pages = 252–255| isbn = 0-201-89685-0}}</ref> खेल प्रतियोगिताओं की तरह, एक एलिमिनेशन टूर्नामेंट पर आधारित है। प्रत्येक गेम में, दो इनपुट तत्व प्रतिस्पर्धा करते हैं। विजेता को अगले दौर में पदोन्नत किया जाता है। इसलिए, हमें खेलों का एक [[द्विआधारी वृक्ष|द्विआधारी ट्री]] मिलता है। सूची को आरोही क्रम में क्रमबद्ध किया गया है, इसलिए गेम का विजेता दोनों तत्वों में से छोटा होता है।


[[File:Loser tree.png|thumb|हारे हुए पेड़]]के-वे विलय के लिए, केवल प्रत्येक गेम के हारने वाले को स्टोर करना अधिक कुशल है (छवि देखें)। इसलिए डेटा संरचना को लूज़र ट्री कहा जाता है। पेड़ बनाते समय या किसी तत्व को उसकी सूची में से अगले तत्व से प्रतिस्थापित करते समय, हम अभी भी गेम के विजेता को शीर्ष पर बढ़ावा देते हैं। पेड़ एक खेल मैच की तरह भरा हुआ है किन्तु नोड्स केवल हारने वाले को ही संग्रहीत करते हैं। सामान्यतः, रूट के ऊपर एक अतिरिक्त नोड जोड़ा जाता है जो समग्र विजेता का प्रतिनिधित्व करता है। प्रत्येक पत्ता किसी एक इनपुट ऐरे में एक पॉइंटर संग्रहीत करता है। प्रत्येक आंतरिक नोड एक मान और एक सूचकांक संग्रहीत करता है। आंतरिक नोड का सूचकांक इंगित करता है कि मान किस इनपुट सरणी से आता है। मान में संबंधित इनपुट सरणी के पहले तत्व की एक प्रति सम्मिलित है।
[[File:Loser tree.png|thumb|हारे हुए ट्री ]]के-वे विलय के लिए, केवल प्रत्येक गेम के हारने वाले को स्टोर करना अधिक कुशल है (छवि देखें)। इसलिए डेटा संरचना को लूज़र ट्री कहा जाता है। इस प्रकार ट्री बनाते समय या किसी तत्व को उसकी सूची में से अगले तत्व से प्रतिस्थापित करते समय, हम अभी भी गेम के विजेता को शीर्ष पर बढ़ावा देते हैं। इस प्रकार ट्री एक खेल मैच की तरह भरा हुआ है किन्तु नोड्स केवल हारने वाले को ही संग्रहीत करते हैं। सामान्यतः, रूट के ऊपर एक अतिरिक्त नोड जोड़ा जाता है जो समग्र विजेता का प्रतिनिधित्व करता है। प्रत्येक पत्ता किसी एक इनपुट ऐरे में एक पॉइंटर संग्रहीत करता है। प्रत्येक आंतरिक नोड एक मान और एक सूचकांक संग्रहीत करता है। इस प्रकार आंतरिक नोड का सूचकांक इंगित करता है कि मान किस इनपुट सरणी से आता है। मान में संबंधित इनपुट सरणी के पहले तत्व की एक प्रति सम्मिलित है।


एल्गोरिथ्म पुनरावृत्त रूप से न्यूनतम तत्व को परिणाम में जोड़ता है और फिर तत्व को संबंधित इनपुट सूची से हटा देता है। यह अद्यतन पत्ती से रूट (प्रतिस्थापन चयन) तक पथ पर नोड्स को अद्यतन करता है। हटाया गया तत्व समग्र विजेता है। इसलिए, इसने इनपुट ऐरे से रूट तक के पथ पर प्रत्येक गेम जीता है। इनपुट ऐरे से एक नया तत्व चुनते समय, तत्व को रूट के पथ पर पिछले हारे हुए तत्वों के विरुद्ध प्रतिस्पर्धा करने की आवश्यकता होती है। हारे हुए पेड़ का उपयोग करते समय, गेम को दोबारा खेलने के लिए भागीदार पहले से ही नोड्स में संग्रहीत होता है। दोबारा खेले गए प्रत्येक गेम के हारने वाले को नोड में लिखा जाता है और विजेता को पुनरावृत्त रूप से शीर्ष पर पदोन्नत किया जाता है। जब रूट पर पहुंच जाता है, तब नया समग्र विजेता मिल जाता है और विलय के अगले दौर में इसका उपयोग किया जा सकता है।
एल्गोरिथ्म पुनरावृत्त रूप से न्यूनतम तत्व को परिणाम में जोड़ता है और फिर तत्व को संबंधित इनपुट सूची से हटा देता है। यह अद्यतन पत्ती से रूट (प्रतिस्थापन चयन) तक पथ पर नोड्स को अद्यतन करता है। इस प्रकार हटाया गया तत्व समग्र विजेता है। इसलिए, इसने इनपुट ऐरे से रूट तक के पथ पर प्रत्येक गेम जीता है। इनपुट ऐरे से एक नया तत्व चुनते समय, तत्व को रूट के पथ पर पिछले हारे हुए तत्वों के विरुद्ध प्रतिस्पर्धा करने की आवश्यकता होती है। इस प्रकार हारे हुए ट्री का उपयोग करते समय, गेम को दोबारा खेलने के लिए भागीदार पहले से ही नोड्स में संग्रहीत होता है। दोबारा खेले गए प्रत्येक गेम के हारने वाले को नोड में लिखा जाता है और विजेता को पुनरावृत्त रूप से शीर्ष पर पदोन्नत किया जाता है। जब रूट पर पहुंच जाता है, तब नया समग्र विजेता मिल जाता है और विलय के अगले दौर में इसका उपयोग किया जा सकता है।


इस अनुभाग में टूर्नामेंट ट्री और हारने वाले ट्री की छवियां समान डेटा का उपयोग करती हैं और हारने वाले ट्री के काम करने के तरीके को समझने के लिए उनकी तुलना की जा सकती है।
इस अनुभाग में टूर्नामेंट ट्री और हारने वाले ट्री की छवियां समान डेटा का उपयोग करती हैं और हारने वाले ट्री के काम करने के तरीके को समझने के लिए उनकी तुलना की जा सकती है।
Line 103: Line 104:
===== एल्गोरिथम =====
===== एल्गोरिथम =====


एक टूर्नामेंट ट्री को इनपुट सूचियों में सेंटिनल्स जोड़कर (अर्थात अनंत के मूल्य के साथ प्रत्येक सूची के अंत में एक सदस्य जोड़कर) और संख्या तक शून्य सूचियां (केवल एक सेंटिनल सम्मिलित करके) जोड़कर एक संतुलित बाइनरी ट्री के रूप में दर्शाया जा सकता है। सूचियाँ दो की शक्ति है। संतुलित वृक्ष को एक ही सारणी में संग्रहित किया जा सकता है। वर्तमान सूचकांक को दो से विभाजित करके मूल तत्व तक पहुंचा जा सकता है।
एक टूर्नामेंट ट्री को इनपुट सूचियों में सेंटिनल्स जोड़कर (अर्थात अनंत के मूल्य के साथ प्रत्येक सूची के अंत में एक सदस्य जोड़कर) और संख्या तक शून्य सूचियां (केवल एक सेंटिनल सम्मिलित करके) जोड़कर एक संतुलित बाइनरी ट्री के रूप में दर्शाया जा सकता है। सूचियाँ दो की शक्ति है। संतुलित ट्री को एक ही सारणी में संग्रहित किया जा सकता है। वर्तमान सूचकांक को दो से विभाजित करके मूल तत्व तक पहुंचा जा सकता है।


जब पत्तबं में से एक को अद्यतन किया जाता है, तब पत्ते से जड़ तक सभी खेल दोबारा खेले जाते हैं। निम्नलिखित [[छद्मकोड]] में, एक सरणी के अतिरिक्त एक ऑब्जेक्ट ओरिएंटेड ट्री का उपयोग किया जाता है क्योंकि इसे समझना आसान है। इसके अतिरिक्त, विलय की जाने वाली सूचियों की संख्या दो की घात मानी जाती है।
जब पत्तों में से एक को अद्यतन किया जाता है, तब पत्ते से जड़ तक सभी खेल दोबारा खेले जाते हैं। इस प्रकार निम्नलिखित [[छद्मकोड|स्यूडोकोड]] में, एक सरणी के अतिरिक्त एक ऑब्जेक्ट ओरिएंटेड ट्री का उपयोग किया जाता है क्योंकि इसे समझना आसान है। इसके अतिरिक्त, विलय की जाने वाली सूचियों की संख्या दो की घात मानी जाती है।
  '''function''' merge(L1, ..., Ln)
  '''function''' merge(L1, ..., Ln)
    buildTree(heads of L1, ..., Ln)
  buildTree(heads of L1, ..., Ln)
    '''while''' tree has elements
  '''while''' tree has elements
        winner := tree.winner
  winner := tree.winner
        output winner.value
  output winner.value
        new := winner.index.next
  new := winner.index.next
        replayGames(winner, new) // Replacement selection
  replayGames(winner, new) // Replacement selection


  '''function''' replayGames(node, new)
  '''function''' replayGames(node, new)
    loser, winner := playGame(node, new)
  loser, winner := playGame(node, new)
    node.value := loser.value
  node.value := loser.value
    node.index := loser.index
  node.index := loser.index
    '''if''' node != root
  '''if''' node != root
        replayGames(node.parent, winner)
  replayGames(node.parent, winner)


  '''function''' buildTree(elements)
  '''function''' buildTree(elements)
    nextLayer := new Array()
  nextLayer := new Array()
    '''while''' elements not empty
  '''while''' elements not empty
        el1 := elements.take()
  el1 := elements.take()
        el2 := elements.take()
  el2 := elements.take()
        loser, winner := playGame(el1, el2)
  loser, winner := playGame(el1, el2)
        parent := new Node(el1, el2, loser)
  parent := new Node(el1, el2, loser)
        nextLayer.add(parent)
  nextLayer.add(parent)
    '''if''' nextLayer.size == 1
  '''if''' nextLayer.size == 1
        '''return''' nextLayer // only root
  '''return''' nextLayer // only root
    '''else'''
  '''else'''
        '''return''' buildTree(nextLayer)
  '''return''' buildTree(nextLayer)


===== चलने का समय =====
===== कार्यकारी समय =====


शुरुआत में, पेड़ पहली बार Θ(k) समय में बनाया गया है। विलय के प्रत्येक चरण में, केवल नए तत्व से रूट तक के पथ पर गेम को फिर से चलाने की आवश्यकता होती है। प्रत्येक परत में, केवल एक तुलना की आवश्यकता है। चूँकि पेड़ संतुलित है, इनपुट सरणियों में से एक से रूट तक के पथ में केवल Θ(लॉग k) तत्व होते हैं। कुल मिलाकर, ऐसे n तत्व हैं जिन्हें स्थानांतरित करने की आवश्यकता है। परिणामस्वरूप कुल चलने का समय Θ(n log k) में है।<ref name="knuth98" />
शुरुआत में, ट्री पहली बार Θ(k) समय में बनाया गया है। विलय के प्रत्येक चरण में, केवल नए तत्व से रूट तक के पथ पर गेम को फिर से चलाने की आवश्यकता होती है। इस प्रकार प्रत्येक परत में, केवल एक तुलना की आवश्यकता है। चूँकि ट्री संतुलित है, इनपुट सरणियों में से एक से रूट तक के पथ में केवल Θ(लॉग k) तत्व होते हैं। कुल मिलाकर, ऐसे n तत्व हैं जिन्हें स्थानांतरित करने की आवश्यकता है। परिणामस्वरूप कुल चलने का समय Θ(n log k) में है।<ref name="knuth98" />
===== उदाहरण =====
===== उदाहरण =====


Line 143: Line 144:
====== प्रतिस्थापन चयन ======
====== प्रतिस्थापन चयन ======


खेल नीचे से ऊपर तक दोबारा खेले जाते हैं। पेड़ की प्रत्येक परत में, नोड का वर्तमान में संग्रहीत तत्व और नीचे की परत से प्रदान किया गया तत्व प्रतिस्पर्धा करते हैं। विजेता को तब तक शीर्ष पर पदोन्नत किया जाता है जब तक हमें नया समग्र विजेता नहीं मिल जाता। हारने वाला पेड़ के नोड में संग्रहीत होता है।
खेल नीचे से ऊपर तक दोबारा खेले जाते हैं। ट्री की प्रत्येक परत में, नोड का वर्तमान में संग्रहीत तत्व और नीचे की परत से प्रदान किया गया तत्व प्रतिस्पर्धा करते हैं। इस प्रकार विजेता को तब तक शीर्ष पर पदोन्नत किया जाता है जब तक हमें नया समग्र विजेता नहीं मिल जाता हैं। हारने वाला ट्री के नोड में संग्रहीत होता है।


[[File:Loser tree replacement selection.gif|केंद्र|अंगूठा|प्रतिस्थापन चयन के लिए उदाहरण]]
[[File:Loser tree replacement selection.gif|केंद्र|अंगूठा|प्रतिस्थापन चयन के लिए उदाहरण]]
Line 149: Line 150:
{| class="wikitable"
{| class="wikitable"
|-
|-
! स्टेप !! कार्य
! चरण !! कार्य
|-
|-
| 1 || लीफ 1 (समग्र विजेता) को इनपुट सूची से अगले तत्व 9 से बदल दिया गया है।
| 1 || लीफ 1 (समग्र विजेता) को इनपुट सूची से अगले तत्व 9 से बदल दिया गया है।
Line 162: Line 163:
|}
|}
====== मर्ज ======
====== मर्ज ======
मर्ज को निष्पादित करने के लिए, समग्र सबसे छोटे तत्व को बार-बार अगले इनपुट तत्व के साथ प्रतिस्थापित किया जाता है। उसके पश्चात्, शीर्ष तक के खेल दोबारा खेले जाते हैं।
मर्ज को निष्पादित करने के लिए, समग्र सबसे छोटे तत्व को बार-बार अगले इनपुट तत्व के साथ प्रतिस्थापित किया जाता है। इस प्रकार उसके पश्चात्, शीर्ष तक के खेल दोबारा खेले जाते हैं।


यह उदाहरण इनपुट के रूप में चार क्रमबद्ध सरणियों का उपयोग करता है।
यह उदाहरण इनपुट के रूप में चार क्रमबद्ध सरणियों का उपयोग करता है।
Line 171: Line 172:
  {4, 8, 9}
  {4, 8, 9}


एल्गोरिदम की शुरुआत प्रत्येक इनपुट सूची के प्रमुखों से की जाती है। इन तत्वों का उपयोग करके, हारे हुए लोगों का एक द्विआधारी वृक्ष बनाया जाता है। विलय के लिए, निम्नतम सूची तत्व 2 को पेड़ के शीर्ष पर समग्र न्यूनतम तत्व को देखकर निर्धारित किया जाता है। फिर उस मान को हटा दिया जाता है, और उसके पत्ते को 7 से भर दिया जाता है, जो इनपुट सूची में अगला मान है। प्रतिस्थापन चयन के बारे में पिछले अनुभाग की तरह शीर्ष पर जाने वाले खेल दोबारा खेले जाते हैं। हटाया जाने वाला अगला तत्व 3 है। सूची में अगले मान 6 से प्रारंभ करके, गेम को रूट तक दोबारा खेला जाता है। इसे तब तक दोहराया जा रहा है जब तक कि पेड़ का न्यूनतम मान अनंत के सामान्तर न हो जाए।
एल्गोरिदम की शुरुआत प्रत्येक इनपुट सूची के प्रमुखों से की जाती है। इन तत्वों का उपयोग करके, हारे हुए लोगों का एक द्विआधारी ट्री बनाया जाता है। इस प्रकार विलय के लिए, निम्नतम सूची तत्व 2 को ट्री के शीर्ष पर समग्र न्यूनतम तत्व को देखकर निर्धारित किया जाता है। फिर उस मान को हटा दिया जाता है, और उसके पत्ते को 7 से भर दिया जाता है, जो इनपुट सूची में अगला मान है। प्रतिस्थापन चयन के बारे में पिछले अनुभाग की तरह शीर्ष पर जाने वाले खेल दोबारा खेले जाते हैं। इस प्रकार हटाया जाने वाला अगला तत्व 3 है। सूची में अगले मान 6 से प्रारंभ करके, गेम को रूट तक दोबारा खेला जाता है। इसे तब तक दोहराया जा रहा है जब तक कि ट्री का न्यूनतम मान अनंत के सामान्तर न हो जाए।


[[File:Loser tree merge.gif|संपूर्ण एल्गोरिथम के लिए केंद्र|अंगूठा|विज़ुअलाइज़ेशन]]
[[File:Loser tree merge.gif|संपूर्ण एल्गोरिथम के लिए केंद्र|अंगूठा|विज़ुअलाइज़ेशन]]
Line 177: Line 178:
=== चलने के समय की निचली सीमा ===
=== चलने के समय की निचली सीमा ===


कोई यह दिखा सकता है कि O(n f(k)) में चलने वाले समय के साथ कोई तुलना-आधारित k-वे मर्ज एल्गोरिदम उपस्तिथ नहीं है, जहां f एक लघुगणक की तुलना में असम्बद्ध रूप से धीमी गति से बढ़ता है, और n तत्वों की कुल संख्या है।
कोई यह दिखा सकता है कि O(n f(k)) में चलने वाले समय के साथ कोई तुलना-आधारित k-वे मर्ज एल्गोरिदम उपस्तिथ नहीं है, इस प्रकार जहां f एक लघुगणक की तुलना में असम्बद्ध रूप से धीमी गति से बढ़ता है, और n तत्वों की कुल संख्या है।


(असंयुक्त श्रेणियों जैसे वांछनीय वितरण वाले डेटा को छोड़कर।)
(असंयुक्त श्रेणियों जैसे वांछनीय वितरण वाले डेटा को छोड़कर।)


इसका प्रमाण तुलना-आधारित छँटाई से एक सीधा-सीधा कमी है।
इसका प्रमाण तुलना-आधारित छँटाई से एक सीधी कमी है।
मान लीजिए कि ऐसा कोई एल्गोरिदम उपस्तिथ है, तब हम निम्न प्रकार से रनिंग टाइम O(n f(n)) के साथ तुलना-आधारित सॉर्टिंग एल्गोरिदम का निर्माण कर सकते हैं:
 
मान लीजिए कि ऐसा कोई एल्गोरिदम उपस्तिथ है, तब हम निम्न प्रकार से रनिंग टाइम O(n f(n)) के साथ तुलना-आधारित सॉर्टिंग एल्गोरिदम का निर्माण इस प्रकार कर सकते हैं:
 
इनपुट ऐरे को आकार 1 के n ऐरे में काटें।
इनपुट ऐरे को आकार 1 के n ऐरे में काटें।


इन n सरणियों को k-वे मर्ज एल्गोरिथम के साथ मर्ज करें।
इन n सरणियों को k-वे मर्ज एल्गोरिथम के साथ मर्ज करें।
परिणामी सरणी को क्रमबद्ध किया गया है और एल्गोरिथ्म में O(n f(n)) में चलने का समय है।
परिणामी सरणी को क्रमबद्ध किया गया है और एल्गोरिथ्म में O(n f(n)) में चलने का समय है।


Line 191: Line 195:


== बाहरी छँटाई ==
== बाहरी छँटाई ==
के-वे मर्ज का उपयोग बाहरी सॉर्टिंग प्रक्रियाओं में किया जाता है।<ref>{{Cite book|title = C++ में डेटा संरचनाएं और एल्गोरिथम विश्लेषण, तीसरा संस्करण|url = https://books.google.com/books?id=AijEAgAAQBAJ|publisher = Courier Corporation|date = 2012-07-26|isbn = 9780486172620|first = Clifford A.|last = Shaffer}}</ref> बाहरी सॉर्टिंग सॉर्टिंग एल्गोरिदम का एक वर्ग है जो भारी मात्रा में डेटा को संभाल सकता है। बाहरी सॉर्टिंग की आवश्यकता तब होती है जब सॉर्ट किया जा रहा डेटा कंप्यूटिंग डिवाइस (सामान्यतः रैम) की मुख्य मेमोरी में फिट नहीं होता है और इसके अतिरिक्त उन्हें धीमी बाहरी मेमोरी (सामान्यतः हार्ड ड्राइव) में रहना चाहिए। के-वे मर्ज एल्गोरिदम सामान्यतः बाहरी सॉर्टिंग एल्गोरिदम के दूसरे चरण में होते हैं, ठीक वैसे ही जैसे वे मर्ज सॉर्ट के लिए करते हैं।
के-वे मर्ज का उपयोग बाहरी सॉर्टिंग प्रक्रियाओं में किया जाता है।<ref>{{Cite book|title = C++ में डेटा संरचनाएं और एल्गोरिथम विश्लेषण, तीसरा संस्करण|url = https://books.google.com/books?id=AijEAgAAQBAJ|publisher = Courier Corporation|date = 2012-07-26|isbn = 9780486172620|first = Clifford A.|last = Shaffer}}</ref> बाहरी सॉर्टिंग सॉर्टिंग एल्गोरिदम का एक वर्ग है जो भारी मात्रा में डेटा को संभाल सकता है। इस प्रकार बाहरी सॉर्टिंग की आवश्यकता तब होती है जब सॉर्ट किया जा रहा डेटा कंप्यूटिंग डिवाइस (सामान्यतः रैम) की मुख्य मेमोरी में फिट नहीं होता है और इसके अतिरिक्त उन्हें धीमी बाहरी मेमोरी (सामान्यतः हार्ड ड्राइव) में रहना चाहिए। इस प्रकार '''के-वे मर्ज एल्गोरिदम''' सामान्यतः बाहरी सॉर्टिंग एल्गोरिदम के दूसरे चरण में होते हैं, ठीक वैसे ही जैसे वे मर्ज सॉर्ट के लिए करते हैं।


मल्टीवे मर्ज मेमोरी के बाहर की फ़ाइलों को बाइनरी मर्ज की तुलना में कम पास में मर्ज करने की अनुमति देता है। यदि 6 रन हैं जिन्हें मर्ज करने की आवश्यकता है तब एक बाइनरी मर्ज को 3 मर्ज पास लेने की आवश्यकता होगी, 6-वे मर्ज के एकल मर्ज पास के विपरीत। मर्ज पास की यह कमी विशेष रूप से बड़ी मात्रा में जानकारी को ध्यान में रखते हुए महत्वपूर्ण है जिसे सामान्यतः पहले स्थान पर क्रमबद्ध किया जाता है, जिससे अधिक गति-अप की अनुमति मिलती है जबकि धीमी भंडारण तक पहुंच की मात्रा भी कम हो जाती है।
मल्टीवे मर्ज मेमोरी के बाहर की फ़ाइलों को बाइनरी मर्ज की तुलना में कम पास में मर्ज करने की अनुमति देता है। यदि 6 रन हैं जिन्हें मर्ज करने की आवश्यकता है तब एक बाइनरी मर्ज को 3 मर्ज पास लेने की आवश्यकता होगी, 6-वे मर्ज के एकल मर्ज पास के विपरीत। मर्ज पास की यह कमी विशेष रूप से बड़ी मात्रा में जानकारी को ध्यान में रखते हुए महत्वपूर्ण है जिसे सामान्यतः पहले स्थान पर क्रमबद्ध किया जाता है, जिससे अधिक गति-अप की अनुमति मिलती है जबकि धीमी भंडारण तक पहुंच की मात्रा भी कम हो जाती है।
Line 197: Line 201:
== संदर्भ ==
== संदर्भ ==
{{Reflist}}
{{Reflist}}
[[Category: छँटाई एल्गोरिदम]]


[[Category: Machine Translated Page]]
[[Category:Created On 07/07/2023]]
[[Category:Created On 07/07/2023]]
[[Category:Machine Translated Page]]
[[Category:Pages with ignored display titles]]
[[Category:Pages with script errors]]
[[Category:Templates Vigyan Ready]]
[[Category:छँटाई एल्गोरिदम]]

Latest revision as of 11:45, 26 July 2023

कंप्यूटर विज्ञान में, के-वे मर्ज एल्गोरिदम या मल्टीवे मर्ज एक विशिष्ट प्रकार k अनुक्रम मर्ज एल्गोरिदम हैं जो k क्रमबद्ध सूचियों को लेने और उन्हें एक एकल क्रमबद्ध सूची में विलय करने में विशेषज्ञ हैं। यह मर्ज एल्गोरिदम सामान्यतः मर्ज एल्गोरिदम को संदर्भित करते हैं जो दो से अधिक क्रमबद्ध सूचियों को लेते हैं। इस प्रकार दो-तरफा मर्ज को बाइनरी मर्ज भी कहा जाता है। के-वे मर्ज बाहरी सॉर्टिंग एल्गोरिदम भी है।

दोतरफा विलय

मर्ज़ सॉर्ट में इसकी महत्वपूर्ण भूमिका के कारण 2-तरफ़ा मर्ज, या बाइनरी मर्ज का बड़े पैमाने पर अध्ययन किया गया है। इस प्रकार इसका एक उदाहरण क्लासिक मर्ज है जो मर्ज सॉर्ट उदाहरणों में अधिकांशतः दिखाई देता है। क्लासिक मर्ज प्रत्येक चरण में सबसे कम कुंजी के साथ डेटा आइटम को आउटपुट करता है; कुछ क्रमबद्ध सूचियों को देखते हुए, यह एक क्रमबद्ध सूची तैयार करता है जिसमें किसी भी इनपुट सूची में सभी तत्व सम्मिलित होते हैं, और यह इनपुट सूचियों की लंबाई के योग के अनुपात में समय पर ऐसा करता है।

बढ़ते क्रम में क्रमबद्ध दो सरणियों को A[1..p] और B[1..q] द्वारा निरूपित करें।

इसके अतिरिक्त, आउटपुट ऐरे को C[1..n] से निरूपित करें।

कैनोनिकल 2-वे मर्ज एल्गोरिदम[1] सूचकांक i, j, और k को क्रमशः A, B, और C में संग्रहीत करता है।

प्रारंभ में, यह सूचकांक पहले तत्व को संदर्भित करते हैं, अर्थात 1 हैं।

यदि A[i] < B[j], तब एल्गोरिथ्म A[i] को C[k] में कॉपी करता है और i और k को बढ़ाता है।

अन्यथा, एल्गोरिदम B[j] को C[k] में कॉपी करता है और j और k को बढ़ाता है।

एक विशेष मामला उत्पन्न होता है यदि i या j में से कोई भी A या B के अंत तक पहुँच गया है।

इस स्थितियों में एल्गोरिदम B या A के शेष तत्वों को C में कॉपी करता है और समाप्त करता है।

के-वे मर्ज

के-वे मर्ज समस्या में समान तत्वों के साथ एकल क्रमबद्ध सरणी बनाने के लिए k क्रमबद्ध सरणियों को मर्ज करना सम्मिलित है।

तत्वों की कुल संख्या को n से निरूपित करें।

इस प्रकार n आउटपुट ऐरे k आकार और k इनपुट ऐरे k आकार के योग के सामान्तर है।

सरलता के लिए, हम मानते हैं कि कोई भी इनपुट ऐरे खाली नहीं है।

एक परिणाम के रूप में , जो सूची किए गए चलने के समय को सरल बनाता है।

उसमें समस्या का समाधान किया जा सकता है के साथ समय चल रहा है अंतरिक्ष।

इस रनिंग टाइम को प्राप्त करने वाले अनेक एल्गोरिदम उपस्तिथ हैं।

पुनरावृत्तीय 2-तरफा विलय

समस्या को 2-तरफा मर्ज का उपयोग करके दो k सरणियों को पुनरावृत्त रूप से मर्ज करके हल किया जा सकता है जब तक कि केवल एक ही ऐरे न रह जाए। इस प्रकार यदि सरणियों को मनमाने क्रम में मर्ज किया जाता है, तब परिणामी रनिंग समय केवल O(kn) होता है। यह उप-इष्टतम है.

पहले को दूसरे के साथ, तीसरे को चौथे के साथ, इत्यादि को पुनरावृत्त रूप से विलय करके चलने के समय में सुधार किया जा सकता है। चूँकि प्रत्येक पुनरावृत्ति में सरणियों की संख्या आधी हो जाती है, केवल Θ(लॉग k) पुनरावृत्तियाँ होती हैं। इस प्रकार प्रत्येक पुनरावृत्ति में प्रत्येक तत्व को ठीक एक बार स्थानांतरित किया जाता है। इसलिए प्रति पुनरावृत्ति चलने का समय Θ(n) में है क्योंकि n तत्वों की संख्या है। इसलिए कुल चलने का समय Θ(n log k) में है।

हम दो सबसे छोटी सरणियों को पुनरावृत्त रूप से मर्ज करके, इस एल्गोरिदम में और सुधार कर सकते हैं। इस प्रकार यह स्पष्ट है कि यह चलने के समय को कम करता है और इसलिए पिछले पैराग्राफ में वर्णित रणनीति से बदतर नहीं हो सकता है। इसलिए चलने का समय O(n log k) में है। सौभाग्य से, सीमावर्ती स्थितियों में चलने का समय उत्तम हो सकता है। उदाहरण के लिए पतित स्थितियों पर विचार करें, जहां एक सरणी को छोड़कर सभी में केवल एक तत्व होता है। इस प्रकार पिछले पैराग्राफ में बताई गई रणनीति के लिए Θ(n log k) रनिंग टाइम की आवश्यकता होती है, जबकि उत्तम रणनीति के लिए केवल Θ(n + k log k) रनिंग टाइम की आवश्यकता होती है।

डायरेक्ट के-वे मर्ज

इस स्थितियों में, हम एक साथ k-रन को एक साथ मर्ज कर देंगे।

एक सीधा कार्यान्वयन न्यूनतम निर्धारित करने के लिए सभी k सरणियों को स्कैन करेगा।

इस सीधे कार्यान्वयन के परिणामस्वरूप Θ(kn) का रनिंग टाइम प्राप्त होता है।

ध्यान दें कि इसका उल्लेख केवल चर्चा के लिए एक संभावना के रूप में किया गया है। चूँकि यह काम करेगा, किन्तु यह कुशल नहीं है।

हम सबसे छोटे तत्व की तेजी से गणना करके इसमें सुधार कर सकते हैं।

हीप (डेटा संरचना), टूर्नामेंट ट्री, या बिखरा हुआ ट्री का उपयोग करके, सबसे छोटा तत्व O(लॉग k) समय में निर्धारित किया जा सकता है।

इसलिए परिणामी चलने का समय O(n log k) में है।

ढेर का उपयोग सामान्यतः अधिक किया जाता है, चूंकि टूर्नामेंट ट्री व्यवहार में तेज़ होता है। एक ढेर प्रत्येक चरण में लगभग 2*लॉग(k) तुलनाओं का उपयोग करता है क्योंकि यह ट्री को जड़ से नीचे तक संभालता है और प्रत्येक नोड के दोनों बच्चों की तुलना करने की आवश्यकता होती है। इस प्रकार इस मध्य, एक टूर्नामेंट ट्री को केवल लॉग (के) तुलना की आवश्यकता होती है क्योंकि यह ट्री के नीचे से प्रारंभ होता है और जड़ तक काम करता है, प्रत्येक परत में केवल एक ही तुलना करता है। इसलिए टूर्नामेंट ट्री को पसंदीदा कार्यान्वयन होना चाहिए।

ढेर

विचार यह है कि k सूचियों का न्यूनतम-ढेर बनाए रखा जाए, प्रत्येक को उनके सबसे छोटे वर्तमान तत्व द्वारा कुंजीबद्ध किया जाए। इस प्रकार एक सरल एल्गोरिदम ढेर से नोड्स के साथ एक आउटपुट बफर बनाता है। इस प्रकार नोड्स का एक न्यूनतम-ढेर बनाकर प्रारंभ करें, जहां प्रत्येक नोड में सूची का एक प्रमुख तत्व और सूची का शेष (या पूंछ) होता है। चूँकि सूचियाँ प्रारंभ में क्रमबद्ध होती हैं, शीर्ष प्रत्येक सूची का सबसे छोटा तत्व होता है; हीप प्रॉपर्टी गारंटी देती है कि रूट में सभी सूचियों में न्यूनतम तत्व सम्मिलित हैं। हीप से रूट नोड निकालें, हेड एलिमेंट को आउटपुट बफर में जोड़ें, टेल से एक नया नोड बनाएं और इसे हीप में डालें। इस प्रकार तब तक दोहराएं जब तक कि ढेर में केवल एक नोड न रह जाए, उस बिंदु पर बस उस शेष सूची (हेड और टेल) को आउटपुट बफर में जोड़ दें।

पॉइंटर्स का उपयोग करना, एक इन-प्लेस हीप एल्गोरिदम[2] इनपुट सरणियों में पॉइंटर्स का एक न्यूनतम-ढेर आवंटित करता है।

प्रारंभ में यह पॉइंटर्स इनपुट ऐरे के सबसे छोटे तत्वों की ओर संकेत करते हैं।

सूचकों को उस मान के आधार पर क्रमबद्ध किया जाता है जिस पर वे इंगित करते हैं।

O(k) प्रीप्रोसेसिंग चरण में मानक हीपिफ़ाई प्रक्रिया का उपयोग करके ढेर बनाया जाता है।

पश्चात् में, एल्गोरिदम पुनरावृत्त रूप से उस तत्व को स्थानांतरित करता है जिसे रूट पॉइंटर इंगित करता है, इस पॉइंटर को बढ़ाता है और रूट तत्व पर मानक कमी कुंजी प्रक्रिया निष्पादित करता है।

वृद्धि कुंजी प्रक्रिया का चलने का समय O(लॉग k) से घिरा है।

चूँकि n तत्व हैं, कुल चलने का समय O(n log k) है।

ध्यान दें कि कुंजी को बदलने और पुनरावृत्त रूप से कमी-कुंजी या सिफ्ट-डाउन करने का संचालन अनेक प्राथमिकता कतार पुस्तकालयों जैसे सी ++ एसटीएल और जावा द्वारा समर्थित नहीं है। एक्स्ट्रेक्ट-मिन और इंसर्ट फलन करना कम कुशल है।

टूर्नामेंट ट्री

टूर्नामेंट ट्री

टूर्नामेंट ट्री [3] खेल प्रतियोगिताओं की तरह, एक एलिमिनेशन टूर्नामेंट पर आधारित है। प्रत्येक गेम में, दो इनपुट तत्व प्रतिस्पर्धा करते हैं। विजेता को अगले दौर में पदोन्नत किया जाता है। इसलिए, हमें खेलों का एक द्विआधारी ट्री मिलता है। सूची को आरोही क्रम में क्रमबद्ध किया गया है, इसलिए गेम का विजेता दोनों तत्वों में से छोटा होता है।

हारे हुए ट्री

के-वे विलय के लिए, केवल प्रत्येक गेम के हारने वाले को स्टोर करना अधिक कुशल है (छवि देखें)। इसलिए डेटा संरचना को लूज़र ट्री कहा जाता है। इस प्रकार ट्री बनाते समय या किसी तत्व को उसकी सूची में से अगले तत्व से प्रतिस्थापित करते समय, हम अभी भी गेम के विजेता को शीर्ष पर बढ़ावा देते हैं। इस प्रकार ट्री एक खेल मैच की तरह भरा हुआ है किन्तु नोड्स केवल हारने वाले को ही संग्रहीत करते हैं। सामान्यतः, रूट के ऊपर एक अतिरिक्त नोड जोड़ा जाता है जो समग्र विजेता का प्रतिनिधित्व करता है। प्रत्येक पत्ता किसी एक इनपुट ऐरे में एक पॉइंटर संग्रहीत करता है। प्रत्येक आंतरिक नोड एक मान और एक सूचकांक संग्रहीत करता है। इस प्रकार आंतरिक नोड का सूचकांक इंगित करता है कि मान किस इनपुट सरणी से आता है। मान में संबंधित इनपुट सरणी के पहले तत्व की एक प्रति सम्मिलित है।

एल्गोरिथ्म पुनरावृत्त रूप से न्यूनतम तत्व को परिणाम में जोड़ता है और फिर तत्व को संबंधित इनपुट सूची से हटा देता है। यह अद्यतन पत्ती से रूट (प्रतिस्थापन चयन) तक पथ पर नोड्स को अद्यतन करता है। इस प्रकार हटाया गया तत्व समग्र विजेता है। इसलिए, इसने इनपुट ऐरे से रूट तक के पथ पर प्रत्येक गेम जीता है। इनपुट ऐरे से एक नया तत्व चुनते समय, तत्व को रूट के पथ पर पिछले हारे हुए तत्वों के विरुद्ध प्रतिस्पर्धा करने की आवश्यकता होती है। इस प्रकार हारे हुए ट्री का उपयोग करते समय, गेम को दोबारा खेलने के लिए भागीदार पहले से ही नोड्स में संग्रहीत होता है। दोबारा खेले गए प्रत्येक गेम के हारने वाले को नोड में लिखा जाता है और विजेता को पुनरावृत्त रूप से शीर्ष पर पदोन्नत किया जाता है। जब रूट पर पहुंच जाता है, तब नया समग्र विजेता मिल जाता है और विलय के अगले दौर में इसका उपयोग किया जा सकता है।

इस अनुभाग में टूर्नामेंट ट्री और हारने वाले ट्री की छवियां समान डेटा का उपयोग करती हैं और हारने वाले ट्री के काम करने के तरीके को समझने के लिए उनकी तुलना की जा सकती है।

एल्गोरिथम

एक टूर्नामेंट ट्री को इनपुट सूचियों में सेंटिनल्स जोड़कर (अर्थात अनंत के मूल्य के साथ प्रत्येक सूची के अंत में एक सदस्य जोड़कर) और संख्या तक शून्य सूचियां (केवल एक सेंटिनल सम्मिलित करके) जोड़कर एक संतुलित बाइनरी ट्री के रूप में दर्शाया जा सकता है। सूचियाँ दो की शक्ति है। संतुलित ट्री को एक ही सारणी में संग्रहित किया जा सकता है। वर्तमान सूचकांक को दो से विभाजित करके मूल तत्व तक पहुंचा जा सकता है।

जब पत्तों में से एक को अद्यतन किया जाता है, तब पत्ते से जड़ तक सभी खेल दोबारा खेले जाते हैं। इस प्रकार निम्नलिखित स्यूडोकोड में, एक सरणी के अतिरिक्त एक ऑब्जेक्ट ओरिएंटेड ट्री का उपयोग किया जाता है क्योंकि इसे समझना आसान है। इसके अतिरिक्त, विलय की जाने वाली सूचियों की संख्या दो की घात मानी जाती है। 

function merge(L1, ..., Ln)
 buildTree(heads of L1, ..., Ln)
 while tree has elements
 winner := tree.winner
 output winner.value
 new := winner.index.next
 replayGames(winner, new) // Replacement selection

function replayGames(node, new)
 loser, winner := playGame(node, new)
 node.value := loser.value
 node.index := loser.index
 if node != root
 replayGames(node.parent, winner)

function buildTree(elements)
 nextLayer := new Array()
 while elements not empty
 el1 := elements.take()
 el2 := elements.take()
 loser, winner := playGame(el1, el2)
 parent := new Node(el1, el2, loser)
 nextLayer.add(parent)
 if nextLayer.size == 1
 return nextLayer // only root
 else
 return buildTree(nextLayer)
कार्यकारी समय

शुरुआत में, ट्री पहली बार Θ(k) समय में बनाया गया है। विलय के प्रत्येक चरण में, केवल नए तत्व से रूट तक के पथ पर गेम को फिर से चलाने की आवश्यकता होती है। इस प्रकार प्रत्येक परत में, केवल एक तुलना की आवश्यकता है। चूँकि ट्री संतुलित है, इनपुट सरणियों में से एक से रूट तक के पथ में केवल Θ(लॉग k) तत्व होते हैं। कुल मिलाकर, ऐसे n तत्व हैं जिन्हें स्थानांतरित करने की आवश्यकता है। परिणामस्वरूप कुल चलने का समय Θ(n log k) में है।[3]

उदाहरण

निम्नलिखित अनुभाग में प्रतिस्थापन चयन चरण के लिए एक विस्तृत उदाहरण और एकाधिक प्रतिस्थापन चयन वाले पूर्ण मर्ज के लिए एक उदाहरण सम्मिलित है।

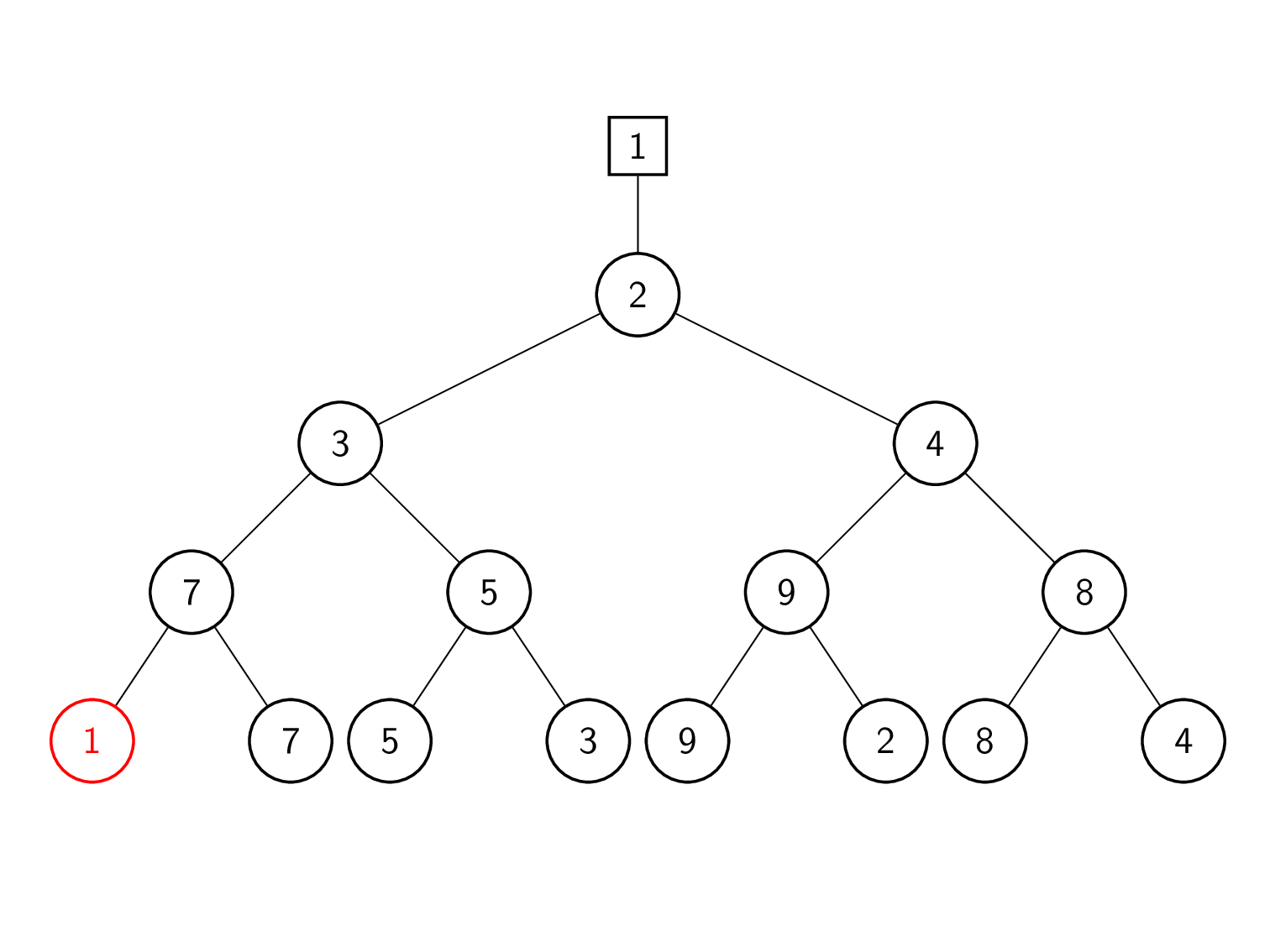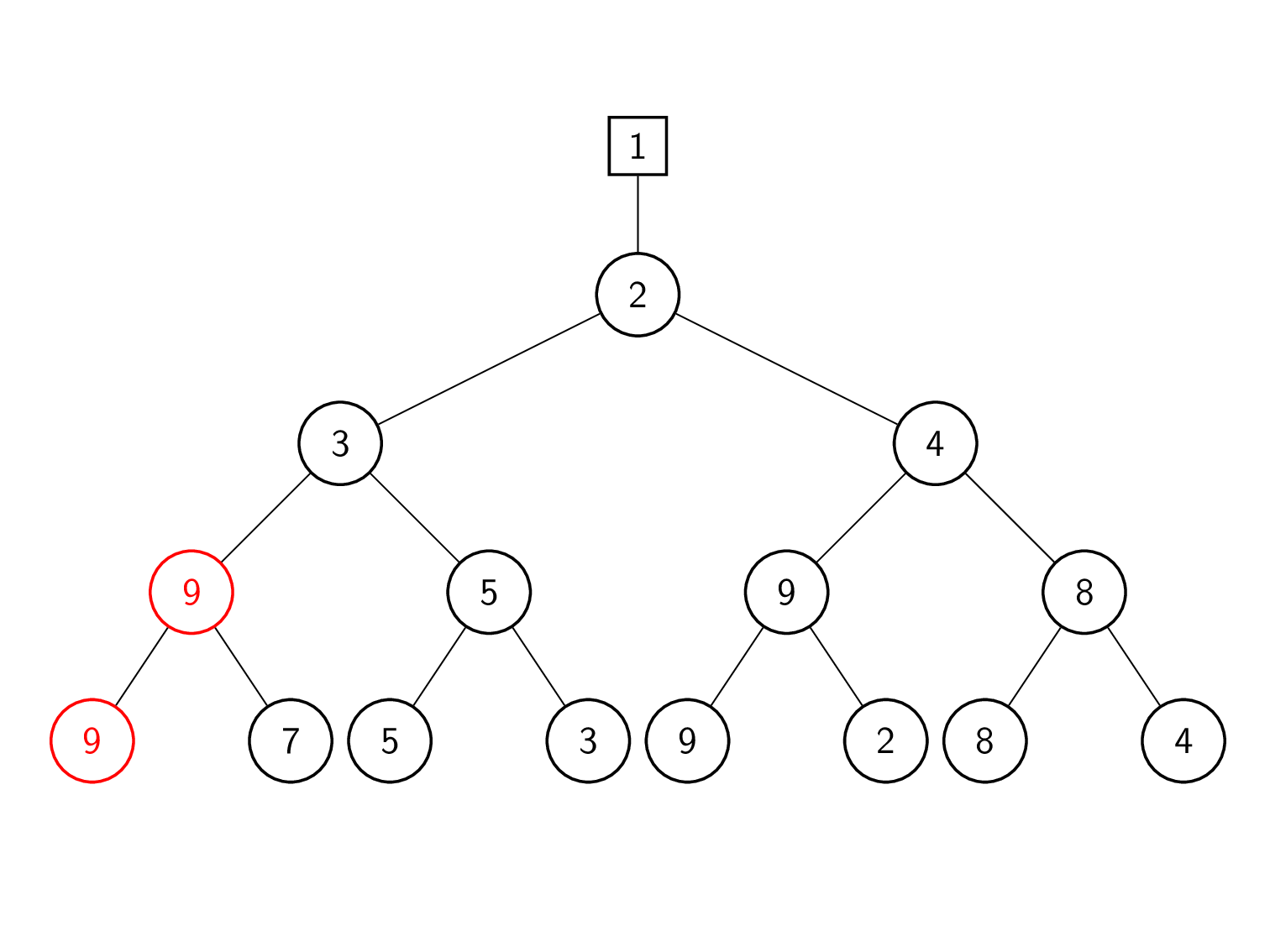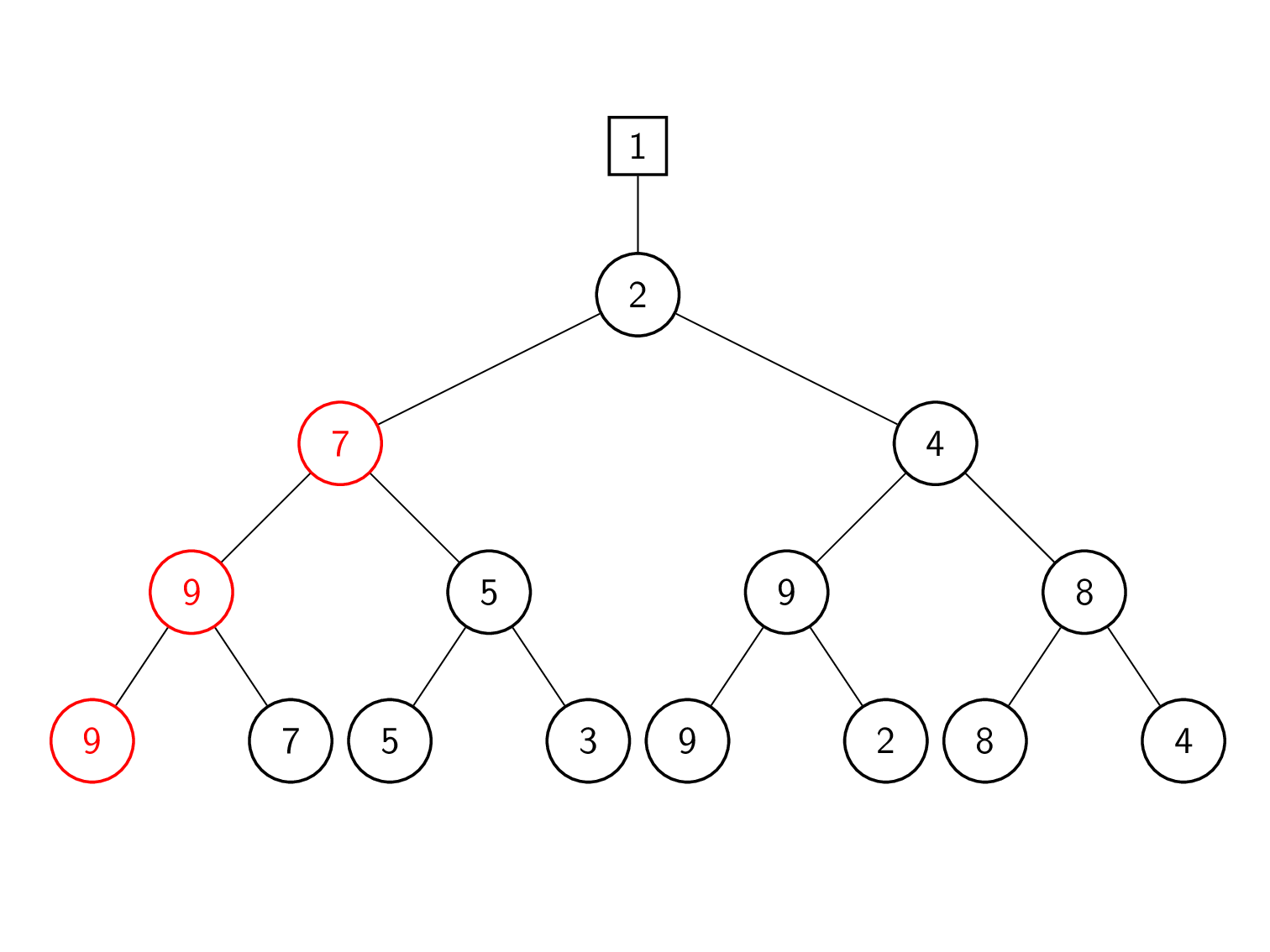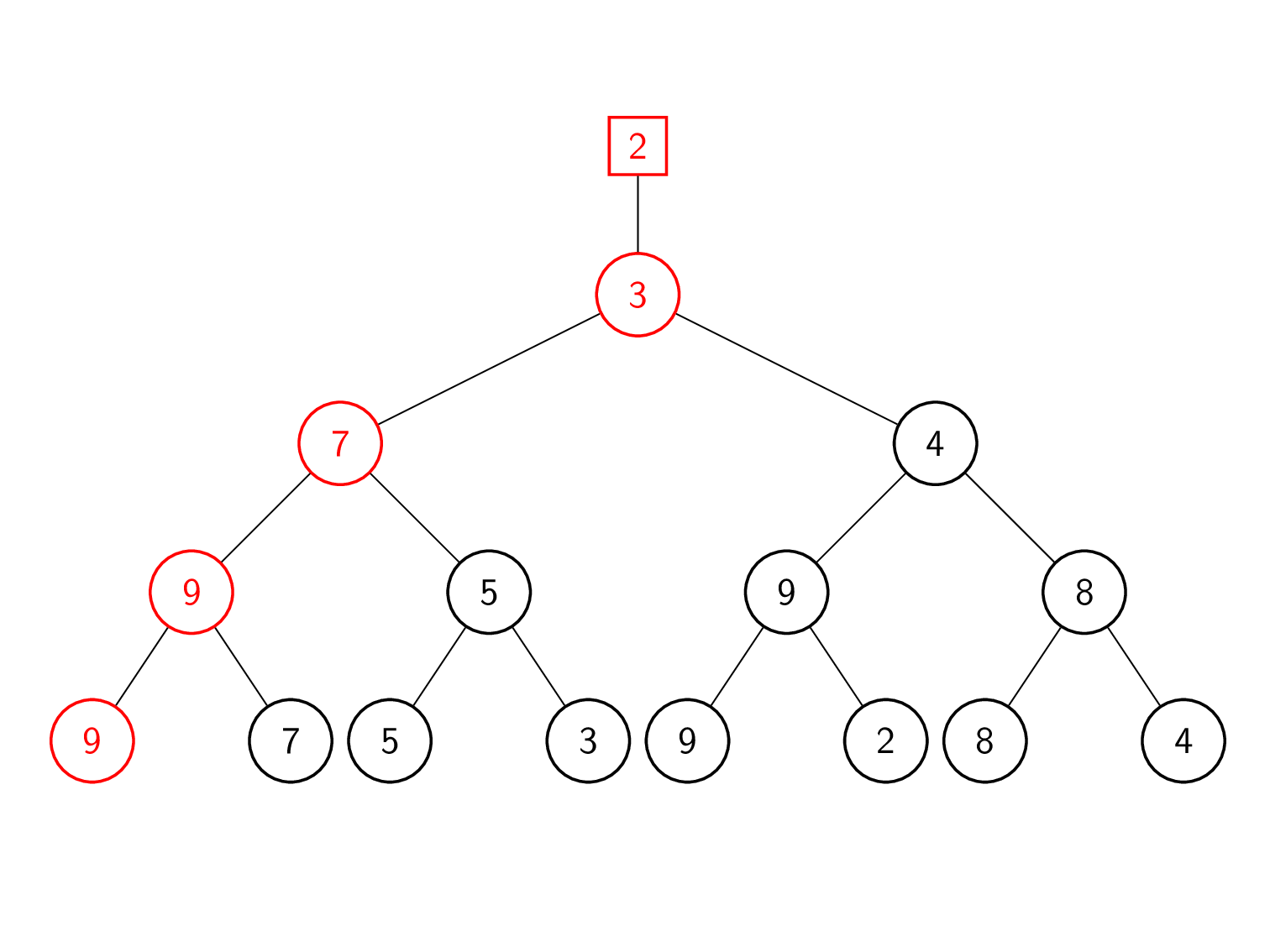
प्रतिस्थापन चयन

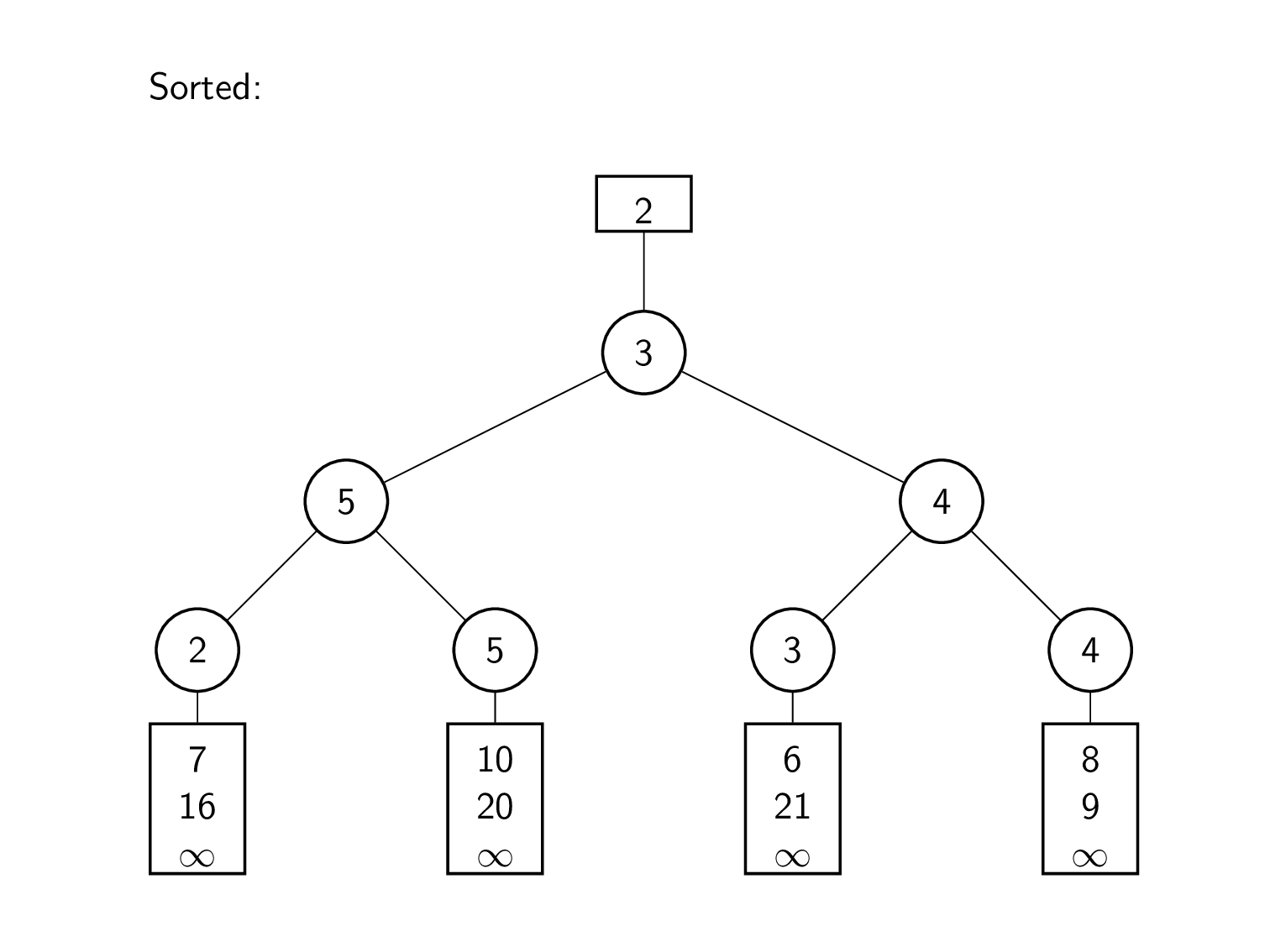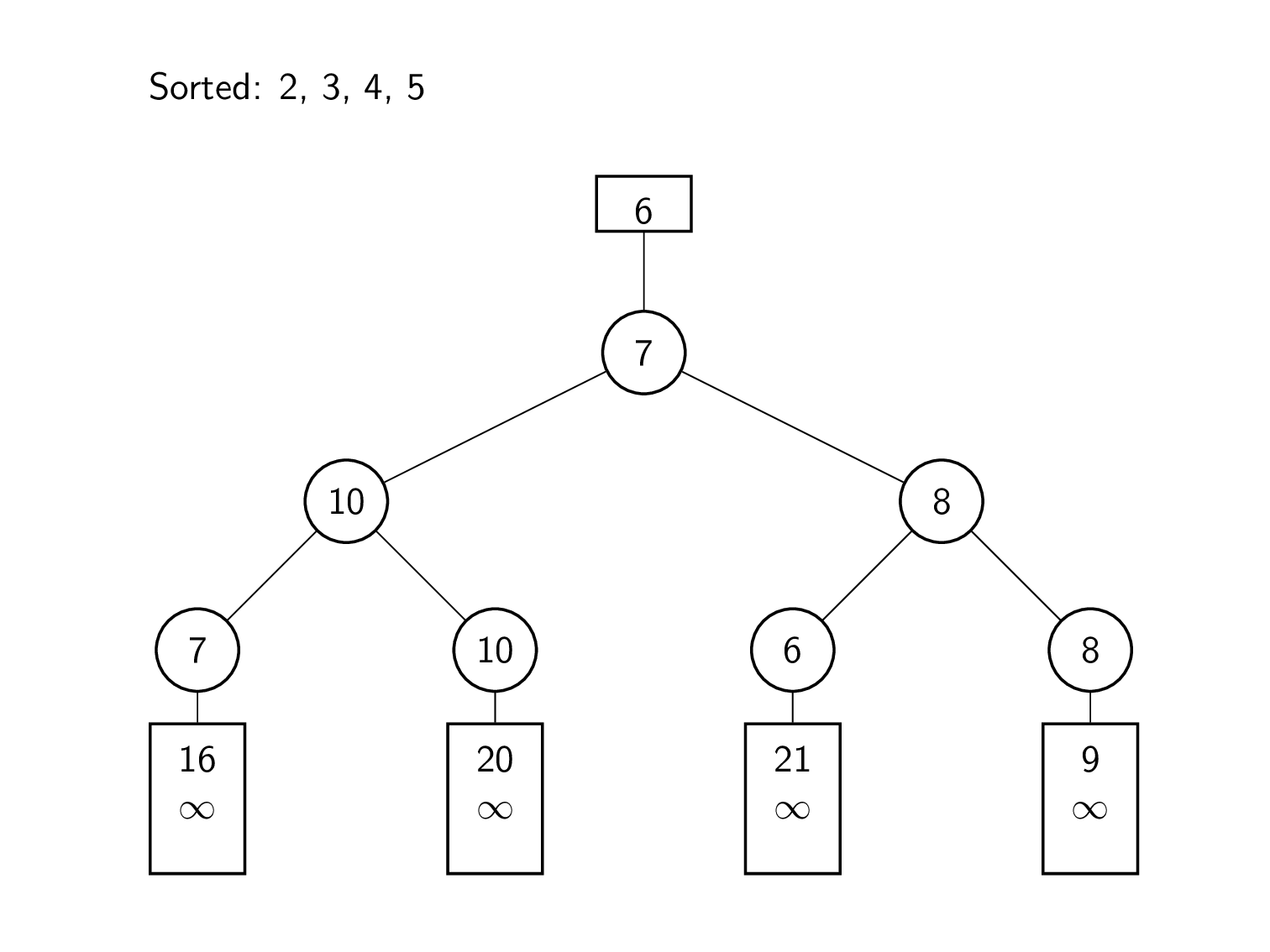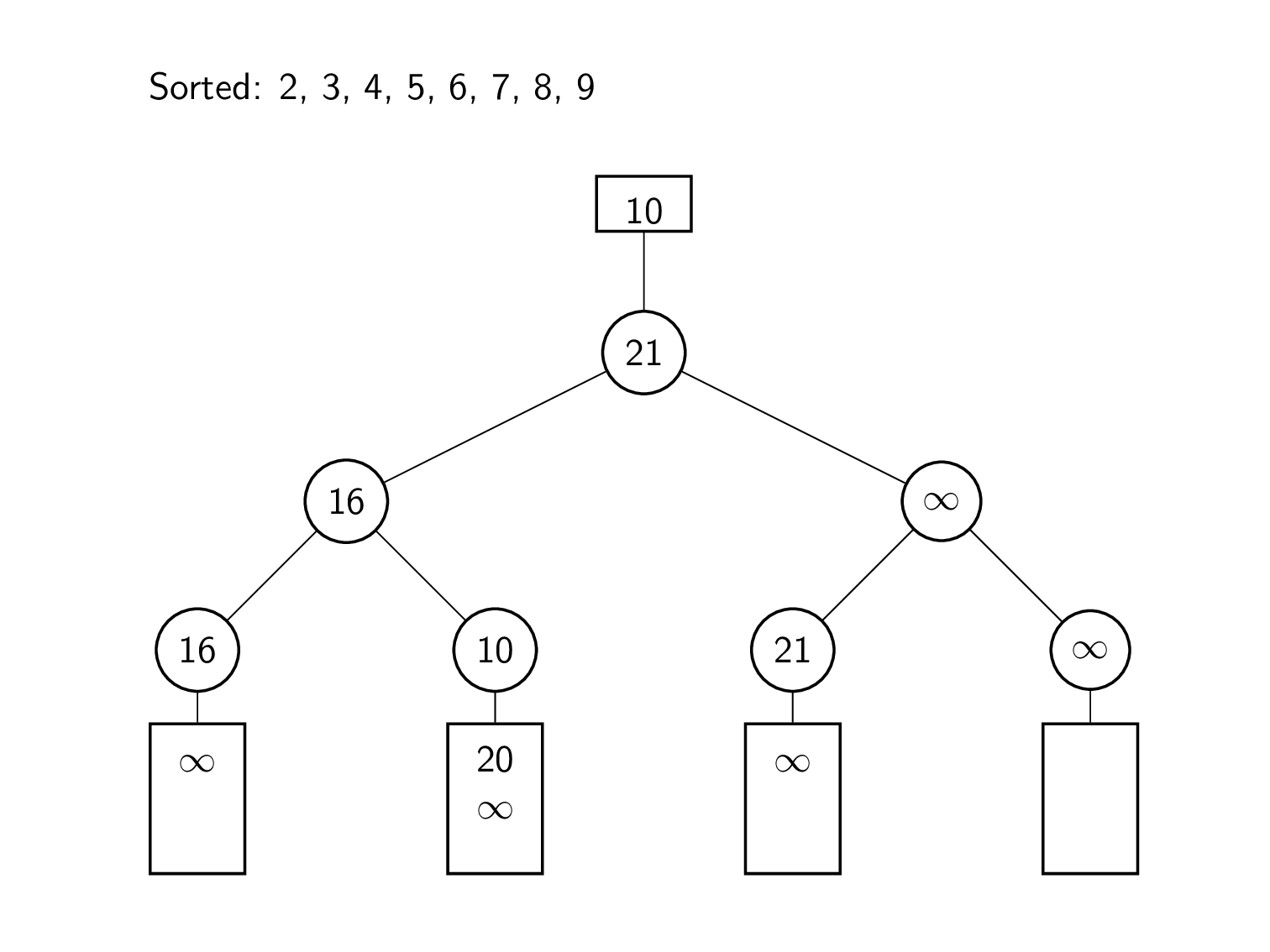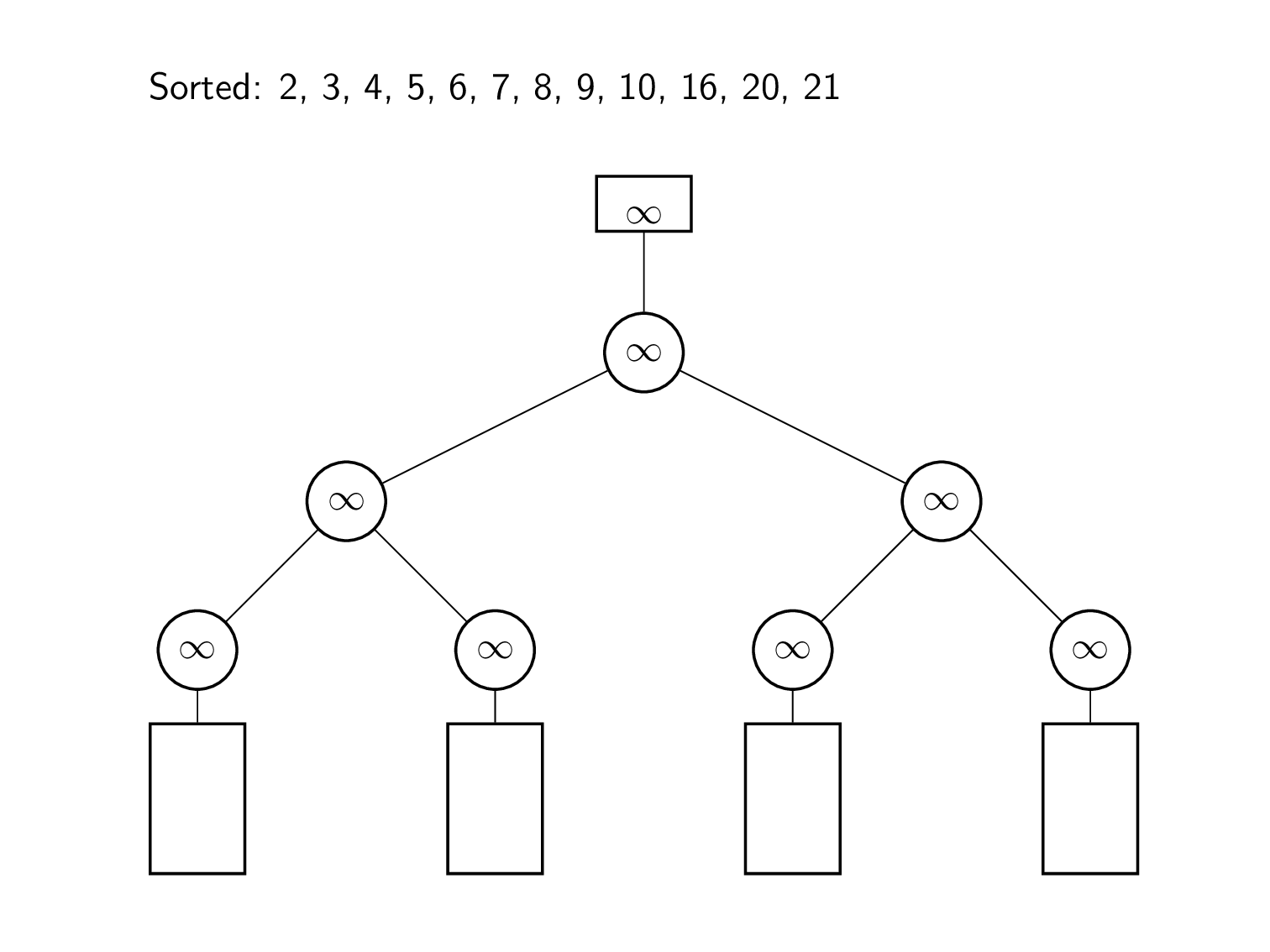
खेल नीचे से ऊपर तक दोबारा खेले जाते हैं। ट्री की प्रत्येक परत में, नोड का वर्तमान में संग्रहीत तत्व और नीचे की परत से प्रदान किया गया तत्व प्रतिस्पर्धा करते हैं। इस प्रकार विजेता को तब तक शीर्ष पर पदोन्नत किया जाता है जब तक हमें नया समग्र विजेता नहीं मिल जाता हैं। हारने वाला ट्री के नोड में संग्रहीत होता है।

प्रतिस्थापन चयन के लिए उदाहरण

चरण कार्य
1 लीफ 1 (समग्र विजेता) को इनपुट सूची से अगले तत्व 9 से बदल दिया गया है।
2 खेल 9 बनाम 7 (पिछला हारा हुआ) दोबारा खेलना। 7 जीतता है क्योंकि यह छोटा है। इसलिए, 7 को शीर्ष पर पदोन्नत किया गया है जबकि 9 को नोड में सहेजा गया है।
3 गेम 7 बनाम 3 (पिछला हारा हुआ) दोबारा खेलना। 3 जीतता है क्योंकि यह छोटा है। इसलिए, 3 को शीर्ष पर पदोन्नत किया गया है जबकि 7 को नोड में सहेजा गया है।
4 गेम 3 बनाम 2 (पिछला हारा हुआ) दोबारा खेलना। 2 जीतता है क्योंकि यह छोटा है। इसलिए, 2 को शीर्ष पर पदोन्नत किया गया है जबकि 3 को नोड में सहेजा गया है।
5 नया समग्र विजेता 2 रूट के ऊपर सहेजा गया है।
मर्ज

मर्ज को निष्पादित करने के लिए, समग्र सबसे छोटे तत्व को बार-बार अगले इनपुट तत्व के साथ प्रतिस्थापित किया जाता है। इस प्रकार उसके पश्चात्, शीर्ष तक के खेल दोबारा खेले जाते हैं।

यह उदाहरण इनपुट के रूप में चार क्रमबद्ध सरणियों का उपयोग करता है। 

{2, 7, 16}
{5, 10, 20}
{3, 6, 21}
{4, 8, 9}

एल्गोरिदम की शुरुआत प्रत्येक इनपुट सूची के प्रमुखों से की जाती है। इन तत्वों का उपयोग करके, हारे हुए लोगों का एक द्विआधारी ट्री बनाया जाता है। इस प्रकार विलय के लिए, निम्नतम सूची तत्व 2 को ट्री के शीर्ष पर समग्र न्यूनतम तत्व को देखकर निर्धारित किया जाता है। फिर उस मान को हटा दिया जाता है, और उसके पत्ते को 7 से भर दिया जाता है, जो इनपुट सूची में अगला मान है। प्रतिस्थापन चयन के बारे में पिछले अनुभाग की तरह शीर्ष पर जाने वाले खेल दोबारा खेले जाते हैं। इस प्रकार हटाया जाने वाला अगला तत्व 3 है। सूची में अगले मान 6 से प्रारंभ करके, गेम को रूट तक दोबारा खेला जाता है। इसे तब तक दोहराया जा रहा है जब तक कि ट्री का न्यूनतम मान अनंत के सामान्तर न हो जाए।

विज़ुअलाइज़ेशन

चलने के समय की निचली सीमा

कोई यह दिखा सकता है कि O(n f(k)) में चलने वाले समय के साथ कोई तुलना-आधारित k-वे मर्ज एल्गोरिदम उपस्तिथ नहीं है, इस प्रकार जहां f एक लघुगणक की तुलना में असम्बद्ध रूप से धीमी गति से बढ़ता है, और n तत्वों की कुल संख्या है।

(असंयुक्त श्रेणियों जैसे वांछनीय वितरण वाले डेटा को छोड़कर।)

इसका प्रमाण तुलना-आधारित छँटाई से एक सीधी कमी है।

मान लीजिए कि ऐसा कोई एल्गोरिदम उपस्तिथ है, तब हम निम्न प्रकार से रनिंग टाइम O(n f(n)) के साथ तुलना-आधारित सॉर्टिंग एल्गोरिदम का निर्माण इस प्रकार कर सकते हैं:

इनपुट ऐरे को आकार 1 के n ऐरे में काटें।

इन n सरणियों को k-वे मर्ज एल्गोरिथम के साथ मर्ज करें।

परिणामी सरणी को क्रमबद्ध किया गया है और एल्गोरिथ्म में O(n f(n)) में चलने का समय है।

यह सुविख्यात परिणाम का विरोधाभास है कि O(n log n) के नीचे सबसे खराब स्थिति में चलने वाले समय के साथ कोई तुलना-आधारित सॉर्टिंग एल्गोरिदम उपस्तिथ नहीं है।

बाहरी छँटाई

के-वे मर्ज का उपयोग बाहरी सॉर्टिंग प्रक्रियाओं में किया जाता है।[4] बाहरी सॉर्टिंग सॉर्टिंग एल्गोरिदम का एक वर्ग है जो भारी मात्रा में डेटा को संभाल सकता है। इस प्रकार बाहरी सॉर्टिंग की आवश्यकता तब होती है जब सॉर्ट किया जा रहा डेटा कंप्यूटिंग डिवाइस (सामान्यतः रैम) की मुख्य मेमोरी में फिट नहीं होता है और इसके अतिरिक्त उन्हें धीमी बाहरी मेमोरी (सामान्यतः हार्ड ड्राइव) में रहना चाहिए। इस प्रकार के-वे मर्ज एल्गोरिदम सामान्यतः बाहरी सॉर्टिंग एल्गोरिदम के दूसरे चरण में होते हैं, ठीक वैसे ही जैसे वे मर्ज सॉर्ट के लिए करते हैं।

मल्टीवे मर्ज मेमोरी के बाहर की फ़ाइलों को बाइनरी मर्ज की तुलना में कम पास में मर्ज करने की अनुमति देता है। यदि 6 रन हैं जिन्हें मर्ज करने की आवश्यकता है तब एक बाइनरी मर्ज को 3 मर्ज पास लेने की आवश्यकता होगी, 6-वे मर्ज के एकल मर्ज पास के विपरीत। मर्ज पास की यह कमी विशेष रूप से बड़ी मात्रा में जानकारी को ध्यान में रखते हुए महत्वपूर्ण है जिसे सामान्यतः पहले स्थान पर क्रमबद्ध किया जाता है, जिससे अधिक गति-अप की अनुमति मिलती है जबकि धीमी भंडारण तक पहुंच की मात्रा भी कम हो जाती है।

संदर्भ

  1. ↑ Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein (2001). एल्गोरिदम का परिचय. MIT Press. pp. 28–29. ISBN 978-0-262-03293-3.
  2. ↑ Bentley, Jon Louis (2000). Programming Pearls (2nd ed.). Addison Wesley. pp. 147–162. ISBN 0201657880.
  3. ↑ 3.0 3.1 Knuth, Donald (1998). "Chapter 5.4.1. Multiway Merging and Replacement Selection". Sorting and Searching. The Art of Computer Programming. Vol. 3 (2nd ed.). Addison-Wesley. pp. 252–255. ISBN 0-201-89685-0.
  4. ↑ Shaffer, Clifford A. (2012-07-26). C++ में डेटा संरचनाएं और एल्गोरिथम विश्लेषण, तीसरा संस्करण. Courier Corporation. ISBN 9780486172620.
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=के-वे_मर्ज_एल्गोरिदम&oldid=225419’