कैंटर फलन: Difference between revisions
No edit summary |
|||
| (8 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Continuous function that is not absolutely continuous}} | {{Short description|Continuous function that is not absolutely continuous}} | ||
[[File:CantorEscalier-2.svg|thumb|right| | [[File:CantorEscalier-2.svg|thumb|right|179x179px|[[इकाई अंतराल]] पर कैंटर फलन का ग्राफ़]]गणित में, '''कैंटर फलन''' एक [[फ़ंक्शन (गणित)|फलन (गणित)]] का उदाहरण है जो सतत फलन है, लेकिन [[पूर्ण निरंतरता|निरपेक्ष सांतत्य]] नहीं है। यह विश्लेषण में विशेष रूप से प्रतिउदाहरण है, क्योंकि यह सतत, व्युत्पन्न और माप के बारे में अनुभवहीन अंतर्ज्ञान को चुनौती देता है। हालाँकि यह हर जगह सतत है और इसका लगभग हर जगह शून्य व्युत्पन्न है, फिर भी इसका मान 0 से 1 हो जाता है क्योंकि इसका तर्क 0 से 1 तक पहुँच जाता है। इस प्रकार, एक अर्थ में फलन बहुत हद तक स्थिरांक जैसा लगता है जो बढ़ नहीं सकता है, और दूसरे में, यह वास्तव में दिष्ट रूप से बढ़ता है। | ||
इसे '''कैंटर त्रिक फलन''', '''लेबेस्ग्यू फलन''' भी कहा जाता है।<ref>{{harvnb|Vestrup|2003|loc=Section 4.6.}}</ref> '''लेबेस्ग्यू एकल फलन, कैंटोर-विटाली फलन, डेविल्स स्टेरकेस''',<ref>{{harvnb|Thomson|Bruckner|Bruckner|2008|p=252}}.</ref> '''कैंटर स्टेरकेस फलन''',<ref>{{Cite web|url=http://mathworld.wolfram.com/CantorStaircaseFunction.html|title=Cantor Staircase Function}}</ref> और '''कैंटर-लेब्सग फल'''न भी कहा जाता है।<ref>{{harvnb|Bass|2013|p=28}}.</ref> {{harvs|txt|first=जॉर्ज कैंटर |last=Cantor|authorlink=जॉर्ज कैंटर|year=1884}} ने कैंटर फलन प्रारंभ | इसे '''कैंटर त्रिक फलन''', '''लेबेस्ग्यू फलन''' भी कहा जाता है।<ref>{{harvnb|Vestrup|2003|loc=Section 4.6.}}</ref> '''लेबेस्ग्यू एकल फलन, कैंटोर-विटाली फलन, डेविल्स स्टेरकेस''',<ref>{{harvnb|Thomson|Bruckner|Bruckner|2008|p=252}}.</ref> '''कैंटर स्टेरकेस फलन''',<ref>{{Cite web|url=http://mathworld.wolfram.com/CantorStaircaseFunction.html|title=Cantor Staircase Function}}</ref> और '''कैंटर-लेब्सग फल'''न भी कहा जाता है।<ref>{{harvnb|Bass|2013|p=28}}.</ref> {{harvs|txt|first=जॉर्ज कैंटर |last=Cantor|authorlink=जॉर्ज कैंटर|year=1884}} ने कैंटर फलन प्रारंभ किया और उल्लेख किया कि शेफ़र ने बताया कि यह [[कार्ल गुस्ताव एक्सल हार्नैक]] द्वारा दावा किए गए कलन का मूलभूत प्रमेय के विस्तार का प्रति उदाहरण था। कैंटर फलन पर {{harvtxt|शेफ़र |1884}}, {{harvtxt|लेब्सग्यू|1904}} और {{harvtxt|विटाली|1905}} द्वारा चर्चा की गई और इसे लोकप्रिय बनाया गया है। | ||
==परिभाषा== | ==परिभाषा== | ||
[[File:Cantor function.gif|thumb | [[File:Cantor function.gif|thumb|कैंटर फलन का पुनरावृत्त निर्माण|184x184px]]कैंटर फलन को परिभाषित करने के लिए <math>c:[0,1]\to[0,1]</math>, मान लीजिये <math>x</math>, <math>[0,1]</math> में कोई भी संख्या हो और प्राप्त <math>c(x)</math> है निम्नलिखित चरणों द्वारा: | ||
#<math>x</math> आधार 3 में अभिव्यक्त करना। | #<math>x</math> आधार 3 में अभिव्यक्त करना। | ||
| Line 18: | Line 17: | ||
*<math>\tfrac{200}{243}</math> इसका त्रिक प्रतिरूपण 0.21102 (या 0.211012222...) है। 0.21 उत्पन्न करने के लिए पहले 1 के बाद के अंकों को 0s से प्रतिस्थापित किया जाता है। इसे 0.11 के रूप में पुनः लिखा गया है। यह <math>\tfrac34</math> का द्विआधारी प्रतिरूपण है , इसलिए <math>c(\tfrac{200}{243})=\tfrac34</math>। | *<math>\tfrac{200}{243}</math> इसका त्रिक प्रतिरूपण 0.21102 (या 0.211012222...) है। 0.21 उत्पन्न करने के लिए पहले 1 के बाद के अंकों को 0s से प्रतिस्थापित किया जाता है। इसे 0.11 के रूप में पुनः लिखा गया है। यह <math>\tfrac34</math> का द्विआधारी प्रतिरूपण है , इसलिए <math>c(\tfrac{200}{243})=\tfrac34</math>। | ||
समान रूप से, यदि <math>\mathcal{C}</math> कैंटर समुच्चय | समान रूप से, यदि <math>\mathcal{C}</math> कैंटर समुच्चय [0,1] है, फिर कैंटर फलन को <math>c:[0,1]\to[0,1]</math> के रूप में परिभाषित किया जा सकता है | ||
:<math>c(x) =\begin{cases} | :<math>c(x) =\begin{cases} | ||
| Line 25: | Line 24: | ||
\\ \sup_{y\leq x,\, y\in\mathcal{C}} c(y), & x\in [0,1]\setminus \mathcal{C}.\\ \end{cases} | \\ \sup_{y\leq x,\, y\in\mathcal{C}} c(y), & x\in [0,1]\setminus \mathcal{C}.\\ \end{cases} | ||
</math> | </math> | ||
यह सूत्र अच्छी तरह से परिभाषित है, क्योंकि कैंटर समुच्चय के प्रत्येक सदस्य का | यह सूत्र अच्छी तरह से परिभाषित है, क्योंकि कैंटर समुच्चय के प्रत्येक सदस्य का अद्वितीय आधार 3 प्रतिरूपण होता है जिसमें केवल अंक 0 या 2 होते हैं। (कुछ सदस्यों के लिए) <math>\mathcal{C}</math>, त्रिक विस्तार 2's के अनुगामी के साथ दोहराया जा रहा है और 1 में समाप्त होने वाला वैकल्पिक गैर-दोहराया जाने वाला विस्तार है। उदाहरण के लिए, <math>\tfrac13</math> = 0.1<sub>3</sub> = 0.02222...<sub>3</sub> कैंटर समुच्चय का सदस्य है)। तब से <math>c(0)=0</math> और <math>c(1)=1</math>, और <math>c</math> पर <math>\mathcal{C}</math> एकदिष्ट है, यह स्पष्ट है कि <math>0\le c(x)\le 1</math> सभी <math>x\in[0,1]\setminus\mathcal{C}</math> के लिए भी धारण करता है। | ||
==गुण== | ==गुण== | ||
कैंटर फलन सतत फलन और [[माप (गणित)]] के बारे में अनुभवहीन अंतर्ज्ञान को चुनौती देता है; यद्यपि यह हर जगह सतत है और [[लगभग हर जगह]] इसका व्युत्पन्न शून्य है, <math display="inline">c(x)</math> 0 से 1 तक चला जाता है <math display="inline>x</math>, 0 से 1 तक जाता है, और बीच में प्रत्येक मान लेता है। कैंटर फलन वास्तविक फलन का सबसे | कैंटर फलन सतत फलन और [[माप (गणित)]] के बारे में अनुभवहीन अंतर्ज्ञान को चुनौती देता है; यद्यपि यह हर जगह सतत है और [[लगभग हर जगह]] इसका व्युत्पन्न शून्य है, <math display="inline">c(x)</math> 0 से 1 तक चला जाता है <math display="inline>x</math>, 0 से 1 तक जाता है, और बीच में प्रत्येक मान लेता है। कैंटर फलन वास्तविक फलन का सबसे अधिकांशतः उद्धृत उदाहरण है जो [[समान रूप से निरंतर|एकसमान सतत]] है (सटीकता से, यह घातांक ''α'' = log 2/log 3 का होल्डर सतत है) लेकिन निरपेक्ष सांतत्य नहीं है। यह फॉर्म के अंतराल पर स्थिर है (0.x<sub>1</sub>x<sub>2</sub>x<sub>3</sub>...''x''<sub>n</sub>022222..., 0.x<sub>1</sub>x<sub>2</sub>x<sub>3</sub>....''x''<sub>n</sub>200000...), और कैंटर समुच्चय में सम्मिलित प्रत्येक बिंदु इन अंतरालों में से एक में नहीं है, इसलिए इसका व्युत्पन्न कैंटर समुच्चय के बाहर 0 है। दूसरी ओर, ऊपर वर्णित अंतराल समापन बिंदु वाले कैंटर समुच्चय के [[बेशुमार|अगणनीय]] उपसमुच्चय में किसी भी बिंदु पर इसका कोई व्युत्पन्न नहीं है। | ||
कैंटर फलन को कैंटर समुच्चय पर समर्थित 1/2-1/2 [[बर्नौली माप]] μ के संचयी वितरण फलन के रूप में भी देखा जा सकता है: <math display="inline">c(x)=\mu([0,x])</math>। इस संभाव्यता वितरण, जिसे [[कैंटर वितरण]] कहा जाता है, का कोई अलग भाग नहीं है। अर्थात् संगत माप [[परमाणु (माप सिद्धांत)]] है। यही कारण है कि फलन में कोई वृद्धि असंततता नहीं है; ऐसी कोई भी वृद्धि माप में एक परमाणु के अनुरूप होगी। | कैंटर फलन को कैंटर समुच्चय पर समर्थित 1/2-1/2 [[बर्नौली माप]] μ के संचयी वितरण फलन के रूप में भी देखा जा सकता है: <math display="inline">c(x)=\mu([0,x])</math>। इस संभाव्यता वितरण, जिसे [[कैंटर वितरण]] कहा जाता है, का कोई अलग भाग नहीं है। अर्थात् संगत माप [[परमाणु (माप सिद्धांत)]] है। यही कारण है कि फलन में कोई वृद्धि असंततता नहीं है; ऐसी कोई भी वृद्धि माप में एक परमाणु के अनुरूप होगी। | ||
हालाँकि, कैंटर फलन के किसी भी गैर-स्थिर भाग को संभाव्यता घनत्व फलन के अभिन्न अंग के रूप में प्रस्तुत नहीं किया जा सकता है; किसी भी अनुमानित संभाव्यता घनत्व फलन को एकीकृत करना जो किसी भी अंतराल पर लगभग हर जगह शून्य नहीं है, कुछ अंतराल को सुनिश्चित संभावना देगा जिसके लिए यह वितरण संभाव्यता शून्य प्रदान करता है। विशेष रूप से, जैसे {{harvtxt|विटाली|1905}} बताया गया है, फलन इसके व्युत्पन्न का अभिन्न अंग नहीं है, भले ही व्युत्पन्न लगभग हर जगह | हालाँकि, कैंटर फलन के किसी भी गैर-स्थिर भाग को संभाव्यता घनत्व फलन के अभिन्न अंग के रूप में प्रस्तुत नहीं किया जा सकता है; किसी भी अनुमानित संभाव्यता घनत्व फलन को एकीकृत करना जो किसी भी अंतराल पर लगभग हर जगह शून्य नहीं है, कुछ अंतराल को सुनिश्चित संभावना देगा जिसके लिए यह वितरण संभाव्यता शून्य प्रदान करता है। विशेष रूप से, जैसे {{harvtxt|विटाली|1905}} बताया गया है, फलन इसके व्युत्पन्न का अभिन्न अंग नहीं है, भले ही व्युत्पन्न लगभग हर जगह सम्मिलित है। | ||
कैंटर फलन एकल फलन का मानक उदाहरण है। | कैंटर फलन एकल फलन का मानक उदाहरण है। | ||
| Line 39: | Line 38: | ||
===निरपेक्ष सांतत्य का अभाव=== | ===निरपेक्ष सांतत्य का अभाव=== | ||
क्योंकि [[बेशुमार सेट|अगणनीय समुच्चय]] कैंटर समुच्चय का [[लेब्सेग माप]] 0 है, किसी भी सुनिश्चित ε < 1 और δ के लिए, कुल लंबाई <δ के साथ युग्मानूसार असंयुक्त उप-अंतराल का सीमित अनुक्रम | क्योंकि [[बेशुमार सेट|अगणनीय समुच्चय]] कैंटर समुच्चय का [[लेब्सेग माप]] 0 है, किसी भी सुनिश्चित ε < 1 और δ के लिए, कुल लंबाई <δ के साथ युग्मानूसार असंयुक्त उप-अंतराल का सीमित अनुक्रम सम्मिलित है, जिस पर कैंटर फलन संचयी रूप से ε से अधिक बढ़ जाता है। | ||
वास्तव में, प्रत्येक δ > 0 के लिए परिमित रूप से कई युग्मानूसार असंयुक्त अंतराल (''x<sub>k</sub>'',''y<sub>k</sub>'') (1 ≤ ''k'' ≤ ''M'') के साथ होते हैं <SUB><math>\sum\limits_{k=1}^M (y_k-x_k)<\delta</math> और <SUB><math>\sum\limits_{k=1}^M (c(y_k)-c(x_k))=1</math>. | वास्तव में, प्रत्येक δ > 0 के लिए परिमित रूप से कई युग्मानूसार असंयुक्त अंतराल (''x<sub>k</sub>'',''y<sub>k</sub>'') (1 ≤ ''k'' ≤ ''M'') के साथ होते हैं <SUB><math>\sum\limits_{k=1}^M (y_k-x_k)<\delta</math> और <SUB><math>\sum\limits_{k=1}^M (c(y_k)-c(x_k))=1</math>. | ||
| Line 46: | Line 45: | ||
=== पुनरावृत्तीय निर्माण === | === पुनरावृत्तीय निर्माण === | ||
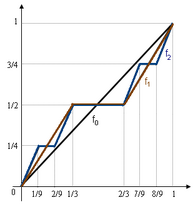
[[File:Cantor function sequence.png| | [[File:Cantor function sequence.png|206x206px|right]]नीचे हम इकाई अंतराल पर फलन का अनुक्रम {''f<sub>n</sub>''} को परिभाषित करते हैं जो कैंटर फलन में परिवर्तित होता है। | ||
मान लीजिये ''f''<sub>0</sub>(''x'') = ''x''. | मान लीजिये ''f''<sub>0</sub>(''x'') = ''x''. | ||
| Line 54: | Line 53: | ||
मान लीजिये ''f<sub>n</sub>''<sub>+1</sub>(''x'') = 1/2 × ''f<sub>n</sub>''(3''x''), जब {{nowrap|0 ≤ ''x'' ≤ 1/3 }}; | मान लीजिये ''f<sub>n</sub>''<sub>+1</sub>(''x'') = 1/2 × ''f<sub>n</sub>''(3''x''), जब {{nowrap|0 ≤ ''x'' ≤ 1/3 }}; | ||
मान लीजिये ''f<sub>n</sub>''<sub>+1</sub>(''x'') = 1/2 | मान लीजिये ''f<sub>n</sub>''<sub>+1</sub>(''x'') = 1/2, जब {{nowrap|1/3 ≤ ''x'' ≤ 2/3 }}; | ||
मान लीजिये ''f<sub>n</sub>''<sub>+1</sub>(''x'') = 1/2 + 1/2 × ''f<sub>n</sub>''(3 ''x'' − 2), | मान लीजिये ''f<sub>n</sub>''<sub>+1</sub>(''x'') = 1/2 + 1/2 × ''f<sub>n</sub>''(3 ''x'' − 2), जब {{nowrap|2/3 ≤ ''x'' ≤ 1}}. | ||
तीन परिभाषाएँ अंत-बिंदु 1/3 और 2/3 पर संगत हैं, प्रवर्तन द्वारा क्योंकि f<sub>''n''</sub>(0)=0 और ''f<sub>n</sub>''(1) = 1 प्रत्येक ''n'' के लिए है। कोई यह जांच सकता है कि ''f<sub>n</sub>'' ऊपर परिभाषित कैंटर फलन में बिंदुवार अभिसरण होता है। इसके | तीन परिभाषाएँ अंत-बिंदु 1/3 और 2/3 पर संगत हैं, प्रवर्तन द्वारा क्योंकि f<sub>''n''</sub>(0)=0 और ''f<sub>n</sub>''(1) = 1 प्रत्येक ''n'' के लिए है। कोई यह जांच सकता है कि ''f<sub>n</sub>'' ऊपर परिभाषित कैंटर फलन में बिंदुवार अभिसरण होता है। इसके अतिरिक्त, अभिसरण एक समान है। दरअसल, ''f<sub>n</sub>''<sub>+1</sub> की परिभाषा के अनुसार, तीन स्थितियों में अलग करना है | ||
:<math>\max_{x \in [0, 1]} |f_{n+1}(x) - f_n(x)| \le \frac 1 2 \, \max_{x \in [0, 1]} |f_{n}(x) - f_{n-1}(x)|, \quad n \ge 1.</math> | :<math>\max_{x \in [0, 1]} |f_{n+1}(x) - f_n(x)| \le \frac 1 2 \, \max_{x \in [0, 1]} |f_{n}(x) - f_{n-1}(x)|, \quad n \ge 1.</math> | ||
| Line 64: | Line 63: | ||
:<math>\max_{x \in [0, 1]} |f(x) - f_n(x)| \le 2^{-n+1} \, \max_{x \in [0, 1]} |f_1(x) - f_0(x)|.</math> | :<math>\max_{x \in [0, 1]} |f(x) - f_n(x)| \le 2^{-n+1} \, \max_{x \in [0, 1]} |f_1(x) - f_0(x)|.</math> | ||
इसके | इसके अतिरिक्त आरंभिक फलन का चुनाव वास्तव में कोई मायने नहीं रखता, बशर्ते कि ''f''<sub>0</sub>(0) = 0, ''f''<sub>0</sub>(1) = 1 और ''f''<sub>0</sub> [[बंधा हुआ कार्य|परिबद्ध फलन]] है। | ||
=== फ्रैक्टल आयतन === | === फ्रैक्टल आयतन === | ||
कैंटर फलन का कैंटर समुच्चय से गहरा संबंध है। कैंटर समुच्चय ''C'' को अंतराल [0,1] में उन संख्याओं के समुच्चय के रूप में परिभाषित किया जा सकता है, जिनके [[आधार (घातांक)|आधार-3 (त्रिकोणीय) विस्तार]] में अंक 1 | कैंटर फलन का कैंटर समुच्चय से गहरा संबंध है। कैंटर समुच्चय ''C'' को अंतराल [0,1] में उन संख्याओं के समुच्चय के रूप में परिभाषित किया जा सकता है, जिनके [[आधार (घातांक)|आधार-3 (त्रिकोणीय) विस्तार]] में अंक 1 सम्मिलित नहीं है, सिवाय इसके कि 1 के बाद आता है केवल शून्य (जिस स्थिति में पिछला 1000<math>\ldots</math> 0222 द्वारा प्रतिस्थापित किया जा सकता है<math>\ldots</math> किसी एक से छुटकारा पाने के लिए 1)। यह पता चला है कि कैंटर समुच्चय[[ भग्न | फ्रैक्टल]] है जिसमें (अगणनीय) अनंत कई बिंदु (शून्य-आयामी मात्रा) हैं, लेकिन शून्य लंबाई (एक-आयामी मात्रा) है। केवल ''D''-आयामी आयतन <math> H_D </math> ([[हॉसडॉर्फ़ आयाम]] के अर्थ में) सीमित मान लेता है, जहां <math> D = \log(2)/\log(3) </math> ''C'' का फ्रैक्टल आयाम है। हम कैंटर फलन को कैंटर समुच्चय के अनुभागों के ''D''-आयामी आयतन के रूप में वैकल्पिक रूप से परिभाषित कर सकते हैं | ||
: <math> | : <math> | ||
| Line 83: | Line 82: | ||
प्रथम स्व-समरूपता को इस प्रकार व्यक्त किया जा सकता है | प्रथम स्व-समरूपता को इस प्रकार व्यक्त किया जा सकता है | ||
:<math>r\circ c = c\circ r</math> | :<math>r\circ c = c\circ r</math> | ||
जहां प्रतीक <math>\circ</math> फलन संरचना को दर्शाता है। वह है, <math>(r\circ c)(x)=r(c(x))=1-c(x)</math> और इसी तरह अन्य | जहां प्रतीक <math>\circ</math> फलन संरचना को दर्शाता है। वह है, <math>(r\circ c)(x)=r(c(x))=1-c(x)</math> और इसी तरह अन्य स्थितियों के लिए भी है। बाएँ और दाएँ आवर्धन के लिए, बाएँ-प्रतिचित्रण लिखें | ||
:<math>L_D(x)= \frac{x}{2}</math> और <math>L_C(x)= \frac{x}{3}</math> | :<math>L_D(x)= \frac{x}{2}</math> और <math>L_C(x)= \frac{x}{3}</math> | ||
तब कैंटर फलन का पालन होता है | तब कैंटर फलन का पालन होता है | ||
| Line 97: | Line 96: | ||
इन परिचालनों को अक्रमतः से क्रमबद्ध किया जा सकता है। उदाहरण के लिए, बाएँ-दाएँ चालों के क्रम <math>LRLLR.</math> पर विचार करें सबस्क्रिप्ट C और D जोड़ना, और स्पष्टता के लिए, कंपोज़िशन ऑपरेटर <math>\circ</math> को हटाना कुछ स्थानों को छोड़कर सभी में, एक है: | इन परिचालनों को अक्रमतः से क्रमबद्ध किया जा सकता है। उदाहरण के लिए, बाएँ-दाएँ चालों के क्रम <math>LRLLR.</math> पर विचार करें सबस्क्रिप्ट C और D जोड़ना, और स्पष्टता के लिए, कंपोज़िशन ऑपरेटर <math>\circ</math> को हटाना कुछ स्थानों को छोड़कर सभी में, एक है: | ||
:<math>L_D R_D L_D L_D R_D \circ c = c \circ L_C R_C L_C L_C R_C</math> | :<math>L_D R_D L_D L_D R_D \circ c = c \circ L_C R_C L_C L_C R_C</math> | ||
L और R अक्षरों में यादृच्छिक परिमित-लंबाई वाले तार द्वैयकीय परिमेय के अनुरूप हैं, जिसमें प्रत्येक द्वैयकीय परिमेय को दोनों <math>y=n/2^m</math>के रूप में पूर्णांक ''n'' और ''m'' के लिए और बिट्स की सीमित लंबाई के रूप में <math>y=0.b_1b_2b_3\cdots b_m</math> साथ <math>b_k\in \{0,1\}.</math> लिखा जा सकता है इस प्रकार, प्रत्येक द्वैयकीय परिमेय कैंटर फलन की कुछ स्व-समरूपता के साथ एकैक पत्राचार में है। | L और R अक्षरों में यादृच्छिक परिमित-लंबाई वाले तार द्वैयकीय परिमेय के अनुरूप हैं, जिसमें प्रत्येक द्वैयकीय परिमेय को दोनों <math>y=n/2^m</math> के रूप में पूर्णांक ''n'' और ''m'' के लिए और बिट्स की सीमित लंबाई के रूप में <math>y=0.b_1b_2b_3\cdots b_m</math> साथ <math>b_k\in \{0,1\}.</math> लिखा जा सकता है इस प्रकार, प्रत्येक द्वैयकीय परिमेय कैंटर फलन की कुछ स्व-समरूपता के साथ एकैक पत्राचार में है। | ||
कुछ सांकेतिक पुनर्व्यवस्थाएं उपरोक्त को व्यक्त करना थोड़ा आसान बना सकती हैं। मान लीजिये <math>g_0</math> और <math>g_1</math> L और R के लिए है। फलन संरचना इसे [[मोनोइड|एकाभ]] तक विस्तारित करती है, जिसमें कोई भी लिख सकता है <math>g_{010}=g_0g_1g_0</math> और | कुछ सांकेतिक पुनर्व्यवस्थाएं उपरोक्त को व्यक्त करना थोड़ा आसान बना सकती हैं। मान लीजिये <math>g_0</math> और <math>g_1</math> L और R के लिए है। फलन संरचना इसे [[मोनोइड|एकाभ]] तक विस्तारित करती है, जिसमें कोई भी लिख सकता है <math>g_{010}=g_0g_1g_0</math> और सामान्यतः, <math>g_Ag_B=g_{AB}</math> अंक ''A, B'' की कुछ द्विआधारी स्ट्रिंग के लिए, जहां ''AB'' ऐसी स्ट्रिंग का सामान्य संयोजन है। द्वैयकीय एकाभ ''M'' तब ऐसी सभी परिमित-लंबाई वाली बाएँ-दाएँ का एकाभ है। <math>\gamma\in M</math> लिखना एकाभ के सामान्य तत्व के रूप में, कैंटर फलन की समान स्व-समरूपता है: | ||
:<math>\gamma_D\circ c= c\circ \gamma_C</math> | :<math>\gamma_D\circ c= c\circ \gamma_C</math> | ||
द्वैयकीय एकाभ में स्वयं कई दिलचस्प गुण हैं। इसे अनंत [[ द्विआधारी वृक्ष |द्वयी तरू]] के नीचे बाएँ-दाएँ चालों की सीमित संख्या के रूप में देखा जा सकता है; तरू पर असीम रूप से दूर की "पत्तियाँ" कैंटर समुच्चय के बिंदुओं से मेल खाती हैं, और इसलिए, एकाभ कैंटर समुच्चय की स्व-समरूपता का भी प्रतिरूपण करता है। वास्तव में, | द्वैयकीय एकाभ में स्वयं कई दिलचस्प गुण हैं। इसे अनंत [[ द्विआधारी वृक्ष |द्वयी तरू]] के नीचे बाएँ-दाएँ चालों की सीमित संख्या के रूप में देखा जा सकता है; तरू पर असीम रूप से दूर की "पत्तियाँ" कैंटर समुच्चय के बिंदुओं से मेल खाती हैं, और इसलिए, एकाभ कैंटर समुच्चय की स्व-समरूपता का भी प्रतिरूपण करता है। वास्तव में, सामान्यतः पाए जाने वाले फ्रैक्टल्स के बड़े वर्ग का वर्णन द्वैयकीय एकाभ द्वारा किया जाता है; अतिरिक्त उदाहरण [[राम का वक्र|डी राम वक्र]] पर लेख में पाए जा सकते हैं। स्व-समानता रखने वाले अन्य फ्रैक्टल्स को अन्य प्रकार के एकाभ के साथ वर्णित किया गया है। द्वैयकीय एकाभ स्वयं [[मॉड्यूलर समूह]] <math>SL(2,\mathbb{Z}).</math> का उप-एकाभ है। | ||
ध्यान दें कि कैंटर फलन मिंकोव्स्की के प्रश्न-चिह्न फलन से कहीं अधिक समानता रखता है। विशेष रूप से, यह बिल्कुल उसी समरूपता संबंधों का पालन यद्यपि परिवर्तित रूप में करता है। | ध्यान दें कि कैंटर फलन मिंकोव्स्की के प्रश्न-चिह्न फलन से कहीं अधिक समानता रखता है। विशेष रूप से, यह बिल्कुल उसी समरूपता संबंधों का पालन यद्यपि परिवर्तित रूप में करता है। | ||
| Line 114: | Line 113: | ||
''z'' = 1/3 के लिए, फलन का व्युत्क्रम ''x'' = 2 ''C''<sub>1/3</sub>(''y'') कैंटर फलन है। अर्थात्, ''y'' = ''y''(''x'') कैंटर फलन है। सामान्य तौर पर, किसी भी ''z'' < 1/2, ''C<sub>z</sub>''(''y'') के लिए ऐसा लगता है जैसे कैंटर फलन अपनी तरफ मुड़ गया है, जैसे-जैसे z शून्य के करीब पहुंचता है, चरणों की चौड़ाई चौड़ी होती जाती है। | ''z'' = 1/3 के लिए, फलन का व्युत्क्रम ''x'' = 2 ''C''<sub>1/3</sub>(''y'') कैंटर फलन है। अर्थात्, ''y'' = ''y''(''x'') कैंटर फलन है। सामान्य तौर पर, किसी भी ''z'' < 1/2, ''C<sub>z</sub>''(''y'') के लिए ऐसा लगता है जैसे कैंटर फलन अपनी तरफ मुड़ गया है, जैसे-जैसे z शून्य के करीब पहुंचता है, चरणों की चौड़ाई चौड़ी होती जाती है। | ||
जैसा कि ऊपर उल्लेख किया गया है, कैंटर फलन कैंटर समुच्चय पर माप का संचयी वितरण फलन भी है। कैंटर समुच्चय या अन्य फ्रैक्टल्स पर समर्थित विभिन्न परमाणु-कम संभाव्यता उपायों पर विचार करके विभिन्न कैंटर फलन, या डेविल्स स्टेरकेस प्राप्त की जा सकती हैं। जबकि कैंटर फलन में लगभग हर जगह व्युत्पन्न 0 है, वर्तमान शोध उन बिंदुओं के समुच्चय के आकार के सवाल पर केंद्रित है जहां ऊपरी दाएं व्युत्पन्न निचले दाएं व्युत्पन्न से अलग है, जिससे व्युत्पन्न | जैसा कि ऊपर उल्लेख किया गया है, कैंटर फलन कैंटर समुच्चय पर माप का संचयी वितरण फलन भी है। कैंटर समुच्चय या अन्य फ्रैक्टल्स पर समर्थित विभिन्न परमाणु-कम संभाव्यता उपायों पर विचार करके विभिन्न कैंटर फलन, या डेविल्स स्टेरकेस प्राप्त की जा सकती हैं। जबकि कैंटर फलन में लगभग हर जगह व्युत्पन्न 0 है, वर्तमान शोध उन बिंदुओं के समुच्चय के आकार के सवाल पर केंद्रित है जहां ऊपरी दाएं व्युत्पन्न निचले दाएं व्युत्पन्न से अलग है, जिससे व्युत्पन्न सम्मिलित नहीं है। भिन्नता का यह विश्लेषण सामान्यतः फ्रैक्टल आयाम के संदर्भ में दिया जाता है, जिसमें हॉसडॉर्फ आयाम सबसे लोकप्रिय विकल्प है। अनुसंधान की यह श्रृंखला 1990 के दशक में डर्स्ट द्वारा प्रारंभ की गई थी,<ref>{{Cite journal|title = The Hausdorff Dimension of the Nondifferentiability Set of the Cantor Function is [ ln(2)/ln(3) ]2|jstor = 2159830|journal = Proceedings of the American Mathematical Society|date = 1993-09-01|pages = 105–108|volume = 119|issue = 1|doi = 10.2307/2159830|first = Richard|last = Darst}}</ref> जिन्होंने दिखाया कि कैंटर फलन की गैर-भिन्नता के समुच्चय का हॉसडॉर्फ आयाम कैंटर समुच्चय के आयाम का वर्ग है, <math>(\log2/\log3)^2</math>। इसके बाद [[केनेथ फाल्कनर (गणितज्ञ)]]<ref>{{Cite journal|title = एक तरफा मल्टीफ्रैक्टल विश्लेषण और शैतान की सीढ़ियों की गैर-विभेदीकरण के बिंदु|journal = Mathematical Proceedings of the Cambridge Philosophical Society|date = 2004-01-01|issn = 1469-8064|pages = 167–174|volume = 136|issue = 1|doi = 10.1017/S0305004103006960|first = Kenneth J.|last = Falconer|bibcode = 2004MPCPS.136..167F|s2cid = 122381614}}</ref> पता चला कि यह वर्ग संबंध अहलफोर के सभी नियमित, एकल उपायों के लिए लागू होता है, अर्थात<math display="block">\dim_H\left\{x : f'(x)=\lim_{h\to0^+}\frac{\mu([x,x+h])}{h}\text{ does not exist}\right\}=\left(\dim_H\operatorname{supp}(\mu)\right)^2</math>बाद में, ट्रोस्चिट<ref>{{Cite journal|title = Hölder differentiability of self-conformal devil's staircases|journal = Mathematical Proceedings of the Cambridge Philosophical Society|date = 2014-03-01|issn = 1469-8064|pages = 295–311|volume = 156|issue = 2|doi = 10.1017/S0305004113000698|first = Sascha|last = Troscheit|arxiv = 1301.1286|bibcode = 2014MPCPS.156..295T|s2cid = 56402751}}</ref> समुच्चय की अधिक व्यापक तस्वीर प्राप्त करें जहां स्व-अनुरूप और स्व-समानता समुच्चय पर समर्थित अधिक सामान्यीकृत गिब के उपायों के लिए व्युत्पन्न सम्मिलित नहीं है। | ||
[[हरमन मिन्कोव्स्की]] का मिन्कोव्स्की का प्रश्न चिह्न फलन देखने में कैंटर फलन से मिलता-जुलता है, जो बाद वाले के | [[हरमन मिन्कोव्स्की]] का मिन्कोव्स्की का प्रश्न चिह्न फलन देखने में कैंटर फलन से मिलता-जुलता है, जो बाद वाले के "सुचारू" रूप के रूप में दिखाई देता है; इसका निर्माण सतत अंश विस्तार से द्विआधारी विस्तार में जाकर किया जा सकता है, जैसे कैंटर फलन का निर्माण त्रिक विस्तार से द्विआधारी विस्तार में जाकर किया जा सकता है। प्रश्न चिह्न फलन में सभी परिमेय संख्याओं के लुप्त हो जाने वाले व्युत्पन्न होने का दिलचस्प गुण है। | ||
==यह भी देखें== | ==यह भी देखें== | ||
| Line 124: | Line 123: | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
<references /> | <references /> | ||
==संदर्भ== | ==संदर्भ== | ||
* {{cite book|first1=Richard Franklin|last1=Bass|author1-link=Richard F. Bass|title=Real analysis for graduate students|year=2013|orig-year=2011|edition=Second|publisher=Createspace Independent Publishing|isbn=978-1-4818-6914-0}} | * {{cite book|first1=Richard Franklin|last1=Bass|author1-link=Richard F. Bass|title=Real analysis for graduate students|year=2013|orig-year=2011|edition=Second|publisher=Createspace Independent Publishing|isbn=978-1-4818-6914-0}} | ||
| Line 140: | Line 137: | ||
*{{cite book|title=The theory of measures and integration|last=Vestrup|first=E.M.|series=Wiley series in probability and statistics|publisher=John Wiley & sons|year=2003|isbn=978-0471249771}} | *{{cite book|title=The theory of measures and integration|last=Vestrup|first=E.M.|series=Wiley series in probability and statistics|publisher=John Wiley & sons|year=2003|isbn=978-0471249771}} | ||
*{{citation|first=A.|last= Vitali|title=Sulle funzioni integrali|journal=Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur.|volume= 40 |year=1905 |pages= 1021–1034 |trans-title=On the integral functions}} | *{{citation|first=A.|last= Vitali|title=Sulle funzioni integrali|journal=Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur.|volume= 40 |year=1905 |pages= 1021–1034 |trans-title=On the integral functions}} | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* [https://www.encyclopediaofmath.org/index.php/Cantor_ternary_function ''Cantor ternary function'' at Encyclopaedia of Mathematics] | * [https://www.encyclopediaofmath.org/index.php/Cantor_ternary_function ''Cantor ternary function'' at Encyclopaedia of Mathematics] | ||
| Line 147: | Line 142: | ||
* {{MathWorld |title= Cantor Function |urlname= CantorFunction}} | * {{MathWorld |title= Cantor Function |urlname= CantorFunction}} | ||
[[Category:Created On 04/07/2023]] | [[Category:Created On 04/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:जॉर्ज कैंटर]] | |||
[[Category:दे राम घटता है]] | |||
[[Category:भग्न]] | |||
[[Category:माप सिद्धांत]] | |||
[[Category:विशेष कार्य]] | |||
Latest revision as of 11:46, 26 July 2023

गणित में, कैंटर फलन एक फलन (गणित) का उदाहरण है जो सतत फलन है, लेकिन निरपेक्ष सांतत्य नहीं है। यह विश्लेषण में विशेष रूप से प्रतिउदाहरण है, क्योंकि यह सतत, व्युत्पन्न और माप के बारे में अनुभवहीन अंतर्ज्ञान को चुनौती देता है। हालाँकि यह हर जगह सतत है और इसका लगभग हर जगह शून्य व्युत्पन्न है, फिर भी इसका मान 0 से 1 हो जाता है क्योंकि इसका तर्क 0 से 1 तक पहुँच जाता है। इस प्रकार, एक अर्थ में फलन बहुत हद तक स्थिरांक जैसा लगता है जो बढ़ नहीं सकता है, और दूसरे में, यह वास्तव में दिष्ट रूप से बढ़ता है।
इसे कैंटर त्रिक फलन, लेबेस्ग्यू फलन भी कहा जाता है।[1] लेबेस्ग्यू एकल फलन, कैंटोर-विटाली फलन, डेविल्स स्टेरकेस,[2] कैंटर स्टेरकेस फलन,[3] और कैंटर-लेब्सग फलन भी कहा जाता है।[4] जॉर्ज कैंटर Cantor (1884) ने कैंटर फलन प्रारंभ किया और उल्लेख किया कि शेफ़र ने बताया कि यह कार्ल गुस्ताव एक्सल हार्नैक द्वारा दावा किए गए कलन का मूलभूत प्रमेय के विस्तार का प्रति उदाहरण था। कैंटर फलन पर शेफ़र (1884), लेब्सग्यू (1904) और विटाली (1905) द्वारा चर्चा की गई और इसे लोकप्रिय बनाया गया है।
परिभाषा
कैंटर फलन को परिभाषित करने के लिए , मान लीजिये , में कोई भी संख्या हो और प्राप्त है निम्नलिखित चरणों द्वारा:
- आधार 3 में अभिव्यक्त करना।
- यदि आधार-3 का प्रतिरूपण में 1 है, प्रत्येक अंक के पहले 1 को 0 से बदलें।
- किसी भी शेष 2s को 1s से बदलें।
- परिणाम को द्विआधारी संख्या के रूप में समझें। परिणाम है।
उदाहरण के लिए:
- इसका त्रिक प्रतिरूपण 0.02020202 है... कोई 1s नहीं है इसलिए अगला चरण अभी भी 0.02020202 है... इसे 0.01010101 के रूप में फिर से लिखा गया है... यह का द्विआधारी प्रतिरूपण है , इसलिए ।
- इसका त्रिक प्रतिरूपण 0.01210121 है... पहले 1 के बाद के अंकों को 0s से प्रतिस्थापित करके 0.01000000 उत्पन्न किया जाता है... इसे दोबारा नहीं लिखा गया है क्योंकि इसमें कोई 2s नहीं है। यह का द्विआधारी प्रतिरूपण है, इसलिए ।
- इसका त्रिक प्रतिरूपण 0.21102 (या 0.211012222...) है। 0.21 उत्पन्न करने के लिए पहले 1 के बाद के अंकों को 0s से प्रतिस्थापित किया जाता है। इसे 0.11 के रूप में पुनः लिखा गया है। यह का द्विआधारी प्रतिरूपण है , इसलिए ।
समान रूप से, यदि कैंटर समुच्चय [0,1] है, फिर कैंटर फलन को के रूप में परिभाषित किया जा सकता है
यह सूत्र अच्छी तरह से परिभाषित है, क्योंकि कैंटर समुच्चय के प्रत्येक सदस्य का अद्वितीय आधार 3 प्रतिरूपण होता है जिसमें केवल अंक 0 या 2 होते हैं। (कुछ सदस्यों के लिए) , त्रिक विस्तार 2's के अनुगामी के साथ दोहराया जा रहा है और 1 में समाप्त होने वाला वैकल्पिक गैर-दोहराया जाने वाला विस्तार है। उदाहरण के लिए, = 0.13 = 0.02222...3 कैंटर समुच्चय का सदस्य है)। तब से और , और पर एकदिष्ट है, यह स्पष्ट है कि सभी के लिए भी धारण करता है।
गुण
कैंटर फलन सतत फलन और माप (गणित) के बारे में अनुभवहीन अंतर्ज्ञान को चुनौती देता है; यद्यपि यह हर जगह सतत है और लगभग हर जगह इसका व्युत्पन्न शून्य है, 0 से 1 तक चला जाता है , 0 से 1 तक जाता है, और बीच में प्रत्येक मान लेता है। कैंटर फलन वास्तविक फलन का सबसे अधिकांशतः उद्धृत उदाहरण है जो एकसमान सतत है (सटीकता से, यह घातांक α = log 2/log 3 का होल्डर सतत है) लेकिन निरपेक्ष सांतत्य नहीं है। यह फॉर्म के अंतराल पर स्थिर है (0.x1x2x3...xn022222..., 0.x1x2x3....xn200000...), और कैंटर समुच्चय में सम्मिलित प्रत्येक बिंदु इन अंतरालों में से एक में नहीं है, इसलिए इसका व्युत्पन्न कैंटर समुच्चय के बाहर 0 है। दूसरी ओर, ऊपर वर्णित अंतराल समापन बिंदु वाले कैंटर समुच्चय के अगणनीय उपसमुच्चय में किसी भी बिंदु पर इसका कोई व्युत्पन्न नहीं है।
कैंटर फलन को कैंटर समुच्चय पर समर्थित 1/2-1/2 बर्नौली माप μ के संचयी वितरण फलन के रूप में भी देखा जा सकता है: । इस संभाव्यता वितरण, जिसे कैंटर वितरण कहा जाता है, का कोई अलग भाग नहीं है। अर्थात् संगत माप परमाणु (माप सिद्धांत) है। यही कारण है कि फलन में कोई वृद्धि असंततता नहीं है; ऐसी कोई भी वृद्धि माप में एक परमाणु के अनुरूप होगी।
हालाँकि, कैंटर फलन के किसी भी गैर-स्थिर भाग को संभाव्यता घनत्व फलन के अभिन्न अंग के रूप में प्रस्तुत नहीं किया जा सकता है; किसी भी अनुमानित संभाव्यता घनत्व फलन को एकीकृत करना जो किसी भी अंतराल पर लगभग हर जगह शून्य नहीं है, कुछ अंतराल को सुनिश्चित संभावना देगा जिसके लिए यह वितरण संभाव्यता शून्य प्रदान करता है। विशेष रूप से, जैसे विटाली (1905) बताया गया है, फलन इसके व्युत्पन्न का अभिन्न अंग नहीं है, भले ही व्युत्पन्न लगभग हर जगह सम्मिलित है।
कैंटर फलन एकल फलन का मानक उदाहरण है।
कैंटर फलन गैर-न्यूनता नहीं है, और इसलिए विशेष रूप से इसका ग्राफ संशोधनीय वक्र को परिभाषित करता है। शेफ़र (1884) दिखाया कि इसके ग्राफ की चाप लंबाई 2 है। ध्यान दें कि किसी भी गैर-न्यूनता फलन का ग्राफ ऐसा है कि और इसकी लंबाई 2 से अधिक नहीं है। इस अर्थ में, कैंटर फलन चरम है।
निरपेक्ष सांतत्य का अभाव
क्योंकि अगणनीय समुच्चय कैंटर समुच्चय का लेब्सेग माप 0 है, किसी भी सुनिश्चित ε < 1 और δ के लिए, कुल लंबाई <δ के साथ युग्मानूसार असंयुक्त उप-अंतराल का सीमित अनुक्रम सम्मिलित है, जिस पर कैंटर फलन संचयी रूप से ε से अधिक बढ़ जाता है।
वास्तव में, प्रत्येक δ > 0 के लिए परिमित रूप से कई युग्मानूसार असंयुक्त अंतराल (xk,yk) (1 ≤ k ≤ M) के साथ होते हैं और .
वैकल्पिक परिभाषाएँ
पुनरावृत्तीय निर्माण
नीचे हम इकाई अंतराल पर फलन का अनुक्रम {fn} को परिभाषित करते हैं जो कैंटर फलन में परिवर्तित होता है।
मान लीजिये f0(x) = x.
फिर, प्रत्येक पूर्णांक के लिए n ≥ 0, अगला फलन fn+1(x) को fn+1(x) के संदर्भ में परिभाषित किया जाएगा इस प्रकार है:
मान लीजिये fn+1(x) = 1/2 × fn(3x), जब 0 ≤ x ≤ 1/3 ;
मान लीजिये fn+1(x) = 1/2, जब 1/3 ≤ x ≤ 2/3 ;
मान लीजिये fn+1(x) = 1/2 + 1/2 × fn(3 x − 2), जब 2/3 ≤ x ≤ 1.
तीन परिभाषाएँ अंत-बिंदु 1/3 और 2/3 पर संगत हैं, प्रवर्तन द्वारा क्योंकि fn(0)=0 और fn(1) = 1 प्रत्येक n के लिए है। कोई यह जांच सकता है कि fn ऊपर परिभाषित कैंटर फलन में बिंदुवार अभिसरण होता है। इसके अतिरिक्त, अभिसरण एक समान है। दरअसल, fn+1 की परिभाषा के अनुसार, तीन स्थितियों में अलग करना है
यदि f सीमा फलन को दर्शाता है, तो यह इस प्रकार है कि, प्रत्येक n ≥ 0 के लिए,
इसके अतिरिक्त आरंभिक फलन का चुनाव वास्तव में कोई मायने नहीं रखता, बशर्ते कि f0(0) = 0, f0(1) = 1 और f0 परिबद्ध फलन है।
फ्रैक्टल आयतन
कैंटर फलन का कैंटर समुच्चय से गहरा संबंध है। कैंटर समुच्चय C को अंतराल [0,1] में उन संख्याओं के समुच्चय के रूप में परिभाषित किया जा सकता है, जिनके आधार-3 (त्रिकोणीय) विस्तार में अंक 1 सम्मिलित नहीं है, सिवाय इसके कि 1 के बाद आता है केवल शून्य (जिस स्थिति में पिछला 1000 0222 द्वारा प्रतिस्थापित किया जा सकता है किसी एक से छुटकारा पाने के लिए 1)। यह पता चला है कि कैंटर समुच्चय फ्रैक्टल है जिसमें (अगणनीय) अनंत कई बिंदु (शून्य-आयामी मात्रा) हैं, लेकिन शून्य लंबाई (एक-आयामी मात्रा) है। केवल D-आयामी आयतन (हॉसडॉर्फ़ आयाम के अर्थ में) सीमित मान लेता है, जहां C का फ्रैक्टल आयाम है। हम कैंटर फलन को कैंटर समुच्चय के अनुभागों के D-आयामी आयतन के रूप में वैकल्पिक रूप से परिभाषित कर सकते हैं
स्व-समानता
कैंटर फलन में कई समरूपताएं होती हैं। के लिए, प्रतिबिंब समरूपता है
और आवर्धन की युग्म, एक बाईं ओर और दाईं ओर:
और
आवर्धन को सोपानित किया जा सकता है; वे द्वैयकीय एकाभ उत्पन्न करते हैं। इसे कई सहायक फलन को परिभाषित करके प्रदर्शित किया जाता है। प्रतिबिंब को इस प्रकार परिभाषित करें
प्रथम स्व-समरूपता को इस प्रकार व्यक्त किया जा सकता है
जहां प्रतीक फलन संरचना को दर्शाता है। वह है, और इसी तरह अन्य स्थितियों के लिए भी है। बाएँ और दाएँ आवर्धन के लिए, बाएँ-प्रतिचित्रण लिखें
- और
तब कैंटर फलन का पालन होता है
इसी प्रकार, सही प्रतिचित्रण को इस प्रकार परिभाषित करें
- और
फिर, इसी तरह,
उसमें दोनों पक्षों को एक दूसरे पर प्रतिबिंबित किया जा सकता है
और इसी तरह,
इन परिचालनों को अक्रमतः से क्रमबद्ध किया जा सकता है। उदाहरण के लिए, बाएँ-दाएँ चालों के क्रम पर विचार करें सबस्क्रिप्ट C और D जोड़ना, और स्पष्टता के लिए, कंपोज़िशन ऑपरेटर को हटाना कुछ स्थानों को छोड़कर सभी में, एक है:
L और R अक्षरों में यादृच्छिक परिमित-लंबाई वाले तार द्वैयकीय परिमेय के अनुरूप हैं, जिसमें प्रत्येक द्वैयकीय परिमेय को दोनों के रूप में पूर्णांक n और m के लिए और बिट्स की सीमित लंबाई के रूप में साथ लिखा जा सकता है इस प्रकार, प्रत्येक द्वैयकीय परिमेय कैंटर फलन की कुछ स्व-समरूपता के साथ एकैक पत्राचार में है।
कुछ सांकेतिक पुनर्व्यवस्थाएं उपरोक्त को व्यक्त करना थोड़ा आसान बना सकती हैं। मान लीजिये और L और R के लिए है। फलन संरचना इसे एकाभ तक विस्तारित करती है, जिसमें कोई भी लिख सकता है और सामान्यतः, अंक A, B की कुछ द्विआधारी स्ट्रिंग के लिए, जहां AB ऐसी स्ट्रिंग का सामान्य संयोजन है। द्वैयकीय एकाभ M तब ऐसी सभी परिमित-लंबाई वाली बाएँ-दाएँ का एकाभ है। लिखना एकाभ के सामान्य तत्व के रूप में, कैंटर फलन की समान स्व-समरूपता है:
द्वैयकीय एकाभ में स्वयं कई दिलचस्प गुण हैं। इसे अनंत द्वयी तरू के नीचे बाएँ-दाएँ चालों की सीमित संख्या के रूप में देखा जा सकता है; तरू पर असीम रूप से दूर की "पत्तियाँ" कैंटर समुच्चय के बिंदुओं से मेल खाती हैं, और इसलिए, एकाभ कैंटर समुच्चय की स्व-समरूपता का भी प्रतिरूपण करता है। वास्तव में, सामान्यतः पाए जाने वाले फ्रैक्टल्स के बड़े वर्ग का वर्णन द्वैयकीय एकाभ द्वारा किया जाता है; अतिरिक्त उदाहरण डी राम वक्र पर लेख में पाए जा सकते हैं। स्व-समानता रखने वाले अन्य फ्रैक्टल्स को अन्य प्रकार के एकाभ के साथ वर्णित किया गया है। द्वैयकीय एकाभ स्वयं मॉड्यूलर समूह का उप-एकाभ है।
ध्यान दें कि कैंटर फलन मिंकोव्स्की के प्रश्न-चिह्न फलन से कहीं अधिक समानता रखता है। विशेष रूप से, यह बिल्कुल उसी समरूपता संबंधों का पालन यद्यपि परिवर्तित रूप में करता है।
सामान्यीकरण
मान लीजिये
वास्तविक संख्या 0 ≤ y ≤ 1 का द्विआधारी अंक bk ∈ {0,1} के संदर्भ में द्विघात परिमेय (द्विआधारी) विस्तार है। द्वैयकीय परिवर्तन पर लेख में इस विस्तार पर अधिक विस्तार से चर्चा की गई है। फिर फलन पर विचार करें
z = 1/3 के लिए, फलन का व्युत्क्रम x = 2 C1/3(y) कैंटर फलन है। अर्थात्, y = y(x) कैंटर फलन है। सामान्य तौर पर, किसी भी z < 1/2, Cz(y) के लिए ऐसा लगता है जैसे कैंटर फलन अपनी तरफ मुड़ गया है, जैसे-जैसे z शून्य के करीब पहुंचता है, चरणों की चौड़ाई चौड़ी होती जाती है।
जैसा कि ऊपर उल्लेख किया गया है, कैंटर फलन कैंटर समुच्चय पर माप का संचयी वितरण फलन भी है। कैंटर समुच्चय या अन्य फ्रैक्टल्स पर समर्थित विभिन्न परमाणु-कम संभाव्यता उपायों पर विचार करके विभिन्न कैंटर फलन, या डेविल्स स्टेरकेस प्राप्त की जा सकती हैं। जबकि कैंटर फलन में लगभग हर जगह व्युत्पन्न 0 है, वर्तमान शोध उन बिंदुओं के समुच्चय के आकार के सवाल पर केंद्रित है जहां ऊपरी दाएं व्युत्पन्न निचले दाएं व्युत्पन्न से अलग है, जिससे व्युत्पन्न सम्मिलित नहीं है। भिन्नता का यह विश्लेषण सामान्यतः फ्रैक्टल आयाम के संदर्भ में दिया जाता है, जिसमें हॉसडॉर्फ आयाम सबसे लोकप्रिय विकल्प है। अनुसंधान की यह श्रृंखला 1990 के दशक में डर्स्ट द्वारा प्रारंभ की गई थी,[5] जिन्होंने दिखाया कि कैंटर फलन की गैर-भिन्नता के समुच्चय का हॉसडॉर्फ आयाम कैंटर समुच्चय के आयाम का वर्ग है, । इसके बाद केनेथ फाल्कनर (गणितज्ञ)[6] पता चला कि यह वर्ग संबंध अहलफोर के सभी नियमित, एकल उपायों के लिए लागू होता है, अर्थात
हरमन मिन्कोव्स्की का मिन्कोव्स्की का प्रश्न चिह्न फलन देखने में कैंटर फलन से मिलता-जुलता है, जो बाद वाले के "सुचारू" रूप के रूप में दिखाई देता है; इसका निर्माण सतत अंश विस्तार से द्विआधारी विस्तार में जाकर किया जा सकता है, जैसे कैंटर फलन का निर्माण त्रिक विस्तार से द्विआधारी विस्तार में जाकर किया जा सकता है। प्रश्न चिह्न फलन में सभी परिमेय संख्याओं के लुप्त हो जाने वाले व्युत्पन्न होने का दिलचस्प गुण है।
यह भी देखें
- द्वैयकीय परिवर्तन
- वीयरस्ट्रैस फलन, एक ऐसा फलन जो हर जगह सतत है लेकिन कहीं भी भिन्न नहीं है।
टिप्पणियाँ
- ↑ Vestrup 2003, Section 4.6.
- ↑ Thomson, Bruckner & Bruckner 2008, p. 252.
- ↑ "Cantor Staircase Function".
- ↑ Bass 2013, p. 28.
- ↑ Darst, Richard (1993-09-01). "The Hausdorff Dimension of the Nondifferentiability Set of the Cantor Function is [ ln(2)/ln(3) ]2". Proceedings of the American Mathematical Society. 119 (1): 105–108. doi:10.2307/2159830. JSTOR 2159830.
- ↑ Falconer, Kenneth J. (2004-01-01). "एक तरफा मल्टीफ्रैक्टल विश्लेषण और शैतान की सीढ़ियों की गैर-विभेदीकरण के बिंदु". Mathematical Proceedings of the Cambridge Philosophical Society. 136 (1): 167–174. Bibcode:2004MPCPS.136..167F. doi:10.1017/S0305004103006960. ISSN 1469-8064. S2CID 122381614.
- ↑ Troscheit, Sascha (2014-03-01). "Hölder differentiability of self-conformal devil's staircases". Mathematical Proceedings of the Cambridge Philosophical Society. 156 (2): 295–311. arXiv:1301.1286. Bibcode:2014MPCPS.156..295T. doi:10.1017/S0305004113000698. ISSN 1469-8064. S2CID 56402751.
संदर्भ
- Bass, Richard Franklin (2013) [2011]. Real analysis for graduate students (Second ed.). Createspace Independent Publishing. ISBN 978-1-4818-6914-0.
- Cantor, G. (1884). "De la puissance des ensembles parfaits de points: Extrait d'une lettre adressée à l'éditeur" [The power of perfect sets of points: Extract from a letter addressed to the editor]. Acta Mathematica. International Press of Boston. 4: 381–392. doi:10.1007/bf02418423. ISSN 0001-5962. Reprinted in: E. Zermelo (Ed.), Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts, Springer, New York, 1980.
- Darst, Richard B.; Palagallo, Judith A.; Price, Thomas E. (2010), Curious curves, Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd., ISBN 978-981-4291-28-6, MR 2681574
- Dovgoshey, O.; Martio, O.; Ryazanov, V.; Vuorinen, M. (2006). "The Cantor function". Expositiones Mathematicae. Elsevier BV. 24 (1): 1–37. doi:10.1016/j.exmath.2005.05.002. ISSN 0723-0869. MR 2195181.
- Fleron, Julian F. (1994-04-01). "A Note on the History of the Cantor Set and Cantor Function". Mathematics Magazine. Informa UK Limited. 67 (2): 136–140. doi:10.2307/2690689. ISSN 0025-570X. JSTOR 2690689.
- Lebesgue, H. (1904), Leçons sur l'intégration et la recherche des fonctions primitives [Lessons on integration and search for primitive functions], Paris: Gauthier-Villars
- Leoni, Giovanni (2017). A first course in Sobolev spaces. Vol. 181 (2nd ed.). Providence, Rhode Island: American Mathematical Society. p. 734. ISBN 978-1-4704-2921-8. OCLC 976406106.
- Scheeffer, Ludwig (1884). "Allgemeine Untersuchungen über Rectification der Curven" [General investigations on rectification of the curves]. Acta Mathematica. International Press of Boston. 5: 49–82. doi:10.1007/bf02421552. ISSN 0001-5962.
- Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2008) [2001]. Elementary real analysis (Second ed.). ClassicalRealAnalysis.com. ISBN 978-1-4348-4367-8.
- Vestrup, E.M. (2003). The theory of measures and integration. Wiley series in probability and statistics. John Wiley & sons. ISBN 978-0471249771.
- Vitali, A. (1905), "Sulle funzioni integrali" [On the integral functions], Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur., 40: 1021–1034