टैग यूनियन: Difference between revisions
No edit summary |
(→2000s) |
||
| Line 1: | Line 1: | ||
[[कंप्यूटर विज्ञान]] में, '''टैग यूनियन''', जिसे '''वैरिएंट''', '''वैरिएंट रिकॉर्ड''', '''चयन प्रकार''', '''विभेदित यूनियन''', [[ असंयुक्त संघ |'''असंयुक्त यूनियन''']], '''योग प्रकार''' या [[सहउत्पाद|'''सहउत्पाद''']] भी कहा जाता है, [[डेटा संरचना]] है जिसका उपयोग मान रखने के लिए किया जाता है जो कई अलग-अलग, लेकिन निश्चित, प्रकारों पर ले जा सकता है। किसी भी समय केवल एक ही प्रकार का उपयोग किया जा सकता है, और '''टैग''' क्षेत्र स्पष्ट रूप से इंगित करता है कि कौन सा प्रकार उपयोग में है। इसे एक ऐसे प्रकार के रूप में सोचा जा सकता है जिसमें कई " | [[कंप्यूटर विज्ञान]] में, '''टैग यूनियन''', जिसे '''वैरिएंट''', '''वैरिएंट रिकॉर्ड''', '''चयन प्रकार''', '''विभेदित यूनियन''', [[ असंयुक्त संघ |'''असंयुक्त यूनियन''']], '''योग प्रकार''' या [[सहउत्पाद|'''सहउत्पाद''']] भी कहा जाता है, [[डेटा संरचना]] है जिसका उपयोग मान रखने के लिए किया जाता है जो कई अलग-अलग, लेकिन निश्चित, प्रकारों पर ले जा सकता है। किसी भी समय केवल एक ही प्रकार का उपयोग किया जा सकता है, और '''टैग''' क्षेत्र स्पष्ट रूप से इंगित करता है कि कौन सा प्रकार उपयोग में है। इसे एक ऐसे प्रकार के रूप में सोचा जा सकता है जिसमें कई "केस" होतो हैं, जिनमें से प्रत्येक को उस प्रकार में युक्तियोजित किए जाने पर सही ढंग से संभाला जाना चाहिए। यह पुनरावर्ती डेटाटाइप को परिभाषित करने में महत्वपूर्ण है, जिसमें किसी मान के कुछ घटक का प्रकार उस मान के समान हो सकता है, उदाहरण के लिए ट्रीस का प्रतिनिधित्व करने के लिए एक प्रकार को परिभाषित करने में, जहां मल्टी-नोड सबट्रीस और लीव्स को अलग करना आवश्यक है। सामान्य यूनियनों की तरह, टैग यूनियन प्रत्येक प्रकार के लिए स्टोरेज क्षेत्रों को ओवरलैप करके स्टोरेज बचा सकता हैं, क्योंकि एक समय में केवल एक ही उपयोग में होता है। | ||
==विवरण== | ==विवरण== | ||
[[प्रोग्रामिंग भाषा|एमएल (ML)]] और [[हास्केल]] जैसी [[कार्यात्मक प्रोग्रामिंग]] भाषाओं में टैग यूनियन सबसे महत्वपूर्ण हैं, जहां उन्हें ''डेटाप्रकार'' कहा जाता है (बीजगणितीय डेटा प्रकार देखें) और [[ संकलक |संकलक]] यह सत्यापित करने में सक्षम है कि टैग यूनियनों की सभी | [[प्रोग्रामिंग भाषा|एमएल (ML)]] और [[हास्केल]] जैसी [[कार्यात्मक प्रोग्रामिंग]] भाषाओं में टैग यूनियन सबसे महत्वपूर्ण हैं, जहां उन्हें ''डेटाप्रकार'' कहा जाता है (बीजगणितीय डेटा प्रकार देखें) और [[ संकलक |संकलक]] यह सत्यापित करने में सक्षम है कि टैग यूनियनों की सभी केसेस को कई प्रकार की त्रुटियों से बचते हुए सदैव नियंत्रित किया जाता है। हालाँकि, इन्हें लगभग किसी भी प्रोग्रामिंग भाषा में बनाया जा सकता है, और अनटैग यूनियनों की तुलना में अधिक सुरक्षित हैं, जिन्हें प्रायः यूनियन कहा जाता है, जो समान हैं लेकिन स्पष्ट रूप से ट्रैक नहीं करते हैं कि यूनियन का कौन सा सदस्य वर्तमान में उपयोग में है। | ||
टैग यूनियनों के साथ प्रायः एक प्रकार के निर्माता की अवधारणा जुड़ी होती है, जो [[क्लास (कंप्यूटर प्रोग्रामिंग)| | टैग यूनियनों के साथ प्रायः एक प्रकार के निर्माता की अवधारणा जुड़ी होती है, जो [[क्लास (कंप्यूटर प्रोग्रामिंग)|क्लास]] के लिए [[कंस्ट्रक्टर (ऑब्जेक्ट-ओरिएंटेड प्रोग्रामिंग)|निर्माता]] के समान है लेकिन समान नहीं होता है। प्रारंभिक टैग प्रकार और संबंधित प्रकार को ध्यान में रखते हुए, प्रकार [[कंस्ट्रक्टर टाइप करें|निर्माता]] टैग यूनियन प्रकार का उत्पादन करते हैं। | ||
गणितीय रूप से, टैग यूनियन असंयुक्त या विभेदित टैगों के अनुरूप होते हैं, जिन्हें प्रायः + का उपयोग करके लिखा जाता है। असंयुक्त टैग ''A'' + ''B'' के तत्व को देखते हुए, यह निर्धारित करना संभव है कि यह ''A'' या ''B'' से आया है या नहीं। यदि कोई तत्व दोनों में निहित है, तो ''A'' + ''B'' में मान की दो प्रभावी रूप से भिन्न प्रतियां होंगी, एक ''A'' से और एक ''B'' से। | गणितीय रूप से, टैग यूनियन असंयुक्त या विभेदित टैगों के अनुरूप होते हैं, जिन्हें प्रायः + का उपयोग करके लिखा जाता है। असंयुक्त टैग ''A'' + ''B'' के तत्व को देखते हुए, यह निर्धारित करना संभव है कि यह ''A'' या ''B'' से आया है या नहीं। यदि कोई तत्व दोनों में निहित है, तो ''A'' + ''B'' में मान की दो प्रभावी रूप से भिन्न प्रतियां होंगी, एक ''A'' से और एक ''B'' से। | ||
[[प्रकार सिद्धांत]] में, टैग यूनियन को ''योग प्रकार'' कहा जाता है। योग प्रकार उत्पाद प्रकारों के द्वैत हैं। संकेतन अलग-अलग होते हैं, लेकिन प्रायः योग प्रकार {{math|''A'' + ''B''}} ([[इंजेक्शन (गणित)|अंतःक्षेपों]]) के लिए दो परिचय के साथ आता है- {{math|inj<sub>1</sub>: ''A'' → ''A'' + ''B''}} और {{nowrap|{{math|inj<sub>2</sub>: ''B'' → ''A'' + ''B''}}}}। उन्मूलन रूप | [[प्रकार सिद्धांत]] में, टैग यूनियन को ''योग प्रकार'' कहा जाता है। योग प्रकार उत्पाद प्रकारों के द्वैत हैं। संकेतन अलग-अलग होते हैं, लेकिन प्रायः योग प्रकार {{math|''A'' + ''B''}} ([[इंजेक्शन (गणित)|अंतःक्षेपों]]) के लिए दो परिचय के साथ आता है- {{math|inj<sub>1</sub>: ''A'' → ''A'' + ''B''}} और {{nowrap|{{math|inj<sub>2</sub>: ''B'' → ''A'' + ''B''}}}}। उन्मूलन रूप केस विश्लेषण है, जिसे एमएल-शैली भाषाओं में [[पैटर्न मिलान]] के रूप में जाना जाता है- यदि {{mvar|e}} में प्रकार {{math|''A'' + ''B''}} है और {{math|''e''<sub>1</sub>}} और {{math|''e''<sub>2</sub>}} में क्रमशः {{math|''x'': ''A''}} और {{math|''y'': ''B''}} की मान्यताओं के तहत <math>\tau</math> प्रकार है, तो शब्द <math>\mathsf{case}\ e\ \mathsf{of}\ x \Rightarrow e_1 \mid y \Rightarrow e_2</math> में <math>\tau</math> प्रकार है। योग प्रकार करी-हावर्ड समानता के तहत अंतर्ज्ञानवादी [[तार्किक विच्छेदन]] से मेल खाता है। | ||
[[प्रगणित प्रकार]] को विकृत | [[प्रगणित प्रकार]] को विकृत केस के रूप में देखा जा सकता है- [[इकाई प्रकार|इकाई प्रकारों]] का टैग यूनियन है। यह अशक्त निर्माताओं के समुच्चय से मेल खाता है और इसे साधारण टैग वेरिएबल के रूप में कार्यान्वित किया जा सकता है, क्योंकि इसमें टैग के मान के अलावा कोई अतिरिक्त डेटा नहीं है। | ||
कई प्रोग्रामिंग तकनीक और डेटा संरचनाएं, जिनमें रोप, [[आलसी मूल्यांकन|अनुयोगी मूल्यांकन]], [[वर्ग पदानुक्रम]] (नीचे देखें), मनमानी-सटीक अंकगणित, [[सीडीआर कोडिंग|सीडीआर (CDR) कोडिंग]], [[अप्रत्यक्ष बिट]] और अन्य प्रकार के टैग संकेतों आदि सम्मिलित हैं, प्रायः कुछ प्रकार के टैग यूनियनों का उपयोग करके कार्यान्वित किए जाते हैं। | कई प्रोग्रामिंग तकनीक और डेटा संरचनाएं, जिनमें रोप, [[आलसी मूल्यांकन|अनुयोगी मूल्यांकन]], [[वर्ग पदानुक्रम|क्लास पदानुक्रम]] (नीचे देखें), मनमानी-सटीक अंकगणित, [[सीडीआर कोडिंग|सीडीआर (CDR) कोडिंग]], [[अप्रत्यक्ष बिट]] और अन्य प्रकार के टैग संकेतों आदि सम्मिलित हैं, प्रायः कुछ प्रकार के टैग यूनियनों का उपयोग करके कार्यान्वित किए जाते हैं। | ||
टैग यूनियन को सबसे सरल प्रकार के स्व-वर्णन डेटा प्रारूप के रूप में देखा जा सकता है। टैग यूनियन के टैग को सबसे सरल प्रकार के [[ मेटा डेटा |मेटाडेटा]] के रूप में देखा जा सकता है। | टैग यूनियन को सबसे सरल प्रकार के स्व-वर्णन डेटा प्रारूप के रूप में देखा जा सकता है। टैग यूनियन के टैग को सबसे सरल प्रकार के [[ मेटा डेटा |मेटाडेटा]] के रूप में देखा जा सकता है। | ||
==लाभ और हानि== | ==लाभ और हानि== | ||
अनटैग यूनियन की तुलना में टैग यूनियन का प्राथमिक लाभ यह है कि सभी एक्सेस सुरक्षित हैं, और संकलक यह भी जांच सकता है कि सभी | अनटैग यूनियन की तुलना में टैग यूनियन का प्राथमिक लाभ यह है कि सभी एक्सेस सुरक्षित हैं, और संकलक यह भी जांच सकता है कि सभी केसेस को संभाला गया है। अनटैग यूनियन वर्तमान में सक्रिय क्षेत्र की सही पहचान करने के लिए प्रोग्राम तर्क पर निर्भर करता हैं, जिसके परिणामस्वरूप अजीब व्यवहार हो सकता है और यदि वह तर्क विफल हो जाता है तो बग ढूंढना मुश्किल हो सकता है। | ||
प्रत्येक प्रकार के लिए क्षेत्र वाले साधारण [[रिकॉर्ड (कंप्यूटर विज्ञान)|रिकॉर्ड]] की तुलना में टैग यूनियन का प्राथमिक लाभ यह है कि यह सभी प्रकार के लिए स्टोरेज को ओवरलैप करके स्टोरेज बचाता है। कुछ कार्यान्वयन सबसे बड़े प्रकार के लिए पर्याप्त स्टोरेज आरक्षित रखते हैं, जबकि अन्य आवश्यकतानुसार टैग यूनियन मान के आकार को गतिशील रूप से समायोजित करते हैं। जब मान [[अपरिवर्तनीय वस्तु|अपरिवर्तनीय]] होता है, तो उतनी ही स्टोरेज अलोकेट करना आसान होता है जितनी आवश्यकता होती है। | प्रत्येक प्रकार के लिए क्षेत्र वाले साधारण [[रिकॉर्ड (कंप्यूटर विज्ञान)|रिकॉर्ड]] की तुलना में टैग यूनियन का प्राथमिक लाभ यह है कि यह सभी प्रकार के लिए स्टोरेज को ओवरलैप करके स्टोरेज बचाता है। कुछ कार्यान्वयन सबसे बड़े प्रकार के लिए पर्याप्त स्टोरेज आरक्षित रखते हैं, जबकि अन्य आवश्यकतानुसार टैग यूनियन मान के आकार को गतिशील रूप से समायोजित करते हैं। जब मान [[अपरिवर्तनीय वस्तु|अपरिवर्तनीय]] होता है, तो उतनी ही स्टोरेज अलोकेट करना आसान होता है जितनी आवश्यकता होती है। | ||
टैग यूनियनों की मुख्य हानि यह है कि टैग स्थान घेरता है। चूँकि प्रायः बहुत कम संख्या में विकल्प होते हैं, टैग को प्रायः जहां भी स्थान मिलता है, 2 या 3 बिट्स में निष्पीडित किया जा सकता है, लेकिन कभी-कभी ये बिट्स भी उपलब्ध नहीं होते हैं। इस | टैग यूनियनों की मुख्य हानि यह है कि टैग स्थान घेरता है। चूँकि प्रायः बहुत कम संख्या में विकल्प होते हैं, टैग को प्रायः जहां भी स्थान मिलता है, 2 या 3 बिट्स में निष्पीडित किया जा सकता है, लेकिन कभी-कभी ये बिट्स भी उपलब्ध नहीं होते हैं। इस केस में, सहायक विकल्प टैग को '''फोल्ड करना''', '''गणना करना''' या '''एन्कोड करना''' हो सकता है, जहां टैग मान की गणना यूनियन क्षेत्र की सामग्री से गतिशील रूप से की जाती है। इसके सामान्य उदाहरण आरक्षित मानों का उपयोग हैं, उदाहरण के लिए, सकारात्मक संख्या वापस लाने वाला फ़ंक्शन विफलता को इंगित करने के लिए -1 वापस कर सकता है, और प्रहरी मान, जो प्रायः टैग संकेतों में उपयोग किए जाते हैं। | ||
कभी-कभी, अनटैग यूनियनों का उपयोग प्रकारों के बीच बिट-स्तरीय रूपांतरण करने के लिए किया जाता है, जिन्हें सी++ (C++) में पुनः व्याख्या विक्षेप कहा जाता है। टैग यूनियन इस उद्देश्य के लिए अभिप्रेत नहीं हैं प्रायः जब भी टैग बदला जाता है तो एक नया मान निर्दिष्ट किया जाता है। | कभी-कभी, अनटैग यूनियनों का उपयोग प्रकारों के बीच बिट-स्तरीय रूपांतरण करने के लिए किया जाता है, जिन्हें सी++ (C++) में पुनः व्याख्या विक्षेप कहा जाता है। टैग यूनियन इस उद्देश्य के लिए अभिप्रेत नहीं हैं प्रायः जब भी टैग बदला जाता है तो एक नया मान निर्दिष्ट किया जाता है। | ||
कई भाषाएँ, कुछ हद तक, सार्वभौमिक डेटा [[शीर्ष प्रकार|प्रकार]] का सपोर्ट करती हैं, जो एक ऐसा प्रकार है जिसमें प्रत्येक दूसरे प्रकार का प्रत्येक मान सम्मिलित होता है, और प्रायः सार्वभौमिक प्रकार के मान के वास्तविक प्रकार का परीक्षण करने का तरीका प्रदान किया जाता है। इन्हें कभी-कभी ''वैरिएंट्स'' के रूप में भी जाना जाता है। जबकि सार्वभौमिक डेटा प्रकार उनकी औपचारिक परिभाषा में टैग यूनियनों के साथ तुलनीय हैं, विशिष्ट टैग यूनियनों में अपेक्षाकृत कम संख्या में | कई भाषाएँ, कुछ हद तक, सार्वभौमिक डेटा [[शीर्ष प्रकार|प्रकार]] का सपोर्ट करती हैं, जो एक ऐसा प्रकार है जिसमें प्रत्येक दूसरे प्रकार का प्रत्येक मान सम्मिलित होता है, और प्रायः सार्वभौमिक प्रकार के मान के वास्तविक प्रकार का परीक्षण करने का तरीका प्रदान किया जाता है। इन्हें कभी-कभी ''वैरिएंट्स'' के रूप में भी जाना जाता है। जबकि सार्वभौमिक डेटा प्रकार उनकी औपचारिक परिभाषा में टैग यूनियनों के साथ तुलनीय हैं, विशिष्ट टैग यूनियनों में अपेक्षाकृत कम संख्या में केसेस सम्मिलित होते हैं, और ये केसेस एकल सुसंगत अवधारणा को व्यक्त करने के विभिन्न तरीके बनाते हैं, जैसे डेटा संरचना नोड या निर्देश। साथ ही, यह भी अपेक्षा है कि टैग यूनियन का उपयोग किए जाने पर उसकी प्रत्येक संभावित केस से निपटा जाएगा। सार्वभौमिक डेटा प्रकार के मान संबंधित नहीं हैं और उन सभी से निपटने का कोई व्यवहार्य तरीका नहीं है। | ||
[[विकल्प प्रकार]] और अपवाद प्रबंधन की तरह, टैग यूनियनों का उपयोग कभी-कभी असाधारण परिणामों की घटना को संभालने के लिए किया जाता है। प्रायः इन टैगों को आरक्षित मानों के रूप में मोड़ दिया जाता है, और उनकी घटना की लगातार जांच नहीं की जाती है- यह प्रोग्रामिंग त्रुटियों का पूरी तरह से सामान्य सोर्स है। टैग यूनियनों के इस उपयोग को निम्नलिखित कार्यों के साथ [[मोनाड (कार्यात्मक प्रोग्रामिंग)|मोनाड]] के रूप में औपचारिक रूप दिया जा सकता है- | [[विकल्प प्रकार]] और अपवाद प्रबंधन की तरह, टैग यूनियनों का उपयोग कभी-कभी असाधारण परिणामों की घटना को संभालने के लिए किया जाता है। प्रायः इन टैगों को आरक्षित मानों के रूप में मोड़ दिया जाता है, और उनकी घटना की लगातार जांच नहीं की जाती है- यह प्रोग्रामिंग त्रुटियों का पूरी तरह से सामान्य सोर्स है। टैग यूनियनों के इस उपयोग को निम्नलिखित कार्यों के साथ [[मोनाड (कार्यात्मक प्रोग्रामिंग)|मोनाड]] के रूप में औपचारिक रूप दिया जा सकता है- | ||
| Line 31: | Line 31: | ||
:<math>\text{return}\colon A \to \left( A + E \right) = a \mapsto \text{value} \, a</math> | :<math>\text{return}\colon A \to \left( A + E \right) = a \mapsto \text{value} \, a</math> | ||
:<math>\text{bind}\colon \left( A + E \right) \to \left(A \to \left(B + E \right) \right) \to \left( B + E \right) = a \mapsto f \mapsto \begin{cases} \text{err} \, e & \text{if} \ a = \text{err} \, e\\ f \, a' & \text{if} \ a = \text{value} \, a' \end{cases}</math> | :<math>\text{bind}\colon \left( A + E \right) \to \left(A \to \left(B + E \right) \right) \to \left( B + E \right) = a \mapsto f \mapsto \begin{cases} \text{err} \, e & \text{if} \ a = \text{err} \, e\\ f \, a' & \text{if} \ a = \text{value} \, a' \end{cases}</math> | ||
जहां "मान" और "त्रुटि" यूनियन प्रकार के निर्माता हैं, ''A'' और ''B'' वैध परिणाम प्रकार हैं और ''E'' त्रुटि | जहां "मान" और "त्रुटि" यूनियन प्रकार के निर्माता हैं, ''A'' और ''B'' वैध परिणाम प्रकार हैं और ''E'' त्रुटि केसेस का प्रकार है। वैकल्पिक रूप से, उसी मोनाड को वापस और दो अतिरिक्त कार्यों, एफएमएपी (''fmap'') और ''संबद्ध'' द्वारा वर्णित किया जा सकता है- | ||
:<math>\text{fmap} \colon (A \to B) \to \left( \left( A + E \right) \to \left( B + E \right) \right) = f \mapsto a \mapsto \begin{cases} \text{err} \, e & \text{if} \ a = \text{err} \, e \\ \text{value} \, \text{(} \, f \, a' \, \text{)} & \text{if} \ a = \text{value} \, a' \end{cases}</math> | :<math>\text{fmap} \colon (A \to B) \to \left( \left( A + E \right) \to \left( B + E \right) \right) = f \mapsto a \mapsto \begin{cases} \text{err} \, e & \text{if} \ a = \text{err} \, e \\ \text{value} \, \text{(} \, f \, a' \, \text{)} & \text{if} \ a = \text{value} \, a' \end{cases}</math> | ||
| Line 42: | Line 42: | ||
| Node of (int * tree * tree) | | Node of (int * tree * tree) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
यह दो | यह दो केसेस के साथ टैग यूनियन है- एक, लीफ, का उपयोग ट्री के पथ को समाप्त करने के लिए किया जाता है, और अनिवार्य भाषाओं में शून्य मान की तरह कार्य करता है। दूसरी शाखा में नोड होता है, जिसमें एक पूर्णांक और बाएं और दाएं सबट्री होता है। लीफ और नोड निर्माता हैं, जो हमें वास्तव में विशेष ट्री बनाने में सक्षम बनाते हैं, जैसे- | ||
<syntaxhighlight lang="sml"> | <syntaxhighlight lang="sml"> | ||
| Line 76: | Line 76: | ||
===1970s और 1980s=== | ===1970s और 1980s=== | ||
हालाँकि मुख्य रूप से केवल कार्यात्मक प्रोग्रामिंग भाषाएँ जैसे एमएल (1970 के दशक से) और हास्केल (1990 के दशक से) टैग यूनियनों को केंद्रीय भूमिका देती हैं और यह जाँचने की शक्ति रखती हैं कि सभी | हालाँकि मुख्य रूप से केवल कार्यात्मक प्रोग्रामिंग भाषाएँ जैसे एमएल (1970 के दशक से) और हास्केल (1990 के दशक से) टैग यूनियनों को केंद्रीय भूमिका देती हैं और यह जाँचने की शक्ति रखती हैं कि सभी केसेस को संभाला जाता है, अन्य भाषाएँ भी टैग यूनियनों का सपोर्ट करती हैं। हालाँकि, व्यवहार में वे कार्यात्मक भाषा संकलकों द्वारा सक्षम किए गए अनुकूलन के कारण गैर-कार्यात्मक भाषाओं में कम कुशल हो सकते हैं जो स्पष्ट टैग जांच को समाप्त कर सकते हैं और टैग के स्पष्ट स्टोरेज से बच सकते हैं।{{Citation needed|date=January 2017}} | ||
[[पास्कल (प्रोग्रामिंग भाषा)|पास्कल]], [[एडा (प्रोग्रामिंग भाषा)|एडा]] और [[मॉड्यूल-2|मोडुला-2]] उन्हें ''वैरिएंट रिकॉर्ड'' (एडा में औपचारिक रूप से विभेदित प्रकार) कहते हैं, और टैग क्षेत्र को मैन्युअल रूप से बनाने और टैग मान निर्दिष्ट करने की आवश्यकता होती है, जैसा कि इस पास्कल उदाहरण में है- | [[पास्कल (प्रोग्रामिंग भाषा)|पास्कल]], [[एडा (प्रोग्रामिंग भाषा)|एडा]] और [[मॉड्यूल-2|मोडुला-2]] उन्हें ''वैरिएंट रिकॉर्ड'' (एडा में औपचारिक रूप से विभेदित प्रकार) कहते हैं, और टैग क्षेत्र को मैन्युअल रूप से बनाने और टैग मान निर्दिष्ट करने की आवश्यकता होती है, जैसा कि इस पास्कल उदाहरण में है- | ||
| Line 143: | Line 143: | ||
C और C++ में विशेष टैग यूनियन के लिए भाषा सपोर्ट भी है- संभवतः-शून्य [[पॉइंटर (कंप्यूटर प्रोग्रामिंग)|सूचक]]। इसकी तुलना एमएल में <code>ऑप्शन</code> प्रकार या हास्केल में <code>मेबी</code> प्रकार से की जा सकती है, और इसे [[नल पॉइंटर|टैग सूचक]] के रूप में देखा जा सकता है- दो प्रकार का टैग यूनियन (एन्कोडेड टैग के साथ)- | C और C++ में विशेष टैग यूनियन के लिए भाषा सपोर्ट भी है- संभवतः-शून्य [[पॉइंटर (कंप्यूटर प्रोग्रामिंग)|सूचक]]। इसकी तुलना एमएल में <code>ऑप्शन</code> प्रकार या हास्केल में <code>मेबी</code> प्रकार से की जा सकती है, और इसे [[नल पॉइंटर|टैग सूचक]] के रूप में देखा जा सकता है- दो प्रकार का टैग यूनियन (एन्कोडेड टैग के साथ)- | ||
* मान्य सूचक, | * मान्य सूचक, | ||
* केवल एक मान वाला शून्य सूचक प्रकार, <code>नल</code>, असाधारण | * केवल एक मान वाला शून्य सूचक प्रकार, <code>नल (null)</code>, असाधारण केस का संकेत देता है। | ||
दुर्भाग्य से, C संकलक यह सत्यापित नहीं करते हैं कि अशक्त | दुर्भाग्य से, C संकलक यह सत्यापित नहीं करते हैं कि अशक्त केस को सदैव संभाला जाता है, और यह C कोड में त्रुटियों का विशेष रूप से प्रचलित सोर्स है, क्योंकि असाधारण केसेस को अनदेखा करने की प्रवृत्ति होती है। | ||
===2000s=== | ===2000s=== | ||
| Line 171: | Line 171: | ||
boost::apply_visitor(display(), v); | boost::apply_visitor(display(), v); | ||
</syntaxhighlight> | </syntaxhighlight> | ||
[[स्काला (प्रोग्रामिंग भाषा)|स्काला]] में | [[स्काला (प्रोग्रामिंग भाषा)|स्काला]] में केस क्लास हैं- | ||
<syntaxhighlight lang="scala"> | <syntaxhighlight lang="scala"> | ||
sealed abstract class Tree | sealed abstract class Tree | ||
| Line 179: | Line 179: | ||
val tree = Node(5, Node(1, Leaf, Leaf), Node(3, Leaf, Node(4, Leaf, Leaf))) | val tree = Node(5, Node(1, Leaf, Leaf), Node(3, Leaf, Node(4, Leaf, Leaf))) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
क्योंकि | क्योंकि क्लास पदानुक्रम क्लोज कर दिया गया है, संकलक यह जांच सकता है कि सभी केसेस को पैटर्न मिलान में संभाला गया है- | ||
<syntaxhighlight lang="scala"> | <syntaxhighlight lang="scala"> | ||
tree match { | tree match { | ||
| Line 186: | Line 186: | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
स्काला | स्काला केस क्लास उपप्रकार के माध्यम से पुन: उपयोग की अनुमति भी देते हैं- | ||
<syntaxhighlight lang="scala"> | <syntaxhighlight lang="scala"> | ||
| Line 203: | Line 203: | ||
let tree = Node(5, Node(1, Leaf, Leaf), Node(3, Leaf, Node(4, Leaf, Leaf))) | let tree = Node(5, Node(1, Leaf, Leaf), Node(3, Leaf, Node(4, Leaf, Leaf))) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
क्योंकि परिभाषित | क्योंकि परिभाषित केस संपूर्ण हैं, संकलक यह जांच सकता है कि सभी केसेस को पैटर्न मिलान में नियंत्रित किया गया है- | ||
<syntaxhighlight lang="fsharp"> | <syntaxhighlight lang="fsharp"> | ||
match tree with | match tree with | ||
| Line 416: | Line 416: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
== टैग यूनियनों के रूप में | == टैग यूनियनों के रूप में क्लास पदानुक्रम == | ||
[[ ऑब्जेक्ट ओरिएंटेड प्रोग्रामिंग |ऑब्जेक्ट-ओरिएंटेड प्रोग्रामिंग]] में विशिष्ट | [[ ऑब्जेक्ट ओरिएंटेड प्रोग्रामिंग |ऑब्जेक्ट-ओरिएंटेड प्रोग्रामिंग]] में विशिष्ट क्लास पदानुक्रम में, प्रत्येक सबक्लास उस क्लास के लिए अद्वितीय डेटा को समाहित कर सकती है। आभासी विधि लुकअप करने के लिए उपयोग किया जाने वाला मेटाडेटा (उदाहरण के लिए, अधिकांश C++ कार्यान्वयन में ऑब्जेक्ट का [[आभासी विधि|वेटेबल]] सूचक) सबक्लास की पहचान करता है और उदाहरण के द्वारा संग्रहीत विशेष डेटा की पहचान करने वाले टैग के रूप में प्रभावी ढंग से कार्य करता है ([[RTTI|आरटीटीआई (RTTI)]] देखें)। किसी ऑब्जेक्ट का निर्माता इस टैग को सेट करता है, और यह ऑब्जेक्ट के पूरे जीवनकाल में स्थिर रहता है। | ||
फिर भी, | फिर भी, क्लास पदानुक्रम में वास्तविक [[उपप्रकार बहुरूपता]] सम्मिलित होती है इसे उसी आधार प्रकार के और सबक्लास बनाकर बढ़ाया जा सकता है, जिसे टैग/डिस्पैच मॉडल के तहत सही ढंग से नियंत्रित नहीं किया जा सकता है। इसलिए, प्रायः किसी सबऑब्जेक्ट के 'टैग' पर केस विश्लेषण करना या प्रेषण करना संभव नहीं है जैसा कि टैग यूनियनों के लिए होता है। स्काला जैसी कुछ भाषाएँ बेस क्लास को "क्लोज" करने की अनुमति देती हैं, और टैग यूनियनों को क्लोज बेस क्लास के साथ एकीकृत करती हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 16:51, 22 July 2023
कंप्यूटर विज्ञान में, टैग यूनियन, जिसे वैरिएंट, वैरिएंट रिकॉर्ड, चयन प्रकार, विभेदित यूनियन, असंयुक्त यूनियन, योग प्रकार या सहउत्पाद भी कहा जाता है, डेटा संरचना है जिसका उपयोग मान रखने के लिए किया जाता है जो कई अलग-अलग, लेकिन निश्चित, प्रकारों पर ले जा सकता है। किसी भी समय केवल एक ही प्रकार का उपयोग किया जा सकता है, और टैग क्षेत्र स्पष्ट रूप से इंगित करता है कि कौन सा प्रकार उपयोग में है। इसे एक ऐसे प्रकार के रूप में सोचा जा सकता है जिसमें कई "केस" होतो हैं, जिनमें से प्रत्येक को उस प्रकार में युक्तियोजित किए जाने पर सही ढंग से संभाला जाना चाहिए। यह पुनरावर्ती डेटाटाइप को परिभाषित करने में महत्वपूर्ण है, जिसमें किसी मान के कुछ घटक का प्रकार उस मान के समान हो सकता है, उदाहरण के लिए ट्रीस का प्रतिनिधित्व करने के लिए एक प्रकार को परिभाषित करने में, जहां मल्टी-नोड सबट्रीस और लीव्स को अलग करना आवश्यक है। सामान्य यूनियनों की तरह, टैग यूनियन प्रत्येक प्रकार के लिए स्टोरेज क्षेत्रों को ओवरलैप करके स्टोरेज बचा सकता हैं, क्योंकि एक समय में केवल एक ही उपयोग में होता है।
विवरण
एमएल (ML) और हास्केल जैसी कार्यात्मक प्रोग्रामिंग भाषाओं में टैग यूनियन सबसे महत्वपूर्ण हैं, जहां उन्हें डेटाप्रकार कहा जाता है (बीजगणितीय डेटा प्रकार देखें) और संकलक यह सत्यापित करने में सक्षम है कि टैग यूनियनों की सभी केसेस को कई प्रकार की त्रुटियों से बचते हुए सदैव नियंत्रित किया जाता है। हालाँकि, इन्हें लगभग किसी भी प्रोग्रामिंग भाषा में बनाया जा सकता है, और अनटैग यूनियनों की तुलना में अधिक सुरक्षित हैं, जिन्हें प्रायः यूनियन कहा जाता है, जो समान हैं लेकिन स्पष्ट रूप से ट्रैक नहीं करते हैं कि यूनियन का कौन सा सदस्य वर्तमान में उपयोग में है।
टैग यूनियनों के साथ प्रायः एक प्रकार के निर्माता की अवधारणा जुड़ी होती है, जो क्लास के लिए निर्माता के समान है लेकिन समान नहीं होता है। प्रारंभिक टैग प्रकार और संबंधित प्रकार को ध्यान में रखते हुए, प्रकार निर्माता टैग यूनियन प्रकार का उत्पादन करते हैं।
गणितीय रूप से, टैग यूनियन असंयुक्त या विभेदित टैगों के अनुरूप होते हैं, जिन्हें प्रायः + का उपयोग करके लिखा जाता है। असंयुक्त टैग A + B के तत्व को देखते हुए, यह निर्धारित करना संभव है कि यह A या B से आया है या नहीं। यदि कोई तत्व दोनों में निहित है, तो A + B में मान की दो प्रभावी रूप से भिन्न प्रतियां होंगी, एक A से और एक B से।
प्रकार सिद्धांत में, टैग यूनियन को योग प्रकार कहा जाता है। योग प्रकार उत्पाद प्रकारों के द्वैत हैं। संकेतन अलग-अलग होते हैं, लेकिन प्रायः योग प्रकार A + B (अंतःक्षेपों) के लिए दो परिचय के साथ आता है- inj1: A → A + B और inj2: B → A + B। उन्मूलन रूप केस विश्लेषण है, जिसे एमएल-शैली भाषाओं में पैटर्न मिलान के रूप में जाना जाता है- यदि e में प्रकार A + B है और e1 और e2 में क्रमशः x: A और y: B की मान्यताओं के तहत प्रकार है, तो शब्द में प्रकार है। योग प्रकार करी-हावर्ड समानता के तहत अंतर्ज्ञानवादी तार्किक विच्छेदन से मेल खाता है।
प्रगणित प्रकार को विकृत केस के रूप में देखा जा सकता है- इकाई प्रकारों का टैग यूनियन है। यह अशक्त निर्माताओं के समुच्चय से मेल खाता है और इसे साधारण टैग वेरिएबल के रूप में कार्यान्वित किया जा सकता है, क्योंकि इसमें टैग के मान के अलावा कोई अतिरिक्त डेटा नहीं है।
कई प्रोग्रामिंग तकनीक और डेटा संरचनाएं, जिनमें रोप, अनुयोगी मूल्यांकन, क्लास पदानुक्रम (नीचे देखें), मनमानी-सटीक अंकगणित, सीडीआर (CDR) कोडिंग, अप्रत्यक्ष बिट और अन्य प्रकार के टैग संकेतों आदि सम्मिलित हैं, प्रायः कुछ प्रकार के टैग यूनियनों का उपयोग करके कार्यान्वित किए जाते हैं।
टैग यूनियन को सबसे सरल प्रकार के स्व-वर्णन डेटा प्रारूप के रूप में देखा जा सकता है। टैग यूनियन के टैग को सबसे सरल प्रकार के मेटाडेटा के रूप में देखा जा सकता है।
लाभ और हानि
अनटैग यूनियन की तुलना में टैग यूनियन का प्राथमिक लाभ यह है कि सभी एक्सेस सुरक्षित हैं, और संकलक यह भी जांच सकता है कि सभी केसेस को संभाला गया है। अनटैग यूनियन वर्तमान में सक्रिय क्षेत्र की सही पहचान करने के लिए प्रोग्राम तर्क पर निर्भर करता हैं, जिसके परिणामस्वरूप अजीब व्यवहार हो सकता है और यदि वह तर्क विफल हो जाता है तो बग ढूंढना मुश्किल हो सकता है।
प्रत्येक प्रकार के लिए क्षेत्र वाले साधारण रिकॉर्ड की तुलना में टैग यूनियन का प्राथमिक लाभ यह है कि यह सभी प्रकार के लिए स्टोरेज को ओवरलैप करके स्टोरेज बचाता है। कुछ कार्यान्वयन सबसे बड़े प्रकार के लिए पर्याप्त स्टोरेज आरक्षित रखते हैं, जबकि अन्य आवश्यकतानुसार टैग यूनियन मान के आकार को गतिशील रूप से समायोजित करते हैं। जब मान अपरिवर्तनीय होता है, तो उतनी ही स्टोरेज अलोकेट करना आसान होता है जितनी आवश्यकता होती है।
टैग यूनियनों की मुख्य हानि यह है कि टैग स्थान घेरता है। चूँकि प्रायः बहुत कम संख्या में विकल्प होते हैं, टैग को प्रायः जहां भी स्थान मिलता है, 2 या 3 बिट्स में निष्पीडित किया जा सकता है, लेकिन कभी-कभी ये बिट्स भी उपलब्ध नहीं होते हैं। इस केस में, सहायक विकल्प टैग को फोल्ड करना, गणना करना या एन्कोड करना हो सकता है, जहां टैग मान की गणना यूनियन क्षेत्र की सामग्री से गतिशील रूप से की जाती है। इसके सामान्य उदाहरण आरक्षित मानों का उपयोग हैं, उदाहरण के लिए, सकारात्मक संख्या वापस लाने वाला फ़ंक्शन विफलता को इंगित करने के लिए -1 वापस कर सकता है, और प्रहरी मान, जो प्रायः टैग संकेतों में उपयोग किए जाते हैं।
कभी-कभी, अनटैग यूनियनों का उपयोग प्रकारों के बीच बिट-स्तरीय रूपांतरण करने के लिए किया जाता है, जिन्हें सी++ (C++) में पुनः व्याख्या विक्षेप कहा जाता है। टैग यूनियन इस उद्देश्य के लिए अभिप्रेत नहीं हैं प्रायः जब भी टैग बदला जाता है तो एक नया मान निर्दिष्ट किया जाता है।
कई भाषाएँ, कुछ हद तक, सार्वभौमिक डेटा प्रकार का सपोर्ट करती हैं, जो एक ऐसा प्रकार है जिसमें प्रत्येक दूसरे प्रकार का प्रत्येक मान सम्मिलित होता है, और प्रायः सार्वभौमिक प्रकार के मान के वास्तविक प्रकार का परीक्षण करने का तरीका प्रदान किया जाता है। इन्हें कभी-कभी वैरिएंट्स के रूप में भी जाना जाता है। जबकि सार्वभौमिक डेटा प्रकार उनकी औपचारिक परिभाषा में टैग यूनियनों के साथ तुलनीय हैं, विशिष्ट टैग यूनियनों में अपेक्षाकृत कम संख्या में केसेस सम्मिलित होते हैं, और ये केसेस एकल सुसंगत अवधारणा को व्यक्त करने के विभिन्न तरीके बनाते हैं, जैसे डेटा संरचना नोड या निर्देश। साथ ही, यह भी अपेक्षा है कि टैग यूनियन का उपयोग किए जाने पर उसकी प्रत्येक संभावित केस से निपटा जाएगा। सार्वभौमिक डेटा प्रकार के मान संबंधित नहीं हैं और उन सभी से निपटने का कोई व्यवहार्य तरीका नहीं है।
विकल्प प्रकार और अपवाद प्रबंधन की तरह, टैग यूनियनों का उपयोग कभी-कभी असाधारण परिणामों की घटना को संभालने के लिए किया जाता है। प्रायः इन टैगों को आरक्षित मानों के रूप में मोड़ दिया जाता है, और उनकी घटना की लगातार जांच नहीं की जाती है- यह प्रोग्रामिंग त्रुटियों का पूरी तरह से सामान्य सोर्स है। टैग यूनियनों के इस उपयोग को निम्नलिखित कार्यों के साथ मोनाड के रूप में औपचारिक रूप दिया जा सकता है-
जहां "मान" और "त्रुटि" यूनियन प्रकार के निर्माता हैं, A और B वैध परिणाम प्रकार हैं और E त्रुटि केसेस का प्रकार है। वैकल्पिक रूप से, उसी मोनाड को वापस और दो अतिरिक्त कार्यों, एफएमएपी (fmap) और संबद्ध द्वारा वर्णित किया जा सकता है-
उदाहरण
मान लें कि हम पूर्णांकों का बाइनरी ट्री बनाना चाहते थे। एमएल में, हम इस तरह डेटाप्रकार बनाकर ऐसा करेंगे-
datatype tree = Leaf
| Node of (int * tree * tree)
यह दो केसेस के साथ टैग यूनियन है- एक, लीफ, का उपयोग ट्री के पथ को समाप्त करने के लिए किया जाता है, और अनिवार्य भाषाओं में शून्य मान की तरह कार्य करता है। दूसरी शाखा में नोड होता है, जिसमें एक पूर्णांक और बाएं और दाएं सबट्री होता है। लीफ और नोड निर्माता हैं, जो हमें वास्तव में विशेष ट्री बनाने में सक्षम बनाते हैं, जैसे-
Node(5, Node(1, Leaf, Leaf), Node(3, Leaf, Node(4, Leaf, Leaf)))
जो इस ट्री के अनुरूप है-
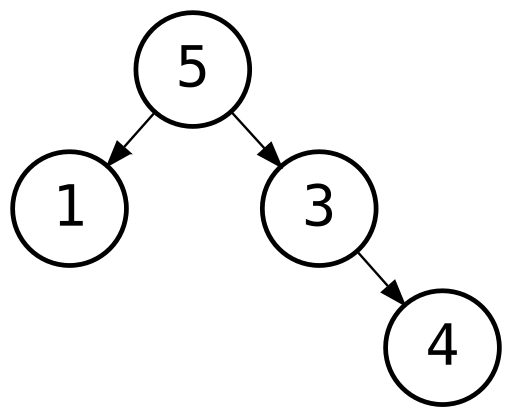 अब हम आसानी से टाइपसेफ़ फ़ंक्शन लिख सकते हैं जो, माना, ट्री में नोड्स की संख्या की गणना करता है-
अब हम आसानी से टाइपसेफ़ फ़ंक्शन लिख सकते हैं जो, माना, ट्री में नोड्स की संख्या की गणना करता है-
fun countNodes(Leaf) = 0
| countNodes(Node(int, left, right)) =
1 + countNodes(left) + countNodes(right)
भाषा समर्थन की समयरेखा
1960s
एएलजीओएल (ALGOL) 68 में, टैग यूनियनों को संयुक्त मोड कहा जाता है, टैग अंतर्निहित है, और case निर्माण का उपयोग यह निर्धारित करने के लिए किया जाता है कि कौन सा क्षेत्र टैग किया गया है-
mode node = union (real, int, compl, string);
नोड के यूनियन केस के लिए उपयोग उदाहरण-
node n := "1234";
case n in
(real r): print(("real:", r)),
(int i): print(("int:", i)),
(compl c): print(("compl:", c)),
(string s): print(("string:", s))
out print(("?:", n))
esac
1970s और 1980s
हालाँकि मुख्य रूप से केवल कार्यात्मक प्रोग्रामिंग भाषाएँ जैसे एमएल (1970 के दशक से) और हास्केल (1990 के दशक से) टैग यूनियनों को केंद्रीय भूमिका देती हैं और यह जाँचने की शक्ति रखती हैं कि सभी केसेस को संभाला जाता है, अन्य भाषाएँ भी टैग यूनियनों का सपोर्ट करती हैं। हालाँकि, व्यवहार में वे कार्यात्मक भाषा संकलकों द्वारा सक्षम किए गए अनुकूलन के कारण गैर-कार्यात्मक भाषाओं में कम कुशल हो सकते हैं जो स्पष्ट टैग जांच को समाप्त कर सकते हैं और टैग के स्पष्ट स्टोरेज से बच सकते हैं।[citation needed]
पास्कल, एडा और मोडुला-2 उन्हें वैरिएंट रिकॉर्ड (एडा में औपचारिक रूप से विभेदित प्रकार) कहते हैं, और टैग क्षेत्र को मैन्युअल रूप से बनाने और टैग मान निर्दिष्ट करने की आवश्यकता होती है, जैसा कि इस पास्कल उदाहरण में है-
type shapeKind = (square, rectangle, circle);
shape = record
centerx : integer;
centery : integer;
case kind : shapeKind of
square : (side : integer);
rectangle : (width, height : integer);
circle : (radius : integer);
end;
और यह एडा समकक्ष हैं-
type Shape_Kind is (Square, Rectangle, Circle);
type Shape (Kind : Shape_Kind) is record
Center_X : Integer;
Center_Y : Integer;
case Kind is
when Square =>
Side : Integer;
when Rectangle =>
Width, Height : Integer;
when Circle =>
Radius : Integer;
end case;
end record;
-- Any attempt to access a member which existence depends
-- on a certain value of the discriminant, while the
-- discriminant is not the expected one, raises an error.
सी(C) और सी++ (C++) में, दृढ़ एक्सेस अनुशासन का उपयोग करके बिना टैग यूनियनों से टैग यूनियन बनाया जा सकता है, जहां टैग की सदैव जांच की जाती है-
enum ShapeKind { Square, Rectangle, Circle };
struct Shape {
int centerx;
int centery;
enum ShapeKind kind;
union {
struct { int side; }; /* Square */
struct { int width, height; }; /* Rectangle */
struct { int radius; }; /* Circle */
};
};
int getSquareSide(struct Shape* s) {
assert(s->kind == Square);
return s->side;
}
void setSquareSide(struct Shape* s, int side) {
s->kind = Square;
s->side = side;
}
/* and so on */
जब तक यूनियन क्षेत्र को केवल फ़ंक्शंस के माध्यम से एक्सेस किया जाता है, तब तक एक्सेस सुरक्षित और सही रहेगा। एन्कोडेड टैग के लिए उसी दृष्टिकोण का उपयोग किया जा सकता है हम केवल टैग को डिकोड करते हैं और फिर प्रत्येक एक्सेस पर इसकी जांच करते हैं। यदि इन टैग जांचों की अक्षमता चिंता का विषय है, तो अंतिम संस्करण में उन्हें स्वचालित रूप से हटाया जा सकता है।
C और C++ में विशेष टैग यूनियन के लिए भाषा सपोर्ट भी है- संभवतः-शून्य सूचक। इसकी तुलना एमएल में ऑप्शन प्रकार या हास्केल में मेबी प्रकार से की जा सकती है, और इसे टैग सूचक के रूप में देखा जा सकता है- दो प्रकार का टैग यूनियन (एन्कोडेड टैग के साथ)-
- मान्य सूचक,
- केवल एक मान वाला शून्य सूचक प्रकार,
नल (null), असाधारण केस का संकेत देता है।
दुर्भाग्य से, C संकलक यह सत्यापित नहीं करते हैं कि अशक्त केस को सदैव संभाला जाता है, और यह C कोड में त्रुटियों का विशेष रूप से प्रचलित सोर्स है, क्योंकि असाधारण केसेस को अनदेखा करने की प्रवृत्ति होती है।
2000s
C की एक उन्नत बोली जिसे साइक्लोन कहा जाता है, में टैग किए गए यूनियनों के लिए व्यापक अंतर्निहित सपोर्ट है।[1]
रस्ट, हेक्स और स्विफ्ट भाषाओं में एनम प्रकार टैग यूनियनों के रूप में भी काम करते हैं।
बूस्ट C++ लाइब्रेरीज़ की वैरिएंट लाइब्रेरी ने प्रदर्शित किया कि C++ में लाइब्रेरी के रूप में सुरक्षित टैग यूनियन को कार्यान्वित करना संभव है, जिसे फ़ंक्शन ऑब्जेक्ट का उपयोग करके देखा जा सकता है।
struct display : boost::static_visitor<void>
{
void operator()(int i)
{
std::cout << "It's an int, with value " << i << std::endl;
}
void operator()(const std::string& s)
{
std::cout << "It's a string, with value " << s << std::endl;
}
};
boost::variant<int, std::string> v = 42;
boost::apply_visitor(display(), v);
boost::variant<int, std::string> v = "hello world";
boost::apply_visitor(display(), v);
स्काला में केस क्लास हैं-
sealed abstract class Tree
case object Leaf extends Tree
case class Node(value: Int, left: Tree, right: Tree) extends Tree
val tree = Node(5, Node(1, Leaf, Leaf), Node(3, Leaf, Node(4, Leaf, Leaf)))
क्योंकि क्लास पदानुक्रम क्लोज कर दिया गया है, संकलक यह जांच सकता है कि सभी केसेस को पैटर्न मिलान में संभाला गया है-
tree match {
case Node(x, _, _) => println("top level node value: " + x)
case Leaf => println("top level node is a leaf")
}
स्काला केस क्लास उपप्रकार के माध्यम से पुन: उपयोग की अनुमति भी देते हैं-
sealed abstract class Shape(centerX: Int, centerY: Int)
case class Square(side: Int, centerX: Int, centerY: Int) extends Shape(centerX, centerY)
case class Rectangle(length: Int, height: Int, centerX: Int, centerY: Int) extends Shape(centerX, centerY)
case class Circle(radius: Int, centerX: Int, centerY: Int) extends Shape(centerX, centerY)
F# ने यूनियनों के साथ विभेदीकृत किया है-
type Tree =
| Leaf
| Node of value: int * left: Tree * right: Tree
let tree = Node(5, Node(1, Leaf, Leaf), Node(3, Leaf, Node(4, Leaf, Leaf)))
क्योंकि परिभाषित केस संपूर्ण हैं, संकलक यह जांच सकता है कि सभी केसेस को पैटर्न मिलान में नियंत्रित किया गया है-
match tree with
| Node (x, _, _) -> printfn "top level node value: %i" x
| Leaf -> printfn "top level node is a leaf"
हेक्स का एनम टैग यूनियनों के रूप में भी काम करता हैं-[2]
enum Color {
Red;
Green;
Blue;
Rgb(r:Int, g:Int, b:Int);
}
इनका मिलान स्विच अभिव्यक्ति का उपयोग करके किया जा सकता है-
switch (color) {
case Red: trace("Color was red");
case Green: trace("Color was green");
case Blue: trace("Color was blue");
case Rgb(r, g, b): trace("Color had a red value of " +r);
}
निम के पास पास्कल और एडा की घोषणा के समान ऑब्जेक्ट वैरिएंट्स[3] हैं-
type
ShapeKind = enum
skSquare, skRectangle, skCircle
Shape = object
centerX, centerY: int
case kind: ShapeKind
of skSquare:
side: int
of skRectangle:
length, height: int
of skCircle:
radius: int
मैक्रोज़ का उपयोग पैटर्न मिलान का अनुकरण करने या ऑब्जेक्ट वैरिएंट्स घोषित करने के लिए सिंटैक्टिक शुगर बनाने के लिए किया जा सकता है, जिसे यहां पैकेज पैटी द्वारा कार्यान्वित किया गया है-
import patty
proc `~`[A](a: A): ref A =
new(result)
result[] = a
variant List[A]:
Nil
Cons(x: A, xs: ref List[A])
proc listHelper[A](xs: seq[A]): List[A] =
if xs.len == 0: Nil[A]()
else: Cons(xs[0], ~listHelper(xs[1 .. xs.high]))
proc list[A](xs: varargs[A]): List[A] = listHelper(@xs)
proc sum(xs: List[int]): int = (block:
match xs:
Nil: 0
Cons(y, ys): y + sum(ys[])
)
echo sum(list(1, 2, 3, 4, 5))
2010s
स्काला 3 में एनम्स जोड़े गए हैं,[4] जिससे हमें पहले के स्काला उदाहरणों को अधिक संक्षेप में रीराइट की अनुमति मिलती है-
enum Tree[+T]:
case Leaf
case Node(x: Int, left: Tree[T], right: Tree[T])
enum Shape(centerX: Int, centerY: Int):
case Square(side: Int, centerX: Int, centerY: Int) extends Shape(centerY, centerX)
case Rectangle(length: Int, height: Int, centerX: Int, centerY: Int) extends Shape(centerX, centerY)
case Circle(radius: Int, centerX: Int, centerY: Int) extends Shape(centerX, centerY)
रस्ट भाषा को टैग यूनियनों, जिन्हें एनम्स कहा जाता है, के लिए व्यापक सपोर्ट प्राप्त है।[5] उदाहरण के लिए-
enum Tree {
Leaf,
Node(i64, Box<Tree>, Box<Tree>)
}
यह यूनियनों पर मिलान की भी अनुमति देता है-
let tree = Tree::Node(
2,
Box::new(Tree::Node(0, Box::new(Tree::Leaf), Box::new(Tree::Leaf))),
Box::new(Tree::Node(3, Box::new(Tree::Leaf),
Box::new(Tree::Node(4, Box::new(Tree::Leaf), Box::new(Tree::Leaf)))))
);
fn add_values(tree: Tree) -> i64 {
match tree {
Tree::Node(v, a, b) => v + add_values(*a) + add_values(*b),
Tree::Leaf => 0
}
}
assert_eq!(add_values(tree), 9);
रस्ट का त्रुटि प्रबंधन मॉडल बड़े पैमाने पर इन टैग यूनियनों पर निर्भर करता है, विशेष रूप से ऑप्शन<T> प्रकार, जो या तो नॉन या सम(T) है, और रिजल्ट<T, E> प्रकार, जो या तो ओके(T) या एरर(E) है।[6]
गणनाओं के माध्यम से टैग यूनियनों के लिए स्विफ्ट को भी पर्याप्त सपोर्ट प्राप्त है।[7] उदाहरण के लिए-
enum Tree {
case leaf
indirect case node(Int, Tree, Tree)
}
let tree = Tree.node(
2,
.node(0, .leaf, .leaf),
.node(3, .leaf, .node(4, .leaf, .leaf))
)
func add_values(_ tree: Tree) -> Int {
switch tree {
case let .node(v, a, b):
return v + add_values(a) + add_values(b)
case .leaf:
return 0
}
}
assert(add_values(tree) == 9)
टाइपस्क्रिप्ट के साथ टैग यूनियन बनाना भी संभव है। उदाहरण के लिए-
interface Leaf { kind: "leaf"; }
interface Node { kind: "node"; value: number; left: Tree; right: Tree; }
type Tree = Leaf | Node
const root: Tree = {
kind: "node",
value: 5,
left: {
kind: "node",
value: 1,
left: { kind: "leaf" },
right: { kind: "leaf" }
},
right: {
kind: "node",
value: 3,
left: { kind: "leaf" },
right: {
kind: "node",
value: 4,
left: { kind: "leaf" },
right: { kind: "leaf" }
}
}
}
function visit(tree: Tree) {
switch (tree.kind) {
case "leaf":
break
case "node":
console.log(tree.value)
visit(tree.left)
visit(tree.right)
break
}
}
पायथन 3.9 एनोटेशन टाइपिंग के लिए सपोर्ट प्रस्तुत करता है जिसका उपयोग टैग यूनियन प्रकार (पीईपी-593[8]) को परिभाषित करने के लिए किया जा सकता है-
Currency = Annotated[
TypedDict('Currency', {'dollars': float, 'pounds': float}, total=False),
TaggedUnion,
]
C++17 std::variant और constexpr if का परिचय देता है
using Tree = std::variant<struct Leaf, struct Node>;
struct Leaf
{
std::string value;
};
struct Node
{
Tree* left = nullptr;
Tree* right = nullptr;
};
struct Transverser
{
template<typename T>
void operator()(T&& v)
{
if constexpr (std::is_same_v<T, Leaf&>)
{
std::cout << v.value << "\n";
}
else if constexpr (std::is_same_v<T, Node&>)
{
if (v.left != nullptr)
std::visit(Transverser{}, *v.left);
if (v.right != nullptr)
std::visit(Transverser{}, *v.right);
}
else
{
// The !sizeof(T) expression is always false
static_assert(!sizeof(T), "non-exhaustive visitor!");
};
}
};
/*Tree forest = ...;
std::visit(Transverser{}, forest);*/
टैग यूनियनों के रूप में क्लास पदानुक्रम
ऑब्जेक्ट-ओरिएंटेड प्रोग्रामिंग में विशिष्ट क्लास पदानुक्रम में, प्रत्येक सबक्लास उस क्लास के लिए अद्वितीय डेटा को समाहित कर सकती है। आभासी विधि लुकअप करने के लिए उपयोग किया जाने वाला मेटाडेटा (उदाहरण के लिए, अधिकांश C++ कार्यान्वयन में ऑब्जेक्ट का वेटेबल सूचक) सबक्लास की पहचान करता है और उदाहरण के द्वारा संग्रहीत विशेष डेटा की पहचान करने वाले टैग के रूप में प्रभावी ढंग से कार्य करता है (आरटीटीआई (RTTI) देखें)। किसी ऑब्जेक्ट का निर्माता इस टैग को सेट करता है, और यह ऑब्जेक्ट के पूरे जीवनकाल में स्थिर रहता है।
फिर भी, क्लास पदानुक्रम में वास्तविक उपप्रकार बहुरूपता सम्मिलित होती है इसे उसी आधार प्रकार के और सबक्लास बनाकर बढ़ाया जा सकता है, जिसे टैग/डिस्पैच मॉडल के तहत सही ढंग से नियंत्रित नहीं किया जा सकता है। इसलिए, प्रायः किसी सबऑब्जेक्ट के 'टैग' पर केस विश्लेषण करना या प्रेषण करना संभव नहीं है जैसा कि टैग यूनियनों के लिए होता है। स्काला जैसी कुछ भाषाएँ बेस क्लास को "क्लोज" करने की अनुमति देती हैं, और टैग यूनियनों को क्लोज बेस क्लास के साथ एकीकृत करती हैं।
यह भी देखें
- विविक्तकर, सीओआरबीए (CORBA) में विभेदित यूनियनों के लिए प्रकार टैग
- वैरिएंट प्रकार (COM)
संदर्भ
- ↑ "Cyclone: Tagged Unions".
- ↑ "एनम्स का उपयोग करना - हेक्स - क्रॉस-प्लेटफ़ॉर्म टूलकिट". Haxe Foundation.
- ↑ "निम मैनुअल". nim-lang.org. Retrieved 2020-01-23.
- ↑ "Scala 3 Language Reference: Enumerations". The Scala Team.
- ↑ "जंग प्रोग्रामिंग भाषा". Mozilla.
- ↑ "उदाहरण के द्वारा जंग". Mozilla.
- ↑ "Enumerations — The Swift Programming Language (Swift 5.4)". docs.swift.org. Retrieved 2021-04-28.
- ↑ "PEP 593 -- Flexible function and variable annotations". Python.org (in English). Retrieved 2021-06-20.
बाहरी संबंध
- boost::variant is a C++ typesafe discriminated union
- std.variant is an implementation of variant type in D 2.0