उभयनिष्ठ संग्राही: Difference between revisions

Latest revision as of 09:18, 11 November 2022

चित्रा 1: मूल एनपीएन उभयनिष्ठ संग्राही परिपथ (पूर्वाग्रह विवरण की उपेक्षा)।

इलेक्ट्रॉनिक्स में, एक सामान्य संग्राही प्रवर्धक जिसे उत्सर्जक अनुगामी भी कहते हैं, तीन मूल एकल चरण के द्विध्रुवी संधि ट्रांजिस्टर (बीजेटी) प्रवर्धक टोपोलॉजी में से एक है, जिसे सामान्यतया वोल्टेज बफर के रूप में प्रयोग किया जाता है।

इस परिपथ में ट्रांजिस्टर का आधार टर्मिनल इनपुट के रूप में कार्य करता है, उत्सर्जक एक आउटपुट होता है और संग्राहक दोनों के लिए सामान्य है। उदाहरण के लिए, इसे क्षेत्रीय या विद्युत आपूर्ति के संदर्भ से संयुक्त किया जा सकता है, इसलिए इसका नाम अनुरूप क्षेत्र प्रभाव ट्रांजिस्टर के परिपथ के लिए सामान्य निर्वात प्रवर्धक होता है और इसलिए समान निर्वात ट्यूब के लिए यह परिपथ कैथोड के अनुगामी होता है।

बेसिक परिपथ

चित्र 2: एक नकारात्मक-प्रतिक्रिया प्रवर्धक

परिपथ की व्याख्या ट्रांजिस्टर को नकारात्मक प्रतिक्रिया के नियंत्रण में रखकर की जा सकती है। इस दृष्टिकोण से, सामान्य संग्राहक चरण ऐसा प्रवर्धक होता है जो पूर्ण श्रृंखला के नकारात्मक प्रतिक्रिया के रूप में होते हैं इसे चित्र -1 में दिखाया गया है। इस विन्यास में चित्र 2 β = 1 के साथ और संपूर्ण आउटपुट वोल्टेज V_out इसके विपरीत इनपुट वोल्टेज V_in के साथ श्रृंखला में रखा गया है। इस प्रकार दो वोल्टेज को किर्चहोफ़ के वोल्टेज नियम केवीएल के अनुसार घटाया जाता है फलन खंड आरेख से व्यवकलक ठीक इनपुट पाश द्वारा कार्यान्वित किया जाता है, और उनका अंतर V_diff = V_in − V_out बेस-उत्सर्जक संधि पर लगाया जाता है। ट्रांजिस्टर लगातार V_diff की निगरानी करता है और इसके उत्सर्जक वोल्टेज को लगभग बराबर कम V_BEO पर समायोजित करता है और उत्सर्जक रेसिस्टर R_E के माध्यम से संग्रहकर्ता करंट को पास करके इनपुट वोल्टेज में बदलता है। नतीजतन, आउटपुट वोल्टेज V_BEO से V₊ तक इनपुट वोल्टेज विविधताओं का अनुसरण करता है इसलिए इसका नाम उत्सर्जक अनुयायी है।

सहज रूप से, इस व्यवहार को यह महसूस करके भी समझा जा सकता है कि द्विध्रुवी ट्रांजिस्टर में बेस-उत्सर्जक वोल्टेज पूर्वाग्रह परिवर्तनों के प्रति बहुत असंवेदनशील है, इसलिए बेस वोल्टेज में कोई भी परिवर्तन सीधे उत्सर्जक को प्रेषित होता है अच्छे अनुमान के लिए यह होने वाली विभिन्न बाधाओं पर निर्भर करता है (ट्रांजिस्टर सहिष्णुता, तापमान भिन्नता, लोड प्रतिरोध, संग्राही प्रतिरोधक द्वारा इसे जोड़ा जाता है), चूंकि ट्रांजिस्टर इन होने वाली विभिन्न बाधाओं पर प्रतिक्रिया करता है और संतुलन बनाये रखता है। इनपुट वोल्टेज सकारात्मक छढ़ तक पहुंचने पर भी यह किसी भी स्थिति में संतृप्त नहीं होता है।

उभयनिष्ठ संग्राही परिपथ को गणितीय रूप से लगभग इकाई वोल्टेज लाभ के लिए दिखाया जा सकता है:

A_{v}={\frac {v_{\text{out}}}{v_{\text{in}}}}\approx 1.

चित्रा 3: उत्सर्जक-अनुयायी परिपथ का पीएनपी संस्करण, सभी ध्रुवीयताएं उलट जाती हैं।

इनपुट टर्मिनल पर एक छोटा वोल्टेज परिवर्तन को आउटपुट पर दोहराया जाता है। ट्रांजिस्टर से होने वाले लाभ और लोड प्रतिरोध के मूल्य पर थोड़ा निर्भर करता है, नीचे चित्र 3 में देखें। यह परिपथ उपयोगी है क्योंकि इसमें व्यापक इनपुट प्रतिबाधा है।

r_{\text{in}}\approx \beta _{0}R_{\text{E}},

इसलिए यह पिछले परिपथ को लोड नहीं करेगा, और एक छोटा आउटपुट प्रतिबाधा है।

r_{\text{out}}\approx {\frac {R_{\text{E}}\parallel R_{\text{source}}}{\beta _{0}}},

इसलिए यह कम प्रतिरोध लोड पर चलन कर सकती है।

साधारणतयः पर, उत्सर्जक रेसिस्टर काफी बड़ा होता है और इसे समीकरण से हटाया जा सकता है।

r_{\text{out}}\approx {\frac {R_{\text{source}}}{\beta _{0}}}.

अनुप्रयोग

चित्रा 4: एकीकृत परिपथ के लिए उपयुक्त धारा स्रोत पूर्वाग्रह के साथ एनपीएन वोल्टेज अनुयायी

कम आउटपुट प्रतिबाधा एक बड़े आउटपुट प्रतिबाधा वाले स्रोत को एक छोटे लोड प्रतिबाधा को चलाने की अनुमति देता है, यह वोल्टेज बफर प्रवर्धक के रूप में कार्य करता है। दूसरे शब्दों में, परिपथ में करंट गेन होता है जो काफी हद तक ट्रांजिस्टर के h_FE पर निर्भर करता है। इसकी विशेषताओं के कारण वोल्टेज गेन कई इलेक्ट्रॉनिक उपकरणों में पसंद किया जाता है। इनपुट करंट में एक छोटा सा बदलाव आउटपुट लोड को सप्लाई किए गए आउटपुट करंट में बहुत बड़ा परिवर्तन करता है।

बफर एक्शन का एक पहलू प्रतिबाधाओं का परिवर्तन है। उदाहरण के लिए, उच्च थेवेनिन प्रतिरोध के साथ वोल्टेज स्रोत द्वारा संचालित वोल्टेज अनुयायी के संयोजन का थेवेनिन प्रतिरोध केवल वोल्टेज अनुयायी के आउटपुट प्रतिरोध के लिए छोटा प्रतिरोध कम हो जाता है। वह प्रतिरोध कमी संयोजन को अधिक आदर्श वोल्टेज स्रोत बनाता है। इसके विपरीत, एक छोटे लोड प्रतिरोध और एक ड्राइविंग चरण के बीच डाला गया वोल्टेज अनुयायी ड्राइविंग चरण में एक बड़ा लोड प्रस्तुत करता है एक वोल्टेज सिग्नल को एक छोटे से लोड में जोड़ने पर लाभ प्रदान करता है।

यह विन्यास सामान्यतः क्लास बी और क्लास एबी प्रवर्धकों के उत्पादन स्तरों में प्रयोग किया जाता है। बेस परिपथ को ट्रांजिस्टर क्लास-बी या एबी मोड में संचालित करने के लिए संशोधित किया गया है। पावर प्रवर्धक क्लास-ए मोड में, और कभी-कभी R_E के बजाय एक सक्रिय धारा स्रोत का उपयोग किया जाता है (चित्र 4) रैखिकता और/दक्षता में सुधार करने के लिए है।^[1]

लक्षण

कम आवृत्तियों पर और एक सरलीकृत हाइब्रिड-पीआई मॉडल का उपयोग करके, निम्नलिखित छोटे- संकेत विशेषताओं को प्राप्त किया जा सकता है। (पैरामीटर $\beta =g_{m}r_{\pi }$ और समानांतर रेखाएं समानांतर में घटकों को दर्शाती हैं

	परिभाषा	अभिव्यक्ति	अनुमानित अभिव्यक्ति	परिस्थिति
धारा लाभ	$A_{\mathrm {i} }={i_{\text{out}} \over i_{\text{in}}}$	$\beta _{0}+1\$	$\approx \beta _{0}$	$\beta _{0}\gg 1$
वोल्टेज बढ़ना	$A_{\mathrm {v} }={v_{\text{out}} \over v_{\text{in}}}$	${g_{m}R_{\text{E}} \over g_{m}R_{\text{E}}+1}$	$\approx 1$	$g_{m}R_{\text{E}}\gg 1$
इनपुट प्रतिरोध	$r_{\text{in}}={\frac {v_{\text{in}}}{i_{\text{in}}}}$	$r_{\pi }+(\beta _{0}+1)R_{\text{E}}\$	$\approx \beta _{0}R_{\text{E}}$	$(g_{m}R_{\text{E}}\gg 1)\wedge (\beta _{0}\gg 1)$
आउटपुट प्रतिरोध	$r_{\text{out}}={\frac {v_{\text{out}}}{i_{\text{out}}}}$	$R_{\text{E}}\parallel {r_{\pi }+R_{\text{source}} \over \beta _{0}+1}$	$\approx {1 \over g_{m}}+{R_{\text{source}} \over \beta _{0}}$	$(\beta _{0}\gg 1)\wedge (r_{\text{in}}\gg R_{\text{source}})$

जहां पे $R_{\text{source}}\$ वेनिन समकक्ष स्रोत प्रतिरोध।

व्युत्पत्ति

चित्रा 5: द्विध्रुवीय ट्रांजिस्टर के लिए हाइब्रिड-पीआई मॉडल का उपयोग करके चित्रा 3 के अनुरूप लघु-संकेत परिपथ द्विध्रुवीय डिवाइस कैपेसिटेंस को अनदेखा करने के लिए पर्याप्त आवृत्तियों पर द्विध्रुवीय ट्रांजिस्टर के लिए

चित्रा 6: आउटपुट प्रतिरोध खोजने के लिए आउटपुट पर टेस्ट करंट के साथ बाइपोलर वोल्टेज फॉलोअर के लिए लो-फ्रीक्वेंसी स्मॉल- संकेत परिपथ। अवरोध

R_{\text{E}}=R_{\text{L}}\parallel r_{\text{O}}

.

चित्रा 5 चित्रा 3 के परिपथ के लिए कम आवृत्ति हाइब्रिड-पीआई मॉडल दिखाता है। ओम के नियम का उपयोग करके, विभिन्न धाराओं को निर्धारित किया गया है, और ये परिणाम आरेख पर दिखाए जाते हैं। किरचॉफ के धारा नियम को उत्सर्जक पर लागू करने पर पाया जाता है:

(\beta +1){\frac {v_{\text{in}}-v_{\text{out}}}{R_{\text{S}}+r_{\pi }}}=v_{\text{out}}\left({\frac {1}{R_{\text{L}}}}+{\frac {1}{r_{\text{O}}}}\right).

निम्नलिखित प्रतिरोध मूल्यों को परिभाषित करें:

{\begin{aligned}{\frac {1}{R_{\text{E}}}}&={\frac {1}{R_{\text{L}}}}+{\frac {1}{r_{\text{O}}}},\\[2pt]R&={\frac {R_{\text{S}}+r_{\pi }}{\beta +1}}.\end{aligned}}

फिर शब्दों को एकत्रित करते हुए वोल्टेज लाभ पाया जाता है:

A_{\text{v}}={\frac {v_{\text{out}}}{v_{\text{in}}}}={\frac {1}{1+{\frac {R}{R_{\text{E}}}}}}.

इस परिणाम से, लाभ एकीकृत जैसा कि बफर प्रवर्धक के अपेक्षित मान तक पहुंचता है यदि हर में प्रतिरोध अनुपात छोटा है। यह अनुपात धारा लाभ β के बड़े मूल्यों के साथ घटता है और $R_{\text{E}}$ के बड़े मूल्यों के साथ है इनपुट प्रतिरोध के रूप में पाया जाता है

{\begin{aligned}R_{\text{in}}&={\frac {v_{\text{in}}}{i_{\text{b}}}}={\frac {R_{\text{S}}+r_{\pi }}{1-A_{\text{v}}}}\\&=\left(R_{\text{S}}+r_{\pi }\right)\left(1+{\frac {R_{\text{E}}}{R}}\right)\\&=R_{\text{S}}+r_{\pi }+(\beta +1)R_{\text{E}}.\end{aligned}}

ट्रांजिस्टर आउटपुट प्रतिरोध $r_{\text{O}}$ लोड की तुलना में सामान्यतः बड़ा होता है $R_{\text{L}}$ , और इसीलिए $R_{\text{L}}$ हावी $R_{\text{E}}$ . इस परिणाम से, प्रवर्धक का इनपुट प्रतिरोध आउटपुट लोड प्रतिरोध से बहुत बड़ा है $R_{\text{L}}$ बड़े धारा लाभ के लिए $\beta$ . अर्थात्, प्रवर्धक को लोड और स्रोत के बीच रखने से स्रोत को प्रत्यक्ष युग्मन की तुलना में एक बड़ा उच्च-प्रतिरोधक लोड प्रस्तुत होता है $R_{\text{L}}$ , जिसके परिणामस्वरूप स्रोत प्रतिबाधा में कम संकेत क्षीणन होता है $R_{\text{S}}$ वोल्टेज विभाजन के परिणामस्वरूप।

चित्रा 6 चित्रा 5 के छोटे- संकेत परिपथ को इनपुट शॉर्ट-परिपथ के साथ दिखाता है और इसके आउटपुट पर एक टेस्ट करंट लगाया जाता है। इस परिपथ का उपयोग करके आउटपुट प्रतिरोध पाया जाता है

R_{\text{out}}={\frac {v_{\text{x}}}{i_{\text{x}}}}.

ओम के नियम का उपयोग करते हुए, विभिन्न धाराएँ पाई गई हैं, जैसा कि चित्र में दर्शाया गया है। बेस करंट के लिए शर्तों को एकत्रित करते हुए, बेस करंट को पाया जाता है

(\beta +1)i_{\text{b}}=i_{\text{x}}-{\frac {v_{\text{x}}}{R_{\text{E}}}},

जहां पे $R_{\text{E}}$ ऊपर परिभाषित किया गया है। बेस धारा के लिए इस मान का उपयोग करते हुए, ओम का नियम प्रदान करता है

v_{\text{x}}=i_{\text{b}}\left(R_{\text{S}}+r_{\pi }\right).

आधार धारा के लिए प्रतिस्थापन, और शर्तों को एकत्रित करना,

R_{\text{out}}={\frac {v_{\text{x}}}{i_{\text{x}}}}=R\parallel R_{\text{E}},

जहां एक समांतर संपर्क को दर्शाता है, और $R$ ऊपर परिभाषित किया गया है। इसलिये $R$ सामान्यतः छोटा प्रतिरोध होता है जब धारा लाभ $\beta$ से बड़ी है, आउटपुट प्रतिबाधा $R$ पर हावी है, ये इसलिए भी छोटा है। एक छोटे उत्पाद प्रतिबाधा का मतलब है कि मूल वोल्टेज स्रोत और वोल्टेज अनुयायी का श्रृंखला संयोजन अपने आउटपुट नोड पर कम थेवेनिन प्रतिरोध के साथ एक थेवेनिन वोल्टेज स्रोत प्रस्तुत करता है, अर्थात वोल्टेज अनुयायी के साथ वोल्टेज स्रोत का संयोजन मूल वोल्टेज की तुलना में अधिक आदर्श वोल्टेज स्रोत बनाता है।

यह भी देखें

संदर्भ

↑ Rod Elliot: 20 Watt Class-A Power Amplifier

बाहरी संबंध

[Elliot-1] Rod Elliot: 20 Watt Class-A Power Amplifier

[1]

@@ Line 1: / Line 1: @@
 {{More footnotes|date=April 2009}}
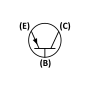
-[[Image:NPN emitter follower.svg|right|thumb|130px|चित्रा 1: मूल एनपीएन आम कलेक्टर परिपथ (पूर्वाग्रह विवरण की उपेक्षा)।]]
+[[Image:NPN emitter follower.svg|right|thumb|130px|चित्रा 1: मूल एनपीएन उभयनिष्ठ संग्राही परिपथ (पूर्वाग्रह विवरण की उपेक्षा)।]]
-[[ इलेक्ट्रानिक्स |इलेक्ट्रानिक्स]] में, एक आम कलेक्टर एम्पलीफायर, को उत्सर्जक अनुगामी के रूप में भी जाना जाता है ये तीन बुनियादी एकल चरण के [[द्विध्रुवी जंक्शन ट्रांजिस्टर]] (बीजेटी) [[एम्पलीफायर]] टोपोलॉजी में से एक है, जिसे सामान्तया एक वोल्टेज बफर के रूप में उपयोग किया जाता है
+[[इलेक्ट्रॉनिक्स]] में, एक सामान्य संग्राही प्रवर्धक जिसे उत्सर्जक अनुगामी भी कहते हैं, तीन मूल एकल चरण के [[द्विध्रुवी संधि ट्रांजिस्टर]] (बीजेटी) प्रवर्धक टोपोलॉजी में से एक है, जिसे सामान्यतया वोल्टेज बफर के रूप में प्रयोग किया जाता है।
-इस परिपथ में ट्रांजिस्टर का आधार टर्मिनल इनपुट के रूप में कार्य करता है, उत्सर्जक एक आउटपुट होता है और संग्राहक दोनों के लिए सामान्य है। उदाहरण के लिए, इसे [[जमीनी संदर्भ]] या बिजली [[आपूर्ति]] रेल से जोड़ा जा सकता है, इसलिए इसका नाम अनुरूप क्षेत्र प्रभाव ट्रांजिस्टर परिपथ सामान्य [[निकासन]] [[प्रवर्धक]] होता है और समान वेक्यूम ट्यूब परिपथ कैथोड के अनुगामी है।
+इस परिपथ में ट्रांजिस्टर का आधार टर्मिनल इनपुट के रूप में कार्य करता है, उत्सर्जक एक आउटपुट होता है और संग्राहक दोनों के लिए सामान्य है। उदाहरण के लिए,  इसे [[क्षेत्रीय]] या विद्युत आपूर्ति के [[संदर्भ]] से संयुक्त किया जा सकता है, इसलिए इसका नाम अनुरूप क्षेत्र प्रभाव ट्रांजिस्टर के परिपथ के लिए सामान्य [[निर्वात प्रवर्धक]] होता है और इसलिए समान निर्वात ट्यूब के लिए यह परिपथ कैथोड के अनुगामी होता है।
 == बेसिक परिपथ ==
 [[Image:Block Diagram for Feedback.svg|thumb|right|चित्र 2: एक नकारात्मक-प्रतिक्रिया प्रवर्धक]]
-परिपथ की व्याख्या ट्रांजिस्टर को नकारात्मक प्रतिक्रिया के नियंत्रण में रखकर की जा सकती है। इस दृष्टिकोण से एक सामान्य-संग्राहक चरण चित्र -1 एक एम्पलीफायर है जिसमें पूर्ण श्रृंखला के नेगेटिव फीडबैक होते हैं। इस कॉन्फ़िगरेशन में (चित्र 2 β = 1 के साथ), संपूर्ण आउटपुट वोल्टेज V<sub>out</sub> इसके विपरीत इनपुट वोल्टेज ''V''<sub>in</sub> के साथ श्रृंखला में रखा गया है। इस प्रकार दो वोल्टेज को किर्चहोफ़ के वोल्टेज कानून (केवीएल) के अनुसार घटाया जाता है फलन खंड आरेख से व्यवकलक ठीक इनपुट पाश द्वारा कार्यान्वित किया जाता है, और उनका अंतर वी<sub>diff</sub> = वी<sub>in</sub> - वी<sub>out</sub> बेस-एमिटर जंक्शन पर लगाया जाता है। ट्रांजिस्टर लगातार ''V''<sub>diff</sub>  की निगरानी करता है और इसके उत्सर्जक वोल्टेज को लगभग बराबर कम ''V''<sub>BEO</sub> पर समायोजित करता है और एमिटर रेसिस्टर R<sub>E</sub> के माध्यम से कलेक्टर करंट को पास करके इनपुट वोल्टेज में में बदलता है। नतीजतन, आउटपुट वोल्टेज ''V''<sub>BEO</sub> से इनपुट वोल्टेज भिन्नताओं का अनुसरण करता है ''V''<sub>+</sub>; तक इसलिए इसका नाम उत्सर्जक अनुयायी है।
+परिपथ की व्याख्या ट्रांजिस्टर को नकारात्मक प्रतिक्रिया के नियंत्रण में रखकर की जा सकती है। इस दृष्टिकोण से, सामान्य संग्राहक चरण ऐसा प्रवर्धक होता है जो  पूर्ण श्रृंखला के नकारात्मक प्रतिक्रिया के रूप में होते हैं इसे चित्र -1 में दिखाया गया है। इस विन्यास में चित्र 2 β = 1 के साथ और संपूर्ण आउटपुट वोल्टेज V<sub>out</sub> इसके विपरीत इनपुट वोल्टेज ''V''<sub>in</sub> के साथ श्रृंखला में रखा गया है। इस प्रकार दो वोल्टेज को किर्चहोफ़ के वोल्टेज नियम केवीएल के अनुसार घटाया जाता है फलन खंड आरेख से व्यवकलक ठीक इनपुट पाश द्वारा कार्यान्वित किया जाता है, और उनका अंतर ''V''<sub>diff</sub> = ''V''<sub>in</sub> − ''V''<sub>out</sub> बेस-उत्सर्जक संधि पर लगाया जाता है। ट्रांजिस्टर लगातार ''V''<sub>diff</sub>  की निगरानी करता है और इसके उत्सर्जक वोल्टेज को लगभग बराबर कम ''V''<sub>BEO</sub> पर समायोजित करता है और उत्सर्जक रेसिस्टर R<sub>E</sub> के माध्यम से संग्रहकर्ता करंट को पास करके इनपुट वोल्टेज में बदलता है। नतीजतन, आउटपुट वोल्टेज ''V''<sub>BEO</sub> से ''V''<sub>+</sub> तक इनपुट वोल्टेज विविधताओं का अनुसरण करता है इसलिए इसका नाम उत्सर्जक अनुयायी है।
-सहज रूप से, इस व्यवहार को यह महसूस करके भी समझा जा सकता है कि द्विध्रुवी ट्रांजिस्टर में बेस-एमिटर वोल्टेज पूर्वाग्रह परिवर्तनों के प्रति बहुत असंवेदनशील है, इसलिए बेस वोल्टेज में कोई भी परिवर्तन सीधे एमिटर को प्रेषित होता है अच्छे अनुमान के लिए। यह विभिन्न गड़बड़ी ट्रांजिस्टर सहिष्णुता, तापमान भिन्नता, भार प्रतिरोध, एक कलेक्टर अवरोधक अगर इसे जोड़ा जाता है, आदि पर थोड़ा निर्भर करता है, क्योंकि ट्रांजिस्टर इन गड़बड़ी पर प्रतिक्रिया करता है और संतुलन को पुनर्स्थापित करता है। इनपुट वोल्टेज सकारात्मक रेल तक पहुंचने पर भी यह कभी भी संतृप्त नहीं होता है।
+सहज रूप से, इस व्यवहार को यह महसूस करके भी समझा जा सकता है कि द्विध्रुवी ट्रांजिस्टर में बेस-उत्सर्जक वोल्टेज पूर्वाग्रह परिवर्तनों के प्रति बहुत असंवेदनशील है, इसलिए बेस वोल्टेज में कोई भी परिवर्तन सीधे उत्सर्जक को प्रेषित होता है अच्छे अनुमान के लिए यह होने वाली विभिन्न बाधाओं पर निर्भर करता है (ट्रांजिस्टर सहिष्णुता, तापमान भिन्नता, लोड प्रतिरोध, संग्राही प्रतिरोधक द्वारा इसे जोड़ा जाता है), चूंकि ट्रांजिस्टर इन होने वाली विभिन्न बाधाओं पर प्रतिक्रिया करता है और संतुलन बनाये रखता है। इनपुट वोल्टेज सकारात्मक छढ़ तक पहुंचने पर भी यह किसी भी स्थिति में संतृप्त नहीं होता है।
-आम कलेक्टर सर्किट को गणितीय रूप से लगभग इकाई के वोल्टेज लाभ के लिए दिखाया जा सकता है:
+उभयनिष्ठ संग्राही परिपथ को गणितीय रूप से लगभग इकाई वोल्टेज लाभ के लिए दिखाया जा सकता है:
 : <math>
 A_v = \frac{v_\text{out}}{v_\text{in}} \approx 1.
 </math>
-[[Image:PNP emitter follower.svg|thumb|130px|चित्रा 3: एमिटर-अनुयायी परिपथ का पीएनपी संस्करण, सभी ध्रुवीयताएं उलट जाती हैं।]]
+[[Image:PNP emitter follower.svg|thumb|130px|चित्रा 3: उत्सर्जक-अनुयायी परिपथ का पीएनपी संस्करण, सभी ध्रुवीयताएं उलट जाती हैं।]]
-इनपुट टर्मिनल पर एक छोटा वोल्टेज परिवर्तन को आउटपुट पर दोहराया जाता है। ट्रांजिस्टर के लाभ और लोड प्रतिरोध के मूल्य पर थोड़ा निर्भर करता है; नीचे लाभ सूत्र देखें। यह परिपथ उपयोगी है क्योंकि इसमें व्यापक इनपुट प्रतिबाधा है।
+इनपुट टर्मिनल पर एक छोटा वोल्टेज परिवर्तन को आउटपुट पर दोहराया जाता है। ट्रांजिस्टर से होने वाले लाभ और लोड प्रतिरोध के मूल्य पर थोड़ा निर्भर करता है, नीचे चित्र 3 में देखें। यह परिपथ उपयोगी है क्योंकि इसमें व्यापक इनपुट प्रतिबाधा है।
 : <math>
 r_\text{in} \approx \beta_0 R_\text{E},
@@ Line 26: / Line 26: @@
 r_\text{out} \approx \frac{R_\text{E} \parallel R_\text{source}}{\beta_0},
 </math>
-इसलिए यह कम-प्रतिरोध भार को चला सकता है।
+इसलिए यह कम प्रतिरोध लोड पर चलन कर सकती है।
-आमतौर पर, एमिटर रेसिस्टर काफी बड़ा होता है और इसे समीकरण से हटाया जा सकता है।
+साधारणतयः पर, उत्सर्जक रेसिस्टर काफी बड़ा होता है और इसे समीकरण से हटाया जा सकता है।
 : <math>
 r_\text{out} \approx \frac{R_\text{source}}{\beta_0}.
@@ Line 35: / Line 35: @@
 == अनुप्रयोग ==
-[[Image:Voltage follower.svg|thumb|302px|चित्रा 4: एकीकृत परिपथ के लिए उपयुक्त [[ वर्तमान स्रोत ]] पूर्वाग्रह के साथ एनपीएन वोल्टेज अनुयायी]]
+[[Image:Voltage follower.svg|thumb|302px|चित्रा 4: एकीकृत परिपथ के लिए उपयुक्त [[ वर्तमान स्रोत | धारा स्रोत]] पूर्वाग्रह के साथ एनपीएन वोल्टेज अनुयायी]]
-कम आउटपुट प्रतिबाधा एक बड़े आउटपुट प्रतिबाधा वाले स्रोत को एक छोटे लोड प्रतिबाधा को चलाने की अनुमति देता है; यह वोल्टेज [[ बफर एम्पलीफायर ]] के रूप में कार्य करता है। दूसरे शब्दों में, परिपथ में करंट गेन होता है (जो काफी हद तक h . पर निर्भर करता है)<sub>FE</sub> ट्रांजिस्टर का) वोल्टेज लाभ के बजाय, इसकी विशेषताओं के कारण इसे कई इलेक्ट्रॉनिक उपकरणों में पसंद किया जाता है। इनपुट करंट में एक छोटा सा बदलाव आउटपुट लोड को सप्लाई किए गए आउटपुट करंट में बहुत बड़ा बदलाव लाता है।
+कम आउटपुट प्रतिबाधा एक बड़े आउटपुट प्रतिबाधा वाले स्रोत को एक छोटे लोड प्रतिबाधा को चलाने की अनुमति देता है, यह वोल्टेज [[ बफर एम्पलीफायर | बफर प्रवर्धक]] के रूप में कार्य करता है। दूसरे शब्दों में, परिपथ में करंट गेन होता है जो काफी हद तक ट्रांजिस्टर के h<sub>FE</sub> पर निर्भर करता है। इसकी विशेषताओं के कारण वोल्टेज गेन कई इलेक्ट्रॉनिक उपकरणों में पसंद किया जाता है। इनपुट करंट में एक छोटा सा बदलाव आउटपुट लोड को सप्लाई किए गए आउटपुट करंट में बहुत बड़ा परिवर्तन करता है।
-बफर एक्शन का एक पहलू प्रतिबाधाओं का परिवर्तन है। उदाहरण के लिए, थेवेनिन के प्रमेय | उच्च थेवेनिन प्रतिरोध वाले वोल्टेज स्रोत द्वारा संचालित वोल्टेज अनुयायी के संयोजन का थेवेनिन प्रतिरोध केवल वोल्टेज अनुयायी (एक छोटा प्रतिरोध) के आउटपुट प्रतिरोध तक कम हो जाता है। वह प्रतिरोध कमी संयोजन को अधिक आदर्श वोल्टेज स्रोत बनाती है। इसके विपरीत, एक छोटे लोड प्रतिरोध और एक ड्राइविंग चरण के बीच डाला गया एक वोल्टेज अनुयायी ड्राइविंग चरण में एक बड़ा भार प्रस्तुत करता है- एक वोल्टेज सिग्नल को एक छोटे से लोड में युग्मित करने में एक फायदा।
+बफर एक्शन का एक पहलू प्रतिबाधाओं का परिवर्तन है। उदाहरण के लिए, उच्च थेवेनिन प्रतिरोध के साथ वोल्टेज स्रोत द्वारा संचालित वोल्टेज अनुयायी के संयोजन का थेवेनिन प्रतिरोध केवल वोल्टेज अनुयायी के आउटपुट प्रतिरोध के लिए  छोटा प्रतिरोध कम हो जाता है। वह प्रतिरोध कमी संयोजन को अधिक आदर्श वोल्टेज स्रोत बनाता है। इसके विपरीत, एक छोटे लोड प्रतिरोध और एक ड्राइविंग चरण के बीच डाला गया वोल्टेज अनुयायी ड्राइविंग चरण में एक बड़ा लोड प्रस्तुत करता है एक वोल्टेज सिग्नल को एक छोटे से लोड में जोड़ने पर लाभ प्रदान करता है।
-यह कॉन्फ़िगरेशन आमतौर पर पावर एम्पलीफायर क्लास # क्लास बी | क्लास-बी और पावर एम्पलीफायर क्लास # क्लास एबी | क्लास-एबी एम्पलीफायरों के आउटपुट चरणों में उपयोग किया जाता है। बेस परिपथ को ट्रांजिस्टर को क्लास-बी या एबी मोड में संचालित करने के लिए संशोधित किया गया है। पावर एम्पलीफायर क्लासेस#क्लास ए|क्लास-ए मोड में, कभी-कभी R . के बजाय एक सक्रिय करंट सोर्स का उपयोग किया जाता है<sub>E</sub> (चित्र 4) रैखिकता और/या दक्षता में सुधार करने के लिए।<ref name=Elliot>[https://sound-au.com/project10.htm Rod Elliot: ''20 Watt Class-A Power Amplifier'']</ref>
+यह विन्यास सामान्यतः क्लास बी और क्लास एबी प्रवर्धकों के उत्पादन स्तरों में प्रयोग किया जाता है। बेस परिपथ को ट्रांजिस्टर क्लास-बी या एबी मोड में संचालित करने के लिए संशोधित किया गया है। पावर प्रवर्धक क्लास-ए मोड में, और कभी-कभी ''R''<sub>E</sub> के बजाय एक सक्रिय धारा स्रोत का उपयोग किया जाता है (चित्र 4) रैखिकता और/दक्षता में सुधार करने के लिए है।<ref name=Elliot>[https://sound-au.com/project10.htm Rod Elliot: ''20 Watt Class-A Power Amplifier'']</ref>
 == लक्षण ==
-कम आवृत्तियों पर और एक सरलीकृत [[ हाइब्रिड-पीआई मॉडल ]] का उपयोग करके, निम्नलिखित छोटे-सिग्नल मॉडल | छोटे-सिग्नल विशेषताओं को प्राप्त किया जा सकता है। (पैरामीटर <math>\beta = g_m r_\pi</math> और [[ समानांतर (ज्यामिति) ]] रेखाएं श्रृंखला और समानांतर परिपथ # समानांतर परिपथ को दर्शाती हैं।)
+कम आवृत्तियों पर और एक सरलीकृत हाइब्रिड-पीआई मॉडल का उपयोग करके, निम्नलिखित छोटे- संकेत विशेषताओं को प्राप्त किया जा सकता है। (पैरामीटर <math>\beta = g_m r_\pi</math> और [[समानांतर रेखाएं]]  समानांतर में घटकों को दर्शाती हैं
 {| class="wikitable" style="background:white;text-align:left"
 !
-! Definition
+! परिभाषा
-! Expression
+! अभिव्यक्ति
-! Approximate expression
+! अनुमानित अभिव्यक्ति
-! Conditions
+! परिस्थिति
 |-
-! '''[[gain (electronics)#Current gain|Current gain]]'''
+! '''[[gain (electronics)#Current gain|धारा लाभ]]'''
 | <math> A_\mathrm{i} = {i_\text{out} \over i_\text{in}} </math>
 | <math> \beta_0 + 1 \ </math>
@@ Line 59: / Line 59: @@
 | <math> \beta_0 \gg 1 </math>
 |-
-! '''[[gain (electronics)#Voltage gain|Voltage gain]]'''
+! '''[[gain (electronics)#Voltage gain|वोल्टेज बढ़ना]]'''
 | <math> A_\mathrm{v} = {v_\text{out} \over v_\text{in}} </math>
 | <math> {g_m R_\text{E} \over g_m R_\text{E} + 1} </math>
@@ Line 65: / Line 65: @@
 | <math> g_m R_\text{E} \gg 1 </math>
 |-
-! '''[[Input resistance]]'''
+! '''[[Input resistance|इनपुट प्रतिरोध]]'''
 | <math> r_\text{in} = \frac{v_\text{in}}{i_\text{in}}</math>
 | <math> r_\pi + (\beta_0 + 1) R_\text{E}\ </math>
@@ Line 71: / Line 71: @@
 | <math> (g_m R_\text{E} \gg 1) \wedge (\beta_0 \gg 1) </math>
 |-
-! '''[[Output resistance]]'''
+! '''[[Output resistance|आउटपुट प्रतिरोध]]'''
 | <math> r_\text{out} = \frac{v_\text{out}}{i_\text{out}}</math>
 | <math> R_\text{E} \parallel {r_\pi + R_\text{source} \over \beta_0 + 1} </math>
@@ Line 77: / Line 77: @@
 | <math> (\beta_0 \gg 1) \wedge (r_\text{in} \gg R_\text{source})</math>
 |}
-कहाँ पे <math>R_\text{source}\ </math> थेवेनिन का प्रमेय है | थेवेनिन समकक्ष स्रोत प्रतिरोध।
+जहां पे <math>R_\text{source}\ </math> वेनिन समकक्ष स्रोत प्रतिरोध।
 === व्युत्पत्ति ===
 [[Image:Voltage follower small-signal.svg|thumb|300px|चित्रा 5: द्विध्रुवीय ट्रांजिस्टर के लिए हाइब्रिड-पीआई मॉडल का उपयोग करके चित्रा 3 के अनुरूप लघु-संकेत परिपथ द्विध्रुवीय डिवाइस कैपेसिटेंस को अनदेखा करने के लिए पर्याप्त आवृत्तियों पर द्विध्रुवीय ट्रांजिस्टर के लिए]]
-[[Image:Voltage follower output resistance.svg|300px |thumb|चित्रा 6: आउटपुट प्रतिरोध खोजने के लिए आउटपुट पर टेस्ट करंट के साथ बाइपोलर वोल्टेज फॉलोअर के लिए लो-फ्रीक्वेंसी स्मॉल-सिग्नल परिपथ। अवरोध <math>R_\text{E} = R_\text{L} \parallel r_\text{O}</math>.]]
+[[Image:Voltage follower output resistance.svg|300px |thumb|चित्रा 6: आउटपुट प्रतिरोध खोजने के लिए आउटपुट पर टेस्ट करंट के साथ बाइपोलर वोल्टेज फॉलोअर के लिए लो-फ्रीक्वेंसी स्मॉल- संकेत परिपथ। अवरोध <math>R_\text{E} = R_\text{L} \parallel r_\text{O}</math>.]]
-चित्रा 5 चित्रा 3 के परिपथ के लिए कम आवृत्ति हाइब्रिड-पीआई मॉडल दिखाता है। ओम के नियम का उपयोग करके, विभिन्न धाराओं को निर्धारित किया गया है, और ये परिणाम आरेख पर दिखाए जाते हैं। किरचॉफ के वर्तमान नियम को उत्सर्जक पर लागू करने पर पाया जाता है:
+चित्रा 5 चित्रा 3 के परिपथ के लिए कम आवृत्ति हाइब्रिड-पीआई मॉडल दिखाता है। ओम के नियम का उपयोग करके, विभिन्न धाराओं को निर्धारित किया गया है, और ये परिणाम आरेख पर दिखाए जाते हैं। किरचॉफ के धारा नियम को उत्सर्जक पर लागू करने पर पाया जाता है:
 : <math>(\beta + 1) \frac{v_\text{in} - v_\text{out}}{R_\text{S} + r_\pi} = v_\text{out} \left(\frac{1}{R_\text{L}} + \frac{1}{r_\text{O}}\right).</math>
 निम्नलिखित प्रतिरोध मूल्यों को परिभाषित करें:
@@ Line 91: / Line 91: @@
 फिर शब्दों को एकत्रित करते हुए वोल्टेज लाभ पाया जाता है:
 : <math>A_\text{v} = \frac{v_\text{out}}{v_\text{in}} = \frac{1}{1 + \frac{R}{R_\text{E}}}.</math>
-इस परिणाम से, लाभ एकता (जैसा कि बफर एम्पलीफायर के लिए अपेक्षित है) तक पहुंचता है यदि हर में प्रतिरोध अनुपात छोटा है। यह अनुपात वर्तमान लाभ β के बड़े मूल्यों और के बड़े मूल्यों के साथ घटता है <math>R_\text{E}</math>.
+इस परिणाम से, लाभ एकीकृत जैसा कि बफर प्रवर्धक के अपेक्षित मान तक पहुंचता है यदि हर में प्रतिरोध अनुपात छोटा है। यह अनुपात धारा लाभ β के बड़े मूल्यों के साथ घटता है और <math>R_\text{E}</math> के बड़े मूल्यों के साथ है
 इनपुट प्रतिरोध के रूप में पाया जाता है
 : <math>\begin{align}
@@ Line 98: / Line 98: @@
                &= R_\text{S} + r_\pi + (\beta + 1) R_\text{E}.
 \end{align}</math>
-ट्रांजिस्टर आउटपुट प्रतिरोध <math>r_\text{O}</math> लोड की तुलना में आमतौर पर बड़ा होता है <math>R_\text{L}</math>, और इसीलिए <math>R_\text{L}</math> हावी <math>R_\text{E}</math>. इस परिणाम से, एम्पलीफायर का इनपुट प्रतिरोध आउटपुट लोड प्रतिरोध से बहुत बड़ा है <math>R_\text{L}</math> बड़े वर्तमान लाभ के लिए <math>\beta</math>. अर्थात्, एम्पलीफायर को लोड और स्रोत के बीच रखने से स्रोत को प्रत्यक्ष युग्मन की तुलना में एक बड़ा (उच्च-प्रतिरोधक) भार प्रस्तुत होता है <math>R_\text{L}</math>, जिसके परिणामस्वरूप स्रोत प्रतिबाधा में कम सिग्नल क्षीणन होता है <math>R_\text{S}</math> [[ वोल्टेज विभाजन ]] के परिणामस्वरूप।
+ट्रांजिस्टर आउटपुट प्रतिरोध <math>r_\text{O}</math> लोड की तुलना में सामान्यतः बड़ा होता है <math>R_\text{L}</math>, और इसीलिए <math>R_\text{L}</math> हावी <math>R_\text{E}</math>. इस परिणाम से, प्रवर्धक का इनपुट प्रतिरोध आउटपुट लोड प्रतिरोध से बहुत बड़ा है <math>R_\text{L}</math> बड़े धारा लाभ के लिए <math>\beta</math>. अर्थात्, प्रवर्धक को लोड और स्रोत के बीच रखने से स्रोत को प्रत्यक्ष युग्मन की तुलना में एक बड़ा उच्च-प्रतिरोधक लोड प्रस्तुत होता है <math>R_\text{L}</math>, जिसके परिणामस्वरूप स्रोत प्रतिबाधा में कम  संकेत क्षीणन होता है <math>R_\text{S}</math> [[ वोल्टेज विभाजन ]] के परिणामस्वरूप।
-चित्रा 6 चित्रा 5 के छोटे-सिग्नल परिपथ को इनपुट शॉर्ट-परिपथ के साथ दिखाता है और इसके आउटपुट पर एक टेस्ट करंट लगाया जाता है। इस परिपथ का उपयोग करके आउटपुट प्रतिरोध पाया जाता है:
+चित्रा 6 चित्रा 5 के छोटे- संकेत परिपथ को इनपुट शॉर्ट-परिपथ के साथ दिखाता है और इसके आउटपुट पर एक टेस्ट करंट लगाया जाता है। इस परिपथ का उपयोग करके आउटपुट प्रतिरोध पाया जाता है
 : <math>R_\text{out} = \frac{v_\text{x}}{i_\text{x}}.</math>
 ओम के नियम का उपयोग करते हुए, विभिन्न धाराएँ पाई गई हैं, जैसा कि चित्र में दर्शाया गया है। बेस करंट के लिए शर्तों को एकत्रित करते हुए, बेस करंट को पाया जाता है
 : <math>(\beta + 1) i_\text{b} = i_\text{x} - \frac{v_\text{x}}{R_\text{E}},</math>
-कहाँ पे <math>R_\text{E}</math> ऊपर परिभाषित किया गया है। बेस करंट के लिए इस मान का उपयोग करते हुए, ओम का नियम प्रदान करता है
+जहां पे <math>R_\text{E}</math> ऊपर परिभाषित किया गया है। बेस धारा के लिए इस मान का उपयोग करते हुए, ओम का नियम प्रदान करता है
 : <math>v_\text{x} = i_\text{b} \left(R_\text{S} + r_\pi\right).</math>
 आधार धारा के लिए प्रतिस्थापन, और शर्तों को एकत्रित करना,
 : <math>R_\text{out} = \frac{v_\text{x}}{i_\text{x}} = R \parallel R_\text{E},</math>
-कहाँ || एक समानांतर कनेक्शन को दर्शाता है, और <math>R</math> ऊपर परिभाषित किया गया है। इसलिये <math>R</math> आम तौर पर एक छोटा प्रतिरोध होता है जब वर्तमान लाभ <math>\beta</math> बड़ी है, <math>R</math> उत्पादन प्रतिबाधा पर हावी है, जो इसलिए भी छोटा है। एक छोटे आउटपुट प्रतिबाधा का मतलब है कि मूल वोल्टेज स्रोत और वोल्टेज अनुयायी का श्रृंखला संयोजन एक थवेनिन के प्रमेय को प्रस्तुत करता है | थेवेनिन वोल्टेज स्रोत इसके आउटपुट नोड पर कम थेवेनिन प्रतिरोध के साथ; अर्थात्, वोल्टेज स्रोत के साथ वोल्टेज स्रोत का संयोजन मूल वोल्टेज स्रोत की तुलना में अधिक आदर्श वोल्टेज स्रोत बनाता है।
+जहां एक समांतर संपर्क को दर्शाता है, और <math>R</math> ऊपर परिभाषित किया गया है। इसलिये <math>R</math> सामान्यतः छोटा प्रतिरोध होता है जब धारा लाभ <math>\beta</math> से बड़ी है, आउटपुट प्रतिबाधा <math>R</math> पर हावी है, ये इसलिए भी छोटा है। एक छोटे उत्पाद प्रतिबाधा का मतलब है कि मूल वोल्टेज स्रोत और वोल्टेज अनुयायी का श्रृंखला संयोजन अपने आउटपुट नोड पर कम थेवेनिन प्रतिरोध के साथ एक थेवेनिन वोल्टेज स्रोत प्रस्तुत करता है, अर्थात वोल्टेज अनुयायी के साथ वोल्टेज स्रोत का संयोजन मूल वोल्टेज की तुलना में अधिक आदर्श वोल्टेज स्रोत बनाता है।
 ==यह भी देखें==
 {{Portal|Electronics}}
-*आम आधार
+*सामान्य आधार
-*[[ आम उत्सर्जक ]]
+*[[ आम उत्सर्जक | सामान्य उत्सर्जक]]
-*आम द्वार*
+*सामान्य द्वार*
-*आम नाली
+*सामान्य नाली
 *[[ सामान्य स्रोत ]]
-* [[ खुला कलेक्टर ]]
+* [[ खुला कलेक्टर | खुला संग्रहकर्ता]]
 * [[ दो बंदरगाह नेटवर्क ]]
@@ Line 130: / Line 130: @@
 {{Transistor amplifiers}}
+[[Category:Machine Translated Page]]
+[[Category:All articles lacking in-text citations]]
+[[Category:Articles lacking in-text citations from April 2009]]
+[[Category:Articles with invalid date parameter in template]]
+[[Category:Collapse templates]]
+[[Category:Navigational boxes| ]]
+[[Category:Navigational boxes without horizontal lists]]
+[[Category:Pages with empty portal template]]
+[[Category:Pages with script errors]]
+[[Category:Portal templates with redlinked portals]]
+[[Category:Sidebars with styles needing conversion]]
+[[Category:Template documentation pages|Documentation/doc]]
+[[Category:Templates generating microformats]]
+[[Category:Templates that are not mobile friendly]]
+[[Category:Templates using TemplateData]]
+[[Category:Wikipedia metatemplates]]

v t e Transistor amplifiers
	Bipolar junction transistor:	Common emitter Common collector Common base
	Field-effect transistor:	Common source Common drain Common gate
	Multiple transistors:	Darlington transistor Complementary feedback pair Cascode Long-tailed pair

Anonymous

Search

उभयनिष्ठ संग्राही: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 09:18, 11 November 2022

Contents

बेसिक परिपथ

अनुप्रयोग

लक्षण

व्युत्पत्ति

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

उभयनिष्ठ संग्राही: Difference between revisions

Latest revision as of 09:18, 11 November 2022

बेसिक परिपथ

अनुप्रयोग

लक्षण

व्युत्पत्ति

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Hidden categories