लाप्लासियन आव्यूह: Difference between revisions

Revision as of 21:25, 19 July 2023

ग्राफ सिद्धांत के गणित क्षेत्र में, लाप्लासियन मैट्रिक्स, जिसे डिस्क्रीट_लाप्लेस_ऑपरेटर#ग्राफ_लाप्लासियन, प्रवेश मैट्रिक्स, किरचॉफ मैट्रिक्स या डिस्क्रीट लाप्लास ऑपरेटर भी कहा जाता है, ग्राफ (असतत गणित) का मैट्रिक्स (गणित) प्रतिनिधित्व है। पियरे-साइमन लाप्लास के नाम पर, ग्राफ लाप्लासियन मैट्रिक्स को परिमित अंतर विधि द्वारा प्राप्त नकारात्मक निरंतर लाप्लासियन का अनुमान लगाने वाले ग्राफ पर नकारात्मक असतत लाप्लास ऑपरेटर के मैट्रिक्स रूप के रूप में देखा जा सकता है।

लाप्लासियन मैट्रिक्स ग्राफ़ के कई उपयोगी गुणों से संबंधित है। किरचॉफ के प्रमेय के साथ, इसका उपयोग किसी दिए गए ग्राफ़ के लिए फैले हुए पेड़ों (गणित) की संख्या की गणना करने के लिए किया जा सकता है। ग्राफ़ के कट (ग्राफ़ सिद्धांत)#सबसे कम कट का अनुमान फिडलर वेक्टर के माध्यम से लगाया जा सकता है - ग्राफ़ लाप्लासियन के दूसरे सबसे छोटे आइगेनवैल्यू के अनुरूप ईजेनवेक्टर - जैसा कि चीगर स्थिरांक (ग्राफ़ सिद्धांत)#चीगर असमानताओं|चीगर की असमानता द्वारा स्थापित किया गया है। लाप्लासियन मैट्रिक्स के मैट्रिक्स का आइगेंडेकंपोजिशन नॉनलाइनर डायमेंशनलिटी रिडक्शन#लाप्लासियन आइजेनमैप्स का निर्माण करने की अनुमति देता है जो कई यंत्र अधिगम अनुप्रयोगों में दिखाई देते हैं और ग्राफ ड्राइंग में वर्णक्रमीय लेआउट निर्धारित करते हैं। ग्राफ-आधारित संकेत आगे बढ़ाना असतत फूरियर रूपांतरण पर आधारित है जो सिग्नल के अनुरूप ग्राफ के लाप्लासियन मैट्रिक्स के ईजेनवेक्टरों के लिए जटिल संख्या साइन तरंगों के मानक आधार को प्रतिस्थापित करके पारंपरिक असतत फूरियर ट्रांसफॉर्म का विस्तार करता है।

लाप्लासियन मैट्रिक्स साधारण ग्राफ के लिए परिभाषित करना सबसे आसान है, लेकिन ग्लोसरी_ऑफ_ग्राफ_थ्योरी#वेटेड_ग्राफ|एज-वेटेड ग्राफ के लिए अनुप्रयोगों में अधिक आम है, यानी, इसके किनारों पर वजन के साथ - ग्राफ आसन्न मैट्रिक्स की प्रविष्टियां। वर्णक्रमीय ग्राफ सिद्धांत ग्राफ के गुणों को स्पेक्ट्रम से जोड़ता है, यानी, आइगेनवैल्यू, और ग्राफ से जुड़े मैट्रिक्स के आइगेनवेक्टर, जैसे कि इसकी आसन्न मैट्रिक्स या लाप्लासियन मैट्रिक्स। असंतुलित भार मैट्रिक्स स्पेक्ट्रम को अवांछित रूप से प्रभावित कर सकता है, जिससे सामान्यीकरण की आवश्यकता होती है - मैट्रिक्स प्रविष्टियों का कॉलम/पंक्ति स्केलिंग - जिसके परिणामस्वरूप सामान्यीकृत आसन्नता और लाप्लासियन मैट्रिक्स होते हैं।

सरल ग्राफ़ के लिए परिभाषाएँ

लाप्लासियन मैट्रिक्स

एक सरल ग्राफ दिया गया है $G$ साथ $n$ कोने $v_{1},\ldots ,v_{n}$ , इसका लाप्लासियन मैट्रिक्स ${\textstyle L_{n\times n}}$ है तत्वानुसार परिभाषित^[1]

L_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j\\-1&{\mbox{if}}\ i\neq j\ {\mbox{and}}\ v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}},\end{cases}}

या मैट्रिक्स द्वारा समकक्ष

L=D-A,

जहां D डिग्री मैट्रिक्स है और A ग्राफ़ का आसन्न मैट्रिक्स है। तब से ${\textstyle G}$ सरल ग्राफ है, ${\textstyle A}$ इसमें केवल 1s या 0s हैं और इसके विकर्ण तत्व सभी 0s हैं।

यहां लेबल, अप्रत्यक्ष ग्राफ़ और उसके लाप्लासियन मैट्रिक्स का सरल उदाहरण दिया गया है।

Labelled graph	Degree matrix	Adjacency matrix	Laplacian matrix
	${\textstyle \left({\begin{array}{rrrrrr}2&0&0&0&0&0\\0&3&0&0&0&0\\0&0&2&0&0&0\\0&0&0&3&0&0\\0&0&0&0&3&0\\0&0&0&0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrrrr}0&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrrrr}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0&-1&3&0\\0&0&0&-1&0&1\\\end{array}}\right)}$

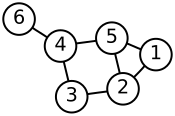
हम अप्रत्यक्ष ग्राफ़ के लिए देखते हैं कि आसन्न मैट्रिक्स और लाप्लासियन मैट्रिक्स दोनों सममित हैं, और लाप्लासियन मैट्रिक्स की पंक्ति और स्तंभ-योग सभी शून्य हैं।

निर्देशित ग्राफ़ के लिए, या तो डिग्री (ग्राफ़ सिद्धांत) का उपयोग किया जा सकता है, जो कि अनुप्रयोग पर निर्भर करता है, जैसा कि निम्नलिखित उदाहरण में है:

Labelled graph	Adjacency matrix	Out-Degree matrix	Out-Degree Laplacian	In-Degree matrix	In-Degree Laplacian
	${\textstyle \left({\begin{array}{rrr}0&1&1\\0&0&1\\1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}2&0&0\\0&1&0\\0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}2&-1&-1\\0&1&-1\\-1&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&0&0\\0&1&0\\0&0&2\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-1&-1\\0&1&-1\\-1&0&2\\\end{array}}\right)}$

निर्देशित ग्राफ़ में, आसन्न मैट्रिक्स और लाप्लासियन मैट्रिक्स दोनों असममित हैं। इसके लाप्लासियन मैट्रिक्स में, कॉलम-योग या पंक्ति-योग शून्य हैं, यह इस बात पर निर्भर करता है कि डिग्री (ग्राफ़ सिद्धांत) का उपयोग किया गया है या नहीं।

=== घटना मैट्रिक्स के माध्यम से सममित लाप्लासियन === ${\textstyle |v|\times |e|}$ h>तत्व बी के साथ घटना मैट्रिक्स बी_ve शीर्ष v और किनारे e के लिए (शीर्षों को जोड़ने वाला)। ${\textstyle v_{i}}$ और ${\textstyle v_{j}}$ , i > j के साथ) द्वारा परिभाषित किया गया है

B_{ve}=\left\{{\begin{array}{rl}1,&{\text{if }}v=v_{i}\\-1,&{\text{if }}v=v_{j}\\0,&{\text{otherwise}}.\end{array}}\right.

भले ही इस परिभाषा में किनारों को तकनीकी रूप से निर्देशित किया गया है, उनकी दिशाएँ मनमाने ढंग से हो सकती हैं, फिर भी समान सममित लाप्लासियन का परिणाम होता है ${\textstyle |v|\times |v|}$ मैट्रिक्स एल के रूप में परिभाषित किया गया है

L=BB^{\textsf {T}}

कहाँ ${\textstyle B^{\textsf {T}}}$ बी का स्थानान्तरण है.

Undirected graph	Incidence matrix	Laplacian matrix
	${\textstyle \left({\begin{array}{rrrr}1&1&1&0\\-1&0&0&0\\0&-1&0&1\\0&0&-1&-1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrr}3&-1&-1&-1\\-1&1&0&0\\-1&0&2&-1\\-1&0&-1&2\\\end{array}}\right)}$

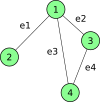
एक वैकल्पिक उत्पाद $B^{\textsf {T}}B$ तथाकथित को परिभाषित करता है ${\textstyle |e|\times |e|}$ किनारे-आधारित लाप्लासियन, आमतौर पर उपयोग किए जाने वाले मूल वर्टेक्स-आधारित लाप्लासियन मैट्रिक्स एल के विपरीत।

निर्देशित ग्राफ़ के लिए सममित लाप्लासियन

एक निर्देशित ग्राफ का लाप्लासियन मैट्रिक्स परिभाषा के अनुसार आम तौर पर गैर-सममित होता है, जबकि, उदाहरण के लिए, पारंपरिक वर्णक्रमीय क्लस्टरिंग मुख्य रूप से सममित आसन्नता और लाप्लासियन मैट्रिक्स के साथ अप्रत्यक्ष ग्राफ के लिए विकसित की जाती है। समरूपता की आवश्यकता वाली तकनीकों को लागू करने के लिए तुच्छ दृष्टिकोण मूल निर्देशित ग्राफ को अप्रत्यक्ष ग्राफ में बदलना और बाद के लिए लाप्लासियन मैट्रिक्स का निर्माण करना है।

मैट्रिक्स नोटेशन में, अप्रत्यक्ष ग्राफ़ के आसन्न मैट्रिक्स को, उदाहरण के लिए, आसन्न मैट्रिक्स के OR गेट के रूप में परिभाषित किया जा सकता है $A$ मूल निर्देशित ग्राफ़ और उसके मैट्रिक्स का स्थानान्तरण $A^{T}$ , जहां शून्य और की प्रविष्टियाँ हैं $A$ मानों को संख्यात्मक के बजाय तार्किक माना जाता है, जैसा कि निम्नलिखित उदाहरण में है:

Adjacency matrix	Symmetrized adjacency	Symmetric Laplacian matrix
${\textstyle \left({\begin{array}{ccc}0&1&1\\0&0&1\\1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{ccc}0&1&1\\1&0&1\\1&1&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{ccc}2&-1&-1\\-1&2&-1\\-1&-1&2\\\end{array}}\right)}$

लाप्लासियन मैट्रिक्स सामान्यीकरण

बड़ी डिग्री वाला शीर्ष, जिसे भारी नोड भी कहा जाता है, के परिणामस्वरूप मैट्रिक्स गुणों पर हावी होने वाले लाप्लासियन मैट्रिक्स में बड़ी विकर्ण प्रविष्टि होती है। सामान्यीकरण का उद्देश्य लाप्लासियन मैट्रिक्स की प्रविष्टियों को शीर्ष डिग्री द्वारा विभाजित करके ऐसे शीर्षों के प्रभाव को अन्य शीर्षों के प्रभाव के बराबर बनाना है। शून्य से विभाजन से बचने के लिए, शून्य डिग्री वाले पृथक शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है।

सममित रूप से सामान्यीकृत लाप्लासियन

सममित रूप से सामान्यीकृत लाप्लासियन मैट्रिक्स को इस प्रकार परिभाषित किया गया है:^[1]

L^{\text{sym}}:=(D^{+})^{1/2}L(D^{+})^{1/2}=I-(D^{+})^{1/2}A(D^{+})^{1/2},

कहाँ $D^{+}$ मूर-पेनरोज़ व्युत्क्रम है।

के तत्व ${\textstyle L^{\text{sym}}}$ इस प्रकार द्वारा दिए गए हैं

L_{i,j}^{\text{sym}}:={\begin{cases}1&{\mbox{if }}i=j{\mbox{ and }}\deg(v_{i})\neq 0\\-{\frac {1}{\sqrt {\deg(v_{i})\deg(v_{j})}}}&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}.\end{cases}}

सममित रूप से सामान्यीकृत लाप्लासियन मैट्रिक्स सममित है यदि और केवल यदि आसन्न मैट्रिक्स सममित है।

Adjacency matrix	Degree matrix	Normalized Laplacian
${\textstyle \left({\begin{array}{rrr}0&1&0\\1&0&1\\0&1&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&0&0\\0&2&0\\0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-{\sqrt {1/2}}&0\\-{\sqrt {1/2}}&1&-{\sqrt {1/2}}\\0&-{\sqrt {1/2}}&1\\\end{array}}\right)}$

निर्देशित ग्राफ़ के गैर-सममित आसन्न मैट्रिक्स के लिए, किसी भी डिग्री (ग्राफ़ सिद्धांत) का उपयोग सामान्यीकरण के लिए किया जा सकता है:

Adjacency matrix	Out-Degree matrix	Out-Degree normalized Laplacian	In-Degree matrix	In-Degree normalized Laplacian
${\textstyle \left({\begin{array}{rrr}0&1&1\\0&0&1\\1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}2&0&0\\0&1&0\\0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-{\sqrt {1/2}}&-{\sqrt {1/2}}\\0&1&-1\\-{\sqrt {1/2}}&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&0&0\\0&1&0\\0&0&2\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-1&-{\sqrt {1/2}}\\0&1&-{\sqrt {1/2}}\\-{\sqrt {1/2}}&0&1\\\end{array}}\right)}$

बाएँ (यादृच्छिक-चलना) और दाएँ सामान्यीकृत लाप्लासियन

बाएं (रैंडम-वॉक) सामान्यीकृत लाप्लासियन मैट्रिक्स को इस प्रकार परिभाषित किया गया है:

L^{\text{rw}}:=D^{+}L=I-D^{+}A,

कहाँ $D^{+}$ मूर-पेनरोज़ व्युत्क्रम है। के तत्व ${\textstyle L^{\text{rw}}}$ द्वारा दिए गए हैं

L_{i,j}^{\text{rw}}:={\begin{cases}1&{\mbox{if }}i=j{\mbox{ and }}\deg(v_{i})\neq 0\\-{\frac {1}{\deg(v_{i})}}&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}.\end{cases}}

इसी प्रकार, सही सामान्यीकृत लाप्लासियन मैट्रिक्स को इस प्रकार परिभाषित किया गया है

LD^{+}=I-AD^{+}

.

यदि सभी पृथक शीर्षों के तुच्छ मामले को छोड़कर, आसन्न मैट्रिक्स सममित है, तो बाएँ या दाएँ सामान्यीकृत लाप्लासियन मैट्रिक्स सममित नहीं है। उदाहरण के लिए,

Adjacency matrix	Degree matrix	Left normalized Laplacian	Right normalized Laplacian
${\textstyle \left({\begin{array}{rrr}0&1&0\\1&0&1\\0&1&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&0&0\\0&2&0\\0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-1&0\\-1/2&1&-1/2\\0&-1&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-1/2&0\\-1&1&-1\\0&-1/2&1\\\end{array}}\right)}$

उदाहरण यह भी दर्शाता है कि यदि $G$ तो फिर, इसका कोई पृथक शीर्ष नहीं है $D^{+}A$ स्टोकेस्टिक मैट्रिक्स और इसलिए यादृच्छिक चलने का मैट्रिक्स है, ताकि बाईं ओर लाप्लासियन सामान्यीकृत हो $L^{\text{rw}}:=D^{+}L=I-D^{+}A$ प्रत्येक पंक्ति का योग शून्य है। इस प्रकार हम कभी-कभी वैकल्पिक रूप से कॉल करते हैं $L^{\text{rw}}$ रैंडम वॉक|रैंडम-वॉक सामान्यीकृत लाप्लासियन। कम असामान्य रूप से उपयोग किए जाने वाले दाएँ सामान्यीकृत लाप्लासियन में $LD^{+}=I-AD^{+}$ चूँकि प्रत्येक कॉलम का योग शून्य है $AD^{+}$ स्टोकेस्टिक मैट्रिक्स है.

निर्देशित ग्राफ़ के गैर-सममित आसन्न मैट्रिक्स के लिए, किसी को सामान्यीकरण के लिए डिग्री (ग्राफ़ सिद्धांत) चुनने की भी आवश्यकता होती है:

Adjacency matrix	Out-Degree matrix	Out-Degree left normalized Laplacian	In-Degree matrix	In-Degree right normalized Laplacian
${\textstyle \left({\begin{array}{rrr}0&1&1\\0&0&1\\1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}2&0&0\\0&1&0\\0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-1/2&-1/2\\0&1&-1\\-1&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&0&0\\0&1&0\\0&0&2\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-1&-1/2\\0&1&-1/2\\-1&0&1\\\end{array}}\right)}$

पंक्ति-योग के साथ लेफ्ट आउट-डिग्री सामान्यीकृत लाप्लासियन सभी 0 स्टोकेस्टिक मैट्रिक्स से संबंधित है $D_{\text{out}}^{+}A$ , जबकि सभी 0 के कॉलम-योग के साथ डिग्री में सामान्यीकृत लाप्लासियन में स्टोकेस्टिक मैट्रिक्स शामिल है $AD_{\text{in}}^{+}$ .

भारित किनारों वाले ग्राफ़ के लिए परिभाषाएँ

अनुप्रयोगों में सामान्य भारित किनारों वाले ग्राफ़ को आसानी से उनके आसन्न मैट्रिक्स द्वारा परिभाषित किया जाता है जहां प्रविष्टियों के मान संख्यात्मक होते हैं और अब शून्य और तक सीमित नहीं होते हैं। वर्णक्रमीय क्लस्टरिंग और ग्राफ़-आधारित सिग्नल प्रोसेसिंग में, जहां ग्राफ़ शीर्ष डेटा बिंदुओं का प्रतिनिधित्व करते हैं, किनारे के वजन की गणना की जा सकती है, उदाहरण के लिए, डेटा बिंदुओं के जोड़े के बीच Distance_matrix के व्युत्क्रमानुपाती के रूप में, जिसके परिणामस्वरूप सभी वजन अनौपचारिक रूप से बड़े मूल्यों के साथ गैर-नकारात्मक होते हैं डेटा बिंदुओं के अधिक समान जोड़े के अनुरूप। डेटा बिंदुओं के बीच सहसंबंध और विरोधी सहसंबंध का उपयोग करने से स्वाभाविक रूप से सकारात्मक और नकारात्मक दोनों प्रकार के भार उत्पन्न होते हैं। सरल ग्राफ़ की अधिकांश परिभाषाएँ गैर-नकारात्मक भार के मानक मामले तक तुच्छ रूप से विस्तारित हैं, जबकि नकारात्मक भार पर अधिक ध्यान देने की आवश्यकता होती है, खासकर सामान्यीकरण में।

लाप्लासियन मैट्रिक्स

लाप्लासियन मैट्रिक्स द्वारा परिभाषित किया गया है

L=D-A,

जहां D डिग्री मैट्रिक्स है और A ग्राफ़ का आसन्न मैट्रिक्स है।

निर्देशित ग्राफ़ के लिए, या तो डिग्री (ग्राफ़ सिद्धांत) का उपयोग किया जा सकता है, जो कि अनुप्रयोग पर निर्भर करता है, जैसा कि निम्नलिखित उदाहरण में है:

Adjacency matrix	In-Degree matrix	In-Degree Laplacian	Out-Degree matrix	Out-Degree Laplacian
${\textstyle \left({\begin{array}{rrr}0&1&2\\3&0&5\\6&7&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}9&0&0\\0&8&0\\0&0&7\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}9&-1&-2\\-3&8&-5\\-6&-7&7\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}3&0&0\\0&8&0\\0&0&13\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}3&-1&-2\\-3&8&-5\\-6&-7&13\\\end{array}}\right)}$

ग्राफ़ सेल्फ-लूप्स, जो आसन्न मैट्रिक्स के मुख्य विकर्ण पर गैर-शून्य प्रविष्टियों द्वारा स्वयं को प्रकट करते हैं, की अनुमति है लेकिन ग्राफ़ लाप्लासियन मानों को प्रभावित नहीं करते हैं।

घटना मैट्रिक्स के माध्यम से सममित लाप्लासियन

एक 2-आयामी स्प्रिंग प्रणाली।

भारित किनारों वाले ग्राफ़ के लिए कोई भारित घटना मैट्रिक्स बी को परिभाषित कर सकता है और इसका उपयोग संबंधित सममित लाप्लासियन के निर्माण के लिए कर सकता है $L=BB^{\textsf {T}}$ . यहां वर्णित वैकल्पिक क्लीनर दृष्टिकोण, वज़न को कनेक्टिविटी से अलग करना है: नियमित ग्राफ़ के लिए घटना मैट्रिक्स का उपयोग करना जारी रखें और केवल वज़न के मान रखने वाले मैट्रिक्स को पेश करें। वसंत प्रणाली इस मॉडल का उदाहरण है जिसका उपयोग यांत्रिकी में दी गई कठोरता और इकाई लंबाई के स्प्रिंग्स की प्रणाली का वर्णन करने के लिए किया जाता है, जहां कठोरता के मूल्य ग्राफ किनारों के वजन की भूमिका निभाते हैं।

इस प्रकार हम भारहीन की परिभाषा का पुन: उपयोग करते हैं ${\textstyle |v|\times |e|}$ तत्व बी के साथ घटना मैट्रिक्स बी_ve शीर्ष v और किनारे e के लिए (शीर्षों को जोड़ने वाला)। ${\textstyle v_{i}}$ और ${\textstyle v_{j}}$ , i > j) द्वारा परिभाषित

B_{ve}=\left\{{\begin{array}{rl}1,&{\text{if }}v=v_{i}\\-1,&{\text{if }}v=v_{j}\\0,&{\text{otherwise}}.\end{array}}\right.

अब हम विकर्ण को भी परिभाषित करते हैं ${\textstyle |e|\times |e|}$ मैट्रिक्स W जिसमें किनारे का भार है। भले ही बी की परिभाषा में किनारों को तकनीकी रूप से निर्देशित किया गया है, उनकी दिशाएं मनमानी हो सकती हैं, फिर भी समान सममित लाप्लासियन का परिणाम होता है ${\textstyle |v|\times |v|}$ मैट्रिक्स एल के रूप में परिभाषित किया गया है

L=BWB^{\textsf {T}}

कहाँ ${\textstyle B^{\textsf {T}}}$ बी का स्थानान्तरण है.

निर्माण को निम्नलिखित उदाहरण में दर्शाया गया है, जहां हर किनारा ${\textstyle e_{i}}$ भार मान i, के साथ निर्दिष्ट किया गया है ${\textstyle i=1,2,3,4.}$

Undirected graph	Incidence matrix	Edge weights	Laplacian matrix
	${\textstyle \left({\begin{array}{rrrr}1&1&1&0\\-1&0&0&0\\0&-1&0&1\\0&0&-1&-1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrr}1&0&0&0\\0&2&0&0\\0&0&3&0\\0&0&0&4\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrr}6&-1&-2&-3\\-1&1&0&0\\-2&0&6&-4\\-3&0&-4&7\\\end{array}}\right)}$

निर्देशित ग्राफ़ के लिए सममित लाप्लासियन

साधारण ग्राफ़ की तरह, निर्देशित भारित ग्राफ़ का लाप्लासियन मैट्रिक्स परिभाषा के अनुसार आम तौर पर गैर-सममित होता है। लाप्लासियन के निर्माण से पहले मूल निर्देशित ग्राफ को अप्रत्यक्ष ग्राफ में बदलकर समरूपता लागू की जा सकती है। अप्रत्यक्ष ग्राफ़ के आसन्न मैट्रिक्स को, उदाहरण के लिए, आसन्न मैट्रिक्स के योग के रूप में परिभाषित किया जा सकता है $A$ मूल निर्देशित ग्राफ़ और उसके मैट्रिक्स का स्थानान्तरण $A^{T}$ जैसा कि निम्नलिखित उदाहरण में है:

Adjacency matrix	Symmetrized adjacency matrix	Symmetric Laplacian matrix
${\textstyle \left({\begin{array}{rrr}0&1&1\\0&0&1\\1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}0&1&2\\1&0&1\\2&1&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}3&-1&-2\\-1&2&-1\\-2&-1&3\\\end{array}}\right)}$

जहाँ शून्य और की प्रविष्टियाँ हैं $A$ सरल ग्राफ़, मानों को तार्किक के बजाय संख्यात्मक माना जाता है, जो परिणामों में अंतर को समझाते हैं - सरल ग्राफ़ के लिए, सममित ग्राफ़ को अभी भी सरल होने की आवश्यकता है, इसके सममित आसन्न मैट्रिक्स में केवल तार्किक होते हैं, संख्यात्मक मान नहीं, उदाहरण के लिए, तार्किक योग 1 v 1 = 1 है, जबकि संख्यात्मक योग 1 + 1 = 2 है।

वैकल्पिक रूप से, सममित लाप्लासियन मैट्रिक्स की गणना डिग्री (ग्राफ सिद्धांत) का उपयोग करके दो लाप्लासियन से की जा सकती है, जैसा कि निम्नलिखित उदाहरण में है:

Adjacency matrix	Out-Degree matrix	Out-Degree Laplacian	In-Degree matrix	In-Degree Laplacian
${\textstyle \left({\begin{array}{rrr}0&1&1\\0&0&1\\1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}2&0&0\\0&1&0\\0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}2&-1&-1\\0&1&-1\\-1&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&0&0\\0&1&0\\0&0&2\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-1&-1\\0&1&-1\\-1&0&2\\\end{array}}\right)}$

आउट-डिग्री लाप्लासियन ट्रांसपोज़्ड और इन-डिग्री लाप्लासियन का योग सममित लाप्लासियन मैट्रिक्स के बराबर होता है।

लाप्लासियन मैट्रिक्स सामान्यीकरण

सामान्यीकरण का लक्ष्य, सरल ग्राफ़ की तरह, लाप्लासियन मैट्रिक्स की विकर्ण प्रविष्टियों को सभी इकाई बनाना है, साथ ही ऑफ-विकर्ण प्रविष्टियों को तदनुसार स्केल करना है। ग्लोसरी_ऑफ_ग्राफ_थ्योरी#वेटेड_ग्राफ में, शीर्ष में जुड़े हुए किनारों की छोटी संख्या के कारण बड़ी डिग्री हो सकती है, लेकिन बड़े वजन के साथ-साथ यूनिट वजन के साथ बड़ी संख्या में जुड़े किनारों के कारण भी।

ग्राफ़ सेल्फ-लूप, यानी, आसन्न मैट्रिक्स के मुख्य विकर्ण पर गैर-शून्य प्रविष्टियाँ, ग्राफ़ लाप्लासियन मानों को प्रभावित नहीं करती हैं, लेकिन सामान्यीकरण कारकों की गणना के लिए गणना करने की आवश्यकता हो सकती है।

सममित रूप से सामान्यीकृत लाप्लासियन

सममित रूप से सामान्यीकृत लाप्लासियन को इस प्रकार परिभाषित किया गया है

L^{\text{sym}}:=(D^{+})^{1/2}L(D^{+})^{1/2}=I-(D^{+})^{1/2}A(D^{+})^{1/2},

जहां एल असामान्य लाप्लासियन है, ए आसन्न मैट्रिक्स है, डी डिग्री मैट्रिक्स है, और $D^{+}$ मूर-पेनरोज़ व्युत्क्रम है। चूँकि डिग्री मैट्रिक्स D विकर्ण है, इसका व्युत्क्रम वर्गमूल है ${\textstyle (D^{+})^{1/2}}$ केवल विकर्ण मैट्रिक्स है जिसकी विकर्ण प्रविष्टियाँ D की विकर्ण प्रविष्टियों के वर्गमूलों के व्युत्क्रम हैं। यदि सभी किनारे के भार गैर-नकारात्मक हैं तो सभी डिग्री मान स्वचालित रूप से भी गैर-नकारात्मक हैं और इसलिए प्रत्येक डिग्री मान का अद्वितीय सकारात्मक वर्गमूल होता है। शून्य से विभाजन से बचने के लिए, शून्य डिग्री वाले शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है, जैसा कि निम्नलिखित उदाहरण में है:

Adjacency matrix	In-Degree matrix	In-Degree normalized Laplacian	Out-Degree matrix	Out-Degree normalized Laplacian
${\textstyle \left({\begin{array}{rrr}0&1&0\\4&0&0\\0&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&0&0\\0&4&0\\0&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-1/2&0\\-2&1&0\\0&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}4&0&0\\0&1&0\\0&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-1/2&0\\-2&1&0\\0&0&0\\\end{array}}\right)}$

सममित रूप से सामान्यीकृत लाप्लासियन सममित मैट्रिक्स है यदि और केवल यदि आसन्न मैट्रिक्स ए सममित है और डी की विकर्ण प्रविष्टियाँ गैर-नकारात्मक हैं, तो उस स्थिति में हम 'सममित सामान्यीकृत लाप्लासियन' शब्द का उपयोग कर सकते हैं।

सममित सामान्यीकृत लाप्लासियन मैट्रिक्स को इस प्रकार भी लिखा जा सकता है

L^{\text{sym}}:=(D^{+})^{1/2}L(D^{+})^{1/2}=(D^{+})^{1/2}BWB^{\textsf {T}}(D^{+})^{1/2}=SS^{T}

भारहीन का उपयोग करना ${\textstyle |v|\times |e|}$ आपतन मैट्रिक्स बी और विकर्ण ${\textstyle |e|\times |e|}$ मैट्रिक्स डब्ल्यू जिसमें किनारे का वजन शामिल है और नए को परिभाषित करता है ${\textstyle |v|\times |e|}$ भारित घटना मैट्रिक्स ${\textstyle S=(D^{+})^{1/2}BW^{{1}/{2}}}$ जिनकी पंक्तियाँ शीर्षों द्वारा अनुक्रमित होती हैं और जिनके स्तंभ G के किनारों द्वारा अनुक्रमित होते हैं, जैसे कि किनारे e = {u, v} के अनुरूप प्रत्येक स्तंभ में प्रविष्टि होती है ${\textstyle {\frac {1}{\sqrt {d_{u}}}}}$ यू के अनुरूप पंक्ति में, प्रविष्टि ${\textstyle -{\frac {1}{\sqrt {d_{v}}}}}$ v के अनुरूप पंक्ति में, और अन्यत्र 0 प्रविष्टियाँ हैं।

रैंडम वॉक सामान्यीकृत लाप्लासियन

रैंडम वॉक सामान्यीकृत लाप्लासियन को इस प्रकार परिभाषित किया गया है

L^{\text{rw}}:=D^{+}L=I-D^{+}A

जहाँ D डिग्री मैट्रिक्स है। चूँकि डिग्री मैट्रिक्स D विकर्ण है, यह व्युत्क्रम है ${\textstyle D^{+}}$ इसे बस विकर्ण मैट्रिक्स के रूप में परिभाषित किया गया है, जिसमें विकर्ण प्रविष्टियाँ हैं जो डी की संगत विकर्ण प्रविष्टियों के व्युत्क्रम हैं। पृथक शीर्षों (डिग्री 0 वाले) के लिए, सामान्य विकल्प संबंधित तत्व को सेट करना है ${\textstyle L_{i,i}^{\text{rw}}}$ से 0. के मैट्रिक्स तत्व ${\textstyle L^{\text{rw}}}$ द्वारा दिए गए हैं

L_{i,j}^{\text{rw}}:={\begin{cases}1&{\mbox{if}}\ i=j\ {\mbox{and}}\ \deg(v_{i})\neq 0\\-{\frac {1}{\deg(v_{i})}}&{\mbox{if}}\ i\neq j\ {\mbox{and}}\ v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}.\end{cases}}

रैंडम-वॉक सामान्यीकृत लाप्लासियन का नाम इस तथ्य से आता है कि यह मैट्रिक्स है ${\textstyle L^{\text{rw}}=I-P}$ , कहाँ ${\textstyle P=D^{+}A}$ गैर-नकारात्मक भार मानते हुए, ग्राफ़ पर यादृच्छिक वॉकर का संक्रमण मैट्रिक्स है। उदाहरण के लिए, चलो ${\textstyle e_{i}}$ i-वें मानक आधार वेक्टर को निरूपित करें। तब ${\textstyle x=e_{i}P}$ संभाव्यता वेक्टर है जो शीर्ष से कदम उठाने के बाद यादृच्छिक वॉकर के स्थानों के वितरण का प्रतिनिधित्व करता है ${\textstyle i}$ ; अर्थात।, ${\textstyle x_{j}=\mathbb {P} \left(v_{i}\to v_{j}\right)}$ . अधिक सामान्यतः, यदि वेक्टर ${\textstyle x}$ तब, ग्राफ़ के शीर्षों पर यादृच्छिक वॉकर के स्थान का संभाव्यता वितरण होता है ${\textstyle x'=xP^{t}}$ बाद में वॉकर का संभाव्यता वितरण है ${\textstyle t}$ कदम।

रैंडम वॉक सामान्यीकृत लाप्लासियन को बायां सामान्यीकृत लाप्लासियन भी कहा जा सकता है $L^{\text{rw}}:=D^{+}L$ चूंकि सामान्यीकरण सामान्यीकरण मैट्रिक्स द्वारा लाप्लासियन को गुणा करके किया जाता है $D^{+}$ बाईं तरफ। तब से इसकी प्रत्येक पंक्ति का योग शून्य है $P=D^{+}A$ स्टोचैस्टिक मैट्रिक्स है, यह मानते हुए कि सभी भार गैर-नकारात्मक हैं।

कम असामान्य रूप से उपयोग किए जाने वाले दाएँ सामान्यीकृत लाप्लासियन में $LD^{+}=I-AD^{+}$ चूँकि प्रत्येक कॉलम का योग शून्य है $AD^{+}$ स्टोकेस्टिक मैट्रिक्स है.

निर्देशित ग्राफ़ के गैर-सममित आसन्न मैट्रिक्स के लिए, किसी को सामान्यीकरण के लिए डिग्री (ग्राफ़ सिद्धांत) चुनने की भी आवश्यकता होती है:

Adjacency matrix	Out-Degree matrix	Out-Degree left normalized Laplacian	In-Degree matrix	In-Degree right normalized Laplacian
${\textstyle \left({\begin{array}{rrr}0&1&0\\0&0&2\\1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&0&0\\0&2&0\\0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-1&0\\0&1&-1\\-1&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&0&0\\0&1&0\\0&0&2\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrr}1&-1&0\\0&1&-1\\-1&0&1\\\end{array}}\right)}$

पंक्ति-योग के साथ लेफ्ट आउट-डिग्री सामान्यीकृत लाप्लासियन सभी 0 स्टोकेस्टिक मैट्रिक्स से संबंधित है $D_{\text{out}}^{+}A$ , जबकि सभी 0 के कॉलम-योग के साथ डिग्री में सामान्यीकृत लाप्लासियन में स्टोकेस्टिक मैट्रिक्स शामिल है $AD_{\text{in}}^{+}$ .

नकारात्मक भार

नकारात्मक भार सामान्यीकरण के लिए कई चुनौतियाँ प्रस्तुत करते हैं:

नकारात्मक भार की उपस्थिति के परिणामस्वरूप गैर-पृथक शीर्षों के लिए स्वाभाविक रूप से शून्य पंक्ति- और/या स्तंभ-योग हो सकता है। सकारात्मक भारों की बड़ी पंक्ति-योग और समान रूप से नकारात्मक भारों की समान रूप से बड़ी पंक्ति-योग वाला शीर्ष, जिसका योग शून्य है, को भारी नोड माना जा सकता है और दोनों बड़े मानों को स्केल किया जा सकता है, जबकि विकर्ण प्रविष्टि शून्य रहती है, जैसे कि पृथक शीर्ष.
नकारात्मक भार नकारात्मक पंक्ति- और/या स्तंभ-योग भी दे सकते हैं, जिससे कि गैर-सामान्यीकृत लाप्लासियन मैट्रिक्स में संबंधित विकर्ण प्रविष्टि नकारात्मक होगी और सममित सामान्यीकरण के लिए आवश्यक सकारात्मक वर्गमूल मौजूद नहीं होगा।
सामान्यीकरण के प्रयोजन के लिए पंक्ति- और/या स्तंभ-योग का पूर्ण मान लेने के लिए तर्क दिए जा सकते हैं, इस प्रकार संभावित मान -1 को सामान्यीकृत लाप्लासियन मैट्रिक्स के मुख्य विकर्ण की वैध इकाई प्रविष्टि के रूप में माना जा सकता है।

गुण

एक (अप्रत्यक्ष) ग्राफ़ G और उसके लाप्लासियन मैट्रिक्स L के लिए eigenvalues के साथ ${\textstyle \lambda _{0}\leq \lambda _{1}\leq \cdots \leq \lambda _{n-1}}$ :

L सममित मैट्रिक्स है.
एल सकारात्मक-निश्चित मैट्रिक्स है | सकारात्मक-अर्ध-निश्चित (अर्थात ${\textstyle \lambda _{i}\geq 0}$ सभी के लिए ${\textstyle i}$ ). इसे इस तथ्य से देखा जा सकता है कि लाप्लासियन सममित और विकर्ण रूप से प्रभावशाली मैट्रिक्स#अनुप्रयोग और गुण है।
एल एम-मैट्रिक्स है (इसकी ऑफ-विकर्ण प्रविष्टियाँ गैर-सकारात्मक हैं, फिर भी इसके स्वदेशी मानों के वास्तविक भाग गैर-नकारात्मक हैं)।
L की प्रत्येक पंक्ति और स्तंभ का योग शून्य है। वास्तव में, योग में, शीर्ष की डिग्री को प्रत्येक पड़ोसी के लिए -1 के साथ जोड़ा जाता है।
परिणामस्वरूप, ${\textstyle \lambda _{0}=0}$ , क्योंकि वेक्टर ${\textstyle \mathbf {v} _{0}=(1,1,\dots ,1)}$ संतुष्ट ${\textstyle L\mathbf {v} _{0}=\mathbf {0} .}$ इसका तात्पर्य यह भी है कि लाप्लासियन मैट्रिक्स एकवचन है।
ग्राफ़ में कनेक्टेड कंपोनेंट (ग्राफ सिद्धांत) की संख्या लाप्लासियन के कर्नेल (रैखिक बीजगणित) का आयाम है और 0 आइगेनवैल्यू की आइगेनवैल्यू और आइजेनवेक्टर#बीजगणितीय बहुलता है।
L के सबसे छोटे गैर-शून्य eigenvalue को वर्णक्रमीय अंतराल कहा जाता है।
L का दूसरा सबसे छोटा eigenvalue (शून्य हो सकता है) G की बीजगणितीय कनेक्टिविटी (या फ़िडलर मान) है और ग्राफ़ के कट (ग्राफ_थ्योरी) #Sparsest कट का अनुमान लगाता है।
लाप्लासियन फ़ंक्शंस के एन-डायमेंशनल वेक्टर स्पेस पर ऑपरेटर है ${\textstyle f:V\to \mathbb {R} }$ , कहाँ ${\textstyle V}$ G का शीर्ष समुच्चय है, और ${\textstyle n=|V|}$ .
जब G, के-नियमित ग्राफ|k-रेगुलर है, तो सामान्यीकृत लाप्लासियन है: ${\textstyle {\mathcal {L}}={\tfrac {1}{k}}L=I-{\tfrac {1}{k}}A}$ , जहां A आसन्नता मैट्रिक्स है और I पहचान मैट्रिक्स है।
एकाधिक कनेक्टेड घटक (ग्राफ़ सिद्धांत) वाले ग्राफ़ के लिए, एल ब्लॉक मैट्रिक्स#ब्लॉक विकर्ण मैट्रिक्स मैट्रिक्स है, जहां प्रत्येक ब्लॉक प्रत्येक घटक के लिए संबंधित लाप्लासियन मैट्रिक्स है, संभवतः शीर्षों को पुन: व्यवस्थित करने के बाद (यानी एल क्रमपरिवर्तन-समान है) ब्लॉक विकर्ण मैट्रिक्स)।
लाप्लासियन मैट्रिक्स एल का ट्रेस बराबर है ${\textstyle 2m}$ कहाँ ${\textstyle m}$ विचारित ग्राफ़ के किनारों की संख्या है।
अब eigendecomposition पर विचार करें ${\textstyle L}$ , यूनिट-मानक eigenvectors के साथ ${\textstyle \mathbf {v} _{i}}$ और संगत eigenvalues ${\textstyle \lambda _{i}}$ :

{\begin{aligned}\lambda _{i}&=\mathbf {v} _{i}^{\textsf {T}}L\mathbf {v} _{i}\\&=\mathbf {v} _{i}^{\textsf {T}}M^{\textsf {T}}M\mathbf {v} _{i}\\&=\left(M\mathbf {v} _{i}\right)^{\textsf {T}}\left(M\mathbf {v} _{i}\right).\\\end{aligned}}

क्योंकि ${\textstyle \lambda _{i}}$ वेक्टर के आंतरिक उत्पाद के रूप में लिखा जा सकता है ${\textstyle M\mathbf {v} _{i}}$ अपने आप से, यह पता चलता है ${\textstyle \lambda _{i}\geq 0}$ और इसलिए के eigenvalues ${\textstyle L}$ सभी गैर-नकारात्मक हैं.

सामान्यीकृत सममित लाप्लासियन के सभी eigenvalues 0 = μ को संतुष्ट करते हैं₀ ≤ … ≤ एम_n−1 ≤ 2. ये eigenvalues (सामान्यीकृत लाप्लासियन के स्पेक्ट्रम के रूप में जाना जाता है) सामान्य ग्राफ़ के लिए अन्य ग्राफ़ अपरिवर्तनीयों से अच्छी तरह से संबंधित हैं।^[1]

कोई इसकी जाँच कर सकता है:

L^{\text{rw}}=I-D^{-{\frac {1}{2}}}\left(I-L^{\text{sym}}\right)D^{\frac {1}{2}}

,

अर्थात।, ${\textstyle L^{\text{rw}}}$ सामान्यीकृत लाप्लासियन के लिए मैट्रिक्स_समानता है ${\textstyle L^{\text{sym}}}$ . इस कारण भले ही ${\textstyle L^{\text{rw}}}$ यह सामान्यतः सममित नहीं है, इसके वास्तविक स्वदेशी मान हैं - बिल्कुल सामान्यीकृत सममित लाप्लासियन के स्वदेशी मूल्यों के समान ${\textstyle L^{\text{sym}}}$ .

निरंतर लाप्लासियन का अनुमान लगाने वाले असतत लाप्लास ऑपरेटर के रूप में व्याख्या

ग्राफ़ लाप्लासियन मैट्रिक्स को परिमित अंतर विधि द्वारा प्राप्त नकारात्मक निरंतर लाप्लासियन ऑपरेटर का अनुमान लगाने वाले ग्राफ़ पर नकारात्मक असतत लाप्लास ऑपरेटर के मैट्रिक्स रूप के रूप में देखा जा सकता है। (असतत पॉइसन समीकरण देखें)^[2] इस व्याख्या में, प्रत्येक ग्राफ शीर्ष को ग्रिड बिंदु के रूप में माना जाता है; शीर्ष की स्थानीय कनेक्टिविटी इस ग्रिड बिंदु पर परिमित अंतर सन्निकटन स्टेंसिल (संख्यात्मक विश्लेषण) निर्धारित करती है, ग्रिड का आकार हमेशा प्रत्येक किनारे के लिए होता है, और किसी भी ग्रिड बिंदु पर कोई बाधा नहीं होती है, जो सजातीय न्यूमैन के मामले से मेल खाती है सीमा की स्थिति, यानी, मुक्त सीमा। इस तरह की व्याख्या किसी को अनुमति देती है, उदाहरण के लिए, अनंत संख्या में शीर्षों और किनारों वाले ग्राफ़ के मामले में लाप्लासियन मैट्रिक्स को सामान्यीकृत करना, जिससे अनंत आकार का लाप्लासियन मैट्रिक्स बनता है।

लाप्लासियन मैट्रिक्स का सामान्यीकरण और विस्तार

सामान्यीकृत लाप्लासियन

सामान्यीकृत लाप्लासियन $Q$ परिभाषित किया जाता है:^[3]

{\begin{cases}Q_{i,j}<0&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is adjacent to }}v_{j}\\Q_{i,j}=0&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is not adjacent to }}v_{j}\\{\mbox{any number}}&{\mbox{otherwise}}.\end{cases}}

ध्यान दें कि साधारण लाप्लासियन सामान्यीकृत लाप्लासियन है।

चुंबकीय लाप्लासियन

आसन्न मैट्रिक्स की प्रविष्टियाँ जटिल-मूल्यवान हो सकती हैं, जिस स्थिति में मैट्रिक्स समरूपता की धारणा को हर्मिटियन मैट्रिक्स के साथ प्रतिस्थापित करने की आवश्यकता होती है। वास्तविक भार के साथ निर्देशित ग्राफ़ के लिए चुंबकीय लाप्लासियन $w_{ij}$ जटिल संख्या प्रविष्टियों के साथ सममित लाप्लासियन और हर्मिटियन चरण मैट्रिक्स के Symmetric_matrix#Real_symmetric_matrices के हैडामर्ड उत्पाद (मैट्रिसेस) के रूप में निर्मित किया गया है।

\gamma _{q}(i,j)=e^{i2\pi q(w_{ij}-w_{ji})}

जो जटिल तल में किनारे की दिशा को चरण में कूटबद्ध करता है। क्वांटम भौतिकी के संदर्भ में, चुंबकीय लाप्लासियन की व्याख्या उस ऑपरेटर के रूप में की जा सकती है जो ग्राफ पर मुक्त आवेशित कण की घटना विज्ञान का वर्णन करता है, जो चुंबकीय क्षेत्र और पैरामीटर की कार्रवाई के अधीन है $q$ विद्युत आवेश कहलाता है।^[4] निम्नलिखित उदाहरण में $q=1/4$ :

Adjacency matrix	Symmetrized Laplacian	Phase matrix	Magnetic Laplacian
${\textstyle \left({\begin{array}{rrrr}0&1&0&0\\1&0&1&0\\0&0&0&0\\0&0&1&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrr}2&-2&0&0\\-2&3&-1&0\\0&-1&2&-1\\0&0&-1&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrr}1&1&1&1\\1&1&i&1\\1&-i&1&-i\\1&1&i&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrr}2&-2&0&0\\-2&3&-i&0\\0&i&2&i\\0&0&-i&1\\\end{array}}\right)}$

विकृत लाप्लासियन

विकृत लाप्लासियन को आमतौर पर इस प्रकार परिभाषित किया जाता है

\Delta (s)=I-sA+s^{2}(D-I)

जहां I पहचान मैट्रिक्स है, A आसन्न मैट्रिक्स है, D डिग्री मैट्रिक्स है, और s (जटिल-मूल्यवान) संख्या है। ^[5]
मानक लाप्लासियन बस है ${\textstyle \Delta (1)}$ और ${\textstyle \Delta (-1)=D+A}$ चिन्हहीन लाप्लासियन है।

साइनलेस लाप्लासियन

साइनलेस लाप्लासियन को इस प्रकार परिभाषित किया गया है

Q=D+A

कहाँ $D$ डिग्री मैट्रिक्स है, और $A$ आसन्नता मैट्रिक्स है.^[6] हस्ताक्षरित लाप्लासियन की तरह $L$ , साइनलेस लाप्लासियन $Q$ यह सकारात्मक अर्ध-निश्चित भी है क्योंकि इसे इस रूप में गुणनखंडित किया जा सकता है

Q=RR^{\textsf {T}}

कहाँ ${\textstyle R}$ घटना मैट्रिक्स है. $Q$ इसमें 0-ईजेनवेक्टर है यदि और केवल तभी जब इसमें पृथक शीर्षों के अलावा कोई द्विदलीय जुड़ा घटक हो। इसे इस प्रकार दर्शाया जा सकता है

\mathbf {x} ^{\textsf {T}}Q\mathbf {x} =\mathbf {x} ^{\textsf {T}}RR^{\textsf {T}}\mathbf {x} \implies R^{\textsf {T}}\mathbf {x} =\mathbf {0} .

इसका समाधान कहां है $\mathbf {x} \neq \mathbf {0}$ यदि और केवल यदि ग्राफ़ में द्विदलीय जुड़ा हुआ घटक है।

निर्देशित मल्टीग्राफ

निर्देशित मल्टीग्राफ के लिए लाप्लासियन मैट्रिक्स का एनालॉग परिभाषित किया जा सकता है।^[7] इस मामले में लाप्लासियन मैट्रिक्स एल को इस प्रकार परिभाषित किया गया है

L=D-A

जहां D, D के साथ विकर्ण मैट्रिक्स है_i,i शीर्ष i और A की आउटडिग्री के बराबर, A के साथ मैट्रिक्स है_i,j i से j तक किनारों की संख्या के बराबर (लूप सहित)।

ओपन सोर्स सॉफ़्टवेयर कार्यान्वयन

एप्लीकेशन सॉफ्टवेयर

स्किकिट-लर्न स्पेक्ट्रल क्लस्टरिंग^[10]
PyGSP: पायथन में ग्राफ़ सिग्नल प्रोसेसिंग^[11]
मेगामैन: लाखों अंकों के लिए मैनिफोल्ड लर्निंग^[12]
चिकनीजी^[13]
डायनामिक ग्राफ़ के लिए लाप्लासियन चेंज पॉइंट डिटेक्शन (KDD 2020)^[14]
लाप्लासियनऑप्ट (लाप्लासियन के भारित ग्राफ़ के दूसरे आइगेनवैल्यू को अधिकतम करने के लिए जूलिया पैकेज) ^[15]
LigMG (बड़ा अनियमित ग्राफ़ मल्टीग्रिड)^[16]
लाप्लासियंस.जे.एल^[17]

यह भी देखें

संदर्भ

↑ ^1.0 ^1.1 ^1.2 Chung, Fan (1997) [1992]. Spectral Graph Theory. American Mathematical Society. ISBN 978-0821803158.
↑ Smola, Alexander J.; Kondor, Risi (2003), "Kernels and regularization on graphs", Learning Theory and Kernel Machines: 16th Annual Conference on Learning Theory and 7th Kernel Workshop, COLT/Kernel 2003, Washington, DC, USA, August 24–27, 2003, Proceedings, Lecture Notes in Computer Science, vol. 2777, Springer, pp. 144–158, CiteSeerX 10.1.1.3.7020, doi:10.1007/978-3-540-45167-9_12, ISBN 978-3-540-40720-1.
↑ Godsil, C.; Royle, G. (2001). बीजगणितीय ग्राफ सिद्धांत, गणित में स्नातक ग्रंथ. Springer-Verlag.
↑ Satoshi Furutani; Toshiki Shibahara; Mitsuaki Akiyama; Kunio Hato; Masaki Aida (2020). हर्मिटियन लाप्लासियन पर आधारित निर्देशित ग्राफ़ के लिए ग्राफ़ सिग्नल प्रोसेसिंग (PDF). ECML PKDD 2019: Machine Learning and Knowledge Discovery in Databases. pp. 447–463. doi:10.1007/978-3-030-46150-8_27.
↑ Morbidi, F. (2013). "विकृत आम सहमति प्रोटोकॉल" (PDF). Automatica. 49 (10): 3049–3055. doi:10.1016/j.automatica.2013.07.006. S2CID 205767404.
↑ Cvetković, Dragoš; Simić, Slobodan K. (2010). "साइनलेस लाप्लासियन पर आधारित ग्राफ़ के एक वर्णक्रमीय सिद्धांत की ओर, III". Applicable Analysis and Discrete Mathematics. 4 (1): 156–166. doi:10.2298/AADM1000001C. ISSN 1452-8630. JSTOR 43671298.
↑ Chaiken, S.; Kleitman, D. (1978). "Matrix Tree Theorems". Journal of Combinatorial Theory, Series A. 24 (3): 377–381. doi:10.1016/0097-3165(78)90067-5. ISSN 0097-3165.
↑ "SciPy". GitHub. 24 March 2022.
↑ "नेटवर्कएक्स". GitHub. 24 March 2022.
↑ "2.3. Clustering".
↑ "PyGSP: Graph Signal Processing in Python". GitHub. 23 March 2022.
↑ "Megaman: Manifold Learning for Millions of Points". GitHub. 14 March 2022.
↑ "स्मूथजी". GitHub. 17 September 2020.
↑ "Announcing Our Paper at KDD 2020".
↑ "Harshangrjn/LaplacianOpt.jl". GitHub. 2 February 2022.
↑ "LigMG (बड़ा अनियमित ग्राफ़ मल्टीग्रिड) - बड़े अनियमित ग्राफ़ के लिए एक वितरित मेमोरी ग्राफ़ लाप्लासियन सॉल्वर". GitHub. 5 January 2022.
↑ "लाप्लासियंस.जे.एल". GitHub. 11 March 2022.

[Fan_Chung-1] 1.0 ^1.1 ^1.2 Chung, Fan (1997) [1992]. Spectral Graph Theory. American Mathematical Society. ISBN 978-0821803158.

[2] Smola, Alexander J.; Kondor, Risi (2003), "Kernels and regularization on graphs", Learning Theory and Kernel Machines: 16th Annual Conference on Learning Theory and 7th Kernel Workshop, COLT/Kernel 2003, Washington, DC, USA, August 24–27, 2003, Proceedings, Lecture Notes in Computer Science, vol. 2777, Springer, pp. 144–158, CiteSeerX 10.1.1.3.7020, doi:10.1007/978-3-540-45167-9_12, ISBN 978-3-540-40720-1.

[3] Godsil, C.; Royle, G. (2001). बीजगणितीय ग्राफ सिद्धांत, गणित में स्नातक ग्रंथ. Springer-Verlag.

[4] Satoshi Furutani; Toshiki Shibahara; Mitsuaki Akiyama; Kunio Hato; Masaki Aida (2020). हर्मिटियन लाप्लासियन पर आधारित निर्देशित ग्राफ़ के लिए ग्राफ़ सिग्नल प्रोसेसिंग (PDF). ECML PKDD 2019: Machine Learning and Knowledge Discovery in Databases. pp. 447–463. doi:10.1007/978-3-030-46150-8_27.

[5] Morbidi, F. (2013). "विकृत आम सहमति प्रोटोकॉल" (PDF). Automatica. 49 (10): 3049–3055. doi:10.1016/j.automatica.2013.07.006. S2CID 205767404.

[6] Cvetković, Dragoš; Simić, Slobodan K. (2010). "साइनलेस लाप्लासियन पर आधारित ग्राफ़ के एक वर्णक्रमीय सिद्धांत की ओर, III". Applicable Analysis and Discrete Mathematics. 4 (1): 156–166. doi:10.2298/AADM1000001C. ISSN 1452-8630. JSTOR 43671298.

[Chaiken1978-7] Chaiken, S.; Kleitman, D. (1978). "Matrix Tree Theorems". Journal of Combinatorial Theory, Series A. 24 (3): 377–381. doi:10.1016/0097-3165(78)90067-5. ISSN 0097-3165.

[8] "SciPy". GitHub. 24 March 2022.

[9] "नेटवर्कएक्स". GitHub. 24 March 2022.

[10] "2.3. Clustering".

[11] "PyGSP: Graph Signal Processing in Python". GitHub. 23 March 2022.

[12] "Megaman: Manifold Learning for Millions of Points". GitHub. 14 March 2022.

[13] "स्मूथजी". GitHub. 17 September 2020.

[14] "Announcing Our Paper at KDD 2020".

[15] "Harshangrjn/LaplacianOpt.jl". GitHub. 2 February 2022.

[16] "LigMG (बड़ा अनियमित ग्राफ़ मल्टीग्रिड) - बड़े अनियमित ग्राफ़ के लिए एक वितरित मेमोरी ग्राफ़ लाप्लासियन सॉल्वर". GitHub. 5 January 2022.

[17] "लाप्लासियंस.जे.एल". GitHub. 11 March 2022.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

@@ Line 1: / Line 1: @@
-{{Use American English|date = March 2019}}
 {{Short description|Matrix representation of a graph}}
-[[ग्राफ सिद्धांत]] के गणित क्षेत्र में, [[लाप्लासियन]] मैट्रिक्स, जिसे डिस्क्रीट_लाप्लेस_ऑपरेटर#ग्राफ_लाप्लासियन, [[प्रवेश मैट्रिक्स]], किरचॉफ मैट्रिक्स या डिस्क्रीट लाप्लास ऑपरेटर भी कहा जाता है, एक ग्राफ (असतत गणित) का एक [[मैट्रिक्स (गणित)]] प्रतिनिधित्व है। [[पियरे-साइमन लाप्लास]] के नाम पर, ग्राफ लाप्लासियन मैट्रिक्स को [[परिमित अंतर विधि]] द्वारा प्राप्त नकारात्मक निरंतर लाप्लासियन का अनुमान लगाने वाले ग्राफ पर नकारात्मक [[असतत लाप्लास ऑपरेटर]] के मैट्रिक्स रूप के रूप में देखा जा सकता है।
+[[ग्राफ सिद्धांत]] के गणित क्षेत्र में, [[लाप्लासियन]] मैट्रिक्स, जिसे डिस्क्रीट_लाप्लेस_ऑपरेटर#ग्राफ_लाप्लासियन, [[प्रवेश मैट्रिक्स]], किरचॉफ मैट्रिक्स या डिस्क्रीट लाप्लास ऑपरेटर भी कहा जाता है, ग्राफ (असतत गणित) का [[मैट्रिक्स (गणित)]] प्रतिनिधित्व है। [[पियरे-साइमन लाप्लास]] के नाम पर, ग्राफ लाप्लासियन मैट्रिक्स को [[परिमित अंतर विधि]] द्वारा प्राप्त नकारात्मक निरंतर लाप्लासियन का अनुमान लगाने वाले ग्राफ पर नकारात्मक [[असतत लाप्लास ऑपरेटर]] के मैट्रिक्स रूप के रूप में देखा जा सकता है।
-लाप्लासियन मैट्रिक्स एक ग्राफ़ के कई उपयोगी गुणों से संबंधित है। किरचॉफ के प्रमेय के साथ, इसका उपयोग किसी दिए गए ग्राफ़ के लिए फैले हुए पेड़ों (गणित) की संख्या की गणना करने के लिए किया जा सकता है। ग्राफ़ के कट (ग्राफ़ सिद्धांत)#सबसे कम कट का अनुमान [[फिडलर वेक्टर]] के माध्यम से लगाया जा सकता है - ग्राफ़ लाप्लासियन के दूसरे सबसे छोटे आइगेनवैल्यू के अनुरूप ईजेनवेक्टर - जैसा कि चीगर स्थिरांक (ग्राफ़ सिद्धांत)#चीगर असमानताओं|चीगर की असमानता द्वारा स्थापित किया गया है। लाप्लासियन मैट्रिक्स के एक मैट्रिक्स का आइगेंडेकंपोजिशन नॉनलाइनर डायमेंशनलिटी रिडक्शन#लाप्लासियन आइजेनमैप्स का निर्माण करने की अनुमति देता है जो कई [[ यंत्र अधिगम ]] अनुप्रयोगों में दिखाई देते हैं और [[ग्राफ ड्राइंग]] में एक [[वर्णक्रमीय लेआउट]] निर्धारित करते हैं। ग्राफ-आधारित [[ संकेत आगे बढ़ाना ]] [[असतत फूरियर रूपांतरण]] पर आधारित है जो सिग्नल के अनुरूप ग्राफ के लाप्लासियन मैट्रिक्स के ईजेनवेक्टरों के लिए [[जटिल संख्या]] साइन तरंगों के मानक आधार को प्रतिस्थापित करके पारंपरिक असतत फूरियर ट्रांसफॉर्म का विस्तार करता है।
+लाप्लासियन मैट्रिक्स ग्राफ़ के कई उपयोगी गुणों से संबंधित है। किरचॉफ के प्रमेय के साथ, इसका उपयोग किसी दिए गए ग्राफ़ के लिए फैले हुए पेड़ों (गणित) की संख्या की गणना करने के लिए किया जा सकता है। ग्राफ़ के कट (ग्राफ़ सिद्धांत)#सबसे कम कट का अनुमान [[फिडलर वेक्टर]] के माध्यम से लगाया जा सकता है - ग्राफ़ लाप्लासियन के दूसरे सबसे छोटे आइगेनवैल्यू के अनुरूप ईजेनवेक्टर - जैसा कि चीगर स्थिरांक (ग्राफ़ सिद्धांत)#चीगर असमानताओं|चीगर की असमानता द्वारा स्थापित किया गया है। लाप्लासियन मैट्रिक्स के मैट्रिक्स का आइगेंडेकंपोजिशन नॉनलाइनर डायमेंशनलिटी रिडक्शन#लाप्लासियन आइजेनमैप्स का निर्माण करने की अनुमति देता है जो कई [[ यंत्र अधिगम ]] अनुप्रयोगों में दिखाई देते हैं और [[ग्राफ ड्राइंग]] में [[वर्णक्रमीय लेआउट]] निर्धारित करते हैं। ग्राफ-आधारित [[ संकेत आगे बढ़ाना ]] [[असतत फूरियर रूपांतरण]] पर आधारित है जो सिग्नल के अनुरूप ग्राफ के लाप्लासियन मैट्रिक्स के ईजेनवेक्टरों के लिए [[जटिल संख्या]] साइन तरंगों के मानक आधार को प्रतिस्थापित करके पारंपरिक असतत फूरियर ट्रांसफॉर्म का विस्तार करता है।
-लाप्लासियन मैट्रिक्स एक साधारण ग्राफ के लिए परिभाषित करना सबसे आसान है, लेकिन ग्लोसरी_ऑफ_ग्राफ_थ्योरी#वेटेड_ग्राफ|एज-वेटेड ग्राफ के लिए अनुप्रयोगों में अधिक आम है, यानी, इसके किनारों पर वजन के साथ - ग्राफ आसन्न मैट्रिक्स की प्रविष्टियां। [[वर्णक्रमीय ग्राफ सिद्धांत]] एक ग्राफ के गुणों को एक स्पेक्ट्रम से जोड़ता है, यानी, आइगेनवैल्यू, और ग्राफ से जुड़े मैट्रिक्स के आइगेनवेक्टर, जैसे कि इसकी आसन्न मैट्रिक्स या लाप्लासियन मैट्रिक्स। असंतुलित भार मैट्रिक्स स्पेक्ट्रम को अवांछित रूप से प्रभावित कर सकता है, जिससे सामान्यीकरण की आवश्यकता होती है - मैट्रिक्स प्रविष्टियों का एक कॉलम/पंक्ति स्केलिंग - जिसके परिणामस्वरूप सामान्यीकृत आसन्नता और लाप्लासियन मैट्रिक्स होते हैं।
+लाप्लासियन मैट्रिक्स साधारण ग्राफ के लिए परिभाषित करना सबसे आसान है, लेकिन ग्लोसरी_ऑफ_ग्राफ_थ्योरी#वेटेड_ग्राफ|एज-वेटेड ग्राफ के लिए अनुप्रयोगों में अधिक आम है, यानी, इसके किनारों पर वजन के साथ - ग्राफ आसन्न मैट्रिक्स की प्रविष्टियां। [[वर्णक्रमीय ग्राफ सिद्धांत]] ग्राफ के गुणों को स्पेक्ट्रम से जोड़ता है, यानी, आइगेनवैल्यू, और ग्राफ से जुड़े मैट्रिक्स के आइगेनवेक्टर, जैसे कि इसकी आसन्न मैट्रिक्स या लाप्लासियन मैट्रिक्स। असंतुलित भार मैट्रिक्स स्पेक्ट्रम को अवांछित रूप से प्रभावित कर सकता है, जिससे सामान्यीकरण की आवश्यकता होती है - मैट्रिक्स प्रविष्टियों का कॉलम/पंक्ति स्केलिंग - जिसके परिणामस्वरूप सामान्यीकृत आसन्नता और लाप्लासियन मैट्रिक्स होते हैं।
 ==सरल ग्राफ़ के लिए परिभाषाएँ==
@@ Line 29: / Line 29: @@
 या मैट्रिक्स द्वारा समकक्ष
 : <math>L = D - A, </math>
-जहां D [[डिग्री मैट्रिक्स]] है और A ग्राफ़ का आसन्न मैट्रिक्स है। तब से <math display="inline">G</math> एक सरल ग्राफ है, <math display="inline">A</math> इसमें केवल 1s या 0s हैं और इसके विकर्ण तत्व सभी 0s हैं।
+जहां D [[डिग्री मैट्रिक्स]] है और A ग्राफ़ का आसन्न मैट्रिक्स है। तब से <math display="inline">G</math> सरल ग्राफ है, <math display="inline">A</math> इसमें केवल 1s या 0s हैं और इसके विकर्ण तत्व सभी 0s हैं।
-यहां एक लेबल, अप्रत्यक्ष ग्राफ़ और उसके लाप्लासियन मैट्रिक्स का एक सरल उदाहरण दिया गया है।
+यहां लेबल, अप्रत्यक्ष ग्राफ़ और उसके लाप्लासियन मैट्रिक्स का सरल उदाहरण दिया गया है।
 {|class="wikitable"
@@ Line 137: / Line 137: @@
 ===निर्देशित ग्राफ़ के लिए सममित लाप्लासियन===
-एक निर्देशित ग्राफ का लाप्लासियन मैट्रिक्स परिभाषा के अनुसार आम तौर पर गैर-सममित होता है, जबकि, उदाहरण के लिए, पारंपरिक [[वर्णक्रमीय क्लस्टरिंग]] मुख्य रूप से सममित आसन्नता और लाप्लासियन मैट्रिक्स के साथ अप्रत्यक्ष ग्राफ के लिए विकसित की जाती है। समरूपता की आवश्यकता वाली तकनीकों को लागू करने के लिए एक तुच्छ दृष्टिकोण मूल निर्देशित ग्राफ को एक अप्रत्यक्ष ग्राफ में बदलना और बाद के लिए लाप्लासियन मैट्रिक्स का निर्माण करना है।
+एक निर्देशित ग्राफ का लाप्लासियन मैट्रिक्स परिभाषा के अनुसार आम तौर पर गैर-सममित होता है, जबकि, उदाहरण के लिए, पारंपरिक [[वर्णक्रमीय क्लस्टरिंग]] मुख्य रूप से सममित आसन्नता और लाप्लासियन मैट्रिक्स के साथ अप्रत्यक्ष ग्राफ के लिए विकसित की जाती है। समरूपता की आवश्यकता वाली तकनीकों को लागू करने के लिए तुच्छ दृष्टिकोण मूल निर्देशित ग्राफ को अप्रत्यक्ष ग्राफ में बदलना और बाद के लिए लाप्लासियन मैट्रिक्स का निर्माण करना है।
-मैट्रिक्स नोटेशन में, अप्रत्यक्ष ग्राफ़ के आसन्न मैट्रिक्स को, उदाहरण के लिए, आसन्न मैट्रिक्स के OR गेट के रूप में परिभाषित किया जा सकता है <math>A</math> मूल निर्देशित ग्राफ़ और उसके मैट्रिक्स का स्थानान्तरण <math>A^T</math>, जहां शून्य और एक की प्रविष्टियाँ हैं <math>A</math> मानों को संख्यात्मक के बजाय तार्किक माना जाता है, जैसा कि निम्नलिखित उदाहरण में है:
+मैट्रिक्स नोटेशन में, अप्रत्यक्ष ग्राफ़ के आसन्न मैट्रिक्स को, उदाहरण के लिए, आसन्न मैट्रिक्स के OR गेट के रूप में परिभाषित किया जा सकता है <math>A</math> मूल निर्देशित ग्राफ़ और उसके मैट्रिक्स का स्थानान्तरण <math>A^T</math>, जहां शून्य और की प्रविष्टियाँ हैं <math>A</math> मानों को संख्यात्मक के बजाय तार्किक माना जाता है, जैसा कि निम्नलिखित उदाहरण में है:
 {|class="wikitable"
 ! [[Adjacency matrix]]
@@ Line 161: / Line 161: @@
 \end{array}\right)</math>
 |}
 === लाप्लासियन मैट्रिक्स सामान्यीकरण ===
-बड़ी डिग्री वाला एक शीर्ष, जिसे भारी नोड भी कहा जाता है, के परिणामस्वरूप मैट्रिक्स गुणों पर हावी होने वाले लाप्लासियन मैट्रिक्स में एक बड़ी विकर्ण प्रविष्टि होती है। सामान्यीकरण का उद्देश्य लाप्लासियन मैट्रिक्स की प्रविष्टियों को शीर्ष डिग्री द्वारा विभाजित करके ऐसे शीर्षों के प्रभाव को अन्य शीर्षों के प्रभाव के बराबर बनाना है। शून्य से विभाजन से बचने के लिए, शून्य डिग्री वाले पृथक शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है।
+बड़ी डिग्री वाला शीर्ष, जिसे भारी नोड भी कहा जाता है, के परिणामस्वरूप मैट्रिक्स गुणों पर हावी होने वाले लाप्लासियन मैट्रिक्स में बड़ी विकर्ण प्रविष्टि होती है। सामान्यीकरण का उद्देश्य लाप्लासियन मैट्रिक्स की प्रविष्टियों को शीर्ष डिग्री द्वारा विभाजित करके ऐसे शीर्षों के प्रभाव को अन्य शीर्षों के प्रभाव के बराबर बनाना है। शून्य से विभाजन से बचने के लिए, शून्य डिग्री वाले पृथक शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है।
 ==== सममित रूप से सामान्यीकृत लाप्लासियन ====
@@ Line 236: / Line 235: @@
 \end{array}\right)</math>
 |}
 ==== बाएँ (यादृच्छिक-चलना) और दाएँ सामान्यीकृत लाप्लासियन ====
@@ Line 280: / Line 278: @@
 \end{array}\right)</math>
 |}
-उदाहरण यह भी दर्शाता है कि यदि <math>G</math> तो फिर, इसका कोई पृथक शीर्ष नहीं है <math>D^+A</math> [[स्टोकेस्टिक मैट्रिक्स]] और इसलिए एक यादृच्छिक चलने का मैट्रिक्स है, ताकि बाईं ओर लाप्लासियन सामान्यीकृत हो <math>L^\text{rw} := D^+L = I - D^+A</math> प्रत्येक पंक्ति का योग शून्य है। इस प्रकार हम कभी-कभी वैकल्पिक रूप से कॉल करते हैं <math>L^\text{rw}</math> रैंडम वॉक|रैंडम-वॉक सामान्यीकृत लाप्लासियन। कम असामान्य रूप से उपयोग किए जाने वाले दाएँ सामान्यीकृत लाप्लासियन में <math>L D^+ = I - A D^+</math> चूँकि प्रत्येक कॉलम का योग शून्य है <math>A D^+</math> स्टोकेस्टिक मैट्रिक्स है.
+उदाहरण यह भी दर्शाता है कि यदि <math>G</math> तो फिर, इसका कोई पृथक शीर्ष नहीं है <math>D^+A</math> [[स्टोकेस्टिक मैट्रिक्स]] और इसलिए यादृच्छिक चलने का मैट्रिक्स है, ताकि बाईं ओर लाप्लासियन सामान्यीकृत हो <math>L^\text{rw} := D^+L = I - D^+A</math> प्रत्येक पंक्ति का योग शून्य है। इस प्रकार हम कभी-कभी वैकल्पिक रूप से कॉल करते हैं <math>L^\text{rw}</math> रैंडम वॉक|रैंडम-वॉक सामान्यीकृत लाप्लासियन। कम असामान्य रूप से उपयोग किए जाने वाले दाएँ सामान्यीकृत लाप्लासियन में <math>L D^+ = I - A D^+</math> चूँकि प्रत्येक कॉलम का योग शून्य है <math>A D^+</math> स्टोकेस्टिक मैट्रिक्स है.
 निर्देशित ग्राफ़ के गैर-सममित आसन्न मैट्रिक्स के लिए, किसी को सामान्यीकरण के लिए डिग्री (ग्राफ़ सिद्धांत) चुनने की भी आवश्यकता होती है:
@@ Line 319: / Line 317: @@
 == भारित किनारों वाले ग्राफ़ के लिए परिभाषाएँ ==
-अनुप्रयोगों में सामान्य भारित किनारों वाले ग्राफ़ को आसानी से उनके आसन्न मैट्रिक्स द्वारा परिभाषित किया जाता है जहां प्रविष्टियों के मान संख्यात्मक होते हैं और अब शून्य और एक तक सीमित नहीं होते हैं। वर्णक्रमीय क्लस्टरिंग और ग्राफ़-आधारित सिग्नल प्रोसेसिंग में, जहां ग्राफ़ शीर्ष डेटा बिंदुओं का प्रतिनिधित्व करते हैं, किनारे के वजन की गणना की जा सकती है, उदाहरण के लिए, डेटा बिंदुओं के जोड़े के बीच Distance_matrix के व्युत्क्रमानुपाती के रूप में, जिसके परिणामस्वरूप सभी वजन अनौपचारिक रूप से बड़े मूल्यों के साथ गैर-नकारात्मक होते हैं डेटा बिंदुओं के अधिक समान जोड़े के अनुरूप। डेटा बिंदुओं के बीच सहसंबंध और विरोधी सहसंबंध का उपयोग करने से स्वाभाविक रूप से सकारात्मक और नकारात्मक दोनों प्रकार के भार उत्पन्न होते हैं। सरल ग्राफ़ की अधिकांश परिभाषाएँ गैर-नकारात्मक भार के मानक मामले तक तुच्छ रूप से विस्तारित हैं, जबकि नकारात्मक भार पर अधिक ध्यान देने की आवश्यकता होती है, खासकर सामान्यीकरण में।
+अनुप्रयोगों में सामान्य भारित किनारों वाले ग्राफ़ को आसानी से उनके आसन्न मैट्रिक्स द्वारा परिभाषित किया जाता है जहां प्रविष्टियों के मान संख्यात्मक होते हैं और अब शून्य और तक सीमित नहीं होते हैं। वर्णक्रमीय क्लस्टरिंग और ग्राफ़-आधारित सिग्नल प्रोसेसिंग में, जहां ग्राफ़ शीर्ष डेटा बिंदुओं का प्रतिनिधित्व करते हैं, किनारे के वजन की गणना की जा सकती है, उदाहरण के लिए, डेटा बिंदुओं के जोड़े के बीच Distance_matrix के व्युत्क्रमानुपाती के रूप में, जिसके परिणामस्वरूप सभी वजन अनौपचारिक रूप से बड़े मूल्यों के साथ गैर-नकारात्मक होते हैं डेटा बिंदुओं के अधिक समान जोड़े के अनुरूप। डेटा बिंदुओं के बीच सहसंबंध और विरोधी सहसंबंध का उपयोग करने से स्वाभाविक रूप से सकारात्मक और नकारात्मक दोनों प्रकार के भार उत्पन्न होते हैं। सरल ग्राफ़ की अधिकांश परिभाषाएँ गैर-नकारात्मक भार के मानक मामले तक तुच्छ रूप से विस्तारित हैं, जबकि नकारात्मक भार पर अधिक ध्यान देने की आवश्यकता होती है, खासकर सामान्यीकरण में।
 === लाप्लासियन मैट्रिक्स ===
@@ Line 363: / Line 361: @@
 === घटना मैट्रिक्स के माध्यम से सममित लाप्लासियन ===
-[[Image:elastic network model.png|thumb|एक 2-आयामी स्प्रिंग प्रणाली।]]भारित किनारों वाले ग्राफ़ के लिए कोई भारित घटना मैट्रिक्स बी को परिभाषित कर सकता है और इसका उपयोग संबंधित सममित लाप्लासियन के निर्माण के लिए कर सकता है <math>L = B B^\textsf{T}</math>. यहां वर्णित एक वैकल्पिक क्लीनर दृष्टिकोण, वज़न को कनेक्टिविटी से अलग करना है: नियमित ग्राफ़ के लिए घटना मैट्रिक्स का उपयोग करना जारी रखें और केवल वज़न के मान रखने वाले मैट्रिक्स को पेश करें। एक [[ वसंत प्रणाली ]] इस मॉडल का एक उदाहरण है जिसका उपयोग [[यांत्रिकी]] में दी गई कठोरता और इकाई लंबाई के स्प्रिंग्स की एक प्रणाली का वर्णन करने के लिए किया जाता है, जहां कठोरता के मूल्य ग्राफ किनारों के वजन की भूमिका निभाते हैं।
+[[Image:elastic network model.png|thumb|एक 2-आयामी स्प्रिंग प्रणाली।]]भारित किनारों वाले ग्राफ़ के लिए कोई भारित घटना मैट्रिक्स बी को परिभाषित कर सकता है और इसका उपयोग संबंधित सममित लाप्लासियन के निर्माण के लिए कर सकता है <math>L = B B^\textsf{T}</math>. यहां वर्णित वैकल्पिक क्लीनर दृष्टिकोण, वज़न को कनेक्टिविटी से अलग करना है: नियमित ग्राफ़ के लिए घटना मैट्रिक्स का उपयोग करना जारी रखें और केवल वज़न के मान रखने वाले मैट्रिक्स को पेश करें। [[ वसंत प्रणाली ]] इस मॉडल का उदाहरण है जिसका उपयोग [[यांत्रिकी]] में दी गई कठोरता और इकाई लंबाई के स्प्रिंग्स की प्रणाली का वर्णन करने के लिए किया जाता है, जहां कठोरता के मूल्य ग्राफ किनारों के वजन की भूमिका निभाते हैं।
 इस प्रकार हम भारहीन की परिभाषा का पुन: उपयोग करते हैं <math display="inline">|v| \times |e|</math> तत्व बी के साथ घटना मैट्रिक्स बी<sub>''ve''</sub> शीर्ष v और किनारे e के लिए (शीर्षों को जोड़ने वाला)। <math display="inline">v_i</math> और <math display="inline">v_j</math>, i > j) द्वारा परिभाषित
@@ Line 371: / Line 369: @@
 , & \text{otherwise}.
 \end{array}\right.</math>
-अब हम एक विकर्ण को भी परिभाषित करते हैं <math display="inline">|e| \times |e|</math> मैट्रिक्स W जिसमें किनारे का भार है। भले ही बी की परिभाषा में किनारों को तकनीकी रूप से निर्देशित किया गया है, उनकी दिशाएं मनमानी हो सकती हैं, फिर भी समान सममित लाप्लासियन का परिणाम होता है <math display="inline">|v| \times |v|</math> मैट्रिक्स एल के रूप में परिभाषित किया गया है
+अब हम विकर्ण को भी परिभाषित करते हैं <math display="inline">|e| \times |e|</math> मैट्रिक्स W जिसमें किनारे का भार है। भले ही बी की परिभाषा में किनारों को तकनीकी रूप से निर्देशित किया गया है, उनकी दिशाएं मनमानी हो सकती हैं, फिर भी समान सममित लाप्लासियन का परिणाम होता है <math display="inline">|v| \times |v|</math> मैट्रिक्स एल के रूप में परिभाषित किया गया है
 :<math>L = B W B^\textsf{T}</math>
 कहाँ <math display="inline">B^\textsf{T}</math> बी का स्थानान्तरण है.
@@ Line 402: / Line 400: @@
 \end{array}\right)</math>
 |}
 ===निर्देशित ग्राफ़ के लिए सममित लाप्लासियन===
-साधारण ग्राफ़ की तरह, एक निर्देशित भारित ग्राफ़ का लाप्लासियन मैट्रिक्स परिभाषा के अनुसार आम तौर पर गैर-सममित होता है। लाप्लासियन के निर्माण से पहले मूल निर्देशित ग्राफ को अप्रत्यक्ष ग्राफ में बदलकर समरूपता लागू की जा सकती है। अप्रत्यक्ष ग्राफ़ के आसन्न मैट्रिक्स को, उदाहरण के लिए, आसन्न मैट्रिक्स के योग के रूप में परिभाषित किया जा सकता है <math>A</math> मूल निर्देशित ग्राफ़ और उसके मैट्रिक्स का स्थानान्तरण <math>A^T</math> जैसा कि निम्नलिखित उदाहरण में है:
+साधारण ग्राफ़ की तरह, निर्देशित भारित ग्राफ़ का लाप्लासियन मैट्रिक्स परिभाषा के अनुसार आम तौर पर गैर-सममित होता है। लाप्लासियन के निर्माण से पहले मूल निर्देशित ग्राफ को अप्रत्यक्ष ग्राफ में बदलकर समरूपता लागू की जा सकती है। अप्रत्यक्ष ग्राफ़ के आसन्न मैट्रिक्स को, उदाहरण के लिए, आसन्न मैट्रिक्स के योग के रूप में परिभाषित किया जा सकता है <math>A</math> मूल निर्देशित ग्राफ़ और उसके मैट्रिक्स का स्थानान्तरण <math>A^T</math> जैसा कि निम्नलिखित उदाहरण में है:
 {|class="wikitable"
 ! [[Adjacency matrix]]
@@ Line 427: / Line 424: @@
 \end{array}\right)</math>
 |}
-जहाँ शून्य और एक की प्रविष्टियाँ हैं <math>A</math> सरल ग्राफ़, मानों को तार्किक के बजाय संख्यात्मक माना जाता है, जो परिणामों में अंतर को समझाते हैं - सरल ग्राफ़ के लिए, सममित ग्राफ़ को अभी भी सरल होने की आवश्यकता है, इसके सममित आसन्न मैट्रिक्स में केवल तार्किक होते हैं, संख्यात्मक मान नहीं, उदाहरण के लिए, तार्किक योग 1 v 1 = 1 है, जबकि संख्यात्मक योग 1 + 1 = 2 है।
+जहाँ शून्य और की प्रविष्टियाँ हैं <math>A</math> सरल ग्राफ़, मानों को तार्किक के बजाय संख्यात्मक माना जाता है, जो परिणामों में अंतर को समझाते हैं - सरल ग्राफ़ के लिए, सममित ग्राफ़ को अभी भी सरल होने की आवश्यकता है, इसके सममित आसन्न मैट्रिक्स में केवल तार्किक होते हैं, संख्यात्मक मान नहीं, उदाहरण के लिए, तार्किक योग 1 v 1 = 1 है, जबकि संख्यात्मक योग 1 + 1 = 2 है।
 वैकल्पिक रूप से, सममित लाप्लासियन मैट्रिक्स की गणना डिग्री (ग्राफ सिद्धांत) का उपयोग करके दो लाप्लासियन से की जा सकती है, जैसा कि निम्नलिखित उदाहरण में है:
@@ Line 466: / Line 463: @@
 ===लाप्लासियन मैट्रिक्स सामान्यीकरण===
-सामान्यीकरण का लक्ष्य, सरल ग्राफ़ की तरह, लाप्लासियन मैट्रिक्स की विकर्ण प्रविष्टियों को सभी इकाई बनाना है, साथ ही ऑफ-विकर्ण प्रविष्टियों को तदनुसार स्केल करना है। ग्लोसरी_ऑफ_ग्राफ_थ्योरी#वेटेड_ग्राफ में, एक शीर्ष में जुड़े हुए किनारों की एक छोटी संख्या के कारण बड़ी डिग्री हो सकती है, लेकिन बड़े वजन के साथ-साथ यूनिट वजन के साथ बड़ी संख्या में जुड़े किनारों के कारण भी।
+सामान्यीकरण का लक्ष्य, सरल ग्राफ़ की तरह, लाप्लासियन मैट्रिक्स की विकर्ण प्रविष्टियों को सभी इकाई बनाना है, साथ ही ऑफ-विकर्ण प्रविष्टियों को तदनुसार स्केल करना है। ग्लोसरी_ऑफ_ग्राफ_थ्योरी#वेटेड_ग्राफ में, शीर्ष में जुड़े हुए किनारों की छोटी संख्या के कारण बड़ी डिग्री हो सकती है, लेकिन बड़े वजन के साथ-साथ यूनिट वजन के साथ बड़ी संख्या में जुड़े किनारों के कारण भी।
 ग्राफ़ सेल्फ-लूप, यानी, आसन्न मैट्रिक्स के मुख्य विकर्ण पर गैर-शून्य प्रविष्टियाँ, ग्राफ़ लाप्लासियन मानों को प्रभावित नहीं करती हैं, लेकिन सामान्यीकरण कारकों की गणना के लिए गणना करने की आवश्यकता हो सकती है।
@@ Line 474: / Line 471: @@
 सममित रूप से सामान्यीकृत लाप्लासियन को इस प्रकार परिभाषित किया गया है
 : <math>L^\text{sym} := (D^+)^{1/2} L (D^+)^{1/2} = I - (D^+)^{1/2} A (D^+)^{1/2},</math>
-जहां एल असामान्य लाप्लासियन है, ए आसन्न मैट्रिक्स है, डी डिग्री मैट्रिक्स है, और <math>D^+</math> मूर-पेनरोज़ व्युत्क्रम है। चूँकि डिग्री मैट्रिक्स D विकर्ण है, इसका व्युत्क्रम वर्गमूल है <math display="inline">(D^+)^{1/2}</math> केवल विकर्ण मैट्रिक्स है जिसकी विकर्ण प्रविष्टियाँ D की विकर्ण प्रविष्टियों के वर्गमूलों के व्युत्क्रम हैं। यदि सभी किनारे के भार गैर-नकारात्मक हैं तो सभी डिग्री मान स्वचालित रूप से भी गैर-नकारात्मक हैं और इसलिए प्रत्येक डिग्री मान का एक अद्वितीय सकारात्मक वर्गमूल होता है। शून्य से विभाजन से बचने के लिए, शून्य डिग्री वाले शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है, जैसा कि निम्नलिखित उदाहरण में है:
+जहां एल असामान्य लाप्लासियन है, ए आसन्न मैट्रिक्स है, डी डिग्री मैट्रिक्स है, और <math>D^+</math> मूर-पेनरोज़ व्युत्क्रम है। चूँकि डिग्री मैट्रिक्स D विकर्ण है, इसका व्युत्क्रम वर्गमूल है <math display="inline">(D^+)^{1/2}</math> केवल विकर्ण मैट्रिक्स है जिसकी विकर्ण प्रविष्टियाँ D की विकर्ण प्रविष्टियों के वर्गमूलों के व्युत्क्रम हैं। यदि सभी किनारे के भार गैर-नकारात्मक हैं तो सभी डिग्री मान स्वचालित रूप से भी गैर-नकारात्मक हैं और इसलिए प्रत्येक डिग्री मान का अद्वितीय सकारात्मक वर्गमूल होता है। शून्य से विभाजन से बचने के लिए, शून्य डिग्री वाले शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है, जैसा कि निम्नलिखित उदाहरण में है:
 {|class="wikitable"
 ! [[Adjacency matrix]]
@@ Line 507: / Line 504: @@
 \end{array}\right)</math>
 |}
-सममित रूप से सामान्यीकृत लाप्लासियन एक सममित मैट्रिक्स है यदि और केवल यदि आसन्न मैट्रिक्स ए सममित है और डी की विकर्ण प्रविष्टियाँ गैर-नकारात्मक हैं, तो उस स्थिति में हम 'सममित सामान्यीकृत लाप्लासियन' शब्द का उपयोग कर सकते हैं।
+सममित रूप से सामान्यीकृत लाप्लासियन सममित मैट्रिक्स है यदि और केवल यदि आसन्न मैट्रिक्स ए सममित है और डी की विकर्ण प्रविष्टियाँ गैर-नकारात्मक हैं, तो उस स्थिति में हम 'सममित सामान्यीकृत लाप्लासियन' शब्द का उपयोग कर सकते हैं।
 सममित सामान्यीकृत लाप्लासियन मैट्रिक्स को इस प्रकार भी लिखा जा सकता है
 : <math>L^\text{sym} := (D^+)^{1/2} L (D^+)^{1/2} = (D^+)^{1/2}B W B^\textsf{T} (D^+)^{1/2} = S S^T</math>
-भारहीन का उपयोग करना <math display="inline">|v| \times |e|</math> आपतन मैट्रिक्स बी और विकर्ण <math display="inline">|e| \times |e|</math> मैट्रिक्स डब्ल्यू जिसमें किनारे का वजन शामिल है और नए को परिभाषित करता है <math display="inline">|v| \times |e|</math> भारित घटना मैट्रिक्स <math display="inline">S=(D^+)^{1/2}B W^{{1}/{2}}</math> जिनकी पंक्तियाँ शीर्षों द्वारा अनुक्रमित होती हैं और जिनके स्तंभ G के किनारों द्वारा अनुक्रमित होते हैं, जैसे कि किनारे e = {u, v} के अनुरूप प्रत्येक स्तंभ में एक प्रविष्टि होती है <math display="inline">\frac{1}{\sqrt{d_u}}</math> यू के अनुरूप पंक्ति में, एक प्रविष्टि <math display="inline">-\frac{1}{\sqrt{d_v}}</math> v के अनुरूप पंक्ति में, और अन्यत्र 0 प्रविष्टियाँ हैं।
+भारहीन का उपयोग करना <math display="inline">|v| \times |e|</math> आपतन मैट्रिक्स बी और विकर्ण <math display="inline">|e| \times |e|</math> मैट्रिक्स डब्ल्यू जिसमें किनारे का वजन शामिल है और नए को परिभाषित करता है <math display="inline">|v| \times |e|</math> भारित घटना मैट्रिक्स <math display="inline">S=(D^+)^{1/2}B W^{{1}/{2}}</math> जिनकी पंक्तियाँ शीर्षों द्वारा अनुक्रमित होती हैं और जिनके स्तंभ G के किनारों द्वारा अनुक्रमित होते हैं, जैसे कि किनारे e = {u, v} के अनुरूप प्रत्येक स्तंभ में प्रविष्टि होती है <math display="inline">\frac{1}{\sqrt{d_u}}</math> यू के अनुरूप पंक्ति में, प्रविष्टि <math display="inline">-\frac{1}{\sqrt{d_v}}</math> v के अनुरूप पंक्ति में, और अन्यत्र 0 प्रविष्टियाँ हैं।
 ==== रैंडम वॉक सामान्यीकृत लाप्लासियन ====
@@ Line 517: / Line 514: @@
 रैंडम वॉक सामान्यीकृत लाप्लासियन को इस प्रकार परिभाषित किया गया है
 : <math>L^\text{rw} := D^+ L = I - D^+ A</math>
-जहाँ D डिग्री मैट्रिक्स है। चूँकि डिग्री मैट्रिक्स D विकर्ण है, यह व्युत्क्रम है <math display="inline">D^+</math> इसे बस एक विकर्ण मैट्रिक्स के रूप में परिभाषित किया गया है, जिसमें विकर्ण प्रविष्टियाँ हैं जो डी की संगत विकर्ण प्रविष्टियों के व्युत्क्रम हैं। पृथक शीर्षों (डिग्री 0 वाले) के लिए, एक सामान्य विकल्प संबंधित तत्व को सेट करना है <math display="inline">L^\text{rw}_{i,i}</math> से 0. के मैट्रिक्स तत्व <math display="inline">L^\text{rw}</math> द्वारा दिए गए हैं
+जहाँ D डिग्री मैट्रिक्स है। चूँकि डिग्री मैट्रिक्स D विकर्ण है, यह व्युत्क्रम है <math display="inline">D^+</math> इसे बस विकर्ण मैट्रिक्स के रूप में परिभाषित किया गया है, जिसमें विकर्ण प्रविष्टियाँ हैं जो डी की संगत विकर्ण प्रविष्टियों के व्युत्क्रम हैं। पृथक शीर्षों (डिग्री 0 वाले) के लिए, सामान्य विकल्प संबंधित तत्व को सेट करना है <math display="inline">L^\text{rw}_{i,i}</math> से 0. के मैट्रिक्स तत्व <math display="inline">L^\text{rw}</math> द्वारा दिए गए हैं
 : <math>L^{\text{rw}}_{i,j} := \begin{cases}
 & \mbox{if}\ i = j\ \mbox{and}\ \deg(v_i) \neq 0\\
@@ Line 523: / Line 520: @@
 & \mbox{otherwise}.
 \end{cases}</math>
-रैंडम-वॉक सामान्यीकृत लाप्लासियन का नाम इस तथ्य से आता है कि यह मैट्रिक्स है <math display="inline">L^\text{rw} = I - P</math>, कहाँ <math display="inline">P = D^+A</math> गैर-नकारात्मक भार मानते हुए, ग्राफ़ पर एक यादृच्छिक वॉकर का संक्रमण मैट्रिक्स है। उदाहरण के लिए, चलो <math display="inline"> e_i </math> i-वें [[मानक आधार]] वेक्टर को निरूपित करें। तब <math display="inline">x = e_i P </math> एक [[संभाव्यता वेक्टर]] है जो शीर्ष से एक कदम उठाने के बाद यादृच्छिक वॉकर के स्थानों के वितरण का प्रतिनिधित्व करता है <math display="inline">i</math>; अर्थात।, <math display="inline">x_j = \mathbb{P}\left(v_i \to v_j\right)</math>. अधिक सामान्यतः, यदि वेक्टर <math display="inline"> x </math> तब, ग्राफ़ के शीर्षों पर एक यादृच्छिक वॉकर के स्थान का संभाव्यता वितरण होता है <math display="inline">x' = x P^t</math> बाद में वॉकर का संभाव्यता वितरण है <math display="inline">t</math> कदम।
+रैंडम-वॉक सामान्यीकृत लाप्लासियन का नाम इस तथ्य से आता है कि यह मैट्रिक्स है <math display="inline">L^\text{rw} = I - P</math>, कहाँ <math display="inline">P = D^+A</math> गैर-नकारात्मक भार मानते हुए, ग्राफ़ पर यादृच्छिक वॉकर का संक्रमण मैट्रिक्स है। उदाहरण के लिए, चलो <math display="inline"> e_i </math> i-वें [[मानक आधार]] वेक्टर को निरूपित करें। तब <math display="inline">x = e_i P </math> [[संभाव्यता वेक्टर]] है जो शीर्ष से कदम उठाने के बाद यादृच्छिक वॉकर के स्थानों के वितरण का प्रतिनिधित्व करता है <math display="inline">i</math>; अर्थात।, <math display="inline">x_j = \mathbb{P}\left(v_i \to v_j\right)</math>. अधिक सामान्यतः, यदि वेक्टर <math display="inline"> x </math> तब, ग्राफ़ के शीर्षों पर यादृच्छिक वॉकर के स्थान का संभाव्यता वितरण होता है <math display="inline">x' = x P^t</math> बाद में वॉकर का संभाव्यता वितरण है <math display="inline">t</math> कदम।
 रैंडम वॉक सामान्यीकृत लाप्लासियन को बायां सामान्यीकृत लाप्लासियन भी कहा जा सकता है <math>L^\text{rw} := D^+L</math> चूंकि सामान्यीकरण सामान्यीकरण मैट्रिक्स द्वारा लाप्लासियन को गुणा करके किया जाता है <math>D^+</math> बाईं तरफ। तब से इसकी प्रत्येक पंक्ति का योग शून्य है <math>P = D^+A</math> स्टोचैस्टिक मैट्रिक्स है, यह मानते हुए कि सभी भार गैर-नकारात्मक हैं।
@@ Line 567: / Line 564: @@
 ====नकारात्मक भार====
 नकारात्मक भार सामान्यीकरण के लिए कई चुनौतियाँ प्रस्तुत करते हैं:
-* नकारात्मक भार की उपस्थिति के परिणामस्वरूप गैर-पृथक शीर्षों के लिए स्वाभाविक रूप से शून्य पंक्ति- और/या स्तंभ-योग हो सकता है। सकारात्मक भारों की एक बड़ी पंक्ति-योग और समान रूप से नकारात्मक भारों की समान रूप से बड़ी पंक्ति-योग वाला एक शीर्ष, जिसका योग शून्य है, को एक भारी नोड माना जा सकता है और दोनों बड़े मानों को स्केल किया जा सकता है, जबकि विकर्ण प्रविष्टि शून्य रहती है, जैसे कि पृथक शीर्ष.
+* नकारात्मक भार की उपस्थिति के परिणामस्वरूप गैर-पृथक शीर्षों के लिए स्वाभाविक रूप से शून्य पंक्ति- और/या स्तंभ-योग हो सकता है। सकारात्मक भारों की बड़ी पंक्ति-योग और समान रूप से नकारात्मक भारों की समान रूप से बड़ी पंक्ति-योग वाला शीर्ष, जिसका योग शून्य है, को भारी नोड माना जा सकता है और दोनों बड़े मानों को स्केल किया जा सकता है, जबकि विकर्ण प्रविष्टि शून्य रहती है, जैसे कि पृथक शीर्ष.
 * नकारात्मक भार नकारात्मक पंक्ति- और/या स्तंभ-योग भी दे सकते हैं, जिससे कि गैर-सामान्यीकृत लाप्लासियन मैट्रिक्स में संबंधित विकर्ण प्रविष्टि नकारात्मक होगी और सममित सामान्यीकरण के लिए आवश्यक सकारात्मक वर्गमूल मौजूद नहीं होगा।
-* सामान्यीकरण के प्रयोजन के लिए पंक्ति- और/या स्तंभ-योग का पूर्ण मान लेने के लिए तर्क दिए जा सकते हैं, इस प्रकार संभावित मान -1 को सामान्यीकृत लाप्लासियन मैट्रिक्स के मुख्य विकर्ण की एक वैध इकाई प्रविष्टि के रूप में माना जा सकता है।
+* सामान्यीकरण के प्रयोजन के लिए पंक्ति- और/या स्तंभ-योग का पूर्ण मान लेने के लिए तर्क दिए जा सकते हैं, इस प्रकार संभावित मान -1 को सामान्यीकृत लाप्लासियन मैट्रिक्स के मुख्य विकर्ण की वैध इकाई प्रविष्टि के रूप में माना जा सकता है।
 == गुण ==
@@ Line 576: / Line 573: @@
 * L [[सममित मैट्रिक्स]] है.
 * एल [[सकारात्मक-निश्चित मैट्रिक्स]] है | सकारात्मक-अर्ध-निश्चित (अर्थात <math display="inline">\lambda_i \ge 0</math> सभी के लिए <math display="inline">i</math>). इसे इस तथ्य से देखा जा सकता है कि लाप्लासियन सममित और विकर्ण रूप से प्रभावशाली मैट्रिक्स#अनुप्रयोग और गुण है।
-* एल एक [[एम-मैट्रिक्स]] है (इसकी ऑफ-विकर्ण प्रविष्टियाँ गैर-सकारात्मक हैं, फिर भी इसके स्वदेशी मानों के वास्तविक भाग गैर-नकारात्मक हैं)।
+* एल [[एम-मैट्रिक्स]] है (इसकी ऑफ-विकर्ण प्रविष्टियाँ गैर-सकारात्मक हैं, फिर भी इसके स्वदेशी मानों के वास्तविक भाग गैर-नकारात्मक हैं)।
 * L की प्रत्येक पंक्ति और स्तंभ का योग शून्य है। वास्तव में, योग में, शीर्ष की डिग्री को प्रत्येक पड़ोसी के लिए -1 के साथ जोड़ा जाता है।
 * परिणामस्वरूप, <math display="inline">\lambda_0 = 0</math>, क्योंकि वेक्टर <math display="inline">\mathbf{v}_0 = (1, 1, \dots, 1)</math> संतुष्ट <math display="inline">L \mathbf{v}_0 = \mathbf{0} .</math> इसका तात्पर्य यह भी है कि लाप्लासियन मैट्रिक्स एकवचन है।
@@ Line 582: / Line 579: @@
 * L के सबसे छोटे गैर-शून्य eigenvalue को [[वर्णक्रमीय अंतराल]] कहा जाता है।
 * L का दूसरा सबसे छोटा eigenvalue (शून्य हो सकता है) G की बीजगणितीय कनेक्टिविटी (या फ़िडलर मान) है और ग्राफ़ के कट (ग्राफ_थ्योरी) #Sparsest कट का अनुमान लगाता है।
-* लाप्लासियन फ़ंक्शंस के एन-डायमेंशनल वेक्टर स्पेस पर एक ऑपरेटर है <math display="inline">f : V \to \mathbb{R}</math>, कहाँ <math display="inline">V</math> G का शीर्ष समुच्चय है, और <math display="inline">n = |V|</math>.
+* लाप्लासियन फ़ंक्शंस के एन-डायमेंशनल वेक्टर स्पेस पर ऑपरेटर है <math display="inline">f : V \to \mathbb{R}</math>, कहाँ <math display="inline">V</math> G का शीर्ष समुच्चय है, और <math display="inline">n = |V|</math>.
-* जब G, [[के-नियमित ग्राफ]]|k-रेगुलर है, तो सामान्यीकृत लाप्लासियन है: <math display="inline">\mathcal{L} = \tfrac{1}{k} L = I - \tfrac{1}{k} A</math>, जहां A आसन्नता मैट्रिक्स है और I एक पहचान मैट्रिक्स है।
+* जब G, [[के-नियमित ग्राफ]]|k-रेगुलर है, तो सामान्यीकृत लाप्लासियन है: <math display="inline">\mathcal{L} = \tfrac{1}{k} L = I - \tfrac{1}{k} A</math>, जहां A आसन्नता मैट्रिक्स है और I पहचान मैट्रिक्स है।
-* एकाधिक कनेक्टेड घटक (ग्राफ़ सिद्धांत) वाले ग्राफ़ के लिए, एल एक ब्लॉक मैट्रिक्स#ब्लॉक विकर्ण मैट्रिक्स मैट्रिक्स है, जहां प्रत्येक ब्लॉक प्रत्येक घटक के लिए संबंधित लाप्लासियन मैट्रिक्स है, संभवतः शीर्षों को पुन: व्यवस्थित करने के बाद (यानी एल क्रमपरिवर्तन-समान है) ब्लॉक विकर्ण मैट्रिक्स)।
+* एकाधिक कनेक्टेड घटक (ग्राफ़ सिद्धांत) वाले ग्राफ़ के लिए, एल ब्लॉक मैट्रिक्स#ब्लॉक विकर्ण मैट्रिक्स मैट्रिक्स है, जहां प्रत्येक ब्लॉक प्रत्येक घटक के लिए संबंधित लाप्लासियन मैट्रिक्स है, संभवतः शीर्षों को पुन: व्यवस्थित करने के बाद (यानी एल क्रमपरिवर्तन-समान है) ब्लॉक विकर्ण मैट्रिक्स)।
 * लाप्लासियन मैट्रिक्स एल का ट्रेस बराबर है <math display="inline">2m</math> कहाँ <math display="inline">m</math> विचारित ग्राफ़ के किनारों की संख्या है।
-* अब एक eigendecomposition पर विचार करें <math display="inline">L</math>, यूनिट-मानक eigenvectors के साथ <math display="inline">\mathbf{v}_i</math> और संगत eigenvalues <math display="inline">\lambda_i</math>:
+* अब eigendecomposition पर विचार करें <math display="inline">L</math>, यूनिट-मानक eigenvectors के साथ <math display="inline">\mathbf{v}_i</math> और संगत eigenvalues <math display="inline">\lambda_i</math>:
 :<math>\begin{align}
    \lambda_i & = \mathbf{v}_i^\textsf{T} L \mathbf{v}_i \\
@@ Line 615: / Line 612: @@
 | isbn = 978-3-540-40720-1
   | citeseerx = 10.1.1.3.7020
-  }}.</ref> इस व्याख्या में, प्रत्येक ग्राफ शीर्ष को ग्रिड बिंदु के रूप में माना जाता है; शीर्ष की स्थानीय कनेक्टिविटी इस ग्रिड बिंदु पर परिमित अंतर सन्निकटन स्टेंसिल (संख्यात्मक विश्लेषण) निर्धारित करती है, ग्रिड का आकार हमेशा प्रत्येक किनारे के लिए एक होता है, और किसी भी ग्रिड बिंदु पर कोई बाधा नहीं होती है, जो सजातीय न्यूमैन के मामले से मेल खाती है सीमा की स्थिति, यानी, मुक्त सीमा। इस तरह की व्याख्या किसी को अनुमति देती है, उदाहरण के लिए, अनंत संख्या में शीर्षों और किनारों वाले ग्राफ़ के मामले में लाप्लासियन मैट्रिक्स को सामान्यीकृत करना, जिससे अनंत आकार का लाप्लासियन मैट्रिक्स बनता है।
+  }}.</ref> इस व्याख्या में, प्रत्येक ग्राफ शीर्ष को ग्रिड बिंदु के रूप में माना जाता है; शीर्ष की स्थानीय कनेक्टिविटी इस ग्रिड बिंदु पर परिमित अंतर सन्निकटन स्टेंसिल (संख्यात्मक विश्लेषण) निर्धारित करती है, ग्रिड का आकार हमेशा प्रत्येक किनारे के लिए होता है, और किसी भी ग्रिड बिंदु पर कोई बाधा नहीं होती है, जो सजातीय न्यूमैन के मामले से मेल खाती है सीमा की स्थिति, यानी, मुक्त सीमा। इस तरह की व्याख्या किसी को अनुमति देती है, उदाहरण के लिए, अनंत संख्या में शीर्षों और किनारों वाले ग्राफ़ के मामले में लाप्लासियन मैट्रिक्स को सामान्यीकृत करना, जिससे अनंत आकार का लाप्लासियन मैट्रिक्स बनता है।
 == लाप्लासियन मैट्रिक्स का सामान्यीकरण और विस्तार ==
@@ Line 626: / Line 623: @@
    \mbox{any number} & \mbox{otherwise}.
 \end{cases}</math>
-ध्यान दें कि साधारण लाप्लासियन एक सामान्यीकृत लाप्लासियन है।
+ध्यान दें कि साधारण लाप्लासियन सामान्यीकृत लाप्लासियन है।
 === चुंबकीय लाप्लासियन ===
@@ Line 632: / Line 629: @@
 :<math>\gamma_q(i, j) = e^{i2 \pi q(w_{ij}-w_{ji})}</math>
 जो जटिल तल में किनारे की दिशा को चरण में कूटबद्ध करता है।
-क्वांटम भौतिकी के संदर्भ में, चुंबकीय लाप्लासियन की व्याख्या उस ऑपरेटर के रूप में की जा सकती है जो एक ग्राफ पर एक मुक्त आवेशित कण की घटना विज्ञान का वर्णन करता है, जो एक चुंबकीय क्षेत्र और पैरामीटर की कार्रवाई के अधीन है <math>q</math> विद्युत आवेश कहलाता है।<ref>{{cite conference|title=हर्मिटियन लाप्लासियन पर आधारित निर्देशित ग्राफ़ के लिए ग्राफ़ सिग्नल प्रोसेसिंग| conference=ECML PKDD 2019: Machine Learning and Knowledge Discovery in Databases |pages=447–463 |year=2020|doi= 10.1007/978-3-030-46150-8_27|url=https://ecmlpkdd2019.org/downloads/paper/499.pdf |author1=Satoshi Furutani |author2=Toshiki Shibahara|author3= Mitsuaki Akiyama|author4= Kunio Hato|author5=Masaki Aida }}</ref>
+क्वांटम भौतिकी के संदर्भ में, चुंबकीय लाप्लासियन की व्याख्या उस ऑपरेटर के रूप में की जा सकती है जो ग्राफ पर मुक्त आवेशित कण की घटना विज्ञान का वर्णन करता है, जो चुंबकीय क्षेत्र और पैरामीटर की कार्रवाई के अधीन है <math>q</math> विद्युत आवेश कहलाता है।<ref>{{cite conference|title=हर्मिटियन लाप्लासियन पर आधारित निर्देशित ग्राफ़ के लिए ग्राफ़ सिग्नल प्रोसेसिंग| conference=ECML PKDD 2019: Machine Learning and Knowledge Discovery in Databases |pages=447–463 |year=2020|doi= 10.1007/978-3-030-46150-8_27|url=https://ecmlpkdd2019.org/downloads/paper/499.pdf |author1=Satoshi Furutani |author2=Toshiki Shibahara|author3= Mitsuaki Akiyama|author4= Kunio Hato|author5=Masaki Aida }}</ref>
 निम्नलिखित उदाहरण में <math>q=1/4</math>:
 {|class="wikitable"
@@ Line 665: / Line 662: @@
 \end{array}\right)</math>
 |}
 === विकृत लाप्लासियन ===
@@ Line 672: / Line 668: @@
 :<math>\Delta(s) = I - sA + s^2(D - I)</math>
-जहां I पहचान मैट्रिक्स है, A आसन्न मैट्रिक्स है, D डिग्री मैट्रिक्स है, और s एक (जटिल-मूल्यवान) संख्या है। <ref>{{cite journal |title=विकृत आम सहमति प्रोटोकॉल|first=F. |last=Morbidi |journal=Automatica |volume=49 |number=10 |pages=3049–3055 |year=2013 |doi=10.1016/j.automatica.2013.07.006|s2cid=205767404 |url=http://hal.archives-ouvertes.fr/docs/00/96/14/91/PDF/Morbidi_AUTO13_ExtVer.pdf }}</ref><br /> मानक लाप्लासियन बस है <math display="inline">\Delta(1)</math> और <math display="inline">\Delta(-1) = D + A</math> चिन्हहीन लाप्लासियन है।
+जहां I पहचान मैट्रिक्स है, A आसन्न मैट्रिक्स है, D डिग्री मैट्रिक्स है, और s (जटिल-मूल्यवान) संख्या है। <ref>{{cite journal |title=विकृत आम सहमति प्रोटोकॉल|first=F. |last=Morbidi |journal=Automatica |volume=49 |number=10 |pages=3049–3055 |year=2013 |doi=10.1016/j.automatica.2013.07.006|s2cid=205767404 |url=http://hal.archives-ouvertes.fr/docs/00/96/14/91/PDF/Morbidi_AUTO13_ExtVer.pdf }}</ref><br /> मानक लाप्लासियन बस है <math display="inline">\Delta(1)</math> और <math display="inline">\Delta(-1) = D + A</math> चिन्हहीन लाप्लासियन है।
 === साइनलेस लाप्लासियन ===
@@ Line 684: / Line 680: @@
 === निर्देशित मल्टीग्राफ ===
-निर्देशित मल्टीग्राफ के लिए लाप्लासियन मैट्रिक्स का एक एनालॉग परिभाषित किया जा सकता है।<ref name="Chaiken1978">{{cite journal
+निर्देशित मल्टीग्राफ के लिए लाप्लासियन मैट्रिक्स का एनालॉग परिभाषित किया जा सकता है।<ref name="Chaiken1978">{{cite journal
   | title = Matrix Tree Theorems
   | author1=Chaiken, S. | author2=Kleitman, D. | author-link2=Daniel Kleitman
@@ Line 697: / Line 693: @@
   }}</ref> इस मामले में लाप्लासियन मैट्रिक्स एल को इस प्रकार परिभाषित किया गया है
 :<math>L = D - A</math>
-जहां D, D के साथ एक विकर्ण मैट्रिक्स है<sub>''i'',''i''</sub> शीर्ष i और A की आउटडिग्री के बराबर, A के साथ एक मैट्रिक्स है<sub>''i'',''j''</sub> i से j तक किनारों की संख्या के बराबर (लूप सहित)।
+जहां D, D के साथ विकर्ण मैट्रिक्स है<sub>''i'',''i''</sub> शीर्ष i और A की आउटडिग्री के बराबर, A के साथ मैट्रिक्स है<sub>''i'',''j''</sub> i से j तक किनारों की संख्या के बराबर (लूप सहित)।
 == ओपन सोर्स सॉफ़्टवेयर कार्यान्वयन ==
 * [[SciPy]]<ref>{{Cite web|url=https://github.com/scipy/scipy/blob/main/scipy/sparse/csgraph/_laplacian.py|title=SciPy|website=[[GitHub]]|date=24 March 2022}}</ref>
 * [[नेटवर्कएक्स]]<ref>{{Cite web|url=https://github.com/networkx/networkx/blob/main/networkx/linalg/laplacianmatrix.py|title=नेटवर्कएक्स|website=[[GitHub]]|date=24 March 2022}}</ref>
 == एप्लीकेशन सॉफ्टवेयर ==
 * [[स्किकिट-लर्न]] स्पेक्ट्रल क्लस्टरिंग<ref>{{Cite web|url=https://scikit-learn.org/stable/modules/clustering.html#spectral-clustering|title=2.3. Clustering}}</ref>
@@ Line 710: / Line 704: @@
 * चिकनीजी<ref>{{Cite web|url=https://github.com/LLNL/smoothG|title = स्मूथजी|website = [[GitHub]]|date = 17 September 2020}}</ref>
 * डायनामिक ग्राफ़ के लिए लाप्लासियन चेंज पॉइंट डिटेक्शन (KDD 2020)<ref>{{Cite web|url=https://complexdatalabmcgill.github.io/papers/post-andy-kdd2020paper/|title=Announcing Our Paper at KDD 2020}}</ref>
-* लाप्लासियनऑप्ट (लाप्लासियन के भारित ग्राफ़ के दूसरे आइगेनवैल्यू को अधिकतम करने के लिए एक जूलिया पैकेज) <ref>{{Cite web|url=https://github.com/harshangrjn/LaplacianOpt.jl|title = Harshangrjn/LaplacianOpt.jl|website = [[GitHub]]|date = 2 February 2022}}</ref>
+* लाप्लासियनऑप्ट (लाप्लासियन के भारित ग्राफ़ के दूसरे आइगेनवैल्यू को अधिकतम करने के लिए जूलिया पैकेज) <ref>{{Cite web|url=https://github.com/harshangrjn/LaplacianOpt.jl|title = Harshangrjn/LaplacianOpt.jl|website = [[GitHub]]|date = 2 February 2022}}</ref>
 * LigMG (बड़ा अनियमित ग्राफ़ मल्टीग्रिड)<ref>{{Cite web|url=https://github.com/ligmg/ligmg|title=LigMG (बड़ा अनियमित ग्राफ़ मल्टीग्रिड) - बड़े अनियमित ग्राफ़ के लिए एक वितरित मेमोरी ग्राफ़ लाप्लासियन सॉल्वर|website=[[GitHub]]|date=5 January 2022}}</ref>
 * लाप्लासियंस.जे.एल<ref>{{Cite web|url=https://github.com/danspielman/लाप्लासियंस.जे.एल|title = लाप्लासियंस.जे.एल|website = [[GitHub]]|date = 11 March 2022}}</ref>
 == यह भी देखें ==
 *[[कठोरता मैट्रिक्स]]

v t e Matrix classes
Explicitly constrained entries	Alternant Anti-diagonal Anti-Hermitian Anti-symmetric Arrowhead Band Bidiagonal Bisymmetric Block-diagonal Block Block tridiagonal Boolean Cauchy Centrosymmetric Conference Complex Hadamard Copositive Diagonally dominant Diagonal Discrete Fourier Transform Elementary Equivalent Frobenius Generalized permutation Hadamard Hankel Hermitian Hessenberg Hollow Integer Logical Matrix unit Metzler Moore Nonnegative Pentadiagonal Permutation Persymmetric Polynomial Quaternionic Signature Skew-Hermitian Skew-symmetric Skyline Sparse Sylvester Symmetric Toeplitz Triangular Tridiagonal Vandermonde Walsh Z
Constant	Exchange Hilbert Identity Lehmer Of ones Pascal Pauli Redheffer Shift Zero
Conditions on eigenvalues or eigenvectors	Companion Convergent Defective Definite Diagonalizable Hurwitz Positive-definite Stieltjes
Satisfying conditions on products or inverses	Congruent Idempotent or Projection Invertible Involutory Nilpotent Normal Orthogonal Unimodular Unipotent Unitary Totally unimodular Weighing
With specific applications	Adjugate Alternating sign Augmented Bézout Carleman Cartan Circulant Cofactor Commutation Confusion Coxeter Distance Duplication and elimination Euclidean distance Fundamental (linear differential equation) Generator Gram Hessian Householder Jacobian Moment Payoff Pick Random Rotation Seifert Shear Similarity Symplectic Totally positive Transformation
Used in statistics	Centering Correlation Covariance Design Doubly stochastic Fisher information Hat Precision Stochastic Transition
Used in graph theory	Adjacency Biadjacency Degree Edmonds Incidence Laplacian Seidel adjacency Tutte
Used in science and engineering	Cabibbo–Kobayashi–Maskawa Density Fundamental (computer vision) Fuzzy associative Gamma Gell-Mann Hamiltonian Irregular Overlap S State transition Substitution Z (chemistry)
Related terms	Jordan normal form Linear independence Matrix exponential Matrix representation of conic sections Perfect matrix Pseudoinverse Row echelon form Wronskian
' List of matrices Category:Matrices

Anonymous

Search

लाप्लासियन आव्यूह: Difference between revisions

Namespaces

More

Page actions

Revision as of 21:25, 19 July 2023

Contents

सरल ग्राफ़ के लिए परिभाषाएँ

लाप्लासियन मैट्रिक्स

निर्देशित ग्राफ़ के लिए सममित लाप्लासियन

लाप्लासियन मैट्रिक्स सामान्यीकरण

सममित रूप से सामान्यीकृत लाप्लासियन

बाएँ (यादृच्छिक-चलना) और दाएँ सामान्यीकृत लाप्लासियन

भारित किनारों वाले ग्राफ़ के लिए परिभाषाएँ

लाप्लासियन मैट्रिक्स

घटना मैट्रिक्स के माध्यम से सममित लाप्लासियन

निर्देशित ग्राफ़ के लिए सममित लाप्लासियन

लाप्लासियन मैट्रिक्स सामान्यीकरण

सममित रूप से सामान्यीकृत लाप्लासियन

रैंडम वॉक सामान्यीकृत लाप्लासियन

नकारात्मक भार

गुण

निरंतर लाप्लासियन का अनुमान लगाने वाले असतत लाप्लास ऑपरेटर के रूप में व्याख्या

लाप्लासियन मैट्रिक्स का सामान्यीकरण और विस्तार

सामान्यीकृत लाप्लासियन

चुंबकीय लाप्लासियन

विकृत लाप्लासियन

साइनलेस लाप्लासियन

निर्देशित मल्टीग्राफ

ओपन सोर्स सॉफ़्टवेयर कार्यान्वयन

एप्लीकेशन सॉफ्टवेयर

यह भी देखें

संदर्भ

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

लाप्लासियन आव्यूह: Difference between revisions

Revision as of 21:25, 19 July 2023

सरल ग्राफ़ के लिए परिभाषाएँ

लाप्लासियन मैट्रिक्स

निर्देशित ग्राफ़ के लिए सममित लाप्लासियन

लाप्लासियन मैट्रिक्स सामान्यीकरण

सममित रूप से सामान्यीकृत लाप्लासियन

बाएँ (यादृच्छिक-चलना) और दाएँ सामान्यीकृत लाप्लासियन

भारित किनारों वाले ग्राफ़ के लिए परिभाषाएँ

लाप्लासियन मैट्रिक्स

घटना मैट्रिक्स के माध्यम से सममित लाप्लासियन

निर्देशित ग्राफ़ के लिए सममित लाप्लासियन

लाप्लासियन मैट्रिक्स सामान्यीकरण

सममित रूप से सामान्यीकृत लाप्लासियन

रैंडम वॉक सामान्यीकृत लाप्लासियन

नकारात्मक भार

गुण

निरंतर लाप्लासियन का अनुमान लगाने वाले असतत लाप्लास ऑपरेटर के रूप में व्याख्या

लाप्लासियन मैट्रिक्स का सामान्यीकरण और विस्तार

सामान्यीकृत लाप्लासियन

चुंबकीय लाप्लासियन

विकृत लाप्लासियन

साइनलेस लाप्लासियन

निर्देशित मल्टीग्राफ

ओपन सोर्स सॉफ़्टवेयर कार्यान्वयन

एप्लीकेशन सॉफ्टवेयर

यह भी देखें

संदर्भ

Navigation

Wiki tools

Page tools

Other projects

Categories