स्पर्शरेखा अर्ध-कोण सूत्र

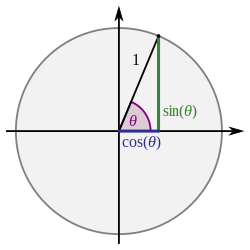
त्रिकोणमिति में, स्पर्शरेखा अर्ध-कोण सूत्र किसी कोण के अर्ध भाग की स्पर्शरेखा को पूरे कोण के त्रिकोणमितीय कार्यों से जोड़ते हैं। अर्ध कोण की स्पर्शरेखा किसी रेखा पर वृत्त का त्रिविम प्रक्षेपण है। इनमें से निम्नलिखित सूत्र हैं:

इनसे अर्ध-कोणों की स्पर्शरेखाओं के कार्यों के रूप में साइन, कोसाइन एवं स्पर्शरेखा को व्यक्त करने वाली पहचान प्राप्त की जा सकती है:

$${\begin{aligned}\sin \alpha &={\frac {2\tan {\tfrac {1}{2}}\alpha }{1+\tan ^{2}{\tfrac {1}{2}}\alpha }}\\[7pt]\cos \alpha &={\frac {1-\tan ^{2}{\tfrac {1}{2}}\alpha }{1+\tan ^{2}{\tfrac {1}{2}}\alpha }}\\[7pt]\tan \alpha &={\frac {2\tan {\tfrac {1}{2}}\alpha }{1-\tan ^{2}{\tfrac {1}{2}}\alpha }}\end{aligned}}$$

प्रमाण

बीजगणितीय प्रमाण

दोहरे कोण सूत्रों एवं पायथागॉरियन पहचान ${\textstyle 1+\tan ^{2}\alpha =1{\big /}\cos ^{2}\alpha }$ का उपयोग करना, देता है,

$$\sin \alpha =2\sin {\tfrac {1}{2}}\alpha \cos {\tfrac {1}{2}}\alpha ={\frac {2\sin {\tfrac {1}{2}}\alpha \,\cos {\tfrac {1}{2}}\alpha {\Big /}\cos ^{2}{\tfrac {1}{2}}\alpha }{1+\tan ^{2}{\tfrac {1}{2}}\alpha }}={\frac {2\tan {\tfrac {1}{2}}\alpha }{1+\tan ^{2}{\tfrac {1}{2}}\alpha }},\quad {\text{and}}$$

$$\cos \alpha =\cos ^{2}{\tfrac {1}{2}}\alpha -\sin ^{2}{\tfrac {1}{2}}\alpha ={\frac {\left(\cos ^{2}{\tfrac {1}{2}}\alpha -\sin ^{2}{\tfrac {1}{2}}\alpha \right){\Big /}\cos ^{2}{\tfrac {1}{2}}\alpha }{1+\tan ^{2}{\tfrac {1}{2}}\alpha }}={\frac {1-\tan ^{2}{\tfrac {1}{2}}\alpha }{1+\tan ^{2}{\tfrac {1}{2}}\alpha }},\quad {\text{and}}$$

साइन एवं कोसाइन पैदावार के लिए सूत्रों का भागफल लेना

$$\tan \alpha ={\frac {2\tan {\tfrac {1}{2}}\alpha }{1-\tan ^{2}{\tfrac {1}{2}}\alpha }}.$$

कोसाइन के लिए पाइथागोरस पहचान को दोहरे कोण सूत्र के साथ जोड़कर, ${\textstyle \cos 2\alpha =\cos ^{2}\alpha -\sin ^{2}\alpha =1-2\sin ^{2}\alpha =2\cos ^{2}\alpha -1,}$पुनर्व्यवस्थित करने एवं वर्गमूल लेने से परिणाम प्राप्त होते हैं,

$$\left|\sin \alpha \right|={\sqrt {\frac {1-\cos 2\alpha }{2}}}$$

एवं

$$\left|\cos \alpha \right|={\sqrt {\frac {1+\cos 2\alpha }{2}}}$$

जो विभाजन करने पर प्राप्त होता है,

$$\left|\tan \alpha \right|={\frac {\sqrt {1-\cos 2\alpha }}{\sqrt {1+\cos 2\alpha }}}={\frac {{\sqrt {1-\cos 2\alpha }}{\sqrt {1+\cos 2\alpha }}}{1+\cos 2\alpha }}={\frac {\sqrt {1-\cos ^{2}2\alpha }}{1+\cos 2\alpha }}={\frac {\left|\sin 2\alpha \right|}{1+\cos 2\alpha }}.$$

वैकल्पिक रूप से,

$$\left|\tan \alpha \right|={\frac {\sqrt {1-\cos 2\alpha }}{\sqrt {1+\cos 2\alpha }}}={\frac {1-\cos 2\alpha }{{\sqrt {1+\cos 2\alpha }}{\sqrt {1-\cos 2\alpha }}}}={\frac {1-\cos 2\alpha }{\sqrt {1-\cos ^{2}2\alpha }}}={\frac {1-\cos 2\alpha }{\left|\sin 2\alpha \right|}}.$$

इससे ज्ञात होता है कि इन अंतिम दो सूत्रों में निरपेक्ष मान चिह्न हटाये जा सकते हैं, चाहे α कोई भी चतुर्थांश में हो। निरपेक्ष मान पट्टियों के साथ या उसके बिना ये सूत्र तब प्रस्तावित नहीं होते जब दाहिनी ओर अंश एवं हर दोनों शून्य हों।

इसके अतिरिक्त, साइन एवं कोसाइन दोनों के लिए कोण जोड़ एवं घटाव सूत्रों का उपयोग करके कोई प्राप्त करता है:

$${\begin{aligned}\cos(a+b)&=\cos a\cos b-\sin a\sin b\\\cos(a-b)&=\cos a\cos b+\sin a\sin b\\\sin(a+b)&=\sin a\cos b+\cos a\sin b\\\sin(a-b)&=\sin a\cos b-\cos a\sin b\end{aligned}}$$

उपरोक्त चार सूत्रों को जोड़ीवार जोड़ने से प्राप्त होता है:

$${\begin{aligned}&\sin(a+b)+\sin(a-b)\\[5mu]&\quad =\sin a\cos b+\cos a\sin b+\sin a\cos b-\cos a\sin b\\[5mu]&\quad =2\sin a\cos b\\[15mu]&\cos(a+b)+\cos(a-b)\\[5mu]&\quad =\cos a\cos b-\sin a\sin b+\cos a\cos b+\sin a\sin b\\[5mu]&\quad =2\cos a\cos b\end{aligned}}$$

समायोजन ${\textstyle a={\tfrac {1}{2}}(p+q)}$ एवं $b={\tfrac {1}{2}}(p-q)$ एवं उपज को प्रतिस्थापित करना:

$${\begin{aligned}&\sin p+\sin q\\[5mu]&\quad =\sin \left({\tfrac {1}{2}}(p+q)+{\tfrac {1}{2}}(p-q)\right)+\sin \left({\tfrac {1}{2}}(p+q)-{\tfrac {1}{2}}(p-q)\right)\\[5mu]&\quad =2\sin {\tfrac {1}{2}}(p+q)\,\cos {\tfrac {1}{2}}(p-q)\\[15mu]&\cos p+\cos q\\[5mu]&\quad =\cos \left({\tfrac {1}{2}}(p+q)+{\tfrac {1}{2}}(p-q)\right)+\cos \left({\tfrac {1}{2}}(p+q)-{\tfrac {1}{2}}(p-q)\right)\\[5mu]&\quad =2\cos {\tfrac {1}{2}}(p+q)\,\cos {\tfrac {1}{2}}(p-q)\end{aligned}}$$

ज्याओं के योग को कोज्याओं के योग से विभाजित करने पर प्राप्त होता है:

$${\frac {\sin p+\sin q}{\cos p+\cos q}}={\frac {2\sin {\tfrac {1}{2}}(p+q)\,\cos {\tfrac {1}{2}}(p-q)}{2\cos {\tfrac {1}{2}}(p+q)\,\cos {\tfrac {1}{2}}(p-q)}}=\tan {\tfrac {1}{2}}(p+q)$$

ज्यामितीय प्रमाण

इस समचतुर्भुज की भुजाओं की लंबाई 1 है। क्षैतिज रेखा एवं दिखाए गए विकर्ण के मध्य का कोण 1/2 (a + b) है। यह विशेष स्पर्शरेखा अर्ध-कोण सूत्र को सिद्ध करने का ज्यामितीय उपाय है जो बताता है कि tan 1/2 (a + b) = (sin a + sin b) / (cos a + cos b) है। सूत्र sin 1/2(a + b) एवं cos 1/2(a + b) विकर्ण की लंबाई से वास्तविक दूरियों का अनुपात है।

ऊपर दिए गए सूत्रों को दाईं ओर समचतुर्भुज आकृति पर प्रस्तावित करने से यह सरलता से प्रदर्शित किया जा सकता है,

$$\tan {\tfrac {1}{2}}(a+b)={\frac {\sin {\tfrac {1}{2}}(a+b)}{\cos {\tfrac {1}{2}}(a+b)}}={\frac {\sin a+\sin b}{\cos a+\cos b}}.$$

यूनिट सर्कल में, उपरोक्त का अनुप्रयोग यह प्रदर्शित करता है कि है${\textstyle t=\tan {\tfrac {1}{2}}\varphi }$ है। समरूप त्रिभुजों द्वारा,

$${\frac {t}{\sin \varphi }}={\frac {1}{1+\cos \varphi }}.$$

यह इस प्रकार है कि

$$t={\frac {\sin \varphi }{1+\cos \varphi }}={\frac {\sin \varphi (1-\cos \varphi )}{(1+\cos \varphi )(1-\cos \varphi )}}={\frac {1-\cos \varphi }{\sin \varphi }}.$$

अभिन्न कलन में स्पर्शरेखा अर्ध-कोण प्रतिस्थापन

Main article: वीयरस्ट्रैस प्रतिस्थापन

वीयरस्ट्रैस प्रतिस्थापन का ज्यामितीय प्रमाण

त्रिकोणमिति के विभिन्न अनुप्रयोगों में, नए चर $t$ के तर्कसंगत कार्यों के संदर्भ में त्रिकोणमितीय कार्यों (जैसे साइन एवं कोसाइन) को पुनः लिखना उपयोगी है। $t$ की परिभाषा के कारण इन सर्वसमिकाओं को सामूहिक रूप से स्पर्शरेखा अर्ध-कोण सूत्र के रूप में जाना जाता है। ये पहचानें साइन एवं कोसाइन में तर्कसंगत कार्यों को उनके प्रतिअवकलज खोजने के लिए t के कार्यों में परिवर्तित करने के लिए कैलकुलसन में उपयोगी हो सकती हैं।

ज्यामितीय रूप से, निर्माण इस प्रकार होता है: इकाई चक्र पर किसी भी बिंदु के लिए (cos φ, sin φ) के लिए, इससे होकर निकलने वाली रेखा एवं बिंदु के लिए (−1, 0) खींची जाती है। यह बिंदु किसी बिंदु y = t पर y-अक्ष को पार करता है। कोई सरल ज्यामिति का उपयोग करके यह दिखा सकता है t = tan(φ/2). खींची गई रेखा का समीकरण y = (1 + x)t है। रेखा एवं वृत्त के प्रतिच्छेदन का समीकरण तब द्विघात समीकरण होता है जिसमें t सम्मिलित होता है। इस समीकरण के दो समाधान हैं (−1, 0) एवं (cos φ, sin φ) हैं। यह हमें पश्चात वाले को t के तर्कसंगत कार्यों के रूप में लिखने की अनुमति देता है (समाधान नीचे दिए गए हैं)।

पैरामीटर t बिंदु के त्रिविम प्रक्षेपण का प्रतिनिधित्व करता है (cos φ, sin φ) उस पर y-प्रक्षेपण के केंद्र के साथ अक्ष (−1, 0). इस प्रकार, स्पर्शरेखा अर्ध-कोण सूत्र त्रिविम निर्देशांक के मध्य रूपांतरण देते हैं t इकाई वृत्त एवं मानक कोणीय निर्देशांक पर φ.

तो हमारे पास हैं

$${\begin{aligned}&\sin \varphi ={\frac {2t}{1+t^{2}}},&&\cos \varphi ={\frac {1-t^{2}}{1+t^{2}}},\\[8pt]&\tan \varphi ={\frac {2t}{1-t^{2}}}&&\cot \varphi ={\frac {1-t^{2}}{2t}},\\[8pt]&\sec \varphi ={\frac {1+t^{2}}{1-t^{2}}},&&\csc \varphi ={\frac {1+t^{2}}{2t}},\end{aligned}}$$

एवं

$$e^{i\varphi }={\frac {1+it}{1-it}},\qquad e^{-i\varphi }={\frac {1-it}{1+it}}.$$

सीधे ऊपर एवं प्रारंभिक परिभाषा के मध्य फाई को समाप्त करके $t$, कोई प्राकृतिक लघुगणक के संदर्भ में आर्कटिक स्पर्शरेखा के लिए निम्नलिखित उपयोगी संबंध पर पहुंचता है

$$2\arctan t=-i\ln {\frac {1+it}{1-it}}.$$

कैलकुलस में, वेयरस्ट्रैस प्रतिस्थापन का उपयोग तर्कसंगत कार्यों के प्रतिअवकलन खोजने के लिए किया जाता है sin φ एवंcos φ. सेटिंग के पश्चात

$$t=\tan {\tfrac {1}{2}}\varphi .$$

इसका अर्थ यह है कि

$$\varphi =2\arctan(t)+2\pi n,$$

कुछ पूर्णांक के लिए n, एवं इसलिए

$$d\varphi ={{2\,dt} \over {1+t^{2}}}.$$

अतिशयोक्तिपूर्ण पहचान कोई भी अतिशयोक्तिपूर्ण कार्यों के साथ पूरी तरह से अनुरूप खेल खेल सकता है। हाइपरबोला की (दाहिनी शाखा पर) बिंदु किसके द्वारा दिया जाता है(cosh ψ, sinh ψ). इसे प्रक्षेपित करना y-केंद्र से अक्ष (−1, 0) निम्नलिखित देता है:

$$t=\tanh {\tfrac {1}{2}}\psi ={\frac {\sinh \psi }{\cosh \psi +1}}={\frac {\cosh \psi -1}{\sinh \psi }}$$

पहचानों के साथ

$${\begin{aligned}&\sinh \psi ={\frac {2t}{1-t^{2}}},&&\cosh \psi ={\frac {1+t^{2}}{1-t^{2}}},\\[8pt]&\tanh \psi ={\frac {2t}{1+t^{2}}},&&\coth \psi ={\frac {1+t^{2}}{2t}},\\[8pt]&\operatorname {sech} \,\psi ={\frac {1-t^{2}}{1+t^{2}}},&&\operatorname {csch} \,\psi ={\frac {1-t^{2}}{2t}},\end{aligned}}$$

एवं

$$e^{\psi }={\frac {1+t}{1-t}},\qquad e^{-\psi }={\frac {1-t}{1+t}}.$$

खोज ψ के अनुसार t व्युत्क्रम अतिशयोक्तिपूर्ण कार्यों के मध्य निम्नलिखित संबंध की ओर ले जाता है $\operatorname {artanh}$ एवं प्राकृतिक लघुगणक:

$$2\operatorname {artanh} t=\ln {\frac {1+t}{1-t}}.$$

गुडरमैनियन फ़ंक्शन

Main article: Gudermannian function

अतिशयोक्तिपूर्ण पहचानों की तुलना वृत्ताकार पहचानों से करने पर, कोई यह नोटिस करता है कि उनमें समान कार्य सम्मिलित हैं t, अभी क्रमपरिवर्तित किया गया। यदि हम पैरामीटर की पहचान करते हैं t दोनों ही मामलों में हम वृत्ताकार फलनों एवं अतिपरवलयिक फलनों के मध्य संबंध पर पहुंचते हैं। अर्थात यदि

$$t=\tan {\tfrac {1}{2}}\varphi =\tanh {\tfrac {1}{2}}\psi$$

तब

$$\varphi =2\arctan {\bigl (}\tanh {\tfrac {1}{2}}\psi \,{\bigr )}\equiv \operatorname {gd} \psi .$$

कहाँ gd(ψ)गुडर्मनियन फ़ंक्शन है। गुडेरमैनियन फ़ंक्शन वृत्ताकार फ़ंक्शंस एवं हाइपरबोलिक फ़ंक्शंस के मध्य सीधा संबंध देता है जिसमें जटिल संख्याएं सम्मिलित नहीं होती हैं। स्पर्शरेखा अर्ध-कोण सूत्रों के उपरोक्त विवरण (इकाई वृत्त एवं मानक हाइपरबोला को प्रक्षेपित करें)। y-अक्ष) इस फ़ंक्शन की ज्यामितीय व्याख्या दें।

तर्कसंगत मान एवं पायथागॉरियन त्रिगुण

Main article: Pythagorean triple

भुजाओं की लंबाई वाले पाइथागोरस त्रिभुज से प्रारंभ करना a, b, एवं c जो धनात्मक पूर्णांक हैं एवं संतुष्ट करते हैं a² + b² = c², इससे तुरंत ज्ञात होता है कि त्रिभुज के प्रत्येक आंतरिक कोण में साइन एवं कोसाइन के लिए तर्कसंगत मान हैं, क्योंकि ये केवल भुजाओं की लंबाई के अनुपात हैं। इस प्रकार, इनमें से प्रत्येक कोण का उपयोग करते हुए, इसके अर्ध-कोण स्पर्शरेखा के लिए तर्कसंगत मान होता है tan φ/2 = sin φ / (1 + cos φ).

विपरीत भी सही है। यदि दो धनात्मक कोण हैं जिनका योग 90° है, प्रत्येक परिमेय अर्ध-कोण स्पर्शरेखा के साथ है, एवं तीसरा कोण समकोण है तो इन आंतरिक कोणों वाला त्रिभुज पाइथागोरस त्रिभुज के समान (ज्यामिति) हो सकता है। यदि तीसरे कोण का समकोण होना आवश्यक नहीं है, लेकिन वह कोण है जो तीन धनात्मक कोणों का योग 180° बनाता है तो तीसरे कोण के पास आवश्यक रूप से अपने अर्ध-कोण स्पर्शरेखा के लिए तर्कसंगत संख्या होगी जब पहले दो ऐसा करते हैं (का उपयोग करके) स्पर्शरेखाओं के लिए कोण जोड़ एवं घटाव सूत्र) एवं त्रिभुज को हेरोनियन त्रिभुज में स्केल किया जा सकता है।

आम तौर पर, अगर K सम्मिश्र संख्याओं का फ़ील्ड विस्तार है tan φ/2 ∈ K ∪ {∞} इसका आशय है {sin φ, cos φ, tan φ, sec φ, csc φ, cot φ} ⊆ K ∪ {∞}.

यह भी देखें

• त्रिकोणमितीय सर्वसमिकाओं की सूची
• अर्ध-पक्षीय सूत्र

बाहरी संबंध

• Tangent Of Halved Angle at Planetmath