अर्ध-घातांकीय फलन: Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
गणित में, अर्ध-घातांकीय फलन किसी घातांकीय फलन का [[कार्यात्मक वर्गमूल]] होता है। | गणित में, '''अर्ध-घातांकीय फलन''' किसी घातांकीय फलन का [[कार्यात्मक वर्गमूल]] होता है। अर्थात [[फ़ंक्शन (गणित)|फलन (गणित)]] <math>f</math> ऐसा है कि <math>f</math> स्वयं से मिलकर घातांकीय फलन में परिणत होता है:<math display=block>f\bigl(f(x)\bigr) = ab^x,</math>कुछ स्थिरांक के लिए {{nowrap|<math>a</math> and <math>b</math>.}} है:{{r|sqrtexp|miltersen}} | ||
<math display=block>f\bigl(f(x)\bigr) = ab^x,</math> | |||
कुछ स्थिरांक के लिए {{nowrap|<math>a</math> and <math>b</math>.}} | |||
== | ==संवृत-फ़ॉर्म सूत्र की असंभवता== | ||
यदि कोई | यदि कोई फलन<math>f</math> को मानक अंकगणितीय संचालन, घातांक, लघुगणक और [[वास्तविक संख्या]]-मूल्यवान स्थिरांक का उपयोग करके परिभाषित किया गया है, फिर <math>f\bigl(f(x)\bigr)</math> या तो उप घातीय | ||
या सुपर घातीय है।{{r|transseries}} इस प्रकार, हार्डी {{mvar|L}}-फलन अर्ध-घातांकीय नहीं हो सकता है। | |||
==निर्माण== | ==निर्माण== | ||
किसी भी घातीय फलन को स्व-रचना के रूप में लिखा जा सकता है <math>f(f(x))</math> के अपरिमित रूप से अनेक संभावित विकल्पों के लिए <math>f</math> | किसी भी घातीय फलन को स्व-रचना के रूप में लिखा जा सकता है <math>f(f(x))</math> के अपरिमित रूप से अनेक संभावित विकल्पों के लिए <math>f</math> विशेष रूप से, प्रत्येक के लिए <math>A</math> विवृत अंतराल में <math>(0,1)</math> और प्रत्येक निरंतर जटिलता से बढ़ते [[विशेषण फलन|फलन]] के लिए <math>g</math> से <math>[0,A]</math> पर <math>[A,1]</math> इस फलन का निरंतर जटिलता से बढ़ते फलन तक विस्तार है। वास्तविक संख्याओं पर <math>f</math> जैसे कि {{nowrap|<math>f\bigl(f(x)\bigr)=\exp x</math>.{{r|croneu}}}}प्रोग्राम <math>f</math> [[कार्यात्मक समीकरण]] का अद्वितीय समाधान है:<math display=block> f (x) = | ||
<math display=block> f (x) = | |||
\begin{cases} | \begin{cases} | ||
g (x) & \mbox{if } x \in [0,A], \\ | g (x) & \mbox{if } x \in [0,A], \\ | ||
| Line 15: | Line 14: | ||
\ln f ( \exp x) & \mbox{if } x \in (-\infty,0). \\ | \ln f ( \exp x) & \mbox{if } x \in (-\infty,0). \\ | ||
\end{cases} | \end{cases} | ||
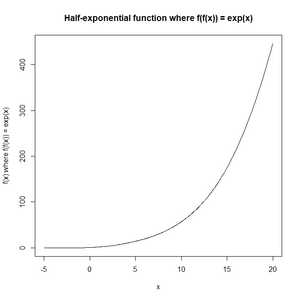
</math> | </math>[[File:Half-exponential_function.png|thumb|right|300px|अर्ध-घातांकीय फलन का उदाहरण]]सरल उदाहरण, जो <math>f</math> की ओर ले जाता है प्रत्येक स्थान सतत प्रथम व्युत्पन्न होने पर <math>A=\tfrac12</math> और <math>g(x)=x+\tfrac12</math> होता है, जो इस प्रकार है: | ||
[[File:Half-exponential_function.png|thumb|right|300px|अर्ध-घातांकीय फलन का उदाहरण]]सरल उदाहरण, जो | |||
<math display=block> f (x) = | <math display=block> f (x) = | ||
\begin{cases} | \begin{cases} | ||
| Line 31: | Line 28: | ||
</math> | </math> | ||
== अनुप्रयोग == | |||
== | बहुपद और घातांक के मध्य मध्यवर्ती विकास दर के लिए [[कम्प्यूटेशनल जटिलता सिद्धांत]] में अर्ध-घातीय कार्यों का उपयोग किया जाता है।{{r|miltersen}}फलन <math>f</math> कम से कम किसी अर्ध-घातांकीय फलन जितनी तीव्रता से बढ़ता है (इसकी संरचना स्वयं के साथ तीव्रता से बढ़ती है)। यदि यह घटता नहीं है और <math>f^{-1}(x^C)=o(\log x)</math>, प्रत्येक के लिए {{nowrap|every <math>C>0</math>.{{r|razrud}}}}है। | ||
बहुपद और घातांक के | |||
==यह भी देखें== | ==यह भी देखें== | ||
*{{annotated link| | *{{annotated link|पुनरावृत्त फलन}} | ||
*{{annotated link| | *{{annotated link|श्रोडर का समीकरण}} | ||
*{{annotated link| | *{{annotated link|हाबिल समीकरण}} | ||
==संदर्भ== | ==संदर्भ== | ||
| Line 113: | Line 109: | ||
* [https://mathoverflow.net/q/12081 Does the exponential function have a (compositional) square root?] | * [https://mathoverflow.net/q/12081 Does the exponential function have a (compositional) square root?] | ||
* [https://mathoverflow.net/q/45477 “Closed-form” functions with half-exponential growth] | * [https://mathoverflow.net/q/45477 “Closed-form” functions with half-exponential growth] | ||
[[Category: | [[Category:CS1 errors]] | ||
[[Category:Created On 04/07/2023]] | [[Category:Created On 04/07/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with reference errors]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:एल्गोरिदम का विश्लेषण]] | |||
[[Category:कम्प्यूटेशनल जटिलता सिद्धांत]] | |||
Latest revision as of 15:16, 2 August 2023
गणित में, अर्ध-घातांकीय फलन किसी घातांकीय फलन का कार्यात्मक वर्गमूल होता है। अर्थात फलन (गणित) ऐसा है कि स्वयं से मिलकर घातांकीय फलन में परिणत होता है:
संवृत-फ़ॉर्म सूत्र की असंभवता
यदि कोई फलन को मानक अंकगणितीय संचालन, घातांक, लघुगणक और वास्तविक संख्या-मूल्यवान स्थिरांक का उपयोग करके परिभाषित किया गया है, फिर या तो उप घातीय
या सुपर घातीय है।[3] इस प्रकार, हार्डी L-फलन अर्ध-घातांकीय नहीं हो सकता है।
निर्माण
किसी भी घातीय फलन को स्व-रचना के रूप में लिखा जा सकता है के अपरिमित रूप से अनेक संभावित विकल्पों के लिए विशेष रूप से, प्रत्येक के लिए विवृत अंतराल में और प्रत्येक निरंतर जटिलता से बढ़ते फलन के लिए से पर इस फलन का निरंतर जटिलता से बढ़ते फलन तक विस्तार है। वास्तविक संख्याओं पर जैसे कि .[4]प्रोग्राम कार्यात्मक समीकरण का अद्वितीय समाधान है:
सरल उदाहरण, जो की ओर ले जाता है प्रत्येक स्थान सतत प्रथम व्युत्पन्न होने पर और होता है, जो इस प्रकार है:
अनुप्रयोग
बहुपद और घातांक के मध्य मध्यवर्ती विकास दर के लिए कम्प्यूटेशनल जटिलता सिद्धांत में अर्ध-घातीय कार्यों का उपयोग किया जाता है।[2]फलन कम से कम किसी अर्ध-घातांकीय फलन जितनी तीव्रता से बढ़ता है (इसकी संरचना स्वयं के साथ तीव्रता से बढ़ती है)। यदि यह घटता नहीं है और , प्रत्येक के लिए every .[5]है।
यह भी देखें
- पुनरावृत्त फलन – Result of repeatedly applying a mathematical function
- श्रोडर का समीकरण
- हाबिल समीकरण – Equation for function that computes iterated values
संदर्भ
- ↑ Kneser, H. (1950). "Reelle analytische Lösungen der Gleichung φ(φ(x) = ex[[Category: Templates Vigyan Ready]] und verwandter Funktionalgleichungen". Journal für die reine und angewandte Mathematik. 187: 56–67. MR 0035385.
{{cite journal}}: URL–wikilink conflict (help) - ↑ 2.0 2.1 Miltersen, Peter Bro; Vinodchandran, N. V.; Watanabe, Osamu (1999). "Super-polynomial versus half-exponential circuit size in the exponential hierarchy". In Asano, Takao; Imai, Hiroshi; Lee, D. T.; Nakano, Shin-ichi; Tokuyama, Takeshi (eds.). Computing and Combinatorics, 5th Annual International Conference, COCOON '99, Tokyo, Japan, July 26–28, 1999, Proceedings. Lecture Notes in Computer Science. Vol. 1627. Springer. pp. 210–220. doi:10.1007/3-540-48686-0_21. MR 1730337.
- ↑ van der Hoeven, J. (2006). Transseries and real differential algebra. Lecture Notes in Mathematics. Vol. 1888. Springer-Verlag, Berlin. doi:10.1007/3-540-35590-1. ISBN 978-3-540-35590-8. MR 2262194. See exercise 4.10, p. 91, according to which every such function has a comparable growth rate to an exponential or logarithmic function iterated an integer number of times, rather than the half-integer that would be required for a half-exponential function.
- ↑ Crone, Lawrence J.; Neuendorffer, Arthur C. (1988). "Functional powers near a fixed point". Journal of Mathematical Analysis and Applications. 132 (2): 520–529. doi:10.1016/0022-247X(88)90080-7. MR 0943525.
- ↑ Razborov, Alexander A.; Rudich, Steven (1997). "Natural proofs". Journal of Computer and System Sciences. 55 (1): 24–35. doi:10.1006/jcss.1997.1494. MR 1473047.