सांस्थितिक वर्गीकरण: Difference between revisions
m (Deepak moved page टोपोलॉजिकल छँटाई to सांस्थितिक वर्गीकरण without leaving a redirect) |
No edit summary |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Node ordering for directed acyclic graphs}} | {{Short description|Node ordering for directed acyclic graphs}} | ||
{{Redirect| | {{Redirect|निर्भरता समाधान|अन्य उपयोग|निर्भरता (बहुविकल्पी)}} | ||
[[कंप्यूटर विज्ञान]] में, | [[कंप्यूटर विज्ञान]] में, [[निर्देशित ग्राफ]] का टोपोलॉजिकल सॉर्ट या टोपोलॉजिकल ऑर्डरिंग इसके शीर्ष (ग्राफ सिद्धांत) का कुल क्रम है, जैसे कि प्रत्येक निर्देशित किनारे ''यूवी'' के लिए शीर्ष ''u'' से शीर्ष ''v'' तक , ''u'' क्रम में ''v'' से पहले आता है। उदाहरण के लिए, ग्राफ़ के शीर्ष निष्पादित किए जाने वाले कार्यों का प्रतिनिधित्व कर सकते हैं, और किनारे उन बाधाओं का प्रतिनिधित्व कर सकते हैं कि कार्य दूसरे से पहले किया जाना चाहिए; इस एप्लिकेशन में, टोपोलॉजिकल ऑर्डरिंग कार्यों के लिए सिर्फ वैध अनुक्रम है। संक्षेप में, टोपोलॉजिकल सॉर्ट ग्राफ़ ट्रैवर्सल है जिसमें प्रत्येक नोड ''v'' पर उसकी सभी निर्भरताओं का दौरा करने के पश्चात ही दौरा किया जाता है।'' टोपोलॉजिकल ऑर्डरिंग तभी संभव है जब ग्राफ़ में कोई [[निर्देशित चक्र]] न हो, अर्थात , यदि यह [[निर्देशित अचक्रीय ग्राफ]] (डीएजी) है। किसी भी डीएजी में कम से कम टोपोलॉजिकल ऑर्डरिंग होती है, और [[कलन विधि]] [[रैखिक समय]] में किसी भी डीएजी के टोपोलॉजिकल ऑर्डरिंग के निर्माण के लिए जाने जाते हैं। टोपोलॉजिकल सॉर्टिंग के कई अनुप्रयोग हैं, विशेष रूप से [[फीडबैक आर्क सेट|फीडबैक आर्क समुच्चय]] जैसी रैंकिंग समस्याओं में डीएजी में [[कनेक्टिविटी (ग्राफ सिद्धांत)]] होने पर भी टोपोलॉजिकल सॉर्टिंग संभव है।'' | ||
== उदाहरण == | == उदाहरण == | ||
टोपोलॉजिकल सॉर्टिंग का विहित अनुप्रयोग जॉब शॉप में उनके [[निर्भरता ग्राफ]] के आधार पर नौकरियों या कार्यों के अनुक्रम को शेड्यूल करना है। कार्यों को शीर्षों द्वारा दर्शाया जाता है, और यदि कार्य x को कार्य y | टोपोलॉजिकल सॉर्टिंग का विहित अनुप्रयोग जॉब शॉप में उनके [[निर्भरता ग्राफ]] के आधार पर नौकरियों या कार्यों के अनुक्रम को शेड्यूल करना है। कार्यों को शीर्षों द्वारा दर्शाया जाता है, और यदि कार्य x को कार्य y प्रारंभ करने से पहले पूरा किया जाना चाहिए तो x से y तक बढ़त होती है (उदाहरण के लिए, कपड़े धोते समय, कपड़े को ड्रायर में डालने से पहले वॉशिंग मशीन को समाप्त करना होगा) . फिर, टोपोलॉजिकल सॉर्ट आदेश देता है जिसमें कार्य करना है। [[परियोजना प्रबंधन]] में शेड्यूलिंग के लिए [[कार्यक्रम मूल्यांकन और समीक्षा तकनीक]] तकनीक के संदर्भ में टोपोलॉजिकल सॉर्टिंग एल्गोरिदम के निकट संबंधी अनुप्रयोग का पहली बार 1960 के दशक की प्रारंभ में अध्ययन किया गया था।{{r|Jarnagin}} इस एप्लिकेशन में, ग्राफ़ के कोने किसी प्रोजेक्ट के मील के पत्थर का प्रतिनिधित्व करते हैं, और किनारे उन कार्यों का प्रतिनिधित्व करते हैं जिन्हें मील के पत्थर और दूसरे के बीच निष्पादित किया जाना चाहिए। टोपोलॉजिकल सॉर्टिंग परियोजना के महत्वपूर्ण पथ विधि, मील के पत्थर और कार्यों के अनुक्रम को खोजने के लिए रैखिक-समय एल्गोरिदम का आधार बनाती है जो समग्र परियोजना अनुसूची की लंबाई को नियंत्रित करती है। | ||
कंप्यूटर विज्ञान में, इस प्रकार के अनुप्रयोग अनुदेश शेड्यूलिंग, [[स्प्रेडशीट]] | कंप्यूटर विज्ञान में, इस प्रकार के अनुप्रयोग अनुदेश शेड्यूलिंग, [[स्प्रेडशीट]] में सूत्र मानों की पुन: गणना करते समय सूत्र सेल मूल्यांकन का क्रम, [[तर्क संश्लेषण]], [[मेकफ़ाइल]] में प्रदर्शन करने के लिए संकलन कार्यों के क्रम का निर्धारण, डेटा [[क्रमबद्धता]], और [[लिंकर (कंप्यूटिंग)]] में प्रतीक निर्भरता को हल करने में उत्पन्न होते हैं। ). इसका उपयोग यह तय करने के लिए भी किया जाता है कि डेटाबेस में विदेशी कुंजियों के साथ तालिकाओं को किस क्रम में लोड किया जाता है। | ||
{| | {| | ||
|[[Image:Directed acyclic graph 2.svg|upright=0.8|left]] | |[[Image:Directed acyclic graph 2.svg|upright=0.8|left]] | ||
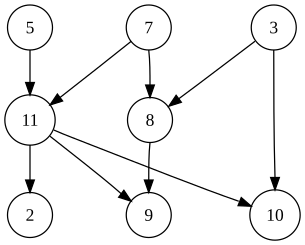
| | | बाईं ओर दिखाए गए ग्राफ़ में कई मान्य टोपोलॉजिकल प्रकार हैं, जिनमें सम्मिलित हैं: | ||
* 5, 7, 3, 11, 8, 2, 9, 10 ( | * 5, 7, 3, 11, 8, 2, 9, 10 (दृश्य ऊपर से नीचे, बाएँ से दाएँ) | ||
* 3, 5, 7, 8, 11, 2, 9, 10 ( | * 3, 5, 7, 8, 11, 2, 9, 10 (सबसे पहले सबसे छोटा क्रमांकित उपलब्ध शीर्ष) | ||
* 5, 7, 3, 8, 11, 10, 9, 2 ( | * 5, 7, 3, 8, 11, 10, 9, 2 (सबसे पहले सबसे कम किनारे) | ||
* 7, 5, 11, 3, 10, 8, 9, 2 ( | * 7, 5, 11, 3, 10, 8, 9, 2 (सबसे बड़ी संख्या वाला उपलब्ध शीर्ष पहले) | ||
* 5, 7, 11, 2, 3, 8, 9, 10 ( | * 5, 7, 11, 2, 3, 8, 9, 10 (ऊपर से नीचे, बाएँ से दाएँ प्रयास करना) | ||
* 3, 7, 8, 5, 11, 10, 2, 9 ( | * 3, 7, 8, 5, 11, 10, 2, 9 (स्वेच्छाचारी) | ||
|} | |} | ||
== एल्गोरिदम == | == एल्गोरिदम == | ||
टोपोलॉजिकल सॉर्टिंग के लिए सामान्य एल्गोरिदम में नोड्स की संख्या और किनारों की संख्या में रैखिक समय चलता है, असममित रूप से, <math>O(\left|{V}\right| + \left|{E}\right|).</math> | टोपोलॉजिकल सॉर्टिंग के लिए सामान्य एल्गोरिदम में नोड्स की संख्या और किनारों की संख्या में रैखिक समय चलता है, असममित रूप से, <math>O(\left|{V}\right| + \left|{E}\right|).</math> किया जाता है | ||
===काह्न का एल्गोरिदम=== | |||
{{Distinguish|कुह्न का एल्गोरिदम}} | |||
इनमें से एल्गोरिदम, जिसका वर्णन सबसे पहले किया गया था {{harvp|काह्न|1962}}, अंतिम टोपोलॉजिकल सॉर्ट के समान क्रम में शीर्षों को चुनकर काम करता है।{{r|Kahn}} सबसे पहले, प्रारंभ नोड्स की सूची खोजे जिनमें कोई आने वाला किनारा नहीं है और उन्हें समुच्चय एस में डालें; गैर-रिक्त चक्रीय ग्राफ़ में कम से कम ऐसा नोड उपस्थित होना चाहिए। तब:<syntaxhighlight lang="abl"> | |||
L ← Empty list that will contain the sorted elements | |||
S ← Set of all nodes with no incoming edge | |||
while S is not empty do | |||
remove a node n from S | |||
add n to L | |||
for each node m with an edge e from n to m do | |||
remove edge e from the graph | |||
if m has no other incoming edges then | |||
insert m into S | |||
if graph has edges then | |||
return error (graph has at least one cycle) | |||
else | |||
return L (a topologically sorted order) | |||
</syntaxhighlight>यदि ग्राफ़ निर्देशित चक्रीय ग्राफ़ है, तो समाधान सूची L में समाहित होगा (समाधान आवश्यक रूप से अद्वितीय नहीं है)। अन्यथा, ग्राफ़ में कम से कम चक्र होना चाहिए और इसलिए टोपोलॉजिकल सॉर्ट असंभव है। | |||
परिणामी प्रकार की गैर-विशिष्टता को दर्शाते हुए, संरचना एस केवल समुच्चय या कतार या स्टैक हो सकती है। समुच्चय एस से नोड्स एन को हटाए जाने के क्रम के आधार पर, अलग समाधान बनाया जाता है। काह्न के एल्गोरिदम का रूपांतर जो [[शब्दकोषीय क्रम]] के संबंधों को तोड़ता है, समानांतर शेड्यूलिंग और स्तरित ग्राफ़ ड्राइंग के लिए कॉफ़मैन-ग्राहम एल्गोरिदम का प्रमुख घटक बनाता है। | |||
===[[गहराई-पहली खोज|डेप्थ-प्रथम खोज]]=== | |||
टोपोलॉजिकल सॉर्टिंग के लिए वैकल्पिक एल्गोरिदम डेप्थ-प्रथम खोज पर आधारित है। एल्गोरिदम ग्राफ़ के प्रत्येक नोड के माध्यम से मनमाना क्रम में लूप करता है, डेप्थ-प्रथम खोज प्रारंभ करता है जो तब समाप्त होता है जब यह किसी भी नोड से टकराता है जो टोपोलॉजिकल सॉर्ट की प्रारंभ के पश्चात से पहले ही देखा जा चुका है या नोड में कोई आउटगोइंग किनारा नहीं है (अर्थात ए) लसीका नोड):<syntaxhighlight> | |||
L ← Empty list that will contain the sorted nodes | |||
while exists nodes without a permanent mark do | |||
select an unmarked node n | |||
visit(n) | |||
function visit(node n) | |||
if n has a permanent mark then | |||
return | |||
if n has a temporary mark then | |||
stop (graph has at least one cycle) | |||
mark n with a temporary mark | |||
for each node m with an edge from n to m do | |||
visit(m) | |||
प्रत्येक नोड n को अन्य सभी नोड्स पर विचार करने के | remove temporary mark from n | ||
mark n with a permanent mark | |||
add n to head of L | |||
</syntaxhighlight>प्रत्येक नोड n को अन्य सभी नोड्स पर विचार करने के पश्चात ही आउटपुट सूची L में जोड़ा जाता है जो n (ग्राफ़ में n के सभी वंशज) पर निर्भर होते हैं। विशेष रूप से, जब एल्गोरिदम नोड एन जोड़ता है, तो हमें गारंटी दी जाती है कि सभी नोड्स जो एन पर निर्भर हैं वे पहले से ही आउटपुट सूची एल में हैं: उन्हें एल में पुनरावर्ती कॉल द्वारा विज़िट() में जोड़ा गया था जो एन पर जाने के लिए कॉल से पहले समाप्त हो गया था, या विज़िट() के लिए कॉल द्वारा जो n पर विज़िट करने के लिए कॉल से पहले ही प्रारंभ हो गया था। चूँकि प्रत्येक किनारे और नोड का बार दौरा किया जाता है, एल्गोरिथ्म रैखिक समय में चलता है। यह गहराई-प्रथम-खोज-आधारित एल्गोरिदम द्वारा वर्णित है {{harvp|कॉर्मेन|लेइसर्सन|Rivest|स्टीन|2001}};{{r|CLRS}} ऐसा लगता है कि इसका वर्णन पहली बार 1976 में टार्जन द्वारा मुद्रित रूप में किया गया था।{{r|Tarjan}} | |||
===समानांतर एल्गोरिदम=== | ===समानांतर एल्गोरिदम=== | ||
एक [[समानांतर रैंडम-एक्सेस मशीन]] पर, O | एक [[समानांतर रैंडम-एक्सेस मशीन]] पर, O<sup>2</sup> लॉग एन में टोपोलॉजिकल ऑर्डरिंग का निर्माण किया जा सकता है प्रोसेसर की बहुपद संख्या का उपयोग करते हुए, समस्या को जटिलता वर्ग [[एनसी (जटिलता)]] में डालें.{{r|Cook}} ऐसा करने का विधि यह है कि दिए गए ग्राफ़ के आसन्न मैट्रिक्स को बार-बार लघुगणकीय रूप से कई बार वर्गाकार किया जाए, जिसमें न्यूनतमकरण के स्थान पर अधिकतमीकरण के साथ [[न्यूनतम-प्लस मैट्रिक्स गुणन]] का उपयोग किया जाता है। परिणामी मैट्रिक्स ग्राफ़ में सबसे लंबी पथ समस्या दूरी का वर्णन करता है। शीर्षों को उनके सबसे लंबे आने वाले पथों की लंबाई के आधार पर क्रमबद्ध करने से टोपोलॉजिकल ऑर्डरिंग उत्पन्न होती है।{{r|DNS}} | ||
ऐसा करने का | |||
वितरित मेमोरी मशीनों पर समानांतर टोपोलॉजिकल सॉर्टिंग के लिए एल्गोरिदम निर्देशित एसाइक्लिक ग्राफ के लिए काह्न के एल्गोरिदम <math>G = (V, E)</math> को समानांतर करता है .{{r|SMDD}} उच्च स्तर पर, काह्न का एल्गोरिदम बार-बार इंडिग्री 0 के शीर्षों को हटाता है और उन्हें उसी क्रम में टोपोलॉजिकल सॉर्टिंग में जोड़ता है जिसमें उन्हें हटाया गया था। चूंकि हटाए गए शीर्षों के आउटगोइंग किनारों को भी हटा दिया गया है, डिग्री 0 के शीर्षों का नया समुच्चय होगा, जहां प्रक्रिया तब तक दोहराई जाती है जब तक कि कोई शीर्ष न बचे। यह एल्गोरिथम कार्य करता है <math>D+1</math> पुनरावृत्तियाँ, जहाँ {{mvar|D}} सबसे लंबा रास्ता है {{mvar|G}}. प्रत्येक पुनरावृत्ति को समानांतर किया जा सकता है, जो निम्नलिखित एल्गोरिदम का विचार है। | |||
निम्नलिखित में यह माना गया है कि ग्राफ़ विभाजन {{mvar|p}} पर संग्रहीत है प्रसंस्करण तत्व (पीई) जिन्हें <math>0, \dots, p-1</math> लेबल किया गया है . प्रत्येक पीई {{mvar|i}} स्थानीय शीर्षों के समुच्चय को प्रारंभ करता है <math>Q_i^1</math> [[डिग्री]] 0 के साथ, जहां ऊपरी सूचकांक वर्तमान पुनरावृत्ति का प्रतिनिधित्व करता है। चूँकि सभी शीर्ष स्थानीय समुच्चय में हैं <math>Q_0^1, \dots, Q_{p-1}^1</math> डिग्री 0 है, अर्थात वे आसन्न नहीं हैं, उन्हें वैध टोपोलॉजिकल सॉर्टिंग के लिए मनमाने विधि से क्रम में दिया जा सकता है। प्रत्येक शीर्ष पर वैश्विक सूचकांक निर्दिष्ट करने के लिए, [[उपसर्ग योग]] की गणना आकारों पर की जाती है <math>Q_0^1, \dots, Q_{p-1}^1</math>. तो हर कदम पर हैं <math display="inline">\sum_{i=0}^{p-1} |Q_i|</math> टोपोलॉजिकल सॉर्टिंग में शीर्ष जोड़े गए थे। | |||
[[File:Parallel_Topological_Sorting.gif|thumb|upright=1.35|दो प्रसंस्करण तत्वों के साथ डीएजी पर समानांतर टोपोलॉजिकल सॉर्टिंग एल्गोरिदम का निष्पादन।]]पहले चरण में पी.ई {{mvar|j}} सूचकांक निर्दिष्ट करता है <math display="inline">\sum_{i=0}^{j-1} |Q_i^1|, \dots, \left(\sum_{i=0}^{j} |Q_i^1|\right) - 1</math> में स्थानीय शिखर तक <math>Q_j^1</math>. इन शिखरों में <math>Q_j^1</math> उनके संगत आउटगोइंग किनारों सहित हटा दिए जाते हैं। प्रत्येक आउटगोइंग किनारे के लिए <math>(u, v)</math> समापन बिंदु के साथ {{mvar|v}} दूसरे पीई में <math>l, j \neq l</math>, संदेश <math>(u, v)</math> पीई में पोस्ट किया गया है {{mvar|l}}. आख़िरकार शिखर में <math>Q_j^1</math> हटा दिए जाते हैं, पोस्ट किए गए संदेश उनके संबंधित पीई को भेज दिए जाते हैं। प्रत्येक संदेश <math>(u, v)</math> स्थानीय वर्टेक्स | |||
की डिग्री {{mvar|v}} के अपडेट प्राप्त हुए . यदि डिग्री शून्य हो जाती है, {{mvar|v}} जोड़ा गया है <math>Q_j^2</math>. फिर अगली पुनरावृत्ति प्रारंभ होती है. | |||
चरण में {{mvar|k}}, पर {{mvar|j}} सूचकांक <math display="inline">a_{k-1} + \sum_{i=0}^{j-1} |Q_i^k|, \dots, a_{k-1} + \left(\sum_{i=0}^{j} |Q_i^k|\right) - 1</math> निर्दिष्ट करता है , जहाँ <math>a_{k-1}</math>चरण दर चरण संसाधित शीर्षों की कुल मात्रा {{tmath|k-1}} है . यह प्रक्रिया तब तक दोहराई जाती है जब तक कि प्रक्रिया <math display="inline">\sum_{i=0}^{p-1} |Q_i^{D+1}| = 0</math> के लिए कोई शीर्ष शेष न रह जाए . नीचे इस एल्गोरिथम का उच्च स्तरीय, एसपीएमडी एकल प्रोग्राम, एकाधिक डेटा छद्म कोड अवलोकन है। | |||
ध्यान दें कि स्थानीय ऑफसेट के लिए उपसर्ग योग समानांतर एल्गोरिदम <math display="inline">a_{k-1} + \sum_{i=0}^{j-1} |Q_i^k|, \dots, a_{k-1} + \left(\sum_{i=0}^{j} |Q_i^k|\right) - 1</math> समानांतर रूप से कुशलतापूर्वक गणना की जा सकती है।<syntaxhighlight> | |||
p processing elements with IDs from 0 to p-1 | |||
Input: G = (V, E) DAG, distributed to PEs, PE index j = 0, ..., p - 1 | |||
Output: topological sorting of G | |||
function traverseDAGDistributed | |||
δ incoming degree of local vertices V | |||
Q = {v ∈ V | δ[v] = 0} // All vertices with indegree 0 | |||
nrOfVerticesProcessed = 0 | |||
do | |||
global build prefix sum over size of Q // get offsets and total amount of vertices in this step | |||
offset = nrOfVerticesProcessed + sum(Qi, i = 0 to j - 1) // j is the processor index | |||
foreach u in Q | |||
localOrder[u] = index++; | |||
foreach (u,v) in E do post message (u, v) to PE owning vertex v | |||
nrOfVerticesProcessed += sum(|Qi|, i = 0 to p - 1) | |||
deliver all messages to neighbors of vertices in Q | |||
receive messages for local vertices V | |||
remove all vertices in Q | |||
foreach message (u, v) received: | |||
if --δ[v] = 0 | |||
add v to Q | |||
while global size of Q > 0 | |||
return localOrder | |||
</syntaxhighlight> | |||
संचार निवेश दिए गए ग्राफ़ विभाजन पर अधिक सीमा तक निर्भर करती है। रनटाइम के लिए, [[CRCW PRAM|सीआरसीडब्ल्यू प्रैम]] मॉडल पर जो निरंतर समय में फ़ेच-एंड-डिक्रीमेंट की अनुमति देता है, यह एल्गोरिदम <math display="inline">\mathcal{O} \left(\frac{m + n}{p} + D (\Delta + \log n)\right)</math> चलता है , जहाँ {{mvar|D}} फिर से सबसे लंबा रास्ता है {{mvar|G}} और {{mvar|Δ}} अधिकतम डिग्री है.{{r|SMDD}} | |||
संचार | |||
==सबसे छोटा पथ खोजने के लिए आवेदन== | ==सबसे छोटा पथ खोजने के लिए आवेदन== | ||
टोपोलॉजिकल ऑर्डरिंग का उपयोग [[भारित ग्राफ]] निर्देशित एसाइक्लिक ग्राफ के माध्यम से सबसे छोटी पथ समस्या की त्वरित गणना करने के लिए भी किया जा सकता है। होने देना {{mvar|V}} ऐसे ग्राफ़ में शीर्षों की सूची टोपोलॉजिकल क्रम में | टोपोलॉजिकल ऑर्डरिंग का उपयोग [[भारित ग्राफ]] निर्देशित एसाइक्लिक ग्राफ के माध्यम से सबसे छोटी पथ समस्या की त्वरित गणना करने के लिए भी किया जा सकता है। होने देना {{mvar|V}} ऐसे ग्राफ़ में शीर्षों की सूची टोपोलॉजिकल क्रम में होटी है। फिर निम्नलिखित एल्गोरिदम कुछ स्रोत शीर्ष से सबसे छोटे पथ की गणना करता है {{mvar|s}} अन्य सभी शीर्षों के लिए:{{r|CLRS}} | ||
<div शैली= मार्जिन-बाएँ: 35px; चौड़ाई: 600px > | <div शैली= मार्जिन-बाएँ: 35px; चौड़ाई: 600px > | ||
{{framebox| | {{framebox|नीला}} | ||
* | * मान लीजिए {{mvar|d}} समान लंबाई की एक सरणी बनें {{mvar|V}}; यह सबसे कम पथ की दूरी बनाए रखेगा {{mvar|s}}. तय करना {{math|1=''d''[''s''] = 0}}, अन्य सभी {{math|1=''d''[''u''] = ∞}}. | ||
* | * मान लीजिए {{mvar|p}} समान लंबाई की एक सरणी बनें {{mvar|V}}, सभी तत्वों को आरंभीकृत करते हुए {{mono|nil}}. प्रत्येक {{math|''p''[''u'']}} का पूर्ववर्ती धारण करेगा {{math|''u''}} से सबसे छोटे रास्ते में {{mvar|s}} को {{mvar|u}}. | ||
* शीर्षों पर लूप करें {{mvar|u}} जैसा आदेश दिया गया है {{mvar|V}}, से | * शीर्षों पर लूप करें {{mvar|u}} जैसा आदेश दिया गया है {{mvar|V}}, से प्रारंभ {{mvar|s}}: | ||
** प्रत्येक शीर्ष के लिए {{mvar|v}} सीधे अनुसरण कर रहा हूँ {{mvar|u}} ( | ** प्रत्येक शीर्ष के लिए {{mvar|v}} सीधे अनुसरण कर रहा हूँ {{mvar|u}} (अर्थात, वहां से एक किनारा उपस्थित है {{mvar|u}} को {{mvar|v}}): | ||
*** | *** माना{{mvar|w}} से किनारे का वजन हो {{mvar|u}} को {{mvar|v}}. | ||
*** किनारे को आराम दें: यदि {{math|''d''[''v''] > ''d''[''u''] + ''w''}}, तय करना | *** किनारे को आराम दें: यदि {{math|''d''[''v''] > ''d''[''u''] + ''w''}}, तय करना | ||
**** {{math|''d''[''v''] ← ''d''[''u''] + ''w''}}, | **** {{math|''d''[''v''] ← ''d''[''u''] + ''w''}}, | ||
| Line 131: | Line 127: | ||
समान रूप से: | समान रूप से: | ||
<div शैली= मार्जिन-बाएँ: 35px; चौड़ाई: 600px > | <div शैली= मार्जिन-बाएँ: 35px; चौड़ाई: 600px > | ||
{{framebox| | {{framebox|नीला}} | ||
* | * माना{{mvar|d}} समान लंबाई की एक सरणी बनें {{mvar|V}}; यह सबसे कम पथ की दूरी बनाए रखेगा {{mvar|s}}. तय करना {{math|1=''d''[''s''] = 0}}, अन्य सभी {{math|1=''d''[''u''] = ∞}}. | ||
* | * माना {{mvar|p}} समान लंबाई की एक सरणी बनें {{mvar|V}}, सभी तत्वों को आरंभीकृत करते हुए {{mono|nil}}. प्रत्येक {{math|''p''[''u'']}} का पूर्ववर्ती धारण करेगा {{mvar|u}} से सबसे छोटे रास्ते में {{mvar|s}} को {{mvar|u}}. | ||
* शीर्षों पर लूप करें {{mvar|u}} जैसा आदेश दिया गया है {{mvar|V}}, से | * शीर्षों पर लूप करें {{mvar|u}} जैसा आदेश दिया गया है {{mvar|V}}, से प्रारंभ {{mvar|s}}: | ||
** प्रत्येक शीर्ष के लिए {{mvar|v}} में {{mvar|u}} ( | ** प्रत्येक शीर्ष के लिए {{mvar|v}} में {{mvar|u}} (अर्थात, वहां से एक किनारा उपस्थित है {{mvar|v}} को {{mvar|u}}): | ||
*** | *** माना {{mvar|w}} से किनारे का वजन हो {{mvar|v}} को {{mvar|u}}. | ||
*** किनारे को आराम दें: यदि {{math|''d''[''u''] > ''d''[''v''] + ''w''}}, तय करना | *** किनारे को आराम दें: यदि {{math|''d''[''u''] > ''d''[''v''] + ''w''}}, तय करना | ||
**** {{math|''d''[''u''] ← ''d''[''v''] + ''w''}}, | **** {{math|''d''[''u''] ← ''d''[''v''] + ''w''}}, | ||
| Line 143: | Line 139: | ||
</div> | </div> | ||
{{mvar|n}} के ग्राफ पर शीर्ष और {{mvar|m}} किनारे, यह एल्गोरिदम {{math|Θ(''n'' + ''m'')}} लेता है अर्थात, रैखिक समय है।{{r|CLRS}} | |||
==अद्वितीयता== | ==अद्वितीयता== | ||
यदि टोपोलॉजिकल सॉर्ट में यह गुण है कि क्रमबद्ध क्रम में | यदि टोपोलॉजिकल सॉर्ट में यह गुण है कि क्रमबद्ध क्रम में निरंतर शीर्षों के सभी जोड़े किनारों से जुड़े हुए हैं, तो ये किनारे निर्देशित एसाइक्लिक ग्राफ में निर्देशित [[हैमिल्टनियन पथ]] बनाते हैं। यदि हैमिल्टनियन पथ उपस्थित है, तो टोपोलॉजिकल सॉर्ट क्रम अद्वितीय है; कोई अन्य आदेश पथ के किनारों का सम्मान नहीं करता है। इसके विपरीत, यदि कोई टोपोलॉजिकल सॉर्ट हैमिल्टनियन पथ नहीं बनाता है, तो डीएजी के पास दो या अधिक वैध टोपोलॉजिकल ऑर्डर होंगे, इस स्थिति में दो निरंतर शीर्षों को स्वैप करके दूसरा वैध ऑर्डर बनाना सदैव संभव होता है जो किनारे से जुड़े नहीं होते हैं दूसरे से इसलिए, रैखिक समय में परीक्षण करना संभव है कि क्या अद्वितीय क्रम उपस्थित है, और क्या हैमिल्टनियन पथ उपस्थित है, अधिक सामान्य निर्देशित ग्राफ़ (अर्थात चक्रीय निर्देशित ग्राफ़) के लिए हैमिल्टनियन पथ समस्या की एनपी-कठोरता के अतिरिक्त होता है।{{r|VM}} | ||
==[[आंशिक आदेश]] | ==[[आंशिक आदेश]] से संबंध== | ||
टोपोलॉजिकल ऑर्डरिंग का गणित में आंशिक ऑर्डर के [[रैखिक विस्तार]] की अवधारणा से भी गहरा संबंध है। आंशिक रूप से ऑर्डर किया गया | टोपोलॉजिकल ऑर्डरिंग का गणित में आंशिक ऑर्डर के [[रैखिक विस्तार]] की अवधारणा से भी गहरा संबंध है। आंशिक रूप से ऑर्डर किया गया समुच्चय ≤ असमानता संबंध की परिभाषा के साथ वस्तुओं का समुच्चय है, जो रिफ्लेक्सिविटी (x ≤ x), एंटीसिममेट्री (यदि x ≤ y और y ≤ x है तो x = y) और [[सकर्मक संबंध]] ( यदि x ≤ y और y ≤ z, तो x ≤ z)। कुल क्रम आंशिक क्रम है, जिसमें समुच्चय में प्रत्येक दो वस्तुओं x और y के लिए, या तो x ≤ y या y ≤ x होता है। कुल ऑर्डर कंप्यूटर विज्ञान में परिचित हैं क्योंकि तुलना संचालको को तुलना सॉर्टिंग एल्गोरिदम निष्पादित करने की आवश्यकता होती है। परिमित सेटों के लिए, कुल आदेशों को वस्तुओं के रैखिक अनुक्रमों से पहचाना जा सकता है, जहां ≤ संबंध सत्य होता है जब भी पहली वस्तु क्रम में दूसरी वस्तु से पहले आती है; इस तरह कुल ऑर्डर को अनुक्रम में बदलने के लिए तुलनात्मक सॉर्टिंग एल्गोरिदम का उपयोग किया जा सकता है। आंशिक क्रम का रैखिक विस्तार कुल क्रम है जो इसके साथ संगत है, इस अर्थ में कि, यदि आंशिक क्रम में x ≤ y है, तो कुल क्रम में x ≤ y भी है। | ||
कोई भी किसी भी | कोई भी किसी भी डीएजी से आंशिक क्रम को परिभाषित कर सकता है, वस्तुओं के समुच्चय को डीएजी का शीर्ष मान सकता है, और किसी भी दो शीर्ष x और y के लिए x ≤ y को सत्य के रूप में परिभाषित कर सकता है, जब भी x से y तक कोई [[निर्देशित पथ]] उपस्थित होता है; अर्थात, जब भी y, x से पहुंच योग्य हो। इन परिभाषाओं के साथ, डीएजी का टोपोलॉजिकल ऑर्डरिंग इस आंशिक ऑर्डर के रैखिक विस्तार के समान है। इसके विपरीत, किसी भी आंशिक आदेश को डीएजी में पहुंच योग्यता संबंध के रूप में परिभाषित किया जा सकता है। ऐसा करने का विधि डीएजी को परिभाषित करना है जिसमें आंशिक रूप से ऑर्डर किए गए समुच्चय में प्रत्येक ऑब्जेक्ट के लिए शीर्ष होता है, और वस्तुओं की प्रत्येक जोड़ी के लिए किनारा xy होता है जिसके लिए x ≤ y होता है। ऐसा करने का वैकल्पिक विधि आंशिक क्रम की [[सकर्मक कमी]] का उपयोग करना है; सामान्यतः, यह कम किनारों वाले डीएजी उत्पन्न करता है, किन्तु इन डीएजी में पहुंच योग्यता संबंध अभी भी वही आंशिक क्रम है। इन निर्माणों का उपयोग करके, कोई आंशिक आदेशों के रैखिक विस्तार को खोजने के लिए टोपोलॉजिकल ऑर्डरिंग एल्गोरिदम का उपयोग कर सकता है। | ||
== शेड्यूलिंग अनुकूलन से संबंध == | == शेड्यूलिंग अनुकूलन से संबंध == | ||
परिभाषा के अनुसार, | परिभाषा के अनुसार, शेड्यूलिंग समस्या का समाधान जिसमें प्राथमिकता ग्राफ सम्मिलित है, टोपोलॉजिकल सॉर्ट (मशीनों की संख्या की परवाह किए बिना) के लिए वैध समाधान है, चूँकि, टोपोलॉजिकल सॉर्ट अपने आप में शेड्यूलिंग अनुकूलन समस्या को उत्तम विधि से हल करने के लिए पर्याप्त नहीं है। एल्गोरिदम लोकप्रिय विधि है जिसका उपयोग शेड्यूलिंग समस्याओं को हल करने के लिए किया जाता है जिसके लिए प्राथमिकता ग्राफ की आवश्यकता होती है और इसमें प्रसंस्करण समय सम्मिलित होता है (जहां लक्ष्य सभी नौकरियों के बीच सबसे बड़े समापन समय को कम करना है)। टोपोलॉजिकल सॉर्ट की तरह, हू का एल्गोरिदम अद्वितीय नहीं है और इसे डीएफएस का उपयोग करके हल किया जा सकता है (सबसे बड़ी पथ लंबाई खोजकर और फिर नौकरियां निर्दिष्ट करके)। | ||
==यह भी देखें== | ==यह भी देखें== | ||
* [[tsort]], टोपोलॉजिकल सॉर्टिंग के लिए | * [[tsort|टीसॉर्ट]], टोपोलॉजिकल सॉर्टिंग के लिए यूनिक्स प्रोग्राम | ||
* फीडबैक आर्क | * फीडबैक आर्क समुच्चय, किनारों का समुच्चय जिसे हटाने से शेष सबग्राफ को टोपोलॉजिकल रूप से क्रमबद्ध किया जा सकता है | ||
* टार्जन का दृढ़ता से जुड़े घटकों का एल्गोरिदम, | * टार्जन का दृढ़ता से जुड़े घटकों का एल्गोरिदम, एल्गोरिदम जो ग्राफ़ में दृढ़ता से जुड़े घटकों की टोपोलॉजिकल रूप से क्रमबद्ध सूची देता है | ||
* [[प्री-टोपोलॉजिकल ऑर्डर]] | * [[प्री-टोपोलॉजिकल ऑर्डर]] | ||
==संदर्भ== | ==संदर्भ == | ||
{{reflist|refs= | {{reflist|refs= | ||
| Line 235: | Line 231: | ||
}} | }} | ||
==अग्रिम पठन == | |||
==अग्रिम पठन== | |||
*[[D. E. Knuth]], [[The Art of Computer Programming]], Volume 1, section 2.2.3, which gives an algorithm for topological sorting of a partial ordering, and a brief history. | *[[D. E. Knuth]], [[The Art of Computer Programming]], Volume 1, section 2.2.3, which gives an algorithm for topological sorting of a partial ordering, and a brief history. | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* [https://xlinux.nist.gov/dads/HTML/topologicalSort.html NIST Dictionary of Algorithms and Data Structures: topological sort] | * [https://xlinux.nist.gov/dads/HTML/topologicalSort.html NIST Dictionary of Algorithms and Data Structures: topological sort] | ||
* {{MathWorld|urlname=TopologicalSort|title=Topological Sort|mode=cs2}} | * {{MathWorld|urlname=TopologicalSort|title=Topological Sort|mode=cs2}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category: | |||
[[Category:Created On 27/06/2023]] | [[Category:Created On 27/06/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Missing redirects]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Pages with syntax highlighting errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:ग्राफ़ एल्गोरिदम]] | |||
[[Category:छँटाई एल्गोरिदम]] | |||
[[Category:निर्देशित अचक्रीय रेखांकन]] | |||
[[Category:स्यूडोकोड उदाहरण सहित लेख]] | |||
Latest revision as of 14:07, 3 August 2023
कंप्यूटर विज्ञान में, निर्देशित ग्राफ का टोपोलॉजिकल सॉर्ट या टोपोलॉजिकल ऑर्डरिंग इसके शीर्ष (ग्राफ सिद्धांत) का कुल क्रम है, जैसे कि प्रत्येक निर्देशित किनारे यूवी के लिए शीर्ष u से शीर्ष v तक , u क्रम में v से पहले आता है। उदाहरण के लिए, ग्राफ़ के शीर्ष निष्पादित किए जाने वाले कार्यों का प्रतिनिधित्व कर सकते हैं, और किनारे उन बाधाओं का प्रतिनिधित्व कर सकते हैं कि कार्य दूसरे से पहले किया जाना चाहिए; इस एप्लिकेशन में, टोपोलॉजिकल ऑर्डरिंग कार्यों के लिए सिर्फ वैध अनुक्रम है। संक्षेप में, टोपोलॉजिकल सॉर्ट ग्राफ़ ट्रैवर्सल है जिसमें प्रत्येक नोड v पर उसकी सभी निर्भरताओं का दौरा करने के पश्चात ही दौरा किया जाता है। टोपोलॉजिकल ऑर्डरिंग तभी संभव है जब ग्राफ़ में कोई निर्देशित चक्र न हो, अर्थात , यदि यह निर्देशित अचक्रीय ग्राफ (डीएजी) है। किसी भी डीएजी में कम से कम टोपोलॉजिकल ऑर्डरिंग होती है, और कलन विधि रैखिक समय में किसी भी डीएजी के टोपोलॉजिकल ऑर्डरिंग के निर्माण के लिए जाने जाते हैं। टोपोलॉजिकल सॉर्टिंग के कई अनुप्रयोग हैं, विशेष रूप से फीडबैक आर्क समुच्चय जैसी रैंकिंग समस्याओं में डीएजी में कनेक्टिविटी (ग्राफ सिद्धांत) होने पर भी टोपोलॉजिकल सॉर्टिंग संभव है।
उदाहरण
टोपोलॉजिकल सॉर्टिंग का विहित अनुप्रयोग जॉब शॉप में उनके निर्भरता ग्राफ के आधार पर नौकरियों या कार्यों के अनुक्रम को शेड्यूल करना है। कार्यों को शीर्षों द्वारा दर्शाया जाता है, और यदि कार्य x को कार्य y प्रारंभ करने से पहले पूरा किया जाना चाहिए तो x से y तक बढ़त होती है (उदाहरण के लिए, कपड़े धोते समय, कपड़े को ड्रायर में डालने से पहले वॉशिंग मशीन को समाप्त करना होगा) . फिर, टोपोलॉजिकल सॉर्ट आदेश देता है जिसमें कार्य करना है। परियोजना प्रबंधन में शेड्यूलिंग के लिए कार्यक्रम मूल्यांकन और समीक्षा तकनीक तकनीक के संदर्भ में टोपोलॉजिकल सॉर्टिंग एल्गोरिदम के निकट संबंधी अनुप्रयोग का पहली बार 1960 के दशक की प्रारंभ में अध्ययन किया गया था।[1] इस एप्लिकेशन में, ग्राफ़ के कोने किसी प्रोजेक्ट के मील के पत्थर का प्रतिनिधित्व करते हैं, और किनारे उन कार्यों का प्रतिनिधित्व करते हैं जिन्हें मील के पत्थर और दूसरे के बीच निष्पादित किया जाना चाहिए। टोपोलॉजिकल सॉर्टिंग परियोजना के महत्वपूर्ण पथ विधि, मील के पत्थर और कार्यों के अनुक्रम को खोजने के लिए रैखिक-समय एल्गोरिदम का आधार बनाती है जो समग्र परियोजना अनुसूची की लंबाई को नियंत्रित करती है।
कंप्यूटर विज्ञान में, इस प्रकार के अनुप्रयोग अनुदेश शेड्यूलिंग, स्प्रेडशीट में सूत्र मानों की पुन: गणना करते समय सूत्र सेल मूल्यांकन का क्रम, तर्क संश्लेषण, मेकफ़ाइल में प्रदर्शन करने के लिए संकलन कार्यों के क्रम का निर्धारण, डेटा क्रमबद्धता, और लिंकर (कंप्यूटिंग) में प्रतीक निर्भरता को हल करने में उत्पन्न होते हैं। ). इसका उपयोग यह तय करने के लिए भी किया जाता है कि डेटाबेस में विदेशी कुंजियों के साथ तालिकाओं को किस क्रम में लोड किया जाता है।
बाईं ओर दिखाए गए ग्राफ़ में कई मान्य टोपोलॉजिकल प्रकार हैं, जिनमें सम्मिलित हैं:
|
एल्गोरिदम
टोपोलॉजिकल सॉर्टिंग के लिए सामान्य एल्गोरिदम में नोड्स की संख्या और किनारों की संख्या में रैखिक समय चलता है, असममित रूप से, किया जाता है
काह्न का एल्गोरिदम
इनमें से एल्गोरिदम, जिसका वर्णन सबसे पहले किया गया था काह्न (1962), अंतिम टोपोलॉजिकल सॉर्ट के समान क्रम में शीर्षों को चुनकर काम करता है।[2] सबसे पहले, प्रारंभ नोड्स की सूची खोजे जिनमें कोई आने वाला किनारा नहीं है और उन्हें समुच्चय एस में डालें; गैर-रिक्त चक्रीय ग्राफ़ में कम से कम ऐसा नोड उपस्थित होना चाहिए। तब:
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edge
while S is not empty do
remove a node n from S
add n to L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least one cycle)
else
return L (a topologically sorted order)
यदि ग्राफ़ निर्देशित चक्रीय ग्राफ़ है, तो समाधान सूची L में समाहित होगा (समाधान आवश्यक रूप से अद्वितीय नहीं है)। अन्यथा, ग्राफ़ में कम से कम चक्र होना चाहिए और इसलिए टोपोलॉजिकल सॉर्ट असंभव है।
परिणामी प्रकार की गैर-विशिष्टता को दर्शाते हुए, संरचना एस केवल समुच्चय या कतार या स्टैक हो सकती है। समुच्चय एस से नोड्स एन को हटाए जाने के क्रम के आधार पर, अलग समाधान बनाया जाता है। काह्न के एल्गोरिदम का रूपांतर जो शब्दकोषीय क्रम के संबंधों को तोड़ता है, समानांतर शेड्यूलिंग और स्तरित ग्राफ़ ड्राइंग के लिए कॉफ़मैन-ग्राहम एल्गोरिदम का प्रमुख घटक बनाता है।
डेप्थ-प्रथम खोज
टोपोलॉजिकल सॉर्टिंग के लिए वैकल्पिक एल्गोरिदम डेप्थ-प्रथम खोज पर आधारित है। एल्गोरिदम ग्राफ़ के प्रत्येक नोड के माध्यम से मनमाना क्रम में लूप करता है, डेप्थ-प्रथम खोज प्रारंभ करता है जो तब समाप्त होता है जब यह किसी भी नोड से टकराता है जो टोपोलॉजिकल सॉर्ट की प्रारंभ के पश्चात से पहले ही देखा जा चुका है या नोड में कोई आउटगोइंग किनारा नहीं है (अर्थात ए) लसीका नोड):
L ← Empty list that will contain the sorted nodes
while exists nodes without a permanent mark do
select an unmarked node n
visit(n)
function visit(node n)
if n has a permanent mark then
return
if n has a temporary mark then
stop (graph has at least one cycle)
mark n with a temporary mark
for each node m with an edge from n to m do
visit(m)
remove temporary mark from n
mark n with a permanent mark
add n to head of Lप्रत्येक नोड n को अन्य सभी नोड्स पर विचार करने के पश्चात ही आउटपुट सूची L में जोड़ा जाता है जो n (ग्राफ़ में n के सभी वंशज) पर निर्भर होते हैं। विशेष रूप से, जब एल्गोरिदम नोड एन जोड़ता है, तो हमें गारंटी दी जाती है कि सभी नोड्स जो एन पर निर्भर हैं वे पहले से ही आउटपुट सूची एल में हैं: उन्हें एल में पुनरावर्ती कॉल द्वारा विज़िट() में जोड़ा गया था जो एन पर जाने के लिए कॉल से पहले समाप्त हो गया था, या विज़िट() के लिए कॉल द्वारा जो n पर विज़िट करने के लिए कॉल से पहले ही प्रारंभ हो गया था। चूँकि प्रत्येक किनारे और नोड का बार दौरा किया जाता है, एल्गोरिथ्म रैखिक समय में चलता है। यह गहराई-प्रथम-खोज-आधारित एल्गोरिदम द्वारा वर्णित है कॉर्मेन et al. (2001);[3] ऐसा लगता है कि इसका वर्णन पहली बार 1976 में टार्जन द्वारा मुद्रित रूप में किया गया था।[4]
समानांतर एल्गोरिदम
एक समानांतर रैंडम-एक्सेस मशीन पर, O2 लॉग एन में टोपोलॉजिकल ऑर्डरिंग का निर्माण किया जा सकता है प्रोसेसर की बहुपद संख्या का उपयोग करते हुए, समस्या को जटिलता वर्ग एनसी (जटिलता) में डालें.[5] ऐसा करने का विधि यह है कि दिए गए ग्राफ़ के आसन्न मैट्रिक्स को बार-बार लघुगणकीय रूप से कई बार वर्गाकार किया जाए, जिसमें न्यूनतमकरण के स्थान पर अधिकतमीकरण के साथ न्यूनतम-प्लस मैट्रिक्स गुणन का उपयोग किया जाता है। परिणामी मैट्रिक्स ग्राफ़ में सबसे लंबी पथ समस्या दूरी का वर्णन करता है। शीर्षों को उनके सबसे लंबे आने वाले पथों की लंबाई के आधार पर क्रमबद्ध करने से टोपोलॉजिकल ऑर्डरिंग उत्पन्न होती है।[6]
वितरित मेमोरी मशीनों पर समानांतर टोपोलॉजिकल सॉर्टिंग के लिए एल्गोरिदम निर्देशित एसाइक्लिक ग्राफ के लिए काह्न के एल्गोरिदम को समानांतर करता है .[7] उच्च स्तर पर, काह्न का एल्गोरिदम बार-बार इंडिग्री 0 के शीर्षों को हटाता है और उन्हें उसी क्रम में टोपोलॉजिकल सॉर्टिंग में जोड़ता है जिसमें उन्हें हटाया गया था। चूंकि हटाए गए शीर्षों के आउटगोइंग किनारों को भी हटा दिया गया है, डिग्री 0 के शीर्षों का नया समुच्चय होगा, जहां प्रक्रिया तब तक दोहराई जाती है जब तक कि कोई शीर्ष न बचे। यह एल्गोरिथम कार्य करता है पुनरावृत्तियाँ, जहाँ D सबसे लंबा रास्ता है G. प्रत्येक पुनरावृत्ति को समानांतर किया जा सकता है, जो निम्नलिखित एल्गोरिदम का विचार है।
निम्नलिखित में यह माना गया है कि ग्राफ़ विभाजन p पर संग्रहीत है प्रसंस्करण तत्व (पीई) जिन्हें लेबल किया गया है . प्रत्येक पीई i स्थानीय शीर्षों के समुच्चय को प्रारंभ करता है डिग्री 0 के साथ, जहां ऊपरी सूचकांक वर्तमान पुनरावृत्ति का प्रतिनिधित्व करता है। चूँकि सभी शीर्ष स्थानीय समुच्चय में हैं डिग्री 0 है, अर्थात वे आसन्न नहीं हैं, उन्हें वैध टोपोलॉजिकल सॉर्टिंग के लिए मनमाने विधि से क्रम में दिया जा सकता है। प्रत्येक शीर्ष पर वैश्विक सूचकांक निर्दिष्ट करने के लिए, उपसर्ग योग की गणना आकारों पर की जाती है . तो हर कदम पर हैं टोपोलॉजिकल सॉर्टिंग में शीर्ष जोड़े गए थे।
पहले चरण में पी.ई j सूचकांक निर्दिष्ट करता है में स्थानीय शिखर तक . इन शिखरों में उनके संगत आउटगोइंग किनारों सहित हटा दिए जाते हैं। प्रत्येक आउटगोइंग किनारे के लिए समापन बिंदु के साथ v दूसरे पीई में , संदेश पीई में पोस्ट किया गया है l. आख़िरकार शिखर में हटा दिए जाते हैं, पोस्ट किए गए संदेश उनके संबंधित पीई को भेज दिए जाते हैं। प्रत्येक संदेश स्थानीय वर्टेक्स
की डिग्री v के अपडेट प्राप्त हुए . यदि डिग्री शून्य हो जाती है, v जोड़ा गया है . फिर अगली पुनरावृत्ति प्रारंभ होती है.
चरण में k, पर j सूचकांक निर्दिष्ट करता है , जहाँ चरण दर चरण संसाधित शीर्षों की कुल मात्रा है . यह प्रक्रिया तब तक दोहराई जाती है जब तक कि प्रक्रिया के लिए कोई शीर्ष शेष न रह जाए . नीचे इस एल्गोरिथम का उच्च स्तरीय, एसपीएमडी एकल प्रोग्राम, एकाधिक डेटा छद्म कोड अवलोकन है।
ध्यान दें कि स्थानीय ऑफसेट के लिए उपसर्ग योग समानांतर एल्गोरिदम समानांतर रूप से कुशलतापूर्वक गणना की जा सकती है।
p processing elements with IDs from 0 to p-1
Input: G = (V, E) DAG, distributed to PEs, PE index j = 0, ..., p - 1
Output: topological sorting of G
function traverseDAGDistributed
δ incoming degree of local vertices V
Q = {v ∈ V | δ[v] = 0} // All vertices with indegree 0
nrOfVerticesProcessed = 0
do
global build prefix sum over size of Q // get offsets and total amount of vertices in this step
offset = nrOfVerticesProcessed + sum(Qi, i = 0 to j - 1) // j is the processor index
foreach u in Q
localOrder[u] = index++;
foreach (u,v) in E do post message (u, v) to PE owning vertex v
nrOfVerticesProcessed += sum(|Qi|, i = 0 to p - 1)
deliver all messages to neighbors of vertices in Q
receive messages for local vertices V
remove all vertices in Q
foreach message (u, v) received:
if --δ[v] = 0
add v to Q
while global size of Q > 0
return localOrderसंचार निवेश दिए गए ग्राफ़ विभाजन पर अधिक सीमा तक निर्भर करती है। रनटाइम के लिए, सीआरसीडब्ल्यू प्रैम मॉडल पर जो निरंतर समय में फ़ेच-एंड-डिक्रीमेंट की अनुमति देता है, यह एल्गोरिदम चलता है , जहाँ D फिर से सबसे लंबा रास्ता है G और Δ अधिकतम डिग्री है.[7]
सबसे छोटा पथ खोजने के लिए आवेदन
टोपोलॉजिकल ऑर्डरिंग का उपयोग भारित ग्राफ निर्देशित एसाइक्लिक ग्राफ के माध्यम से सबसे छोटी पथ समस्या की त्वरित गणना करने के लिए भी किया जा सकता है। होने देना V ऐसे ग्राफ़ में शीर्षों की सूची टोपोलॉजिकल क्रम में होटी है। फिर निम्नलिखित एल्गोरिदम कुछ स्रोत शीर्ष से सबसे छोटे पथ की गणना करता है s अन्य सभी शीर्षों के लिए:[3]
- मान लीजिए d समान लंबाई की एक सरणी बनें V; यह सबसे कम पथ की दूरी बनाए रखेगा s. तय करना d[s] = 0, अन्य सभी d[u] = ∞.
- मान लीजिए p समान लंबाई की एक सरणी बनें V, सभी तत्वों को आरंभीकृत करते हुए nil. प्रत्येक p[u] का पूर्ववर्ती धारण करेगा u से सबसे छोटे रास्ते में s को u.
- शीर्षों पर लूप करें u जैसा आदेश दिया गया है V, से प्रारंभ s:
- प्रत्येक शीर्ष के लिए v सीधे अनुसरण कर रहा हूँ u (अर्थात, वहां से एक किनारा उपस्थित है u को v):
- मानाw से किनारे का वजन हो u को v.
- किनारे को आराम दें: यदि d[v] > d[u] + w, तय करना
- d[v] ← d[u] + w,
- p[v] ← u.
- प्रत्येक शीर्ष के लिए v सीधे अनुसरण कर रहा हूँ u (अर्थात, वहां से एक किनारा उपस्थित है u को v):
समान रूप से:
- मानाd समान लंबाई की एक सरणी बनें V; यह सबसे कम पथ की दूरी बनाए रखेगा s. तय करना d[s] = 0, अन्य सभी d[u] = ∞.
- माना p समान लंबाई की एक सरणी बनें V, सभी तत्वों को आरंभीकृत करते हुए nil. प्रत्येक p[u] का पूर्ववर्ती धारण करेगा u से सबसे छोटे रास्ते में s को u.
- शीर्षों पर लूप करें u जैसा आदेश दिया गया है V, से प्रारंभ s:
- प्रत्येक शीर्ष के लिए v में u (अर्थात, वहां से एक किनारा उपस्थित है v को u):
- माना w से किनारे का वजन हो v को u.
- किनारे को आराम दें: यदि d[u] > d[v] + w, तय करना
- d[u] ← d[v] + w,
- p[u] ← v.
- प्रत्येक शीर्ष के लिए v में u (अर्थात, वहां से एक किनारा उपस्थित है v को u):
n के ग्राफ पर शीर्ष और m किनारे, यह एल्गोरिदम Θ(n + m) लेता है अर्थात, रैखिक समय है।[3]
अद्वितीयता
यदि टोपोलॉजिकल सॉर्ट में यह गुण है कि क्रमबद्ध क्रम में निरंतर शीर्षों के सभी जोड़े किनारों से जुड़े हुए हैं, तो ये किनारे निर्देशित एसाइक्लिक ग्राफ में निर्देशित हैमिल्टनियन पथ बनाते हैं। यदि हैमिल्टनियन पथ उपस्थित है, तो टोपोलॉजिकल सॉर्ट क्रम अद्वितीय है; कोई अन्य आदेश पथ के किनारों का सम्मान नहीं करता है। इसके विपरीत, यदि कोई टोपोलॉजिकल सॉर्ट हैमिल्टनियन पथ नहीं बनाता है, तो डीएजी के पास दो या अधिक वैध टोपोलॉजिकल ऑर्डर होंगे, इस स्थिति में दो निरंतर शीर्षों को स्वैप करके दूसरा वैध ऑर्डर बनाना सदैव संभव होता है जो किनारे से जुड़े नहीं होते हैं दूसरे से इसलिए, रैखिक समय में परीक्षण करना संभव है कि क्या अद्वितीय क्रम उपस्थित है, और क्या हैमिल्टनियन पथ उपस्थित है, अधिक सामान्य निर्देशित ग्राफ़ (अर्थात चक्रीय निर्देशित ग्राफ़) के लिए हैमिल्टनियन पथ समस्या की एनपी-कठोरता के अतिरिक्त होता है।[8]
आंशिक आदेश से संबंध
टोपोलॉजिकल ऑर्डरिंग का गणित में आंशिक ऑर्डर के रैखिक विस्तार की अवधारणा से भी गहरा संबंध है। आंशिक रूप से ऑर्डर किया गया समुच्चय ≤ असमानता संबंध की परिभाषा के साथ वस्तुओं का समुच्चय है, जो रिफ्लेक्सिविटी (x ≤ x), एंटीसिममेट्री (यदि x ≤ y और y ≤ x है तो x = y) और सकर्मक संबंध ( यदि x ≤ y और y ≤ z, तो x ≤ z)। कुल क्रम आंशिक क्रम है, जिसमें समुच्चय में प्रत्येक दो वस्तुओं x और y के लिए, या तो x ≤ y या y ≤ x होता है। कुल ऑर्डर कंप्यूटर विज्ञान में परिचित हैं क्योंकि तुलना संचालको को तुलना सॉर्टिंग एल्गोरिदम निष्पादित करने की आवश्यकता होती है। परिमित सेटों के लिए, कुल आदेशों को वस्तुओं के रैखिक अनुक्रमों से पहचाना जा सकता है, जहां ≤ संबंध सत्य होता है जब भी पहली वस्तु क्रम में दूसरी वस्तु से पहले आती है; इस तरह कुल ऑर्डर को अनुक्रम में बदलने के लिए तुलनात्मक सॉर्टिंग एल्गोरिदम का उपयोग किया जा सकता है। आंशिक क्रम का रैखिक विस्तार कुल क्रम है जो इसके साथ संगत है, इस अर्थ में कि, यदि आंशिक क्रम में x ≤ y है, तो कुल क्रम में x ≤ y भी है।
कोई भी किसी भी डीएजी से आंशिक क्रम को परिभाषित कर सकता है, वस्तुओं के समुच्चय को डीएजी का शीर्ष मान सकता है, और किसी भी दो शीर्ष x और y के लिए x ≤ y को सत्य के रूप में परिभाषित कर सकता है, जब भी x से y तक कोई निर्देशित पथ उपस्थित होता है; अर्थात, जब भी y, x से पहुंच योग्य हो। इन परिभाषाओं के साथ, डीएजी का टोपोलॉजिकल ऑर्डरिंग इस आंशिक ऑर्डर के रैखिक विस्तार के समान है। इसके विपरीत, किसी भी आंशिक आदेश को डीएजी में पहुंच योग्यता संबंध के रूप में परिभाषित किया जा सकता है। ऐसा करने का विधि डीएजी को परिभाषित करना है जिसमें आंशिक रूप से ऑर्डर किए गए समुच्चय में प्रत्येक ऑब्जेक्ट के लिए शीर्ष होता है, और वस्तुओं की प्रत्येक जोड़ी के लिए किनारा xy होता है जिसके लिए x ≤ y होता है। ऐसा करने का वैकल्पिक विधि आंशिक क्रम की सकर्मक कमी का उपयोग करना है; सामान्यतः, यह कम किनारों वाले डीएजी उत्पन्न करता है, किन्तु इन डीएजी में पहुंच योग्यता संबंध अभी भी वही आंशिक क्रम है। इन निर्माणों का उपयोग करके, कोई आंशिक आदेशों के रैखिक विस्तार को खोजने के लिए टोपोलॉजिकल ऑर्डरिंग एल्गोरिदम का उपयोग कर सकता है।
शेड्यूलिंग अनुकूलन से संबंध
परिभाषा के अनुसार, शेड्यूलिंग समस्या का समाधान जिसमें प्राथमिकता ग्राफ सम्मिलित है, टोपोलॉजिकल सॉर्ट (मशीनों की संख्या की परवाह किए बिना) के लिए वैध समाधान है, चूँकि, टोपोलॉजिकल सॉर्ट अपने आप में शेड्यूलिंग अनुकूलन समस्या को उत्तम विधि से हल करने के लिए पर्याप्त नहीं है। एल्गोरिदम लोकप्रिय विधि है जिसका उपयोग शेड्यूलिंग समस्याओं को हल करने के लिए किया जाता है जिसके लिए प्राथमिकता ग्राफ की आवश्यकता होती है और इसमें प्रसंस्करण समय सम्मिलित होता है (जहां लक्ष्य सभी नौकरियों के बीच सबसे बड़े समापन समय को कम करना है)। टोपोलॉजिकल सॉर्ट की तरह, हू का एल्गोरिदम अद्वितीय नहीं है और इसे डीएफएस का उपयोग करके हल किया जा सकता है (सबसे बड़ी पथ लंबाई खोजकर और फिर नौकरियां निर्दिष्ट करके)।
यह भी देखें
- टीसॉर्ट, टोपोलॉजिकल सॉर्टिंग के लिए यूनिक्स प्रोग्राम
- फीडबैक आर्क समुच्चय, किनारों का समुच्चय जिसे हटाने से शेष सबग्राफ को टोपोलॉजिकल रूप से क्रमबद्ध किया जा सकता है
- टार्जन का दृढ़ता से जुड़े घटकों का एल्गोरिदम, एल्गोरिदम जो ग्राफ़ में दृढ़ता से जुड़े घटकों की टोपोलॉजिकल रूप से क्रमबद्ध सूची देता है
- प्री-टोपोलॉजिकल ऑर्डर
संदर्भ
- ↑ Jarnagin, M. P. (1960), Automatic machine methods of testing PERT networks for consistency, Technical Memorandum No. K-24/60, Dahlgren, Virginia: U. S. Naval Weapons Laboratory
- ↑ Kahn, Arthur B. (1962), "Topological sorting of large networks", Communications of the ACM, 5 (11): 558–562, doi:10.1145/368996.369025, S2CID 16728233
- ↑ 3.0 3.1 3.2 Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), "Section 22.4: Topological sort", Introduction to Algorithms (2nd ed.), MIT Press and McGraw-Hill, pp. 549–552, ISBN 0-262-03293-7
- ↑ Tarjan, Robert E. (1976), "Edge-disjoint spanning trees and depth-first search", Acta Informatica, 6 (2): 171–185, doi:10.1007/BF00268499, S2CID 12044793
- ↑ Cook, Stephen A. (1985), "A Taxonomy of Problems with Fast Parallel Algorithms", Information and Control, 64 (1–3): 2–22, doi:10.1016/S0019-9958(85)80041-3
- ↑ Dekel, Eliezer; Nassimi, David; Sahni, Sartaj (1981), "Parallel matrix and graph algorithms", SIAM Journal on Computing, 10 (4): 657–675, doi:10.1137/0210049, MR 0635424
- ↑ 7.0 7.1 Sanders, Peter; Mehlhorn, Kurt; Dietzfelbinger, Martin; Dementiev, Roman (2019), Sequential and Parallel Algorithms and Data Structures: The Basic Toolbox, Springer International Publishing, ISBN 978-3-030-25208-3
- ↑ Vernet, Oswaldo; Markenzon, Lilian (1997), "Hamiltonian problems for reducible flowgraphs" (PDF), Proceedings: 17th International Conference of the Chilean Computer Science Society, pp. 264–267, doi:10.1109/SCCC.1997.637099, hdl:11422/2585, S2CID 206554481
अग्रिम पठन
- D. E. Knuth, The Art of Computer Programming, Volume 1, section 2.2.3, which gives an algorithm for topological sorting of a partial ordering, and a brief history.