दूसरे क्रम की शंकु प्रोग्रामिंग: Difference between revisions
(Created page with "{{Technical|date=October 2011}} दूसरे क्रम का शंकु कार्यक्रम (एसओसीपी) प्रपत्र की उत्...") |
No edit summary |
||
| Line 1: | Line 1: | ||
दूसरे क्रम का शंकु कार्यक्रम (एसओसीपी) प्रपत्र की [[उत्तल अनुकूलन]] समस्या है | दूसरे क्रम का शंकु कार्यक्रम (एसओसीपी) प्रपत्र की [[उत्तल अनुकूलन]] समस्या है | ||
| Line 20: | Line 18: | ||
दूसरे क्रम के शंकु को द्विघात शंकु, आइसक्रीम शंकु या लोरेंत्ज़ शंकु के नाम से भी जाना जाता है। दूसरे क्रम का शंकु <math>\mathbb{R}^3</math> है <math>\left\{(x,y,z) \Big| \sqrt{x^2 + y^2} \leq z \right\}</math>. | दूसरे क्रम के शंकु को द्विघात शंकु, आइसक्रीम शंकु या लोरेंत्ज़ शंकु के नाम से भी जाना जाता है। दूसरे क्रम का शंकु <math>\mathbb{R}^3</math> है <math>\left\{(x,y,z) \Big| \sqrt{x^2 + y^2} \leq z \right\}</math>. | ||
दूसरे क्रम के शंकु बाधा को संतुष्ट करने वाले बिंदुओं का सेट | दूसरे क्रम के शंकु बाधा को संतुष्ट करने वाले बिंदुओं का सेट एफ़िन मैपिंग के तहत इकाई दूसरे क्रम के शंकु की व्युत्क्रम छवि है: | ||
<math>\lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i \Leftrightarrow | <math>\lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i \Leftrightarrow | ||
| Line 30: | Line 28: | ||
<math>||x||\leq t \Leftrightarrow \begin{bmatrix} tI & x \\ x^T & t \end{bmatrix} \succcurlyeq 0,</math> | <math>||x||\leq t \Leftrightarrow \begin{bmatrix} tI & x \\ x^T & t \end{bmatrix} \succcurlyeq 0,</math> | ||
यानी, दूसरे क्रम का शंकु अवरोध | यानी, दूसरे क्रम का शंकु अवरोध रैखिक मैट्रिक्स असमानता के बराबर है (यहां)। <math>M\succcurlyeq 0 </math> साधन <math>M </math> अर्धनिश्चित मैट्रिक्स है)। इसी प्रकार, हमारे पास भी है, | ||
<math>\lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i \Leftrightarrow | <math>\lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i \Leftrightarrow | ||
| Line 36: | Line 34: | ||
== अन्य अनुकूलन समस्याओं के साथ संबंध == | == अन्य अनुकूलन समस्याओं के साथ संबंध == | ||
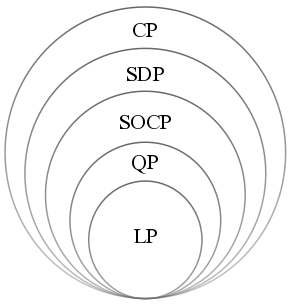
[[File:Hierarchy compact convex.png|thumb|उत्तल अनुकूलन समस्याओं का | [[File:Hierarchy compact convex.png|thumb|उत्तल अनुकूलन समस्याओं का पदानुक्रम. (एलपी: रैखिक कार्यक्रम, क्यूपी: द्विघात कार्यक्रम, एसओसीपी द्वितीय-क्रम शंकु कार्यक्रम, एसडीपी: अर्धनिश्चित कार्यक्रम, सीपी: शंकु कार्यक्रम।)]]कब <math>A_i = 0</math> के लिए <math>i = 1,\dots,m</math>, SOCP [[रैखिक कार्यक्रम]] में परिवर्तित हो जाता है। कब <math>c_i = 0 </math> के लिए <math>i = 1,\dots,m</math>, एसओसीपी उत्तल चतुर्भुज रूप से बाधित रैखिक कार्यक्रम के बराबर है। | ||
उत्तल चतुर्भुज रूप से बाधित द्विघात कार्यक्रमों को उद्देश्य फ़ंक्शन को | उत्तल चतुर्भुज रूप से बाधित द्विघात कार्यक्रमों को उद्देश्य फ़ंक्शन को बाधा के रूप में सुधारकर एसओसीपी के रूप में भी तैयार किया जा सकता है।<ref name=":0" />अर्धनिश्चित प्रोग्रामिंग एसओसीपी को समाहित करती है क्योंकि एसओसीपी बाधाओं को [[रैखिक मैट्रिक्स असमानता]] (एलएमआई) के रूप में लिखा जा सकता है और इसे अर्धनिश्चित कार्यक्रम के उदाहरण के रूप में पुन: तैयार किया जा सकता है।<ref name=":0" />हालाँकि, इसका उलटा मान्य नहीं है: सकारात्मक अर्धनिश्चित शंकु हैं जो किसी भी दूसरे क्रम के शंकु प्रतिनिधित्व को स्वीकार नहीं करते हैं।<ref name="Fawzi">{{Cite journal|last=Fawzi|first=Hamza|date=2019|title=दूसरे क्रम के शंकु का उपयोग करके सकारात्मक अर्धनिश्चित शंकु का प्रतिनिधित्व करने पर|journal=Mathematical Programming|language=en|volume=175|issue=1–2|pages=109–118|doi=10.1007/s10107-018-1233-0|issn=0025-5610|arxiv=1610.04901|s2cid=119324071}}</ref> वास्तव में, जबकि समतल में किसी भी बंद उत्तल अर्ध बीजगणितीय सेट को SOCP के व्यवहार्य क्षेत्र के रूप में लिखा जा सकता है,<ref>{{cite arXiv|last=Scheiderer|first=Claus|date=2020-04-08|title=समतल के उत्तल उपसमुच्चय के लिए दूसरे क्रम का शंकु प्रतिनिधित्व|class=math.OC|eprint=2004.04196}}</ref> यह ज्ञात है कि ऐसे उत्तल अर्ध-बीजगणितीय सेट मौजूद हैं जिन्हें एसडीपी द्वारा प्रस्तुत नहीं किया जा सकता है, यानी, ऐसे उत्तल अर्ध-बीजगणितीय सेट मौजूद हैं जिन्हें एसडीपी के व्यवहार्य क्षेत्र के रूप में नहीं लिखा जा सकता है।<ref>{{Cite journal|last=Scheiderer|first=Claus|date=2018|title=स्पेक्ट्राहेड्रल छायाएँ|journal=SIAM Journal on Applied Algebra and Geometry|language=en|volume=2|issue=1|pages=26–44|doi=10.1137/17M1118981|issn=2470-6566|doi-access=free}}</ref> | ||
| Line 53: | Line 51: | ||
===स्टोकेस्टिक रैखिक प्रोग्रामिंग=== | ===स्टोकेस्टिक रैखिक प्रोग्रामिंग=== | ||
असमानता रूप में | असमानता रूप में [[स्टोकेस्टिक रैखिक कार्यक्रम]] पर विचार करें | ||
:छोटा करना <math>\ c^T x \ </math> :का विषय है | :छोटा करना <math>\ c^T x \ </math> :का विषय है | ||
| Line 67: | Line 65: | ||
हम दूसरे क्रम के शंकु कार्यक्रमों का उल्लेख करते हैं | हम दूसरे क्रम के शंकु कार्यक्रमों का उल्लेख करते हैं | ||
नियतात्मक दूसरे क्रम के शंकु कार्यक्रमों के रूप में क्योंकि उन्हें परिभाषित करने वाला डेटा नियतात्मक है। | नियतात्मक दूसरे क्रम के शंकु कार्यक्रमों के रूप में क्योंकि उन्हें परिभाषित करने वाला डेटा नियतात्मक है। | ||
स्टोकेस्टिक द्वितीय-क्रम शंकु कार्यक्रम अनुकूलन समस्याओं का | स्टोकेस्टिक द्वितीय-क्रम शंकु कार्यक्रम अनुकूलन समस्याओं का वर्ग है जिन्हें नियतात्मक द्वितीय-क्रम शंकु कार्यक्रमों को परिभाषित करने वाले डेटा में अनिश्चितता को संभालने के लिए परिभाषित किया गया है। | ||
==सॉल्वर और स्क्रिप्टिंग (प्रोग्रामिंग) भाषाएँ== | ==सॉल्वर और स्क्रिप्टिंग (प्रोग्रामिंग) भाषाएँ== | ||
Revision as of 17:22, 17 July 2023
दूसरे क्रम का शंकु कार्यक्रम (एसओसीपी) प्रपत्र की उत्तल अनुकूलन समस्या है
- छोटा करना :का विषय है
जहां समस्या पैरामीटर हैं , और . अनुकूलन चर है. यूक्लिडियन मानदंड है और स्थानांतरण को इंगित करता है.[1] एसओसीपी में दूसरे क्रम का शंकु बाधाओं से उत्पन्न होता है, जो एफ़िन फ़ंक्शन की आवश्यकता के बराबर है दूसरे क्रम के Convex_cone में स्थित होना .[1]
एसओसीपी को आंतरिक बिंदु विधियों द्वारा हल किया जा सकता है[2] और सामान्य तौर पर, अर्धनिश्चित प्रोग्रामिंग (एसडीपी) समस्याओं की तुलना में अधिक कुशलता से हल किया जा सकता है।[3]एसओसीपी के कुछ इंजीनियरिंग अनुप्रयोगों में फिल्टर डिजाइन, एंटीना सरणी वजन डिजाइन, ट्रस डिजाइन और रोबोटिक्स में लोभी बल अनुकूलन शामिल हैं।[4] मात्रात्मक वित्त में अनुप्रयोगों में पोर्टफोलियो अनुकूलन शामिल है; कुछ बाज़ार प्रभाव बाधाएँ, क्योंकि वे रैखिक नहीं हैं, द्विघात प्रोग्रामिंग द्वारा हल नहीं की जा सकती हैं, लेकिन उन्हें एसओसीपी समस्याओं के रूप में तैयार किया जा सकता है।[5][6][7]
दूसरे क्रम का शंकु
आयाम का मानक या इकाई दूसरे क्रम का शंकु परिभाषित किया जाता है
.
दूसरे क्रम के शंकु को द्विघात शंकु, आइसक्रीम शंकु या लोरेंत्ज़ शंकु के नाम से भी जाना जाता है। दूसरे क्रम का शंकु है .
दूसरे क्रम के शंकु बाधा को संतुष्ट करने वाले बिंदुओं का सेट एफ़िन मैपिंग के तहत इकाई दूसरे क्रम के शंकु की व्युत्क्रम छवि है:
और इसलिए उत्तल है.
दूसरे क्रम के शंकु को सकारात्मक अर्धनिश्चित मैट्रिक्स के शंकु में एम्बेड किया जा सकता है
यानी, दूसरे क्रम का शंकु अवरोध रैखिक मैट्रिक्स असमानता के बराबर है (यहां)। साधन अर्धनिश्चित मैट्रिक्स है)। इसी प्रकार, हमारे पास भी है,
.
अन्य अनुकूलन समस्याओं के साथ संबंध
कब के लिए , SOCP रैखिक कार्यक्रम में परिवर्तित हो जाता है। कब के लिए , एसओसीपी उत्तल चतुर्भुज रूप से बाधित रैखिक कार्यक्रम के बराबर है।
उत्तल चतुर्भुज रूप से बाधित द्विघात कार्यक्रमों को उद्देश्य फ़ंक्शन को बाधा के रूप में सुधारकर एसओसीपी के रूप में भी तैयार किया जा सकता है।[4]अर्धनिश्चित प्रोग्रामिंग एसओसीपी को समाहित करती है क्योंकि एसओसीपी बाधाओं को रैखिक मैट्रिक्स असमानता (एलएमआई) के रूप में लिखा जा सकता है और इसे अर्धनिश्चित कार्यक्रम के उदाहरण के रूप में पुन: तैयार किया जा सकता है।[4]हालाँकि, इसका उलटा मान्य नहीं है: सकारात्मक अर्धनिश्चित शंकु हैं जो किसी भी दूसरे क्रम के शंकु प्रतिनिधित्व को स्वीकार नहीं करते हैं।[3] वास्तव में, जबकि समतल में किसी भी बंद उत्तल अर्ध बीजगणितीय सेट को SOCP के व्यवहार्य क्षेत्र के रूप में लिखा जा सकता है,[8] यह ज्ञात है कि ऐसे उत्तल अर्ध-बीजगणितीय सेट मौजूद हैं जिन्हें एसडीपी द्वारा प्रस्तुत नहीं किया जा सकता है, यानी, ऐसे उत्तल अर्ध-बीजगणितीय सेट मौजूद हैं जिन्हें एसडीपी के व्यवहार्य क्षेत्र के रूप में नहीं लिखा जा सकता है।[9]
उदाहरण
द्विघात बाधा
प्रपत्र के उत्तल चतुर्भुज रूप से बाधित द्विघात प्रोग्राम पर विचार करें
यह SOCP बाधा के समतुल्य है
स्टोकेस्टिक रैखिक प्रोग्रामिंग
असमानता रूप में स्टोकेस्टिक रैखिक कार्यक्रम पर विचार करें
- छोटा करना :का विषय है
जहां पैरामीटर माध्य के साथ स्वतंत्र गाऊसी यादृच्छिक सदिश हैं और सहप्रसरण और . इस समस्या को SOCP के रूप में व्यक्त किया जा सकता है
- छोटा करना :का विषय है
कहाँ व्युत्क्रम सामान्य संचयी वितरण फलन है।[1]
स्टोकेस्टिक द्वितीय-क्रम शंकु प्रोग्रामिंग
हम दूसरे क्रम के शंकु कार्यक्रमों का उल्लेख करते हैं नियतात्मक दूसरे क्रम के शंकु कार्यक्रमों के रूप में क्योंकि उन्हें परिभाषित करने वाला डेटा नियतात्मक है। स्टोकेस्टिक द्वितीय-क्रम शंकु कार्यक्रम अनुकूलन समस्याओं का वर्ग है जिन्हें नियतात्मक द्वितीय-क्रम शंकु कार्यक्रमों को परिभाषित करने वाले डेटा में अनिश्चितता को संभालने के लिए परिभाषित किया गया है।
सॉल्वर और स्क्रिप्टिंग (प्रोग्रामिंग) भाषाएँ
| Name | License | Brief info |
|---|---|---|
| AMPL | commercial | An algebraic modeling language with SOCP support |
| Artelys Knitro | commercial | |
| CPLEX | commercial | |
| FICO Xpress | commercial | |
| Gurobi Optimizer | commercial | |
| MATLAB | commercial | The coneprog function solves SOCP problems[10] using an interior-point algorithm[11]
|
| MOSEK | commercial | parallel interior-point algorithm |
| NAG Numerical Library | commercial | General purpose numerical library with SOCP solver |
संदर्भ
- ↑ 1.0 1.1 1.2 Boyd, Stephen; Vandenberghe, Lieven (2004). उत्तल अनुकूलन (PDF). Cambridge University Press. ISBN 978-0-521-83378-3. Retrieved July 15, 2019.
- ↑ Potra, lorian A.; Wright, Stephen J. (1 December 2000). "आंतरिक-बिंदु विधियाँ". Journal of Computational and Applied Mathematics. 124 (1–2): 281–302. Bibcode:2000JCoAM.124..281P. doi:10.1016/S0377-0427(00)00433-7.
- ↑ 3.0 3.1 Fawzi, Hamza (2019). "दूसरे क्रम के शंकु का उपयोग करके सकारात्मक अर्धनिश्चित शंकु का प्रतिनिधित्व करने पर". Mathematical Programming (in English). 175 (1–2): 109–118. arXiv:1610.04901. doi:10.1007/s10107-018-1233-0. ISSN 0025-5610. S2CID 119324071.
- ↑ 4.0 4.1 4.2 Lobo, Miguel Sousa; Vandenberghe, Lieven; Boyd, Stephen; Lebret, Hervé (1998). "दूसरे क्रम के शंकु प्रोग्रामिंग के अनुप्रयोग". Linear Algebra and Its Applications (in English). 284 (1–3): 193–228. doi:10.1016/S0024-3795(98)10032-0.
- ↑ "एसओसीपी को हल करना" (PDF).
- ↑ "पोर्टफोलियो अनुकूलन" (PDF).
- ↑ Li, Haksun (16 January 2022). Numerical Methods Using Java: For Data Science, Analysis, and Engineering. APress. pp. Chapter 10. ISBN 978-1484267967.
- ↑ Scheiderer, Claus (2020-04-08). "समतल के उत्तल उपसमुच्चय के लिए दूसरे क्रम का शंकु प्रतिनिधित्व". arXiv:2004.04196 [math.OC].
- ↑ Scheiderer, Claus (2018). "स्पेक्ट्राहेड्रल छायाएँ". SIAM Journal on Applied Algebra and Geometry (in English). 2 (1): 26–44. doi:10.1137/17M1118981. ISSN 2470-6566.
- ↑ "Second-order cone programming solver - MATLAB coneprog". MathWorks. 2021-03-01. Retrieved 2021-07-15.
- ↑ "Second-Order Cone Programming Algorithm - MATLAB & Simulink". MathWorks. 2021-03-01. Retrieved 2021-07-15.