डी कैस्टेलजौ का एल्गोरिदम: Difference between revisions
No edit summary |
No edit summary |
||
| Line 20: | Line 20: | ||
:<math>\beta_0^{(0)},\beta_0^{(1)},\ldots,\beta_0^{(n)}</math> | :<math>\beta_0^{(0)},\beta_0^{(1)},\ldots,\beta_0^{(n)}</math> | ||
:<math>\beta_0^{(n)},\beta_1^{(n-1)},\ldots,\beta_n^{(0)}</math> | :<math>\beta_0^{(n)},\beta_1^{(n-1)},\ldots,\beta_n^{(0)}</math> | ||
=== ज्यामितीय व्याख्या === | === ज्यामितीय व्याख्या === | ||
डी कास्टेलजौ के एल्गोरिदम की ज्यामितीय व्याख्या सीधी है। | डी कास्टेलजौ के एल्गोरिदम की ज्यामितीय व्याख्या सीधी है। | ||
| Line 58: | Line 56: | ||
और | और | ||
:<math>B_2(t) = \sum_{i=0}^n \beta_i^{(n-i)} b_{i,n}\left(\frac{t-t_0}{1-t_0}\right)\!, \quad t \in [t_0,1].</math> | :<math>B_2(t) = \sum_{i=0}^n \beta_i^{(n-i)} b_{i,n}\left(\frac{t-t_0}{1-t_0}\right)\!, \quad t \in [t_0,1].</math> | ||
== बेज़ियर वक्र == | == बेज़ियर वक्र == | ||
[[File:Bézier 2 big.gif|thumb|right|एक बेज़ियर वक्र]]n + 1 नियंत्रण बिंदु 'पी' के साथ 3-आयामी अंतरिक्ष में डिग्री n<sub>''i''</sub> के बेज़ियर वक्र का मूल्यांकन करते समय का प्रोयोग करते है | [[File:Bézier 2 big.gif|thumb|right|एक बेज़ियर वक्र]]n + 1 नियंत्रण बिंदु 'पी' के साथ 3-आयामी अंतरिक्ष में डिग्री n<sub>''i''</sub> के बेज़ियर वक्र का मूल्यांकन करते समय का प्रोयोग करते है | ||
| Line 111: | Line 107: | ||
lerp t a b = t * b + (1 - t) * a | lerp t a b = t * b + (1 - t) * a | ||
</syntaxhighlight> | </syntaxhighlight> | ||
=== [[पायथन (प्रोग्रामिंग भाषा)]] === | === [[पायथन (प्रोग्रामिंग भाषा)]] === | ||
<syntaxhighlight lang="python"> | <syntaxhighlight lang="python"> | ||
| Line 123: | Line 117: | ||
return beta[0] | return beta[0] | ||
</syntaxhighlight> | </syntaxhighlight> | ||
=== [[जावास्क्रिप्ट]] === | === [[जावास्क्रिप्ट]] === | ||
निम्नलिखित फ़ंक्शन डी कास्टेलजौ के एल्गोरिदम को सरणी पर प्रयुक्त करता है {{var|{{code|points}}}}, अतिरिक्त गुणों के साथ अंतिम मध्यबिंदु को हल करना {{code|in}} और {{code|out}} (क्रमशः मध्यबिंदु के अंदर और बाहर स्पर्शरेखाओं के लिए)। | निम्नलिखित फ़ंक्शन डी कास्टेलजौ के एल्गोरिदम को सरणी पर प्रयुक्त करता है {{var|{{code|points}}}}, अतिरिक्त गुणों के साथ अंतिम मध्यबिंदु को हल करना {{code|in}} और {{code|out}} (क्रमशः मध्यबिंदु के अंदर और बाहर स्पर्शरेखाओं के लिए)। | ||
| Line 159: | Line 151: | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
== यह भी देखें == | == यह भी देखें == | ||
*बेज़ियर वक्र | *बेज़ियर वक्र | ||
| Line 169: | Line 159: | ||
==संदर्भ== | ==संदर्भ== | ||
*Farin, Gerald & [[Dianne Hansford|Hansford, Dianne]] (2000). ''The Essentials of CAGD''. Natic, MA: A K Peters, Ltd. {{ISBN|1-56881-123-3}} | *Farin, Gerald & [[Dianne Hansford|Hansford, Dianne]] (2000). ''The Essentials of CAGD''. Natic, MA: A K Peters, Ltd. {{ISBN|1-56881-123-3}} | ||
==बाहरी संबंध == | ==बाहरी संबंध == | ||
* [http://hcklbrrfnn.wordpress.com/2012/08/20/piecewise-linear-approximation-of-bezier-curves/ Piecewise linear approximation of Bézier curves] – description of De Casteljau's algorithm, including a criterion to determine when to stop the recursion | * [http://hcklbrrfnn.wordpress.com/2012/08/20/piecewise-linear-approximation-of-bezier-curves/ Piecewise linear approximation of Bézier curves] – description of De Casteljau's algorithm, including a criterion to determine when to stop the recursion | ||
Revision as of 17:28, 21 July 2023
संख्यात्मक विश्लेषण के गणित क्षेत्र में, डी कास्टेलजौ का एल्गोरिदम बर्नस्टीन फॉर्म या बेज़ियर वक्रों में बहुपदों का मूल्यांकन करने के लिए पुनरावर्ती विधि है, जिसका नाम इसके आविष्कारक पॉल डी कास्टेलजौ के नाम पर रखा गया है। डी कास्टेलजौ के एल्गोरिदम का उपयोग बेज़ियर वक्र को इच्छानुसार मापदंड मान पर दो बेज़ियर वक्रों में विभाजित करने के लिए भी किया जा सकता है।
यद्यपि प्रत्यक्ष दृष्टिकोण की तुलना में अधिकांश आर्किटेक्चर के लिए एल्गोरिदम धीमा है, यह संख्यात्मक रूप से अधिक स्थिर है।
परिभाषा
एक बेज़ियर वक्र (डिग्री का , नियंत्रण बिंदुओं के साथ ) को बर्नस्टीन रूप में इस प्रकार लिखा जा सकता है
जहाँ बर्नस्टीन बहुपद है
बिंदु पर वक्र पुनरावृत्ति संबंध के साथ मूल्यांकन किया जा सकता है
फिर, का मूल्यांकन बिंदु पर में मूल्यांकन किया जा सकता है परिचालन. परिणाम द्वारा दिया गया है
इसके अतिरिक्त, बेज़ियर वक्र बिंदु पर विभाजित किया जा सकता है संबंधित नियंत्रण बिंदुओं के साथ दो वक्रों में:
ज्यामितीय व्याख्या
डी कास्टेलजौ के एल्गोरिदम की ज्यामितीय व्याख्या सीधी है।
- नियंत्रण बिंदुओं वाले बेज़ियर वक्र पर विचार करें . निरंतर बिंदुओं को जोड़कर हम वक्र का नियंत्रण बहुभुज बनाते हैं।
- अब इस बहुभुज के प्रत्येक रेखाखंड को अनुपात के साथ उप-विभाजित करें और जो अंक मिले उन्हें जोड़ दें। इस तरह आप कम खंड वाले नए बहुभुज पर पहुंचते हैं।
- प्रक्रिया को तब तक दोहराएँ जब तक आप एकल बिंदु पर न पहुँच जाएँ यह मापदंड के अनुरूप वक्र का बिंदु है .
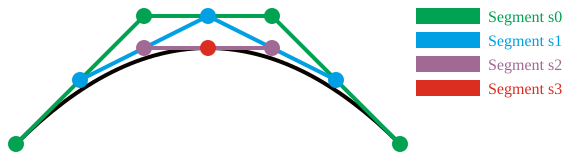
निम्नलिखित चित्र घन बेज़ियर वक्र के लिए इस प्रक्रिया को दर्शाता है:

- ध्यान दें कि जिन मध्यवर्ती बिंदुओं का निर्माण किया गया था वे वास्तव में दो नए बेज़ियर वक्रों के लिए नियंत्रण बिंदु हैं, दोनों बिल्कुल पुराने के साथ मेल खाते हैं। यह एल्गोरिदम न केवल वक्र का मूल्यांकन करता है , किन्तु वक्र को दो टुकड़ों में विभाजित करता है , और बेज़ियर रूप में दो उप-वक्रों के समीकरण प्रदान करता है।
ऊपर दी गई व्याख्या गैर-तर्कसंगत बेज़ियर वक्र के लिए मान्य है। तर्कसंगत बेज़ियर वक्र का मूल्यांकन करने के लिए , हम इस बिंदु को प्रक्षेपित कर सकते हैं ; उदाहरण के लिए, तीन आयामों में वक्र के अपने नियंत्रण बिंदु हो सकते हैं और वजन भारित नियंत्रण बिंदुओं पर प्रक्षेपित किया गया है. फिर एल्गोरिदम सामान्य रूप से आगे बढ़ता है, इंटरपोलेशन करता है . परिणामी चार-आयामी बिंदुओं को परिप्रेक्ष्य विभाजन के साथ तीन-समिष्ट में वापस प्रक्षेपित किया जा सकता है।
सामान्यतः, तर्कसंगत वक्र (या सतह) पर संचालन प्रक्षेप्य समिष्ट में गैर-तर्कसंगत वक्र पर संचालन के समान होता है। तर्कसंगत वक्रों का मूल्यांकन करते समय भारित नियंत्रण बिंदुओं और वज़न के रूप में यह प्रतिनिधित्व अक्सर सुविधाजनक होता है।
संकेतन
हाथ से गणना करते समय गुणांकों को त्रिभुज योजना में लिखना उपयोगी होता है
एक बिंदु चुनते समय t0 बर्नस्टीन बहुपद का मूल्यांकन करने के लिए हम बहुपद का विभाजन बनाने के लिए त्रिभुज योजना के दो विकर्णों का उपयोग कर सकते हैं
में
और
बेज़ियर वक्र
n + 1 नियंत्रण बिंदु 'पी' के साथ 3-आयामी अंतरिक्ष में डिग्री ni के बेज़ियर वक्र का मूल्यांकन करते समय का प्रोयोग करते है
साथ
हमने बेज़ियर वक्र को तीन अलग-अलग समीकरणों में विभाजित किया है
जिसका मूल्यांकन हम डी कैस्टेलजाउ के एल्गोरिदम का उपयोग करके व्यक्तिगत रूप से करते हैं।
उदाहरण
हम बर्नस्टीन गुणांक के साथ डिग्री 2 के बर्नस्टीन बहुपद का मूल्यांकन करना चाहते हैं
बिंदु पर t0.
हम पुनरावृत्ति प्रारंभ करते हैं
और दूसरे पुनरावृत्ति के साथ पुनरावर्तन रुक जाता है
जो घात 2 का अपेक्षित बर्नस्टीन बहुपद है।
कार्यान्वयन
यहां विभिन्न प्रोग्रामिंग भाषाओं में d कैस्टेलजाउ के एल्गोरिदम के उदाहरण कार्यान्वयन दिए गए हैं।
हास्केल (प्रोग्रामिंग भाषा)
deCasteljau :: Double -> [(Double, Double)] -> (Double, Double)
deCasteljau t [b] = b
deCasteljau t coefs = deCasteljau t reduced
where
reduced = zipWith (lerpP t) coefs (tail coefs)
lerpP t (x0, y0) (x1, y1) = (lerp t x0 x1, lerp t y0 y1)
lerp t a b = t * b + (1 - t) * a
पायथन (प्रोग्रामिंग भाषा)
def de_casteljau(t, coefs):
beta = [c for c in coefs] # values in this list are overridden
n = len(beta)
for j in range(1, n):
for k in range(n - j):
beta[k] = beta[k] * (1 - t) + beta[k + 1] * t
return beta[0]
जावास्क्रिप्ट
निम्नलिखित फ़ंक्शन डी कास्टेलजौ के एल्गोरिदम को सरणी पर प्रयुक्त करता है points, अतिरिक्त गुणों के साथ अंतिम मध्यबिंदु को हल करना in और out (क्रमशः मध्यबिंदु के अंदर और बाहर स्पर्शरेखाओं के लिए)।
function deCasteljau(points, position = 0.5){
let a, b, midpoints = [];
while(points.length > 1){
const num = points.length - 1;
for(let i = 0; i < num; ++i){
a = points[i];
b = points[i+1];
midpoints.push([
a[0] + ((b[0] - a[0]) * position),
a[1] + ((b[1] - a[1]) * position),
]);
}
points = midpoints;
midpoints = [];
}
return Object.assign(points[0], {in: a, out: b});
}
निम्नलिखित उदाहरण इस फ़ंक्शन को कॉल करता है हरा नीचे बिंदु, वक्र के बिल्कुल आधे रास्ते पर। परिणामी निर्देशांक समान होने चाहिए , या सबसे केंद्र की स्थिति लाल बिंदु है।
{
/* Definition of deCasteljau() function omitted for brevity */
const nodes = window.document.querySelectorAll("circle.n0-point");
const points = Array.from(nodes).map(({cx, cy}) => [cx.baseVal.value, cy.baseVal.value]);
deCasteljau(points); // Result: [192, 32]
}
यह भी देखें
- बेज़ियर वक्र
- डी बूर का एल्गोरिदम
- एकपदी रूप में बहुपदों का मूल्यांकन करने के लिए हॉर्नर योजना
- चेबीशेव रूप में बहुपदों का मूल्यांकन करने के लिए क्लेंशॉ एल्गोरिथम
संदर्भ
- Farin, Gerald & Hansford, Dianne (2000). The Essentials of CAGD. Natic, MA: A K Peters, Ltd. ISBN 1-56881-123-3
बाहरी संबंध
- Piecewise linear approximation of Bézier curves – description of De Casteljau's algorithm, including a criterion to determine when to stop the recursion
- Bezier Curves and Picasso — Description and illustration of De Casteljau's algorithm applied to cubic Bézier curves.
- de Casteljau's algorithm - Implementation help and interactive demonstration of the algorithm.