आर्किमिडीज़ संपत्ति: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Mathematical property of algebraic structures}} | {{Short description|Mathematical property of algebraic structures}} | ||
{{about|अमूर्त बीजगणित|भौतिक नियम|आर्किमिडीज़ का सिद्धांत}} | {{about|अमूर्त बीजगणित|भौतिक नियम|आर्किमिडीज़ का सिद्धांत}} | ||
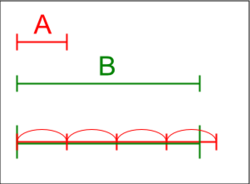
[[File:Archimedean property.png|thumb|250px|आर्किमिडीज़ गुण का चित्रण।]]अमूर्त बीजगणित और [[गणितीय विश्लेषण]] में [[आर्किमिडीज]] गुण का नाम सिरैक्यूज़ के प्राचीन यूनानी गणितज्ञ आर्किमिडीज़ के नाम पर रखा गया है, जो कुछ [[बीजगणितीय संरचना]]ओं जैसे कि आदेशित या मानक [[समूह (बीजगणित)]] और क्षेत्रों के माध्यम से धारित गुण है। गुण, सामान्यतः समझा जाता है, और यह बताता है कि दो सकारात्मक संख्याएं <math>x</math> और <math>y</math> दिए जाने पर एक पूर्णांक <math>n</math> होता है जैसे कि कि <math>nx > y</math> है। इसका अर्थ यह भी है कि [[प्राकृतिक संख्या]]ओं का समूह उपरोक्त परिबद्ध नहीं है।<ref>https://www.math.cuhk.edu.hk/course_builder/2021/math2050c/MATH%202050C%20Lecture%204%20(Jan%2021).pdf {{Bare URL PDF|date=March 2022}}</ref> साधारणतया कहा जाये | [[File:Archimedean property.png|thumb|250px|आर्किमिडीज़ गुण का चित्रण।]]अमूर्त बीजगणित और [[गणितीय विश्लेषण]] में [[आर्किमिडीज]] गुण का नाम सिरैक्यूज़ के प्राचीन यूनानी गणितज्ञ आर्किमिडीज़ के नाम पर रखा गया है, जो कुछ [[बीजगणितीय संरचना]]ओं जैसे कि आदेशित या मानक [[समूह (बीजगणित)]] और क्षेत्रों के माध्यम से धारित गुण है। गुण, सामान्यतः समझा जाता है, और यह बताता है कि दो सकारात्मक संख्याएं <math>x</math> और <math>y</math> दिए जाने पर एक पूर्णांक <math>n</math> होता है जैसे कि कि <math>nx > y</math> है। इसका अर्थ यह भी है कि [[प्राकृतिक संख्या]]ओं का समूह उपरोक्त परिबद्ध नहीं है।<ref>https://www.math.cuhk.edu.hk/course_builder/2021/math2050c/MATH%202050C%20Lecture%204%20(Jan%2021).pdf {{Bare URL PDF|date=March 2022}}</ref> साधारणतया कहा जाये तब यह कोई उन्नत रूप से व्यापक या उन्नत रूप से छोटे घटक न होने का गुण है। यह [[ओटो स्टोल्ज़]] ही थे जिन्होंने आर्किमिडीज़ के सूत्रीकरण को इसका नाम दिया चूँकि यह आर्किमिडीज़ के 'ऑन द स्फीयर एंड सिलेंडर' के सूत्रीकरण V के रूप में प्रकट होता है।<ref>G. Fisher (1994) in P. Ehrlich(ed.), Real Numbers, Generalizations of the Reals, and Theories of continua, 107-145, Kluwer Academic</ref> | ||
यह धारणा प्राचीन ग्रीस के [[परिमाण (गणित)]] के सिद्धांत से उत्पन्न हुई; यह अभी भी आधुनिक गणित में एक महत्वपूर्ण भूमिका निभाता है जैसे कि ज्यामिति के लिए [[डेविड हिल्बर्ट]] के सिद्धांत, [[रैखिक रूप से आदेशित समूह]] के सिद्धांत, [[आदेशित क्षेत्र]] और [[स्थानीय क्षेत्र]] के सिद्धांत है। | यह धारणा प्राचीन ग्रीस के [[परिमाण (गणित)]] के सिद्धांत से उत्पन्न हुई; यह अभी भी आधुनिक गणित में एक महत्वपूर्ण भूमिका निभाता है जैसे कि ज्यामिति के लिए [[डेविड हिल्बर्ट]] के सिद्धांत, [[रैखिक रूप से आदेशित समूह]] के सिद्धांत, [[आदेशित क्षेत्र]] और [[स्थानीय क्षेत्र]] के सिद्धांत है। | ||
एक बीजगणितीय संरचना जिसमें कोई भी दो शून्यतर घटक तुलनीय हैं, इस अर्थ में कि उनमें से कोई भी दूसरे के संबंध में अपरिमेय नहीं है, उसे 'आर्किमिडीयन' कहा जाता है। एक संरचना जिसमें शून्यतर | एक बीजगणितीय संरचना जिसमें कोई भी दो शून्यतर घटक तुलनीय हैं, इस अर्थ में कि उनमें से कोई भी दूसरे के संबंध में अपरिमेय नहीं है, उसे 'आर्किमिडीयन' कहा जाता है। एक संरचना जिसमें शून्यतर घटको की एक युग्म होता है, जिनमें से एक दूसरे के संबंध में अपरिमेय है, उसे 'अ-आर्किमिडीज' कहा जाता है।उदाहरण के रूप मे एक रैखिक रूप से आदेशित समूह जो कि आर्किमिडीज़ है, एक [[आर्किमिडीज़ समूह]] है। | ||
इसे भिन्न-भिन्न संदर्भों में थोड़ा भिन्न सूत्रीकरण के साथ स्पष्ट करा जा सकता है। उदाहरण के रूप मे क्रमित क्षेत्रों के संदर्भ में, एक के | इसे भिन्न-भिन्न संदर्भों में थोड़ा भिन्न सूत्रीकरण के साथ स्पष्ट करा जा सकता है। उदाहरण के रूप मे क्रमित क्षेत्रों के संदर्भ में, एक के समीप आर्किमिडीज़ का सूत्रीकरण है जो इस गुण को सज्जित करता है, जिस स्थान पर वास्तविक संख्याओं का क्षेत्र आर्किमिडीज़ है, किन्तु [[वास्तविक संख्या|वास्तविक गुणांक]] में [[तर्कसंगत कार्य|तर्कसंगत कार्यो]] का क्षेत्र आर्किमिडीज़ नहीं है। | ||
== आर्किमिडीज़ गुण के नाम का इतिहास और उत्पत्ति == | == आर्किमिडीज़ गुण के नाम का इतिहास और उत्पत्ति == | ||
| Line 12: | Line 12: | ||
इस अवधारणा का नाम ओटो स्टोल्ज़ के माध्यम से (1880 के दशक में) [[प्राचीन ग्रीस|प्राचीन ग्रीक]] के ज्यामिति और सिरैक्यूज़ के भौतिक विज्ञानी आर्किमिडीज़ के नाम पर रखा गया था। | इस अवधारणा का नाम ओटो स्टोल्ज़ के माध्यम से (1880 के दशक में) [[प्राचीन ग्रीस|प्राचीन ग्रीक]] के ज्यामिति और सिरैक्यूज़ के भौतिक विज्ञानी आर्किमिडीज़ के नाम पर रखा गया था। | ||
आर्किमिडीज़ गुण यूक्लिड के | आर्किमिडीज़ गुण यूक्लिड के घटको की पुस्तक V में परिभाषा 4 के रूप में प्रदर्शित करी गई है: | ||
{{Blockquote|कहा जाता है कि परिमाण का एक दूसरे से अनुपात होता है जिसे गुणा करने पर एक दूसरे से अधिक हो सकता है।}} | {{Blockquote|कहा जाता है कि परिमाण का एक दूसरे से अनुपात होता है जिसे गुणा करने पर एक दूसरे से अधिक हो सकता है।}} | ||
| Line 22: | Line 22: | ||
== रैखिक रूप से आदेशित समूहों के लिए परिभाषा == | == रैखिक रूप से आदेशित समूहों के लिए परिभाषा == | ||
{{Main|आर्किमिडीज़ समूह}} | {{Main|आर्किमिडीज़ समूह}} | ||
मान लीजिए कि x और y एक रैखिक क्रम वाले समूह G के सकारात्मक घटक हैं। तत्पश्चात <math>y</math> के संबंध में <math>x</math> | मान लीजिए कि x और y एक रैखिक क्रम वाले समूह G के सकारात्मक घटक हैं। तत्पश्चात <math>y</math> के संबंध में <math>x</math> अपरिमेय है (या समकक्ष <math>y</math>, <math>x</math> के संबंध में अनंत है) यदि किसी [[प्राकृतिक संख्या]] <math>n</math> के लिए <math>nx</math> का गुणज <math>y</math> से न्यूनतम है, तब निम्नलिखित असमानता है: | ||
<math display="block"> \underbrace{x+\cdots+x}_{n\text{ terms}} < y. \, </math> | <math display="block"> \underbrace{x+\cdots+x}_{n\text{ terms}} < y. \, </math> | ||
निरपेक्ष मान लेकर इस परिभाषा को समस्त समूह तक प्रेषित करा जा सकता है। | निरपेक्ष मान लेकर इस परिभाषा को समस्त समूह तक प्रेषित करा जा सकता है। | ||
| Line 28: | Line 28: | ||
समूह <math>G</math> आर्किमिडीज़ है यदि कोई जोड़ी नहीं है <math>(x,y)</math> ऐसा है कि <math>x</math> एवं <math>y</math> के संबंध में अपरिमेय है। | समूह <math>G</math> आर्किमिडीज़ है यदि कोई जोड़ी नहीं है <math>(x,y)</math> ऐसा है कि <math>x</math> एवं <math>y</math> के संबंध में अपरिमेय है। | ||
इसके अतिरिक्त, यदि <math>K</math> इकाई (1) के साथ एक बीजगणितीय संरचना है - उदाहरण के रूप मे, एक [[अंगूठी (गणित)|चक्र (गणित)]] - | इसके अतिरिक्त, यदि <math>K</math> इकाई (1) के साथ एक बीजगणितीय संरचना है - उदाहरण के रूप मे, एक [[अंगूठी (गणित)|चक्र (गणित)]] - तब एक समान परिभाषा <math>K</math> पर प्रयुक्त होती है। यदि <math>1</math> के संबंध में {{mvar|x}} अपरिमेय है तब {{mvar|x}} एक अपरिमेय घटक है। इसी प्रकार, यदि <math>1</math> के संबंध में <math>y</math> अनंत है, तब <math>y</math> एक अनंत घटक है। बीजगणितीय संरचना <math>K</math> आर्किमिडीयन है यदि इसमें कोई अनंत घटक और कोई अपरिमेय घटक नहीं है। | ||
=== आदेशित किए गए क्षेत्र === | === आदेशित किए गए क्षेत्र === | ||
आदेशित क्षेत्र में कुछ अतिरिक्त गुण होते हैं: | आदेशित क्षेत्र में कुछ अतिरिक्त गुण होते हैं: | ||
* परिमेय संख्याएँ किसी भी क्रमित क्षेत्र में [[एम्बेडिंग]] | * परिमेय संख्याएँ किसी भी क्रमित क्षेत्र में [[एम्बेडिंग|अंतर्निहित]] होती हैं। अर्थात्, किसी भी क्रमित क्षेत्र में अभिलक्षणिक (बीजगणित) शून्य होता है। | ||
* यदि <math>x</math> अनंत है, तब <math>1/x</math> अनंत है, और इसके | * यदि <math>x</math> अनंत है, तब <math>1/x</math> अनंत है, और इसके विपरीत है। इसलिए, यह सत्यापित करने के लिए कि एक क्षेत्र आर्किमिडीयन है, यह मात्र यह परीक्षण के लिए पर्याप्त है कि कोई अपरिमेय घटक नहीं हैं, या यह परीक्षण के लिए कि कोई अनंत घटक नहीं हैं। | ||
* यदि <math>x</math> | * यदि <math>x</math> अपरिमेय है और <math>r</math> तब एक परिमेय संख्या है, तब <math>rx</math> अपरिमेय भी है। परिणामस्वरूप दिए गए एक सामान्य घटक <math>c</math> के परिणामस्वरूप दिए गए सामान्य घटक <math>c/2</math>, <math>c</math> और <math>2c</math> या तब समस्त अनंतसूक्ष्म हैं या समस्त अनंतसूक्ष्म नही हैं। | ||
इस | इस समूहों में एक क्रमबद्ध क्षेत्र {{mvar|K}} आर्किमिडीज़ है, जब निम्नलिखित कथन को आर्किमिडीज़ का स्वयंसिद्ध कहा जाता है: | ||
: | : मान लीजिए <math>x</math> एवं <math>K</math> का कोई भी घटक नहीं है। तत्पश्चात एक प्राकृतिक संख्या <math>n</math> is प्रकार उपस्थित है कि <math>n > x</math> है। | ||
वैकल्पिक रूप से कोई निम्नलिखित लक्षण वर्णन का उपयोग कर सकता है: | वैकल्पिक रूप से कोई निम्नलिखित लक्षण वर्णन का उपयोग कर सकता है: | ||
<math display="block">\forall\, \varepsilon \in K\big(\varepsilon > 0 \implies \exists\ n \in N : 1/n < \varepsilon\big).</math> | <math display="block">\forall\, \varepsilon \in K\big(\varepsilon > 0 \implies \exists\ n \in N : 1/n < \varepsilon\big).</math> | ||
== आदर्श क्षेत्रों के लिए परिभाषा == | == आदर्श क्षेत्रों के लिए परिभाषा == | ||
विशेषण "आर्किमिडीयन" को [[वैल्यूएशन रिंग|मान ांकन श्रेणी]] एक मान वान क्षेत्र और श्रेणी एक मान वान क्षेत्र पर मानक रिक्त स्थान के सिद्धांत में निम्नानुसार तैयार किया गया है। मान लीजिए <math>K</math> एक क्षेत्र है जो एक निरपेक्ष मान फलन से संपन्न है, अर्थात, एक फलन जो वास्तविक संख्या <math>0</math> को क्षेत्र घटक 0 के साथ संबद्ध करता है और प्रत्येक शून्यतर <math>x \in K</math> के साथ एक धनात्मक वास्तविक संख्या <math>|x|</math> को संबद्ध करता है और <math>|xy|=|x| |y|</math> और <math>|x+y| \le |x|+|y|</math> को संतुष्ट करता है। तत्पश्चात, <math>K</math> को आर्किमिडीयन कहा जाता है यदि किसी शून्यतर <math>x \in K</math> के लिए एक प्राकृतिक संख्या <math>n</math> उपस्थित हो | |||
<math>|xy|=|x| |y|</math> और <math>|x+y| \le |x|+|y|</math> | |||
<math display="block">|\underbrace{x+\cdots+x}_{n\text{ terms}}| > 1. </math> | <math display="block">|\underbrace{x+\cdots+x}_{n\text{ terms}}| > 1. </math> | ||
इसी | इसी प्रकार, एक आदर्श स्थान आर्किमिडीयन है यदि <math>n</math> पदों का योग, प्रत्येक एक शून्यतर सदिश <math>x</math> के सामान्तर है, तब पर्याप्त रूप से व्यापक <math>n</math> के लिए एक से अधिक मानक है। एक निरपेक्ष मान या एक आदर्श स्थान वाला क्षेत्र या तब आर्किमिडीयन है या अधिकार शाली स्थिति को संतुष्ट करता है, जिसे [[अल्ट्रामेट्रिक]] त्रिकोण असमानता कहा जाता है, | ||
एक निरपेक्ष मान या एक आदर्श स्थान वाला क्षेत्र या तब आर्किमिडीयन है या | |||
<math display="block">|x+y| \le \max(|x|,|y|) ,</math> | <math display="block">|x+y| \le \max(|x|,|y|) ,</math> | ||
क्रमश: अल्ट्रामैट्रिक त्रिकोण असमानता को संतुष्ट करने वाले क्षेत्र या आदर्श स्थान को आर्किमिडीयन नही कहा जाता है। | |||
अल्ट्रामैट्रिक त्रिकोण असमानता को संतुष्ट करने वाले क्षेत्र या आदर्श स्थान को | |||
एक गैर-आर्किमिडीयन मानक रैखिक स्थान की अवधारणा ए.एफ. मोन्ना के माध्यम से प्रस्तुत की गई थी।<ref name=monna1943>{{cite journal |last1=Monna |first1=A. F. |title=Over een lineaire ''P''-adische ruimte |journal=Nederl. Akad. Wetensch. Verslag Afd. Natuurk. |issue=52 |date=1943 |pages=74–84 |mr=15678 }}</ref> | एक गैर-आर्किमिडीयन मानक रैखिक स्थान की अवधारणा ए.एफ. मोन्ना के माध्यम से प्रस्तुत की गई थी।<ref name=monna1943>{{cite journal |last1=Monna |first1=A. F. |title=Over een lineaire ''P''-adische ruimte |journal=Nederl. Akad. Wetensch. Verslag Afd. Natuurk. |issue=52 |date=1943 |pages=74–84 |mr=15678 }}</ref> | ||
== उदाहरण और विपरीत उदाहरण == | |||
== | === वास्तविक संख्या का आर्किमिडीयन गुण === | ||
=== वास्तविक संख्या का आर्किमिडीयन गुण | तर्कसंगत संख्याओं के क्षेत्र को अनेक निरपेक्ष मान फलन में से एक अभिहस्तांकित करा जा सकता है, जिसमें निरर्थक फलन <math>|x|=1</math> भी सम्मलित है जब <math>x \neq 0</math> अधिक सामान्य <math display="inline">|x| = \sqrt{x^2}</math> और <math>p</math> एडिक निरपेक्ष मान फलन है। ओस्ट्रोव्स्की के प्रमेय के अनुसार, तर्कसंगत संख्याओं पर प्रत्येक अ-निरर्थक निरपेक्ष मान या तब सामान्य निरपेक्ष मान या कुछ <math>p</math> एडिक निरपेक्ष मान के समान्तर होता है। अ-निरर्थक निरपेक्ष मानों के संबंध में तर्कसंगत क्षेत्र पूर्ण नहीं है, निरर्थक निरपेक्ष मान के संबंध में, तर्कसंगत क्षेत्र एक असतत स्थलीय स्थान है इसलिए यह पूर्ण है। सामान्य निरपेक्ष मान (क्रम से) के संबंध में पूर्णता वास्तविक संख्याओं का क्षेत्र है। इस तर्कसाध्य के के माध्यम से वास्तविक संख्या का क्षेत्र एक आदेशित क्षेत्र और एक मानक क्षेत्र के रूप में आर्किमिडीयन है।<ref>[[Neal Koblitz]], "p-adic Numbers, p-adic Analysis, and Zeta-Functions", Springer-Verlag,1977.</ref> दूसरी ओर, अन्य अ-निरर्थक निरपेक्ष मानों के संबंध में पूर्णताएं [[मेरा मतलब संख्या है|पी-एडिक]] संख्या प्रणाली के क्षेत्र प्रदान करती हैं, जिस स्थान पर <math>p</math> एक अभाज्य पूर्णांक संख्या है (नीचे देखें); चूंकि <math>p</math> एडिक निरपेक्ष मान अल्ट्रामेट्रिक गुण को संतुष्ट करते हैं, तब <math>p</math> एडिक संख्या क्षेत्र मानक क्षेत्र के रूप में आर्किमिडीयन नही हैं (उन्हें आदेशित किए गए क्षेत्र में निर्मित नही करा जा सकता है)। | ||
वास्तविक संख्याओं के सूत्रीकरण सिद्धांत में, शून्येतर | वास्तविक संख्याओं के सूत्रीकरण सिद्धांत में, शून्येतर अपरिमेय वास्तविक संख्याओं की अ-उपस्थित निम्नतम ऊपरी बाध्य गुण के माध्यम से निहित है। समस्त धनात्मक अपरिमित गुण से युक्त समुच्चय को <math>Z</math> के माध्यम से निरूपित करें। यह समुच्चय उपर्युक्त <math>1</math> से परिबद्ध है। अब एक विरोधाभास के लिए मान लें कि <math>Z</math> अरिक्त है। तत्पश्चात इसकी [[कम से कम ऊपरी सीमा|न्यूनतम उच्च सीमा]] <math>c</math> है जो धनात्मक भी है इसलिए <math>c/2 < c < 2c</math> है। चूँकि c, <math>Z</math> की [[ऊपरी सीमा|उच्च परिबंध]] है और <math>2c</math>, <math>c</math>, <math>2c</math> से पूर्णतः दीर्घतर है, यह एक धनात्मक अपरिमेय नहीं है। अर्थात् कुछ प्राकृतिक संख्या <math>n</math> होती है जिसके लिए <math>1/n < 2c</math> होता है। दूसरी ओर <math>c/2</math> एक धनात्मक अपरिमेय है क्योंकि न्यूनतम ऊपरी सीमा की परिभाषा के अनुसार <math>c/2</math> और <math>c</math>, के मध्य एक अपरिमेय <math>x</math> होना चाहिए और यदि <math>1/k < c/2 \leq x</math> है तब <math>x</math> अपरिमेय नहीं है। किन्तु <math>1/(4n) < c/2</math> इसलिए <math>c/2</math> अपरिमेय नहीं है, और यह एक विरोधाभास है। इसका अर्थ यह है कि Z अंततः रिक्त है: कोई धनात्मक, अपरिमेय वास्तविक संख्याएँ नहीं हैं। | ||
यह समुच्चय | |||
दूसरी ओर | |||
वास्तविक संख्याओं की | वास्तविक संख्याओं की आर्किमिडीज़ गुण भी [[रचनात्मक विश्लेषण]] में भी प्रयुक्त होती है, तथापि न्यूनतम ऊपरी परिबंध वाले गुण उस संदर्भ में विफल हो सकते है। | ||
=== गैर-आर्किमिडीयन आदेशित क्षेत्र === | === गैर-आर्किमिडीयन आदेशित क्षेत्र === | ||
{{main article|गैर-आर्किमिडीयन आदेशित क्षेत्र}} | {{main article|गैर-आर्किमिडीयन आदेशित क्षेत्र}} | ||
एक आदेशित क्षेत्र के उदाहरण के रूप मे जो आर्किमिडीयन नहीं है, वास्तविक गुणांक वाले [[तर्कसंगत कार्य]] | एक आदेशित क्षेत्र के उदाहरण के रूप मे जो आर्किमिडीयन नहीं है, वास्तविक गुणांक वाले [[तर्कसंगत कार्य]] के क्षेत्र को लें। (एक परिमेय फलन वह फलन है जिसे एक [[बहुपद]] के माध्यम से दूसरे बहुपद से विभाजित करके व्यक्त किया जा सकता है; हम मानेंगे कि यह इस प्रकार से किया गया है कि प्रत्येक का प्रमुख गुणांक धनात्मक है।) इसे एक आदेशित किया गया और इसे क्षेत्र बनाने के लिए, किसी को जोड़ और गुणन संचालन के साथ संगत आदेशित निर्दिष्ट करना होगा। अब <math>f > g</math> यदि और मात्र <math>f - g > 0</math> है तब हमें मात्र यह वर्णन करना है कि कौन से तर्कसंगत कार्य धनात्मक माने जाते हैं। यदि अंश का प्रमुख गुणांक धनात्मक है, तब फलन धनात्मक कहा जाता है। (किसी को यह परीक्षण चाहिए कि यह क्रम उचित प्रकार से परिभाषित है और जोड़ और गुणा के साथ संगत है।) इस परिभाषा के अनुसार परिमेय फलन <math>1/x</math> धनात्मक है, किन्तु परिमेय फलन <math>1</math> से न्यूनतम है। वास्तव में यदि <math>n</math> कोई प्राकृतिक संख्या है तब <math>n(1/x) = n/x</math> धनात्मक है किन्तु तब भी <math>1</math> से न्यूनतम है चाहे <math>n</math> कितना भी दीर्घतर क्यों न हो। इसलिए, <math>1/x</math> इस क्षेत्र में एक अपरिमेय है। | ||
(एक परिमेय फलन | |||
इसे एक आदेशित क्षेत्र बनाने के लिए, किसी को जोड़ और | |||
यदि अंश का प्रमुख गुणांक धनात्मक है, तब फलन | |||
इस परिभाषा के अनुसार | |||
वास्तव में | |||
इसलिए, <math>1/x</math> इस क्षेत्र में एक अपरिमेय है। | |||
यह उदाहरण अन्य गुणांकों का सामान्यीकरण करता है। वास्तविक गुणांकों के अतिरिक्त तर्कसंगत कार्यों को तर्कसंगत के साथ लेने से एक गणनीय अ-आर्किमिडीयन आदेशित क्षेत्र उत्पन्न होता है। गुणांकों को एक भिन्न चर में तर्कसंगत कार्यों के रूप में लेने से, मान लीजिए y, एक भिन्न आदेशित प्रकार के साथ एक उदाहरण निर्मित करता है। | |||
=== अ-आर्किमिडीयन मूल्यवान क्षेत्र === | |||
p-एडिक आव्युह और p-एडिक अंक क्षेत्र से संपन्न परिमेय संख्याओं का क्षेत्र जो पूर्णताएँ हैं, उनके समीप निरपेक्ष मान वाले क्षेत्र के रूप में आर्किमिडीज़ गुण नहीं होता है। समस्त आर्किमिडीयन मूल्यवान क्षेत्र सामान्य निरपेक्ष मान की अधिकार के साथ जटिल संख्याओं के एक उपक्षेत्र के लिए सममितीय रूप से समरूपी हैं।<ref name="shell1">Shell, Niel, Topological Fields and Near Valuations, Dekker, New York, 1990. {{ISBN|0-8247-8412-X}}</ref> | |||
'''आर्किमिडीयन आदेशित क्षेत्र की समतुल्य परिभाषाएँ''' | |||
प्रत्येक रैखिक रूप से क्रमित क्षेत्र <math>K</math> में एक क्रमित उपक्षेत्र के रूप में परिमेय (एक समरूपी प्रतिलिपि) सम्मिलित है, अर्थात् <math>K</math> की गुणक इकाई <math>1</math> के माध्यम से उत्पन्न उपक्षेत्र, जिसमें प्रवर्तित होकर एक आदेशित उपसमूह के रूप में पूर्णांक सम्मिलित होते हैं, जिसमें एक आदेशित [[मोनोइड]] के रूप में प्राकृतिक संख्याएं सम्मिलित होती हैं। परिमेय को अंतर्निहित करने पर <math>K</math> में परिमेय, पूर्णांक और प्राकृतिक संख्याओं के विषय में वर्णन की एक विधि प्राप्त होती है। इन अवसंरचनाओं के संदर्भ में आर्किमिडीयन क्षेत्रों के समतुल्य लक्षण निम्नलिखित हैं।<ref name="Schechter">{{harvnb|Schechter|1997|loc=§10.3}}</ref> | |||
# प्राकृतिक संख्याएँ <math>K</math> [[कोफिनल (गणित)|सह-अंतिम (गणित)]] में होती हैं। अर्थात <math>K</math> का प्रत्येक घटक किसी प्राकृतिक संख्या से न्यूनतम है। (यह वह स्थिति नहीं है जब अनंत घटक उपस्थित हों।) इस प्रकार एक आर्किमिडीयन क्षेत्र वह है जिसकी प्राकृतिक संख्या बिना किसी सीमा के विकसित होती है। | |||
# समुच्चय <math>\{1/2, 1/3, 1/4, \dots\}</math> के <math>K</math> में शून्य [[सबसे कम|न्यूनतम]] है। (यदि <math>K</math> एक धनात्मक अपरिमेय समाहित करता है, तब यह समुच्चय के लिए एक निम्म सीमा होगी जिस स्थान पर शून्य सबसे दीर्घतर निम्म सीमा नहीं होगी।) | |||
# धनात्मक और ऋणात्मक परिमेय के मध्य <math>K</math> के घटको का समुच्चय विवृत नही है। इसका कारण यह है कि समुच्चय में समस्त अपरिमेय होते हैं, जो मात्र समुच्चय <math>\{0\}</math> होता है जब कोई शून्येतर अपरिमेय नहीं होते हैं, और अन्यथा विवृत होता है, तब न कोई न्यूनतम और न ही दीर्घतर शून्यतर अपरिमेय होता है। ध्यान दें कि दोनों स्थितियों में, अत्यंत सूक्ष्म का समुच्चय संवृत है। बाद वाले मामले में, (i) प्रत्येक अपरिमेय प्रत्येक धनात्मक परिमेय से न्यूनतम है, (ii) न तब कोई सबसे दीर्घतर अपरिमेय है और न ही सबसे न्यूनतम धनात्मक परिमेय है, और (iii) मध्य में और कुछ भी और नहीं है। परिणामस्वरूप, कोई भी अ-आर्किमिडीयन आदेशित क्षेत्र अपूर्ण और असंबद्ध दोनों है। | |||
# <math>K</math> में किसी <math>x</math> के लिए <math>x</math> से दीर्घतर पूर्णांकों के समूहों में न्यूनतम घटक होता है। (यदि <math>x</math> एक ऋणात्मक अनंत मात्रा होती तब प्रत्येक पूर्णांक इससे दीर्घतर होता है।) | |||
# | # <math>K</math> के प्रत्येक अरिक्त विवृत अंतराल में एक परिमेय सम्मिलित होता है। (यदि <math>x</math> एक धनात्मक अपरिमेय है, तब विवृत अंतराल <math>(x,2x)</math> में अपरिमित रूप से अनेक अपरिमेय हैं किन्तु एक भी परिमेय नहीं है।) | ||
# के | # <math>K</math> में सुप० और इन्फ़० दोनों के संबंध में परिमेय सघन हैं। (अर्थात्, <math>K</math> का प्रत्येक घटक परिमेय के कुछ समुच्चय का पूरक है, और परिमेय के कुछ अन्य समुच्चय का इन्फ़० है।) इस प्रकार एक आर्किमिडीयन क्षेत्र किसी भी क्रमित क्षेत्र के अर्थ में परिमेय का कोई सघन क्रमित विस्तार है, जो अपने परिमेय घटको को संघनित रूप से अंतःस्थापित करता है। | ||
# | |||
# | |||
# | |||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 00:38, 24 July 2023
अमूर्त बीजगणित और गणितीय विश्लेषण में आर्किमिडीज गुण का नाम सिरैक्यूज़ के प्राचीन यूनानी गणितज्ञ आर्किमिडीज़ के नाम पर रखा गया है, जो कुछ बीजगणितीय संरचनाओं जैसे कि आदेशित या मानक समूह (बीजगणित) और क्षेत्रों के माध्यम से धारित गुण है। गुण, सामान्यतः समझा जाता है, और यह बताता है कि दो सकारात्मक संख्याएं और दिए जाने पर एक पूर्णांक होता है जैसे कि कि है। इसका अर्थ यह भी है कि प्राकृतिक संख्याओं का समूह उपरोक्त परिबद्ध नहीं है।[1] साधारणतया कहा जाये तब यह कोई उन्नत रूप से व्यापक या उन्नत रूप से छोटे घटक न होने का गुण है। यह ओटो स्टोल्ज़ ही थे जिन्होंने आर्किमिडीज़ के सूत्रीकरण को इसका नाम दिया चूँकि यह आर्किमिडीज़ के 'ऑन द स्फीयर एंड सिलेंडर' के सूत्रीकरण V के रूप में प्रकट होता है।[2]
यह धारणा प्राचीन ग्रीस के परिमाण (गणित) के सिद्धांत से उत्पन्न हुई; यह अभी भी आधुनिक गणित में एक महत्वपूर्ण भूमिका निभाता है जैसे कि ज्यामिति के लिए डेविड हिल्बर्ट के सिद्धांत, रैखिक रूप से आदेशित समूह के सिद्धांत, आदेशित क्षेत्र और स्थानीय क्षेत्र के सिद्धांत है।
एक बीजगणितीय संरचना जिसमें कोई भी दो शून्यतर घटक तुलनीय हैं, इस अर्थ में कि उनमें से कोई भी दूसरे के संबंध में अपरिमेय नहीं है, उसे 'आर्किमिडीयन' कहा जाता है। एक संरचना जिसमें शून्यतर घटको की एक युग्म होता है, जिनमें से एक दूसरे के संबंध में अपरिमेय है, उसे 'अ-आर्किमिडीज' कहा जाता है।उदाहरण के रूप मे एक रैखिक रूप से आदेशित समूह जो कि आर्किमिडीज़ है, एक आर्किमिडीज़ समूह है।
इसे भिन्न-भिन्न संदर्भों में थोड़ा भिन्न सूत्रीकरण के साथ स्पष्ट करा जा सकता है। उदाहरण के रूप मे क्रमित क्षेत्रों के संदर्भ में, एक के समीप आर्किमिडीज़ का सूत्रीकरण है जो इस गुण को सज्जित करता है, जिस स्थान पर वास्तविक संख्याओं का क्षेत्र आर्किमिडीज़ है, किन्तु वास्तविक गुणांक में तर्कसंगत कार्यो का क्षेत्र आर्किमिडीज़ नहीं है।
आर्किमिडीज़ गुण के नाम का इतिहास और उत्पत्ति
इस अवधारणा का नाम ओटो स्टोल्ज़ के माध्यम से (1880 के दशक में) प्राचीन ग्रीक के ज्यामिति और सिरैक्यूज़ के भौतिक विज्ञानी आर्किमिडीज़ के नाम पर रखा गया था।
आर्किमिडीज़ गुण यूक्लिड के घटको की पुस्तक V में परिभाषा 4 के रूप में प्रदर्शित करी गई है:
कहा जाता है कि परिमाण का एक दूसरे से अनुपात होता है जिसे गुणा करने पर एक दूसरे से अधिक हो सकता है।
चूँकि आर्किमिडीज़ ने इसका श्रेय कनिडस के यूडोक्सस को दिया है, इसलिए इसे "यूडोक्सस का प्रमेय" या यूडोक्सस सूत्रीकरण के रूप में भी जाना जाता है।[3]
आर्किमिडीज़ ने अनुमानी तर्कों में अत्यंत सूक्ष्म का उपयोग किया है, चूंकि उन्होंने अस्वीकार किया कि वह पूर्ण गणितीय प्रमाण थे।
रैखिक रूप से आदेशित समूहों के लिए परिभाषा
मान लीजिए कि x और y एक रैखिक क्रम वाले समूह G के सकारात्मक घटक हैं। तत्पश्चात के संबंध में अपरिमेय है (या समकक्ष , के संबंध में अनंत है) यदि किसी प्राकृतिक संख्या के लिए का गुणज से न्यूनतम है, तब निम्नलिखित असमानता है:
समूह आर्किमिडीज़ है यदि कोई जोड़ी नहीं है ऐसा है कि एवं के संबंध में अपरिमेय है।
इसके अतिरिक्त, यदि इकाई (1) के साथ एक बीजगणितीय संरचना है - उदाहरण के रूप मे, एक चक्र (गणित) - तब एक समान परिभाषा पर प्रयुक्त होती है। यदि के संबंध में x अपरिमेय है तब x एक अपरिमेय घटक है। इसी प्रकार, यदि के संबंध में अनंत है, तब एक अनंत घटक है। बीजगणितीय संरचना आर्किमिडीयन है यदि इसमें कोई अनंत घटक और कोई अपरिमेय घटक नहीं है।
आदेशित किए गए क्षेत्र
आदेशित क्षेत्र में कुछ अतिरिक्त गुण होते हैं:
- परिमेय संख्याएँ किसी भी क्रमित क्षेत्र में अंतर्निहित होती हैं। अर्थात्, किसी भी क्रमित क्षेत्र में अभिलक्षणिक (बीजगणित) शून्य होता है।
- यदि अनंत है, तब अनंत है, और इसके विपरीत है। इसलिए, यह सत्यापित करने के लिए कि एक क्षेत्र आर्किमिडीयन है, यह मात्र यह परीक्षण के लिए पर्याप्त है कि कोई अपरिमेय घटक नहीं हैं, या यह परीक्षण के लिए कि कोई अनंत घटक नहीं हैं।
- यदि अपरिमेय है और तब एक परिमेय संख्या है, तब अपरिमेय भी है। परिणामस्वरूप दिए गए एक सामान्य घटक के परिणामस्वरूप दिए गए सामान्य घटक , और या तब समस्त अनंतसूक्ष्म हैं या समस्त अनंतसूक्ष्म नही हैं।
इस समूहों में एक क्रमबद्ध क्षेत्र K आर्किमिडीज़ है, जब निम्नलिखित कथन को आर्किमिडीज़ का स्वयंसिद्ध कहा जाता है:
- मान लीजिए एवं का कोई भी घटक नहीं है। तत्पश्चात एक प्राकृतिक संख्या is प्रकार उपस्थित है कि है।
वैकल्पिक रूप से कोई निम्नलिखित लक्षण वर्णन का उपयोग कर सकता है:
आदर्श क्षेत्रों के लिए परिभाषा
विशेषण "आर्किमिडीयन" को मान ांकन श्रेणी एक मान वान क्षेत्र और श्रेणी एक मान वान क्षेत्र पर मानक रिक्त स्थान के सिद्धांत में निम्नानुसार तैयार किया गया है। मान लीजिए एक क्षेत्र है जो एक निरपेक्ष मान फलन से संपन्न है, अर्थात, एक फलन जो वास्तविक संख्या को क्षेत्र घटक 0 के साथ संबद्ध करता है और प्रत्येक शून्यतर के साथ एक धनात्मक वास्तविक संख्या को संबद्ध करता है और और को संतुष्ट करता है। तत्पश्चात, को आर्किमिडीयन कहा जाता है यदि किसी शून्यतर के लिए एक प्राकृतिक संख्या उपस्थित हो
एक गैर-आर्किमिडीयन मानक रैखिक स्थान की अवधारणा ए.एफ. मोन्ना के माध्यम से प्रस्तुत की गई थी।[4]
उदाहरण और विपरीत उदाहरण
वास्तविक संख्या का आर्किमिडीयन गुण
तर्कसंगत संख्याओं के क्षेत्र को अनेक निरपेक्ष मान फलन में से एक अभिहस्तांकित करा जा सकता है, जिसमें निरर्थक फलन भी सम्मलित है जब अधिक सामान्य और एडिक निरपेक्ष मान फलन है। ओस्ट्रोव्स्की के प्रमेय के अनुसार, तर्कसंगत संख्याओं पर प्रत्येक अ-निरर्थक निरपेक्ष मान या तब सामान्य निरपेक्ष मान या कुछ एडिक निरपेक्ष मान के समान्तर होता है। अ-निरर्थक निरपेक्ष मानों के संबंध में तर्कसंगत क्षेत्र पूर्ण नहीं है, निरर्थक निरपेक्ष मान के संबंध में, तर्कसंगत क्षेत्र एक असतत स्थलीय स्थान है इसलिए यह पूर्ण है। सामान्य निरपेक्ष मान (क्रम से) के संबंध में पूर्णता वास्तविक संख्याओं का क्षेत्र है। इस तर्कसाध्य के के माध्यम से वास्तविक संख्या का क्षेत्र एक आदेशित क्षेत्र और एक मानक क्षेत्र के रूप में आर्किमिडीयन है।[5] दूसरी ओर, अन्य अ-निरर्थक निरपेक्ष मानों के संबंध में पूर्णताएं पी-एडिक संख्या प्रणाली के क्षेत्र प्रदान करती हैं, जिस स्थान पर एक अभाज्य पूर्णांक संख्या है (नीचे देखें); चूंकि एडिक निरपेक्ष मान अल्ट्रामेट्रिक गुण को संतुष्ट करते हैं, तब एडिक संख्या क्षेत्र मानक क्षेत्र के रूप में आर्किमिडीयन नही हैं (उन्हें आदेशित किए गए क्षेत्र में निर्मित नही करा जा सकता है)।
वास्तविक संख्याओं के सूत्रीकरण सिद्धांत में, शून्येतर अपरिमेय वास्तविक संख्याओं की अ-उपस्थित निम्नतम ऊपरी बाध्य गुण के माध्यम से निहित है। समस्त धनात्मक अपरिमित गुण से युक्त समुच्चय को के माध्यम से निरूपित करें। यह समुच्चय उपर्युक्त से परिबद्ध है। अब एक विरोधाभास के लिए मान लें कि अरिक्त है। तत्पश्चात इसकी न्यूनतम उच्च सीमा है जो धनात्मक भी है इसलिए है। चूँकि c, की उच्च परिबंध है और , , से पूर्णतः दीर्घतर है, यह एक धनात्मक अपरिमेय नहीं है। अर्थात् कुछ प्राकृतिक संख्या होती है जिसके लिए होता है। दूसरी ओर एक धनात्मक अपरिमेय है क्योंकि न्यूनतम ऊपरी सीमा की परिभाषा के अनुसार और , के मध्य एक अपरिमेय होना चाहिए और यदि है तब अपरिमेय नहीं है। किन्तु इसलिए अपरिमेय नहीं है, और यह एक विरोधाभास है। इसका अर्थ यह है कि Z अंततः रिक्त है: कोई धनात्मक, अपरिमेय वास्तविक संख्याएँ नहीं हैं।
वास्तविक संख्याओं की आर्किमिडीज़ गुण भी रचनात्मक विश्लेषण में भी प्रयुक्त होती है, तथापि न्यूनतम ऊपरी परिबंध वाले गुण उस संदर्भ में विफल हो सकते है।
गैर-आर्किमिडीयन आदेशित क्षेत्र
एक आदेशित क्षेत्र के उदाहरण के रूप मे जो आर्किमिडीयन नहीं है, वास्तविक गुणांक वाले तर्कसंगत कार्य के क्षेत्र को लें। (एक परिमेय फलन वह फलन है जिसे एक बहुपद के माध्यम से दूसरे बहुपद से विभाजित करके व्यक्त किया जा सकता है; हम मानेंगे कि यह इस प्रकार से किया गया है कि प्रत्येक का प्रमुख गुणांक धनात्मक है।) इसे एक आदेशित किया गया और इसे क्षेत्र बनाने के लिए, किसी को जोड़ और गुणन संचालन के साथ संगत आदेशित निर्दिष्ट करना होगा। अब यदि और मात्र है तब हमें मात्र यह वर्णन करना है कि कौन से तर्कसंगत कार्य धनात्मक माने जाते हैं। यदि अंश का प्रमुख गुणांक धनात्मक है, तब फलन धनात्मक कहा जाता है। (किसी को यह परीक्षण चाहिए कि यह क्रम उचित प्रकार से परिभाषित है और जोड़ और गुणा के साथ संगत है।) इस परिभाषा के अनुसार परिमेय फलन धनात्मक है, किन्तु परिमेय फलन से न्यूनतम है। वास्तव में यदि कोई प्राकृतिक संख्या है तब धनात्मक है किन्तु तब भी से न्यूनतम है चाहे कितना भी दीर्घतर क्यों न हो। इसलिए, इस क्षेत्र में एक अपरिमेय है।
यह उदाहरण अन्य गुणांकों का सामान्यीकरण करता है। वास्तविक गुणांकों के अतिरिक्त तर्कसंगत कार्यों को तर्कसंगत के साथ लेने से एक गणनीय अ-आर्किमिडीयन आदेशित क्षेत्र उत्पन्न होता है। गुणांकों को एक भिन्न चर में तर्कसंगत कार्यों के रूप में लेने से, मान लीजिए y, एक भिन्न आदेशित प्रकार के साथ एक उदाहरण निर्मित करता है।
अ-आर्किमिडीयन मूल्यवान क्षेत्र
p-एडिक आव्युह और p-एडिक अंक क्षेत्र से संपन्न परिमेय संख्याओं का क्षेत्र जो पूर्णताएँ हैं, उनके समीप निरपेक्ष मान वाले क्षेत्र के रूप में आर्किमिडीज़ गुण नहीं होता है। समस्त आर्किमिडीयन मूल्यवान क्षेत्र सामान्य निरपेक्ष मान की अधिकार के साथ जटिल संख्याओं के एक उपक्षेत्र के लिए सममितीय रूप से समरूपी हैं।[6]
आर्किमिडीयन आदेशित क्षेत्र की समतुल्य परिभाषाएँ
प्रत्येक रैखिक रूप से क्रमित क्षेत्र में एक क्रमित उपक्षेत्र के रूप में परिमेय (एक समरूपी प्रतिलिपि) सम्मिलित है, अर्थात् की गुणक इकाई के माध्यम से उत्पन्न उपक्षेत्र, जिसमें प्रवर्तित होकर एक आदेशित उपसमूह के रूप में पूर्णांक सम्मिलित होते हैं, जिसमें एक आदेशित मोनोइड के रूप में प्राकृतिक संख्याएं सम्मिलित होती हैं। परिमेय को अंतर्निहित करने पर में परिमेय, पूर्णांक और प्राकृतिक संख्याओं के विषय में वर्णन की एक विधि प्राप्त होती है। इन अवसंरचनाओं के संदर्भ में आर्किमिडीयन क्षेत्रों के समतुल्य लक्षण निम्नलिखित हैं।[7]
- प्राकृतिक संख्याएँ सह-अंतिम (गणित) में होती हैं। अर्थात का प्रत्येक घटक किसी प्राकृतिक संख्या से न्यूनतम है। (यह वह स्थिति नहीं है जब अनंत घटक उपस्थित हों।) इस प्रकार एक आर्किमिडीयन क्षेत्र वह है जिसकी प्राकृतिक संख्या बिना किसी सीमा के विकसित होती है।
- समुच्चय के में शून्य न्यूनतम है। (यदि एक धनात्मक अपरिमेय समाहित करता है, तब यह समुच्चय के लिए एक निम्म सीमा होगी जिस स्थान पर शून्य सबसे दीर्घतर निम्म सीमा नहीं होगी।)
- धनात्मक और ऋणात्मक परिमेय के मध्य के घटको का समुच्चय विवृत नही है। इसका कारण यह है कि समुच्चय में समस्त अपरिमेय होते हैं, जो मात्र समुच्चय होता है जब कोई शून्येतर अपरिमेय नहीं होते हैं, और अन्यथा विवृत होता है, तब न कोई न्यूनतम और न ही दीर्घतर शून्यतर अपरिमेय होता है। ध्यान दें कि दोनों स्थितियों में, अत्यंत सूक्ष्म का समुच्चय संवृत है। बाद वाले मामले में, (i) प्रत्येक अपरिमेय प्रत्येक धनात्मक परिमेय से न्यूनतम है, (ii) न तब कोई सबसे दीर्घतर अपरिमेय है और न ही सबसे न्यूनतम धनात्मक परिमेय है, और (iii) मध्य में और कुछ भी और नहीं है। परिणामस्वरूप, कोई भी अ-आर्किमिडीयन आदेशित क्षेत्र अपूर्ण और असंबद्ध दोनों है।
- में किसी के लिए से दीर्घतर पूर्णांकों के समूहों में न्यूनतम घटक होता है। (यदि एक ऋणात्मक अनंत मात्रा होती तब प्रत्येक पूर्णांक इससे दीर्घतर होता है।)
- के प्रत्येक अरिक्त विवृत अंतराल में एक परिमेय सम्मिलित होता है। (यदि एक धनात्मक अपरिमेय है, तब विवृत अंतराल में अपरिमित रूप से अनेक अपरिमेय हैं किन्तु एक भी परिमेय नहीं है।)
- में सुप० और इन्फ़० दोनों के संबंध में परिमेय सघन हैं। (अर्थात्, का प्रत्येक घटक परिमेय के कुछ समुच्चय का पूरक है, और परिमेय के कुछ अन्य समुच्चय का इन्फ़० है।) इस प्रकार एक आर्किमिडीयन क्षेत्र किसी भी क्रमित क्षेत्र के अर्थ में परिमेय का कोई सघन क्रमित विस्तार है, जो अपने परिमेय घटको को संघनित रूप से अंतःस्थापित करता है।
यह भी देखें
- 0.999...
- आर्किमिडीज़ ने वेक्टर स्पेस का आदेश दिया
- वास्तविक संख्याओं का निर्माण – Axiomatic definitions of the real numbers
टिप्पणियाँ
- ↑ https://www.math.cuhk.edu.hk/course_builder/2021/math2050c/MATH%202050C%20Lecture%204%20(Jan%2021).pdf[bare URL PDF]
- ↑ G. Fisher (1994) in P. Ehrlich(ed.), Real Numbers, Generalizations of the Reals, and Theories of continua, 107-145, Kluwer Academic
- ↑ Knopp, Konrad (1951). Theory and Application of Infinite Series (English 2nd ed.). London and Glasgow: Blackie & Son, Ltd. p. 7. ISBN 0-486-66165-2.
- ↑ Monna, A. F. (1943). "Over een lineaire P-adische ruimte". Nederl. Akad. Wetensch. Verslag Afd. Natuurk. (52): 74–84. MR 0015678.
- ↑ Neal Koblitz, "p-adic Numbers, p-adic Analysis, and Zeta-Functions", Springer-Verlag,1977.
- ↑ Shell, Niel, Topological Fields and Near Valuations, Dekker, New York, 1990. ISBN 0-8247-8412-X
- ↑ Schechter 1997, §10.3
संदर्भ
- Schechter, Eric (1997). Handbook of Analysis and its Foundations. Academic Press. ISBN 0-12-622760-8. Archived from the original on 2015-03-07. Retrieved 2009-01-30.