दूसरे क्रम की शंकु प्रोग्रामिंग: Difference between revisions
No edit summary |
No edit summary |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
दूसरे क्रम का शंकु | '''दूसरे क्रम का शंकु प्रोग्राम''' (एसओसीपी) प्रपत्र की [[उत्तल अनुकूलन]] समस्या है | ||
:छोटा करना <math>\ f^T x \ </math> :का विषय है | :छोटा करना <math>\ f^T x \ </math> :का विषय है | ||
::<math>\lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i,\quad i = 1,\dots,m</math> | ::<math>\lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i,\quad i = 1,\dots,m</math> | ||
::<math>Fx = g \ </math> | ::<math>Fx = g \ </math> | ||
जहां समस्या | जहां समस्या मापदंड <math>f \in \mathbb{R}^n, \ A_i \in \mathbb{R}^{{n_i}\times n}, \ b_i \in \mathbb{R}^{n_i}, \ c_i \in \mathbb{R}^n, \ d_i \in \mathbb{R}, \ F \in \mathbb{R}^{p\times n}</math> हैं , और <math>g \in \mathbb{R}^p</math>. <math>x\in\mathbb{R}^n</math> अनुकूलन चर है. [[यूक्लिडियन मानदंड]] <math>\lVert x \rVert_2 </math><math>^T</math> है और स्थानांतरण को इंगित करता है.<ref name="boyd">{{cite book |last1=Boyd |first1=Stephen |last2=Vandenberghe |first2=Lieven |title=उत्तल अनुकूलन|publisher=Cambridge University Press |year=2004 |isbn=978-0-521-83378-3 |url=https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf |accessdate=July 15, 2019}}</ref> एसओसीपी में दूसरे क्रम का शंकु बाधाओं से उत्पन्न होता है, जो एफ़िन फलन की आवश्यकता के समान है <math>(A x + b, c^T x + d)</math> दूसरे क्रम के उत्तल शंकु में स्थित <math>\mathbb{R}^{n_i + 1}</math> होता है .<ref name="boyd"/> | ||
<math>\lVert x \rVert_2 </math> | |||
एसओसीपी को आंतरिक बिंदु विधियों द्वारा हल किया जा सकता है <ref>{{cite journal|last1=Potra|first1=lorian A.|last2=Wright|first2=Stephen J.|date=1 December 2000|title=आंतरिक-बिंदु विधियाँ|journal=Journal of Computational and Applied Mathematics|volume=124|issue=1–2|pages=281–302|doi=10.1016/S0377-0427(00)00433-7|bibcode=2000JCoAM.124..281P|doi-access=free}}</ref> और सामान्यतः, [[अर्धनिश्चित प्रोग्रामिंग]] (एसडीपी) समस्याओं की तुलना में अधिक कुशलता से हल किया जा सकता है।<ref name="Fawzi" /> एसओसीपी के कुछ इंजीनियरिंग अनुप्रयोगों में फिल्टर डिजाइन, एंटीना सरणी वजन डिजाइन, ट्रस डिजाइन और रोबोटिक्स में लोभी बल अनुकूलन सम्मिलित हैं।<ref name=":0">{{Cite journal|last1=Lobo|first1=Miguel Sousa|last2=Vandenberghe|first2=Lieven|last3=Boyd|first3=Stephen|last4=Lebret|first4=Hervé|date=1998|title=दूसरे क्रम के शंकु प्रोग्रामिंग के अनुप्रयोग|journal=Linear Algebra and Its Applications|language=en|volume=284|issue=1–3|pages=193–228|doi=10.1016/S0024-3795(98)10032-0|doi-access=free}}</ref> [[मात्रात्मक वित्त]] में अनुप्रयोगों में [[पोर्टफोलियो अनुकूलन]] सम्मिलित है; कुछ बाज़ार प्रभाव बाधाएँ, क्योंकि वे रैखिक नहीं हैं, [[द्विघात प्रोग्रामिंग]] द्वारा हल नहीं की जा सकती हैं, किन्तु उन्हें एसओसीपी समस्याओं के रूप में तैयार किया जा सकता है।<ref>{{cite web |title=एसओसीपी को हल करना|url=https://docs.mosek.com/slides/2017/shanghai/talk.pdf}}</ref><ref>{{cite web |title=पोर्टफोलियो अनुकूलन|url=https://nmfin.tech/wp-content/uploads/2020/06/new-technologies-in-portfolio-optimization.20200612.pdf}}</ref><ref>{{cite book |last1=Li |first1=Haksun |title=Numerical Methods Using Java: For Data Science, Analysis, and Engineering |date=16 January 2022 |publisher=APress |pages=Chapter 10 |isbn=978-1484267967 }}</ref> | |||
== दूसरे क्रम का शंकु == | == दूसरे क्रम का शंकु == | ||
आयाम का मानक या इकाई दूसरे क्रम का शंकु <math>n+1</math> परिभाषित किया जाता है | आयाम का मानक या इकाई दूसरे क्रम का शंकु <math>n+1</math> परिभाषित किया जाता है | ||
| Line 18: | Line 15: | ||
दूसरे क्रम के शंकु को द्विघात शंकु, आइसक्रीम शंकु या लोरेंत्ज़ शंकु के नाम से भी जाना जाता है। दूसरे क्रम का शंकु <math>\mathbb{R}^3</math> है <math>\left\{(x,y,z) \Big| \sqrt{x^2 + y^2} \leq z \right\}</math>. | दूसरे क्रम के शंकु को द्विघात शंकु, आइसक्रीम शंकु या लोरेंत्ज़ शंकु के नाम से भी जाना जाता है। दूसरे क्रम का शंकु <math>\mathbb{R}^3</math> है <math>\left\{(x,y,z) \Big| \sqrt{x^2 + y^2} \leq z \right\}</math>. | ||
दूसरे क्रम के शंकु बाधा को संतुष्ट करने वाले बिंदुओं का | दूसरे क्रम के शंकु बाधा को संतुष्ट करने वाले बिंदुओं का समुच्चय एफ़िन मैपिंग के अनुसार इकाई दूसरे क्रम के शंकु की व्युत्क्रम छवि है: | ||
<math>\lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i \Leftrightarrow | <math>\lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i \Leftrightarrow | ||
| Line 25: | Line 22: | ||
और इसलिए उत्तल है. | और इसलिए उत्तल है. | ||
दूसरे क्रम के शंकु को | दूसरे क्रम के शंकु को धनात्मक अर्धनिश्चित आव्यूह के शंकु में एम्बेड किया जा सकता है | ||
<math>||x||\leq t \Leftrightarrow \begin{bmatrix} tI & x \\ x^T & t \end{bmatrix} \succcurlyeq 0,</math> | <math>||x||\leq t \Leftrightarrow \begin{bmatrix} tI & x \\ x^T & t \end{bmatrix} \succcurlyeq 0,</math> | ||
अर्थात, दूसरे क्रम का शंकु अवरोध रैखिक आव्यूह असमानता के समान है (यहां)। <math>M\succcurlyeq 0 </math> साधन <math>M </math> अर्धनिश्चित आव्यूह है)। इसी प्रकार, हमारे पास भी है, | |||
<math>\lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i \Leftrightarrow | <math>\lVert A_i x + b_i \rVert_2 \leq c_i^T x + d_i \Leftrightarrow | ||
\begin{bmatrix} (c_i^T x+d_i)I & A_i x+b_i \\ (A_i x + b_i)^T & c_i^T x + d_i \end{bmatrix} \succcurlyeq 0</math>. | \begin{bmatrix} (c_i^T x+d_i)I & A_i x+b_i \\ (A_i x + b_i)^T & c_i^T x + d_i \end{bmatrix} \succcurlyeq 0</math>. | ||
== अन्य अनुकूलन समस्याओं के साथ संबंध == | == अन्य अनुकूलन समस्याओं के साथ संबंध == | ||
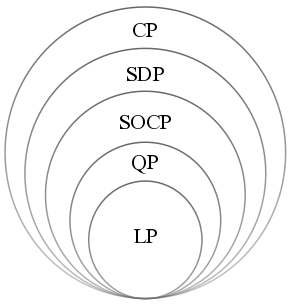
[[File:Hierarchy compact convex.png|thumb|उत्तल अनुकूलन समस्याओं का पदानुक्रम. (एलपी: रैखिक | [[File:Hierarchy compact convex.png|thumb|उत्तल अनुकूलन समस्याओं का पदानुक्रम. (एलपी: रैखिक प्रोग्राम, क्यूपी: द्विघात प्रोग्राम, एसओसीपी द्वितीय-क्रम शंकु प्रोग्राम, एसडीपी: अर्धनिश्चित प्रोग्राम, सीपी: शंकु प्रोग्राम।)]]जब <math>A_i = 0</math> के लिए <math>i = 1,\dots,m</math>, एसओसीपी [[रैखिक कार्यक्रम|रैखिक प्रोग्राम]] में परिवर्तित हो जाता है। जब <math>c_i = 0 </math> के लिए <math>i = 1,\dots,m</math>, एसओसीपी उत्तल चतुर्भुज रूप से बाधित रैखिक प्रोग्राम के समान है। | ||
उत्तल चतुर्भुज रूप से बाधित द्विघात फलन को उद्देश्य फलन को बाधा के रूप में सुधारकर एसओसीपी के रूप में भी तैयार किया जा सकता है।<ref name=":0" /> अर्धनिश्चित प्रोग्रामिंग एसओसीपी को समाहित करती है क्योंकि एसओसीपी बाधाओं को [[रैखिक मैट्रिक्स असमानता|रैखिक आव्यूह असमानता]] (एलएमआई) के रूप में लिखा जा सकता है और इसे अर्धनिश्चित प्रोग्राम के उदाहरण के रूप में पुन: तैयार किया जा सकता है।<ref name=":0" /> चूँकि, इसका उलटा मान्य नहीं है: धनात्मक अर्धनिश्चित शंकु हैं जो किसी भी दूसरे क्रम के शंकु प्रतिनिधित्व को स्वीकार नहीं करते हैं।<ref name="Fawzi">{{Cite journal|last=Fawzi|first=Hamza|date=2019|title=दूसरे क्रम के शंकु का उपयोग करके सकारात्मक अर्धनिश्चित शंकु का प्रतिनिधित्व करने पर|journal=Mathematical Programming|language=en|volume=175|issue=1–2|pages=109–118|doi=10.1007/s10107-018-1233-0|issn=0025-5610|arxiv=1610.04901|s2cid=119324071}}</ref> वास्तव में, जबकि समतल में किसी भी बंद उत्तल अर्ध बीजगणितीय समुच्चय को एसओसीपी के व्यवहार्य क्षेत्र के रूप में लिखा जा सकता है,<ref>{{cite arXiv|last=Scheiderer|first=Claus|date=2020-04-08|title=समतल के उत्तल उपसमुच्चय के लिए दूसरे क्रम का शंकु प्रतिनिधित्व|class=math.OC|eprint=2004.04196}}</ref> यह ज्ञात है कि ऐसे उत्तल अर्ध-बीजगणितीय समुच्चय उपस्थित हैं जिन्हें एसडीपी द्वारा प्रस्तुत नहीं किया जा सकता है, अर्थात, ऐसे उत्तल अर्ध-बीजगणितीय समुच्चय उपस्थित हैं जिन्हें एसडीपी के व्यवहार्य क्षेत्र के रूप में नहीं लिखा जा सकता है।<ref>{{Cite journal|last=Scheiderer|first=Claus|date=2018|title=स्पेक्ट्राहेड्रल छायाएँ|journal=SIAM Journal on Applied Algebra and Geometry|language=en|volume=2|issue=1|pages=26–44|doi=10.1137/17M1118981|issn=2470-6566|doi-access=free}}</ref> | |||
== उदाहरण == | == उदाहरण == | ||
=== द्विघात बाधा === | === द्विघात बाधा === | ||
| Line 45: | Line 40: | ||
:<math> x^T A x + b^T x + c \leq 0. </math> | :<math> x^T A x + b^T x + c \leq 0. </math> | ||
यह | यह एसओसीपी बाधा के समतुल्य है | ||
:<math> \lVert A^{1/2} x + \frac{1}{2}A^{-1/2}b \rVert \leq \left(\frac{1}{4}b^T A^{-1} b - c \right)^{\frac{1}{2}} </math> | :<math> \lVert A^{1/2} x + \frac{1}{2}A^{-1/2}b \rVert \leq \left(\frac{1}{4}b^T A^{-1} b - c \right)^{\frac{1}{2}} </math> | ||
===स्टोकेस्टिक रैखिक प्रोग्रामिंग=== | ===स्टोकेस्टिक रैखिक प्रोग्रामिंग=== | ||
असमानता रूप में [[स्टोकेस्टिक रैखिक कार्यक्रम]] पर विचार करें | असमानता रूप में [[स्टोकेस्टिक रैखिक कार्यक्रम|स्टोकेस्टिक रैखिक प्रोग्राम]] पर विचार करें | ||
: | :मिनीमाइज <math>\ c^T x \ </math> :का विषय है | ||
::<math>\mathbb{P}(a_i^Tx \leq b_i) \geq p, \quad i = 1,\dots,m </math> | ::<math>\mathbb{P}(a_i^Tx \leq b_i) \geq p, \quad i = 1,\dots,m </math> | ||
जहां | जहां मापदंड <math>a_i \ </math> माध्य के साथ स्वतंत्र गाऊसी यादृच्छिक सदिश <math>\bar{a}_i</math> हैं और सहप्रसरण <math>\Sigma_i \ </math> और <math>p\geq0.5</math>. इस समस्या को एसओसीपी के रूप में व्यक्त किया जा सकता है | ||
:छोटा करना <math>\ c^T x \ </math> :का विषय है | :छोटा करना <math>\ c^T x \ </math> :का विषय है | ||
:: <math>\bar{a}_i^T x + \Phi^{-1}(p) \lVert \Sigma_i^{1/2} x \rVert_2 \leq b_i , \quad i = 1,\dots,m </math> | :: <math>\bar{a}_i^T x + \Phi^{-1}(p) \lVert \Sigma_i^{1/2} x \rVert_2 \leq b_i , \quad i = 1,\dots,m </math> | ||
जहाँ <math>\Phi^{-1}(\cdot) \ </math> व्युत्क्रम सामान्य संचयी वितरण फलन है।<ref name="boyd"/> | |||
===स्टोकेस्टिक द्वितीय-क्रम शंकु प्रोग्रामिंग=== | ===स्टोकेस्टिक द्वितीय-क्रम शंकु प्रोग्रामिंग=== | ||
हम दूसरे क्रम के शंकु | हम दूसरे क्रम के शंकु फलन का उल्लेख करते हैं नियतात्मक दूसरे क्रम के शंकु फलन के रूप में क्योंकि उन्हें परिभाषित करने वाला डेटा नियतात्मक है। स्टोकेस्टिक द्वितीय-क्रम शंकु प्रोग्राम अनुकूलन समस्याओं का वर्ग है जिन्हें नियतात्मक द्वितीय-क्रम शंकु फलन को परिभाषित करने वाले डेटा में अनिश्चितता को संभालने के लिए परिभाषित किया गया है। | ||
नियतात्मक दूसरे क्रम के शंकु | |||
स्टोकेस्टिक द्वितीय-क्रम शंकु | |||
==सॉल्वर और स्क्रिप्टिंग (प्रोग्रामिंग) भाषाएँ== | ==सॉल्वर और स्क्रिप्टिंग (प्रोग्रामिंग) भाषाएँ== | ||
| Line 71: | Line 60: | ||
{| class="wikitable sortable" | {| class="wikitable sortable" | ||
|- | |- | ||
! | !नाम | ||
! | !लाइसेंस | ||
! | !संक्षिप्त सूचना | ||
|- | |- | ||
|[[AMPL]]|| | |[[AMPL|एएमपीएल]]||व्यावसायिक|| सीएससीपी समर्थन के साथ एक बीजगणितीय मॉडलिंग भाषा | ||
|- | |- | ||
|[[Artelys Knitro]]|| | |[[Artelys Knitro|आर्टेलिस निट्रो]]||व्यावसायिक|| | ||
|- | |- | ||
|[[CPLEX]]|| | |[[CPLEX|सीप्लेक्स]]||व्यावसायिक|| | ||
|- | |- | ||
|[[FICO Xpress]]|| | |[[FICO Xpress|फीको एक्सप्रेस]]||व्यावसायिक|| | ||
|- | |- | ||
|[[Gurobi Optimizer]]|| | |[[Gurobi Optimizer|गुरोबी ऑप्टिमाइज़र]]||व्यावसायिक|| | ||
|- | |- | ||
|[[MATLAB]]|| | |[[MATLAB|मैटलैब]]||व्यावसायिक||कॉनप्रोग फलन इलेक्ट्रिसिटीसीपी समस्याओं का समाधान करता है<ref>{{cite web | title=Second-order cone programming solver - MATLAB coneprog | website=MathWorks | date=2021-03-01 | url=https://www.mathworks.com/help/optim/ug/coneprog.html | access-date=2021-07-15}}</ref> आंतरिक-बिंदु एल्गोरिदम का उपयोग करना<ref>{{cite web | title=Second-Order Cone Programming Algorithm - MATLAB & Simulink | website=MathWorks | date=2021-03-01 | url=https://www.mathworks.com/help/optim/ug/cone-programming-algorithm.html | access-date=2021-07-15}}</ref> | ||
|- | |- | ||
|[[MOSEK]]|| | |[[MOSEK|मोसेक]]||व्यावसायिक|| समानांतर आंतरिक-बिंदु एल्गोरिथ्म | ||
|- | |- | ||
|[[NAG Numerical Library]]|| | |[[NAG Numerical Library|एनएजी न्यूमेरिकल लाइब्रेरी]]||व्यावसायिक|| एसओसीपी सॉल्वर के साथ सामान्य प्रयोजन संख्यात्मक लाइब्रेरी | ||
|} | |} | ||
==संदर्भ == | |||
==संदर्भ== | |||
{{reflist}} | {{reflist}} | ||
[[Category: | [[Category:CS1 English-language sources (en)]] | ||
[[Category:Created On 10/07/2023]] | [[Category:Created On 10/07/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:अनुकूलन एल्गोरिदम और विधियाँ]] | |||
[[Category:उत्तल अनुकूलन]] | |||
Latest revision as of 10:18, 4 August 2023
दूसरे क्रम का शंकु प्रोग्राम (एसओसीपी) प्रपत्र की उत्तल अनुकूलन समस्या है
- छोटा करना :का विषय है
जहां समस्या मापदंड हैं , और . अनुकूलन चर है. यूक्लिडियन मानदंड है और स्थानांतरण को इंगित करता है.[1] एसओसीपी में दूसरे क्रम का शंकु बाधाओं से उत्पन्न होता है, जो एफ़िन फलन की आवश्यकता के समान है दूसरे क्रम के उत्तल शंकु में स्थित होता है .[1]
एसओसीपी को आंतरिक बिंदु विधियों द्वारा हल किया जा सकता है [2] और सामान्यतः, अर्धनिश्चित प्रोग्रामिंग (एसडीपी) समस्याओं की तुलना में अधिक कुशलता से हल किया जा सकता है।[3] एसओसीपी के कुछ इंजीनियरिंग अनुप्रयोगों में फिल्टर डिजाइन, एंटीना सरणी वजन डिजाइन, ट्रस डिजाइन और रोबोटिक्स में लोभी बल अनुकूलन सम्मिलित हैं।[4] मात्रात्मक वित्त में अनुप्रयोगों में पोर्टफोलियो अनुकूलन सम्मिलित है; कुछ बाज़ार प्रभाव बाधाएँ, क्योंकि वे रैखिक नहीं हैं, द्विघात प्रोग्रामिंग द्वारा हल नहीं की जा सकती हैं, किन्तु उन्हें एसओसीपी समस्याओं के रूप में तैयार किया जा सकता है।[5][6][7]
दूसरे क्रम का शंकु
आयाम का मानक या इकाई दूसरे क्रम का शंकु परिभाषित किया जाता है
.
दूसरे क्रम के शंकु को द्विघात शंकु, आइसक्रीम शंकु या लोरेंत्ज़ शंकु के नाम से भी जाना जाता है। दूसरे क्रम का शंकु है .
दूसरे क्रम के शंकु बाधा को संतुष्ट करने वाले बिंदुओं का समुच्चय एफ़िन मैपिंग के अनुसार इकाई दूसरे क्रम के शंकु की व्युत्क्रम छवि है:
और इसलिए उत्तल है.
दूसरे क्रम के शंकु को धनात्मक अर्धनिश्चित आव्यूह के शंकु में एम्बेड किया जा सकता है
अर्थात, दूसरे क्रम का शंकु अवरोध रैखिक आव्यूह असमानता के समान है (यहां)। साधन अर्धनिश्चित आव्यूह है)। इसी प्रकार, हमारे पास भी है,
.
अन्य अनुकूलन समस्याओं के साथ संबंध
जब के लिए , एसओसीपी रैखिक प्रोग्राम में परिवर्तित हो जाता है। जब के लिए , एसओसीपी उत्तल चतुर्भुज रूप से बाधित रैखिक प्रोग्राम के समान है।
उत्तल चतुर्भुज रूप से बाधित द्विघात फलन को उद्देश्य फलन को बाधा के रूप में सुधारकर एसओसीपी के रूप में भी तैयार किया जा सकता है।[4] अर्धनिश्चित प्रोग्रामिंग एसओसीपी को समाहित करती है क्योंकि एसओसीपी बाधाओं को रैखिक आव्यूह असमानता (एलएमआई) के रूप में लिखा जा सकता है और इसे अर्धनिश्चित प्रोग्राम के उदाहरण के रूप में पुन: तैयार किया जा सकता है।[4] चूँकि, इसका उलटा मान्य नहीं है: धनात्मक अर्धनिश्चित शंकु हैं जो किसी भी दूसरे क्रम के शंकु प्रतिनिधित्व को स्वीकार नहीं करते हैं।[3] वास्तव में, जबकि समतल में किसी भी बंद उत्तल अर्ध बीजगणितीय समुच्चय को एसओसीपी के व्यवहार्य क्षेत्र के रूप में लिखा जा सकता है,[8] यह ज्ञात है कि ऐसे उत्तल अर्ध-बीजगणितीय समुच्चय उपस्थित हैं जिन्हें एसडीपी द्वारा प्रस्तुत नहीं किया जा सकता है, अर्थात, ऐसे उत्तल अर्ध-बीजगणितीय समुच्चय उपस्थित हैं जिन्हें एसडीपी के व्यवहार्य क्षेत्र के रूप में नहीं लिखा जा सकता है।[9]
उदाहरण
द्विघात बाधा
प्रपत्र के उत्तल चतुर्भुज रूप से बाधित द्विघात प्रोग्राम पर विचार करें
यह एसओसीपी बाधा के समतुल्य है
स्टोकेस्टिक रैखिक प्रोग्रामिंग
असमानता रूप में स्टोकेस्टिक रैखिक प्रोग्राम पर विचार करें
- मिनीमाइज :का विषय है
जहां मापदंड माध्य के साथ स्वतंत्र गाऊसी यादृच्छिक सदिश हैं और सहप्रसरण और . इस समस्या को एसओसीपी के रूप में व्यक्त किया जा सकता है
- छोटा करना :का विषय है
जहाँ व्युत्क्रम सामान्य संचयी वितरण फलन है।[1]
स्टोकेस्टिक द्वितीय-क्रम शंकु प्रोग्रामिंग
हम दूसरे क्रम के शंकु फलन का उल्लेख करते हैं नियतात्मक दूसरे क्रम के शंकु फलन के रूप में क्योंकि उन्हें परिभाषित करने वाला डेटा नियतात्मक है। स्टोकेस्टिक द्वितीय-क्रम शंकु प्रोग्राम अनुकूलन समस्याओं का वर्ग है जिन्हें नियतात्मक द्वितीय-क्रम शंकु फलन को परिभाषित करने वाले डेटा में अनिश्चितता को संभालने के लिए परिभाषित किया गया है।
सॉल्वर और स्क्रिप्टिंग (प्रोग्रामिंग) भाषाएँ
| नाम | लाइसेंस | संक्षिप्त सूचना |
|---|---|---|
| एएमपीएल | व्यावसायिक | सीएससीपी समर्थन के साथ एक बीजगणितीय मॉडलिंग भाषा |
| आर्टेलिस निट्रो | व्यावसायिक | |
| सीप्लेक्स | व्यावसायिक | |
| फीको एक्सप्रेस | व्यावसायिक | |
| गुरोबी ऑप्टिमाइज़र | व्यावसायिक | |
| मैटलैब | व्यावसायिक | कॉनप्रोग फलन इलेक्ट्रिसिटीसीपी समस्याओं का समाधान करता है[10] आंतरिक-बिंदु एल्गोरिदम का उपयोग करना[11] |
| मोसेक | व्यावसायिक | समानांतर आंतरिक-बिंदु एल्गोरिथ्म |
| एनएजी न्यूमेरिकल लाइब्रेरी | व्यावसायिक | एसओसीपी सॉल्वर के साथ सामान्य प्रयोजन संख्यात्मक लाइब्रेरी |
संदर्भ
- ↑ 1.0 1.1 1.2 Boyd, Stephen; Vandenberghe, Lieven (2004). उत्तल अनुकूलन (PDF). Cambridge University Press. ISBN 978-0-521-83378-3. Retrieved July 15, 2019.
- ↑ Potra, lorian A.; Wright, Stephen J. (1 December 2000). "आंतरिक-बिंदु विधियाँ". Journal of Computational and Applied Mathematics. 124 (1–2): 281–302. Bibcode:2000JCoAM.124..281P. doi:10.1016/S0377-0427(00)00433-7.
- ↑ 3.0 3.1 Fawzi, Hamza (2019). "दूसरे क्रम के शंकु का उपयोग करके सकारात्मक अर्धनिश्चित शंकु का प्रतिनिधित्व करने पर". Mathematical Programming (in English). 175 (1–2): 109–118. arXiv:1610.04901. doi:10.1007/s10107-018-1233-0. ISSN 0025-5610. S2CID 119324071.
- ↑ 4.0 4.1 4.2 Lobo, Miguel Sousa; Vandenberghe, Lieven; Boyd, Stephen; Lebret, Hervé (1998). "दूसरे क्रम के शंकु प्रोग्रामिंग के अनुप्रयोग". Linear Algebra and Its Applications (in English). 284 (1–3): 193–228. doi:10.1016/S0024-3795(98)10032-0.
- ↑ "एसओसीपी को हल करना" (PDF).
- ↑ "पोर्टफोलियो अनुकूलन" (PDF).
- ↑ Li, Haksun (16 January 2022). Numerical Methods Using Java: For Data Science, Analysis, and Engineering. APress. pp. Chapter 10. ISBN 978-1484267967.
- ↑ Scheiderer, Claus (2020-04-08). "समतल के उत्तल उपसमुच्चय के लिए दूसरे क्रम का शंकु प्रतिनिधित्व". arXiv:2004.04196 [math.OC].
- ↑ Scheiderer, Claus (2018). "स्पेक्ट्राहेड्रल छायाएँ". SIAM Journal on Applied Algebra and Geometry (in English). 2 (1): 26–44. doi:10.1137/17M1118981. ISSN 2470-6566.
- ↑ "Second-order cone programming solver - MATLAB coneprog". MathWorks. 2021-03-01. Retrieved 2021-07-15.
- ↑ "Second-Order Cone Programming Algorithm - MATLAB & Simulink". MathWorks. 2021-03-01. Retrieved 2021-07-15.