डब्ल्यू अवस्था: Difference between revisions

From Vigyanwiki
(Created page with "{{Use American English|date = February 2019}} {{Short description|Entangled 3-qubit quantum state}} {{Use mdy dates|date = February 2019}} डब्ल्यू अवस्...")
 
No edit summary
 
(9 intermediate revisions by 3 users not shown)
Line 1: Line 1:
{{Use American English|date = February 2019}}
{{Short description|Entangled 3-qubit quantum state}}
{{Short description|Entangled 3-qubit quantum state}}
{{Use mdy dates|date = February 2019}}


डब्ल्यू अवस्था तीन क्वैबिट की एक क्वांटम उलझाव [[कितना राज्य]] है जिसका [[अच्छा संकेतन]] में निम्नलिखित आकार होता है
'''डब्ल्यू''' अवस्था तीन क्वैबिट की एक उलझी हुई [[कितना राज्य|क्वांटम अवस्था]] है जिसका ब्रा-केट नोटेशन में निम्नलिखित आकार होता है


: <math>|\mathrm{W}\rangle = \frac{1}{\sqrt{3}}(|001\rangle + |010\rangle + |100\rangle)</math>
: <math>|\mathrm{W}\rangle = \frac{1}{\sqrt{3}}(|001\rangle + |010\rangle + |100\rangle)</math>
और जो एक विशिष्ट प्रकार के [[बहुपक्षीय उलझाव]] का प्रतिनिधित्व करने और [[क्वांटम सूचना सिद्धांत]] में कई अनुप्रयोगों में होने के लिए उल्लेखनीय है। इस अवस्था में तैयार किए गए कण बेल के प्रमेय के गुणों को पुन: उत्पन्न करते हैं, जो बताता है कि स्थानीय छिपे हुए चर का कोई भी शास्त्रीय सिद्धांत क्वांटम यांत्रिकी की भविष्यवाणियां नहीं कर सकता है। राज्य का नाम वोल्फगैंग ड्यूर के नाम पर रखा गया है,<ref>{{Cite journal|last=Cabello|first=Adán|date=2002-02-05|title=थ्री-क्विट ग्रीनबर्गर-हॉर्न-ज़ीलिंगर और डब्ल्यू राज्यों के लिए असमानताओं के साथ और बिना बेल का प्रमेय|url=https://link.aps.org/doi/10.1103/PhysRevA.65.032108|journal=Physical Review A|language=en|volume=65|issue=3|pages=032108|doi=10.1103/PhysRevA.65.032108|issn=1050-2947|arxiv=quant-ph/0107146|bibcode=2002PhRvA..65c2108C |s2cid=55659305 }}</ref> जिन्होंने सबसे पहले 2002 में गुइफ़्रे विडाल और [[जुआन इग्नासियो सिराक सस्टुरैन]] के साथ मिलकर राज्य की रिपोर्ट की थी।<ref name="Duer2000">{{cite journal|author1=W. Dür |author2=G. Vidal |author3=J. I. Cirac  |name-list-style=amp |title=तीन क्वैबिट को दो असमान तरीकों से उलझाया जा सकता है|journal=Phys. Rev. A|volume=62|pages=062314|year=2000|issue=6 | doi=10.1103/PhysRevA.62.062314|arxiv=quant-ph/0005115|bibcode = 2000PhRvA..62f2314D |s2cid=16636159 }}</ref>
और जो विशिष्ट प्रकार के [[बहुपक्षीय उलझाव|बहुपक्षीय सम्मिश्रता]] का प्रतिनिधित्व करने और [[क्वांटम सूचना सिद्धांत]] में कई अनुप्रयोगों में होने के लिए उल्लेखनीय है। इस प्रकार इस अवस्था में तैयार किए गए कण बेल के प्रमेय के गुणों को पुन: उत्पन्न करते हैं, जो बताता है कि स्थानीय छिपे हुए चर का कोई भी मौलिक सिद्धांत क्वांटम यांत्रिकी की पूर्वानुमान नहीं हो सकता है। इस प्रकार अवस्था का नाम वोल्फगैंग ड्यूर के नाम पर रखा गया है,<ref>{{Cite journal|last=Cabello|first=Adán|date=2002-02-05|title=थ्री-क्विट ग्रीनबर्गर-हॉर्न-ज़ीलिंगर और डब्ल्यू राज्यों के लिए असमानताओं के साथ और बिना बेल का प्रमेय|url=https://link.aps.org/doi/10.1103/PhysRevA.65.032108|journal=Physical Review A|language=en|volume=65|issue=3|pages=032108|doi=10.1103/PhysRevA.65.032108|issn=1050-2947|arxiv=quant-ph/0107146|bibcode=2002PhRvA..65c2108C |s2cid=55659305 }}</ref> जिन्होंने सबसे पहले 2002 में गुइफ़्रे विडाल और [[जुआन इग्नासियो सिराक सस्टुरैन]] के साथ मिलकर अवस्था की रिपोर्ट की थी।<ref name="Duer2000">{{cite journal|author1=W. Dür |author2=G. Vidal |author3=J. I. Cirac  |name-list-style=amp |title=तीन क्वैबिट को दो असमान तरीकों से उलझाया जा सकता है|journal=Phys. Rev. A|volume=62|pages=062314|year=2000|issue=6 | doi=10.1103/PhysRevA.62.062314|arxiv=quant-ph/0005115|bibcode = 2000PhRvA..62f2314D |s2cid=16636159 }}</ref>
==गुण                                                                                                                                                                                                                      ==
[[File:Wstate quantumcircuit.png|thumb|400x400px|राई-रोटेशन गेट, नियंत्रित [[हैडमार्ड गेट]], 2 नियंत्रित नॉट गेट और क्वांटम लॉजिक गेट#एक्स गेट। घूर्णन का कोण है <math display="inline">\phi_3=2\arccos\left(1/\sqrt{3}\right)</math>.]]डब्ल्यू अवस्था दो गैर-विभाज्य में से का प्रतिनिधि है <ref>A pure state <math>|\psi\rangle</math> of <math>N</math> parties is called ''biseparable'', if one can find a partition of the parties in two disjoint subsets <math>A</math> and <math>B</math> with <math>A\cup B=\{1,...,N\}</math> such that <math>|\psi\rangle = |\phi\rangle_A\otimes|\gamma\rangle_B</math>, i.e. <math>|\psi\rangle</math> is a [[product state]] with respect to the partition <math>A|B</math>.</ref> तीन-क्विबिट अवस्थाों की कक्षाएं, दूसरा ग्रीनबर्गर-हॉर्न-ज़ीलिंगर <math>|\mathrm{GHZ}\rangle = (|000\rangle + |111\rangle)/\sqrt{2}</math> अवस्था है, जिन्हें [[LOCC|एलओसीसी]] द्वारा दूसरे में परिवर्तित नहीं किया जा सकता (संभावित रूप से भी नहीं)।<ref name="Duer2000">{{cite journal|author1=W. Dür |author2=G. Vidal |author3=J. I. Cirac  |name-list-style=amp |title=तीन क्वैबिट को दो असमान तरीकों से उलझाया जा सकता है|journal=Phys. Rev. A|volume=62|pages=062314|year=2000|issue=6 | doi=10.1103/PhysRevA.62.062314|arxiv=quant-ph/0005115|bibcode = 2000PhRvA..62f2314D |s2cid=16636159 }}</ref> इस प्रकार <math>|\mathrm{W}\rangle</math> और <math>|\mathrm{GHZ}\rangle</math> दो बहुत भिन्न प्रकार के त्रिपक्षीय सम्मिश्रता का प्रतिनिधित्व करते हैं।


यह अंतर, उदाहरण के लिए, डब्ल्यू अवस्था की निम्नलिखित रोचक प्रोपर्टी द्वारा चित्रित किया गया है: इस प्रकार यदि तीन क्विबिट में से खो जाता है, जिससे शेष 2-क्विबिट प्रणाली की स्थिति अभी भी उलझी हुई है। इस प्रकार डब्ल्यू-प्रकार के सम्मिश्रता की यह सशक्त जीएचजेड स्थिति के साथ दृढ़ता से विपरीत है, जो क्विबिट के हानि के बाद पूरी तरह से अलग हो जाती है।


==गुण==
डब्ल्यू वर्ग के अवस्थाों को मल्टीपार्टाइट सम्मिश्रता शुद्ध अवस्थाों के लिए मल्टीपार्टाइट सम्मिश्रता उपायों के माध्यम से अन्य सभी 3-क्विबिट अवस्थाों से अलग किया जा सकता है। विशेष रूप से, डब्ल्यू अवस्थाों में किसी भी द्विविभाजन में गैर-शून्य सम्मिश्रता होता है,<ref>A bipartition of the three qubits <math>1,2,3</math> is any grouping <math>(12) 3, 1 (23)</math> and <math>(13) 2</math> in which two qubits are considered to belong to the same party. The 3-qubit state can then be considered as a state on <math>\mathbb{C}^4 \otimes \mathbb{C}^2</math> and studied with bipartite entanglement measures.</ref> जबकि 3-टेंगल विलुप्त हो जाता है, जो गीगाहर्ट्ज-प्रकार के अवस्थाों के लिए भी गैर-शून्य है।<ref name="Duer2000" />
[[File:Wstate quantumcircuit.png|thumb|400x400px|क्वांटम सर्किट जो 3 क्यूबिट उत्पन्न करता है-<math>|\mathrm{W}\rangle </math> दो और एकल क्वबिट [[क्वांटम गेट]]्स का उपयोग करके स्थिति बताएं, यानी क्वांटम लॉजिक गेट्स की एक सूची#रोटेशन ऑपरेटर गेट्स|राई-रोटेशन गेट, एक नियंत्रित [[हैडमार्ड गेट]], 2 नियंत्रित नॉट गेट और एक क्वांटम लॉजिक गेट#एक्स गेट। घूर्णन का कोण है <math display="inline">\phi_3=2\arccos\left(1/\sqrt{3}\right)</math>.]]डब्ल्यू राज्य दो गैर-विभाज्य में से एक का प्रतिनिधि है<ref>A pure state <math>|\psi\rangle</math> of <math>N</math> parties is called ''biseparable'', if one can find a partition of the parties in two disjoint subsets <math>A</math> and <math>B</math> with <math>A\cup B=\{1,...,N\}</math> such that <math>|\psi\rangle = |\phi\rangle_A\otimes|\gamma\rangle_B</math>, i.e. <math>|\psi\rangle</math> is a [[product state]] with respect to the partition <math>A|B</math>.</ref> तीन-क्विबिट राज्यों की कक्षाएं, दूसरा ग्रीनबर्गर-हॉर्न-ज़ीलिंगर राज्य है, <math>|\mathrm{GHZ}\rangle = (|000\rangle + |111\rangle)/\sqrt{2}</math>, जिन्हें [[LOCC]] द्वारा एक दूसरे में परिवर्तित नहीं किया जा सकता (संभावित रूप से भी नहीं)।<ref name="Duer2000">{{cite journal|author1=W. Dür |author2=G. Vidal |author3=J. I. Cirac  |name-list-style=amp |title=तीन क्वैबिट को दो असमान तरीकों से उलझाया जा सकता है|journal=Phys. Rev. A|volume=62|pages=062314|year=2000|issue=6 | doi=10.1103/PhysRevA.62.062314|arxiv=quant-ph/0005115|bibcode = 2000PhRvA..62f2314D |s2cid=16636159 }}</ref> इस प्रकार <math>|\mathrm{W}\rangle</math> और <math>|\mathrm{GHZ}\rangle</math> दो बहुत भिन्न प्रकार के त्रिपक्षीय उलझाव का प्रतिनिधित्व करते हैं।
== सामान्यीकरण                                                                                                                                                                                  ==


यह अंतर, उदाहरण के लिए, डब्ल्यू राज्य की निम्नलिखित दिलचस्प संपत्ति द्वारा चित्रित किया गया है: यदि तीन क्विबिट में से एक खो जाता है, तो शेष 2-क्विबिट प्रणाली की स्थिति अभी भी उलझी हुई है। डब्ल्यू-प्रकार के उलझाव की यह मजबूती जीएचजेड स्थिति के साथ दृढ़ता से विपरीत है, जो एक क्विबिट के नुकसान के बाद पूरी तरह से अलग हो जाती है।
डब्ल्यू अवस्था की धारणा <math>n</math> क्वैबिट्स को सामान्यीकृत किया गया है <ref name="Duer2000" /> और इस प्रकार फिर सभी संभावित शुद्ध अवस्थाओं के समान विस्तार गुणांक वाले क्वांटम सुपरपोजिशन को संदर्भित करता है जिसमें वास्तव में क्वैबिट उत्तेजित अवस्था <math> |1\rangle</math> में होता है जबकि अन्य सभी जमीनी अवस्था <math> |0\rangle</math> में हैं :
 
W वर्ग के राज्यों को मल्टीपार्टाइट उलझाव#शुद्ध राज्यों के लिए मल्टीपार्टाइट उलझाव उपायों के माध्यम से अन्य सभी 3-क्विबिट राज्यों से अलग किया जा सकता है। विशेष रूप से, W राज्यों में किसी भी द्विविभाजन में गैर-शून्य उलझाव होता है,<ref>A bipartition of the three qubits <math>1,2,3</math> is any grouping <math>(12) 3, 1 (23)</math> and <math>(13) 2</math> in which two qubits are considered to belong to the same party. The 3-qubit state can then be considered as a state on <math>\mathbb{C}^4 \otimes \mathbb{C}^2</math> and studied with bipartite entanglement measures.</ref> जबकि 3-टेंगल गायब हो जाता है, जो GHZ-प्रकार के राज्यों के लिए भी गैर-शून्य है।<ref name="Duer2000" />
 
 
== सामान्यीकरण ==
 
डब्ल्यू राज्य की धारणा को सामान्यीकृत किया गया है <math>n</math> qubits<ref name="Duer2000" />और फिर सभी संभावित शुद्ध अवस्थाओं के समान विस्तार गुणांक वाले क्वांटम सुपरपोजिशन को संदर्भित करता है जिसमें वास्तव में एक क्वैबिट उत्तेजित अवस्था में होता है <math> |1\rangle</math>, जबकि अन्य सभी जमीनी अवस्था में हैं <math> |0\rangle</math>:
: <math>|\mathrm{W}\rangle = \frac{1}{\sqrt{n}}(|100...0\rangle + |010...0\rangle + ... + |00...01\rangle).</math>
: <math>|\mathrm{W}\rangle = \frac{1}{\sqrt{n}}(|100...0\rangle + |010...0\rangle + ... + |00...01\rangle).</math>
कण हानि के विरुद्ध मजबूती और (सामान्यीकृत) GHZ अवस्था के साथ LOCC-असमानता दोनों भी इसके लिए मान्य हैं <math>n</math>-क्विबिट डब्ल्यू अवस्था।
इस प्रकार कण हानि के विरुद्ध सशक्त और (सामान्यीकृत) गीगाहर्ट्ज अवस्था के साथ एलओसीसी-असमानता दोनों भी <math>n</math>-क्विबिट डब्ल्यू अवस्था इसके लिए मान्य हैं।


== अनुप्रयोग ==
== अनुप्रयोग ==
जिन प्रणालियों में एक एकल क्वबिट को कई दो-स्तरीय प्रणालियों के समूह में संग्रहीत किया जाता है, तार्किक 1 को अक्सर डब्ल्यू राज्य द्वारा दर्शाया जाता है, जबकि तार्किक 0 को राज्य द्वारा दर्शाया जाता है। <math>|00...0\rangle</math>. यहां कण हानि के खिलाफ डब्ल्यू राज्य की मजबूती एक बहुत ही लाभकारी संपत्ति है जो इन संयोजन-आधारित क्वांटम यादों के अच्छे भंडारण गुणों को सुनिश्चित करती है।<ref>{{cite journal|title=Quantum memory for photons: Dark-state polaritons|author1=M. Fleischhauer  |author2=M. D. Lukin |name-list-style=amp |journal=Phys. Rev. A|volume=65|pages=022314|year=2002|issue=2 |doi=10.1103/PhysRevA.65.022314|arxiv=quant-ph/0106066|bibcode = 2002PhRvA..65b2314F |s2cid=54532771 }}</ref>
जिन प्रणालियों में एकल क्वबिट को कई दो-स्तरीय प्रणालियों के समूह में संग्रहीत किया जाता है, इस प्रकार तार्किक 1 को अधिकांशतः डब्ल्यू अवस्था द्वारा दर्शाया जाता है, जबकि तार्किक 0 को अवस्था <math>|00...0\rangle</math> द्वारा दर्शाया जाता है। यहां कण हानि के विरुद्ध डब्ल्यू अवस्था की सशक्त बहुत ही लाभकारी प्रोपर्टी है जो इन संयोजन-आधारित क्वांटम यादों के अच्छे संग्रहण गुणों को सुनिश्चित करती है।<ref>{{cite journal|title=Quantum memory for photons: Dark-state polaritons|author1=M. Fleischhauer  |author2=M. D. Lukin |name-list-style=amp |journal=Phys. Rev. A|volume=65|pages=022314|year=2002|issue=2 |doi=10.1103/PhysRevA.65.022314|arxiv=quant-ph/0106066|bibcode = 2002PhRvA..65b2314F |s2cid=54532771 }}</ref>
 
== यह भी देखें                                                                             ==
 
* [[दोपहर की अवस्था|नून अवस्था]]
== यह भी देखें ==
* [[दोपहर की अवस्था]]


== संदर्भ ==
== संदर्भ ==
{{reflist}}
{{reflist}}


{{DEFAULTSORT:W State}}[[Category: क्वांटम सूचना सिद्धांत]]
{{DEFAULTSORT:W State}}
 
 


[[Category: Machine Translated Page]]
[[Category:CS1 English-language sources (en)]]
[[Category:Created On 10/07/2023]]
[[Category:Created On 10/07/2023|W State]]
[[Category:Lua-based templates|W State]]
[[Category:Machine Translated Page|W State]]
[[Category:Pages with script errors|W State]]
[[Category:Short description with empty Wikidata description|W State]]
[[Category:Templates Vigyan Ready|W State]]
[[Category:Templates that add a tracking category|W State]]
[[Category:Templates that generate short descriptions|W State]]
[[Category:Templates using TemplateData|W State]]
[[Category:क्वांटम सूचना सिद्धांत|W State]]

Latest revision as of 10:20, 4 August 2023

डब्ल्यू अवस्था तीन क्वैबिट की एक उलझी हुई क्वांटम अवस्था है जिसका ब्रा-केट नोटेशन में निम्नलिखित आकार होता है

और जो विशिष्ट प्रकार के बहुपक्षीय सम्मिश्रता का प्रतिनिधित्व करने और क्वांटम सूचना सिद्धांत में कई अनुप्रयोगों में होने के लिए उल्लेखनीय है। इस प्रकार इस अवस्था में तैयार किए गए कण बेल के प्रमेय के गुणों को पुन: उत्पन्न करते हैं, जो बताता है कि स्थानीय छिपे हुए चर का कोई भी मौलिक सिद्धांत क्वांटम यांत्रिकी की पूर्वानुमान नहीं हो सकता है। इस प्रकार अवस्था का नाम वोल्फगैंग ड्यूर के नाम पर रखा गया है,[1] जिन्होंने सबसे पहले 2002 में गुइफ़्रे विडाल और जुआन इग्नासियो सिराक सस्टुरैन के साथ मिलकर अवस्था की रिपोर्ट की थी।[2]

गुण

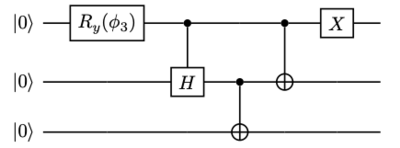
राई-रोटेशन गेट, नियंत्रित हैडमार्ड गेट, 2 नियंत्रित नॉट गेट और क्वांटम लॉजिक गेट#एक्स गेट। घूर्णन का कोण है .

डब्ल्यू अवस्था दो गैर-विभाज्य में से का प्रतिनिधि है [3] तीन-क्विबिट अवस्थाों की कक्षाएं, दूसरा ग्रीनबर्गर-हॉर्न-ज़ीलिंगर अवस्था है, जिन्हें एलओसीसी द्वारा दूसरे में परिवर्तित नहीं किया जा सकता (संभावित रूप से भी नहीं)।[2] इस प्रकार और दो बहुत भिन्न प्रकार के त्रिपक्षीय सम्मिश्रता का प्रतिनिधित्व करते हैं।

यह अंतर, उदाहरण के लिए, डब्ल्यू अवस्था की निम्नलिखित रोचक प्रोपर्टी द्वारा चित्रित किया गया है: इस प्रकार यदि तीन क्विबिट में से खो जाता है, जिससे शेष 2-क्विबिट प्रणाली की स्थिति अभी भी उलझी हुई है। इस प्रकार डब्ल्यू-प्रकार के सम्मिश्रता की यह सशक्त जीएचजेड स्थिति के साथ दृढ़ता से विपरीत है, जो क्विबिट के हानि के बाद पूरी तरह से अलग हो जाती है।

डब्ल्यू वर्ग के अवस्थाों को मल्टीपार्टाइट सम्मिश्रता शुद्ध अवस्थाों के लिए मल्टीपार्टाइट सम्मिश्रता उपायों के माध्यम से अन्य सभी 3-क्विबिट अवस्थाों से अलग किया जा सकता है। विशेष रूप से, डब्ल्यू अवस्थाों में किसी भी द्विविभाजन में गैर-शून्य सम्मिश्रता होता है,[4] जबकि 3-टेंगल विलुप्त हो जाता है, जो गीगाहर्ट्ज-प्रकार के अवस्थाों के लिए भी गैर-शून्य है।[2]

सामान्यीकरण

डब्ल्यू अवस्था की धारणा क्वैबिट्स को सामान्यीकृत किया गया है [2] और इस प्रकार फिर सभी संभावित शुद्ध अवस्थाओं के समान विस्तार गुणांक वाले क्वांटम सुपरपोजिशन को संदर्भित करता है जिसमें वास्तव में क्वैबिट उत्तेजित अवस्था में होता है जबकि अन्य सभी जमीनी अवस्था में हैं :

इस प्रकार कण हानि के विरुद्ध सशक्त और (सामान्यीकृत) गीगाहर्ट्ज अवस्था के साथ एलओसीसी-असमानता दोनों भी -क्विबिट डब्ल्यू अवस्था इसके लिए मान्य हैं।

अनुप्रयोग

जिन प्रणालियों में एकल क्वबिट को कई दो-स्तरीय प्रणालियों के समूह में संग्रहीत किया जाता है, इस प्रकार तार्किक 1 को अधिकांशतः डब्ल्यू अवस्था द्वारा दर्शाया जाता है, जबकि तार्किक 0 को अवस्था द्वारा दर्शाया जाता है। यहां कण हानि के विरुद्ध डब्ल्यू अवस्था की सशक्त बहुत ही लाभकारी प्रोपर्टी है जो इन संयोजन-आधारित क्वांटम यादों के अच्छे संग्रहण गुणों को सुनिश्चित करती है।[5]

यह भी देखें

संदर्भ

  1. ↑ Cabello, Adán (2002-02-05). "थ्री-क्विट ग्रीनबर्गर-हॉर्न-ज़ीलिंगर और डब्ल्यू राज्यों के लिए असमानताओं के साथ और बिना बेल का प्रमेय". Physical Review A (in English). 65 (3): 032108. arXiv:quant-ph/0107146. Bibcode:2002PhRvA..65c2108C. doi:10.1103/PhysRevA.65.032108. ISSN 1050-2947. S2CID 55659305.
  2. ↑ 2.0 2.1 2.2 2.3 W. Dür; G. Vidal & J. I. Cirac (2000). "तीन क्वैबिट को दो असमान तरीकों से उलझाया जा सकता है". Phys. Rev. A. 62 (6): 062314. arXiv:quant-ph/0005115. Bibcode:2000PhRvA..62f2314D. doi:10.1103/PhysRevA.62.062314. S2CID 16636159.
  3. ↑ A pure state of parties is called biseparable, if one can find a partition of the parties in two disjoint subsets and with such that , i.e. is a product state with respect to the partition .
  4. ↑ A bipartition of the three qubits is any grouping and in which two qubits are considered to belong to the same party. The 3-qubit state can then be considered as a state on and studied with bipartite entanglement measures.
  5. ↑ M. Fleischhauer & M. D. Lukin (2002). "Quantum memory for photons: Dark-state polaritons". Phys. Rev. A. 65 (2): 022314. arXiv:quant-ph/0106066. Bibcode:2002PhRvA..65b2314F. doi:10.1103/PhysRevA.65.022314. S2CID 54532771.
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=डब्ल्यू_अवस्था&oldid=236916’