अपेक्षित रैखिक समय एमएसटी एल्गोरिदम: Difference between revisions
No edit summary |
No edit summary |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 17: | Line 17: | ||
===बोरोव्का चरण=== | ===बोरोव्का चरण=== | ||
इस प्रकार से एल्गोरिदम का प्रत्येक पुनरावृत्ति बोरोव्का के एल्गोरिदम के अनुकूलन पर निर्भर करता है जिसे बोरोव्का चरण कहा जाता है: | इस प्रकार से एल्गोरिदम का प्रत्येक पुनरावृत्ति बोरोव्का के एल्गोरिदम के अनुकूलन पर निर्भर करता है जिसे बोरोव्का चरण कहा जाता है:<syntaxhighlight lang="abl"> | ||
Input: A graph G with no isolated vertices | |||
1 For each vertex v, select the lightest edge incident on v | |||
2 Create a contracted graph G' by replacing each component of G connected by the edges selected in step 1 with a single vertex | |||
3 Remove all isolated vertices, self-loops, and non-minimal repetitive edges from G' | |||
Output: The edges selected in step 1 and the contracted graph G' | |||
</syntaxhighlight>बोरोव्का चरण बोरोव्का के एल्गोरिदम के आंतरिक लूप के समान है, जो ओ (एम) समय में चलता है जहां एम G में किनारों की संख्या है। इसके अतिरिक्त , चूंकि प्रत्येक किनारे को अधिकतम दो बार चुना जा सकता है (प्रत्येक घटना शीर्ष पर एक बार) चरण 1 के पश्चात डिस्कनेक्ट किए गए घटकों की अधिकतम संख्या शीर्षों की आधी संख्या के समान है। इस प्रकार, बोरोव्का चरण ग्राफ़ में शीर्षों की संख्या को कम से कम दो गुना कम कर देता है और कम से कम n/2 किनारों को हटा देता है जहां n G में शीर्षों की संख्या है। | |||
बोरोव्का चरण बोरोव्का के एल्गोरिदम के आंतरिक लूप के समान है, जो ओ (एम) समय में चलता है जहां एम G में किनारों की संख्या है। इसके अतिरिक्त , चूंकि प्रत्येक किनारे को अधिकतम दो बार चुना जा सकता है (प्रत्येक घटना शीर्ष पर एक बार) चरण 1 के पश्चात डिस्कनेक्ट किए गए घटकों की अधिकतम संख्या शीर्षों की आधी संख्या के समान है। इस प्रकार, बोरोव्का चरण ग्राफ़ में शीर्षों की संख्या को कम से कम दो गुना कम कर देता है और कम से कम n/2 किनारों को हटा देता है जहां n G में शीर्षों की संख्या है। | |||
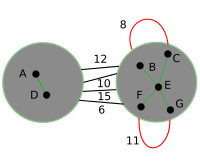
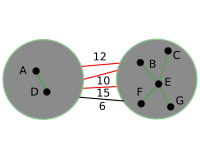
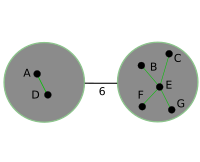
इस प्रकार से बोरोव्का चरण का उदाहरण निष्पादन | इस प्रकार से बोरोव्का चरण का उदाहरण निष्पादन | ||
| Line 59: | Line 57: | ||
==शुद्धता== | ==शुद्धता== | ||
इस प्रकार से ग्राफ़ में शीर्षों की संख्या को उपस्तिथ करके शुद्धता सिद्ध की जाती है।चूंकि आधार स्तिथि तुच्छ रूप से सत्य है। मान लीजिये कि T* G का न्यूनतम फैला हुआ वृक्ष है। बोरोव्का चरण में चयनित प्रत्येक किनारा कट प्रॉपर्टी द्वारा T* में है और अनुबंधित ग्राफ़ बनाने के लिए हटाए गए किनारों में से कोई भी कट प्रॉपर्टी द्वारा T* में नहीं है (अनावश्यक किनारों के लिए) और चक्र संपत्ति (स्वयं लूप के लिए)। चरण 2 में चयनित नहीं किए गए T* के शेष किनारे कट प्रॉपर्टी द्वारा अनुबंधित ग्राफ के न्यूनतम फैले हुए ट्री का निर्माण करते हैं (प्रत्येक कट को एक सुपरनोड होने दें)। हटाया गया प्रत्येक F-हैवी | इस प्रकार से ग्राफ़ में शीर्षों की संख्या को उपस्तिथ करके शुद्धता सिद्ध की जाती है।चूंकि आधार स्तिथि तुच्छ रूप से सत्य है। मान लीजिये कि T* G का न्यूनतम फैला हुआ वृक्ष है। बोरोव्का चरण में चयनित प्रत्येक किनारा कट प्रॉपर्टी द्वारा T* में है और अनुबंधित ग्राफ़ बनाने के लिए हटाए गए किनारों में से कोई भी कट प्रॉपर्टी द्वारा T* में नहीं है (अनावश्यक किनारों के लिए) और चक्र संपत्ति (स्वयं लूप के लिए)। चरण 2 में चयनित नहीं किए गए T* के शेष किनारे कट प्रॉपर्टी द्वारा अनुबंधित ग्राफ के न्यूनतम फैले हुए ट्री का निर्माण करते हैं (प्रत्येक कट को एक सुपरनोड होने दें)। हटाया गया प्रत्येक F-हैवी किनारा चक्र संपत्ति द्वारा न्यूनतम स्पैनिंग ट्री में नहीं है। अंततः F' आगमनात्मक परिकल्पना द्वारा अनुबंधित ग्राफ का न्यूनतम फैलाव वाला वृक्ष है। इस प्रकार F' और बोरोव्का चरणों से अनुबंधित किनारे न्यूनतम फैले हुए ट्री का निर्माण करते हैं। | ||
==प्रदर्शन== | ==प्रदर्शन== | ||
अपेक्षित प्रदर्शन यादृच्छिक | अपेक्षित प्रदर्शन यादृच्छिक प्रारूप चरण का परिणाम है। यादृच्छिक नमूनाकरण चरण की प्रभावशीलता को निम्नलिखित लेम्मा द्वारा वर्णित किया गया है जो G में या F-हैवी और F-लाइट किनारों F-लाइट किनारों की संख्या पर सीमा लगाता है जिससे दूसरे उप-समस्या का आकार सीमित हो जाता है। | ||
===यादृच्छिक नमूनाकरण प्रमेय=== | ===यादृच्छिक नमूनाकरण प्रमेय=== | ||
| Line 90: | Line 88: | ||
==अग्रिम पठन== | ==अग्रिम पठन== | ||
* [https://www.cs.technion.ac.il/~idddo/mstverif.pdf Minimum Spanning Tree Verification in Linear Time] | * [https://www.cs.technion.ac.il/~idddo/mstverif.pdf Minimum Spanning Tree Verification in Linear Time] | ||
[[Category:Created On 10/07/2023]] | [[Category:Created On 10/07/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:फैले पेड़]] | |||
[[Category:यादृच्छिक एल्गोरिदम]] | |||
Latest revision as of 12:53, 4 August 2023
अपेक्षित रैखिक समय एमएसटी एल्गोरिदम बिना किसी पृथक शीर्ष वाले भारित ग्राफ के न्यूनतम फैले हुए फॉरेस्ट की गणना के लिए यादृच्छिक एल्गोरिदम है। इसे डेविड कार्गर, फिलिप क्लेन और रॉबर्ट टार्जन द्वारा विकसित किया गया था।[1] एल्गोरिथ्म रैखिक समय में न्यूनतम फैले हुए ट्री को सत्यापित करने के लिए एल्गोरिदम के साथ-साथ बोरोव्का के एल्गोरिदम की तकनीकों पर निर्भर करता है।[2][3] यह अपेक्षित मूल्य रैखिक समय प्राप्त करने के लिए विभाजित करें और जीतो एल्गोरिदम, ग्रेडी एल्गोरिदम और यादृच्छिक एल्गोरिदम के डिजाइन प्रतिमानों को जोड़ती है।
इस प्रकार से न्यूनतम स्पैनिंग ट्री खोजने वाले नियतात्मक एल्गोरिदम में प्राइम का एल्गोरिदम, क्रुस्कल का एल्गोरिदम, रिवर्स-डिलीट एल्गोरिदम और बोरव्का का एल्गोरिदम भी सम्मिलित हैं।
अवलोकन
किन्तु एल्गोरिथम की मुख्य अंतर्दृष्टि यादृच्छिक नमूनाकरण चरण है जो प्रत्येक सबग्राफ में सम्मिलित करने के लिए किनारों को यादृच्छिक रूप से चुनकर ग्राफ़ को दो में विभाजित करता है। एल्गोरिथ्म पुनरावर्ती रूप से पहले उप-समस्या के न्यूनतम फैलाव वाला ट्री को खोजता है और ग्राफ़ में किनारों को हटाने के लिए रैखिक समय सत्यापन एल्गोरिदम के साथ समाधान का उपयोग करता है जो न्यूनतम स्पैनिंग ट्री में नहीं हो सकता है। बोरोव्का के एल्गोरिदम से ली गई प्रक्रिया का उपयोग प्रत्येक रिकर्सन (कंप्यूटर विज्ञान) में ग्राफ़ के आकार को कम करने के लिए भी किया जाता है।
बोरोव्का चरण
इस प्रकार से एल्गोरिदम का प्रत्येक पुनरावृत्ति बोरोव्का के एल्गोरिदम के अनुकूलन पर निर्भर करता है जिसे बोरोव्का चरण कहा जाता है:
Input: A graph G with no isolated vertices
1 For each vertex v, select the lightest edge incident on v
2 Create a contracted graph G' by replacing each component of G connected by the edges selected in step 1 with a single vertex
3 Remove all isolated vertices, self-loops, and non-minimal repetitive edges from G'
Output: The edges selected in step 1 and the contracted graph G'
बोरोव्का चरण बोरोव्का के एल्गोरिदम के आंतरिक लूप के समान है, जो ओ (एम) समय में चलता है जहां एम G में किनारों की संख्या है। इसके अतिरिक्त , चूंकि प्रत्येक किनारे को अधिकतम दो बार चुना जा सकता है (प्रत्येक घटना शीर्ष पर एक बार) चरण 1 के पश्चात डिस्कनेक्ट किए गए घटकों की अधिकतम संख्या शीर्षों की आधी संख्या के समान है। इस प्रकार, बोरोव्का चरण ग्राफ़ में शीर्षों की संख्या को कम से कम दो गुना कम कर देता है और कम से कम n/2 किनारों को हटा देता है जहां n G में शीर्षों की संख्या है।
इस प्रकार से बोरोव्का चरण का उदाहरण निष्पादन
एफ-हैवी और एफ-हल्के किनारे
इस प्रकार से प्रत्येक पुनरावृत्ति में एल्गोरिथ्म विशेष गुणों वाले किनारों को हटा देता है जो की उन्हें न्यूनतम स्पैनिंग ट्री से बाहर कर देता है। इन्हें एफ-हैवी किनारे कहा जाता है और इन्हें निम्नानुसार परिभाषित किया गया है। मान लीजिए F ग्राफ़ एच पर एक फॉरेस्ट है। एक एफ-हैवी किनारा एक किनारा है जो शीर्ष यू, वी को जोड़ता है जिसका वजन F में यू से वी तक पथ पर अधिक भारी किनारे के वजन से अधिक है। (यदि कोई पथ F में उपस्तिथ नहीं है, इसे अनंत भार माना जाता है)। कोई भी किनारा जो एफ-हैवी नहीं है वह एफ-लाइट है। यदि एफ, G का उपसमूह है तो G में कोई भी एफ-हैवी किनारा चक्र गुण के अनुसार G के न्यूनतम फैले हुए ट्री में नहीं हो सकता है। एक फॉरेस्ट को देखते हुए, एफ-हैवी किनारों की गणना न्यूनतम फैले हुए ट्री सत्यापन एल्गोरिदम का उपयोग करके रैखिक समय में की जा सकती है[2][3]
एल्गोरिदम
इनपुट: ग्राफ़ G जिसमें कोई पृथक शीर्ष नहीं है
- यदि G खाली है तो खाली फॉरेस्ट लौटाएं
- G पर निरंतर दो बोरोव्का चरण चलाकर अनुबंधित ग्राफ G' बनाएं
- प्रायिकता 1/2 के साथ G' में प्रत्येक किनारे का चयन करके सबग्राफ H बनाएं। न्यूनतम फैले हुए वन F को प्राप्त करने के लिए एल्गोरिदम को H पर पुनरावर्ती रूप से प्रयुक्त करें।
- रैखिक समय न्यूनतम फैले वृक्ष सत्यापन एल्गोरिदम का उपयोग करके G' (जहां F चरण 3 से फॉरेस्ट है) से सभी एफ-हैवी किनारों को हटा दें।[2][3] न्यूनतम फैले हुए फॉरेस्ट को प्राप्त करने के लिए एल्गोरिदम को G' पर पुनरावर्ती रूप से प्रयुक्त करें।
आउटपुट: जी' का न्यूनतम फैला हुआ फॉरेस्ट और बोरोव्का चरणों से अनुबंधित किनारे है
शुद्धता
इस प्रकार से ग्राफ़ में शीर्षों की संख्या को उपस्तिथ करके शुद्धता सिद्ध की जाती है।चूंकि आधार स्तिथि तुच्छ रूप से सत्य है। मान लीजिये कि T* G का न्यूनतम फैला हुआ वृक्ष है। बोरोव्का चरण में चयनित प्रत्येक किनारा कट प्रॉपर्टी द्वारा T* में है और अनुबंधित ग्राफ़ बनाने के लिए हटाए गए किनारों में से कोई भी कट प्रॉपर्टी द्वारा T* में नहीं है (अनावश्यक किनारों के लिए) और चक्र संपत्ति (स्वयं लूप के लिए)। चरण 2 में चयनित नहीं किए गए T* के शेष किनारे कट प्रॉपर्टी द्वारा अनुबंधित ग्राफ के न्यूनतम फैले हुए ट्री का निर्माण करते हैं (प्रत्येक कट को एक सुपरनोड होने दें)। हटाया गया प्रत्येक F-हैवी किनारा चक्र संपत्ति द्वारा न्यूनतम स्पैनिंग ट्री में नहीं है। अंततः F' आगमनात्मक परिकल्पना द्वारा अनुबंधित ग्राफ का न्यूनतम फैलाव वाला वृक्ष है। इस प्रकार F' और बोरोव्का चरणों से अनुबंधित किनारे न्यूनतम फैले हुए ट्री का निर्माण करते हैं।
प्रदर्शन
अपेक्षित प्रदर्शन यादृच्छिक प्रारूप चरण का परिणाम है। यादृच्छिक नमूनाकरण चरण की प्रभावशीलता को निम्नलिखित लेम्मा द्वारा वर्णित किया गया है जो G में या F-हैवी और F-लाइट किनारों F-लाइट किनारों की संख्या पर सीमा लगाता है जिससे दूसरे उप-समस्या का आकार सीमित हो जाता है।
यादृच्छिक नमूनाकरण प्रमेय
लेम्मा- मान लीजिए H, G का एक उपसमूह है जो G के प्रत्येक किनारे को स्वतंत्र रूप से प्रायिकता p के साथ सम्मिलित करके बनता है और F को H का न्यूनतम फैला हुआ जंगल है। G में F-लाइट किनारों की अपेक्षित संख्या अधिकतम n/p है जहां n है G में शीर्षों की संख्या है '.
लेम्मा को प्रमाणित करने के लिए G के किनारों की जांच करें क्योंकि उन्हें H में जोड़ा जा रहा है। G में F-हैवी और F-लाइट किनारों | F-लाइट किनारों की संख्या उस क्रम से स्वतंत्र है जिसमें H के न्यूनतम फैले फॉरेस्ट के बाद से H के किनारों का चयन किया जाता है। 'सभी चयन आदेशों के लिए समान है। प्रमाण के लिए G के किनारों को हल्के से हैवी तक किनारे के वजन के क्रम में बार में लेकर H के लिए किनारों का चयन करने पर विचार करें। मान लीजिए ई को वर्तमान बढ़त माना जा रहा है। यदि e के अंतिम बिंदु H के दो अलग किए गए घटकों में हैं तो e उन घटकों को जोड़ने वाला अधिक लाइट किनारा है और यदि इसे H में जोड़ा जाता है तो यह में होगा F मिनिमम स्पैनिंग ट्री कट प्रॉपर्टी द्वारा। इसका तथ्य यह भी है कि e F -हैवी है और F -लाइट किनारे F -लाइट है, भले ही इसे H में जोड़ा गया हो या नहीं, क्योंकि इसके अतिरिक्त केवल भारी किनारों पर ही विचार किया जाता है। यदि e के दोनों समापन बिंदु H के ही घटक में हैं तो यह मिनिमम स्पैनिंग ट्री साइकिल प्रॉपर्टी द्वारा F -हैवी है (और हमेशा रहेगा)। फिर H e को प्रायिकता p के साथ H में जोड़ा जाता है।
इस प्रकार से H में जोड़े गए F-लाइट किनारों की अधिकतम संख्या n-1 है क्योंकि H के किसी भी न्यूनतम फैले हुए पेड़ में n-1 किनारे होते हैं। एक बार n -1 F-लाइट किनारों को H में जोड़ दिया गया है तत्पश्चात के किसी भी किनारे को चक्र संपत्ति द्वारा F-लाइट नहीं माना जाता है। इस प्रकार, G में F-प्रकाश किनारों की संख्या n-1 F-प्रकाश किनारों को वास्तव में H में जोड़ने से पहले H के लिए माने जाने वाले F-प्रकाश किनारों की संख्या से बंधी होती है। चूंकि किसी भी F-प्रकाश किनारे को संभाव्यता p के साथ जोड़ा जाता है। यह एक सिक्के को उछालने के समान है जिसमें चित आने की प्रायिकता p तब तक है जब तक कि n-1 चित सामने न आ जाए। इस प्रकार से सिक्का उछालने की कुल संख्या G में F-लाइट किनारों की संख्या के समान है। चूंकि सिक्का उछालने की संख्या का वितरण पैरामीटर n-1 और p के साथ व्युत्क्रम द्विपद वितरण द्वारा दिया जाता है। इन मापदंडों के लिए इस वितरण का अपेक्षित मूल्य (n-1)/p है।
अपेक्षित विश्लेषण
पुनरावर्ती उपसमस्याओं में किए गए कार्य को अनदेखा करते हुए एल्गोरिदम के एकल आह्वान में किए गए कार्य की कुल मात्रा इनपुट ग्राफ़ में किनारों की संख्या में रैखिक समय है। चरण 1 में निरंतर समय लगता है। जैसा कि बोरोव्का चरण बोरोव्का चरण अनुभाग में बताया गया है, बोरोव्का चरणों को किनारों की संख्या में रैखिक समय में निष्पादित किया जा सकता है। चरण 3 किनारों के माध्यम से पुनरावृत्त करता है और प्रत्येक के लिए सिक्का उछालता है जिससे यह किनारों की संख्या में रैखिक हो। चरण 4 को संशोधित रैखिक समय न्यूनतम फैले हुए वृक्ष सत्यापन एल्गोरिदम का उपयोग करके रैखिक समय में निष्पादित किया जा सकता है।[2][3] चूंकि एल्गोरिदम के पुनरावृत्ति में किया गया कार्य किनारों की संख्या में रैखिक होता है, इसलिए एल्गोरिदम के पूर्ण रन में किया गया कार्य (सभी पुनरावर्ती कॉल सहित) मूल समस्या में किनारों की कुल संख्या के गुणा स्थिर कारक से घिरा होता है और सभी पुनरावर्ती उपसमस्याएँ होती है ।
एल्गोरिदम का प्रत्येक आह्वान अधिकतम दो उपसमस्याएं उत्पन्न करता है इसलिए उपसमस्याओं का समुच्चय द्विआधारी वृक्ष बनाता है। प्रत्येक बोरोव्का चरण बोरोव्का चरण शीर्षों की संख्या को कम से कम दो गुना कम कर देता है, इसलिए दो बोरोव्का चरणों के पश्चात् शीर्षों की संख्या चार गुना कम हो गई है। इस प्रकार, यदि मूल ग्राफ़ में n कोने और m किनारे हैं तो ट्री की गहराई d पर प्रत्येक उपसमस्या अधिकतम n/4d के ग्राफ़ पर है शीर्ष. इसके अतिरिक्त ट्री में अधिकतम लॉग4n है स्तर.
इस प्रकार से रिकर्सन ट्री के बारे में तर्क करने के लिए चरण 3 में पुनरावर्ती कॉल में बाएं चाइल्ड समस्या को उपसमस्या होने दें और चरण 5 में रिकर्सिव कॉल में दाएं चाइल्ड समस्या को उपसमस्या होने दें। मूल समस्या और सभी उपसमस्याओं में किनारों की कुल संख्या की गणना करें ट्री के प्रत्येक बाएँ पथ में किनारों की संख्या की गणना करके। बायाँ पथ या तो दाएँ बच्चे या मूल से प्रारंभ होता है और इसमें बाएँ बच्चे के पथ के माध्यम से पहुँचने योग्य सभी नोड्स सम्मिलित होते हैं। दाईं ओर के चित्र में बाइनरी ट्री के बाएँ पथ को नीले रंग में परिक्रमा करते हुए दिखाया गया है।
बाएं बच्चे की समस्या में प्रत्येक किनारे को उसकी मूल समस्या के किनारों से चुना जाता है (बोरोव्का चरण बोरोव्का चरणों में अनुबंधित किनारों को छोड़कर) प्रायिकता 1/2 के साथ है । यदि मूल समस्या में x किनारे हैं तो बाएं बच्चे की समस्या में किनारों का अपेक्षित मान अधिकतम x/2 है। यदि x को यादृच्छिक वरिएबल . इस प्रकार यदि किसी समस्या में बाएं पथ के शीर्ष पर किनारों की अपेक्षित संख्या k है तो बाएं पथ में प्रत्येक उपसमस्या में किनारों की अपेक्षित संख्या का योग अधिकतम होता है (ज्यामितीय श्रृंखला देखें)। मूलमें m किनारे हैं इसलिए किनारों का अपेक्षित मान 2m के समान है और प्रत्येक दाएँ उपसमस्या में किनारों की अपेक्षित संख्या दोगुनी है।
प्रत्येक दाएँ उपसमस्या में किनारों की अपेक्षित संख्या मूल समस्या में F-हैवी और F-प्रकाश किनारों F-प्रकाश किनारों की संख्या के समान है जहाँ F बाएँ उपसमस्या का न्यूनतम फैला हुआ वृक्ष है। F-लाइट किनारों की संख्या रैंडम सैंपलिंग लेम्मा द्वारा उप-समस्या में शीर्षों की संख्या से दोगुनी से कम या उसके समान है। गहराई d पर उपसमस्या में शीर्षों की संख्या n/4d है तो सभी सही उपसमस्याओं में शीर्षों की कुल संख्या दी गई है . इस प्रकार, मूल समस्या और सभी उपसमस्याओं में किनारों की अपेक्षित संख्या अधिकतम 2m+n है। चूंकि बिना किसी पृथक शीर्ष वाले ग्राफ़ के लिए n अधिकतम 2m है, इसलिए एल्गोरिथम अपेक्षित समय O(m) में चलता है।
अधिक निकृष्टतम स्थिति का विश्लेषण
इस प्रकार से अधिक निकृष्टतम स्थिति का रनटाइम बोरोव्का के एल्गोरिदम के रनटाइम के समान है। ऐसा तब होता है जब प्रत्येक आह्वान पर सभी किनारों को बाएँ या दाएँ उपसमस्या में जोड़ा जाता है। इस मामले में एल्गोरिथ्म बोरोव्का के एल्गोरिदम के समान है जो n शीर्षों और m किनारों वाले ग्राफ़ पर O(min{n2, mlogn}) में चलता है।
संदर्भ
- ↑ Karger, David R.; Klein, Philip N.; Tarjan, Robert E. (1995). "न्यूनतम फैले हुए पेड़ों को खोजने के लिए एक यादृच्छिक रैखिक-समय एल्गोरिथ्म". Journal of the ACM. 42 (2): 321. CiteSeerX 10.1.1.39.9012. doi:10.1145/201019.201022. S2CID 832583.
- ↑ 2.0 2.1 2.2 2.3 Dixon, Brandon; Rauch, Monika; Tarjan, Robert E. (1992). "रैखिक समय में न्यूनतम फैले पेड़ों का सत्यापन और संवेदनशीलता विश्लेषण". SIAM Journal on Computing. 21 (6): 1184. CiteSeerX 10.1.1.49.25. doi:10.1137/0221070.
- ↑ 3.0 3.1 3.2 3.3 King, Valerie (1995). A Simpler Minimum Spanning Tree Verification Algorithm. Proceedings of the 4th International Workshop on Algorithms and Data Structures. London, UK, UK: Springer-Verlag. pp. 440–448.