निश्चित-बिंदु गणना

नियत-बिंदु गणना किसी दिए गए प्रकार्य के सटीक या अनुमानित नियत बिंदु (गणित) की गणना करने की प्रक्रिया को संदर्भित करती है। इसके सबसे सामान्य रूप में, हमें एक प्रकार्य f दिया गया है जो ब्रौवर नियत-बिंदु प्रमेय की स्थिति को संतुष्ट करता है, अर्थात: f सतत है और इकाई d-क्यूब को अपने आप में चित्रित(मानचित्र) करता है। ब्रौवर नियत-बिंदु प्रमेय गारंटी देता है कि f का एक नियत बिंदु है, लेकिन प्रमाण रचनात्मक नहीं है। अनुमानित नियत बिंदु की गणना के लिए विभिन्न एल्गोरिदम तैयार किए गए हैं। ऐसे एल्गोरिदम का उपयोग अर्थशास्त्र में बाजार संतुलन की गणना के लिए, गेम थ्योरी(खेल सिद्धांत) में नैश संतुलन की गणना के लिए और गतिशील प्रणाली विश्लेषण में उपयोग किया जाता है।

निश्चित-बिंदु उनके भिन्नात्मक भाग के अंकों की एक निश्चित संख्या को संग्रहीत करके भिन्नात्मक (गैर-पूर्णांक) संख्याओं का प्रतिनिधित्व करने की एक विधि है। उदाहरण के लिए, डॉलर की रकम को प्रायः सेंट (डॉलर का 1/100) का प्रतिनिधित्व करने वाले दो आंशिक अंकों के साथ संग्रहित किया जाता है।

परिभाषाएँ

तीन निश्चित बिंदुओं के साथ एक उदाहरण प्रकार्य का ग्राफ़

इकाई अंतराल को निरूपित किया जाता है $E:=[0,1]$, और इकाई d-आयामी घन को E^d द्वारा निरूपित किया जाता है। एक सतत फलन f को E^d (E^d से स्वयं तक) पर परिभाषित किया गया है। प्रायः, यह माना जाता है कि f न केवल सतत है, बल्कि लिप्सचिट्ज़ सतत भी है, अर्थात, कुछ स्थिरांक L के लिए, $|f(x)-f(y)|\leq L\cdot |x-y|$ E^d में सभी x,y के लिए।

F का एक 'नियत बिंदु' E^d में एक बिंदु x है जैसे कि f(x) = x । ब्रौवर नियत-बिंदु प्रमेय के अनुसार, E^d से कोई भी सतत कार्य का अपने आप में एक नियत बिंदु होता है। लेकिन सामान्य कार्यों के लिए, एक नियत बिंदु की सटीक गणना करना असंभव है, क्योंकि यह एक मनमानी वास्तविक संख्या हो सकती है। नियत-बिंदु गणना एल्गोरिदम अनुमानित निश्चित बिंदुओं की खोज करते हैं। अनुमानित निश्चित बिंदु के लिए कई मानदंड हैं। कई सामान्य मानदंड हैं:

• अवशिष्ट मानदंड: एक सन्निकटन पैरामीटर दिया गया है $\varepsilon >0$ , f का एक ε-अवशिष्ट निश्चित-बिंदु E^d में एक बिंदु x है जैसे कि $|f(x)-x|\leq \varepsilon$, यहाँ कहाँ |.| अधिकतम मानदंड को दर्शाता है| अर्थात सभी d निर्देशांक में अंतर है $f(x)-x$ अधिक से अधिक ε होना चाहिए |
• पूर्ण मानदंड: एक सन्निकटन पैरामीटर दिया गया है $\delta >0$, f का एक δ-पूर्ण नियत-बिंदु E^d में एक बिंदु x है जैसे कि $|x-x_{0}|\leq \delta$, कहाँ $x_{0}$ f का कोई निश्चित-बिंदु है।
• 'सापेक्ष मानदंड': एक सन्निकटन पैरामीटर दिया गया है $\delta >0$, f का एक δ-सापेक्ष नियत-बिंदु E^d में एक बिंदु x है जैसे कि $|x-x_{0}|/|x_{0}|\leq \delta$, कहाँ $x_{0}$ f का कोई निश्चित-बिंदु है।

लिप्सचिट्ज़-सतत कार्यों के लिए, पूर्ण मानदंड अवशिष्ट मानदंड से अधिक मजबूत है: यदि f स्थिर L के साथ लिप्सचिट्ज़-सतत है, तो $|x-x_{0}|\leq \delta$ का तात्पर्य है $|f(x)-f(x_{0})|\leq L\cdot \delta$ | तब से $x_{0}$ f का एक नियत बिंदु है, इसका तात्पर्य है $|f(x)-x_{0}|\leq L\cdot \delta$, इसलिए $|f(x)-x|\leq (1+L)\cdot \delta$. इसलिए, एक δ-पूर्ण नियत-बिंदु भी एक ε-अवशिष्ट नियत-बिंदु के साथ $\varepsilon =(1+L)\cdot \delta$ है|

नियत-बिंदु गणना एल्गोरिदम का सबसे बुनियादी चरण एक मान क्वेरी है: E^d में कोई भी x दिया गया है,^{[वाक्य खंड]}

प्रकार्य f 'मूल्यांकन' प्रश्नों के माध्यम से सुलभ है: किसी भी x के लिए, एल्गोरिदम f(x) का मूल्यांकन कर सकता है। किसी एल्गोरिदम की रन-टाइम जटिलता समान्यता आवश्यक मूल्यांकनों की संख्या द्वारा दी जाती है।

संविदात्मक कार्य

यदि L < 1 स्थिरांक L के साथ एक लिप्सचिट्ज़-सतत प्रकार्य को 'संविदात्मक' कहा जाता है; यदि L ≤ 1 इसे 'कमजोर-संकुचन' कहा जाता है| ब्रौवर की शर्तों को संतुष्ट करने वाले प्रत्येक संविदात्मक कार्य का एक अद्वितीय नियत बिंदु होता है। इसके अतिरिक्त, संविदात्मक कार्यों के लिए नियत-बिंदु गणना सामान्य कार्यों की तुलना में आसान है।

प्रकार्य पुनरावृत्ति का उपयोग करके एक नियत बिंदु की गणना करना

नियत-बिंदु गणना के लिए पहला एल्गोरिदम बानाच का नियत-बिंदु पुनरावृत्ति एल्गोरिदम था। बानाच का नियत-बिंदु प्रमेय का तात्पर्य है कि, जब नियत-बिंदु पुनरावृत्ति को संकुचन मानचित्रण पर लागू किया जाता है, तो t पुनरावृत्तियों के बाद त्रुटि है $O(L^{t})$| इसलिए, δ-सापेक्ष नियत-बिंदु के लिए आवश्यक मूल्यांकनों की संख्या लगभग $\log _{L}(\delta )=\log(\delta )/\log(L)=\log(1/\delta )/\log(1/L)$ है| सिकोरस्की और वोज्नियाकोव्स्की ने दिखाया गया कि जब आयाम बड़ा होता है तो बानाच का एल्गोरिदम इष्टतम होता है। विशेष रूप से, जब $d\geq \log(1/\delta )/\log(1/L)$, δ-सापेक्ष नियत-बिंदु के लिए किसी भी एल्गोरिदम के आवश्यक मूल्यांकन की संख्या पुनरावृत्ति एल्गोरिदम द्वारा आवश्यक मूल्यांकन की संख्या 50% से अधिक है। ध्यान दें कि जब L 1 के करीब पहुंचता है, तो मूल्यांकन की संख्या अनंत तक पहुंच जाती है। वास्तव में, कोई भी परिमित एल्गोरिथ्म L=1 वाले सभी कार्यों के लिए δ-पूर्ण नियत बिंदु की गणना नहीं कर सकता है।

जब L <1 और d = 1, इष्टतम एल्गोरिदम सिकोरस्की और वोज्नियाकोव्स्की का 'नियत बिन्दु आवरण' (FPE) एल्गोरिदम है। इसका उपयोग करके δ-सापेक्ष नियत बिंदु पाया जाता है $O(\log(1/\delta )+\log \log(1/(1-L)))$ क्वेरीज़(प्रश्न), और एक δ-पूर्ण नियत बिंदु $O(\log(1/\delta ))$ का उपयोग करना | यह नियत-बिंदु पुनरावृत्ति एल्गोरिथ्म से बहुत तेज़ है।

जब d>1 लेकिन बहुत बड़ा नहीं है, और L ≤ 1, इष्टतम एल्गोरिथ्म आंतरिक-दीर्घवृत्ताभ एल्गोरिथ्म (दीर्घवृत्ताभ विधि पर आधारित) है। यह पाता है कि ε-अवशिष्ट नियत-बिंदु $O(d\cdot \log(1/\varepsilon ))$ मूल्यांकन का उपयोग किया जा रहा है | जब L<1, यह एक δ-निरपेक्ष नियत बिंदु $O(d\cdot [\log(1/\delta )+\log(1/(1-L))])$ मूल्यांकन का उपयोग करके पाता है|

शेलमैन और सिकोरस्की ने केवल L ≤ 1 के साथ दो-आयामी प्रकार्य के ε-अवशिष्ट निश्चित-बिंदु की गणना के लिए BEFix (बाइसेक्शन लिफाफा निश्चित-बिंदु) $2\lceil \log _{2}(1/\varepsilon )\rceil +1$ नामक एक एल्गोरिदम प्रस्तुत किया, वे बाद में समान सबसे खराब स्थिति की गारंटी लेकिन बेहतर अनुभवजन्य प्रदर्शन के साथ, BEDFix (बाइसेक्शन लिफाफा डीप-कट निश्चित-बिंदु) नामक एक सुधार प्रस्तुत किया। जब L<1, BEDFix का उपयोग करके δ-पूर्ण नियत-बिंदु $O(\log(1/\varepsilon )+\log(1/(1-L)))$ की गणना भी की जा सकती है|

शेलमैन और सिकोरस्की ने L ≤ 1 के साथ एक d-आयामी प्रकार्य के ε- अवशिष्ट नियत-बिंदुकी गणना के लिए PFix नामक एक एल्गोरिदम $O(\log ^{d}(1/\varepsilon ))$ प्रस्तुत किया, जिसका उपयोग किया गया | जब L <1, PFix को निष्पादित किया जा सकता है $\varepsilon =(1-L)\cdot \delta$, और उस स्थिति में, यह उपयोग करके δ-पूर्ण नियत-बिंदु $O(\log ^{d}(1/[(1-L)\delta ]))$ की गणना करता है | जब L 1 के करीब होता है तो यह पुनरावृत्ति एल्गोरिथ्म से अधिक कुशल होता है। एल्गोरिदम पुनरावर्ती है: यह (d-1)-आयामी कार्यों पर पुनरावर्ती कॉल द्वारा एक d-आयामी प्रकार्य को संभालता है।

विभिन्न कार्यों के लिए एल्गोरिदम

जब प्रकार्य f अवकलनीय होता है, और एल्गोरिदम इसके व्युत्पन्न (केवल f ही नहीं) का मूल्यांकन कर सकता है, तो अनुकूलन में न्यूटन की विधि का उपयोग किया जा सकता है और यह बहुत तेज़ है।

सामान्य कार्य

लिप्सचिट्ज़ स्थिरांक L > 1 वाले कार्यों के लिए, एक नियत-बिंदु की गणना करना बहुत कठिन है।

एक आयाम

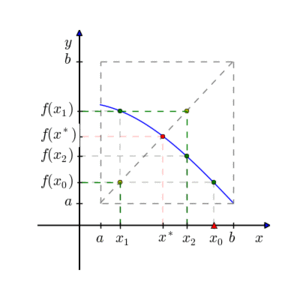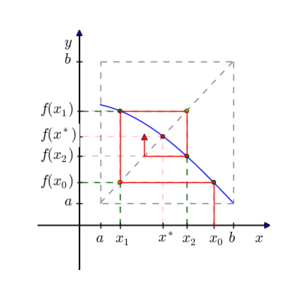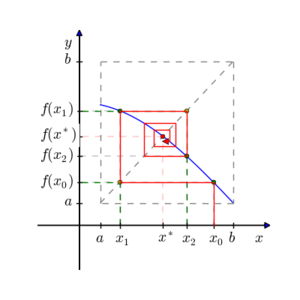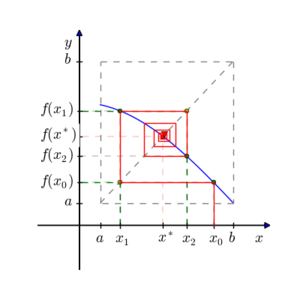
1-आयामी प्रकार्य (d = 1) के लिए, एक δ-पूर्ण नियत-बिंदु का उपयोग करके पाया जा सकता है $O(\log(1/\delta ))$ द्विभाजन विधि का उपयोग करते हुए प्रश्न: अंतराल से प्रारंभ करें $E:=[0,1]$; प्रत्येक पुनरावृत्ति पर, मान लीजिए कि x वर्तमान अंतराल का केंद्र है, और f(x) की गणना करता है; यदि f(x) > x तो x के दाईं ओर उप-अंतराल पर पुनरावृत्ति करें; अन्यथा, x के बाईं ओर के अंतराल पर पुनरावृत्ति करें। ध्यान दें कि वर्तमान अंतराल में हमेशा एक नियत बिंदु होता है, इसलिए बाद में $O(\log(1/\delta ))$, शेष अंतराल में कोई भी बिंदु f का δ-पूर्ण नियत-बिंदु है। सेटिंग $\delta :=\varepsilon /(L+1)$, जहां L लिप्सचिट्ज़ स्थिरांक है,$O(\log(L/\varepsilon )=\log(L)+\log(1/\varepsilon ))$ का उपयोग करके एक ε-अवशिष्ट निश्चित-बिंदु देता है|

दो या दो से अधिक आयाम

दो या दो से अधिक आयामों वाले कार्यों के लिए, समस्या अधिक चुनौतीपूर्ण है। शेलमैन और सिकोरस्की ने साबित किया कि, किसी भी पूर्णांक d ≥ 2 और L > 1 के लिए, d-आयामी L-लिप्सचिट्ज़ कार्यों का δ-पूर्ण नियत-बिंदु को खोजने के लिए अनंत-कई मूल्यांकन की आवश्यकता हो सकती है। प्रमाण विचार इस प्रकार है कि किसी भी पूर्णांक T > 1 के लिए, और मूल्यांकन प्रश्नों (संभवतः अनुकूली) के T के किसी भी अनुक्रम के लिए, कोई दो कार्यों का निर्माण कर सकता है जो सतत L के साथ लिप्सचिट्ज़-सतत हैं, और इन सभी प्रश्नों का एक ही उत्तर दे सकते हैं, लेकिन उनमें से एक का (x, 0) पर एक अद्वितीय निश्चित-बिंदु है और दूसरे का (x, 1) पर एक अद्वितीय निश्चित-बिंदु है। T मूल्यांकन का उपयोग करने वाला कोई भी एल्गोरिदम इन कार्यों के बीच अंतर नहीं कर सकता है, इसलिए δ-पूर्ण नियत-बिंदु नहीं ढूंढ सकता है। यह किसी भी परिमित पूर्णांक T के लिए सत्य है।

ε-अवशिष्ट नियत-बिंदु, इसे खोजने के लिए प्रकार्य मूल्यांकन पर आधारित कई एल्गोरिदम विकसित किए गए हैं

• किसी सामान्य प्रकार्य के एक नियत बिंदु का अनुमान लगाने वाला पहला एल्गोरिदम 1967 में हर्बर्ट स्कार्फ द्वारा विकसित किया गया था। स्कार्फ का एल्गोरिदम स्पर्नर के लेम्मा के समान एक निर्माण में, एक पूर्ण-लेबल वाले आदिम सेट को ढूंढकर एक ε-अवशिष्ट निश्चित बिंदु ढूंढता है।
• हेरोल्ड कुह्न द्वारा एक बाद के एल्गोरिदम आदिम सेटों के सिवाय सरल और सरल विभाजन का उपयोग किया गया।
• सरल दृष्टिकोण को और विकसित करते हुए, ओरिन हैरिसन मेरिल ने पुनरारंभ एल्गोरिथ्म प्रस्तुत किया।
• B कर्टिस ईव्स होमोटॉपी एल्गोरिदम प्रस्तुत किया। एल्गोरिथ्म एक एफ़िन प्रकार्य से शुरू करके काम करता है जो f का अनुमान लगाता है, और नियत बिंदु का पालन करते हुए इसे f की ओर विकृत करता है। माइकल टॉड की एक किताब1976 तक विकसित विभिन्न एल्गोरिदम का सर्वेक्षण करती है।
• डेविड गेल ने दिखाया गया है कि n-आयामी प्रकार्य (इकाई d-आयामी क्यूब पर) के एक नियत बिंदु की गणना करना यह तय करने के बराबर है कि हेक्स (बोर्ड गेम) के d-आयामी खेल में विजेता कौन है (d खिलाड़ियों वाला एक गेम, प्रत्येक जिसे d-घन के दो विपरीत फलकों को जोड़ने की आवश्यकता है)। वांछित सटीकता को देखते हुए ε
  • kd आकार का एक हेक्स बोर्ड बनाएं, जहां $k>1/\varepsilon$. प्रत्येक शीर्ष z इकाई n-घन में एक बिंदु z/k से मेल खाता है।
  • अंतर की गणना करें f(z/k) - z/k; ध्यान दें कि अंतर एक n-वेक्टर है।
  • शीर्ष z को 1, ..., d में एक लेबल द्वारा लेबल करें, जो अंतर वेक्टर में सबसे बड़े निर्देशांक को दर्शाता है।
  • परिणामस्वरूप लेबलिंग d खिलाड़ियों के बीच d-आयामी हेक्स गेम के संभावित खेल से मेल खाती है। इस खेल में एक विजेता होना चाहिए, और गेल विजयी पथ के निर्माण के लिए एक एल्गोरिदम प्रस्तुत करता है।
  • जीत की राह में, एक बिंदु ऐसा होना चाहिए जिसमें f_i(z/k) - z/k धनात्मक है, और एक आसन्न बिंदु जिसमें f_i(z/k) - z/k ऋणात्मक है। इसका मतलब यह है कि इन दोनों बिंदुओं के बीच f का एक निश्चित बिंदु है।

सबसे खराब स्थिति में, इन सभी एल्गोरिदम द्वारा आवश्यक प्रकार्य मूल्यांकन की संख्या सटीकता के द्विआधारी प्रतिनिधित्व में घातीय है, अर्थात $\Omega (1/\varepsilon )$.

क्वेरी(प्रश्न) जटिलता

हिर्श, क्रिस्टोस पापादिमित्रियोउ और वावसिस ने यह साबित किया कि कोई भी एल्गोरिदम प्रकार्य मूल्यांकन के आधार पर ,इसके लिए f का ε-अवशिष्ट नियत-बिंदु खोजना आवश्यक है $\Omega (L'/\varepsilon )$ प्रकार्य मूल्यांकन, जहां $L'$ प्रकार्य का लिप्सचिट्ज़ स्थिरांक है $f(x)-x$ (ध्यान दें कि $L-1\leq L'\leq L+1$). ज्यादा ठीक:

• 2-आयामी प्रकार्य (d=2) के लिए, वे एक कड़े बंधन में बंधे हुए साबित होते हैं $\Theta (L'/\varepsilon )$.
• किसी भी d ≥ 3 के लिए, d-आयामी प्रकार्य के ε-अवशिष्ट नियत-बिंदु को खोजने आवश्यकता होती है $\Omega ((L'/\varepsilon )^{d-2})$ क्वेरीज़ और $O((L'/\varepsilon )^{d})$ क्वेरीज़ |

बाद वाला परिणाम घातांक में एक अंतर छोड़ देता है। चेन और डेंग ने अंतर को कम कर दिया| उन्होंने यह साबित कर दिया कि, किसी भी d ≥ 2 और के लिए $1/\varepsilon >4d$ और $L'/\varepsilon >192d^{3}$, ε-अवशिष्ट निश्चित-बिंदु की गणना के लिए आवश्यक प्रश्नों की संख्या $\Theta ((L'/\varepsilon )^{d-1})$ है |

पृथक निश्चित-बिंदु गणना

पृथक प्रकार्य के उपसमुच्चय पर परिभाषित एक प्रकार्य है $\mathbb {Z} ^{d}$(d-आयामी पूर्णांक ग्रिड)। कई अलग-अलग निश्चित-बिंदु प्रमेय हैं, जो उन स्थितियों को बताते हैं जिनके तहत एक अलग प्रकार्य का एक निश्चित बिंदु होता है। उदाहरण के लिए, 'आईमुरा-मुरोता-तमुरा प्रमेय' बताता है कि (विशेष रूप से) यदि f एक आयत उपसमुच्चय से एक प्रकार्य है $\mathbb {Z} ^{d}$स्वयं के लिए, और f हाइपरक्यूबिक(अतिघन) दिशा-संरक्षण , तो f का एक नियत बिंदु है।

मान लीजिए f पूर्णांक घन से एक दिशा-संरक्षण प्रकार्य है $\{1,\dots ,n\}^{d}$ अपने आप में। चेन और डेंगसाबित करते हैं कि, किसी भी d ≥ 2 और n > 48d के लिए, ऐसे नियत बिंदु $\Theta (n^{d-1})$ कार्य मूल्यांकन की गणना करना आवश्यक है|

चेन और डेंग एक अलग पृथक-नियत-बिंदु समस्या को परिभाषित करते हैं, जिसे वे 2D-ब्रॉउवर कहते हैं। यह एक पृथक फलन f पर विचार करता है $\{0,\dots ,n\}^{2}$ जैसे कि, ग्रिड पर प्रत्येक x के लिए, f(x) - x या तो (0, 1) या (1, 0) या (-1, -1) है। लक्ष्य ग्रिड में एक वर्ग ढूंढना है, जिसमें सभी तीन लेबल होते हैं। प्रकार्य f को वर्ग को चित्रित(मानचित्र) करना होगा $\{0,\dots ,n\}^{2}$स्वयं के लिए, इसलिए इसे रेखाओं x = 0 और y = 0 को या तो (0, 1) या (1, 0) पर चित्रित(मानचित्र) करना होगा; रेखा x = n से या तो (-1, -1) या (0, 1); और रेखा y = n से या तो (-1, -1) या (1,0)। समस्या को '2D-स्पर्नर' तक कम किया जा सकता है (स्पर्नर के लेम्मा की शर्तों को पूरा करने वाले त्रिभुज में एक पूर्ण-लेबल वाले त्रिकोण की गणना करना), और इसलिए यह PPAD-पूर्ण है। इसका तात्पर्य यह है कि अनुमानित नियत-बिंदु की गणना बहुत सरल कार्यों के लिए भी PPAD-पूर्ण है।

निश्चित-बिंदु गणना और रूट-फाइंडिंग(मूल-खोज) एल्गोरिदम के बीच संबंध

E^d से R तक एक प्रकार्य g दिया गया है, g का 'मूल' E^d में एक बिंदु x है जैसे कि g(x)=0 | g का ε-मूल E^d में एक बिंदु x है, जैसे कि $g(x)\leq \varepsilon$ |

निश्चित-बिंदु गणना मूल-खोज का एक विशेष कारक है: E^d पर एक प्रकार्य f दिया गया है, परिभाषित करें $g(x):=|f(x)-x|$ | स्पष्ट रूप से, x, f का एक नियत-बिंदु है यदि और केवल यदि x, g का मूल है, और x f का एक ε-अवशिष्ट निश्चित-बिंदु है यदि और केवल यदि x, g का एक ε-मूल है। इसलिए, किसी भी मूल-खोज एल्गोरिदम (एक एल्गोरिदम जो किसी प्रकार्य के अनुमानित रूट की गणना करता है) का उपयोग अनुमानित नियत-बिंदु खोजने के लिए किया जा सकता है।

इसके विपरीत सत्य नहीं है: किसी सामान्य प्रकार्य का अनुमानित मूल ढूँढ़ना किसी अनुमानित नियत बिंदु को ढूँढ़ने से अधिक कठिन हो सकता है। विशेष रूप से, सिकोरस्की ने यह साबित कर दिया कि $\Omega (1/\varepsilon ^{d})$ कार्य मूल्यांकन ε-रूट खोजने की आवश्यकता है| यह एक-आयामी प्रकार्य के लिए भी एक घातीय निचली सीमा देता है (इसके विपरीत, एक ε-एक-आयामी प्रकार्य का ε-अवशिष्ट नियत-बिंदु का उपयोग करके पाया जा सकता है $O(\log(1/\varepsilon ))$ द्विभाजन विधि का उपयोग कर प्रश्न)। यहाँ एक प्रमाण रेखाचित्र है। एक प्रकार्य g का निर्माण करें जो कि E^d में हर जगह ε से थोड़ा बड़ा है, कुछ बिंदु x₀ के आसपास कुछ छोटे घन को छोड़कर, जहां x₀ g की अद्वितीय मूल है| यदि g स्थिरांक L के साथ निरंतर लिप्सचिट्ज़ है, तो x₀ के आसपास के घन की भुजा-लंबाई $\varepsilon /L$ हो सकती है| कोई भी एल्गोरिदम जो g का ε-रूट पाता है, उसे पूरे E^d को कवर करने वाले घनों के एक सेट की जांच करनी चाहिए; ऐसे घनों की संख्या न्यूनतम है$(L/\varepsilon )^{d}$

यद्यपि, कार्यों के ऐसे वर्ग हैं जिनके लिए अनुमानित मूल ढूंढना अनुमानित नियत बिंदु खोजने के बराबर है। एक उदाहरण कार्यों का वर्ग g इस प्रकार है $g(x)+x$ E^d को अपने पास मानचित्र करता है (अर्थात: $g(x)+x$ सभी के लिए E^d में है x E^d में)। ऐसा इसलिए है, क्योंकि ऐसे प्रत्येक प्रकार्य के लिए, प्रकार्य $f(x):=g(x)+x$ ब्रौवर के नियत-बिंदु प्रमेय की शर्तों को संतुष्ट करता है। स्पष्ट रूप से, x, f का एक नियत-बिंदु है यदि और केवल यदि x, g का मूल है, औरx, f का एक ε-अवशिष्ट निश्चित-बिंदु है यदि और केवल यदि x, g का एक ε-मूल है। चेन और डेंग दिखाएँ हैं कि इन समस्याओं के अलग-अलग रूप कम्प्यूटेशनल रूप से समतुल्य $\Theta (n^{d-1})$ कार्य मूल्यांकन: दोनों समस्याओं की आवश्यकता है |

संचार जटिलता

रफ़गार्डन और वीनस्टीन ने अनुमानित नियत-बिंदु की गणना की संचार जटिलता का अध्ययन किया। उनके मॉडल में, दो अभिकर्ता हैं: उनमें से एक प्रकार्य f को जानता है और दूसरा प्रकार्य g को जानता है। दोनों कार्य लिप्सचिट्ज़ सतत हैं और ब्रौवर की शर्तों को पूरा करते हैं। लक्ष्य समग्र प्रकार्य के अनुमानित नियत बिंदु $g\circ f$ की गणना करना है | वे दिखाते हैं कि नियतिवादी संचार जटिलता$\Omega (2^{d})$ मौजूद है |

अग्रिम पठन

• Yannakakis, Mihalis (May 2009). "Equilibria, fixed points, and complexity classes". Computer Science Review. 3 (2): 71–85. doi:10.1016/j.cosrev.2009.03.004.