थ्रेडेड बाइनरी ट्री: Difference between revisions
(Created page with "{{cleanup-rewrite|date=October 2011}} Image:Threaded tree.svg|right|thumb|धराशायी तीरों द्वारा दिखाए गए विशेष थ...") |
No edit summary |
||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
[[Image:Threaded tree.svg|right|thumb|डैशड एरोस द्वारा दिखाए गए विशेष थ्रेडिंग लिंक के साथ थ्रेडेड ट्री]][[ कम्प्यूटिंग |कम्प्यूटिंग]] में, '''थ्रेडेड [[ द्विआधारी वृक्ष |बाइनरी ट्री]]''' बाइनरी ट्री वैरिएंट है जो की विशेष क्रम में [[ वृक्ष परिभ्रमण |ट्रैवर्सल]] की सुविधा देता है (प्रायः वही क्रम जो पूर्व से ही ट्री के लिए परिभाषित है)। | |||
[[Image:Threaded tree.svg|right|thumb| | |||
इस प्रकार से संपूर्ण बाइनरी सर्च ट्री को मुख्य कीय के क्रम में सरलता से पार किया जा सकता है, किन्तु [[नोड (कंप्यूटर विज्ञान)]] को केवल [[पॉइंटर (कंप्यूटर प्रोग्रामिंग)]] दिया जाता है, इसके पश्चात आने वाले नोड को खोजना धीमा या असंभव हो सकता है। अतः उदाहरण के लिए, परिलैंग्वेज के अनुसार लीफ नोड्स का कोई वंशज नहीं होता है, इसलिए लीफ नोड के लिए केवल पॉइंटर दिए जाने पर किसी अन्य नोड तक नहीं पहुंचा जा सकता है। और थ्रेडेड ट्री कुछ या सभी नोड्स में अतिरिक्त जानकारी जोड़ता है, जिससे किसी भी एकल नोड के लिए "नेक्स्ट" नोड शीघ्रता से पाया जा सकता है, जिससे रिकर्सन के बिना ट्री ट्रैवर्सल और रिकर्सन के लिए आवश्यक अतिरिक्त स्टोरेज (ट्री की गहराई के आनुपातिक) की अनुमति मिलती है। | |||
==थ्रेडिंग== | ==थ्रेडिंग== | ||
एक बाइनरी ट्री को सभी दाएं चाइल्ड पॉइंटर्स बनाकर पिरोया जाता है जो सामान्यतः नोड के इन-ऑर्डर उत्तराधिकारी के लिए शून्य बिंदु होंगे ('यदि'यह उपस्तिथ है), और सभी बाएं चाइल्ड पॉइंटर्स जो सामान्य रूप से नोड के इन-ऑर्डर पूर्ववर्ती के लिए शून्य बिंदु होते है।<ref>Van Wyk, Christopher J. <u>Data Structures and C Programs</u>, Addison-Wesley, 1988, p. 175. {{ISBN|978-0-201-16116-8}}.</ref> | |||
इस प्रकार से माना जाता है कि ट्रैवर्सल क्रम ट्री के [[इन-ऑर्डर ट्रैवर्सल]] के समान है। चूंकि, पॉइंटर्स को प्रतिस्थापित करने के अतिरिक्त (या इसके अतिरिक्त) ट्री नोड्स में जोड़ा जा सकता है। इस प्रकार परिभाषित लिंक्ड सूचियों को सामान्यतः थ्रेड्स भी कहा जाता है, और इसका उपयोग किसी भी वांछित क्रम में ट्रैवर्सल को सक्षम करने के लिए किया जा सकता है। अतः उदाहरण के लिए, ट्री जिसके नोड्स लोगों के बारे में जानकारी का प्रतिनिधित्व करते हैं, किन्तु इन्हें नाम के आधार पर क्रमबद्ध किया जा सकता है, किन्तु जन्म तिथि, वेट या किसी अन्य ज्ञात विशेषता के क्रम में त्वरित ट्रैवर्सल की अनुमति देने वाले अतिरिक्त धागे होते हैं। | |||
==प्रेरणा== | ==प्रेरणा== | ||
[[बाइनरी सर्च ट्री]] सहित ( | अतः [[बाइनरी सर्च ट्री]] सहित (किन्तु इन्हीं तक सीमित नहीं) ट्री के उपयोग वस्तुओं को विशेष क्रम में स्टोर्ड करने के लिए किया जा सकता है, जैसे कि प्रत्येक नोड में स्टोर्ड कुछ गुण का मूल्य है, जिसे प्रायः कीय मान कहा जाता है। इस प्रकार से ट्री पर उपयोगी ऑपरेशन ट्रैवर्सल होते है: जो की कीय के क्रम में सभी वस्तुओं पर जाना। | ||
एक सरल पुनरावर्ती ट्रैवर्सल एल्गोरिदम जो बाइनरी सर्च ट्री के प्रत्येक नोड पर जाता है वह निम्नलिखित है। मान लीजिए {{mvar|t}} | एक सरल पुनरावर्ती ट्रैवर्सल एल्गोरिदम जो बाइनरी सर्च ट्री के प्रत्येक नोड पर जाता है वह निम्नलिखित है। मान लीजिए {{mvar|t}} नोड के लिए पॉइंटर है, या {{math|nil}}. है। "विज़िट" {{mvar|t}} का अर्थ नोड {{mvar|t}} या इसकी सामग्री पर कोई भी क्रिया करना हो सकता है. | ||
<div शैली= मार्जिन-बाएँ: 35px; चौड़ाई: 600px > | <div शैली= मार्जिन-बाएँ: 35px; चौड़ाई: 600px > | ||
{{framebox| | {{framebox|नीला}} | ||
एल्गोरिथम ट्रैवर्स({{mvar|t}}): | एल्गोरिथम ट्रैवर्स({{mvar|t}}): | ||
* इनपुट: | * इनपुट: पॉइंटर्स {{mvar|t}} एक नोड के लिए (या {{math|nil}}) | ||
* | * यदि {{math|''t'' {{=}} nil}}, वापस करना। | ||
* अन्य: | * अन्य: | ||
** ट्रैवर्स (बाएं-बच्चे ({{mvar|t}})) | ** ट्रैवर्स (बाएं-बच्चे ({{mvar|t}})) | ||
** | ** विजिट {{mvar|t}} | ||
** ट्रैवर्स (राइट-चाइल्ड ({{mvar|t}})) | ** ट्रैवर्स (राइट-चाइल्ड ({{mvar|t}})) | ||
{{frame-footer}} | {{frame-footer}} | ||
</div> | </div> | ||
इस एल्गोरिदम के साथ | इस प्रकार से एल्गोरिदम के साथ समस्या यह है कि, इसकी पुनरावृत्ति के कारण, यह ट्री की ऊंचाई के अनुपात में स्टैक स्पेस का उपयोग करता है। यदि ट्री अधिक संतुलित है, तो यह {{mvar|n }} तत्वों वाले ट्री के लिए {{math|''O''(log ''n'') }} स्थान जिसमें सम्मिलित है तत्व. अधिक व्यर्थ स्थिति में, जब ट्री [[पथ ग्राफ|चैन]] का रूप लेता है, तो ट्री की ऊंचाई {{mvar|n}} होती है इसलिए एल्गोरिथ्म {{math|''O''(''n'') }} लेता है। द्वतीय समस्या यह है कि सभी ट्रैवर्सल मूल से प्रारंभ होने चाहिए जब नोड्स में केवल उनके चाइल्ड के लिए पॉइंटर्स होते है। किसी विशेष नोड के लिए पॉइंटर होना समान बात है, किन्तु जब तक थ्रेड पॉइंटर्स जैसी अतिरिक्त जानकारी नहीं जोड़ी जाती है, तब तक वह बाकी ट्री पर वापस जाने के लिए पर्याप्त नहीं है। | ||
इस दृष्टिकोण में, यह बताना संभव नहीं हो सकता है कि किसी दिए गए नोड में बाएँ और/या | इस दृष्टिकोण में, यह बताना संभव नहीं हो सकता है कि किसी दिए गए नोड में बाएँ और/या राइट पॉइंटर वास्तव में चाइल्ड को इंगित करते हैं, या थ्रेडिंग का परिणाम हैं। यदि अंतर आवश्यक है, तो प्रत्येक नोड में बिट जोड़ना इसे रिकॉर्ड करने के लिए पर्याप्त है। | ||
1968 की पाठ्यपुस्तक में, [[डोनाल्ड नुथ]] ने पूछा कि क्या इन-ऑर्डर ट्रैवर्सल के लिए | अतः 1968 की पाठ्यपुस्तक में, [[डोनाल्ड नुथ]] ने पूछा कि क्या इन-ऑर्डर ट्रैवर्सल के लिए गैर-पुनरावर्ती एल्गोरिदम उपस्तिथ होते है, जो की किसी स्टैक का उपयोग नहीं करता है और ट्री को अपरिवर्तित छोड़ देता है।<ref>{{cite book |last=Knuth |first=D.E. |authorlink=Donald Knuth |year=1968 |title=मौलिक एल्गोरिदम|edition=1st |series=The Art of Computer Programming |publisher=Addison Wesley |location=Reading/MA |volume=1 }}<!---according to Mateti.Manghirmalani.1988, p.29---></ref> इस समस्या का समाधान ट्री थ्रेडिंग है, जिसे जोसेफ एम. मॉरिस ने 1979 में प्रस्तुत किया था।<ref>{{cite journal |last=Morris |first=Joseph H. |year=1979 |title=बाइनरी पेड़ों को आसानी से और सस्ते में पार करना|journal=[[Information Processing Letters]] |doi=10.1016/0020-0190(79)90068-1 |volume=9 |issue=5}}</ref><ref>{{cite journal |last1=Mateti |first1=Prabhaker |last2=Manghirmalani |first2=Ravi |year=1988 |title=मॉरिस के ट्री ट्रैवर्सल एल्गोरिदम पर पुनर्विचार किया गया|journal=Science of Computer Programming |doi=10.1016/0167-6423(88)90063-9 |volume=11 |pages=29–43|doi-access=free }}</ref> | ||
इस प्रकार से 1969 के अनुवर्ती संस्करण में,<ref>{{cite book |last=Knuth |first=D.E. |authorlink=Donald Knuth |year=1969 |title=मौलिक एल्गोरिदम|edition=2 |publisher=Addison Wesley |series=The Art of Computer Programming |volume=1}} Hre: Sect.2.3.1 "Traversing Binary Trees".</ref> नुथ ने थ्रेडेड ट्री प्रतिनिधित्व का श्रेय [[एलन पर्लिस]] और थॉर्नटन (1960) को दिया गया था।<ref>{{cite journal |last1=Perlis |first1=Alan Jay |last2=Thornton |first2=C. |date=Apr 1960 |title=थ्रेडेड सूचियों द्वारा प्रतीक हेरफेर|journal=Communications of the ACM |doi=10.1145/367177.367202 |volume=3 |number=4 |pages=195–204}}</ref> | |||
===मूल पॉइंटरो से संबंध=== | |||
समान लक्ष्यों को प्राप्त करने की द्वतीय विधि प्रत्येक नोड में उस नोड के मूल नोड में पॉइंटर सम्मिलित करना है। यह देखते हुए, "नेक्स्ट" नोड तक सदैव पहुंचा जा सकता है। जब भी कोई सही चाइल्ड नहीं होते हैं तब भी राईट पॉइंटर शून्य होते हैं। उस नोड से "नेक्स्ट" नोड खोजने के लिए जिसका दायां पॉइंटर शून्य है, और मूल पॉइंटर्स के माध्यम से तब तक चलें जब तक कि उस नोड तक न पहुंच जाएं जिसका दायां पॉइंटर शून्य नहीं है, और यह वह चाइल्ड नहीं है जहां से आप अभी आए हैं। वह नोड नेक्स्ट नोड है, और इसके पश्चात उसके वंशज दाईं ओर आते हैं। | |||
इस प्रकार से पैरेंट पॉइंटर्स या स्टैक के स्पष्ट उपयोग के बिना, थ्रेडेड बाइनरी ट्री से नोड के पैरेंट की खोज करना भी संभव है, चूंकि यह धीमा है। इसे देखने के लिए, दाएं चाइल्ड r के साथ नोड k पर विचार करें। यदि r का बायां पॉइंटर या तो चाइल्ड होना चाहिए या k पर वापस थ्रेड होना चाहिए। इस प्रकार की स्तिथि में जब r का लेफ्ट चाइल्ड है, तो उस बाएँ चाइल्ड के समीप या तो अपना लेफ्ट चाइल्ड होना चाहिए या k की ओर धागा होना चाहिए, और इसी तरह सभी क्रमिक बाएँ चाइल्ड के लिए है। जब r से बाएँ पॉइंटर की श्रृंखला का अनुसरण करके, हम अंततः k की ओर इंगित करने वाला धागा पाएंगे। किन्तु स्थिति सममित रूप से समान है जब q, p का लेफ्ट चाइल्ड है - हम q के राइट चाइल्ड का अनुसरण p की ओर इंगित करने वाले धागे तक कर सकते हैं। | |||
[[पायथन (प्रोग्रामिंग भाषा)|पायथन (प्रोग्रामिंग लैंग्वेज)]] में:<syntaxhighlight lang="python"> | |||
[[पायथन (प्रोग्रामिंग भाषा)]] में:<syntaxhighlight lang="python"> | |||
def parent(node): | def parent(node): | ||
if node is node.tree.root: | if node is node.tree.root: | ||
| Line 76: | Line 72: | ||
== इन-ऑर्डर ट्रैवर्सल की सरणी == | == इन-ऑर्डर ट्रैवर्सल की सरणी == | ||
[[क्रम में]] ट्रैवर्सल के अनुसार थ्रेड्स नोड के पूर्ववर्तियों और उत्तराधिकारियों के संदर्भ हैं। | इस प्रकार से [[क्रम में]] ट्रैवर्सल के अनुसार थ्रेड्स नोड के पूर्ववर्तियों और उत्तराधिकारियों के संदर्भ हैं। | ||
थ्रेडेड ट्री का इन-ऑर्डर ट्रैवर्सल <code>A,B,C,D,E,F,G,H,I</code>है, <code>E</code> का पूर्ववर्ती <code>D</code> है, <code>E</code> का उत्तराधिकारी <code>F</code> है। | |||
[[File:ThreadTree Inorder Array.png]] | [[File:ThreadTree Inorder Array.png]] | ||
== उदाहरण == | == उदाहरण == | ||
[[File:ThreadTree Inorder Array123456789.png]]आइए | [[File:ThreadTree Inorder Array123456789.png]]आइए सामान्य बाइनरी ट्री से थ्रेडेड बाइनरी ट्री बनाएं: | ||
[[File:Normal Binary Tree.png]]उपरोक्त | [[File:Normal Binary Tree.png]]उपरोक्त ट्री के लिए इन-ऑर्डर ट्रैवर्सल है - D B A E C. तो, संबंधित थ्रेडेड बाइनरी ट्री होगा - | ||
[[File:Threaded Binary Tree.png]] | [[File:Threaded Binary Tree.png]] | ||
| Line 95: | Line 91: | ||
== संदर्भ == | == संदर्भ == | ||
{{reflist}} | {{reflist}} | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* [http://adtinfo.org/libavl.html/Threaded-Binary-Search-Trees.html GNU libavl 2.0.2, Section on threaded binary search trees] | * [http://adtinfo.org/libavl.html/Threaded-Binary-Search-Trees.html GNU libavl 2.0.2, Section on threaded binary search trees] | ||
{{DEFAULTSORT:Threaded Binary Tree}} | {{DEFAULTSORT:Threaded Binary Tree}} | ||
[[Category: Machine Translated Page]] | [[Category:Created On 25/07/2023|Threaded Binary Tree]] | ||
[[Category: | [[Category:Machine Translated Page|Threaded Binary Tree]] | ||
[[Category:Pages with script errors|Threaded Binary Tree]] | |||
[[Category:Templates Vigyan Ready|Threaded Binary Tree]] | |||
[[Category:उदाहरण के लिए पायथन (प्रोग्रामिंग भाषा) कोड वाले लेख|Threaded Binary Tree]] | |||
[[Category:पेड़ खोजें|Threaded Binary Tree]] | |||
[[Category:बाइनरी पेड़|Threaded Binary Tree]] | |||
Latest revision as of 10:46, 10 August 2023
कम्प्यूटिंग में, थ्रेडेड बाइनरी ट्री बाइनरी ट्री वैरिएंट है जो की विशेष क्रम में ट्रैवर्सल की सुविधा देता है (प्रायः वही क्रम जो पूर्व से ही ट्री के लिए परिभाषित है)।
इस प्रकार से संपूर्ण बाइनरी सर्च ट्री को मुख्य कीय के क्रम में सरलता से पार किया जा सकता है, किन्तु नोड (कंप्यूटर विज्ञान) को केवल पॉइंटर (कंप्यूटर प्रोग्रामिंग) दिया जाता है, इसके पश्चात आने वाले नोड को खोजना धीमा या असंभव हो सकता है। अतः उदाहरण के लिए, परिलैंग्वेज के अनुसार लीफ नोड्स का कोई वंशज नहीं होता है, इसलिए लीफ नोड के लिए केवल पॉइंटर दिए जाने पर किसी अन्य नोड तक नहीं पहुंचा जा सकता है। और थ्रेडेड ट्री कुछ या सभी नोड्स में अतिरिक्त जानकारी जोड़ता है, जिससे किसी भी एकल नोड के लिए "नेक्स्ट" नोड शीघ्रता से पाया जा सकता है, जिससे रिकर्सन के बिना ट्री ट्रैवर्सल और रिकर्सन के लिए आवश्यक अतिरिक्त स्टोरेज (ट्री की गहराई के आनुपातिक) की अनुमति मिलती है।
थ्रेडिंग
एक बाइनरी ट्री को सभी दाएं चाइल्ड पॉइंटर्स बनाकर पिरोया जाता है जो सामान्यतः नोड के इन-ऑर्डर उत्तराधिकारी के लिए शून्य बिंदु होंगे ('यदि'यह उपस्तिथ है), और सभी बाएं चाइल्ड पॉइंटर्स जो सामान्य रूप से नोड के इन-ऑर्डर पूर्ववर्ती के लिए शून्य बिंदु होते है।[1]
इस प्रकार से माना जाता है कि ट्रैवर्सल क्रम ट्री के इन-ऑर्डर ट्रैवर्सल के समान है। चूंकि, पॉइंटर्स को प्रतिस्थापित करने के अतिरिक्त (या इसके अतिरिक्त) ट्री नोड्स में जोड़ा जा सकता है। इस प्रकार परिभाषित लिंक्ड सूचियों को सामान्यतः थ्रेड्स भी कहा जाता है, और इसका उपयोग किसी भी वांछित क्रम में ट्रैवर्सल को सक्षम करने के लिए किया जा सकता है। अतः उदाहरण के लिए, ट्री जिसके नोड्स लोगों के बारे में जानकारी का प्रतिनिधित्व करते हैं, किन्तु इन्हें नाम के आधार पर क्रमबद्ध किया जा सकता है, किन्तु जन्म तिथि, वेट या किसी अन्य ज्ञात विशेषता के क्रम में त्वरित ट्रैवर्सल की अनुमति देने वाले अतिरिक्त धागे होते हैं।
प्रेरणा
अतः बाइनरी सर्च ट्री सहित (किन्तु इन्हीं तक सीमित नहीं) ट्री के उपयोग वस्तुओं को विशेष क्रम में स्टोर्ड करने के लिए किया जा सकता है, जैसे कि प्रत्येक नोड में स्टोर्ड कुछ गुण का मूल्य है, जिसे प्रायः कीय मान कहा जाता है। इस प्रकार से ट्री पर उपयोगी ऑपरेशन ट्रैवर्सल होते है: जो की कीय के क्रम में सभी वस्तुओं पर जाना।
एक सरल पुनरावर्ती ट्रैवर्सल एल्गोरिदम जो बाइनरी सर्च ट्री के प्रत्येक नोड पर जाता है वह निम्नलिखित है। मान लीजिए t नोड के लिए पॉइंटर है, या nil. है। "विज़िट" t का अर्थ नोड t या इसकी सामग्री पर कोई भी क्रिया करना हो सकता है.
एल्गोरिथम ट्रैवर्स(t):
- इनपुट: पॉइंटर्स t एक नोड के लिए (या nil)
- यदि t = nil, वापस करना।
- अन्य:
- ट्रैवर्स (बाएं-बच्चे (t))
- विजिट t
- ट्रैवर्स (राइट-चाइल्ड (t))
इस प्रकार से एल्गोरिदम के साथ समस्या यह है कि, इसकी पुनरावृत्ति के कारण, यह ट्री की ऊंचाई के अनुपात में स्टैक स्पेस का उपयोग करता है। यदि ट्री अधिक संतुलित है, तो यह n तत्वों वाले ट्री के लिए O(log n) स्थान जिसमें सम्मिलित है तत्व. अधिक व्यर्थ स्थिति में, जब ट्री चैन का रूप लेता है, तो ट्री की ऊंचाई n होती है इसलिए एल्गोरिथ्म O(n) लेता है। द्वतीय समस्या यह है कि सभी ट्रैवर्सल मूल से प्रारंभ होने चाहिए जब नोड्स में केवल उनके चाइल्ड के लिए पॉइंटर्स होते है। किसी विशेष नोड के लिए पॉइंटर होना समान बात है, किन्तु जब तक थ्रेड पॉइंटर्स जैसी अतिरिक्त जानकारी नहीं जोड़ी जाती है, तब तक वह बाकी ट्री पर वापस जाने के लिए पर्याप्त नहीं है।
इस दृष्टिकोण में, यह बताना संभव नहीं हो सकता है कि किसी दिए गए नोड में बाएँ और/या राइट पॉइंटर वास्तव में चाइल्ड को इंगित करते हैं, या थ्रेडिंग का परिणाम हैं। यदि अंतर आवश्यक है, तो प्रत्येक नोड में बिट जोड़ना इसे रिकॉर्ड करने के लिए पर्याप्त है।
अतः 1968 की पाठ्यपुस्तक में, डोनाल्ड नुथ ने पूछा कि क्या इन-ऑर्डर ट्रैवर्सल के लिए गैर-पुनरावर्ती एल्गोरिदम उपस्तिथ होते है, जो की किसी स्टैक का उपयोग नहीं करता है और ट्री को अपरिवर्तित छोड़ देता है।[2] इस समस्या का समाधान ट्री थ्रेडिंग है, जिसे जोसेफ एम. मॉरिस ने 1979 में प्रस्तुत किया था।[3][4]
इस प्रकार से 1969 के अनुवर्ती संस्करण में,[5] नुथ ने थ्रेडेड ट्री प्रतिनिधित्व का श्रेय एलन पर्लिस और थॉर्नटन (1960) को दिया गया था।[6]
मूल पॉइंटरो से संबंध
समान लक्ष्यों को प्राप्त करने की द्वतीय विधि प्रत्येक नोड में उस नोड के मूल नोड में पॉइंटर सम्मिलित करना है। यह देखते हुए, "नेक्स्ट" नोड तक सदैव पहुंचा जा सकता है। जब भी कोई सही चाइल्ड नहीं होते हैं तब भी राईट पॉइंटर शून्य होते हैं। उस नोड से "नेक्स्ट" नोड खोजने के लिए जिसका दायां पॉइंटर शून्य है, और मूल पॉइंटर्स के माध्यम से तब तक चलें जब तक कि उस नोड तक न पहुंच जाएं जिसका दायां पॉइंटर शून्य नहीं है, और यह वह चाइल्ड नहीं है जहां से आप अभी आए हैं। वह नोड नेक्स्ट नोड है, और इसके पश्चात उसके वंशज दाईं ओर आते हैं।
इस प्रकार से पैरेंट पॉइंटर्स या स्टैक के स्पष्ट उपयोग के बिना, थ्रेडेड बाइनरी ट्री से नोड के पैरेंट की खोज करना भी संभव है, चूंकि यह धीमा है। इसे देखने के लिए, दाएं चाइल्ड r के साथ नोड k पर विचार करें। यदि r का बायां पॉइंटर या तो चाइल्ड होना चाहिए या k पर वापस थ्रेड होना चाहिए। इस प्रकार की स्तिथि में जब r का लेफ्ट चाइल्ड है, तो उस बाएँ चाइल्ड के समीप या तो अपना लेफ्ट चाइल्ड होना चाहिए या k की ओर धागा होना चाहिए, और इसी तरह सभी क्रमिक बाएँ चाइल्ड के लिए है। जब r से बाएँ पॉइंटर की श्रृंखला का अनुसरण करके, हम अंततः k की ओर इंगित करने वाला धागा पाएंगे। किन्तु स्थिति सममित रूप से समान है जब q, p का लेफ्ट चाइल्ड है - हम q के राइट चाइल्ड का अनुसरण p की ओर इंगित करने वाले धागे तक कर सकते हैं।
पायथन (प्रोग्रामिंग लैंग्वेज) में:
def parent(node):
if node is node.tree.root:
return None
x = node
y = node
while True:
if is_thread(y):
p = y.right
if p is None or p.left is not node:
p = x
while not is_thread(p.left):
p = p.left
p = p.left
return p
elif is_thread(x):
p = x.left
if p is None or p.right is not node:
p = y
while not is_thread(p.right):
p = p.right
p = p.right
return p
x = x.left
y = y.right
प्रकार
- एकल थ्रेडेड: प्रत्येक नोड को या तो इन-ऑर्डर पूर्ववर्ती या उत्तराधिकारी (बाएं या दाएं) की ओर पिरोया गया है।
- डबल थ्रेडेड: प्रत्येक नोड को इन-ऑर्डर पूर्ववर्ती और उत्तराधिकारी (बाएं और दाएं) दोनों की ओर पिरोया गया है।
इन-ऑर्डर ट्रैवर्सल की सरणी
इस प्रकार से क्रम में ट्रैवर्सल के अनुसार थ्रेड्स नोड के पूर्ववर्तियों और उत्तराधिकारियों के संदर्भ हैं।
थ्रेडेड ट्री का इन-ऑर्डर ट्रैवर्सल A,B,C,D,E,F,G,H,Iहै, E का पूर्ववर्ती D है, E का उत्तराधिकारी F है।
उदाहरण
आइए सामान्य बाइनरी ट्री से थ्रेडेड बाइनरी ट्री बनाएं:
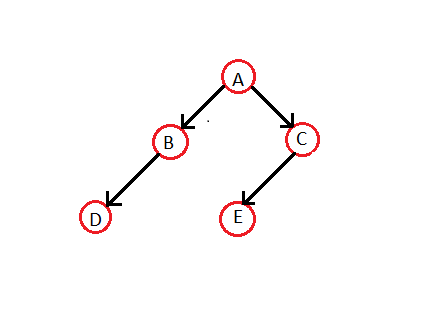उपरोक्त ट्री के लिए इन-ऑर्डर ट्रैवर्सल है - D B A E C. तो, संबंधित थ्रेडेड बाइनरी ट्री होगा -
शून्य लिंक
n नोड्स वाले एम-वे थ्रेडेड बाइनरी ट्री में, 'n×m - (n−1)' शून्य लिंक होते हैं।
संदर्भ
- ↑ Van Wyk, Christopher J. Data Structures and C Programs, Addison-Wesley, 1988, p. 175. ISBN 978-0-201-16116-8.
- ↑ Knuth, D.E. (1968). मौलिक एल्गोरिदम. The Art of Computer Programming. Vol. 1 (1st ed.). Reading/MA: Addison Wesley.
- ↑ Morris, Joseph H. (1979). "बाइनरी पेड़ों को आसानी से और सस्ते में पार करना". Information Processing Letters. 9 (5). doi:10.1016/0020-0190(79)90068-1.
- ↑ Mateti, Prabhaker; Manghirmalani, Ravi (1988). "मॉरिस के ट्री ट्रैवर्सल एल्गोरिदम पर पुनर्विचार किया गया". Science of Computer Programming. 11: 29–43. doi:10.1016/0167-6423(88)90063-9.
- ↑ Knuth, D.E. (1969). मौलिक एल्गोरिदम. The Art of Computer Programming. Vol. 1 (2 ed.). Addison Wesley. Hre: Sect.2.3.1 "Traversing Binary Trees".
- ↑ Perlis, Alan Jay; Thornton, C. (Apr 1960). "थ्रेडेड सूचियों द्वारा प्रतीक हेरफेर". Communications of the ACM. 3 (4): 195–204. doi:10.1145/367177.367202.
