कर्नेल रिग्रेशन: Difference between revisions
No edit summary |
m (Abhishek moved page कर्नेल प्रतिगमन to कर्नेल रिग्रेशन without leaving a redirect) |
(No difference)
| |
Revision as of 13:10, 4 August 2023
आंकड़ों में, कर्नेल रिग्रेशन यादृच्छिक वैरीएबल की नियमबद्ध अपेक्षा का अनुमान लगाने के लिए गैर पैरामीट्रिक तकनीक है। इस प्रकार इसका उद्देश्य यादृच्छिक वैरीएबल X और Y की जोड़ी के मध्य गैर-रैखिक संबंध खोजना है।
किसी भी गैरपैरामीट्रिक रिग्रेशन में, एक वैरीएबल के सापेक्ष एक वैरीएबल की नियमबद्ध अपेक्षा लिखी जा सकती है:
जहाँ अज्ञात फ़ंक्शन है.
नादारया-वाटसन कर्नेल रिग्रेशन
1964 में नदारया और जेफ्री वॉटसन दोनों ने वेटिंग फ़ंक्शन के रूप में कर्नेल (सांख्यिकी) का उपयोग करके स्थानीय रूप से भारित औसत के रूप में का अनुमान लगाने का प्रस्ताव रखा था।[1][2][3] नादारया-वाटसन अनुमानक है:
जहां एक बैंडविड्थ वाला कर्नेल है जैसे कि कम से कम 1 क्रम का है, अर्थात
व्युत्पत्ति
कर्नेल 'K' के साथ संयुक्त वितरण f(x,y) और f(x) के लिए कर्नेल घनत्व अनुमान का उपयोग करना है,
हम पाते हैं
जो नादारया-वाटसन अनुमानक है।
प्रीस्टली-चाओ कर्नेल अनुमानक
जहाँ बैंडविड्थ (या स्मूथिंग मापदंड) है।
गैसर-मुलर कर्नेल अनुमानक[4]
जहाँ
उदाहरण
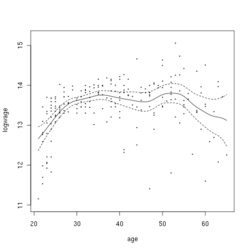
यह उदाहरण कनाडाई क्रॉस-सेक्शन वेतन डेटा पर आधारित है जिसमें सामान्य शिक्षा (ग्रेड 13) वाले पुरुष व्यक्तियों के लिए 1971 की कनाडाई जनगणना सार्वजनिक उपयोग टेप से लिया गया यादृच्छिक नमूना सम्मिलित है। कुल 205 अवलोकन हैं।
दाईं ओर का आंकड़ा स्पर्शोन्मुख परिवर्तनशीलता सीमा के साथ दूसरे क्रम के गॉसियन कर्नेल का उपयोग करके अनुमानित रिग्रेशन फ़ंक्शन को दर्शाता है।
उदाहरण के लिए स्क्रिप्ट
R प्रोग्रामिंग लैंग्वेज के निम्नलिखित कमांड का उपयोग करते हैं अधिकांशतः स्मूथिंग प्रदान करने और ऊपर दिए गए चित्र को बनाने का कार्य इन कमांड को कमांड प्रॉम्प्ट पर कट और पेस्ट के माध्यम से अंकित किया जा सकता है।
install.packages("np")
library(np) # non parametric library
data(cps71)
attach(cps71)
m <- npreg(logwage~age)
plot(m, plot.errors.method="asymptotic",
plot.errors.style="band",
ylim=c(11, 15.2))
points(age, logwage, cex=.25)
detach(cps71)
संबंधित
डेविड साल्सबर्ग के अनुसार, कर्नेल रिग्रेशन में उपयोग किए जाने वाले एल्गोरिदम स्वतंत्र रूप से विकसित किए गए थे और फजी सिस्टम में उपयोग किए गए थे: इस प्रकार पूर्णतः समान कंप्यूटर एल्गोरिदम के साथ, फ़ज़ी सिस्टम और कर्नेल घनत्व-आधारित रिग्रेशन दूसरे से पूरी तरह से स्वतंत्र रूप से विकसित किए गए प्रतीत होते हैं।[5]
सांख्यिकीय कार्यान्वयन
- जीएनयू ऑक्टेव गणितीय प्रोग्राम पैकेज
- जूलिया (प्रोग्रामिंग लैंग्वेज): KernelEstimator.jl
- मैटलैब: कर्नेल रिग्रेशन, कर्नेल घनत्व अनुमान, हैजर्ड फ़ंक्शन के कर्नेल अनुमान और कई अन्य के कार्यान्वयन के साथ मुफ्त मैटलैब टूलबॉक्स इन पृष्ठों पर उपलब्ध है (यह टूलबॉक्स पुस्तक का भाग है) [6]).
- पायथन (प्रोग्रामिंग लैंग्वेज): द
KernelRegमिश्रित डेटा प्रकारों के लिए वर्गstatsmodels.nonparametricउप-पैकेज (अन्य कर्नेल घनत्व से संबंधित वर्ग सम्मिलित हैं), पैकेज [1] स्किकिट-लर्न के विस्तार के रूप में (अक्षम मेमोरी-वार, केवल छोटे डेटासेट के लिए उपयोगी) - आर (प्रोग्रामिंग लैंग्वेज): फ़ंक्शन
npregएनपी पैकेज कर्नेल रिग्रेशन निष्पादित कर सकता है।[7][8] - Stata: : npregress, kernreg2
यह भी देखें
संदर्भ
- ↑ Nadaraya, E. A. (1964). "On Estimating Regression". Theory of Probability and Its Applications. 9 (1): 141–2. doi:10.1137/1109020.
- ↑ Watson, G. S. (1964). "सहज प्रतिगमन विश्लेषण". Sankhyā: The Indian Journal of Statistics, Series A. 26 (4): 359–372. JSTOR 25049340.
- ↑ Bierens, Herman J. (1994). "The Nadaraya–Watson kernel regression function estimator". उन्नत अर्थमिति में विषय. New York: Cambridge University Press. pp. 212–247. ISBN 0-521-41900-X.
- ↑ Gasser, Theo; Müller, Hans-Georg (1979). "प्रतिगमन कार्यों का कर्नेल अनुमान". Springer: 23–68.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Salsburg, D. (2002). The Lady Tasting Tea: How Statistics Revolutionized Science in the Twentieth Century. W.H. Freeman. pp. 290–91. ISBN 0-8050-7134-2.
- ↑ Horová, I.; Koláček, J.; Zelinka, J. (2012). Kernel Smoothing in MATLAB: Theory and Practice of Kernel Smoothing. Singapore: World Scientific Publishing. ISBN 978-981-4405-48-5.
- ↑ np: Nonparametric kernel smoothing methods for mixed data types
- ↑ Kloke, John; McKean, Joseph W. (2014). आर का उपयोग करते हुए गैर-पैरामीट्रिक सांख्यिकीय तरीके. CRC Press. pp. 98–106. ISBN 978-1-4398-7343-4.
अग्रिम पठन
- Henderson, Daniel J.; Parmeter, Christopher F. (2015). Applied Nonparametric Econometrics. Cambridge University Press. ISBN 978-1-107-01025-3.
- Li, Qi; Racine, Jeffrey S. (2007). Nonparametric Econometrics: Theory and Practice. Princeton University Press. ISBN 978-0-691-12161-1.
- Pagan, A.; Ullah, A. (1999). Nonparametric Econometrics. Cambridge University Press. ISBN 0-521-35564-8.
- Racine, Jeffrey S. (2019). An Introduction to the Advanced Theory and Practice of Nonparametric Econometrics: A Replicable Approach Using R. Cambridge University Press. ISBN 9781108483407.
- Simonoff, Jeffrey S. (1996). Smoothing Methods in Statistics. Springer. ISBN 0-387-94716-7.
बाहरी संबंध
- Scale-adaptive kernel regression (with मैटलैब software).
- Tutorial of Kernel regression using spreadsheet (with Microsoft Excel).
- An online kernel regression demonstration Requires .NET 3.0 or later.
- Kernel regression with automatic bandwidth selection (with Python)