बर्स्ट त्रुटि-सुधार करने वाले कोड: Difference between revisions

Revision as of 13:12, 2 August 2023

कोडिंग सिद्धांत में, बर्स्ट त्रुटि-सुधार करने वाले कोड बर्स्ट त्रुटियों को ठीक करने के विधियों को नियोजित करते हैं, जो त्रुटियां हैं जो एक-दूसरे से स्वतंत्र रूप से बिट्स में होने के अतिरिक्त निरंतर अनेक बिट्स में होती हैं।

यादृच्छिक त्रुटियों को ठीक करने के लिए अनेक कोड डिज़ाइन किए गए हैं। चूँकि, कभी-कभी चैनल त्रुटियाँ प्रस्तुत कर सकते हैं जो थोड़े अंतराल में स्थानीयकृत होती हैं। ऐसी त्रुटियाँ बर्स्ट में होती हैं (जिन्हें बर्स्ट त्रुटियाँ कहा जाता है) क्योंकि वे निरंतर अनेक बिट्स में होती हैं। बर्स्ट त्रुटियों के उदाहरण भंडारण माध्यमों में बड़े पैमाने पर पाए जा सकते हैं। ये त्रुटियाँ शारीरिक क्षति जैसे डिस्क पर खरोंच या वायरलेस चैनलों के उपस्तिथि में बिजली के झटके के कारण हो सकती हैं। वे स्वतंत्र नहीं हैं; वे स्थानिक रूप से केंद्रित होते हैं। यदि बिट में कोई त्रुटि है, तो संभावना है कि आसन्न बिट्स भी दूषित हो सकते हैं। यादृच्छिक त्रुटियों को ठीक करने के लिए उपयोग की जाने वाली विधियाँ बर्स्ट त्रुटियों को ठीक करने में अक्षम हैं।

परिभाषाएँ

लम्बाई का बर्स्ट 5

इस प्रकार की लम्बाई का बर्स्ट $ℓ$ ^[1] कोडवर्ड बोलो $C$ प्रसारित किया जाता है, और इसे $Y=C+E.$ प्राप्त किया जाता है फिर, त्रुटि सदिश $E$ लम्बाई का बर्स्ट $\ell$ कहलाता है यदि $E$ के गैर-शून्य अवयव $\ell$ तक निरंतर अवयव ही सीमित हैं . उदाहरण के लिए, $E=(0{\textbf {1000011}}0)$ लम्बाई का बर्स्ट $\ell =7.$ है

चूँकि यह परिभाषा यह बताने के लिए पर्याप्त है कि बर्स्ट त्रुटि क्या है, बर्स्ट त्रुटि सुधार के लिए विकसित अधिकांश उपकरण चक्रीय कोड पर निर्भर करते हैं। यह हमारी अगली परिभाषा को प्रेरित करता है।

त्रुटि सदिश $E$ को $\ell$ लंबाई की चक्रीय बर्स्ट त्रुटि कहलाती है यदि इसके गैरशून्य अवयव $\ell$ चक्रीय रूप से निरंतर अवयव तक ही सीमित हैं। उदाहरण के लिए, पहले माना गया त्रुटि सदिश $E=(010000110)$ , लंबाई का चक्रीय बर्स्ट है $\ell =5$ , चूंकि हम स्थिति से प्रारंभ होने वाली त्रुटि पर विचार करते हैं $6$ और स्थिति $1$ पर समाप्त हो रहा है. ध्यान दें कि सूचकांक हैं $0$ -आधारित, यानी पहला तत्व स्थिति पर है $0$ .

इस लेख के शेष भाग के लिए, हम चक्रीय बर्स्ट को संदर्भित करने के लिए बर्स्ट शब्द का उपयोग करेंगे, जब तक कि अन्यथा उल्लेख न किया गया हो।

बर्स्ट विवरण

बर्स्ट त्रुटि की संक्षिप्त परिभाषा रखना अधिकांशतः उपयोगी होता है, जिसमें न केवल इसकी लंबाई, किंतु ऐसी त्रुटि का पैटर्न और स्थान भी सम्मिलित होता है। हम बर्स्ट विवरण को $(P,L)$ टुपल के रूप में परिभाषित करते हैं जहाँ $P$ त्रुटि का पैटर्न है (जो कि त्रुटि पैटर्न में पहली गैर-शून्य प्रविष्टि से प्रारंभ होने वाले और अंतिम गैर-शून्य प्रतीक के साथ समाप्त होने वाले प्रतीकों की स्ट्रिंग है), और $L$ कोडवर्ड पर वह स्थान है, जहां बर्स्ट पाया जा सकता है।^[1]

उदाहरण के लिए, त्रुटि पैटर्न $E=(010000110)$ का बर्स्ट विवरण $D=(1000011,1)$ है ध्यान दें कि ऐसा वर्णन अद्वितीय नहीं है, क्योंकि $D'=(11001,6)$ उसी बर्स्ट त्रुटि का वर्णन करता है। सामान्यतः , यदि $E$ में गैर-शून्य अवयव की संख्या $w$ है , तब $E$ में $w$ भिन्न -भिन्न बर्स्ट विवरण होगा, जिनमें से प्रत्येक $E$ भिन्न गैर-शून्य प्रविष्टि पर प्रारंभ होता है . नीचे दिए गए प्रमेय के साथ बर्स्ट विवरण की अस्पष्टता से उत्पन्न होने वाले विवादों को हल करने के लिए, चूंकि ऐसा करने से पहले हमें पहले परिभाषा की आवश्यकता है।

परिभाषा। किसी दिए गए त्रुटि $y,$ पैटर्न में प्रतीकों की संख्या $\mathrm {length} (y).$ द्वारा निरूपित किया जाता है

Theorem (Uniqueness of burst descriptions) — मान लीजिए $E$ लंबाई का त्रुटि सदिश है $n$ दो बर्स्ट विवरण के साथ $(P_{1},L_{1})$ and $(P_{2},L_{2})$ . If $\mathrm {length} (P_{1})+\mathrm {length} (P_{2})\leqslant n+1,$ तो दोनों विवरण समान हैं अर्थात् उनके अवयव समतुल्य हैं.^[2]

{{math proof | proof = $w$ हैमिंग वज़न (या गैर-शून्य प्रविष्टियों की संख्या) हो $E$ . तब $E$ बिलकुल है $w$ त्रुटि विवरण. के लिए $w=0,1,$ साबित करने के लिए कुछ भी नहीं है. तो हम ऐसा मान लेते हैं $w\geqslant 2$ और यह कि विवरण समान नहीं हैं। हम देखते हैं कि प्रत्येक गैर-शून्य प्रविष्टि $E$ wमैं पैटर्न में दिखाई दूंगा, और इसी तरह, इसके अवयव भी $E$ पैटर्न में सम्मिलित नहीं किए जाने पर शून्यों का चक्रीय क्रम बनेगा, जो अंतिम गैर-शून्य प्रविष्टि के पश्चात प्रारंभ होगा, और पैटर्न की पहली गैर-शून्य प्रविष्टि से ठीक पहले जारी रहेगा। हम इस रन के अनुरूप सूचकांकों के सेट को शून्य रन कहते हैं। हमने तुरंत देखा कि प्रत्येक बर्स्ट विवरण के साथ एक शून्य रन जुड़ा हुआ है और प्रत्येक शून्य रन असंयुक्त है। चूंकि हमारे पास है $w$ शून्य रन, और प्रत्येक असंयुक्त है, हमारे पास कुल है $n-w$ सभी शून्य रन में विशिष्ट तत्व। दूसरी ओर हमारे पास है:

{\begin{aligned}n-w={\text{number of zeros in }}E&\geqslant (n-\mathrm {length} (P_{1}))+(n-\mathrm {length} (P_{2}))\\&=2n-\left(\mathrm {length} (P_{1})+\mathrm {length} (P_{2})\right)\\&\geqslant 2n-(n+1)&&\mathrm {length} (P_{1})+\mathrm {length} (P_{2})\leqslant n+1\\&=n-1\end{aligned}}

यह विरोधाभासी है

w\geqslant 2.

इस प्रकार, बर्स्ट त्रुटि विवरण समान हैं.}}

उपरोक्त प्रमेय का परिणाम यह है कि हमारे पास लंबाई के बर्स्ट के लिए दो भिन्न -भिन्न बर्स्ट ${\tfrac {1}{2}}(n+1).$ विवरण नहीं हो सकते हैं

बर्स्ट त्रुटि सुधार के लिए चक्रीय कोड

चक्रीय कोड को इस प्रकार परिभाषित किया गया है: $q$ प्रतीक को $\mathbb {F} _{q}$ के तत्वों के रूप के बारे में सोचें. अब, हम शब्दों को $\mathbb {F} _{q},$ से अधिक बहुपद के रूप में सोच सकते हैं जहां किसी शब्द के भिन्न -भिन्न प्रतीक बहुपद के विभिन्न गुणांकों से मेल खाते हैं। चक्रीय कोड को परिभाषित करने के लिए, हम निश्चित बहुपद चुनते हैं, जिसे जनरेटर बहुपद कहा जाता है। इस चक्रीय कोड के कोडवर्ड वे सभी बहुपद हैं जो इस जनरेटर बहुपद से विभाज्य हैं।

कोडवर्ड डिग्री $\leqslant n-1$ के बहुपद हैं. मान लीजिए कि जनरेटर बहुपद $g(x)$ की डिग्री $r$ है . तथा $\leqslant n-1$ डिग्री के बहुपद जिनसे $g(x)$ विभाज्य होते हैं $g(x)$ को घात $\leqslant n-1-r$ के बहुपदों से गुणा करने से परिणाम प्राप्त होते है . अपने पास $q^{n-r}$ ऐसे बहुपद है. उनमें से प्रत्येक कोडवर्ड से मेल खाता है। इसलिए, $k=n-r$ चक्रीय कोड के लिए उपयोग किये जाते है .

चक्रीय कोड $\ell =n-k=r$ तक की लंबाई के सभी बर्स्ट का पता लगा सकते हैं . हम पश्चात में देखेंगे कि किसी की $(n,k)$ बर्स्ट त्रुटि का पता लगाने की क्षमता कोड ऊपर से $\ell \leqslant n-k$ तक सीमित है। . बर्स्ट त्रुटि का पता लगाने के लिए चक्रीय कोड को इष्टतम माना जाता है क्योंकि वे इस ऊपरी सीमा को पूरा करते हैं:

Theorem (Cyclic burst correction capability) — डिग्री के जनरेटर बहुपद के साथ प्रत्येक चक्रीय कोड $r$ लंबाई के सभी विस्फोटों का पता लगा सकता है $\leqslant r.$

{{math proof | proof = $\leqslant r$ कोडवर्ड के लिए (अर्थात एक बहुपद के लिए जो विभाज्य है $g(x)$ ), तब परिणाम कोई कोडवर्ड नहीं होगा (अर्थात संबंधित बहुपद इससे विभाज्य नहीं है) $g(x)$ ). यह दिखाने के लिए पर्याप्त है कि लंबाई में कोई उछाल नहीं है $\leqslant r$ से विभाज्य है $g(x)$ .ऐसे फूटने का रूप होता है $x^{i}b(x)$ , जहाँ $\deg(b(x))<r.$ इसलिए, $b(x)$ से विभाज्य नहीं है $g(x)$ (क्योंकि पश्चात वाले के पास डिग्री है $r$ ). $g(x)$ से विभाज्य नहीं है $x$ (अन्यथा, सभी कोडवर्ड से प्रारंभ होंगे $0$ ). इसलिए, $x^{i}$ से विभाज्य नहीं है $g(x)$ as well.}}

उपरोक्त प्रमाण चक्रीय कोड में बर्स्ट त्रुटि का पता लगाने/सुधार के लिए सरल एल्गोरिदम का सुझाव देता है: संचरित शब्द (यानी डिग्री $\leqslant n-1$ का बहुपद) दिया गया है ), जो कि $g(x)$ से विभाजित करने पर इस शब्द के शेषफल की गणना करता और यदि शेषफल शून्य है (अर्थात् यदि शब्द $g(x)$ विभाज्य है ), तो यह वैध कोडवर्ड है। अन्यथा, त्रुटि की रिपोर्ट करें. इस त्रुटि को ठीक करने के लिए, इस शेषफल को प्रेषित शब्द से घटाएँ। घटाव का परिणाम $g(x)$ व से िभाजित होने वाला है (अर्थात यह वैध कोडवर्ड होगा)।

बर्स्ट त्रुटि का पता लगाने पर $\ell \leqslant n-k=r$ की ऊपरी सीमा द्वारा हम जानते हैं कि चक्रीय कोड लंबाई $\ell >r$ के सभी बर्स्ट का पता नहीं लगा सकता है. चूँकि चक्रीय कोड वास्तव में लंबाई $>r$ के अधिकांश बर्स्ट का पता लगा सकते हैं .जिसका कारण यह है कि पता लगाना तभी विफल होता है जब बर्स्ट $g(x)$ विभाज्य हो . द्विआधारी वर्णमाला से अधिक, वहाँ मौजूद हैं $2^{\ell -2}$ लंबाई का फटना $\ell$ . उनमें से ही $2^{\ell -2-r}$ से विभाज्य हैं $g(x)$ . इसलिए,) लंबाई $\ell$ के सभी बर्स्ट पर समान वितरण मानते हुए पता लगाने में विफलता की संभावना बहुत कम है ( $g(x)$ .

अब हम चक्रीय कोड के बारे में मौलिक प्रमेय पर विचार करते हैं जो बर्स्ट को भिन्न -भिन्न कोसेट में वर्गीकृत करके कुशल बर्स्ट-त्रुटि सुधार कोड को डिजाइन करने में सहायता करेगा।

Theorem (Distinct Cosets) — एक रेखीय कोड $C$ एक $\ell$ -बर्स्ट-एरर-सही कोड यदि लंबाई की सभी बर्स्ट त्रुटियां $\leqslant \ell$ भिन्न -भिन्न कोसेट में झूठ बोलें $C$ .

{{math proof | proof = $\mathbf {e} _{1},\mathbf {e} _{2}$ लंबाई की भिन्न -भिन्न बर्स्ट त्रुटियाँ हों $\leqslant \ell$ जो कोड के एक ही कोसेट में स्थित हैं $C$ . Then $\mathbf {c} =\mathbf {e} _{1}-\mathbf {e} _{2}$ कोडवर्ड है. इसलिए, यदि हम प्राप्त करते हैं $\mathbf {e} _{1},$ हम इसे या तो डिकोड कर सकते हैं $\mathbf {0}$ or $\mathbf {c}$ . इसके विपरीत, यदि सभी विस्फोट त्रुटियाँ $\mathbf {e} _{1}$ and $\mathbf {e} _{2}$ एक ही कोसेट में न रहें, तो प्रत्येक बर्स्ट त्रुटि उसके सिंड्रोम द्वारा निर्धारित होती है। फिर त्रुटि को उसके सिंड्रोम के माध्यम से ठीक किया जा सकता है। इस प्रकार, एक रैखिक कोड $C$ is an $\ell$ -बर्स्ट-त्रुटि-सही कोड यदि और केवल यदि लंबाई की सभी बर्स्ट त्रुटियां $\leqslant \ell$ के भिन्न-भिन्न कोसेट में स्थित हैं $C$ .}}

Theorem (Burst error codeword classification) — मान लीजिये $C$ एक रेखीय हो $\ell$ -विस्फोट-त्रुटि-सुधार कोड। फिर लंबाई का कोई शून्येतर विस्फोट नहीं $\leqslant 2\ell$ कोडवर्ड हो सकता है.

Proof

$c$ be a codeword with a burst of length $\leqslant 2\ell$ . Thus it has the pattern $(0,1,u,v,1,0)$ , where $u$ and $v$ are words of length $\leqslant \ell -1.$ Hence, the words $w=(0,1,u,0,0,0)$ and $c-w=(0,0,0,v,1,0)$ are two bursts of length $\leqslant \ell$ . For binary linear codes, they belong to the same coset. This contradicts the Distinct Cosets Theorem, therefore no nonzero burst of length $\leqslant 2\ell$ can be a codeword.

बर्स्ट त्रुटि सुधार सीमा

बर्स्ट त्रुटि का पता लगाने और सुधार पर ऊपरी सीमा

ऊपरी सीमा से हमारा तात्पर्य हमारी त्रुटि पता लगाने की क्षमता की सीमा से है जिसे हम कभी भी पार नहीं कर सकते। मान लीजिए कि हम डिज़ाइन बनाना चाहते हैं $(n,k)$ कोड जो लंबाई की सभी बर्स्ट त्रुटियों का पता लगा सकता है $\leqslant \ell .$ पूछने के लिए स्वाभाविक प्रश्न है: दिया गया $n$ और $k$ , अधिकतम क्या है $\ell$ कि हम इससे आगे कभी हासिल नहीं कर सकते? दूसरे शब्दों में, लंबाई की ऊपरी सीमा क्या है $\ell$ हम किसी भी बर्स्ट का पता लगा सकते हैं $(n,k)$ कोड? निम्नलिखित प्रमेय इस प्रश्न का उत्तर प्रदान करता है।

Theorem (Burst error detection ability) — किसी की भी बर्स्ट त्रुटि का पता लगाने की क्षमता $(n,k)$ code is $\ell \leqslant n-k.$

Proof

पहले हम देखते हैं कि एक कोड लंबाई के सभी विस्फोटों का पता लगा सकता है $\leqslant \ell$ यदि और केवल यदि कोई भी दो कोडवर्ड लंबाई के हिसाब से भिन्न न हों $\leqslant \ell$ . मान लीजिए कि हमारे पास दो कोड वर्ड हैं $\mathbf {c} _{1}$ and $\mathbf {c} _{2}$ जो विस्फोट से भिन्न होता है $\mathbf {b}$ लम्बाई का $\leqslant \ell$ . प्राप्त करने पर $\mathbf {c} _{1}$ , हम यह नहीं बता सकते कि प्रेषित शब्द वास्तव में है या नहीं $\mathbf {c} _{1}$ बिना किसी ट्रांसमिशन त्रुटि के, या चाहे वह हो $\mathbf {c} _{2}$ बर्स्ट त्रुटि के साथ $\mathbf {b}$ जो प्रसारण के दौरान घटित हुआ। अब, मान लीजिए कि प्रत्येक दो कोडवर्ड की लंबाई में बहुत अधिक अंतर होता है $\ell .$ भले ही प्रेषित कोडवर्ड $\mathbf {c} _{1}$ विस्फोट की चपेट में आ गया है $\mathbf {b}$ लम्बाई का $\ell$ ,यह किसी अन्य वैध कोडवर्ड में परिवर्तित नहीं होगा. इसे प्राप्त करने पर, हम बता सकते हैं कि यह है $\mathbf {c} _{1}$ विस्फोट के साथ $\mathbf {b} .$ उपरोक्त अवलोकन से, हम जानते हैं कि कोई भी दो कोडवर्ड पहले को साझा नहीं कर सकते हैं $n-\ell$ प्रतीक. कारण यह है कि भले ही वे सभी में भिन्न हों $\ell$ प्रतीक, वे अभी भी लंबाई के आधार पर भिन्न होंगे $\ell .$ इसलिए, कोडवर्ड की संख्या $q^{k}$ संतुष्ट $q^{k}\leqslant q^{n-\ell }.$ को प्रयुक्त करने $\log _{q}$ दोनों तरफ और पुनर्व्यवस्थित करके, हम इसे देख सकते हैं $\ell \leqslant n-k$ .

अब, हम वही प्रश्न दोहराते हैं लेकिन त्रुटि सुधार के लिए: दिया गया है $n$ और $k$ , लंबाई पर ऊपरी सीमा क्या है $\ell$ बर्स्ट ों का जिन्हें हम किसी का उपयोग करके ठीक कर सकते हैं $(n,k)$ कोड? निम्नलिखित प्रमेय इस प्रश्न का प्रारंभिक उत्तर प्रदान करता है:

Theorem (Burst error correction ability) — किसी की भी बर्स्ट त्रुटि सुधार क्षमता $(n,k)$ कोड संतुष्ट करता है $\ell \leqslant n-k-\log _{q}(n-\ell )+2$

Proof

पहले हम देखते हैं कि एक कोड लंबाई के सभी विस्फोटों को ठीक कर सकता है $\leqslant \ell$ यदि और केवल यदि कोई भी दो कोडवर्ड लंबाई के दो बर्स्ट के योग से भिन्न न हों $\leqslant \ell .$ मान लीजिए कि दो कोडवर्ड $\mathbf {c} _{1}$ और $\mathbf {c} _{2}$ विस्फोट से भिन्न $\mathbf {b} _{1}$ and $\mathbf {b} _{2}$ लम्बाई का $\leqslant \ell$ each.प्राप्त करने पर $\mathbf {c} _{1}$ विस्फोट से मारा गया $\mathbf {b} _{1}$ , हम इसकी व्याख्या ऐसे कर सकते हैं जैसे कि यह था $\mathbf {c} _{2}$ विस्फोट से मारा गया $-\mathbf {b} _{2}$ . हम यह नहीं बता सकते कि प्रेषित शब्द है या नहीं $\mathbf {c} _{1}$ or $\mathbf {c} _{2}$ . अब, मान लीजिए कि प्रत्येक दो कोडवर्ड की लंबाई दो से अधिक भिन्न होती है $\ell$ . तदपि प्रेषित कोडवर्ड $\mathbf {c} _{1}$ लम्बाई के विस्फोट से मारा जाता है $\ell$ , यह किसी अन्य कोडवर्ड की तरह नहीं दिखने वाला है जो एक और विस्फोट से प्रभावित हुआ है. For each codeword $\mathbf {c} ,$ मान लीजिये $B(\mathbf {c} )$ से भिन्न सभी शब्दों के समुच्चय को निरूपित करें $\mathbf {c}$ bआप लंबाई का एक विस्फोट $\leqslant \ell .$ नोटिस जो $B(\mathbf {c} )$ सम्मिलित $\mathbf {c}$ अपने आप। उपरोक्त अवलोकन से, हम जानते हैं कि दो भिन्न-भिन्न कोडवर्ड के लिए $\mathbf {c} _{i}$ और $\mathbf {c} _{j},B(\mathbf {c} _{i})$ और $B(\mathbf {c} _{j})$ असंयुक्त हैं. अपने पास $q^{k}$ कोडवर्ड इसलिए हम ऐसा कह सकते हैं $q^{k}|B(\mathbf {c} )|\leqslant q^{n}$ . इसके अतिरिक्त, हमारे पास है $(n-\ell )q^{\ell -2}\leqslant |B(\mathbf {c} )|$ . पश्चात वाली असमानता को पहले वाली असमानता से जोड़कर, फिर आधार लेकर $q$ लघुगणक और पुनर्व्यवस्थित करने पर, हमें उपरोक्त प्रमेय प्राप्त होता है।

रीगर बाउंड द्वारा मजबूत परिणाम दिया गया है:

Theorem (Rieger bound) — यदि $\ell$ की बर्स्ट त्रुटि सुधार करने की क्षमता है $(n,k)$ रैखिक ब्लॉक कोड, फिर $2\ell \leqslant n-k$ .

Proof

कोई भी रैखिक कोड जो लंबाई के किसी भी विस्फोट पैटर्न को सही कर सकता है $\leqslant \ell$ लम्बाई का विस्फोट नहीं हो सकता $\leqslant 2\ell$ एक कोडवर्ड के रूप में. यदि इसकी लम्बाई में वृद्धि होती $\leqslant 2\ell$ एक कोडवर्ड के रूप में, फिर लंबाई का विस्फोट $\ell$ कोडवर्ड को लंबाई के बर्स्ट पैटर्न में बदल सकता है $\ell$ , जिसे लंबाई की बर्स्ट त्रुटि बनाकर भी प्राप्त किया जा सकता है $\ell$ बिल्कुल शून्य कोडवर्ड में. यदि सदिश पहले शून्येतर हैं $2\ell$ प्रतीकों, तो सदिश एक सरणी के विभिन्न उपसमूहों से होने चाहिए ताकि उनका अंतर लंबाई के फटने का कोडवर्ड न हो $2\ell$ . इस शर्त को सुनिश्चित करते हुए, ऐसे उपसमुच्चय की संख्या कम से कम सदिश की संख्या के समान्तर है। इस प्रकार, उपसमुच्चय की संख्या कम से कम होगी $q^{2\ell }$ .इसलिए, हमारे पास कम से कम है $2\ell$ अलग-अलग प्रतीक, अन्यथा, ऐसे दो बहुपदों का अंतर एक कोडवर्ड होगा जो लंबाई के दो विस्फोटों का योग है $\leqslant \ell .$ इस प्रकार, यह रीगर बाउंड सिद्ध होता है।

परिभाषा। उपरोक्त रीगर सीमा को प्राप्त करने वाले रैखिक बर्स्ट-त्रुटि-सुधार करने वाले कोड को इष्टतम बर्स्ट-त्रुटि-सुधार करने वाला कोड कहा जाता है।

बर्स्ट त्रुटि सुधार पर आगे की सीमाएं

एकाधिक चरणबद्ध-बर्स्ट सुधार (एमपीबीसी) के लिए रैखिक ब्लॉक कोड की प्राप्त कोड दर पर से अधिक ऊपरी सीमा होती है। ऐसी सीमा प्रत्येक उपब्लॉक के अंदर अधिकतम सुधार योग्य चक्रीय बर्स्ट लंबाई तक सीमित है, या समकक्ष रूप से प्रत्येक चरण-बर्स्ट के अंदर न्यूनतम त्रुटि मुक्त लंबाई या अंतराल पर बाधा है। यह सीमा, जब एकल बर्स्ट सुधार के लिए बाध्य के विशेष उपस्तिथियां में कम हो जाती है, अब्रामसन बाध्य (बर्स्ट -त्रुटि सुधार के लिए हैमिंग बाध्य का परिणाम) है जब चक्रीय बर्स्ट की लंबाई ब्लॉक लंबाई के आधे से कम होती है।^[3]

Theorem (number of bursts) — इसके लिए $1\leqslant \ell \leqslant {\tfrac {1}{2}}(n+1),$ एक द्विआधारी वर्णमाला पर, वहाँ हैं $n2^{\ell -1}+1$ लंबाई के सदिश $n$ जो लम्बाई के विस्फोट हैं $\leqslant \ell$ .^[1]

Proof

Since the burst length is $\leqslant {\tfrac {1}{2}}(n+1),$ there is a unique burst description associated with the burst. The burst can begin at any of the $n$ positions of the pattern. Each pattern begins with $1$ and contain a length of $\ell$ . We can think of it as the set of all strings that begin with $1$ and have length $\ell$ . Thus, there are a total of $2^{\ell -1}$ possible such patterns, and a total of $n2^{\ell -1}$ bursts of length $\leqslant \ell .$ If we include the all-zero burst, we have $n2^{\ell -1}+1$ vectors representing bursts of length $\leqslant \ell .$

Theorem (Bound on the number of codewords) — If $1\leqslant \ell \leqslant {\tfrac {1}{2}}(n+1),$ a binary $\ell$ -burst error correcting code has at most $2^{n}/(n2^{\ell -1}+1)$ codewords.

Proof

Since $\ell \leqslant {\tfrac {1}{2}}(n+1)$ , we know that there are $n2^{\ell -1}+1$ bursts of length $\leqslant \ell$ . Say the code has $M$ codewords, then there are $Mn2^{\ell -1}$ codewords that differ from a codeword by a burst of length $\leqslant \ell$ . Each of the $M$ words must be distinct, otherwise the code would have distance $<1$ . Therefore, $M(2^{\ell -1}+1)\leqslant 2^{n}$ implies $M\leqslant 2^{n}/(n2^{\ell -1}+1).$

Theorem (Abramson's bounds) — If $1\leqslant \ell \leqslant {\tfrac {1}{2}}(n+1)$ is a binary linear $(n,k),\ell$ -burst error correcting code, its block-length must satisfy:

n\leqslant 2^{n-k-\ell +1}-1.

Proof

For a linear $(n,k)$ code, there are $2^{k}$ codewords. By our previous result, we know that

2^{k}\leqslant {\frac {2^{n}}{n2^{\ell -1}+1}}.

Isolating

n

, we get

n\leqslant 2^{n-k-\ell +1}-2^{-\ell +1}

. Since

\ell \geqslant 1

and

n

must be an integer, we have

n\leqslant 2^{n-k-\ell +1}-1

.

टिप्पणी। $r=n-k$ कोड की अतिरेक कहा जाता है और अब्रामसन की सीमा के लिए वैकल्पिक सूत्रीकरण में है $r\geqslant \lceil \log _{2}(n+1)\rceil +\ell -1.$

अग्नि कोड^[3]^[4]^[5]

जबकि सामान्यतः चक्रीय कोड बर्स्ट त्रुटियों का पता लगाने के लिए शक्तिशाली उपकरण होते हैं, अब हम फायर कोड नामक बाइनरी चक्रीय कोड के परिवार पर विचार करते हैं, जिसमें अच्छी एकल बर्स्ट त्रुटि सुधार क्षमताएं होती हैं। एकल बर्स्ट से, लंबाई के बारे में कहें $\ell$ , हमारा मतलब है कि प्राप्त कोडवर्ड में मौजूद सभी त्रुटियां निश्चित अवधि के अंदर होती हैं $\ell$ अंक.

होने देना $p(x)$ डिग्री का अपरिवर्तनीय बहुपद बनें $m$ ऊपर $\mathbb {F} _{2}$ , और जाने $p$ की अवधि हो $p(x)$ . की अवधि $p(x)$ , और वास्तव में किसी भी बहुपद को सबसे कम धनात्मक पूर्णांक के रूप में परिभाषित किया गया है $r$ ऐसा है कि $p(x)|x^{r}-1.$ होने देना $\ell$ सकारात्मक पूर्णांक संतोषजनक हो $\ell \leqslant m$ और $2\ell -1$ से विभाज्य नहीं है $p$ , जहाँ $p$ की अवधि है $p(x)$ . अग्नि संहिता को परिभाषित करें $G$ निम्नलिखित जनरेटर बहुपद द्वारा:

g(x)=\left(x^{2\ell -1}+1\right)p(x).

हम वो दिखाएंगे

G

\ell

-बर्स्ट -त्रुटि सुधार कोड।

Lemma 1 — $\gcd \left(p(x),x^{2\ell -1}+1\right)=1.$

Proof

Let $d(x)$ be the greatest common divisor of the two polynomials. Since $p(x)$ is irreducible, $\deg(d(x))=0$ or $\deg(p(x))$ . Assume $\deg(d(x))\neq 0,$ then $p(x)=cd(x)$ for some constant $c$ . But, $(1/c)p(x)$ is a divisor of $x^{2\ell -1}+1$ since $d(x)$ is a divisor of $x^{2\ell -1}+1$ . But this contradicts our assumption that $p(x)$ does not divide $x^{2\ell -1}+1.$ Thus, $\deg(d(x))=0,$ proving the lemma.

Lemma 2 — If $p(x)$ is a polynomial of period $p$ , then $p(x)|x^{k}-1$ if and only if $p|k.$

Proof

If $p|k$ , then $x^{k}-1=(x^{p}-1)(1+x^{p}+x^{2p}+\dots +x^{k/p})$ . Thus, $p(x)|x^{k}-1.$

Now suppose $p(x)|x^{k}-1$ . Then, $k\geqslant p$ . We show that $k$ is divisible by $p$ by induction on $k$ . The base case $k=p$ follows. Therefore, assume $k>p$ . We know that $p(x)$ divides both (since it has period $p$ )

x^{p}-1=(x-1)\left(1+x+\dots +x^{p-1}\right)\quad {\text{and}}\quad x^{k}-1=(x-1)\left(1+x+\dots +x^{k-1}\right).

But

p(x)

is irreducible, therefore it must divide both

(1+x+\dots +x^{p-1})

and

(1+x+\dots +x^{k-1})

; thus, it also divides the difference of the last two polynomials,

x^{p}(1+x+\dots +x^{p-k-1})

. Then, it follows that

p(x)

divides

(1+x+\cdots +x^{p-k-1})

. Finally, it also divides:

x^{k-p}-1=(x-1)(1+x+\dots +x^{p-k-1})

. By the induction hypothesis,

p|k-p

, then

p|k

.

A corollary to Lemma 2 is that since $p(x)=x^{p}-1$ has period $p$ , then $p(x)$ divides $x^{k}-1$ if and only if $p|k$ .

Theorem — The Fire Code is $\ell$ -burst error correcting^[4]^[5]

यदि हम यह दिखा सकें कि लंबाई के सभी बर्स्ट $\ell$ या कम भिन्न -भिन्न सह समुच्चय में होते हैं, हम उन्हें कोसेट नेता के रूप में उपयोग कर सकते हैं जो सुधार योग्य त्रुटि पैटर्न बनाते हैं। कारण सरल है: हम जानते हैं कि प्रत्येक कोसेट में अद्वितीय सिंड्रोम डिकोडिंग जुड़ी होती है, और यदि भिन्न -भिन्न लंबाई के सभी बर्स्ट भिन्न -भिन्न कोसेट में होते हैं, तो सभी में अद्वितीय सिंड्रोम होते हैं, जिससे त्रुटि सुधार की सुविधा मिलती है।

प्रमेय का प्रमाण

होने देना $x^{i}a(x)$ और $x^{j}b(x)$ डिग्री वाले बहुपद बनें $\ell _{1}-1$ और $\ell _{2}-1$ , लंबाई के बर्स्ट का प्रतिनिधित्व करता है $\ell _{1}$ और $\ell _{2}$ क्रमशः साथ $\ell _{1},\ell _{2}\leqslant \ell .$ पूर्णांक $i,j$ बर्स्ट की प्रारंभिक स्थिति का प्रतिनिधित्व करते हैं, और कोड की ब्लॉक लंबाई से कम होते हैं। विरोधाभास के लिए, यह मान लें $x^{i}a(x)$ और $x^{j}b(x)$ ही कोसेट में हैं. तब, $v(x)=x^{i}a(x)+x^{j}b(x)$ वैध कोडवर्ड है (क्योंकि दोनों पद ही कोसेट में हैं)। व्यापकता की हानि के बिना, चुनें $i\leqslant j$ . विभाजन प्रमेय द्वारा हम लिख सकते हैं: $j-i=g(2\ell -1)+r,$ पूर्णांकों के लिए $g$ और $r,0\leqslant r<2\ell -1$ . हम बहुपद को फिर से लिखते हैं $v(x)$ निम्नलिखित नुसार:

v(x)=x^{i}a(x)+x^{i+g(2\ell -1)+r}=x^{i}a(x)+x^{i+g(2\ell -1)+r}+2x^{i+r}b(x)=x^{i}\left(a(x)+x^{b}b(x)\right)+x^{i+r}b(x)\left(x^{g(2\ell -1)}+1\right)

ध्यान दें कि दूसरे हेरफेर में, हमने शब्द प्रस्तुत किया

2x^{i+r}b(x)

. हमें ऐसा करने की अनुमति है, क्योंकि फायर कोड चालू हैं

\mathbb {F} _{2}

. हमारी धारणा से,

v(x)

वैध कोडवर्ड है, और इस प्रकार, इसका गुणज होना चाहिए

g(x)

. जैसा कि पहले उल्लेख किया गया है, के कारकों के पश्चात से

g(x)

अपेक्षाकृत प्रमुख हैं,

v(x)

से विभाज्य होना चाहिए

x^{2\ell -1}+1

. के लिए व्युत्पन्न अंतिम अभिव्यक्ति को करीब से देख रहे हैं

v(x)

हम उस पर ध्यान देते हैं

x^{g(2\ell -1)}+1

से विभाज्य है

x^{2\ell -1}+1

(लेम्मा 2 के परिणाम से)। इसलिए,

a(x)+x^{b}b(x)

या तो विभाज्य है

x^{2\ell -1}+1

या है

0

. विभाजन प्रमेय को दोबारा लागू करने पर, हम देखते हैं कि बहुपद मौजूद है

d(x)

डिग्री के साथ

\delta

ऐसा है कि:

a(x)+x^{b}b(x)=d(x)(x^{2\ell -1}+1)

तब हम लिख सकते हैं:

{\begin{aligned}\delta +2\ell -1&=\deg \left(d(x)\left(x^{2\ell -1}+1\right)\right)\\&=\deg \left(a(x)+x^{b}b(x)\right)\\&=\deg \left(x^{b}b(x)\right)&&\deg(a(x))=\ell _{1}-1<2\ell -1\\&=b+\ell _{2}-1\end{aligned}}

दोनों पक्षों की डिग्री को बराबर करने से हमें प्राप्त होता है

b=2\ell -\ell _{2}+\delta .

तब से

\ell _{1},\ell _{2}\leqslant \ell

हम निष्कर्ष निकाल सकते हैं

b\geqslant \ell +\delta ,

जो ये दर्शाता हे

b>\ell -1

और

b>\delta

. ध्यान दें कि विस्तार में:

a(x)+x^{b}b(x)=1+a_{1}x+a_{2}x^{2}+\dots +x^{\ell _{1}-1}+x^{b}\left(1+b_{1}x+b_{2}x^{2}+\dots +x^{\ell _{2}-1}\right).

शब्द

x^{b}

प्रकट होता है, लेकिन तब से

\delta <b<2\ell -1

, परिणामी अभिव्यक्ति

d(x)(x^{2\ell -1}+1)

सम्मिलित नहीं है

x^{b}

, इसलिए

d(x)=0

और पश्चात में

a(x)+x^{b}b(x)=0.

इसके लिए इसकी आवश्यकता है

b=0

, और

a(x)=b(x)

. हम अपने विभाजन को और संशोधित कर सकते हैं

j-i

द्वारा

g(2\ell -1)

प्रतिबिंबित करना

b=0,

वह है

j-i=g(2\ell -1)

. वापस प्रतिस्थापित करना

v(x)

हमें देता है,

v(x)=x^{i}b(x)\left(x^{j-1}+1\right).

तब से

\deg(b(x))=\ell _{2}-1<\ell

, अपने पास

\deg(b(x))<\deg(p(x))=m

. लेकिन

p(x)

इसलिए, अपरिवर्तनीय है

b(x)

और

p(x)

अपेक्षाकृत प्रधान होना चाहिए। तब से

v(x)

कोडवर्ड है,

x^{j-1}+1

से विभाज्य होना चाहिए

p(x)

, क्योंकि इसे विभाज्य नहीं किया जा सकता

x^{2\ell -1}+1

. इसलिए,

j-i

का गुणज होना चाहिए

p

. लेकिन इसका गुणज भी होना चाहिए

2\ell -1

, जिसका अर्थ है कि यह का गुणज होना चाहिए

n={\text{lcm}}(2\ell -1,p)

लेकिन वह बिल्कुल कोड की ब्लॉक-लंबाई है। इसलिए,

j-i

का गुणज नहीं हो सकता

n

चूँकि वे दोनों इससे कम हैं

n

. इस प्रकार, हमारी धारणा

v(x)

कोडवर्ड होना गलत है, और इसलिए

x^{i}a(x)

और

x^{j}b(x)

अद्वितीय सिंड्रोम के साथ भिन्न -भिन्न कोसेट में हैं, और इसलिए सुधार योग्य हैं।

उदाहरण: फायर कोड को सही करने में 5-बर्स्ट त्रुटि

उपरोक्त अनुभाग में प्रस्तुत सिद्धांत के साथ, के निर्माण पर विचार करें $5$ -फ़ायर कोड को सही करने में बर्स्ट त्रुटि। याद रखें कि फायर कोड बनाने के लिए, हमें अपरिवर्तनीय बहुपद की आवश्यकता होती है $p(x)$ , पूर्णांक $\ell$ , हमारे कोड की बर्स्ट त्रुटि सुधार क्षमता का प्रतिनिधित्व करता है, और हमें उस संपत्ति को संतुष्ट करने की आवश्यकता है

  $2\ell -1$  की अवधि से विभाज्य नहीं है  $p(x)$ . इन आवश्यकताओं को ध्यान में रखते हुए, अपरिवर्तनीय बहुपद पर विचार करें  $p(x)=1+x^{2}+x^{5}$ , और जाने  $\ell =5$ . तब से  $p(x)$  आदिम बहुपद है, इसका आवर्त है  $2^{5}-1=31$ . हम इसकी पुष्टि करते हैं  $2\ell -1=9$  से विभाज्य नहीं है  $31$ . इस प्रकार,

g(x)=(x^{9}+1)\left(1+x^{2}+x^{5}\right)=1+x^{2}+x^{5}+x^{9}+x^{11}+x^{14}

एक फायर कोड जनरेटर है. हम न्यूनतम समापवर्त्य का मूल्यांकन करके कोड की ब्लॉक-लंबाई की गणना कर सकते हैं

p

और

2\ell -1

. दूसरे शब्दों में,

n={\text{lcm}}(9,31)=279

. इस प्रकार, उपरोक्त फायर कोड चक्रीय कोड है जो लंबाई के किसी भी बर्स्ट को ठीक करने में सक्षम है

5

या कम।

बाइनरी रीड-सोलोमन कोड

कोड के कुछ परिवार, जैसे रीड-सोलोमन त्रुटि सुधार|रीड-सोलोमन, बाइनरी से बड़े वर्णमाला आकार पर काम करते हैं। यह संपत्ति ऐसे कोड को शक्तिशाली बर्स्ट त्रुटि सुधार क्षमताएं प्रदान करती है। उस कोड पर विचार करें जिस पर काम चल रहा है $\mathbb {F} _{2^{m}}$ . वर्णमाला के प्रत्येक प्रतीक को किसके द्वारा दर्शाया जा सकता है? $m$ बिट्स अगर $C$ $(n,k)$ रीड-सोलोमन कोड ख़त्म $\mathbb {F} _{2^{m}}$ , हम सोच सकते हैं $C$ के रूप में $[mn,mk]_{2}$ कोड ख़त्म $\mathbb {F} _{2}$ .

बर्स्ट त्रुटि सुधार के लिए ऐसे कोड शक्तिशाली होने का कारण यह है कि प्रत्येक प्रतीक का प्रतिनिधित्व किया जाता है $m$ बिट्स, और सामान्यतः , यह अप्रासंगिक है कि उनमें से कितने हैं $m$ बिट्स ग़लत हैं; चाहे बिट, या सभी $m$ बिट्स में त्रुटियाँ हैं, डिकोडिंग परिप्रेक्ष्य से यह अभी भी एकल प्रतीक त्रुटि है। दूसरे शब्दों में, चूंकि क्लस्टर में बर्स्ट त्रुटियां होती हैं, इसलिए एकल प्रतीक त्रुटि में अनेक बाइनरी त्रुटियों के योगदान की प्रबल संभावना होती है।

ध्यान दें कि बर्स्ट $(m+1)$ त्रुटियाँ अधिकतम प्रभावित कर सकती हैं $2$ प्रतीकों, और का बर्स्ट $2m+1$ ज्यादा से ज्यादा प्रभावित कर सकता है $3$ प्रतीक. फिर, बर्स्ट $tm+1$ ज्यादा से ज्यादा प्रभावित कर सकता है $t+1$ प्रतीक; इसका तात्पर्य यह है कि ए $t$ -प्रतीक-त्रुटि सुधार कोड अधिकतम लंबाई के बर्स्ट को ठीक कर सकता है $(t-1)m+1$ .

सामान्यतः , ए $t$ -रीड-सोलोमन कोड को सही करने में त्रुटि $\mathbb {F} _{2^{m}}$ के किसी भी संयोजन को ठीक कर सकता है

{\frac {t}{1+\lfloor (l+m-2)/m\rfloor }}

या लंबाई के कम बर्स्ट

l

, सही करने में सक्षम होने के शीर्ष पर

t

-यादृच्छिक सबसे खराब स्थिति त्रुटियाँ।

बाइनरी आरएस कोड का उदाहरण

होने देना $G$ हो $[255,223,33]$ आरएस कोड ख़त्म $\mathbb {F} _{2^{8}}$ . इस कोड को नासा ने अपने कैसिनी-हुय्गेंस अंतरिक्ष यान में नियोजित किया था।^[6] यह ठीक करने में सक्षम है $\lfloor 33/2\rfloor =16$ प्रतीक त्रुटियाँ. अब हम बाइनरी आरएस कोड बनाते हैं $G'$ से $G$ . प्रत्येक चिन्ह का प्रयोग करके लिखा जायेगा $\lceil \log _{2}(255)\rceil =8$ बिट्स इसलिए, बाइनरी आरएस कोड होगा $[2040,1784,33]_{2}$ इसके पैरामीटर के रूप में। यह लंबाई के किसी भी बर्स्ट को ठीक करने में सक्षम है $l=121$ .

इंटरलीव्ड कोड

इंटरलीविंग का उपयोग कनवल्शनल कोड को यादृच्छिक त्रुटि सुधारकों से बर्स्ट त्रुटि सुधारकों में परिवर्तित करने के लिए किया जाता है। इंटरलीव्ड कोड के उपयोग के पीछे मूल विचार ट्रांसमीटर पर प्रतीकों को मिलाना है। इससे प्राप्त त्रुटियों के बर्स्ट ों का यादृच्छिककरण होता है जो निकट स्थित होते हैं और फिर हम यादृच्छिक चैनल के लिए विश्लेषण लागू कर सकते हैं। इस प्रकार, ट्रांसमीटर पर इंटरलीवर द्वारा किया जाने वाला मुख्य कार्य इनपुट प्रतीक अनुक्रम को बदलना है। रिसीवर पर, डिइंटरलीवर ट्रांसमीटर पर मूल अपरिवर्तित अनुक्रम को वापस पाने के लिए प्राप्त अनुक्रम को बदल देगा।

इंटरलीवर की बर्स्ट त्रुटि सुधार क्षमता

पंक्ति और स्तंभ-प्रमुख क्रम का चित्रण

Theorem — If the burst error correcting ability of some code is $\ell ,$ then the burst error correcting ability of its $\lambda$ -way interleave is $\lambda \ell .$

Proof

Suppose that we have an $(n,k)$ code that can correct all bursts of length $\leqslant \ell .$ Interleaving can provide us with a $(\lambda n,\lambda k)$ code that can correct all bursts of length $\leqslant \lambda \ell ,$ for any given $\lambda$ . If we want to encode a message of an arbitrary length using interleaving, first we divide it into blocks of length $\lambda k$ . We write the $\lambda k$ entries of each block into a $\lambda \times k$ matrix using row-major order. Then, we encode each row using the $(n,k)$ code. What we will get is a $\lambda \times n$ matrix. Now, this matrix is read out and transmitted in column-major order. The trick is that if there occurs a burst of length $h$ in the transmitted word, then each row will contain approximately ${\tfrac {h}{\lambda }}$ consecutive errors (More specifically, each row will contain a burst of length at least $\lfloor {\tfrac {h}{\lambda }}\rfloor$ and at most $\lceil {\tfrac {h}{\lambda }}\rceil$ ). If $h\leqslant \lambda \ell ,$ then ${\tfrac {h}{\lambda }}\leqslant \ell$ and the $(n,k)$ code can correct each row. Therefore, the interleaved $(\lambda n,\lambda k)$ code can correct the burst of length $h$ . Conversely, if $h>\lambda \ell ,$ then at least one row will contain more than ${\tfrac {h}{\lambda }}$ consecutive errors, and the $(n,k)$ code might fail to correct them. Therefore, the error correcting ability of the interleaved $(\lambda n,\lambda k)$ code is exactly $\lambda \ell .$ The BEC efficiency of the interleaved code remains the same as the original $(n,k)$ code. This is true because:

{\frac {2\lambda \ell }{\lambda n-\lambda k}}={\frac {2\ell }{n-k}}

ब्लॉक इंटरलीवर

नीचे दिया गया चित्र 4 बाय 3 इंटरलीवर दिखाता है।

ब्लॉक इंटरलीवर का उदाहरण

उपरोक्त इंटरलीवर को ब्लॉक इंटरलीवर कहा जाता है। यहां, इनपुट प्रतीकों को पंक्तियों में क्रमिक रूप से लिखा जाता है और आउटपुट प्रतीकों को कॉलम को क्रमिक रूप से पढ़कर प्राप्त किया जाता है। इस प्रकार, यह इस रूप में है $M\times N$ सरणी. आम तौर पर, $N$ कोडवर्ड की लंबाई है.

ब्लॉक इंटरलीवर की क्षमता: के लिए $M\times N$ ब्लॉक इंटरलीवर और लंबाई का फटना $\ell ,$ त्रुटियों की संख्या की ऊपरी सीमा है ${\tfrac {\ell }{M}}.$ यह इस तथ्य से स्पष्ट है कि हम आउटपुट को कॉलम के अनुसार पढ़ रहे हैं और पंक्तियों की संख्या है $M$ . उपरोक्त प्रमेय के अनुसार त्रुटि सुधार क्षमता तक $t,$ अनुमत अधिकतम बर्स्ट लंबाई है $Mt.$ की बर्स्ट लंबाई के लिए $Mt+1$ , डिकोडर विफल हो सकता है।

ब्लॉक इंटरलीवर की दक्षता ( $\gamma$ ): यह बर्स्ट लंबाई का अनुपात लेकर पाया जाता है जहां डिकोडर इंटरलीवर मेमोरी में विफल हो सकता है। इस प्रकार, हम सूत्रीकरण कर सकते हैं $\gamma$ जैसा

\gamma ={\frac {Mt+1}{MN}}\approx {\frac {t}{N}}.

ब्लॉक इंटरलीवर की कमियाँ: जैसा कि चित्र से स्पष्ट है, कॉलम क्रमिक रूप से पढ़े जाते हैं, रिसीवर पूर्ण संदेश प्राप्त करने के पश्चात ही एकल पंक्ति की व्याख्या कर सकता है, उससे पहले नहीं। साथ ही, प्राप्त प्रतीकों को संग्रहीत करने के लिए रिसीवर को काफी मात्रा में मेमोरी की आवश्यकता होती है और उसे पूरा संदेश संग्रहीत करना होता है। इस प्रकार, ये कारक दो कमियों को जन्म देते हैं, है विलंबता और दूसरा है भंडारण (काफी बड़ी मात्रा में मेमोरी)। नीचे वर्णित कनवल्शनल इंटरलीवर का उपयोग करके इन कमियों से बचा जा सकता है।

कन्वेंशनल इंटरलीवर

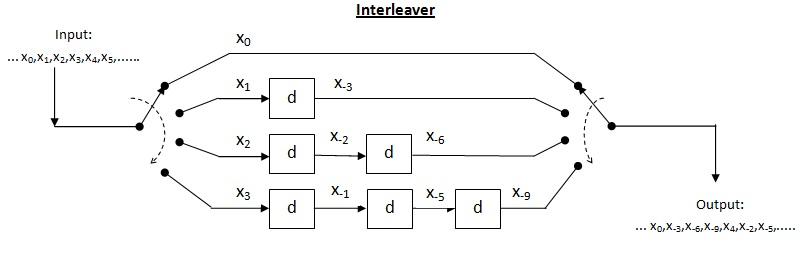
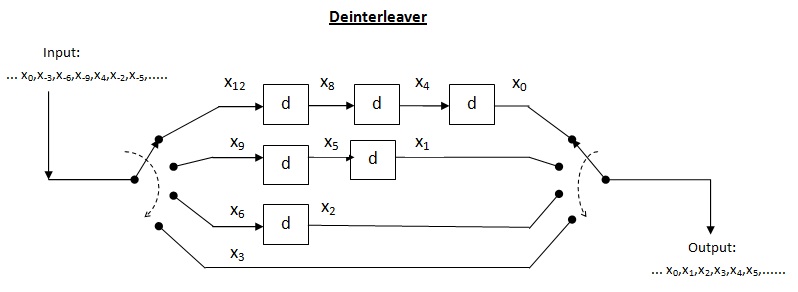
क्रॉस इंटरलीवर प्रकार का मल्टीप्लेक्सर-डेमल्टीप्लेक्सर सिस्टम है। इस प्रणाली में, लंबाई को उत्तरोत्तर बढ़ाने के लिए विलंब रेखाओं का उपयोग किया जाता है। विलंब रेखा मूल रूप से इलेक्ट्रॉनिक सर्किट है जिसका उपयोग सिग्नल को निश्चित समय अवधि तक विलंबित करने के लिए किया जाता है। होने देना $n$ विलंब रेखाओं की संख्या हो और $d$ प्रत्येक विलंब रेखा द्वारा प्रस्तुत प्रतीकों की संख्या हो। इस प्रकार, निरंतर इनपुट के बीच भिन्न ाव = $nd$ प्रतीक. कोडवर्ड की लंबाई बताएं $\leqslant n.$ इस प्रकार, इनपुट कोडवर्ड में प्रत्येक प्रतीक भिन्न विलंब रेखा पर होगा। लंबाई की बर्स्ट त्रुटि दें $\ell$ घटित होना। चूँकि क्रमागत प्रतीकों के बीच पृथक्करण है $nd,$ डीइंटरलीव्ड आउटपुट में त्रुटियों की संख्या हो सकती है ${\tfrac {\ell }{nd+1}}.$ उपरोक्त प्रमेय के अनुसार, त्रुटि सुधार क्षमता तक $t$ , अनुमत अधिकतम बर्स्ट लंबाई है $(nd+1)(t-1).$ की बर्स्ट लंबाई के लिए $(nd+1)(t-1)+1,$ डिकोडर विफल हो सकता है.

कन्वेल्यूशनल इंटरलीवर का उदाहरण

डिइंटरलीवर का उदाहरण

क्रॉस इंटरलीवर की दक्षता ( $\gamma$ ): यह बर्स्ट लंबाई के अनुपात को लेकर पाया जाता है जहां डिकोडर इंटरलीवर मेमोरी में विफल हो सकता है। इस उपस्तिथियां में, इंटरलीवर की मेमोरी की गणना इस प्रकार की जा सकती है

(0+1+2+3+\cdots +(n-1))d={\frac {n(n-1)}{2}}d.

इस प्रकार, हम सूत्रीकरण कर सकते हैं

\gamma

निम्नलिखित नुसार:

\gamma ={\frac {(nd+1)(t-1)+1}{{\frac {n(n-1)}{2}}d}}.

क्रॉस इंटरलीवर का प्रदर्शन: जैसा कि उपरोक्त इंटरलीवर चित्र में दिखाया गया है, आउटपुट प्रत्येक विलंब रेखा के अंत में उत्पन्न विकर्ण प्रतीकों के अलावा कुछ नहीं है। इस उपस्तिथियां में, जब इनपुट मल्टीप्लेक्सर स्विच लगभग आधा स्विचिंग पूरा कर लेता है, तो हम रिसीवर पर पहली पंक्ति पढ़ सकते हैं। इस प्रकार, हमें पहली पंक्ति को पढ़ने के लिए रिसीवर पर अधिकतम लगभग आधा संदेश संग्रहीत करने की आवश्यकता है। इससे भंडारण की आवश्यकता आधे से भी कम हो जाती है। चूँकि अब पहली पंक्ति को पढ़ने के लिए केवल आधे संदेश की आवश्यकता होती है, विलंबता भी आधी कम हो जाती है जो ब्लॉक इंटरलीवर की तुलना में अच्छा सुधार है। इस प्रकार, कुल इंटरलीवर मेमोरी ट्रांसमीटर और रिसीवर के बीच विभाजित हो जाती है।

अनुप्रयोग

कॉम्पैक्ट डिस्क

त्रुटि सुधार कोड के बिना, डिजिटल ऑडियो तकनीकी रूप से संभव नहीं होगा।^[7] रीड-सोलोमन त्रुटि सुधार|रीड-सोलोमन कोड एकल बिट त्रुटि वाले दूषित प्रतीक को उतनी ही आसानी से ठीक कर सकते हैं जितनी आसानी से यह सभी बिट गलत वाले प्रतीक को ठीक कर सकता है। यह आरएस कोड को बर्स्ट त्रुटियों को ठीक करने के लिए विशेष रूप से उपयुक्त बनाता है।^[5]अब तक, आरएस कोड का सबसे आम अनुप्रयोग कॉम्पैक्ट डिस्क में है। आरएस कोड द्वारा प्रदान की गई बुनियादी त्रुटि सुधार के अलावा, डिस्क पर खरोंच के कारण होने वाली बर्स्ट त्रुटियों से सुरक्षा क्रॉस इंटरलीवर द्वारा प्रदान की जाती है।^[3]

वर्तमान कॉम्पैक्ट डिस्क डिजिटल ऑडियो सिस्टम नीदरलैंड के एन. वी. फिलिप्स और जापान के सोनी कॉरपोरेशन (1979 में हस्ताक्षरित समझौते) द्वारा विकसित किया गया था।

एक कॉम्पैक्ट डिस्क में स्पष्ट प्लास्टिक कोटिंग के साथ लेपित 120 मिमी एल्युमिनाइज्ड डिस्क होती है, जिसमें सर्पिल ट्रैक होता है, जिसकी लंबाई लगभग 5 किमी होती है, जिसे ~ 0.8 माइक्रोमीटर तरंग दैर्ध्य के लेजर द्वारा ~ 1.25 मीटर/सेकेंड की निरंतर गति से ऑप्टिकली स्कैन किया जाता है। इस स्थिर गति को प्राप्त करने के लिए, ट्रैक के आंतरिक भाग पर स्कैन करते समय डिस्क का घुमाव ~8 रेव/सेकेंड से लेकर बाहरी भाग पर ~3.5 रेव/सेकेंड तक भिन्न होता है। गड्ढे और भूमि अवसाद (0.12 माइक्रोमीटर गहरे) और समतल खंड हैं जो ट्रैक के साथ बाइनरी डेटा बनाते हैं (0.6 माइक्रोमीटर चौड़ाई)।^[8] सीडी प्रक्रिया को निम्नलिखित उप-प्रक्रियाओं के अनुक्रम के रूप में समझा जा सकता है:

सिग्नल के स्रोत का चैनल एन्कोडिंग
मास्टर डिस्क तैयार करने, उपयोगकर्ता डिस्क का उत्पादन करने और खेलते समय उपयोगकर्ता डिस्क पर एम्बेडेड संकेतों को महसूस करने की यांत्रिक उप-प्रक्रियाएँ - चैनल
उपयोगकर्ता डिस्क से प्राप्त संकेतों को डिकोड करना

यह प्रक्रिया बर्स्ट त्रुटियों और यादृच्छिक त्रुटियों दोनों के अधीन है।^[7]बर्स्ट त्रुटियों में डिस्क सामग्री (एल्यूमीनियम प्रतिबिंबित फिल्म के दोष, पारदर्शी डिस्क सामग्री का खराब प्रतिबिंबित सूचकांक), डिस्क उत्पादन (डिस्क बनाने और डिस्क काटने आदि के दौरान दोष), डिस्क हैंडलिंग (स्क्रैच - आम तौर पर पतली, रेडियल और रिकॉर्डिंग की दिशा में ऑर्थोगोनल) और प्ले-बैक तंत्र में भिन्नताएं सम्मिलित हैं। यादृच्छिक त्रुटियों में पुनर्निर्मित सिग्नल तरंग की घबराहट और सिग्नल में हस्तक्षेप के कारण होने वाली त्रुटियां सम्मिलित हैं। सीआईआरसी (क्रॉस-इंटरलीव्ड रीड-सोलोमन कोडिंग|क्रॉस-इंटरलीव्ड रीड-सोलोमन कोड) सीडी प्रक्रिया में त्रुटि का पता लगाने और सुधार का आधार है। यह क्रमिक रूप से 3,500 बिट्स (सीडी सतह पर देखी गई लंबाई में 2.4 मिमी) तक त्रुटि बर्स्ट ों को ठीक करता है और 12,000 बिट्स (8.5 मिमी) तक त्रुटि बर्स्ट ों की भरपाई करता है जो मामूली खरोंच के कारण हो सकते हैं।

एन्कोडिंग: ध्वनि-तरंगों का नमूना लिया जाता है और ए/डी कनवर्टर द्वारा डिजिटल रूप में परिवर्तित किया जाता है। ध्वनि तरंग का नमूना आयाम के लिए लिया जाता है (44.1 kHz या 44,100 जोड़े पर, स्टीरियो ध्वनि के बाएँ और दाएँ चैनलों के लिए एक-एक)। उदाहरण पर आयाम को लंबाई 16 की बाइनरी स्ट्रिंग सौंपी गई है। इस प्रकार, प्रत्येक नमूना दो बाइनरी वैक्टर उत्पन्न करता है $\mathbb {F} _{2}^{16}$ या 4 $\mathbb {F} _{2}^{8}$ डेटा के बाइट्स. रिकॉर्ड की गई ध्वनि के प्रत्येक सेकंड में 44,100 × 32 = 1,411,200 बिट्स (176,400 बाइट्स) डेटा प्राप्त होता है।^[5]1.41 Mbit/s नमूना डेटा स्ट्रीम त्रुटि सुधार प्रणाली से होकर गुजरती है और अंततः 1.88 Mbit/s की स्ट्रीम में परिवर्तित हो जाती है।

एनकोडर के लिए इनपुट में 24 8-बिट प्रतीकों (ए/डी कनवर्टर से 12 16-बिट नमूने, बाएं और दाएं डेटा (ध्वनि) स्रोतों से 6 प्रत्येक) के इनपुट फ्रेम होते हैं। फ़्रेम का प्रतिनिधित्व किया जा सकता है $L_{1}R_{1}L_{2}R_{2}\ldots L_{6}R_{6}$ जहाँ $L_{i}$ और $R_{i}$ से बाएँ और दाएँ चैनल से बाइट्स हैं $i^{th}$ फ़्रेम का नमूना.

प्रारंभ में, बाइट्स को नए फ़्रेम बनाने के लिए क्रमपरिवर्तित किया जाता है $L_{1}L_{3}L_{5}R_{1}R_{3}R_{5}L_{2}L_{4}L_{6}R_{2}R_{4}R_{6}$ जहाँ $L_{i},R_{i}$ प्रतिनिधित्व करना $i$ -2 मध्यवर्ती फ़्रेमों के पश्चात फ़्रेम से बाएँ और दाएँ नमूने।

इसके पश्चात , इन 24 संदेश प्रतीकों को C2 (28,24,5) रीड-सोलोमन कोड का उपयोग करके एन्कोड किया गया है जो कि संक्षिप्त RS कोड है $\mathbb {F} _{256}$ . यह दो-त्रुटि-सुधार करने वाला है, न्यूनतम दूरी 5 का है। यह अतिरेक के 4 बाइट्स जोड़ता है, $P_{1}P_{2}$ नया फ्रेम बनाना: $L_{1}L_{3}L_{5}R_{1}R_{3}R_{5}P_{1}P_{2}L_{2}L_{4}L_{6}R_{2}R_{4}R_{6}$ . परिणामी 28-प्रतीक कोडवर्ड को (28.4) क्रॉस इंटरलीवर के माध्यम से पारित किया जाता है, जिससे 28 इंटरलीव्ड प्रतीक बन जाते हैं। फिर इन्हें C1 (32,28,5) RS कोड से गुजारा जाता है, जिसके परिणामस्वरूप 32 कोडित आउटपुट प्रतीकों के कोडवर्ड प्राप्त होते हैं। किसी कोडवर्ड के विषम संख्या वाले प्रतीकों को अगले कोडवर्ड के सम संख्या वाले प्रतीकों के साथ फिर से समूहीकृत किया जाता है ताकि किसी भी छोटे बर्स्ट को तोड़ा जा सके जो उपरोक्त 4-फ्रेम विलंब इंटरलीविंग के पश्चात भी मौजूद हो सकता है। इस प्रकार, प्रत्येक 24 इनपुट प्रतीकों के लिए 32 आउटपुट प्रतीक होंगे $R=24/32$ . अंत में नियंत्रण और प्रदर्शन जानकारी की बाइट जोड़ी जाती है।^[5]33 बाइट्स में से प्रत्येक को ईएफएम (आठ से चौदह मॉड्यूलेशन) के माध्यम से 17 बिट्स में परिवर्तित किया जाता है और 3 मर्ज बिट्स को जोड़ा जाता है। इसलिए, छह नमूनों के फ्रेम का परिणाम 33 बाइट्स × 17 बिट्स (561 बिट्स) होता है, जिसमें 24 सिंक्रोनाइज़ेशन बिट्स और 3 मर्जिंग बिट्स जोड़े जाते हैं, जिससे कुल 588 बिट्स प्राप्त होते हैं।

डिकोडिंग: सीडी प्लेयर (सीआईआरसी डिकोडर) 32 आउटपुट सिंबल डेटा स्ट्रीम प्राप्त करता है। यह धारा पहले डिकोडर D1 से होकर गुजरती है। डिकोडिंग विधियों पर निर्णय लेना और अपने उत्पाद प्रदर्शन को अनुकूलित करना सीडी सिस्टम के व्यक्तिगत डिजाइनरों पर निर्भर है। न्यूनतम दूरी 5 होने के कारण D1, D2 डिकोडर प्रत्येक के संयोजन को सही कर सकते हैं $e$ त्रुटियाँ और $f$ ऐसे मिटाता है $2e+f<5$ .^[5]अधिकांश डिकोडिंग समाधानों में, D1 को एकल त्रुटि को ठीक करने के लिए डिज़ाइन किया गया है। और 1 से अधिक त्रुटि के उपस्तिथियां में, यह डिकोडर 28 इरेज़र आउटपुट करता है। अगले चरण में डीइंटरलीवर इन विलोपनों को 28 डी2 कोडवर्ड में वितरित करता है। पुनः अधिकांश समाधानों में, D2 को केवल मिटाने से निपटने के लिए सेट किया गया है (एक सरल और कम महंगा समाधान)। यदि 4 से अधिक विलोपन का सामना करना पड़ता है, तो 24 विलोपन D2 द्वारा आउटपुट होते हैं। इसके पश्चात , त्रुटि छुपाने वाली प्रणाली अचूक प्रतीकों के उपस्तिथियां में (पड़ोसी प्रतीकों से) प्रक्षेप करने का प्रयास करती है, जिसमें विफल रहने पर ऐसे गलत प्रतीकों के अनुरूप ध्वनियाँ म्यूट हो जाती हैं।

सीआईआरसी का प्रदर्शन:^[7]सीआईआरसी सरल रैखिक प्रक्षेप द्वारा लंबी बस्ट त्रुटियों को छुपाता है। 2.5 मिमी ट्रैक लंबाई (4000 बिट्स) अधिकतम पूरी तरह से सुधार योग्य बर्स्ट लंबाई है। 7.7 मिमी ट्रैक लंबाई (12,300 बिट्स) अधिकतम बर्स्ट लंबाई है जिसे इंटरपोल किया जा सकता है। बिट त्रुटि दर (बीईआर) पर नमूना प्रक्षेप दर हर 10 घंटे में होती है $=10^{-4}$ और बीईआर पर प्रति मिनट 1000 नमूने = $10^{-3}$ अज्ञात त्रुटि नमूने (क्लिक): बीईआर = पर हर 750 घंटे में से कम $10^{-3}$ और BER = पर नगण्य $10^{-4}$ .

यह भी देखें

त्रुटि का पता लगाना और सुधार करना
प्रतिक्रिया के साथ त्रुटि-सुधार कोड
कोड दर
रीड-सोलोमन त्रुटि सुधार

संदर्भ

↑ ^1.0 ^1.1 ^1.2 Coding Bounds for Multiple Phased-Burst Correction and Single Burst Correction Codes
↑ सूचना और कोडिंग का सिद्धांत: छात्र संस्करण,आर जे मैकलीस द्वारा
↑ ^3.0 ^3.1 ^3.2 Ling, San, and Chaoping Xing. Coding Theory: A First Course. Cambridge, UK: Cambridge UP, 2004. Print
↑ ^4.0 ^4.1 Moon, Todd K. Error Correction Coding: Mathematical Methods and Algorithms. Hoboken, NJ: Wiley-Interscience, 2005. Print
↑ ^5.0 ^5.1 ^5.2 ^5.3 ^5.4 ^5.5 Lin, Shu, and Daniel J. Costello. Error Control Coding: Fundamentals and Applications. Upper Saddle River, NJ: Pearson-Prentice Hall, 2004. Print
↑ quest.arc.nasa.gov https://web.archive.org/web/20120627022807/http://quest.arc.nasa.gov/saturn/qa/cassini/Error_correction.txt. Archived from the original on 2012-06-27. {{cite web}}: Missing or empty |title= (help)
↑ ^7.0 ^7.1 ^7.2 Algebraic Error Control Codes (Autumn 2012) – Handouts from Stanford University
↑ McEliece, Robert J. The Theory of Information and Coding: A Mathematical Framework for Communication. Reading, MA: Addison-Wesley Pub., Advanced Book Program, 1977. Print

[Coding_Bounds-1] 1.0 ^1.1 ^1.2 Coding Bounds for Multiple Phased-Burst Correction and Single Burst Correction Codes

[2] सूचना और कोडिंग का सिद्धांत: छात्र संस्करण,आर जे मैकलीस द्वारा

[Ling,_San-3] 3.0 ^3.1 ^3.2 Ling, San, and Chaoping Xing. Coding Theory: A First Course. Cambridge, UK: Cambridge UP, 2004. Print

[Moon,_Todd-4] 4.0 ^4.1 Moon, Todd K. Error Correction Coding: Mathematical Methods and Algorithms. Hoboken, NJ: Wiley-Interscience, 2005. Print

[Lin,_Shu-5] 5.0 ^5.1 ^5.2 ^5.3 ^5.4 ^5.5 Lin, Shu, and Daniel J. Costello. Error Control Coding: Fundamentals and Applications. Upper Saddle River, NJ: Pearson-Prentice Hall, 2004. Print

[6] quest.arc.nasa.gov https://web.archive.org/web/20120627022807/http://quest.arc.nasa.gov/saturn/qa/cassini/Error_correction.txt. Archived from the original on 2012-06-27. {{cite web}}: Missing or empty |title= (help)

[Algebraic_Error_Control_Codes-7] 7.0 ^7.1 ^7.2 Algebraic Error Control Codes (Autumn 2012) – Handouts from Stanford University

[8] McEliece, Robert J. The Theory of Information and Coding: A Mathematical Framework for Communication. Reading, MA: Addison-Wesley Pub., Advanced Book Program, 1977. Print

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

@@ Line 16: / Line 16: @@
 बर्स्ट त्रुटि की संक्षिप्त परिभाषा रखना अधिकांशतः उपयोगी होता है, जिसमें न केवल इसकी लंबाई, किंतु  ऐसी त्रुटि का पैटर्न और स्थान भी सम्मिलित होता है। हम बर्स्ट विवरण को <math>(P,L)</math> टुपल के रूप में परिभाषित करते हैं  जहाँ <math>P</math> त्रुटि का पैटर्न है (जो कि त्रुटि पैटर्न में पहली गैर-शून्य प्रविष्टि से प्रारंभ  होने वाले और अंतिम गैर-शून्य प्रतीक के साथ समाप्त होने वाले प्रतीकों की स्ट्रिंग है), और <math>L</math> कोडवर्ड पर वह स्थान है, जहां बर्स्ट पाया जा सकता है।<ref name = "Coding Bounds" />
-उदाहरण के लिए, त्रुटि पैटर्न <math>E = (010000110)</math> का बर्स्ट विवरण <math>D = (1000011,1)</math> है ध्यान दें कि ऐसा वर्णन अद्वितीय नहीं है, क्योंकि <math>D' = (11001,6)</math> उसी बर्स्ट त्रुटि का वर्णन करता है। सामान्य तौर पर, यदि <math>E</math> में गैर-शून्य अवयव की संख्या <math>w</math> है , तब <math>E</math> में <math>w</math> भिन्न -भिन्न बर्स्ट विवरण होगा, जिनमें से प्रत्येक <math>E</math> भिन्न  गैर-शून्य प्रविष्टि पर प्रारंभ होता है . नीचे दिए गए प्रमेय के साथ बर्स्ट विवरण की अस्पष्टता से उत्पन्न होने वाले मुद्दों को हल करने के लिए, चूंकि ऐसा करने से पहले हमें पहले परिभाषा की आवश्यकता है।
+उदाहरण के लिए, त्रुटि पैटर्न <math>E = (010000110)</math> का बर्स्ट विवरण <math>D = (1000011,1)</math> है ध्यान दें कि ऐसा वर्णन अद्वितीय नहीं है, क्योंकि<math>D' = (11001,6)</math> उसी बर्स्ट त्रुटि का वर्णन करता है। सामान्यतः , यदि <math>E</math> में गैर-शून्य अवयव की संख्या <math>w</math> है , तब <math>E</math> में <math>w</math> भिन्न -भिन्न बर्स्ट विवरण होगा, जिनमें से प्रत्येक <math>E</math> भिन्न  गैर-शून्य प्रविष्टि पर प्रारंभ होता है . नीचे दिए गए प्रमेय के साथ बर्स्ट विवरण की अस्पष्टता से उत्पन्न होने वाले विवादों को हल करने के लिए, चूंकि ऐसा करने से पहले हमें पहले परिभाषा की आवश्यकता है।
 परिभाषा। किसी दिए गए त्रुटि <math>y,</math> पैटर्न में प्रतीकों की संख्या <math>\mathrm{length}(y).</math>द्वारा निरूपित किया जाता है
@@ Line 22: / Line 22: @@
 {{math theorem | name = Theorem (Uniqueness of burst descriptions) | math_statement = मान लीजिए <math>E</math> लंबाई का त्रुटि सदिश  है <math>n</math> दो बर्स्ट विवरण के साथ <math>(P_1,L_1)</math> and <math>(P_2,L_2)</math>. If <math>\mathrm{length}(P_1) + \mathrm{length}(P_2) \leqslant n + 1,</math> तो दोनों विवरण समान हैं अर्थात् उनके अवयव समतुल्य हैं.<ref>''सूचना और कोडिंग का सिद्धांत: छात्र संस्करण'',आर जे मैकलीस द्वारा</ref>
-{{गणित प्रमाण | प्रमाण = चलो}} <math>w</math> [[हैमिंग वज़न]] (या गैर-शून्य प्रविष्टियों की संख्या) हो <math>E</math>. तब <math>E</math> बिलकुल है <math>w</math>त्रुटि विवरण. के लिए <math>w = 0, 1,</math>साबित करने के लिए कुछ भी नहीं है. तो हम ऐसा मान लेते हैं <math>w \geqslant 2</math> और यह कि विवरण समान नहीं हैं। हम देखते हैं कि प्रत्येक गैर-शून्य प्रविष्टि<math>E</math> wमैं पैटर्न में दिखाई दूंगा, और इसी तरह, इसके अवयव  भी<math>E</math> पैटर्न में सम्मिलित नहीं किए जाने पर शून्यों का चक्रीय क्रम बनेगा, जो अंतिम गैर-शून्य प्रविष्टि के पश्चात  प्रारंभ  होगा, और पैटर्न की पहली गैर-शून्य प्रविष्टि से ठीक पहले जारी रहेगा। हम इस रन के अनुरूप सूचकांकों के सेट को शून्य रन कहते हैं। हमने तुरंत देखा कि प्रत्येक बर्स्ट विवरण के साथ एक शून्य रन जुड़ा हुआ है और प्रत्येक शून्य रन असंयुक्त है। चूंकि हमारे पास है <math>w</math> शून्य रन, और प्रत्येक असंयुक्त है, हमारे पास कुल है <math>n-w</math>सभी शून्य रन में विशिष्ट तत्व। दूसरी ओर हमारे पास है: <math display="block">\begin{align}
+<nowiki>{{math proof | proof =</nowiki><math>w</math> [[हैमिंग वज़न]] (या गैर-शून्य प्रविष्टियों की संख्या) हो <math>E</math>. तब <math>E</math> बिलकुल है <math>w</math>त्रुटि विवरण. के लिए <math>w = 0, 1,</math>साबित करने के लिए कुछ भी नहीं है. तो हम ऐसा मान लेते हैं <math>w \geqslant 2</math> और यह कि विवरण समान नहीं हैं। हम देखते हैं कि प्रत्येक गैर-शून्य प्रविष्टि<math>E</math> wमैं पैटर्न में दिखाई दूंगा, और इसी तरह, इसके अवयव  भी<math>E</math> पैटर्न में सम्मिलित नहीं किए जाने पर शून्यों का चक्रीय क्रम बनेगा, जो अंतिम गैर-शून्य प्रविष्टि के पश्चात  प्रारंभ  होगा, और पैटर्न की पहली गैर-शून्य प्रविष्टि से ठीक पहले जारी रहेगा। हम इस रन के अनुरूप सूचकांकों के सेट को शून्य रन कहते हैं। हमने तुरंत देखा कि प्रत्येक बर्स्ट विवरण के साथ एक शून्य रन जुड़ा हुआ है और प्रत्येक शून्य रन असंयुक्त है। चूंकि हमारे पास है <math>w</math> शून्य रन, और प्रत्येक असंयुक्त है, हमारे पास कुल है <math>n-w</math>सभी शून्य रन में विशिष्ट तत्व। दूसरी ओर हमारे पास है: <math display="block">\begin{align}
 n-w = \text{number of zeros in } E &\geqslant  (n - \mathrm{length}(P_1)) + (n - \mathrm{length}(P_2))\\
 &= 2n - \left ( \mathrm{length}(P_1) +  \mathrm{length}(P_2) \right ) \\
@@ Line 39: / Line 39: @@
 कोडवर्ड डिग्री  <math>\leqslant n-1</math> के बहुपद हैं. मान लीजिए कि जनरेटर बहुपद <math>g(x)</math> की डिग्री <math>r</math> है . तथा <math>\leqslant n-1</math> डिग्री के बहुपद  जिनसे <math>g(x)</math> विभाज्य होते हैं <math>g(x)</math> को घात <math>\leqslant n-1-r</math> के बहुपदों से गुणा करने से परिणाम प्राप्त होते है . अपने पास <math>q^{n-r}</math> ऐसे बहुपद है. उनमें से प्रत्येक कोडवर्ड से मेल खाता है। इसलिए, <math>k=n-r</math> चक्रीय कोड के लिए उपयोग किये जाते है .
-चक्रीय कोड <math>\ell = n-k = r</math> तक की लंबाई के सभी बर्स्ट का पता लगा सकते हैं . हम बाद में देखेंगे कि किसी की <math>(n, k)</math> बर्स्ट त्रुटि का पता लगाने की क्षमता   कोड ऊपर से <math>\ell \leqslant n-k</math> तक सीमित है। . बर्स्ट त्रुटि का पता लगाने के लिए चक्रीय कोड को इष्टतम माना जाता है क्योंकि वे इस ऊपरी सीमा को पूरा करते हैं:
+चक्रीय कोड <math>\ell = n-k = r</math> तक की लंबाई के सभी बर्स्ट का पता लगा सकते हैं . हम पश्चात  में देखेंगे कि किसी की <math>(n, k)</math> बर्स्ट त्रुटि का पता लगाने की क्षमता   कोड ऊपर से <math>\ell \leqslant n-k</math> तक सीमित है। . बर्स्ट त्रुटि का पता लगाने के लिए चक्रीय कोड को इष्टतम माना जाता है क्योंकि वे इस ऊपरी सीमा को पूरा करते हैं:
-{{math theorem | name = Theorem (Cyclic burst correction capability) | math_statement = डिग्री के जनरेटर बहुपद के साथ प्रत्येक चक्रीय कोड<math>r</math> लंबाई के सभी विस्फोटों का पता लगा सकता है  <math>\leqslant r.</math>
+{{math theorem | name = Theorem (Cyclic burst correction capability) | math_statement = डिग्री के जनरेटर बहुपद के साथ प्रत्येक चक्रीय कोड <math>r</math> लंबाई के सभी विस्फोटों का पता लगा सकता है  <math>\leqslant r.</math>
-{{गणित प्रमाण | प्रमाण = हमें यह साबित करने की आवश्यकता है कि यदि आप लंबाई का विस्फोट जोड़ते हैं}} <math>\leqslant r</math> कोडवर्ड के लिए (अर्थात एक बहुपद के लिए जो विभाज्य है <math>g(x)</math>), तब परिणाम कोई कोडवर्ड नहीं होगा (अर्थात संबंधित बहुपद इससे विभाज्य नहीं है) <math>g(x)</math>). यह दिखाने के लिए पर्याप्त है कि लंबाई में कोई उछाल नहीं है <math>\leqslant r</math>से विभाज्य है <math>g(x)</math>.ऐसे फूटने का रूप होता है <math>x^i b(x)</math>, जहाँ <math>\deg(b(x)) < r.</math> इसलिए, <math>b(x)</math>से विभाज्य नहीं है <math>g(x)</math> (क्योंकि पश्चात  वाले के पास डिग्री है<math>r</math>). <math>g(x)</math>से विभाज्य नहीं है <math>x</math> (अन्यथा, सभी कोडवर्ड से प्रारंभ होंगे <math>0</math>). इसलिए, <math>x^i</math>से विभाज्य नहीं है<math>g(x)</math><nowiki> as well.}}</nowiki>
+<nowiki>{{math proof | proof = </nowiki><math>\leqslant r</math> कोडवर्ड के लिए (अर्थात एक बहुपद के लिए जो विभाज्य है <math>g(x)</math>), तब परिणाम कोई कोडवर्ड नहीं होगा (अर्थात संबंधित बहुपद इससे विभाज्य नहीं है) <math>g(x)</math>). यह दिखाने के लिए पर्याप्त है कि लंबाई में कोई उछाल नहीं है <math>\leqslant r</math>से विभाज्य है <math>g(x)</math>.ऐसे फूटने का रूप होता है <math>x^i b(x)</math>, जहाँ <math>\deg(b(x)) < r.</math> इसलिए, <math>b(x)</math>से विभाज्य नहीं है <math>g(x)</math> (क्योंकि पश्चात  वाले के पास डिग्री है<math>r</math>). <math>g(x)</math>से विभाज्य नहीं है <math>x</math> (अन्यथा, सभी कोडवर्ड से प्रारंभ होंगे <math>0</math>). इसलिए, <math>x^i</math>से विभाज्य नहीं है<math>g(x)</math><nowiki> as well.}}</nowiki>
 }}
@@ Line 54: / Line 54: @@
 {{math theorem | name = Theorem (Distinct [[Coset]]s) | math_statement = एक रेखीय कोड <math>C</math>एक<math>\ell</math>-बर्स्ट-एरर-सही कोड यदि लंबाई की सभी बर्स्ट त्रुटियां <math>\leqslant \ell</math> भिन्न -भिन्न  [[कोसेट]] में झूठ बोलें<math>C</math>.
-{{गणित प्रमाण | प्रमाण = चलो}} <math>\mathbf{e}_1, \mathbf{e}_2</math>लंबाई की भिन्न -भिन्न बर्स्ट त्रुटियाँ हों <math> \leqslant \ell</math> जो कोड के एक ही कोसेट में स्थित हैं <math>C</math>.  Then <math>\mathbf{c} = \mathbf{e}_1 - \mathbf{e}_2</math> कोडवर्ड है. इसलिए, यदि हम प्राप्त करते हैं <math>\mathbf{e}_1,</math> हम इसे या तो डिकोड कर सकते हैं <math>\mathbf{0}</math> or <math>\mathbf{c}</math>. इसके विपरीत, यदि सभी विस्फोट त्रुटियाँ <math>\mathbf{e}_1</math> and <math>\mathbf{e}_2</math> एक ही कोसेट में न रहें, तो प्रत्येक बर्स्ट त्रुटि उसके सिंड्रोम द्वारा निर्धारित होती है। फिर त्रुटि को उसके सिंड्रोम के माध्यम से ठीक किया जा सकता है। इस प्रकार, एक रैखिक कोड <math>C</math> is an <math>\ell</math>-बर्स्ट-त्रुटि-सही कोड यदि और केवल यदि लंबाई की सभी बर्स्ट त्रुटियां<math>\leqslant \ell</math> के भिन्न-भिन्न कोसेट में स्थित हैं<math>C</math><nowiki>.}}</nowiki>}}
+<nowiki>{{math proof | proof = </nowiki><math>\mathbf{e}_1, \mathbf{e}_2</math>लंबाई की भिन्न -भिन्न बर्स्ट त्रुटियाँ हों <math> \leqslant \ell</math> जो कोड के एक ही कोसेट में स्थित हैं <math>C</math>.  Then <math>\mathbf{c} = \mathbf{e}_1 - \mathbf{e}_2</math> कोडवर्ड है. इसलिए, यदि हम प्राप्त करते हैं <math>\mathbf{e}_1,</math> हम इसे या तो डिकोड कर सकते हैं <math>\mathbf{0}</math> or <math>\mathbf{c}</math>. इसके विपरीत, यदि सभी विस्फोट त्रुटियाँ <math>\mathbf{e}_1</math> and <math>\mathbf{e}_2</math> एक ही कोसेट में न रहें, तो प्रत्येक बर्स्ट त्रुटि उसके सिंड्रोम द्वारा निर्धारित होती है। फिर त्रुटि को उसके सिंड्रोम के माध्यम से ठीक किया जा सकता है। इस प्रकार, एक रैखिक कोड <math>C</math> is an <math>\ell</math>-बर्स्ट-त्रुटि-सही कोड यदि और केवल यदि लंबाई की सभी बर्स्ट त्रुटियां<math>\leqslant \ell</math> के भिन्न-भिन्न कोसेट में स्थित हैं<math>C</math><nowiki>.}}</nowiki>}}
 {{math theorem | name = Theorem (Burst error codeword classification) | math_statement = मान लीजिये  <math>C</math> एक रेखीय हो <math>\ell</math>-विस्फोट-त्रुटि-सुधार कोड। फिर लंबाई का कोई शून्येतर विस्फोट नहीं <math>\leqslant 2\ell</math>  कोडवर्ड हो सकता है.
-{{math proof | proof = Let <math>c</math> be a codeword with a burst of length <math>\leqslant 2\ell</math>. Thus it has the pattern <math>(0,1,u,v,1,0)</math>, where <math>u</math> and <math>v</math> are words of length <math>\leqslant \ell -1.</math> Hence, the words <math>w = (0,1,u,0,0,0)</math> and <math>c-w =  (0,0,0,v,1,0)</math> are two bursts of length <math> \leqslant \ell</math>. For binary linear codes, they belong to the same coset. This contradicts the Distinct Cosets Theorem, therefore no nonzero burst of length <math>\leqslant 2\ell</math> can be a codeword.}}
+{{math proof | proof =  <math>c</math> be a codeword with a burst of length <math>\leqslant 2\ell</math>. Thus it has the pattern <math>(0,1,u,v,1,0)</math>, where <math>u</math> and <math>v</math> are words of length <math>\leqslant \ell -1.</math> Hence, the words <math>w = (0,1,u,0,0,0)</math> and <math>c-w =  (0,0,0,v,1,0)</math> are two bursts of length <math> \leqslant \ell</math>. For binary linear codes, they belong to the same coset. This contradicts the Distinct Cosets Theorem, therefore no nonzero burst of length <math>\leqslant 2\ell</math> can be a codeword.}}
 }}
@@ Line 67: / Line 67: @@
 ऊपरी सीमा से हमारा तात्पर्य हमारी त्रुटि पता लगाने की क्षमता की सीमा से है जिसे हम कभी भी पार नहीं कर सकते। मान लीजिए कि हम डिज़ाइन बनाना चाहते हैं <math>(n, k)</math> कोड जो लंबाई की सभी बर्स्ट त्रुटियों का पता लगा सकता है <math>\leqslant \ell.</math> पूछने के लिए स्वाभाविक प्रश्न है: दिया गया <math>n</math> और <math>k</math>, अधिकतम क्या है <math>\ell</math> कि हम इससे आगे कभी हासिल नहीं कर सकते? दूसरे शब्दों में, लंबाई की ऊपरी सीमा क्या है <math>\ell</math> हम किसी भी बर्स्ट  का पता लगा सकते हैं <math>(n, k)</math> कोड? निम्नलिखित प्रमेय इस प्रश्न का उत्तर प्रदान करता है।
-{{math theorem | name = Theorem (Burst error detection ability) | math_statement = The burst error detection ability of any <math>(n, k)</math> code is <math>\ell \leqslant  n-k.</math>
+{{math theorem | name = Theorem (Burst error detection ability) | math_statement = किसी की भी बर्स्ट त्रुटि का पता लगाने की क्षमता <math>(n, k)</math> code is <math>\ell \leqslant  n-k.</math>
-{{math proof | proof = First we observe that a code can detect all bursts of length <math>\leqslant  \ell</math> if and only if no two codewords differ by a burst of length <math>\leqslant  \ell</math>. Suppose that we have two code words <math>\mathbf{c}_1</math> and <math>\mathbf{c}_2</math> that differ by a burst <math>\mathbf{b}</math> of length <math>\leqslant  \ell</math>. Upon receiving <math>\mathbf{c}_1</math>, we can not tell whether the transmitted word is indeed <math>\mathbf{c}_1</math> with no transmission errors, or whether it is <math>\mathbf{c}_2</math> with a burst error <math>\mathbf{b}</math> that occurred during transmission. Now, suppose that every two codewords differ by more than a burst of length <math>\ell.</math> Even if the transmitted codeword <math>\mathbf{c}_1</math> is hit by a burst <math>\mathbf{b}</math> of length <math>\ell</math>, it is not going to change into another valid codeword. Upon receiving it, we can tell that this is <math>\mathbf{c}_1</math> with a burst <math>\mathbf{b}.</math> By the above observation, we know that no two codewords can share the first <math>n-\ell</math> symbols. The reason is that even if they differ in all the other <math>\ell</math> symbols, they are still going to be different by a burst of length <math>\ell.</math> Therefore, the number of codewords <math>q^k</math> satisfies <math>q^k \leqslant  q^{n-\ell}.</math> Applying <math>\log_q</math> to both sides and rearranging, we can see that <math>\ell \leqslant  n-k</math>.}}
+{{math proof | proof = पहले हम देखते हैं कि एक कोड लंबाई के सभी विस्फोटों का पता लगा सकता है <math>\leqslant  \ell</math> यदि और केवल यदि कोई भी दो कोडवर्ड लंबाई के हिसाब से भिन्न न हों <math>\leqslant  \ell</math>. मान लीजिए कि हमारे पास दो कोड वर्ड हैं <math>\mathbf{c}_1</math> and <math>\mathbf{c}_2</math>जो विस्फोट से भिन्न होता है <math>\mathbf{b}</math> लम्बाई का <math>\leqslant  \ell</math>. प्राप्त करने पर <math>\mathbf{c}_1</math>, हम यह नहीं बता सकते कि प्रेषित शब्द वास्तव में है या नहीं <math>\mathbf{c}_1</math> बिना किसी ट्रांसमिशन त्रुटि के, या चाहे वह हो <math>\mathbf{c}_2</math>बर्स्ट त्रुटि के साथ<math>\mathbf{b}</math>जो प्रसारण के दौरान घटित हुआ। अब, मान लीजिए कि प्रत्येक दो कोडवर्ड की लंबाई में बहुत अधिक अंतर होता है <math>\ell.</math> भले ही प्रेषित कोडवर्ड <math>\mathbf{c}_1</math> विस्फोट की चपेट में आ गया है <math>\mathbf{b}</math> लम्बाई का <math>\ell</math>,यह किसी अन्य वैध कोडवर्ड में परिवर्तित नहीं होगा. इसे प्राप्त करने पर, हम बता सकते हैं कि यह है <math>\mathbf{c}_1</math> विस्फोट के साथ<math>\mathbf{b}.</math> उपरोक्त अवलोकन से, हम जानते हैं कि कोई भी दो कोडवर्ड पहले को साझा नहीं कर सकते हैं <math>n-\ell</math>प्रतीक. कारण यह है कि भले ही वे सभी में भिन्न हों <math>\ell</math> प्रतीक, वे अभी भी लंबाई के आधार पर भिन्न होंगे <math>\ell.</math> इसलिए, कोडवर्ड की संख्या <math>q^k</math>संतुष्ट<math>q^k \leqslant  q^{n-\ell}.</math> को प्रयुक्त करने <math>\log_q</math> दोनों तरफ और पुनर्व्यवस्थित करके, हम इसे देख सकते हैं <math>\ell \leqslant  n-k</math>.}}
 }}
 अब, हम वही प्रश्न दोहराते हैं लेकिन त्रुटि सुधार के लिए: दिया गया है <math>n</math> और <math>k</math>, लंबाई पर ऊपरी सीमा क्या है <math>\ell</math> बर्स्ट ों का जिन्हें हम किसी का उपयोग करके ठीक कर सकते हैं <math>(n, k)</math> कोड? निम्नलिखित प्रमेय इस प्रश्न का प्रारंभिक उत्तर प्रदान करता है:
@@ Line 79: / Line 79: @@
 रीगर बाउंड द्वारा मजबूत परिणाम दिया गया है:
-{{math theorem | name = Theorem (Rieger bound) | math_statement = If <math>\ell</math> is the burst error correcting ability of an <math>(n, k)</math> linear block code, then <math>2\ell \leqslant n - k</math>.
+{{math theorem | name = Theorem (Rieger bound) | math_statement = यदि  <math>\ell</math>की बर्स्ट त्रुटि सुधार करने की क्षमता है <math>(n, k)</math>रैखिक ब्लॉक कोड, फिर<math>2\ell \leqslant n - k</math>.
-{{math proof | proof = Any linear code that can correct any burst pattern of length <math>\leqslant \ell</math> cannot have a burst of length <math>\leqslant 2\ell</math> as a codeword. If it had a burst of length <math>\leqslant 2\ell</math> as a codeword, then a burst of length <math>\ell</math> could change the codeword to a burst pattern of length <math>\ell</math>, which also could be obtained by making a burst error of length <math>\ell</math> in all zero codeword. If vectors are non-zero in first <math>2\ell</math> symbols, then the vectors should be from different subsets of an array so that their difference is not a codeword of bursts of length <math>2\ell</math>. Ensuring this condition, the number of such subsets is at least equal to number of vectors. Thus, the number of subsets would be at least <math>q^{2\ell}</math>. Hence, we have at least <math>2\ell</math> distinct symbols, otherwise, the difference of two such polynomials would be a codeword that is a sum of two bursts of length <math>\leqslant  \ell.</math> Thus, this proves the Rieger Bound.}}}}
+{{math proof | proof = कोई भी रैखिक कोड जो लंबाई के किसी भी विस्फोट पैटर्न को सही कर सकता है <math>\leqslant \ell</math>लम्बाई का विस्फोट नहीं हो सकता <math>\leqslant 2\ell</math> एक कोडवर्ड के रूप में. यदि इसकी लम्बाई में वृद्धि होती <math>\leqslant 2\ell</math> एक कोडवर्ड के रूप में, फिर लंबाई का विस्फोट<math>\ell</math> कोडवर्ड को लंबाई के बर्स्ट पैटर्न में बदल सकता है <math>\ell</math>, जिसे लंबाई की बर्स्ट त्रुटि बनाकर भी प्राप्त किया जा सकता है <math>\ell</math> बिल्कुल शून्य कोडवर्ड में. यदि सदिश पहले शून्येतर हैं<math>2\ell</math> प्रतीकों, तो सदिश एक सरणी के विभिन्न उपसमूहों से होने चाहिए ताकि उनका अंतर लंबाई के फटने का कोडवर्ड न हो<math>2\ell</math>. इस शर्त को सुनिश्चित करते हुए, ऐसे उपसमुच्चय की संख्या कम से कम सदिश की संख्या के समान्तर है। इस प्रकार, उपसमुच्चय की संख्या कम से कम होगी<math>q^{2\ell}</math>.इसलिए, हमारे पास कम से कम है <math>2\ell</math> अलग-अलग प्रतीक, अन्यथा, ऐसे दो बहुपदों का अंतर एक कोडवर्ड होगा जो लंबाई के दो विस्फोटों का योग है <math>\leqslant  \ell.</math> इस प्रकार, यह रीगर बाउंड सिद्ध होता है।}}}}
 परिभाषा। उपरोक्त रीगर सीमा को प्राप्त करने वाले रैखिक बर्स्ट-त्रुटि-सुधार करने वाले कोड को इष्टतम बर्स्ट-त्रुटि-सुधार करने वाला कोड कहा जाता है।
@@ Line 87: / Line 87: @@
 === बर्स्ट त्रुटि सुधार पर आगे की सीमाएं ===
-एकाधिक चरणबद्ध-बर्स्ट  सुधार (एमपीबीसी) के लिए रैखिक ब्लॉक कोड की प्राप्त कोड दर पर से अधिक ऊपरी सीमा होती है। ऐसी सीमा प्रत्येक उपब्लॉक के भीतर अधिकतम सुधार योग्य चक्रीय बर्स्ट  लंबाई तक सीमित है, या समकक्ष रूप से प्रत्येक चरण-बर्स्ट  के भीतर न्यूनतम त्रुटि मुक्त लंबाई या अंतराल पर बाधा है। यह सीमा, जब एकल बर्स्ट  सुधार के लिए बाध्य के विशेष उपस्तिथियां  में कम हो जाती है, अब्रामसन बाध्य (बर्स्ट -त्रुटि सुधार के लिए हैमिंग बाध्य का परिणाम) है जब चक्रीय बर्स्ट  की लंबाई ब्लॉक लंबाई के आधे से कम होती है।<ref name = "Ling, San">Ling, San, and Chaoping Xing. Coding Theory: A First Course. Cambridge, UK: Cambridge UP, 2004. Print</ref>
+एकाधिक चरणबद्ध-बर्स्ट  सुधार (एमपीबीसी) के लिए रैखिक ब्लॉक कोड की प्राप्त कोड दर पर से अधिक ऊपरी सीमा होती है। ऐसी सीमा प्रत्येक उपब्लॉक के अंदर  अधिकतम सुधार योग्य चक्रीय बर्स्ट  लंबाई तक सीमित है, या समकक्ष रूप से प्रत्येक चरण-बर्स्ट  के अंदर न्यूनतम त्रुटि मुक्त लंबाई या अंतराल पर बाधा है। यह सीमा, जब एकल बर्स्ट  सुधार के लिए बाध्य के विशेष उपस्तिथियां  में कम हो जाती है, अब्रामसन बाध्य (बर्स्ट -त्रुटि सुधार के लिए हैमिंग बाध्य का परिणाम) है जब चक्रीय बर्स्ट  की लंबाई ब्लॉक लंबाई के आधे से कम होती है।<ref name = "Ling, San">Ling, San, and Chaoping Xing. Coding Theory: A First Course. Cambridge, UK: Cambridge UP, 2004. Print</ref>
-{{math theorem | name = Theorem (number of bursts) | math_statement = For <math>1 \leqslant \ell \leqslant \tfrac{1}{2}(n+1),</math> over a binary alphabet, there are <math>n2^{\ell-1}+1</math> vectors of length <math>n</math> which are bursts of length <math>\leqslant \ell</math>.<ref name = "Coding Bounds" />
+{{math theorem | name = Theorem (number of bursts) | math_statement = इसके लिए <math>1 \leqslant \ell \leqslant \tfrac{1}{2}(n+1),</math> एक द्विआधारी वर्णमाला पर, वहाँ हैं <math>n2^{\ell-1}+1</math> लंबाई के सदिश<math>n</math> जो लम्बाई के विस्फोट हैं <math>\leqslant \ell</math>.<ref name = "Coding Bounds" />
 {{math proof | proof = Since the burst length is <math>\leqslant \tfrac{1}{2}(n+1),</math> there is a unique burst description associated with the burst. The burst can begin at any of the <math>n</math> positions of the pattern. Each pattern begins with <math>1</math> and contain a length of <math>\ell</math>. We can think of it as the set of all strings that begin with <math>1</math> and have length <math>\ell</math>. Thus, there are a total of <math>2^{\ell-1}</math> possible such patterns, and a total of <math>n2^{\ell-1}</math> bursts of length <math>\leqslant \ell.</math> If we include the all-zero burst, we have <math>n2^{\ell-1}+1</math> vectors representing bursts of length <math>\leqslant \ell.</math>}}}}
@@ Line 107: / Line 107: @@
 ==अग्नि कोड<ref name = "Ling, San" /><ref name = "Moon, Todd">Moon, Todd K. Error Correction Coding: Mathematical Methods and Algorithms. Hoboken, NJ: Wiley-Interscience, 2005. Print</ref><ref name = "Lin, Shu">Lin, Shu, and Daniel J. Costello. Error Control Coding: Fundamentals and Applications. Upper Saddle River, NJ: Pearson-Prentice Hall, 2004. Print</ref>==
-जबकि सामान्य तौर पर चक्रीय कोड बर्स्ट त्रुटियों का पता लगाने के लिए शक्तिशाली उपकरण होते हैं, अब हम फायर कोड नामक बाइनरी चक्रीय कोड के परिवार पर विचार करते हैं, जिसमें अच्छी एकल बर्स्ट त्रुटि सुधार क्षमताएं होती हैं। एकल बर्स्ट  से, लंबाई के बारे में कहें <math>\ell</math>, हमारा मतलब है कि प्राप्त कोडवर्ड में मौजूद सभी त्रुटियां निश्चित अवधि के भीतर होती हैं <math>\ell</math> अंक.
+जबकि सामान्यतः  चक्रीय कोड बर्स्ट त्रुटियों का पता लगाने के लिए शक्तिशाली उपकरण होते हैं, अब हम फायर कोड नामक बाइनरी चक्रीय कोड के परिवार पर विचार करते हैं, जिसमें अच्छी एकल बर्स्ट त्रुटि सुधार क्षमताएं होती हैं। एकल बर्स्ट  से, लंबाई के बारे में कहें <math>\ell</math>, हमारा मतलब है कि प्राप्त कोडवर्ड में मौजूद सभी त्रुटियां निश्चित अवधि के अंदर  होती हैं <math>\ell</math> अंक.
 होने देना <math>p(x)</math> डिग्री का अपरिवर्तनीय बहुपद बनें <math>m</math> ऊपर <math>\mathbb{F}_2</math>, और जाने <math>p</math> की अवधि हो <math>p(x)</math>. की अवधि <math>p(x)</math>, और वास्तव में किसी भी बहुपद को सबसे कम धनात्मक पूर्णांक के रूप में परिभाषित किया गया है <math>r</math> ऐसा है कि <math>p(x) |x^r - 1.</math> होने देना <math>\ell</math> सकारात्मक पूर्णांक संतोषजनक हो <math>\ell \leqslant m</math> और <math>2\ell -1</math> से विभाज्य नहीं है <math>p</math>, जहाँ  <math>p</math> की अवधि है <math>p(x)</math>. अग्नि संहिता को परिभाषित करें <math>G</math> निम्नलिखित जनरेटर बहुपद द्वारा:
@@ Line 132: / Line 132: @@
 होने देना <math>x^i a(x)</math> और <math>x^j b(x)</math> डिग्री वाले बहुपद बनें <math>\ell_1-1</math> और <math>\ell_2-1</math>, लंबाई के बर्स्ट  का प्रतिनिधित्व करता है <math>\ell_1</math> और <math>\ell_2</math> क्रमशः साथ <math>\ell_1, \ell_2 \leqslant \ell.</math> पूर्णांक <math>i, j</math> बर्स्ट की प्रारंभिक स्थिति का प्रतिनिधित्व करते हैं, और कोड की ब्लॉक लंबाई से कम होते हैं। विरोधाभास के लिए, यह मान लें <math>x^i a(x)</math> और <math>x^j b(x)</math> ही कोसेट में हैं. तब, <math>v(x) = x^i a(x) + x^j b(x)</math> वैध कोडवर्ड है (क्योंकि दोनों पद ही कोसेट में हैं)। व्यापकता की हानि के बिना, चुनें <math>i \leqslant j</math>. [[विभाजन प्रमेय]] द्वारा हम लिख सकते हैं: <math>j-i = g(2\ell -1)+r,</math> पूर्णांकों के लिए <math>g</math> और <math>r, 0 \leqslant r < 2\ell -1</math>. हम बहुपद को फिर से लिखते हैं <math>v(x)</math> निम्नलिखित नुसार:
 <math display="block">v(x) = x^ia(x) + x^{i + g(2\ell -1) + r} =  x^ia(x) + x^{i + g(2\ell -1) + r} + 2x^{i+r}b(x) = x^i \left (a(x) + x^b b(x) \right ) + x^{i+r}b(x) \left (x^{g(2\ell -1)}+1 \right )</math>
-ध्यान दें कि दूसरे हेरफेर में, हमने शब्द प्रस्तुत  किया <math>2x^{i+r}b(x)</math>. हमें ऐसा करने की अनुमति है, क्योंकि फायर कोड चालू हैं <math>\mathbb{F}_2</math>. हमारी धारणा से, <math>v(x)</math> वैध कोडवर्ड है, और इस प्रकार, इसका गुणज होना चाहिए <math>g(x)</math>. जैसा कि पहले उल्लेख किया गया है, के कारकों के बाद से <math>g(x)</math> अपेक्षाकृत प्रमुख हैं, <math>v(x)</math> से विभाज्य होना चाहिए <math>x^{2\ell -1} + 1</math>. के लिए व्युत्पन्न अंतिम अभिव्यक्ति को करीब से देख रहे हैं <math>v(x)</math> हम उस पर ध्यान देते हैं <math>x^{g(2\ell -1)} + 1</math> से विभाज्य है <math>x^{2\ell -1} + 1</math> (लेम्मा 2 के परिणाम से)। इसलिए, <math>a(x) + x^bb(x)</math> या तो विभाज्य है <math>x^{2\ell -1} + 1</math> या है <math>0</math>. विभाजन प्रमेय को दोबारा लागू करने पर, हम देखते हैं कि बहुपद मौजूद है <math>d(x)</math> डिग्री के साथ <math>\delta</math> ऐसा है कि:
+ध्यान दें कि दूसरे हेरफेर में, हमने शब्द प्रस्तुत  किया <math>2x^{i+r}b(x)</math>. हमें ऐसा करने की अनुमति है, क्योंकि फायर कोड चालू हैं <math>\mathbb{F}_2</math>. हमारी धारणा से, <math>v(x)</math> वैध कोडवर्ड है, और इस प्रकार, इसका गुणज होना चाहिए <math>g(x)</math>. जैसा कि पहले उल्लेख किया गया है, के कारकों के पश्चात  से <math>g(x)</math> अपेक्षाकृत प्रमुख हैं, <math>v(x)</math> से विभाज्य होना चाहिए <math>x^{2\ell -1} + 1</math>. के लिए व्युत्पन्न अंतिम अभिव्यक्ति को करीब से देख रहे हैं <math>v(x)</math> हम उस पर ध्यान देते हैं <math>x^{g(2\ell -1)} + 1</math> से विभाज्य है <math>x^{2\ell -1} + 1</math> (लेम्मा 2 के परिणाम से)। इसलिए, <math>a(x) + x^bb(x)</math> या तो विभाज्य है <math>x^{2\ell -1} + 1</math> या है <math>0</math>. विभाजन प्रमेय को दोबारा लागू करने पर, हम देखते हैं कि बहुपद मौजूद है <math>d(x)</math> डिग्री के साथ <math>\delta</math> ऐसा है कि:
 <math display="block">a(x) + x^b b(x) = d(x) (x^{2\ell -1}+1)</math>
 तब हम लिख सकते हैं:
@@ Line 143: / Line 143: @@
 दोनों पक्षों की डिग्री को बराबर करने से हमें प्राप्त होता है <math>b = 2\ell  - \ell_2 + \delta.</math> तब से <math>\ell_1, \ell_2 \leqslant \ell</math> हम निष्कर्ष निकाल सकते हैं <math>b \geqslant \ell + \delta,</math> जो ये दर्शाता हे <math>b > \ell -1</math> और <math>b > \delta</math>. ध्यान दें कि विस्तार में:
 <math display="block">a(x) + x^bb(x) = 1 + a_1x + a_2x^2 + \dots + x^{\ell_1-1} + x^b \left (1 + b_1x + b_2x^2 + \dots + x^{\ell_2-1} \right ). </math>
-शब्द <math>x^b</math> प्रकट होता है, लेकिन तब से <math>\delta < b < 2\ell -1</math>, परिणामी अभिव्यक्ति <math>d(x)(x^{2\ell -1} + 1)</math> सम्मिलित  नहीं है <math>x^b</math>, इसलिए <math>d(x) = 0</math> और बाद में <math>a(x) + x^b b(x) = 0.</math> इसके लिए इसकी आवश्यकता है <math>b = 0</math>, और <math>a(x) = b(x)</math>. हम अपने विभाजन को और संशोधित कर सकते हैं <math>j-i</math> द्वारा <math>g(2\ell -1)</math> प्रतिबिंबित करना <math>b = 0,</math> वह है {{nowrap|<math>j-i = g(2\ell -1)</math>.}} वापस प्रतिस्थापित करना <math>v(x)</math> हमें देता है,
+शब्द <math>x^b</math> प्रकट होता है, लेकिन तब से <math>\delta < b < 2\ell -1</math>, परिणामी अभिव्यक्ति <math>d(x)(x^{2\ell -1} + 1)</math> सम्मिलित  नहीं है <math>x^b</math>, इसलिए <math>d(x) = 0</math> और पश्चात  में <math>a(x) + x^b b(x) = 0.</math> इसके लिए इसकी आवश्यकता है <math>b = 0</math>, और <math>a(x) = b(x)</math>. हम अपने विभाजन को और संशोधित कर सकते हैं <math>j-i</math> द्वारा <math>g(2\ell -1)</math> प्रतिबिंबित करना <math>b = 0,</math> वह है {{nowrap|<math>j-i = g(2\ell -1)</math>.}} वापस प्रतिस्थापित करना <math>v(x)</math> हमें देता है,
 <math display="block">v(x) = x^i b(x) \left (x^{j-1}+1 \right ).</math>
 तब से <math>\deg(b(x)) = \ell_2-1 < \ell</math>, अपने पास <math>\deg(b(x)) < \deg(p(x)) = m</math>. लेकिन <math>p(x)</math> इसलिए, अपरिवर्तनीय है <math>b(x)</math> और <math>p(x)</math> अपेक्षाकृत प्रधान होना चाहिए। तब से <math>v(x)</math> कोडवर्ड है, <math>x^{j-1}+1</math> से विभाज्य होना चाहिए <math>p(x)</math>, क्योंकि इसे विभाज्य नहीं किया जा सकता <math>x^{2\ell -1} + 1</math>. इसलिए, <math>j-i</math> का गुणज होना चाहिए <math>p</math>. लेकिन इसका गुणज भी होना चाहिए <math>2\ell -1</math>, जिसका अर्थ है कि यह का गुणज होना चाहिए <math>n = \text{lcm}(2\ell -1,p)</math> लेकिन वह बिल्कुल कोड की ब्लॉक-लंबाई है। इसलिए, <math>j-i</math> का गुणज नहीं हो सकता <math>n</math> चूँकि वे दोनों इससे कम हैं <math>n</math>. इस प्रकार, हमारी धारणा <math>v(x)</math> कोडवर्ड होना गलत है, और इसलिए <math>x^i a(x)</math> और <math>x^j b(x)</math> अद्वितीय सिंड्रोम के साथ भिन्न -भिन्न  कोसेट में हैं, और इसलिए सुधार योग्य हैं।
@@ Line 156: / Line 156: @@
 कोड के कुछ परिवार, जैसे रीड-सोलोमन त्रुटि सुधार|रीड-सोलोमन, बाइनरी से बड़े वर्णमाला आकार पर काम करते हैं। यह संपत्ति ऐसे कोड को शक्तिशाली बर्स्ट त्रुटि सुधार क्षमताएं प्रदान करती है। उस कोड पर विचार करें जिस पर काम चल रहा है <math>\mathbb{F}_{2^m}</math>. वर्णमाला के प्रत्येक प्रतीक को किसके द्वारा दर्शाया जा सकता है? <math>m</math> बिट्स अगर <math>C</math> <math>(n,k)</math> रीड-सोलोमन कोड ख़त्म <math>\mathbb{F}_{2^m}</math>, हम सोच सकते हैं <math>C</math> के रूप में <math>[mn,mk]_2</math> कोड ख़त्म <math>\mathbb{F}_{2}</math>.
-बर्स्ट त्रुटि सुधार के लिए ऐसे कोड शक्तिशाली होने का कारण यह है कि प्रत्येक प्रतीक का प्रतिनिधित्व किया जाता है <math>m</math> बिट्स, और सामान्य तौर पर, यह अप्रासंगिक है कि उनमें से कितने हैं <math>m</math> बिट्स ग़लत हैं; चाहे बिट, या सभी <math>m</math> बिट्स में त्रुटियाँ हैं, डिकोडिंग परिप्रेक्ष्य से यह अभी भी एकल प्रतीक त्रुटि है। दूसरे शब्दों में, चूंकि क्लस्टर में बर्स्ट त्रुटियां होती हैं, इसलिए एकल प्रतीक त्रुटि में अनेक बाइनरी त्रुटियों के योगदान की प्रबल संभावना होती है।
+बर्स्ट त्रुटि सुधार के लिए ऐसे कोड शक्तिशाली होने का कारण यह है कि प्रत्येक प्रतीक का प्रतिनिधित्व किया जाता है <math>m</math> बिट्स, और सामान्यतः , यह अप्रासंगिक है कि उनमें से कितने हैं <math>m</math> बिट्स ग़लत हैं; चाहे बिट, या सभी <math>m</math> बिट्स में त्रुटियाँ हैं, डिकोडिंग परिप्रेक्ष्य से यह अभी भी एकल प्रतीक त्रुटि है। दूसरे शब्दों में, चूंकि क्लस्टर में बर्स्ट त्रुटियां होती हैं, इसलिए एकल प्रतीक त्रुटि में अनेक बाइनरी त्रुटियों के योगदान की प्रबल संभावना होती है।
 ध्यान दें कि बर्स्ट  <math>(m+1)</math> त्रुटियाँ अधिकतम प्रभावित कर सकती हैं <math>2</math> प्रतीकों, और का बर्स्ट  <math>2m + 1</math> ज्यादा से ज्यादा प्रभावित कर सकता है <math>3</math> प्रतीक. फिर, बर्स्ट  <math>tm+1</math> ज्यादा से ज्यादा प्रभावित कर सकता है <math>t + 1</math> प्रतीक; इसका तात्पर्य यह है कि ए <math>t</math>-प्रतीक-त्रुटि सुधार कोड अधिकतम लंबाई के बर्स्ट  को ठीक कर सकता है <math>(t-1)m+1</math>.
-सामान्य तौर पर, ए <math>t</math>-रीड-सोलोमन कोड को सही करने में त्रुटि <math>\mathbb{F}_{2^m}</math> के किसी भी संयोजन को ठीक कर सकता है
+सामान्यतः , ए <math>t</math>-रीड-सोलोमन कोड को सही करने में त्रुटि <math>\mathbb{F}_{2^m}</math> के किसी भी संयोजन को ठीक कर सकता है
 <math display="block">\frac{t}{1+\lfloor (l+m-2)/m \rfloor}</math>
 या लंबाई के कम बर्स्ट  <math>l</math>, सही करने में सक्षम होने के शीर्ष पर <math>t</math>-यादृच्छिक सबसे खराब स्थिति त्रुटियाँ।
@@ Line 186: / Line 186: @@
 ब्लॉक इंटरलीवर की दक्षता (<math>\gamma</math>): यह बर्स्ट लंबाई का अनुपात लेकर पाया जाता है जहां डिकोडर इंटरलीवर मेमोरी में विफल हो सकता है। इस प्रकार, हम सूत्रीकरण कर सकते हैं <math>\gamma</math> जैसा
 <math display="block">\gamma=\frac{Mt+1}{MN} \approx \frac{t}{N}.</math>
-ब्लॉक इंटरलीवर की कमियाँ: जैसा कि चित्र से स्पष्ट है, कॉलम क्रमिक रूप से पढ़े जाते हैं, रिसीवर पूर्ण संदेश प्राप्त करने के बाद ही एकल पंक्ति की व्याख्या कर सकता है, उससे पहले नहीं। साथ ही, प्राप्त प्रतीकों को संग्रहीत करने के लिए रिसीवर को काफी मात्रा में मेमोरी की आवश्यकता होती है और उसे पूरा संदेश संग्रहीत करना होता है। इस प्रकार, ये कारक दो कमियों को जन्म देते हैं, है विलंबता और दूसरा है भंडारण (काफी बड़ी मात्रा में मेमोरी)। नीचे वर्णित कनवल्शनल इंटरलीवर का उपयोग करके इन कमियों से बचा जा सकता है।
+ब्लॉक इंटरलीवर की कमियाँ: जैसा कि चित्र से स्पष्ट है, कॉलम क्रमिक रूप से पढ़े जाते हैं, रिसीवर पूर्ण संदेश प्राप्त करने के पश्चात  ही एकल पंक्ति की व्याख्या कर सकता है, उससे पहले नहीं। साथ ही, प्राप्त प्रतीकों को संग्रहीत करने के लिए रिसीवर को काफी मात्रा में मेमोरी की आवश्यकता होती है और उसे पूरा संदेश संग्रहीत करना होता है। इस प्रकार, ये कारक दो कमियों को जन्म देते हैं, है विलंबता और दूसरा है भंडारण (काफी बड़ी मात्रा में मेमोरी)। नीचे वर्णित कनवल्शनल इंटरलीवर का उपयोग करके इन कमियों से बचा जा सकता है।
 ===कन्वेंशनल इंटरलीवर===
@@ Line 217: / Line 217: @@
 एनकोडर के लिए इनपुट में 24 8-बिट प्रतीकों (ए/डी कनवर्टर से 12 16-बिट नमूने, बाएं और दाएं डेटा (ध्वनि) स्रोतों से 6 प्रत्येक) के इनपुट फ्रेम होते हैं। फ़्रेम का प्रतिनिधित्व किया जा सकता है <math>L_1 R_1 L_2 R_2 \ldots L_6 R_6</math> जहाँ  <math> L_i </math> और <math>R_i</math> से बाएँ और दाएँ चैनल से बाइट्स हैं <math>i^{th}</math> फ़्रेम का नमूना.
-प्रारंभ में, बाइट्स को नए फ़्रेम बनाने के लिए क्रमपरिवर्तित किया जाता है <math>L_1 L_3 L_5 R_1 R_3 R_5 L_2 L_4 L_6 R_2 R_4 R_6</math> जहाँ  <math>L_i,R_i </math>प्रतिनिधित्व करना <math>i</math>-2 मध्यवर्ती फ़्रेमों के बाद फ़्रेम से बाएँ और दाएँ नमूने।
+प्रारंभ में, बाइट्स को नए फ़्रेम बनाने के लिए क्रमपरिवर्तित किया जाता है <math>L_1 L_3 L_5 R_1 R_3 R_5 L_2 L_4 L_6 R_2 R_4 R_6</math> जहाँ  <math>L_i,R_i </math>प्रतिनिधित्व करना <math>i</math>-2 मध्यवर्ती फ़्रेमों के पश्चात  फ़्रेम से बाएँ और दाएँ नमूने।
-इसके बाद, इन 24 संदेश प्रतीकों को C2 (28,24,5) रीड-सोलोमन कोड का उपयोग करके एन्कोड किया गया है जो कि संक्षिप्त RS कोड है <math>\mathbb{F}_{256}</math>. यह दो-त्रुटि-सुधार करने वाला है, न्यूनतम दूरी 5 का है। यह अतिरेक के 4 बाइट्स जोड़ता है, <math>P_1 P_2</math> नया फ्रेम बनाना: <math>L_1 L_3 L_5 R_1 R_3 R_5 P_1 P_2 L_2 L_4 L_6 R_2 R_4 R_6</math>. परिणामी 28-प्रतीक कोडवर्ड को (28.4) क्रॉस इंटरलीवर के माध्यम से पारित किया जाता है, जिससे 28 इंटरलीव्ड प्रतीक बन जाते हैं। फिर इन्हें C1 (32,28,5) RS कोड से गुजारा जाता है, जिसके परिणामस्वरूप 32 कोडित आउटपुट प्रतीकों के कोडवर्ड प्राप्त होते हैं। किसी कोडवर्ड के विषम संख्या वाले प्रतीकों को अगले कोडवर्ड के सम संख्या वाले प्रतीकों के साथ फिर से समूहीकृत किया जाता है ताकि किसी भी छोटे बर्स्ट  को तोड़ा जा सके जो उपरोक्त 4-फ्रेम विलंब इंटरलीविंग के बाद भी मौजूद हो सकता है। इस प्रकार, प्रत्येक 24 इनपुट प्रतीकों के लिए 32 आउटपुट प्रतीक होंगे <math> R = 24/32 </math>. अंत में नियंत्रण और प्रदर्शन जानकारी की बाइट जोड़ी जाती है।<ref name = "Lin, Shu" />33 बाइट्स में से प्रत्येक को ईएफएम (आठ से चौदह मॉड्यूलेशन) के माध्यम से 17 बिट्स में परिवर्तित किया जाता है और 3 मर्ज बिट्स को जोड़ा जाता है। इसलिए, छह नमूनों के फ्रेम का परिणाम 33 बाइट्स × 17 बिट्स (561 बिट्स) होता है, जिसमें 24 सिंक्रोनाइज़ेशन बिट्स और 3 मर्जिंग बिट्स जोड़े जाते हैं, जिससे कुल 588 बिट्स प्राप्त होते हैं।
+इसके पश्चात , इन 24 संदेश प्रतीकों को C2 (28,24,5) रीड-सोलोमन कोड का उपयोग करके एन्कोड किया गया है जो कि संक्षिप्त RS कोड है <math>\mathbb{F}_{256}</math>. यह दो-त्रुटि-सुधार करने वाला है, न्यूनतम दूरी 5 का है। यह अतिरेक के 4 बाइट्स जोड़ता है, <math>P_1 P_2</math> नया फ्रेम बनाना: <math>L_1 L_3 L_5 R_1 R_3 R_5 P_1 P_2 L_2 L_4 L_6 R_2 R_4 R_6</math>. परिणामी 28-प्रतीक कोडवर्ड को (28.4) क्रॉस इंटरलीवर के माध्यम से पारित किया जाता है, जिससे 28 इंटरलीव्ड प्रतीक बन जाते हैं। फिर इन्हें C1 (32,28,5) RS कोड से गुजारा जाता है, जिसके परिणामस्वरूप 32 कोडित आउटपुट प्रतीकों के कोडवर्ड प्राप्त होते हैं। किसी कोडवर्ड के विषम संख्या वाले प्रतीकों को अगले कोडवर्ड के सम संख्या वाले प्रतीकों के साथ फिर से समूहीकृत किया जाता है ताकि किसी भी छोटे बर्स्ट  को तोड़ा जा सके जो उपरोक्त 4-फ्रेम विलंब इंटरलीविंग के पश्चात  भी मौजूद हो सकता है। इस प्रकार, प्रत्येक 24 इनपुट प्रतीकों के लिए 32 आउटपुट प्रतीक होंगे <math> R = 24/32 </math>. अंत में नियंत्रण और प्रदर्शन जानकारी की बाइट जोड़ी जाती है।<ref name = "Lin, Shu" />33 बाइट्स में से प्रत्येक को ईएफएम (आठ से चौदह मॉड्यूलेशन) के माध्यम से 17 बिट्स में परिवर्तित किया जाता है और 3 मर्ज बिट्स को जोड़ा जाता है। इसलिए, छह नमूनों के फ्रेम का परिणाम 33 बाइट्स × 17 बिट्स (561 बिट्स) होता है, जिसमें 24 सिंक्रोनाइज़ेशन बिट्स और 3 मर्जिंग बिट्स जोड़े जाते हैं, जिससे कुल 588 बिट्स प्राप्त होते हैं।
-डिकोडिंग: सीडी प्लेयर (सीआईआरसी डिकोडर) 32 आउटपुट सिंबल डेटा स्ट्रीम प्राप्त करता है। यह धारा पहले डिकोडर D1 से होकर गुजरती है। डिकोडिंग विधियों पर निर्णय लेना और अपने उत्पाद प्रदर्शन को अनुकूलित करना सीडी सिस्टम के व्यक्तिगत डिजाइनरों पर निर्भर है। न्यूनतम दूरी 5 होने के कारण D1, D2 डिकोडर प्रत्येक के संयोजन को सही कर सकते हैं <math>e</math> त्रुटियाँ और <math>f</math> ऐसे मिटाता है <math>2e+f<5</math>.<ref name = "Lin, Shu" />अधिकांश डिकोडिंग समाधानों में, D1 को एकल त्रुटि को ठीक करने के लिए डिज़ाइन किया गया है। और 1 से अधिक त्रुटि के उपस्तिथियां  में, यह डिकोडर 28 इरेज़र आउटपुट करता है। अगले चरण में डीइंटरलीवर इन विलोपनों को 28 डी2 कोडवर्ड में वितरित करता है। पुनः अधिकांश समाधानों में, D2 को केवल मिटाने से निपटने के लिए सेट किया गया है (एक सरल और कम महंगा समाधान)। यदि 4 से अधिक विलोपन का सामना करना पड़ता है, तो 24 विलोपन D2 द्वारा आउटपुट होते हैं। इसके बाद, त्रुटि छुपाने वाली प्रणाली अचूक प्रतीकों के उपस्तिथियां  में (पड़ोसी प्रतीकों से) प्रक्षेप करने का प्रयास करती है, जिसमें विफल रहने पर ऐसे गलत प्रतीकों के अनुरूप ध्वनियाँ म्यूट हो जाती हैं।
+डिकोडिंग: सीडी प्लेयर (सीआईआरसी डिकोडर) 32 आउटपुट सिंबल डेटा स्ट्रीम प्राप्त करता है। यह धारा पहले डिकोडर D1 से होकर गुजरती है। डिकोडिंग विधियों पर निर्णय लेना और अपने उत्पाद प्रदर्शन को अनुकूलित करना सीडी सिस्टम के व्यक्तिगत डिजाइनरों पर निर्भर है। न्यूनतम दूरी 5 होने के कारण D1, D2 डिकोडर प्रत्येक के संयोजन को सही कर सकते हैं <math>e</math> त्रुटियाँ और <math>f</math> ऐसे मिटाता है <math>2e+f<5</math>.<ref name = "Lin, Shu" />अधिकांश डिकोडिंग समाधानों में, D1 को एकल त्रुटि को ठीक करने के लिए डिज़ाइन किया गया है। और 1 से अधिक त्रुटि के उपस्तिथियां  में, यह डिकोडर 28 इरेज़र आउटपुट करता है। अगले चरण में डीइंटरलीवर इन विलोपनों को 28 डी2 कोडवर्ड में वितरित करता है। पुनः अधिकांश समाधानों में, D2 को केवल मिटाने से निपटने के लिए सेट किया गया है (एक सरल और कम महंगा समाधान)। यदि 4 से अधिक विलोपन का सामना करना पड़ता है, तो 24 विलोपन D2 द्वारा आउटपुट होते हैं। इसके पश्चात , त्रुटि छुपाने वाली प्रणाली अचूक प्रतीकों के उपस्तिथियां  में (पड़ोसी प्रतीकों से) प्रक्षेप करने का प्रयास करती है, जिसमें विफल रहने पर ऐसे गलत प्रतीकों के अनुरूप ध्वनियाँ म्यूट हो जाती हैं।
 सीआईआरसी का प्रदर्शन:<ref name = "Algebraic Error Control Codes" />सीआईआरसी सरल रैखिक प्रक्षेप द्वारा लंबी बस्ट त्रुटियों को छुपाता है। 2.5 मिमी ट्रैक लंबाई (4000 बिट्स) अधिकतम पूरी तरह से सुधार योग्य बर्स्ट लंबाई है। 7.7 मिमी ट्रैक लंबाई (12,300 बिट्स) अधिकतम बर्स्ट लंबाई है जिसे इंटरपोल किया जा सकता है। बिट त्रुटि दर (बीईआर) पर नमूना प्रक्षेप दर हर 10 घंटे में होती है <math>= 10^{-4}</math> और बीईआर पर प्रति मिनट 1000 नमूने = <math>10^{-3}</math> अज्ञात त्रुटि नमूने (क्लिक): बीईआर = पर हर 750 घंटे में से कम <math>10^{-3}</math> और BER = पर नगण्य <math>10^{-4}</math>.

Anonymous

Search

बर्स्ट त्रुटि-सुधार करने वाले कोड: Difference between revisions

Namespaces

More

Page actions

Revision as of 13:12, 2 August 2023

Contents

परिभाषाएँ

बर्स्ट विवरण

बर्स्ट त्रुटि सुधार के लिए चक्रीय कोड

बर्स्ट त्रुटि सुधार सीमा

बर्स्ट त्रुटि का पता लगाने और सुधार पर ऊपरी सीमा

बर्स्ट त्रुटि सुधार पर आगे की सीमाएं

अग्नि कोड^[3]^[4]^[5]

प्रमेय का प्रमाण

उदाहरण: फायर कोड को सही करने में 5-बर्स्ट त्रुटि

बाइनरी रीड-सोलोमन कोड

बाइनरी आरएस कोड का उदाहरण

इंटरलीव्ड कोड

इंटरलीवर की बर्स्ट त्रुटि सुधार क्षमता

ब्लॉक इंटरलीवर

कन्वेंशनल इंटरलीवर

अनुप्रयोग

कॉम्पैक्ट डिस्क

यह भी देखें

संदर्भ

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

बर्स्ट त्रुटि-सुधार करने वाले कोड: Difference between revisions

Revision as of 13:12, 2 August 2023

परिभाषाएँ

बर्स्ट विवरण

बर्स्ट त्रुटि सुधार के लिए चक्रीय कोड

बर्स्ट त्रुटि सुधार सीमा

बर्स्ट त्रुटि का पता लगाने और सुधार पर ऊपरी सीमा

बर्स्ट त्रुटि सुधार पर आगे की सीमाएं

अग्नि कोड[3][4][5]

प्रमेय का प्रमाण

उदाहरण: फायर कोड को सही करने में 5-बर्स्ट त्रुटि

बाइनरी रीड-सोलोमन कोड

बाइनरी आरएस कोड का उदाहरण

इंटरलीव्ड कोड

इंटरलीवर की बर्स्ट त्रुटि सुधार क्षमता

ब्लॉक इंटरलीवर

कन्वेंशनल इंटरलीवर

अनुप्रयोग

कॉम्पैक्ट डिस्क

यह भी देखें

संदर्भ

Navigation

Wiki tools

Page tools

Other projects

Categories

अग्नि कोड^[3]^[4]^[5]