जाल के प्रकार: Difference between revisions
No edit summary |
No edit summary |
||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 4: | Line 4: | ||
===द्वि-आयामी=== | ===द्वि-आयामी=== | ||
[[File:Two Dim Grid.PNG|right|260px|thumb| | [[File:Two Dim Grid.PNG|right|260px|thumb|मूलभूत द्वि-आयामी सेल आकृतियाँ]]सामान्यतः दो प्रकार की द्वि-आयामी सेल आकृतियाँ उपयोग की जाती हैं। यह त्रिभुज और चतुर्भुज हैं। | ||
कम्प्यूटेशनल रूप से निर्गुण तत्वों में तेज [[आंतरिक कोण]] या छोटे किनारे या दोनों होंगे। | कम्प्यूटेशनल रूप से निर्गुण तत्वों में तेज [[आंतरिक कोण]] या छोटे किनारे या दोनों होंगे। | ||
| Line 17: | Line 17: | ||
===त्रि-आयामी=== | ===त्रि-आयामी=== | ||
[[File:Three Dim Grid.PNG|right|thumb|320px| | [[File:Three Dim Grid.PNG|right|thumb|320px|आधारभूत त्रि-आयामी सेल आकृतियाँ]]मूल 3-आयामी तत्व [[ चतुर्पाश्वीय ]], [[चतुर्भुज पिरामिड]], [[त्रिकोणीय प्रिज्म]] और [[ षट्फलक ]] हैं। उन सभी के फलक त्रिकोणीय और चतुर्भुज हैं। | ||
एक्सट्रूडेड 2-आयामी मॉडल को पूरी तरह से प्रिज्म और हेक्साहेड्रा द्वारा एक्सट्रूडेड त्रिकोण और चतुर्भुज के रूप में दर्शाया जा सकता है। | एक्सट्रूडेड 2-आयामी मॉडल को पूरी तरह से प्रिज्म और हेक्साहेड्रा द्वारा एक्सट्रूडेड त्रिकोण और चतुर्भुज के रूप में दर्शाया जा सकता है। | ||
| Line 27: | Line 27: | ||
====पिरामिड==== | ====पिरामिड==== | ||
चतुर्भुज-आधारित [[वर्गाकार पिरामिड]] में 5 शीर्ष, 8 किनारे होते हैं, जो 4 त्रिकोणीय और 1 चतुर्भुज फलक से घिरा होता है। इन्हें प्रभावी रूप से वर्गाकार और त्रिकोणीय फलक वाले तत्वों और अन्य संकर मेशों और ग्रिडों के | चतुर्भुज-आधारित [[वर्गाकार पिरामिड]] में 5 शीर्ष, 8 किनारे होते हैं, जो 4 त्रिकोणीय और 1 चतुर्भुज फलक से घिरा होता है। इन्हें प्रभावी रूप से वर्गाकार और त्रिकोणीय फलक वाले तत्वों और अन्य संकर मेशों और ग्रिडों के मध्य संक्रमण तत्वों के रूप में उपयोग किया जाता है। | ||
====त्रिकोणीय प्रिज्म ==== | ====त्रिकोणीय प्रिज्म ==== | ||
| Line 33: | Line 33: | ||
====हेक्साहेड्रोन==== | ====हेक्साहेड्रोन==== | ||
हेक्साहेड्रोन, टोपोलॉजिकल [[ घनक्षेत्र ]], में 8 शीर्ष, 12 किनारे होते हैं, जो 6 चतुर्भुज | हेक्साहेड्रोन, टोपोलॉजिकल [[ घनक्षेत्र ]], में 8 शीर्ष, 12 किनारे होते हैं, जो 6 चतुर्भुज फलकों से घिरा होता है। इसे हेक्स या ईंट भी कहा जाता है।<ref>{{Cite web |url=http://www.colorado.edu/engineering/CAS/courses.d/AFEM.d/AFEM.Ch11.d/AFEM.Ch11.pdf |title=हेक्साहेड्रोन तत्व|access-date=2015-04-13 |archive-date=2015-02-24 |archive-url=https://web.archive.org/web/20150224172824/http://www.colorado.edu/engineering/CAS/courses.d/AFEM.d/AFEM.Ch11.d/AFEM.Ch11.pdf |url-status=dead }}</ref> समान सेल मात्रा के लिए, हेक्साहेड्रल मेश में समाधान की शुद्धता सबसे अधिक है। | ||
पिरामिड और त्रिकोणीय प्रिज्म क्षेत्रों को कम्प्यूटेशनल रूप से पतित हेक्साहेड्रोन के रूप में माना जा सकता है, जहां कुछ किनारों को शून्य कर दिया गया है। हेक्साहेड्रोन के अन्य विकृत रूपों का भी प्रतिनिधित्व किया जा सकता है। | पिरामिड और त्रिकोणीय प्रिज्म क्षेत्रों को कम्प्यूटेशनल रूप से पतित हेक्साहेड्रोन के रूप में माना जा सकता है, जहां कुछ किनारों को शून्य कर दिया गया है। हेक्साहेड्रोन के अन्य विकृत रूपों का भी प्रतिनिधित्व किया जा सकता है। | ||
====उन्नत सेल ([[ बहुतल ]])==== | ====उन्नत सेल ([[ बहुतल ]])==== | ||
बहुफलकीय (दोहरे) तत्व में किसी भी संख्या में शीर्ष, किनारे और फलक होते हैं। | बहुफलकीय (दोहरे) तत्व में किसी भी संख्या में शीर्ष, किनारे और फलक होते हैं। मध्य की संख्या (सामान्यतः 10) के कारण इसे सामान्यतः प्रति सेल अधिक कंप्यूटिंग संचालन की आवश्यकता होती है।<ref>{{Cite web |url=http://www.plmmarketplace.com/upload/Temp/The_Advantage_of_polyhedral.pdf |title=संग्रहीत प्रति|access-date=2018-01-10 |archive-date=2013-12-06 |archive-url=https://web.archive.org/web/20131206232340/http://www.plmmarketplace.com/upload/Temp/The_Advantage_of_polyhedral.pdf |url-status=dead }}</ref> चूँकि इसकी भरपाई गणना की शुद्धता से की जाती है। | ||
==ग्रिडों का वर्गीकरण== | ==ग्रिडों का वर्गीकरण== | ||
| Line 46: | Line 46: | ||
===संरचित ग्रिड=== | ===संरचित ग्रिड=== | ||
संरचित ग्रिडों की पहचान नियमित कनेक्टिविटी द्वारा की जाती है। संभावित तत्व विकल्प द्वि-आयामी में चतुर्भुज और त्रि-आयामी में हेक्साहेड्रा हैं। यह मॉडल अत्यधिक स्थान कुशल है, क्योंकि निकट के | संरचित ग्रिडों की पहचान नियमित कनेक्टिविटी द्वारा की जाती है। संभावित तत्व विकल्प द्वि-आयामी में चतुर्भुज और त्रि-आयामी में हेक्साहेड्रा हैं। यह मॉडल अत्यधिक स्थान कुशल है, क्योंकि निकट के संबंध संचयन व्यवस्था द्वारा परिभाषित होते हैं। असंरचित ग्रिड की तुलना में संरचित ग्रिड के कुछ अन्य लाभ उत्तम अभिसरण और उच्च रिज़ॉल्यूशन हैं।<ref>{{Cite web | url=http://www.pointwise.com/theconnector/March-2013/Structured-Grids-in-Pointwise.shtml | title=Quality and Control - Two Reasons Why Structured Grids Aren't Going Away}}</ref><ref>{{citation | journal=Society for Industrial and Applied Mathematics, Philadelphia | first=J.E. | last=Castillo | year=1991 | title=Mathematical aspects of grid Generation }}</ref><ref>{{citation | first=P.L. | last=George | year=1991 | title=Automatic Mesh Generation }}</ref> | ||
===असंरचित ग्रिड=== | ===असंरचित ग्रिड=== | ||
असंरचित ग्रिड की पहचान अनियमित कनेक्टिविटी से होती है। इसे आसानी से कंप्यूटर मेमोरी में द्वि-आयामी या त्रि-आयामी सरणी के रूप में व्यक्त नहीं किया जा सकता है। यह किसी भी संभावित तत्व की अनुमति देता है जिसे सॉल्वर उपयोग करने में सक्षम हो सकता है। संरचित मेशों की तुलना में, जिनके लिए निकट के | असंरचित ग्रिड की पहचान अनियमित कनेक्टिविटी से होती है। इसे आसानी से कंप्यूटर मेमोरी में द्वि-आयामी या त्रि-आयामी सरणी के रूप में व्यक्त नहीं किया जा सकता है। यह किसी भी संभावित तत्व की अनुमति देता है जिसे सॉल्वर उपयोग करने में सक्षम हो सकता है। संरचित मेशों की तुलना में, जिनके लिए निकट के संबंध अंतर्निहित हैं, यह मॉडल अत्यधिक स्थान अक्षम हो सकता है क्योंकि इसमें निकट के संबंधों के स्पष्ट संचयन की आवश्यकता होती है। चूँकि, यह ध्यान दिया जाना चाहिए कि संरचित ग्रिड और असंरचित ग्रिड की संचयन आवश्यकताएँ स्थिर कारक के अन्दर हैं। यह ग्रिड सामान्यतः द्वि-आयामी में त्रिकोण और त्रि-आयामी में टेट्राहेड्रल का उपयोग करते हैं।<ref>{{Citation | last1=Mavriplis | first1=D.J. | title=Mesh Generation and adaptivity for complex geometries and flows | work=Handbook of Computational Fluid Mechanics | year=1996 }}</ref> | ||
===हाइब्रिड ग्रिड=== | ===हाइब्रिड ग्रिड=== | ||
हाइब्रिड ग्रिड में संरचित भागों और असंरचित भागों का मिश्रण होता है। यह संरचित मेशों और असंरचित मेशों को कुशल प्रणाली से एकीकृत करता है। ज्यामिति के | हाइब्रिड ग्रिड में संरचित भागों और असंरचित भागों का मिश्रण होता है। यह संरचित मेशों और असंरचित मेशों को कुशल प्रणाली से एकीकृत करता है। ज्यामिति के वह भाग जो नियमित हैं उनमें संरचित ग्रिड हो सकते हैं और जो जटिल हैं उनमें असंरचित ग्रिड हो सकते हैं। यह ग्रिड गैर-अनुरूप हो सकते हैं जिसका अर्थ है कि ग्रिड लाइनों को ब्लॉक सीमाओं पर मेल खाने की आवश्यकता नहीं है।<ref>{{Citation | last1=Bern | first1=Marshall | last2=Plassmann | first2=Paul | title=Mesh Generation | work=Handbook of Computational Geometry. Elsevier Science | year=2000 }}</ref> | ||
==मेष गुणवत्ता== | ==मेष गुणवत्ता== | ||
यदि अधिक त्रुटिहीन समाधान की गणना अधिक तेज़ी से की जाती है | यदि अधिक त्रुटिहीन समाधान की गणना अधिक तेज़ी से की जाती है तब मेश को उच्च गुणवत्ता वाला माना जाता है। शुद्धता और गति तनाव में हैं। मेश का आकार कम करने से सदैव शुद्धता बढ़ती है किन्तु कम्प्यूटेशनल निवेश भी बढ़ जाती है। | ||
शुद्धता विवेकाधीन त्रुटि और समाधान त्रुटि दोनों पर निर्भर करती है। विवेकाधीन त्रुटि के लिए, दिया गया मेश अंतरिक्ष का | शुद्धता विवेकाधीन त्रुटि और समाधान त्रुटि दोनों पर निर्भर करती है। विवेकाधीन त्रुटि के लिए, दिया गया मेश अंतरिक्ष का भिन्न अनुमान है, और इसलिए केवल अनुमानित समाधान प्रदान कर सकता है, तथापि समीकरण बिल्कुल समाधान हो जाएं। (कंप्यूटर ग्राफिक्स रे ट्रेसिंग (ग्राफिक्स) में, छोड़ी गई किरणों की संख्या विवेकाधीन त्रुटि का अन्य स्रोत है।) समाधान त्रुटि के लिए, पीडीई के लिए पूरे मेश पर अनेक पुनरावृत्तियों की आवश्यकता होती है। समीकरणों को त्रुटिहीन रूप से समाधान करने से पहले, गणना जल्दी समाप्त कर दी जाती है। मेश तत्व प्रकार का चयन विवेकीकरण और समाधान त्रुटि दोनों को प्रभावित करता है। | ||
शुद्धता तत्वों की कुल संख्या और व्यक्तिगत तत्वों के आकार दोनों पर निर्भर करती है। प्रत्येक पुनरावृत्ति की गति तत्वों की संख्या के साथ (रैखिक रूप से) बढ़ती है, और आवश्यक पुनरावृत्तियों की संख्या स्थानीय तत्वों के आकार और आकार की तुलना में स्थानीय समाधान | शुद्धता तत्वों की कुल संख्या और व्यक्तिगत तत्वों के आकार दोनों पर निर्भर करती है। प्रत्येक पुनरावृत्ति की गति तत्वों की संख्या के साथ (रैखिक रूप से) बढ़ती है, और आवश्यक पुनरावृत्तियों की संख्या स्थानीय तत्वों के आकार और आकार की तुलना में स्थानीय समाधान मान और ढाल पर निर्भर करती है। | ||
===समाधान परिशुद्धता=== | ===समाधान परिशुद्धता=== | ||
यदि समाधान स्थिर है | यदि समाधान स्थिर है तब मोटा मेश त्रुटिहीन समाधान प्रदान कर सकता है, इसलिए शुद्धता विशेष समस्या उदाहरण पर निर्भर करती है। | ||
कोई उन क्षेत्रों में मेश को | |||
कोई उन क्षेत्रों में मेश को श्रेष्ठ रूप से परिष्कृत कर सकता है जहां समाधान प्रवणता अधिक है, इस प्रकार वहां निष्ठा बढ़ जाती है। किसी तत्व के अन्दर प्रक्षेपित मूल्यों सहित शुद्धता, तत्व के प्रकार और आकार पर निर्भर करती है। | |||
===अभिसरण की दर=== | ===अभिसरण की दर=== | ||
प्रत्येक पुनरावृत्ति गणना और सही समाधान के | प्रत्येक पुनरावृत्ति गणना और सही समाधान के मध्य त्रुटि को कम करती है। | ||
[[अभिसरण (गणित)]] की तेज़ दर का अर्थ | |||
[[अभिसरण (गणित)]] की तेज़ दर का अर्थ कम पुनरावृत्तियों के साथ छोटी त्रुटि होता है। | |||
निम्न गुणवत्ता का मेश द्रव प्रवाह के लिए सीमा परत जैसी महत्वपूर्ण विशेषताओं को छोड़ सकता है। विवेकाधीन त्रुटि बड़ी होगी और अभिसरण की दर ख़राब हो जाएगी; समाधान बिल्कुल भी नहीं मिल सकता है। | निम्न गुणवत्ता का मेश द्रव प्रवाह के लिए सीमा परत जैसी महत्वपूर्ण विशेषताओं को छोड़ सकता है। विवेकाधीन त्रुटि बड़ी होगी और अभिसरण की दर ख़राब हो जाएगी; समाधान बिल्कुल भी नहीं मिल सकता है। | ||
===ग्रिड स्वतंत्रता=== | ===ग्रिड स्वतंत्रता=== | ||
समाधान को ग्रिड-स्वतंत्र माना जाता है यदि पर्याप्त पुनरावृत्तियों को देखते हुए विवेकीकरण और समाधान त्रुटि | समाधान को ग्रिड-स्वतंत्र माना जाता है यदि पर्याप्त पुनरावृत्तियों को देखते हुए विवेकीकरण और समाधान त्रुटि अधिक छोटी हो। तुलनात्मक परिणामों के लिए यह जानना आवश्यक है। मेश अभिसरण अध्ययन में तत्वों को परिष्कृत करना और परिष्कृत समाधानों की मोटे समाधानों से तुलना करना सम्मिलित है। यदि आगे परिशोधन (या अन्य परिवर्तन) से समाधान में महत्वपूर्ण परिवर्तन नहीं होता है, तब मेश स्वतंत्र ग्रिड है। | ||
==मेश का प्रकार तय करना== | ==मेश का प्रकार तय करना== | ||
[[File:Skweness.PNG|thumb|right|150px|समबाहु आयतन पर आधारित तिरछापन]]यदि शुद्धता सबसे अधिक चिंता का विषय है | [[File:Skweness.PNG|thumb|right|150px|समबाहु आयतन पर आधारित तिरछापन]]यदि शुद्धता सबसे अधिक चिंता का विषय है तब हेक्साहेड्रल मेश सबसे उत्तम है। सभी प्रवाह सुविधाओं को कैप्चर करने के लिए मेश का घनत्व पर्याप्त रूप से उच्च होना आवश्यक है, किन्तु ही नोट पर, यह इतना अधिक नहीं होना चाहिए कि यह प्रवाह के अनावश्यक विवरणों को कैप्चर कर ले, इस प्रकार सीपीयू पर लोड पड़ेगा और अधिक समय बर्बाद होगा। जब भी कोई दीवार उपस्थित होती है, तब दीवार से सटा हुआ मेश सीमा परत के प्रवाह का समाधान करने के लिए अधिक सूक्ष्म होता है और सामान्यतः त्रिकोण, टेट्राहेड्रोन और पिरामिड की तुलना में क्वाड, हेक्स और प्रिज्म सेलों को प्राथमिकता दी जाती है। क्वाड और हेक्स सेलों को प्रसारित किया जा सकता है जहां प्रवाह पूरी तरह से विकसित और एक-आयामी है। | ||
[[File:Skewnessquad.PNG|thumb|right|250px|चतुर्भुज की विषमता को दर्शाता है]]तिरछापन, चिकनापन और | [[File:Skewnessquad.PNG|thumb|right|250px|चतुर्भुज की विषमता को दर्शाता है]]तिरछापन, चिकनापन और आयाम अनुपात के आधार पर, मेश की उपयुक्तता तय की जा सकती है।<ref>{{cite web | url =http://www.bakker.org| title= Meshing,Lecture 7 | accessdate=2012-11-10 |publisher= Andre Bakker }}</ref> | ||
<ref>{{cite web | url =http://www.bakker.org| title= Meshing,Lecture 7 | accessdate=2012-11-10 |publisher= Andre Bakker }}</ref> | |||
| Line 88: | Line 89: | ||
====समबाहु आयतन के आधार पर==== | ====समबाहु आयतन के आधार पर==== | ||
यह विधि केवल त्रिभुजों और चतुष्फलकीय पर | यह विधि केवल त्रिभुजों और चतुष्फलकीय पर प्रायुक्त होती है और डिफ़ॉल्ट विधि है। | ||
:<math>\text{ Skewness }=\frac{\text{ optimal cell size - cell size }}{\text{optimal cell size}}</math> | :<math>\text{ Skewness }=\frac{\text{ optimal cell size - cell size }}{\text{optimal cell size}}</math> | ||
[[File:Smooth and Large Jump.PNG|right|300px|thumb|चिकनी और बड़ी | [[File:Smooth and Large Jump.PNG|right|300px|thumb|चिकनी और बड़ी जम्प परिवर्तन]] | ||
====सामान्यीकृत समबाहु कोण से विचलन के आधार पर==== | ====सामान्यीकृत समबाहु कोण से विचलन के आधार पर==== | ||
यह विधि सभी सेल और फलक के आकार पर | यह विधि सभी सेल और फलक के आकार पर प्रायुक्त होती है और लगभग सदैव प्रिज्म और पिरामिड के लिए उपयोग की जाती है | ||
:<math>\text{ Skewness ( for a quad ) } = \max{ \left[\frac{\theta_\text{max} - 90}{90}, \frac{90 - \theta_\text{min}}{90}\right] }</math> | :<math>\text{ Skewness ( for a quad ) } = \max{ \left[\frac{\theta_\text{max} - 90}{90}, \frac{90 - \theta_\text{min}}{90}\right] }</math> | ||
| Line 100: | Line 101: | ||
गुणवत्ता का अन्य सामान्य माप समकोणीय तिरछापन पर आधारित है। | गुणवत्ता का अन्य सामान्य माप समकोणीय तिरछापन पर आधारित है। | ||
:<math>\text{ Equiangle Skew } =\max{ \left[\frac{\theta_\text{max} - \theta_e}{180 - \theta_e},\frac{\theta_e - \theta_\text{min}}{\theta_e} \right]}</math> | :<math>\text{ Equiangle Skew } =\max{ \left[\frac{\theta_\text{max} - \theta_e}{180 - \theta_e},\frac{\theta_e - \theta_\text{min}}{\theta_e} \right]}</math> | ||
जहाँ: | |||
*<math>\theta_\text{max}\,</math> किसी फलक या सेल में सबसे बड़ा कोण है, | *<math>\theta_\text{max}\,</math> किसी फलक या सेल में सबसे बड़ा कोण है, | ||
*<math>\theta_\text{min}\,</math> किसी फलक या सेल का सबसे छोटा कोण है, | *<math>\theta_\text{min}\,</math> किसी फलक या सेल का सबसे छोटा कोण है, | ||
*<math>\theta_{e}\,</math> समकोणीय फलक या सेल के लिए कोण है अर्थात त्रिभुज के लिए 60 और वर्ग के लिए | *<math>\theta_{e}\,</math> समकोणीय फलक या सेल के लिए कोण है अर्थात त्रिभुज के लिए 60 और वर्ग के लिए 90 है। | ||
0 का तिरछापन सर्वोत्तम संभव है और किसी का तिरछापन लगभग कभी भी पसंद नहीं किया जाता है। हेक्स और क्वाड सेलों के लिए, | 0 का तिरछापन सर्वोत्तम संभव है और किसी का तिरछापन लगभग कभी भी पसंद नहीं किया जाता है। हेक्स और क्वाड सेलों के लिए, अधिक त्रुटिहीन समाधान प्राप्त करने के लिए तिरछापन 0.85 से अधिक नहीं होना चाहिए। | ||
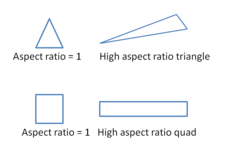
[[File:Aspect ratio grid.PNG|thumb|right|225px|पक्षानुपात में परिवर्तन को दर्शाता है]]त्रिकोणीय सेलों के लिए, तिरछापन 0.85 से अधिक नहीं होना चाहिए और चतुर्भुज सेलों के लिए, तिरछापन 0.9 से अधिक नहीं होना चाहिए। | [[File:Aspect ratio grid.PNG|thumb|right|225px|पक्षानुपात में परिवर्तन को दर्शाता है]]त्रिकोणीय सेलों के लिए, तिरछापन 0.85 से अधिक नहीं होना चाहिए और चतुर्भुज सेलों के लिए, तिरछापन 0.9 से अधिक नहीं होना चाहिए। | ||
===चिकनापन=== | ===चिकनापन=== | ||
आकार में परिवर्तन भी सहज होना चाहिए। सेल के आकार में अचानक उछाल नहीं होना चाहिए क्योंकि इससे | आकार में परिवर्तन भी सहज होना चाहिए। सेल के आकार में अचानक उछाल नहीं होना चाहिए क्योंकि इससे निकटतम के नोड्स पर गलत परिणाम हो सकते हैं। | ||
=== | ===आयाम अनुपात=== | ||
यह किसी सेल में सबसे लंबी और सबसे छोटी भुजा का अनुपात है। सर्वोत्तम परिणाम सुनिश्चित करने के लिए आदर्श रूप से यह 1 के | यह किसी सेल में सबसे लंबी और सबसे छोटी भुजा का अनुपात है। सर्वोत्तम परिणाम सुनिश्चित करने के लिए आदर्श रूप से यह 1 के समान होना चाहिए। [[बहुआयामी]] प्रवाह के लिए यह के निकट होना चाहिए। इसके अतिरिक्त सेल आकार में स्थानीय भिन्नताएं न्यूनतम होनी चाहिए, अर्थात् आसन्न सेल आकार में 20% से अधिक अंतर नहीं होना चाहिए। बड़े आयाम अनुपात होने से अस्वीकार्य परिमाण की इंटरपोलेशन त्रुटि हो सकती है। | ||
==मेष निर्माण और सुधार== | ==मेष निर्माण और सुधार== | ||
मेश निर्माण और [[ग्रिड निर्माण के सिद्धांत]] भी देखें। | मेश निर्माण और [[ग्रिड निर्माण के सिद्धांत]] भी देखें। | ||
दो आयामों में, फ़्लिपिंग और स्मूथिंग ख़राब मेश को अच्छे मेश में बदलने के लिए शक्तिशाली उपकरण हैं। फ़्लिपिंग में दो त्रिभुजों को मिलाकर चतुर्भुज बनाया जाता है, फिर चतुर्भुज को दूसरी दिशा में विभाजित करके दो नए त्रिभुज बनाए जाते हैं। फ़्लिपिंग का उपयोग तिरछापन जैसे त्रिभुज की गुणवत्ता माप में सुधार के लिए किया जाता है। मेश स्मूथनिंग मेश शीर्षों के स्थान को समायोजित करके तत्व के आकार और समग्र मेश गुणवत्ता को बढ़ाता है। मेश स्मूथिंग में, [[रैखिक प्रणाली]] के गैर-शून्य पैटर्न जैसी मुख्य विशेषताओं को संरक्षित किया जाता है क्योंकि मेश की टोपोलॉजी अपरिवर्तित रहती है। [[लाप्लासियन चौरसाई]] सबसे अधिक | |||
दो आयामों में, फ़्लिपिंग और स्मूथिंग ख़राब मेश को अच्छे मेश में बदलने के लिए शक्तिशाली उपकरण हैं। फ़्लिपिंग में दो त्रिभुजों को मिलाकर चतुर्भुज बनाया जाता है, फिर चतुर्भुज को दूसरी दिशा में विभाजित करके दो नए त्रिभुज बनाए जाते हैं। फ़्लिपिंग का उपयोग तिरछापन जैसे त्रिभुज की गुणवत्ता माप में सुधार के लिए किया जाता है। मेश स्मूथनिंग मेश शीर्षों के स्थान को समायोजित करके तत्व के आकार और समग्र मेश गुणवत्ता को बढ़ाता है। मेश स्मूथिंग में, [[रैखिक प्रणाली]] के गैर-शून्य पैटर्न जैसी मुख्य विशेषताओं को संरक्षित किया जाता है क्योंकि मेश की टोपोलॉजी अपरिवर्तित रहती है। [[लाप्लासियन चौरसाई|लाप्लासियन स्मूथिंग]] सबसे अधिक उपयोग की जाने वाली स्मूथिंग प्रणाली है। | |||
== यह भी देखें == | == यह भी देखें == | ||
*{{annotated link| | *{{annotated link|मेश पीढ़ी}} | ||
*{{annotated link| | *{{annotated link|असंरचित ग्रिड}} | ||
*{{annotated link| | *{{annotated link|नियमित ग्रिड}} | ||
*{{annotated link| | *{{annotated link|विस्तारित ग्रिड विधि}} | ||
== संदर्भ == | == संदर्भ == | ||
| Line 129: | Line 131: | ||
{{Mesh generation|state=autocollapse}} | {{Mesh generation|state=autocollapse}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Collapse templates]] | |||
[[Category:Created On 24/07/2023]] | [[Category:Created On 24/07/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:कम्प्यूटेशनल तरल सक्रिय]] | |||
[[Category:जाल पीढ़ी]] | |||
Latest revision as of 14:34, 11 August 2023
बहुभुज मेश छोटे असतत सेलों द्वारा बड़े ज्यामितीय डोमेन का प्रतिनिधित्व है। मेश का उपयोग सामान्यतः आंशिक अंतर समीकरणों के समाधान की गणना करने और कंप्यूटर ग्राफिक्स प्रस्तुत करने और भौगोलिक और कार्टोग्राफिक डेटा का विश्लेषण करने के लिए किया जाता है। एक मेश स्थान को तत्वों (या सेलों या क्षेत्रों) में विभाजित करता है, जिस पर समीकरणों का समाधान किया जा सकता है, जो तब बड़े डोमेन पर समाधान का अनुमान लगाता है। किसी मॉडल के अन्दर तत्व की सीमाएँ आंतरिक या बाहरी सीमाओं पर स्थित होने के लिए बाध्य हो सकती हैं। उच्च गुणवत्ता वाले (उत्तम आकार वाले) तत्वों में उत्तम संख्यात्मक गुण होते हैं, जहां उत्तम तत्व का गठन सामान्य शासी समीकरणों और मॉडल उदाहरण के विशेष समाधान पर निर्भर करता है।
सामान्य सेल आकार
द्वि-आयामी
सामान्यतः दो प्रकार की द्वि-आयामी सेल आकृतियाँ उपयोग की जाती हैं। यह त्रिभुज और चतुर्भुज हैं।
कम्प्यूटेशनल रूप से निर्गुण तत्वों में तेज आंतरिक कोण या छोटे किनारे या दोनों होंगे।
त्रिभुज
इस सेल के आकार में 3 भुजाएँ होती हैं और यह मेश के सबसे सरल प्रकारों में से है। त्रिकोणीय सतह मेश सदैव त्वरित और आसान होता है। यह असंरचित ग्रिड्स में सबसे सामान्य है।
चतुर्भुज
जैसा कि चित्र में दिखाया गया है, यह सेल का आकार मूल 4 पक्षीय है। यह संरचित ग्रिडों में सबसे सामान्य है।
चतुर्भुज तत्वों को सामान्यतः अवतल होने या बनने से बाहर रखा जाता है।
त्रि-आयामी
मूल 3-आयामी तत्व चतुर्पाश्वीय , चतुर्भुज पिरामिड, त्रिकोणीय प्रिज्म और षट्फलक हैं। उन सभी के फलक त्रिकोणीय और चतुर्भुज हैं।
एक्सट्रूडेड 2-आयामी मॉडल को पूरी तरह से प्रिज्म और हेक्साहेड्रा द्वारा एक्सट्रूडेड त्रिकोण और चतुर्भुज के रूप में दर्शाया जा सकता है।
सामान्यतः, 3-आयामों में चतुर्भुज फलक पूरी तरह से समतल नहीं हो सकते हैं। गैर-तलीय चतुर्भुज फलक को पतला चतुष्फलकीय आयतन माना जा सकता है जो दो निकटतम तत्वों द्वारा साझा किया जाता है।
चतुष्फलक
चतुष्फलक में 4 शीर्ष, 6 किनारे होते हैं और यह 4 त्रिकोणीय फलकों से घिरा होता है। अधिकांश स्थितियों में टेट्राहेड्रल वॉल्यूम मेश स्वचालित रूप से उत्पन्न किया जा सकता है।
पिरामिड
चतुर्भुज-आधारित वर्गाकार पिरामिड में 5 शीर्ष, 8 किनारे होते हैं, जो 4 त्रिकोणीय और 1 चतुर्भुज फलक से घिरा होता है। इन्हें प्रभावी रूप से वर्गाकार और त्रिकोणीय फलक वाले तत्वों और अन्य संकर मेशों और ग्रिडों के मध्य संक्रमण तत्वों के रूप में उपयोग किया जाता है।
त्रिकोणीय प्रिज्म
त्रिकोणीय प्रिज्म में 6 शीर्ष, 9 किनारे हैं, जो 2 त्रिकोणीय और 3 चतुर्भुज फलकों से घिरा है। इस प्रकार की परत का लाभ यह है कि यह सीमा परत को कुशलतापूर्वक समाधान करती है।
हेक्साहेड्रोन
हेक्साहेड्रोन, टोपोलॉजिकल घनक्षेत्र , में 8 शीर्ष, 12 किनारे होते हैं, जो 6 चतुर्भुज फलकों से घिरा होता है। इसे हेक्स या ईंट भी कहा जाता है।[1] समान सेल मात्रा के लिए, हेक्साहेड्रल मेश में समाधान की शुद्धता सबसे अधिक है।
पिरामिड और त्रिकोणीय प्रिज्म क्षेत्रों को कम्प्यूटेशनल रूप से पतित हेक्साहेड्रोन के रूप में माना जा सकता है, जहां कुछ किनारों को शून्य कर दिया गया है। हेक्साहेड्रोन के अन्य विकृत रूपों का भी प्रतिनिधित्व किया जा सकता है।
उन्नत सेल (बहुतल )
बहुफलकीय (दोहरे) तत्व में किसी भी संख्या में शीर्ष, किनारे और फलक होते हैं। मध्य की संख्या (सामान्यतः 10) के कारण इसे सामान्यतः प्रति सेल अधिक कंप्यूटिंग संचालन की आवश्यकता होती है।[2] चूँकि इसकी भरपाई गणना की शुद्धता से की जाती है।
ग्रिडों का वर्गीकरण
संरचित ग्रिड
संरचित ग्रिडों की पहचान नियमित कनेक्टिविटी द्वारा की जाती है। संभावित तत्व विकल्प द्वि-आयामी में चतुर्भुज और त्रि-आयामी में हेक्साहेड्रा हैं। यह मॉडल अत्यधिक स्थान कुशल है, क्योंकि निकट के संबंध संचयन व्यवस्था द्वारा परिभाषित होते हैं। असंरचित ग्रिड की तुलना में संरचित ग्रिड के कुछ अन्य लाभ उत्तम अभिसरण और उच्च रिज़ॉल्यूशन हैं।[3][4][5]
असंरचित ग्रिड
असंरचित ग्रिड की पहचान अनियमित कनेक्टिविटी से होती है। इसे आसानी से कंप्यूटर मेमोरी में द्वि-आयामी या त्रि-आयामी सरणी के रूप में व्यक्त नहीं किया जा सकता है। यह किसी भी संभावित तत्व की अनुमति देता है जिसे सॉल्वर उपयोग करने में सक्षम हो सकता है। संरचित मेशों की तुलना में, जिनके लिए निकट के संबंध अंतर्निहित हैं, यह मॉडल अत्यधिक स्थान अक्षम हो सकता है क्योंकि इसमें निकट के संबंधों के स्पष्ट संचयन की आवश्यकता होती है। चूँकि, यह ध्यान दिया जाना चाहिए कि संरचित ग्रिड और असंरचित ग्रिड की संचयन आवश्यकताएँ स्थिर कारक के अन्दर हैं। यह ग्रिड सामान्यतः द्वि-आयामी में त्रिकोण और त्रि-आयामी में टेट्राहेड्रल का उपयोग करते हैं।[6]
हाइब्रिड ग्रिड
हाइब्रिड ग्रिड में संरचित भागों और असंरचित भागों का मिश्रण होता है। यह संरचित मेशों और असंरचित मेशों को कुशल प्रणाली से एकीकृत करता है। ज्यामिति के वह भाग जो नियमित हैं उनमें संरचित ग्रिड हो सकते हैं और जो जटिल हैं उनमें असंरचित ग्रिड हो सकते हैं। यह ग्रिड गैर-अनुरूप हो सकते हैं जिसका अर्थ है कि ग्रिड लाइनों को ब्लॉक सीमाओं पर मेल खाने की आवश्यकता नहीं है।[7]
मेष गुणवत्ता
यदि अधिक त्रुटिहीन समाधान की गणना अधिक तेज़ी से की जाती है तब मेश को उच्च गुणवत्ता वाला माना जाता है। शुद्धता और गति तनाव में हैं। मेश का आकार कम करने से सदैव शुद्धता बढ़ती है किन्तु कम्प्यूटेशनल निवेश भी बढ़ जाती है।
शुद्धता विवेकाधीन त्रुटि और समाधान त्रुटि दोनों पर निर्भर करती है। विवेकाधीन त्रुटि के लिए, दिया गया मेश अंतरिक्ष का भिन्न अनुमान है, और इसलिए केवल अनुमानित समाधान प्रदान कर सकता है, तथापि समीकरण बिल्कुल समाधान हो जाएं। (कंप्यूटर ग्राफिक्स रे ट्रेसिंग (ग्राफिक्स) में, छोड़ी गई किरणों की संख्या विवेकाधीन त्रुटि का अन्य स्रोत है।) समाधान त्रुटि के लिए, पीडीई के लिए पूरे मेश पर अनेक पुनरावृत्तियों की आवश्यकता होती है। समीकरणों को त्रुटिहीन रूप से समाधान करने से पहले, गणना जल्दी समाप्त कर दी जाती है। मेश तत्व प्रकार का चयन विवेकीकरण और समाधान त्रुटि दोनों को प्रभावित करता है।
शुद्धता तत्वों की कुल संख्या और व्यक्तिगत तत्वों के आकार दोनों पर निर्भर करती है। प्रत्येक पुनरावृत्ति की गति तत्वों की संख्या के साथ (रैखिक रूप से) बढ़ती है, और आवश्यक पुनरावृत्तियों की संख्या स्थानीय तत्वों के आकार और आकार की तुलना में स्थानीय समाधान मान और ढाल पर निर्भर करती है।
समाधान परिशुद्धता
यदि समाधान स्थिर है तब मोटा मेश त्रुटिहीन समाधान प्रदान कर सकता है, इसलिए शुद्धता विशेष समस्या उदाहरण पर निर्भर करती है।
कोई उन क्षेत्रों में मेश को श्रेष्ठ रूप से परिष्कृत कर सकता है जहां समाधान प्रवणता अधिक है, इस प्रकार वहां निष्ठा बढ़ जाती है। किसी तत्व के अन्दर प्रक्षेपित मूल्यों सहित शुद्धता, तत्व के प्रकार और आकार पर निर्भर करती है।
अभिसरण की दर
प्रत्येक पुनरावृत्ति गणना और सही समाधान के मध्य त्रुटि को कम करती है।
अभिसरण (गणित) की तेज़ दर का अर्थ कम पुनरावृत्तियों के साथ छोटी त्रुटि होता है।
निम्न गुणवत्ता का मेश द्रव प्रवाह के लिए सीमा परत जैसी महत्वपूर्ण विशेषताओं को छोड़ सकता है। विवेकाधीन त्रुटि बड़ी होगी और अभिसरण की दर ख़राब हो जाएगी; समाधान बिल्कुल भी नहीं मिल सकता है।
ग्रिड स्वतंत्रता
समाधान को ग्रिड-स्वतंत्र माना जाता है यदि पर्याप्त पुनरावृत्तियों को देखते हुए विवेकीकरण और समाधान त्रुटि अधिक छोटी हो। तुलनात्मक परिणामों के लिए यह जानना आवश्यक है। मेश अभिसरण अध्ययन में तत्वों को परिष्कृत करना और परिष्कृत समाधानों की मोटे समाधानों से तुलना करना सम्मिलित है। यदि आगे परिशोधन (या अन्य परिवर्तन) से समाधान में महत्वपूर्ण परिवर्तन नहीं होता है, तब मेश स्वतंत्र ग्रिड है।
मेश का प्रकार तय करना
यदि शुद्धता सबसे अधिक चिंता का विषय है तब हेक्साहेड्रल मेश सबसे उत्तम है। सभी प्रवाह सुविधाओं को कैप्चर करने के लिए मेश का घनत्व पर्याप्त रूप से उच्च होना आवश्यक है, किन्तु ही नोट पर, यह इतना अधिक नहीं होना चाहिए कि यह प्रवाह के अनावश्यक विवरणों को कैप्चर कर ले, इस प्रकार सीपीयू पर लोड पड़ेगा और अधिक समय बर्बाद होगा। जब भी कोई दीवार उपस्थित होती है, तब दीवार से सटा हुआ मेश सीमा परत के प्रवाह का समाधान करने के लिए अधिक सूक्ष्म होता है और सामान्यतः त्रिकोण, टेट्राहेड्रोन और पिरामिड की तुलना में क्वाड, हेक्स और प्रिज्म सेलों को प्राथमिकता दी जाती है। क्वाड और हेक्स सेलों को प्रसारित किया जा सकता है जहां प्रवाह पूरी तरह से विकसित और एक-आयामी है।
तिरछापन, चिकनापन और आयाम अनुपात के आधार पर, मेश की उपयुक्तता तय की जा सकती है।[8]
तिरछापन
ग्रिड का तिरछापन मेश की गुणवत्ता और उपयुक्तता का उपयुक्त संकेतक है। बड़ा तिरछापन प्रक्षेपित क्षेत्रों की शुद्धता से समझौता करता है। ग्रिड की विषमता निर्धारित करने की तीन विधियाँ हैं।
समबाहु आयतन के आधार पर
यह विधि केवल त्रिभुजों और चतुष्फलकीय पर प्रायुक्त होती है और डिफ़ॉल्ट विधि है।
सामान्यीकृत समबाहु कोण से विचलन के आधार पर
यह विधि सभी सेल और फलक के आकार पर प्रायुक्त होती है और लगभग सदैव प्रिज्म और पिरामिड के लिए उपयोग की जाती है
समकोणीय तिरछा
गुणवत्ता का अन्य सामान्य माप समकोणीय तिरछापन पर आधारित है।
जहाँ:
- किसी फलक या सेल में सबसे बड़ा कोण है,
- किसी फलक या सेल का सबसे छोटा कोण है,
- समकोणीय फलक या सेल के लिए कोण है अर्थात त्रिभुज के लिए 60 और वर्ग के लिए 90 है।
0 का तिरछापन सर्वोत्तम संभव है और किसी का तिरछापन लगभग कभी भी पसंद नहीं किया जाता है। हेक्स और क्वाड सेलों के लिए, अधिक त्रुटिहीन समाधान प्राप्त करने के लिए तिरछापन 0.85 से अधिक नहीं होना चाहिए।
त्रिकोणीय सेलों के लिए, तिरछापन 0.85 से अधिक नहीं होना चाहिए और चतुर्भुज सेलों के लिए, तिरछापन 0.9 से अधिक नहीं होना चाहिए।
चिकनापन
आकार में परिवर्तन भी सहज होना चाहिए। सेल के आकार में अचानक उछाल नहीं होना चाहिए क्योंकि इससे निकटतम के नोड्स पर गलत परिणाम हो सकते हैं।
आयाम अनुपात
यह किसी सेल में सबसे लंबी और सबसे छोटी भुजा का अनुपात है। सर्वोत्तम परिणाम सुनिश्चित करने के लिए आदर्श रूप से यह 1 के समान होना चाहिए। बहुआयामी प्रवाह के लिए यह के निकट होना चाहिए। इसके अतिरिक्त सेल आकार में स्थानीय भिन्नताएं न्यूनतम होनी चाहिए, अर्थात् आसन्न सेल आकार में 20% से अधिक अंतर नहीं होना चाहिए। बड़े आयाम अनुपात होने से अस्वीकार्य परिमाण की इंटरपोलेशन त्रुटि हो सकती है।
मेष निर्माण और सुधार
मेश निर्माण और ग्रिड निर्माण के सिद्धांत भी देखें।
दो आयामों में, फ़्लिपिंग और स्मूथिंग ख़राब मेश को अच्छे मेश में बदलने के लिए शक्तिशाली उपकरण हैं। फ़्लिपिंग में दो त्रिभुजों को मिलाकर चतुर्भुज बनाया जाता है, फिर चतुर्भुज को दूसरी दिशा में विभाजित करके दो नए त्रिभुज बनाए जाते हैं। फ़्लिपिंग का उपयोग तिरछापन जैसे त्रिभुज की गुणवत्ता माप में सुधार के लिए किया जाता है। मेश स्मूथनिंग मेश शीर्षों के स्थान को समायोजित करके तत्व के आकार और समग्र मेश गुणवत्ता को बढ़ाता है। मेश स्मूथिंग में, रैखिक प्रणाली के गैर-शून्य पैटर्न जैसी मुख्य विशेषताओं को संरक्षित किया जाता है क्योंकि मेश की टोपोलॉजी अपरिवर्तित रहती है। लाप्लासियन स्मूथिंग सबसे अधिक उपयोग की जाने वाली स्मूथिंग प्रणाली है।
यह भी देखें
- मेश पीढ़ी
- असंरचित ग्रिड
- नियमित ग्रिड – Tessellation of n-dimensional Euclidean space by congruent parallelotopes
- विस्तारित ग्रिड विधि
संदर्भ
- ↑ "हेक्साहेड्रोन तत्व" (PDF). Archived from the original (PDF) on 2015-02-24. Retrieved 2015-04-13.
- ↑ "संग्रहीत प्रति" (PDF). Archived from the original (PDF) on 2013-12-06. Retrieved 2018-01-10.
- ↑ "Quality and Control - Two Reasons Why Structured Grids Aren't Going Away".
- ↑ Castillo, J.E. (1991), "Mathematical aspects of grid Generation", Society for Industrial and Applied Mathematics, Philadelphia
- ↑ George, P.L. (1991), Automatic Mesh Generation
- ↑ Mavriplis, D.J. (1996), "Mesh Generation and adaptivity for complex geometries and flows", Handbook of Computational Fluid Mechanics
- ↑ Bern, Marshall; Plassmann, Paul (2000), "Mesh Generation", Handbook of Computational Geometry. Elsevier Science
- ↑ "Meshing,Lecture 7". Andre Bakker. Retrieved 2012-11-10.