त्रिकोण तरंग: Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Non-sinusoidal waveform}} | {{Short description|Non-sinusoidal waveform}} | ||
{{Infobox mathematical function | {{Infobox mathematical function | ||
| name = | | name = त्रिकोण तरंग | ||
| image = triangle-td and fd.png | | image = triangle-td and fd.png | ||
| imagesize = | | imagesize = 400पीएक्स | ||
| imagealt = | | imagealt = समय क्षेत्र और आवृत्ति क्षेत्र में चित्रित बैंडलिमिटेड त्रिकोण तरंग। | ||
| caption = A [[Bandlimiting| | | caption = A [[Bandlimiting|बैंडलिमिटेड]] त्रिकोण तरंग<ref name="bandlimited-synthesis">{{cite conference |title=LP-BLIT: Bandlimited Impulse Train Synthesis of Lowpass-filtered Waveforms |last1=Kraft |first1=Sebastian |last2=Zölzer |first2=Udo |date=5 September 2017 |book-title=Proceedings of the 20th [[International Conference on Digital Audio Effects]] (DAFx-17) |pages=255–259 |location=Edinburgh |conference=20th International Conference on Digital Audio Effects (DAFx-17) |conference-url=http://www.dafx17.eca.ed.ac.uk/}}</ref> समय डोमेन (ऊपर) और आवृत्ति डोमेन (नीचे) में चित्रित मौलिक 220 Hz (A<sub>3</sub>) पर होता है। | ||
| general_definition = <math>x(t) = 4 \left\vert t - \left\lfloor t + 3/4 \right\rfloor + 1/4 \right\vert - 1</math> | | general_definition = <math>x(t) = 4 \left\vert t - \left\lfloor t + 3/4 \right\rfloor + 1/4 \right\vert - 1</math> | ||
| fields_of_application = | | fields_of_application = इलेक्ट्रॉनिक्स, सिंथेसाइज़र | ||
| domain = <math>\mathbb{R}</math> | | domain = <math>\mathbb{R}</math> | ||
| codomain = <math>\left[ -1, 1 \right]</math> | | codomain = <math>\left[ -1, 1 \right]</math> | ||
| parity = | | parity = ओडीडी | ||
| period = 1 | | period = 1 | ||
| root = <math>\left\{ \tfrac{n}{2} \right\}, n \in \mathbb{Z}</math> | | root = <math>\left\{ \tfrac{n}{2} \right\}, n \in \mathbb{Z}</math> | ||
| derivative = [[ | | derivative = [[वर्ग तरंग]] | ||
| fourier_series = <math>x(t) = -\frac{8}{{\pi}^{2}}\sum_{k=1}^{\infty} \frac{{\left( -1 \right)}^{k}}{\left( 2 k - 1 \right)^{2}} \sin \left(2 \pi \left( 2 k - 1 \right) t\right)</math> | | fourier_series = <math>x(t) = -\frac{8}{{\pi}^{2}}\sum_{k=1}^{\infty} \frac{{\left( -1 \right)}^{k}}{\left( 2 k - 1 \right)^{2}} \sin \left(2 \pi \left( 2 k - 1 \right) t\right)</math> | ||
}} | }} | ||
| Line 20: | Line 20: | ||
{{Listen|filename=Additive_220Hz_Triangle_Wave.wav|title=Additive Triangle wave sound sample|description=After each second, a harmonic is added to a sine wave creating a triangle 220 Hz wave|format=[[Ogg]]}} | {{Listen|filename=Additive_220Hz_Triangle_Wave.wav|title=Additive Triangle wave sound sample|description=After each second, a harmonic is added to a sine wave creating a triangle 220 Hz wave|format=[[Ogg]]}} | ||
[[त्रिकोण]] तरंग या त्रिकोणीय तरंग [[गैर-साइनसॉइडल तरंग]]रूप है जिसका नाम इसके त्रिभुज आकार के कारण रखा गया है। यह वास्तविक चर का [[आवधिक कार्य]], [[टुकड़े-टुकड़े रैखिक कार्य]], निरंतर कार्य | '''[[त्रिकोण]] तरंग''' या '''त्रिकोणीय तरंग''' [[गैर-साइनसॉइडल तरंग]]रूप होता है जिसका नाम इसके त्रिभुज आकार के कारण रखा गया है। यह वास्तविक चर का [[आवधिक कार्य]], [[टुकड़े-टुकड़े रैखिक कार्य]], निरंतर वास्तविक कार्य होते है। | ||
वर्गाकार तरंग की | वर्गाकार तरंग की भांति, त्रिभुज तरंग में केवल विषम [[ लयबद्ध |लयबद्ध]] होते हैं। चूँकि, उच्च हार्मोनिक्स वर्ग तरंग की तुलना में अधिक तेजी से [[धड़ल्ले से बोलना|लुढ़कता]] है (केवल व्युत्क्रम के विपरीत हार्मोनिक संख्या के व्युत्क्रम वर्ग के आनुपातिक)। | ||
==परिभाषाएँ== | ==परिभाषाएँ== | ||
| Line 28: | Line 28: | ||
=== परिभाषा === | === परिभाषा === | ||
अवधि पी की त्रिकोण तरंग जो सीमा [0,1] तक फैली हुई है, | अवधि पी की त्रिकोण तरंग जो सीमा [0,1] तक फैली हुई है, इसको इस प्रकार परिभाषित किया गया है। | ||
<math display="block">x(t)= 2 \left| \frac{t}{p} - \left \lfloor \frac{t}{p} + \frac{1}{2} \right \rfloor \right|</math> | <math display="block">x(t)= 2 \left| \frac{t}{p} - \left \lfloor \frac{t}{p} + \frac{1}{2} \right \rfloor \right|</math> | ||
जहाँ <math>\lfloor\,\ \rfloor</math> फर्श और छत का कार्य होता है। इसे स्थानांतरित सॉटूथ तरंग के पूर्ण मान के रूप में देखा जा सकता है। | |||
सीमा में फैली त्रिभुज तरंग के लिए {{closed-closed|−1,1}} अभिव्यक्ति बन जाती है। | |||
<math display="block"> x(t)= 2 \left | 2 \left ( \frac{t}{p} - \left \lfloor {t \over p} + {1 \over 2} \right \rfloor \right) \right | - 1. </math> | <math display="block"> x(t)= 2 \left | 2 \left ( \frac{t}{p} - \left \lfloor {t \over p} + {1 \over 2} \right \rfloor \right) \right | - 1. </math> | ||
आयाम वाली त्रिभुज तरंग के लिए अधिक सामान्य समीकरण <math>a</math> और अवधि <math>p</math> [[मॉड्यूलो ऑपरेशन]] और निरपेक्ष मान का उपयोग करना | सामान्यतः आयाम वाली त्रिभुज तरंग के लिए अधिक सामान्य समीकरण <math>a</math> और अवधि <math>p</math> [[मॉड्यूलो ऑपरेशन]] और निरपेक्ष मान का उपयोग करना है। | ||
आयाम=5, आवर्त=4 के साथ त्रिभुज तरंग | |||
<math display="block">y(x) = \frac{4a}{p} \left| \left( \left(x - \frac{p}{4}\right) \bmod p \right) - \frac{p}{2} \right| - a.</math> | <math display="block">y(x) = \frac{4a}{p} \left| \left( \left(x - \frac{p}{4}\right) \bmod p \right) - \frac{p}{2} \right| - a.</math> | ||
उदाहरण के लिए, आयाम 5 और अवधि 4 वाली त्रिभुज तरंग के लिए: | उदाहरण के लिए, आयाम 5 और अवधि 4 वाली त्रिभुज तरंग के लिए: | ||
<math display="block">y(x) = 5 \bigl | \left( (x - 1) \bmod 4 \right) - 2\bigr | - 5.</math> | <math display="block">y(x) = 5 \bigl | \left( (x - 1) \bmod 4 \right) - 2\bigr | - 5.</math> | ||
इसके मान में परिवर्तन करके चरण परिवर्तन <math>- p/4</math> प्राप्त किया जा सकता है जिसे शब्द, और ऊर्ध्वाधर ऑफसेट को <math>- a</math> अवधि के मूल्य में परिवर्तन करके समायोजित किया जा सकता है। | |||
चूँकि यह केवल मॉड्यूलो ऑपरेशन और निरपेक्ष मान का उपयोग करता है, इसका उपयोग हार्डवेयर इलेक्ट्रॉनिक्स पर त्रिकोण तरंग को | चूँकि यह केवल मॉड्यूलो ऑपरेशन और निरपेक्ष मान का उपयोग करता है, इसका उपयोग हार्डवेयर इलेक्ट्रॉनिक्स पर त्रिकोण तरंग को क्रियान्वित करने के लिए किया जा सकता है। | ||
ध्यान | ध्यान दीजिए कि अनेक प्रोग्रामिंग भाषाओं में, <code>%</code> ऑपरेटर शेष ऑपरेटर होता है (परिणाम लाभांश के समान चिह्न के साथ), मॉड्यूलो ऑपरेशन नहीं प्रोग्रामिंग भाषाओं में, मॉड्यूलो ऑपरेशन का उपयोग करके प्राप्त किया जा सकता है <code>((x % p) + p) % p</code> की स्थान <code>x % p</code>. उदाहरण के लिए जावास्क्रिप्ट, इसका परिणाम फॉर्म का समीकरण होता है। <code>4*a/p * Math.abs((((x-p/4)%p)+p)%p - p/2) - a</code> | ||
===वर्ग तरंग से संबंध === | ===वर्ग तरंग से संबंध === | ||
त्रिभुज तरंग को वर्ग तरंग के [[अभिन्न]] अंग के रूप में भी व्यक्त किया जा सकता | त्रिभुज तरंग को वर्ग तरंग के [[अभिन्न]] अंग के रूप में भी व्यक्त किया जा सकता है। | ||
<math display="block">x(t) = \int_0^t \sgn\left(\sin\frac{u}{p}\right)\,du.</math> | <math display="block">x(t) = \int_0^t \sgn\left(\sin\frac{u}{p}\right)\,du.</math> | ||
=== त्रिकोणमितीय फलनों में अभिव्यक्ति === | === त्रिकोणमितीय फलनों में अभिव्यक्ति === | ||
अवधि पी और आयाम ए के साथ त्रिकोण तरंग को [[ उन लोगों के |उन लोगों के]] और [[ आर्कसीन |आर्कसीन]] के संदर्भ में व्यक्त किया जा सकता है (जिसका मान −π/2 से π/2 तक होता है) | अवधि पी और आयाम ए के साथ त्रिकोण तरंग को [[ उन लोगों के |उन लोगों के]] और [[ आर्कसीन |आर्कसीन]] के संदर्भ में व्यक्त किया जा सकता है (जिसका मान −π/2 से π/2 तक होता है)। | ||
<math display="block">y(x) = \frac{2a}{\pi} \arcsin\left(\sin\left(\frac{2\pi}{p}x\right)\right).</math> | <math display="block">y(x) = \frac{2a}{\pi} \arcsin\left(\sin\left(\frac{2\pi}{p}x\right)\right).</math> | ||
पहचान <math display="inline">\cos{x} = \sin\left(\frac{p}{4}-x\right)</math> इसका उपयोग त्रिभुज साइन तरंग से त्रिकोणीय कोसाइन तरंग में परिवर्तित करने के लिए किया जा सकता है। इस चरण-स्थानांतरित त्रिभुज तरंग को कोसाइन और [[कोटि[[कोज्या]]]] के साथ भी व्यक्त किया जा सकता | पहचान <math display="inline">\cos{x} = \sin\left(\frac{p}{4}-x\right)</math> इसका उपयोग त्रिभुज साइन तरंग से त्रिकोणीय कोसाइन तरंग में परिवर्तित करने के लिए किया जा सकता है। इस चरण-स्थानांतरित त्रिभुज तरंग को कोसाइन और [[कोटि[[कोज्या]]]] के साथ भी व्यक्त किया जा सकता है। | ||
<math display="block">y(x) = a - \frac{2a}{\pi} \arccos\left(\cos\left(\frac{2\pi}{p}x\right)\right).</math> | <math display="block">y(x) = a - \frac{2a}{\pi} \arccos\left(\cos\left(\frac{2\pi}{p}x\right)\right).</math> | ||
=== वैकल्पिक रैखिक कार्यों के रूप में व्यक्त === | === वैकल्पिक रैखिक कार्यों के रूप में व्यक्त === | ||
-1 से 1 तक की सीमा और अवधि पी के साथ त्रिकोण तरंग की और परिभाषा | -1 से 1 तक की सीमा और अवधि पी के साथ त्रिकोण तरंग की और परिभाषा होती है। | ||
<math display="block">x(t) = \frac{4}{p} \left (t-\frac{p}{2} \left \lfloor\frac{2 t}{p}+\frac{1}{2} \right \rfloor \right )(-1)^\left \lfloor\frac{2 t}{p} + \frac{1}{2} \right \rfloor</math> | <math display="block">x(t) = \frac{4}{p} \left (t-\frac{p}{2} \left \lfloor\frac{2 t}{p}+\frac{1}{2} \right \rfloor \right )(-1)^\left \lfloor\frac{2 t}{p} + \frac{1}{2} \right \rfloor</math> | ||
===हार्मोनिक्स=== | ===हार्मोनिक्स=== | ||
[[Image:Synthesis triangle.gif|thumb|upright=1.6|right|हार्मोनिक्स की बढ़ती संख्या के साथ त्रिकोण तरंग के योगात्मक संश्लेषण का | [[Image:Synthesis triangle.gif|thumb|upright=1.6|right|हार्मोनिक्स की बढ़ती संख्या के साथ त्रिकोण तरंग के योगात्मक संश्लेषण का एनीमेशन होता है। अतः गणितीय विवरण के लिए [[फूरियर रूपांतरण]] देखें।]]प्रत्येक अन्य विषम हार्मोनिक को -1 से गुणा करते हुए (या, समकक्ष, इसके चरण को परिवर्तित करते हुए) मौलिक के विषम हार्मोनिक्स को जोड़कर [[योगात्मक संश्लेषण]] के साथ त्रिकोण तरंग {{pi}} का अनुमान लगाना संभव है) और हार्मोनिक्स के आयाम को उनके मोड संख्या के वर्ग से गुणा करके, {{math|''n''}} (जो [[मौलिक आवृत्ति]] के सापेक्ष उनकी आवृत्ति के वर्ग के सामान्तर होती है)। | ||
उपरोक्त को गणितीय रूप से निम्नानुसार संक्षेपित किया जा सकता है | उपरोक्त को गणितीय रूप से निम्नानुसार संक्षेपित किया जा सकता है{{pi}} | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
x_\mathrm{triangle}(t) & {} = \frac8{\pi^2}\sum_{i=0}^{N - 1} (-1)^i n^{-2} \sin\left(2\pi f_0 n t\right) | x_\mathrm{triangle}(t) & {} = \frac8{\pi^2}\sum_{i=0}^{N - 1} (-1)^i n^{-2} \sin\left(2\pi f_0 n t\right) | ||
\end{align}</math> | \end{align}</math> | ||
जहाँ {{math|''N''}} सन्निकटन में सम्मिलित करने के लिए हार्मोनिक्स की संख्या <math>n = 2i + 1</math> होती है, अतः {{mvar|t}} स्वतंत्र चर होता है (जैसे ध्वनि तरंगों के लिए समय), <math> f_0 </math> मौलिक आवृत्ति होती है, और {{math|''i''}} हार्मोनिक लेबल होता है जो इसके मोड नंबर से संबंधित होता है। | |||
यह अनंत फूरियर श्रृंखला तेजी से त्रिभुज तरंग में परिवर्तित हो जाती है {{math|''N''}} अनंत की ओर प्रवृत्त होता है, जैसा कि एनीमेशन में दिखाया गया है। | यह अनंत फूरियर श्रृंखला तेजी से त्रिभुज तरंग में परिवर्तित हो जाती है {{math|''N''}} अनंत की ओर प्रवृत्त होता है, जैसा कि एनीमेशन में दिखाया गया है। | ||
==आर्क लंबाई== | ==आर्क लंबाई== | ||
त्रिभुज तरंग के लिए प्रति आवर्त चाप की लंबाई, | त्रिभुज तरंग के लिए प्रति आवर्त चाप की लंबाई, एस द्वारा निरूपित, आयाम ए और आवर्त लंबाई पी के संदर्भ में दी गई है। | ||
<math display="block">s = \sqrt{(4a)^2 + p^2}.</math> | <math display="block">s = \sqrt{(4a)^2 + p^2}.</math> | ||
==यह भी देखें== | ==यह भी देखें== | ||
* [[आवधिक कार्यों की सूची]] | * [[आवधिक कार्यों की सूची]] | ||
* साइन [[लहर]] | * साइन [[लहर]] | ||
* स्क्वेर | * स्क्वेर तरंग | ||
* सॉटूथ तरंग | * सॉटूथ तरंग | ||
*[[नाड़ी तरंग]] | *[[नाड़ी तरंग]] | ||
* [[आवाज़]] | * [[आवाज़|ध्वनि]] | ||
*त्रिकोण | *त्रिकोण फलन | ||
* | * तरंग | ||
* [[ वक्र ]] | * [[ वक्र |वक्र]] | ||
==संदर्भ== | ==संदर्भ== | ||
| Line 90: | Line 90: | ||
{{Use dmy dates|date=July 2019}} | {{Use dmy dates|date=July 2019}} | ||
{{DEFAULTSORT:Triangle Wave}} | {{DEFAULTSORT:Triangle Wave}} | ||
[[Category:Articles with hAudio microformats|Triangle Wave]] | |||
[[Category:Collapse templates|Triangle Wave]] | |||
[[Category: | [[Category:Created On 25/07/2023|Triangle Wave]] | ||
[[Category:Created On 25/07/2023]] | [[Category:Lua-based templates|Triangle Wave]] | ||
[[Category:Machine Translated Page|Triangle Wave]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Triangle Wave]] | |||
[[Category:Pages with script errors|Triangle Wave]] | |||
[[Category:Short description with empty Wikidata description|Triangle Wave]] | |||
[[Category:Sidebars with styles needing conversion|Triangle Wave]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Triangle Wave]] | |||
[[Category:Templates generating microformats|Triangle Wave]] | |||
[[Category:Templates that add a tracking category|Triangle Wave]] | |||
[[Category:Templates that are not mobile friendly|Triangle Wave]] | |||
[[Category:Templates that generate short descriptions|Triangle Wave]] | |||
[[Category:Templates using TemplateData|Triangle Wave]] | |||
[[Category:Use dmy dates from July 2019|Triangle Wave]] | |||
[[Category:Wikipedia metatemplates|Triangle Wave]] | |||
[[Category:तरंगरूप|Triangle Wave]] | |||
[[Category:फोरियर श्रेणी|Triangle Wave]] | |||
Latest revision as of 14:48, 11 August 2023
| त्रिकोण तरंग | |
|---|---|
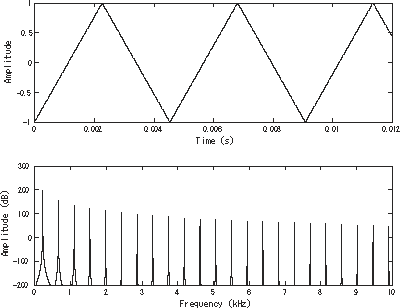 A बैंडलिमिटेड त्रिकोण तरंग[1] समय डोमेन (ऊपर) और आवृत्ति डोमेन (नीचे) में चित्रित मौलिक 220 Hz (A3) पर होता है। | |
| General information | |
| सामान्य परिभाषा | |
| आवेदन के क्षेत्र | इलेक्ट्रॉनिक्स, सिंथेसाइज़र |
| Domain, Codomain and Image | |
| डोमेन | |
| कोडोमेन | |
| Basic features | |
| समता | ओडीडी |
| अवधि | 1 |
| Specific features | |
| रूट | |
| व्युत्पन्न | वर्ग तरंग |
| फोरियर श्रेणी | |
त्रिकोण तरंग या त्रिकोणीय तरंग गैर-साइनसॉइडल तरंगरूप होता है जिसका नाम इसके त्रिभुज आकार के कारण रखा गया है। यह वास्तविक चर का आवधिक कार्य, टुकड़े-टुकड़े रैखिक कार्य, निरंतर वास्तविक कार्य होते है।
वर्गाकार तरंग की भांति, त्रिभुज तरंग में केवल विषम लयबद्ध होते हैं। चूँकि, उच्च हार्मोनिक्स वर्ग तरंग की तुलना में अधिक तेजी से लुढ़कता है (केवल व्युत्क्रम के विपरीत हार्मोनिक संख्या के व्युत्क्रम वर्ग के आनुपातिक)।
परिभाषाएँ
परिभाषा
अवधि पी की त्रिकोण तरंग जो सीमा [0,1] तक फैली हुई है, इसको इस प्रकार परिभाषित किया गया है।
सीमा में फैली त्रिभुज तरंग के लिए [−1,1] अभिव्यक्ति बन जाती है।
आयाम=5, आवर्त=4 के साथ त्रिभुज तरंग
चूँकि यह केवल मॉड्यूलो ऑपरेशन और निरपेक्ष मान का उपयोग करता है, इसका उपयोग हार्डवेयर इलेक्ट्रॉनिक्स पर त्रिकोण तरंग को क्रियान्वित करने के लिए किया जा सकता है।
ध्यान दीजिए कि अनेक प्रोग्रामिंग भाषाओं में, % ऑपरेटर शेष ऑपरेटर होता है (परिणाम लाभांश के समान चिह्न के साथ), मॉड्यूलो ऑपरेशन नहीं प्रोग्रामिंग भाषाओं में, मॉड्यूलो ऑपरेशन का उपयोग करके प्राप्त किया जा सकता है ((x % p) + p) % p की स्थान x % p. उदाहरण के लिए जावास्क्रिप्ट, इसका परिणाम फॉर्म का समीकरण होता है। 4*a/p * Math.abs((((x-p/4)%p)+p)%p - p/2) - a
वर्ग तरंग से संबंध
त्रिभुज तरंग को वर्ग तरंग के अभिन्न अंग के रूप में भी व्यक्त किया जा सकता है।
त्रिकोणमितीय फलनों में अभिव्यक्ति
अवधि पी और आयाम ए के साथ त्रिकोण तरंग को उन लोगों के और आर्कसीन के संदर्भ में व्यक्त किया जा सकता है (जिसका मान −π/2 से π/2 तक होता है)।
वैकल्पिक रैखिक कार्यों के रूप में व्यक्त
-1 से 1 तक की सीमा और अवधि पी के साथ त्रिकोण तरंग की और परिभाषा होती है।
हार्मोनिक्स

प्रत्येक अन्य विषम हार्मोनिक को -1 से गुणा करते हुए (या, समकक्ष, इसके चरण को परिवर्तित करते हुए) मौलिक के विषम हार्मोनिक्स को जोड़कर योगात्मक संश्लेषण के साथ त्रिकोण तरंग π का अनुमान लगाना संभव है) और हार्मोनिक्स के आयाम को उनके मोड संख्या के वर्ग से गुणा करके, n (जो मौलिक आवृत्ति के सापेक्ष उनकी आवृत्ति के वर्ग के सामान्तर होती है)।
उपरोक्त को गणितीय रूप से निम्नानुसार संक्षेपित किया जा सकता हैπ
यह अनंत फूरियर श्रृंखला तेजी से त्रिभुज तरंग में परिवर्तित हो जाती है N अनंत की ओर प्रवृत्त होता है, जैसा कि एनीमेशन में दिखाया गया है।
आर्क लंबाई
त्रिभुज तरंग के लिए प्रति आवर्त चाप की लंबाई, एस द्वारा निरूपित, आयाम ए और आवर्त लंबाई पी के संदर्भ में दी गई है।
यह भी देखें
- आवधिक कार्यों की सूची
- साइन लहर
- स्क्वेर तरंग
- सॉटूथ तरंग
- नाड़ी तरंग
- ध्वनि
- त्रिकोण फलन
- तरंग
- वक्र
संदर्भ
- ↑ Kraft, Sebastian; Zölzer, Udo (5 September 2017). "LP-BLIT: Bandlimited Impulse Train Synthesis of Lowpass-filtered Waveforms". Proceedings of the 20th International Conference on Digital Audio Effects (DAFx-17). 20th International Conference on Digital Audio Effects (DAFx-17). Edinburgh. pp. 255–259.

