डिजिटल इमेज प्रोसेसिंग: Difference between revisions
(→इतिहास) |
No edit summary |
||
| (21 intermediate revisions by 5 users not shown) | |||
| Line 5: | Line 5: | ||
== इतिहास == | == इतिहास == | ||
{{See|Digital image#History|Digital imaging#History}} | {{See|Digital image#History|Digital imaging#History}} | ||
1960 के दशक में, डिजिटल छवि प्रसंस्करण की कई तकनीकें, या जिन्हें प्रायः डिजिटल चित्रण प्रसंस्करण कहा जाता है, बेल प्रयोगशाला, जेट प्रोपल्शन (प्रणोदन) प्रयोगशाला, मैसाचुसेट्स प्राद्योगिकी संस्थान, मैरीलैंड विश्वविद्यालय और कुछ अन्य शोध सुविधाएं उपग्रह बिंबावली (सैटेलाइट इमेजरी), मानक तंत्रिका-फोटो | 1960 के दशक में, डिजिटल छवि प्रसंस्करण की कई तकनीकें, या जिन्हें प्रायः डिजिटल चित्रण प्रसंस्करण कहा जाता है, बेल प्रयोगशाला, जेट प्रोपल्शन (प्रणोदन) प्रयोगशाला, मैसाचुसेट्स प्राद्योगिकी संस्थान, मैरीलैंड विश्वविद्यालय और कुछ अन्य शोध सुविधाएं उपग्रह बिंबावली (सैटेलाइट इमेजरी), मानक तंत्रिका-फोटो संक्रिया(वायर-फोटो स्टैण्डर्ड कन्वर्शन), मेडिकल प्रतिबिंबन, वीडियोफोन, संप्रतीक अभिज्ञान (करैक्टर रिकग्निशन), और छायाचित्र वर्धन के लिए अनुप्रयोगों के साथ विकसित की गई।<ref>Azriel Rosenfeld, ''Picture Processing by Computer'', New York: Academic Press, 1969</ref> प्रारंभिक छवि प्रसंस्करण का उद्देश्य छवि की गुणवत्ता में सुधार तथा मनुष्यों के लिए लोगों के दृश्य प्रभाव में सुधार करना है। छवि प्रसंस्करण में, निविष्ट एक निम्न-कोटि वाली छवि होती है, और निर्गत उच्च कोटि वाली छवि प्राप्त होती है। सामान्य छवि प्रसंस्करण में छवि वर्धन, प्रत्यावर्तन, संकेतन और संपीड़न होता है। पहला सफल अनुप्रयोग अमेरिकन जेट प्रणोदन (प्रोपल्शन) प्रयोगशाला (JPL) था। उन्होंने सूर्य की स्थिति और चंद्रमा के वातावरण को ध्यान में रखते हुए 1964 में अन्तरिक्ष संसूचक रेज़र 7 द्वारा वापस भेजी गई हजारों चंद्र तस्वीरों पर छवि प्रसंस्करण तकनीकों जैसे कि ज्यामितीय सुधार, उन्नयन परिवर्तन, चटकीलापन हटाने आदि का उपयोग किया। संगणक (कंप्यूटर) द्वारा चंद्रमा की सतह के नक्शे की सफल मैपिंग का प्रभाव एक बड़ी सफलता रही है। बाद में, अंतरिक्ष यान द्वारा वापस भेजी गई लगभग 100,000 तस्वीरों पर अधिक जटिल छवि प्रसंस्करण का प्रदर्शन किया गया, ताकि स्थलाकृतिक मानचित्र, रंगीन मानचित्र और चंद्रमा का विशालदर्शी चित्र वर्ण प्राप्त किया जा सके, जिसने असाधारण परिणाम हासिल किए और चांद पर मानव के उतरने की ठोस नींव रखी। <रेफ नाम =: 1>{{Cite book|title=Digital image processing|last=Gonzalez, Rafael C.|date=2008|publisher=Prentice Hall|others=Woods, Richard E. (Richard Eugene), 1954-|isbn=9780131687288|edition= 3rd|location=Upper Saddle River, N.J.|pages=23–28|oclc=137312858}}</ref> | ||
हालाँकि, उस युग के कंप्यूटिंग उपकरणों के साथ प्रसंस्करण की लागत काफी अधिक थी। यह 1970 के दशक में बदल गया, जब डिजिटल | हालाँकि, उस युग के संगणक (कंप्यूटिंग) उपकरणों के साथ प्रसंस्करण की लागत काफी अधिक थी। यह 1970 के दशक में बदल गया, जब डिजिटल छवि प्रसंस्करण सस्ते संगणक (कंप्यूटर) के रूप में आ गई और उपयुक्त हार्डवेयर उपलब्ध हो गया। इससे छवियों को वास्तविक समय में संसाधित किया जाता है, कुछ निष्ठित समस्याओं जैसे कि दूरदर्शन (टेलीविजन) मानकों के संक्रिया के लिए। जैसे-जैसे सामान्य-प्रयोजन वाले संगणक (कंप्यूटर) तीव्रता से कार्य करने लगे, उन्होंने सबसे विशिष्ट और संगणक (कंप्यूटर)-गहन संचालन को छोड़कर सभी के लिए उपयुक्त हार्डवेयर की भूमिका निभानी शुरू कर दी। 2000 के दशक में उपलब्ध तीव्रता से कार्य करने वाला संगणक (कंप्यूटर) और एकल संसाधित्र (प्रोसेसर) के साथ, डिजिटल छवि प्रसंस्करण छवि प्रसंस्करण का सबसे सामान्य रूप बन गया है, और सामान्यतः छवि प्रसंस्करण में इसका उपयोग किया जाता है क्योंकि यह न केवल सबसे बहुमुखी तरीका है, बल्कि सबसे सस्ता भी है। | ||
=== छवि सेंसर === | === छवि संवेदक (सेंसर) === | ||
{{Main|Image sensor}} | {{Main|Image sensor}} | ||
आधुनिक छवि सेंसर | आधुनिक छवि संवेदक (सेंसर) का आधार धातु आक्साइड अर्धचालक (MOS) तकनीक है,<ref name="Williams">{{cite book |last1=Williams |first1=J. B. |title=The Electronics Revolution: Inventing the Future |date=2017 |publisher=Springer |isbn=9783319490885 |pages=245–8 |url=https://books.google.com/books?id=v4QlDwAAQBAJ&pg=PA245}}</ref> जो 1959 में बेल प्रयोगशाला में मोहम्मद एम. अटाला और डॉन कहंग द्वारा MOSFET (MOS क्षेत्र प्रभावी ट्रांजिस्टर (फील्ड-इफेक्ट ट्रांजिस्टर)) के आविष्कार से उत्पन्न की गई।<ref name="computerhistory">{{cite journal|url=https://www.computerhistory.org/siliconengine/metal-oxide-semiconductor-mos-transistor-demonstrated/|title=1960: Metal Oxide Semiconductor (MOS) Transistor Demonstrated|journal=The Silicon Engine|publisher=[[Computer History Museum]]|access-date=31 August 2019|archive-url=https://web.archive.org/web/20191003003452/https://www.computerhistory.org/siliconengine/metal-oxide-semiconductor-mos-transistor-demonstrated/|archive-date=3 October 2019|url-status=live}}</ref> इससे डिजिटल अर्धचालक छवि संवेदक (सेंसर) का विकास हुआ, जिसमें आवेश युग्मित युक्ति (CCD) और बाद में CMOS संवेदक (सेंसर) शामिल हैं।<ref name="Williams"/> | ||
आवेश युग्मित युक्ति का आविष्कार विलार्ड एस. बॉयल और जॉर्ज ई. स्मिथ ने 1969 में बेल प्रयोगशाला में किया।<ref>{{Cite book | title = Scientific charge-coupled devices | author = James R. Janesick | publisher = SPIE Press | year = 2001 | isbn = 978-0-8194-3698-6 | pages = 3–4 | url = https://books.google.com/books?id=3GyE4SWytn4C&pg=PA3 }}</ref> MOS तकनीक पर शोध करते समय, उन्होंने महसूस किया कि विद्युत आवेश चुंबकीय बुद्बुद्द स्मृति का सादृश्य है और इसे छोटे से MOS संधारित्र पर संग्रहीत किया जा सकता है। चूंकि MOS संधारित्र की एक श्रृंखला को एक पंक्ति में बनाना काफी सरल होता है, इसलिए उन्होंने उनमे उपयुक्त वोल्टेज लगाया गया ताकि आवेश को एक से दूसरे तक ले जाया जा सके।<ref name="Williams"/> CCD एक अर्धचालक परिपथ है जिसका उपयोग बाद में दूरदर्शन (टेलीविजन) प्रसारण के लिए पहले डिजिटल वीडियो कैमरों में किया गया।<ref>{{cite journal|last1=Boyle|first1=William S|last2=Smith|first2=George E.|date=1970|title=Charge Coupled Semiconductor Devices|journal=Bell Syst. Tech. J.|volume=49|issue=4|pages=587–593|doi=10.1002/j.1538-7305.1970.tb01790.x}}</ref> | |||
NMOS एक्टिव-पिक्सेल संवेदक (सेंसर) (APS) का आविष्कार 1980 के दशक के मध्य में जापान में ओलंपस द्वारा किया गया था। यह MOS अर्धचालक युक्ति संरचना में अग्रिमों द्वारा सक्षम किया गया, जिसमें MOSFET प्रवर्धन छोटे माइक्रोन और फिर उप-माइक्रोन स्तर तक पहुंच गई।<ref name="fossum93">{{cite book |last1=Fossum |first1=Eric R. |author1-link=Eric Fossum |title= Charge-Coupled Devices and Solid State Optical Sensors III |series=Proceedings of the SPIE |volume=1900 |date=12 July 1993 |doi=10.1117/12.148585 |pages=2–14 |editor1-last=Blouke |editor1-first=Morley M.|citeseerx=10.1.1.408.6558 |bibcode=1993SPIE.1900....2F |chapter=Active pixel sensors: Are CCDS dinosaurs? |s2cid=10556755 }}</ref><ref>{{cite document |last1=Fossum |first1=Eric R. |s2cid=18831792 |author1-link=Eric Fossum |title=Active Pixel Sensors |year=2007 }}</ref> NMOS APS को 1985 में ओलंपस में त्सुतोमु नाकामुरा की टीम द्वारा बनाया गया।<ref>{{cite journal |last1=Matsumoto |first1=Kazuya |last2=Nakamura |first2=Tsutomu |last3=Yusa |first3=Atsushi |last4=Nagai |first4=Shohei |display-authors=1|date=1985 |title=A new MOS phototransistor operating in a non-destructive readout mode |journal=Japanese Journal of Applied Physics |volume=24 |issue=5A |page=L323|doi=10.1143/JJAP.24.L323 |bibcode=1985JaJAP..24L.323M }}</ref> CMOS एक्टिव-पिक्सेल संवेदक (सेंसर) (CMOS संवेदक (सेंसर)) को बाद में एरिक फॉसम की टीम द्वारा 1993 में नासा जेट प्रणोदन (प्रोपल्शन) प्रयोगशाला में विकसित किया गया था।<ref name="Fossum2014">{{cite journal |last1=Fossum |first1=Eric R. |author1-link=Eric Fossum |last2=Hondongwa |first2=D. B. |title=A Review of the Pinned Photodiode for CCD and CMOS Image Sensors |journal=IEEE Journal of the Electron Devices Society |date=2014 |volume=2 |issue=3 |pages=33–43 |doi=10.1109/JEDS.2014.2306412 |doi-access=free }}</ref> 2007 तक, CMOS संवेदक (सेंसर) की बिक्री ने CCD संवेदक (सेंसर) से अधिक बिक्री की।<ref>{{cite news |title=CMOS Image Sensor Sales Stay on Record-Breaking Pace |url=http://www.icinsights.com/news/bulletins/CMOS-Image-Sensor-Sales-Stay-On-RecordBreaking-Pace/ |access-date=6 October 2019 |work=IC Insights |date=8 May 2018 |archive-url=https://web.archive.org/web/20190621180401/http://www.icinsights.com/news/bulletins/CMOS-Image-Sensor-Sales-Stay-On-RecordBreaking-Pace/ |archive-date=21 June 2019 |url-status=live }}</ref> | |||
=== छवि | |||
=== छवि संपीडन === | |||
{{Main|Image compression}} | {{Main|Image compression}} | ||
डिजिटल | डिजिटल छवि संपीडन दूरदर्शन (टेक्नोलॉजी) में महत्वपूर्ण विकास असतत कोज्या रूपांतरण (DCT) है, जो नासिर अहमद द्वारा पहली बार 1972 में प्रस्तावित एक हानिपूर्ण संपीड़न तकनीक थी।<ref name="Ahmed">{{cite journal |last=Ahmed |first=Nasir |author-link=N. Ahmed |title=How I Came Up With the Discrete Cosine Transform |journal=[[Digital Signal Processing (journal)|Digital Signal Processing]] |date=January 1991 |volume=1 |issue=1 |pages=4–5 |doi=10.1016/1051-2004(91)90086-Z |url=https://www.scribd.com/doc/52879771/DCT-History-How-I-Came-Up-with-the-Discrete-Cosine-Transform |access-date=10 October 2019 |archive-url=https://web.archive.org/web/20160610013109/https://www.scribd.com/doc/52879771/DCT-History-How-I-Came-Up-with-the-Discrete-Cosine-Transform |archive-date=10 June 2016 |url-status=live }}</ref> DCT संपीड़न JPEG के लिए आधार बन गया, जिसे 1992 में संयुक्त छायाचित्रित (फोटोग्राफिक) विशेषज्ञों के समूह द्वारा प्रस्तुत किया गया।<ref name="t81">{{cite web |title=T.81 – DIGITAL COMPRESSION AND CODING OF CONTINUOUS-TONE STILL IMAGES – REQUIREMENTS AND GUIDELINES |url=https://www.w3.org/Graphics/JPEG/itu-t81.pdf |publisher=[[CCITT]] |date=September 1992 |access-date=12 July 2019 |archive-url=https://web.archive.org/web/20190717052727/http://www.w3.org/Graphics/JPEG/itu-t81.pdf |archive-date=17 July 2019 |url-status=live }}</ref> JPEG छवियों को बहुत छोटे फ़ाइल आकारों में संकुचित करता है, और इंटरनेट पर सबसे व्यापक रूप से उपयोग की जाने वाली छवि फ़ाइल प्रारूप बन गया है।<ref>{{cite web |title=The JPEG image format explained |url=https://home.bt.com/tech-gadgets/photography/what-is-a-jpeg-11364206889349 |website=[[BT.com]] |publisher=[[BT Group]] |access-date=5 August 2019 |date=31 May 2018 |archive-url=https://web.archive.org/web/20190805194553/https://home.bt.com/tech-gadgets/photography/what-is-a-jpeg-11364206889349 |archive-date=5 August 2019 |url-status=live }}</ref> इसका अत्यधिक कुशल DCT संपीड़न कलन विधि (एल्गोरिथ्म) डिजिटल छवियों और डिजिटल तस्वीरों के व्यापक प्रसार के लिए काफी हद तक जिम्मेदार था,<ref name="Atlantic">{{cite web |title=What Is a JPEG? The Invisible Object You See Every Day |url=https://www.theatlantic.com/technology/archive/2013/09/what-is-a-jpeg-the-invisible-object-you-see-every-day/279954/ |access-date=13 September 2019 |website=[[The Atlantic]] |date=24 September 2013 |archive-url=https://web.archive.org/web/20191009054159/https://www.theatlantic.com/technology/archive/2013/09/what-is-a-jpeg-the-invisible-object-you-see-every-day/279954/ |archive-date=9 October 2019 |url-status=live }}</ref> {{as of|2015|lc=y}} तक हर दिन कई अरब JPEG छवियों का उत्पादन किया गया।<ref>{{cite news |last1=Baraniuk |first1=Chris |title=Copy protections could come to JPEGs |url=https://www.bbc.co.uk/news/technology-34538705 |access-date=13 September 2019 |publisher=[[BBC News]]|date=15 October 2015 |archive-url=https://web.archive.org/web/20191009193610/https://www.bbc.co.uk/news/technology-34538705 |archive-date=9 October 2019 |url-status=live }}</ref> | ||
=== डिजिटल | === डिजिटल संकेत संसाधित्र (प्रोसेसर) (DSP) === | ||
{{Main|Digital signal processor}} | {{Main|Digital signal processor}} | ||
1970 के दशक में | 1970 के दशक में MOS तकनीक को व्यापक रूप से अपनाने से इलेक्ट्रॉनिक संकेत प्रसंस्करण में क्रांति आई।<ref name="Grant">{{cite book |last1=Grant |first1=Duncan Andrew |last2=Gowar |first2=John |title=Power MOSFETS: theory and applications |date=1989 |publisher=[[Wiley (publisher)|Wiley]] |isbn=9780471828679 |page=1 |url=https://books.google.com/books?id=ZiZTAAAAMAAJ |quote=The metal-oxide-semiconductor field-effect transistor (MOSFET) is the most commonly used active device in the very large-scale integration of digital integrated circuits (VLSI). During the 1970s these components revolutionized electronic signal processing, control systems and computers.}}</ref> MOS समाकलित (इंटीग्रेटेड) परिपथ तकनीक 1970 के दशक की शुरुआत में पहले एकल-चिप सूक्ष्म संसाधित्र (माइक्रोप्रोसेसर्स) और माइक्रो नियंत्रक (माइक्रोकंट्रोलर्स) के लिए आधार है,<ref name="ieee">{{cite journal |last1=Shirriff |first1=Ken |title=The Surprising Story of the First Microprocessors |journal=[[IEEE Spectrum]] |date=30 August 2016 |volume=53 |issue=9 |pages=48–54 |publisher=[[Institute of Electrical and Electronics Engineers]] |doi=10.1109/MSPEC.2016.7551353 |s2cid=32003640 |url=https://spectrum.ieee.org/tech-history/silicon-revolution/the-surprising-story-of-the-first-microprocessors |access-date=13 October 2019 |archive-url=https://web.archive.org/web/20191013012248/https://spectrum.ieee.org/tech-history/silicon-revolution/the-surprising-story-of-the-first-microprocessors |archive-date=13 October 2019 |url-status=live }}</ref> और फिर 1970 के दशक के अंत में पहला एकल-चिप डिजिटल संकेत संसाधित्र (प्रोसेसर) (DSP) चिप।<ref name="computerhistory1979">{{cite web |title=1979: Single Chip Digital Signal Processor Introduced |url=https://www.computerhistory.org/siliconengine/single-chip-digital-signal-processor-introduced/ |website=The Silicon Engine |publisher=[[Computer History Museum]] |access-date=14 October 2019 |archive-url=https://web.archive.org/web/20191003072500/https://www.computerhistory.org/siliconengine/single-chip-digital-signal-processor-introduced/ |archive-date=3 October 2019 |url-status=live }}</ref><ref name="Taranovich">{{cite web |last1=Taranovich |first1=Steve |title=30 years of DSP: From a child's toy to 4G and beyond |url=https://www.edn.com/design/systems-design/4394792/30-years-of-DSP--From-a-child-s-toy-to-4G-and-beyond |website=[[EDN (magazine)|EDN]] |access-date=14 October 2019 |date=27 August 2012 |archive-url=https://web.archive.org/web/20191014044347/https://www.edn.com/design/systems-design/4394792/30-years-of-DSP--From-a-child-s-toy-to-4G-and-beyond |archive-date=14 October 2019 |url-status=live }}</ref> DSP चिप तब से डिजिटल छवि प्रसंस्करण में व्यापक रूप से उपयोग किया गया।<ref name="computerhistory1979"/> | ||
असतत | असतत कोज्या रूपांतरण (DCT) छवि संपीडन कलन विधि (एल्गोरिदम) को DSP चिप में व्यापक रूप से लागू किया गया है, जिसमें कई कंपनियां DCT प्रौद्योगिकी के आधार पर DSP चिप विकसित करती हैं। DCTs व्यापक रूप से एन्कोडिंग, डिकोडिंग, वीडियो कोडिंग, श्रव्य कोडिंग, बहुभाजन (मल्टीप्लेक्सिंग), नियंत्रण संकेत (कंट्रोल सिग्नल्स), संकेत (सिग्नल्स), समधर्मी (एनालॉग)-से-डिजिटल रूपांतरण, आरूपण ज्योतिर्मयता (फॉर्मेटिंग ल्यूमिनेंस) और रंग अंतर, और रंग प्रारूप जैसे YUV444 और YUV411 के लिए व्यापक रूप से उपयोग किया जाता है। DCT का उपयोग एन्कोडिंग संचालन के लिए भी किया जाता है जैसे कि गति अनुमान, गति प्रतिकर, अंतर-फ्रेम पूर्वाकलन, परिमाणीकरण, प्रात्यक्षिक भार, एन्ट्रापी एन्कोडिंग, चर (वेरिएबल) एन्कोडिंग, और गति सदिश, और विभिन्न रंग प्रारूपों के बीच विपरीत संचालन (YIQ, YUV और RGB) प्रदर्शनी (डिस्प्ले) प्रयोजन के लिए होते है। DCT का उपयोग सामान्यतः उच्च स्पष्टता दूरदर्शन (हाई-डेफिनिशन टेलीविज़न) (HDTV) एनकोडर/डिकोडर चिप के लिए भी किया जाता है।<ref name="Stankovic">{{cite journal |last1=Stanković |first1=Radomir S. |last2=Astola |first2=Jaakko T. |title=Reminiscences of the Early Work in DCT: Interview with K.R. Rao |journal=Reprints from the Early Days of Information Sciences |date=2012 |volume=60 |url=http://ticsp.cs.tut.fi/reports/ticsp-report-60-reprint-rao-corrected.pdf |access-date=13 October 2019 |archive-url=https://web.archive.org/web/20191013204147/http://ticsp.cs.tut.fi/reports/ticsp-report-60-reprint-rao-corrected.pdf |archive-date=13 October 2019 |url-status=live }}</ref> | ||
=== मेडिकल इमेजिंग === | === चिकित्सीय प्रतिबिंबन (मेडिकल इमेजिंग) === | ||
{{See|Medical imaging}} | {{See|Medical imaging}} | ||
1972 में, ब्रिटिश कंपनी | 1972 में, ब्रिटिश कंपनी EMI हाउसफील्ड के अभियांत्रिक ने मस्तष्क रोगनिदान के लिए एक्स-रे अभिकलित (कंप्यूटेड) टोमोग्राफी उपकरण का आविष्कार किया, जिसे समान्यतः CT (संगणक (कंप्यूटर) टोमोग्राफी) कहा जाता है। CT केन्द्रक (न्यूक्लियस) विधि मानव मस्तष्क के खंड के प्रक्षेपण पर आधारित है और संगणक (कंप्यूटर) द्वारा क्रॉस-अनुभागीय छवि के पुनर्निर्माण के लिए संसाधित की जाती है, जिसे छवि पुनर्निर्माण कहा जाता है। 1975 में, EMI ने सफलतापूर्वक पूरे शरीर के लिए एक CT उपकरण विकसित किया, जिसने मानव शरीर के विभिन्न हिस्सों की एक स्पष्ट टोमोग्राफिक छवि प्राप्त की। 1979 में, इस रोगनिदान तकनीक ने नोबेल पुरस्कार जीता। '''<रेफरी नाम =: 1 />''' चिकित्सा अनुप्रयोगों के लिए डिजिटल छवि प्रसंस्करण तकनीक को 1994 में अंतरिक्ष अनुसंधान अंतरिक्ष प्रौद्योगिकी हॉल ऑफ फ़ेम में शामिल किया गया।<ref name="sf">{{Cite web |url=http://www.spacetechhalloffame.org/inductees_1994_Digital_Image_Processing.html |title=Space Technology Hall of Fame:Inducted Technologies/1994 |year=1994 |publisher=Space Foundation |access-date=7 January 2010 |url-status=dead |archive-url=https://web.archive.org/web/20110704043830/http://www.spacetechhalloffame.org/inductees_1994_Digital_Image_Processing.html |archive-date=4 July 2011 }}</ref> | ||
== कार्य == | == कार्य == | ||
डिजिटल | डिजिटल छवि प्रसंस्करण बहुत अधिक जटिल कलन विधि (एल्गोरिदम) के उपयोग की अनुमति देता है, और इसलिए, सरल कार्यों में अधिक परिष्कृत प्रदर्शन और उन तरीकों के कार्यान्वयन का परिपालन कर सकता है जो समधर्मी (एनालॉग) माध्यमों से असंभव होगा। | ||
विशेष रूप से, डिजिटल छवि प्रसंस्करण एक ठोस अनुप्रयोग है, और एक | विशेष रूप से, डिजिटल छवि प्रसंस्करण का एक ठोस अनुप्रयोग है, और एक प्रायोगिक तकनीक पर आधारित है: | ||
* वर्गीकरण | * वर्गीकरण | ||
* | * विशेषता निकर्ष | ||
* बहु-स्तरीय संकेत विश्लेषण | * बहु-स्तरीय संकेत विश्लेषण | ||
* पैटर्न | * अभिरचना (पैटर्न) पहचान | ||
* प्रक्षेपण | * प्रक्षेपण | ||
डिजिटल | डिजिटल छवि प्रसंस्करण में उपयोग की जाने वाली कुछ तकनीकों में शामिल हैं: | ||
* | * विषमदैशिक विसरण | ||
* | * अप्रत्यक्ष मार्कोव मॉडल | ||
* छवि | * छवि संशोधन | ||
* छवि बहाली | * छवि बहाली (प्रत्यावर्तन) | ||
* स्वतंत्र घटक विश्लेषण | * स्वतंत्र घटक विश्लेषण | ||
* रैखिक फ़िल्टरिंग | * रैखिक फ़िल्टरिंग | ||
* तंत्रिका - तंत्र | * तंत्रिका - तंत्र | ||
* | * आंशिकअवकल समीकरण | ||
* | * पिक्सेलेशन | ||
* | * अभिलक्षण (फीचर) सुमेलन का उल्लेख | ||
* प्रमुख घटक विश्लेषण | * प्रमुख घटक विश्लेषण | ||
* स्व-आयोजन | * स्व-आयोजन मानचित्र | ||
* तरंगिका | * तरंगिका | ||
| Line 62: | Line 64: | ||
=== फ़िल्टरिंग === | === फ़िल्टरिंग === | ||
डिजिटल | डिजिटल फिल्टर का उपयोग डिजिटल छवियों को धुंधला और तेज करने के लिए किया जाता है। फ़िल्टरिंग द्वारा किया जा सकता है: | ||
* स्थानिक | * स्थानिक कार्यक्षेत्र में विशेष रूप से बनाए गए कर्नेल (फ़िल्टर सरणी) के साथ संवलन <रेफ नाम =: 0>{{Cite journal|last1=Zhang|first1=M. Z.|last2=Livingston|first2=A. R.|last3=Asari|first3=V. K.|date=2008|journal=International Journal of Computers and Applications|volume=30|issue=4|pages=298–308|doi=10.1080/1206212x.2008.11441909|title=A High Performance Architecture for Implementation of 2-D Convolution with Quadrant Symmetric Kernels|s2cid=57289814}}</ref> | ||
* आवृत्ति ( | * आवृत्ति (फॉरिएर) कार्यक्षेत्र में विशिष्ट आवृत्ति क्षेत्रों का आवरण करता है | ||
निम्नलिखित उदाहरण दोनों | निम्नलिखित उदाहरण दोनों विधियों को दिखाते हैं: <रेफ नाम = गोंजालेज 2008>{{cite book | ||
रेफ नाम = गोंजालेज 2008>{{cite book | |||
|last = Gonzalez | |last = Gonzalez | ||
|first = Rafael | |first = Rafael | ||
| Line 78: | Line 79: | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! | ! फ़िल्टर का प्रकार | ||
! | ! आवरण | ||
! | ! उदाहरण | ||
|- | |- | ||
| ''' | | '''वास्तविक छवि''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 92: | Line 93: | ||
| [[File:Affine Transformation Original Checkerboard.jpg]] | | [[File:Affine Transformation Original Checkerboard.jpg]] | ||
|- | |- | ||
| '''[[lowpass| | | '''[[lowpass|स्थानिक निम्न पारक]]''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\frac{1}{9}\times | \frac{1}{9}\times | ||
| Line 103: | Line 104: | ||
| [[File:Spatial Mean Filter Checkerboard.png]] | | [[File:Spatial Mean Filter Checkerboard.png]] | ||
|- | |- | ||
| '''[[Edge detection| | | '''[[Edge detection|स्थानिक उच्च पारक]]''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 113: | Line 114: | ||
| [[File:Spatial Laplacian Filter Checkerboard.png]] | | [[File:Spatial Laplacian Filter Checkerboard.png]] | ||
|- | |- | ||
| '''[[Fast Fourier transform| | | '''[[Fast Fourier transform|फॉरिएर निरूपण]]''' | ||
| | | सूडो-कोड: | ||
छवि = शतरंज फलक | |||
F = | F = छवि का फोरिएर रूपांतरण | ||
छवि: लघुगणक(1+निरपेक्ष मान(F)) | |||
| align="center"| [[File:Fourier Space Checkerboard.png]] | | align="center"| [[File:Fourier Space Checkerboard.png]] | ||
|- | |- | ||
| ''' | | '''फॉरिएर निम्न पारक''' | ||
| align="center"| [[File:Lowpass Butterworth Checkerboard.png]] | | align="center"| [[File:Lowpass Butterworth Checkerboard.png]] | ||
| align="center"| [[File:Lowpass FFT Filtered checkerboard.png]] | | align="center"| [[File:Lowpass FFT Filtered checkerboard.png]] | ||
|- | |- | ||
| ''' | | '''फॉरिएर उच्च पारक''' | ||
| align="center"| [[File:Highpass Butterworth Checkerboard.png]] | | align="center"| [[File:Highpass Butterworth Checkerboard.png]] | ||
| align="center"| [[File:Highpass FFT Filtered checkerboard.png]] | | align="center"| [[File:Highpass FFT Filtered checkerboard.png]] | ||
| Line 135: | Line 136: | ||
==== | ==== फॉरिएर कार्यक्षेत्र फ़िल्टरिंग में छवि पैडिंग ==== | ||
छवियों को | छवियों को सामान्यतः फॉरिएर स्पेस में बदलने से पहले स्थूल (पैडेड) किया जाता है, नीचे दिए गए उच्च पारक (हाईपास) फ़िल्टर की गई छवियां विभिन्न पैडिंग तकनीकों के परिणामों को दर्शाती हैं। | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! | ! शून्य स्थूल (पैडेड) | ||
! | ! पुनरावर्ती कोर स्थूल (पैडेड) | ||
|- | |- | ||
| [[File:Highpass FFT Filtered checkerboard.png]] | | [[File:Highpass FFT Filtered checkerboard.png]] | ||
| Line 148: | Line 149: | ||
|- | |- | ||
|} | |} | ||
ध्यान दें कि | ध्यान दें कि पुनरावर्ती कोर वाले पैडिंग की तुलना में शून्य स्थूल (पैडेड) होने पर उच्च पारक (हाईपास) फ़िल्टर अतिरिक्त कोर को दिखाता है। | ||
==== फ़िल्टरिंग कोड उदाहरण ==== | ==== फ़िल्टरिंग कोड उदाहरण ==== | ||
स्थानिक | स्थानिक कार्यक्षेत्र उच्च पारक (हाईपास) फ़िल्टरिंग के लिए MATLAB उदाहरण है। | ||
<syntaxhighlight lang="matlab"> | |||
img=checkerboard(20); % generate checkerboard | |||
% ************************** SPATIAL DOMAIN *************************** | |||
klaplace=[0 -1 0; -1 5 -1; 0 -1 0]; % Laplacian filter kernel | |||
X=conv2(img,klaplace); % convolve test img with | |||
% 3x3 Laplacian kernel | |||
figure() | |||
imshow(X,[]) % show Laplacian filtered | |||
title('Laplacian Edge Detection') | |||
</syntaxhighlight> | |||
=== | === सजातीय संक्रिया === | ||
सजातीय संक्रिया पैमाने, घूर्णन, स्थानांतरण, दर्पण और अपरूपण सहित मूलभूत छवि परिवर्तनों को सक्षम करते हैं जैसा कि निम्नलिखित उदाहरणों में दिखाया गया है। | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! | ! संक्रिया | ||
! | ! सजातीय आव्यूह | ||
! | ! उदाहरण | ||
|- | |- | ||
| '''[[Identity operation| | | '''[[Identity operation|सर्वसमिका]]''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 184: | Line 195: | ||
| [[File:Checkerboard identity.svg]] | | [[File:Checkerboard identity.svg]] | ||
|- | |- | ||
| '''[[Reflection (mathematics)| | | '''[[Reflection (mathematics)|परावर्तन]]''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 194: | Line 205: | ||
| [[File:Checkerboard reflection.svg]] | | [[File:Checkerboard reflection.svg]] | ||
|- | |- | ||
| '''[[Scale (ratio)| | | '''[[Scale (ratio)|पैमाना]]''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 204: | Line 215: | ||
| [[File:Checkerboard scale.svg]] | | [[File:Checkerboard scale.svg]] | ||
|- | |- | ||
| '''[[Rotate]]''' | | '''[[Rotate|घूर्णन]]''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 212: | Line 223: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| [[File:Checkerboard rotate.svg]] | | [[File:Checkerboard rotate.svg]] जहाँ {{math|''θ'' {{=}} {{sfrac|π|6}} {{=}}30°}} | ||
|- | |- | ||
| '''[[Shear matrix| | | '''[[Shear matrix|अपरूपण]]''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 225: | Line 236: | ||
|- | |- | ||
|} | |} | ||
छवि के लिए सजातीय आव्यूह के उपयोग के लिए, छवि को आव्यूह में बदल दिया जाता है जिसमें प्रत्येक प्रविष्टि उस स्थान पर पिक्सेल तीव्रता के सामान होती है। फिर प्रत्येक पिक्सेल के स्थान को सदिश के रूप में दर्शाया जाता है जो छवि में उस पिक्सेल के निर्देशांक को दर्शाता है, [x, y], जहां x और y छवि आव्यूह में पिक्सेल की पंक्ति और स्तंभ हैं। यह निर्देशांक सजातीय-संक्रिया आव्यूह से गुणा करते है, जो यह स्थिति देता है कि निष्पाद (आउटपुट) छवि में पिक्सेल मान की प्रतिलिपि बनाई जाती है। | |||
हालांकि, | हालांकि, उन रूपांतरणों की अनुमति देने के लिए जिन्हें प्रतिश्रवणिक (ट्रांसलेशन) रूपांतरणों की आवश्यकता होती है, त्रि विमीय सजातीय निर्देशांक की आवश्यकता होती है। तीसरी विमा सामान्यतः अशून्य स्थिरांक के लिए समुच्चय होता है, सामान्यतः 1, ताकि नया निर्देशांक [x, y, 1] हो। यह निर्देशांक सदिश को 3 बटा 3 आव्यूह से गुणा करने की अनुमति देता है, जिससे अनुवाद बदलाव सक्षम होते हैं। तो तीसरी विमा, जो स्थिरांक 1 है, स्थानान्तरण की अनुमति देता है। | ||
चूंकि आव्यूह गुणन साहचर्य है, इसलिए कई सजातीय रूपांतरणों को एक ही सजातीय संक्रियामें जोड़ा जा सकता है, ताकि रूपांतरण किए जाने के क्रम में प्रत्येक विशिष्ट संक्रिया के आव्यूह को गुणा किया जा सके। इसका परिणाम एक एकल आव्यूह होता है, जब एक सदिश बिंदु पर लागू किया जाता है, तो वह परिणाम प्राप्त होता है जो अनुक्रम में सदिश [x, y, 1] पर किए गए सभी विशिष्ट परिवर्तनों के समान होता है। इस प्रकार सजातीय संक्रिया आव्यूह के अनुक्रम को एकल सजातीय संक्रिया आव्यूह में घटाया जा सकता है। | |||
उदाहरण के लिए, | उदाहरण के लिए, द्वी विमीय निर्देशांक केवल मूल (0, 0) के चारों ओर में घूर्णन की अनुमति देते हैं। लेकिन त्रि विमीय सजातीय निर्देशांक का उपयोग पहले किसी भी बिंदु को (0, 0) में स्थानान्तरित करने के लिए किया जा सकता है, फिर घूर्णन किया जा सकता है, और अंत में मूल बिंदु (0, 0) का मूल बिंदु (पहले स्थानांतरण के विपरीत) में स्थानांतरण किया जा सकता है। इन 3 सजातीय परिवर्तनों को एकल आव्यूह में जोड़ा जा सकता है, इस प्रकार छवि में किसी भी बिंदु के चारों ओर घूर्णन करता है।<ref>{{Cite book|url=https://people.cs.clemson.edu/~dhouse/courses/401/notes/affines-matrices.pdf|title=Affine Transformations|last=House, Keyser|date=6 December 2016|website=Clemson|series=Foundations of Physically Based Modeling & Animation|publisher=A K Peters/CRC Press|isbn=9781482234602|access-date=26 March 2019|archive-url=https://web.archive.org/web/20170830052734/https://people.cs.clemson.edu/~dhouse/courses/401/notes/affines-matrices.pdf|archive-date=30 August 2017|url-status=live}}</ref> | ||
=== छवि आकृति विज्ञान के साथ | === छवि आकृति विज्ञान के साथ डेनोइसिंग === | ||
गणितीय आकृति विज्ञान छवियों को | गणितीय आकृति विज्ञान छवियों को निरूपित करने के लिए उपयुक्त है। गणितीय आकृति विज्ञान में संरचना तत्व महत्वपूर्ण हैं। | ||
निम्नलिखित उदाहरण | निम्नलिखित उदाहरण संरचना तत्वों के बारे में हैं। डेनोइसे फलन, I के रूप में छवि, और B के रूप में संरचना तत्व को नीचे और तालिका के रूप में दिखाया गया है। | ||
उदहारण के लिए <math>(I') = \begin{bmatrix} | |||
45 & 50 & 65 \\ | 45 & 50 & 65 \\ | ||
40 & 60 & 55 \\ | 40 & 60 & 55 \\ | ||
| Line 249: | Line 260: | ||
1 & 0 & 3 | 1 & 0 & 3 | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
D (i ', b) (1,1) = <math>max(45+1,50+2,65+1,40+2,60+1,55+1,25+1,15+0,5+3) = 66</math> | विस्तारण को परिभाषित करें (i, b) (i, j) = <math>max\{I(i+m, j+n) + B(m,n)\}</math>। माना विस्तारण (i, b) = d (i, b) | ||
D(i ', b) (1,1) = <math>max(45+1,50+2,65+1,40+2,60+1,55+1,25+1,15+0,5+3) = 66</math> | |||
अपक्षरण को परिभाषित करें (i, b) (i, j) = <math>min\{I(i+m, j+n) - B(m,n)\}</math>। माना अपक्षरण (i, b) = e (i, b) | |||
<math>(I') = \begin{bmatrix} | E(i ', b) (1,1) = <math>min(45-1,50-2,65-1,40-2,60-1,55-1,25-1,15-0,5-3) = 2</math> | ||
विस्तारण के बाद <math>(I') = \begin{bmatrix} | |||
45 & 50 & 65 \\ | 45 & 50 & 65 \\ | ||
40 & 66 & 55 \\ | 40 & 66 & 55 \\ | ||
25 & 15 & 5 | 25 & 15 & 5 | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math>अपक्षरण के बाद <math>(I') = \begin{bmatrix} | ||
<math>(I') = \begin{bmatrix} | |||
45 & 50 & 65 \\ | 45 & 50 & 65 \\ | ||
40 & 2 & 55 \\ | 40 & 2 & 55 \\ | ||
| Line 269: | Line 280: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
अभिमुख विधि केवल पहला अपक्षरण है, और फिर विस्तारण होता है जबकि संवरण विधि इसके विपरीत है। वास्तव में, D(i, b) और E(i, b) को संवलन द्वारा कार्यान्वित किया जा सकता है | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! | ! संरचना तत्व | ||
! | ! आवरण | ||
! | ! कोड | ||
! | ! उदाहरण | ||
|- | |- | ||
| ''' | | '''वास्तविक छवि''' | ||
| | | नहीं | ||
| | | मूल छवि पढ़ने के लिए Matlab का प्रयोग करें | ||
<syntaxhighlight lang="matlab"> | <syntaxhighlight lang="matlab"> | ||
original = imread('scene.jpg'); | original = imread('scene.jpg'); | ||
| Line 294: | Line 306: | ||
|- | |- | ||
|- | |- | ||
| '''[[dilation (morphology)| | | '''[[dilation (morphology)|विस्तारण]]''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 302: | Line 314: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| | | विस्तारण के लिए Matlab का प्रयोग करें | ||
<syntaxhighlight lang="matlab"> | <syntaxhighlight lang="matlab"> | ||
imwrite(image, "scene_dil.jpg") | imwrite(image, "scene_dil.jpg") | ||
| Line 324: | Line 336: | ||
| [[File:Lotus free dil.jpg|thumb|Denoising picture with dilation method]] | | [[File:Lotus free dil.jpg|thumb|Denoising picture with dilation method]] | ||
|- | |- | ||
| '''[[erosion (morphology)| | | '''[[erosion (morphology)|अपक्षरण]]''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 332: | Line 344: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| | | अपक्षरण के लिए Matlab का प्रयोग करें | ||
<syntaxhighlight lang="matlab"> | <syntaxhighlight lang="matlab"> | ||
imwrite(image, 'scene_ero.jpg'); | imwrite(image, 'scene_ero.jpg'); | ||
| Line 355: | Line 367: | ||
|- | |- | ||
|- | |- | ||
| '''[[opening (morphology)| | | '''[[opening (morphology)|अभिमुख]]''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 363: | Line 375: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| | | अभिमुख के लिए Matlab का प्रयोग करें | ||
<syntaxhighlight lang="matlab"> | <syntaxhighlight lang="matlab"> | ||
imwrite(extractmin, "scene_opening.jpg") | imwrite(extractmin, "scene_opening.jpg") | ||
| Line 385: | Line 397: | ||
| [[File:Lotus free opening.jpg|thumb|]] | | [[File:Lotus free opening.jpg|thumb|]] | ||
|- | |- | ||
| '''[[closing (morphology)| | | '''[[closing (morphology)|निष्कर्ष]]''' | ||
| align="center" | <math> | | align="center" | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 393: | Line 405: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| | | निष्कर्ष के लिए Matlab का प्रयोग करें | ||
<syntaxhighlight lang="matlab"> | <syntaxhighlight lang="matlab"> | ||
imwrite(extractmax, "scene_closing.jpg") | imwrite(extractmax, "scene_closing.jpg") | ||
| Line 416: | Line 428: | ||
|- | |- | ||
|} | |} | ||
छवि के लिए डेनोइसिंग विधि के उपयोग के लिए, छवि को ग्रे स्केल में परिवर्तित कर दिया जाता है। डेनोइसिंग विधि वाला आवरण तार्किक मैट्रिक्स <math>[1 1 1 ; 1 1 1 ; 1 1 1]</math> है। डेनोइसिंग विधियां चित्र के केंद्र से आधी ऊंचाई, आधी चौड़ाई से शुरू होती हैं, और पंक्ति संख्या, स्तंभ संख्या की छवि सीमा के साथ समाप्त होती हैं। सीमा के साथ मूल छवि में सहवासी (नेबर) अवरोध (ब्लॉक) [केंद्र के नीचे का बिंदु: ऊपर का बिंदु, केंद्र के बाईं ओर का बिंदु: केंद्र के दाईं ओर का बिंदु] है। संवलन सहवासी (नेबर) और संरचना तत्व और फिर केंद्र को न्यूनतम सहवासी (नेबर) से बदलें।। | |||
उदाहरण के लिए संवरण विधि लें। | |||
प्रथम विस्तारण | |||
# छवि पढ़ें और इसे Matlab के साथ ग्रेस्केल में बदलें। | |||
## छवि की माप प्राप्त करें। प्रत्युत्तर (रिटर्न) मान पंक्ति संख्याएँ और स्तंभ संख्याएँ सीमाओ का बाद में उपयोग किया जाता है। | |||
## संरचना तत्व आपके विस्तारण या अपक्षरण फलन पर निर्भर करते हैं। पिक्सेल के सहवासी (नेबर) का न्यूनतम अपक्षरण विधि की ओर अग्रसित है और अधिकतम सहवासी (नेबर) विस्तारण विधि की ओर अग्रसित है। | |||
## विस्तारण, अपक्षरण और संवरण के लिए समय निर्धारित करें। | |||
# मूल छवि के समान आकार का शून्य आव्यूह बनाएं। | |||
#संरचना गवाक्ष (विंडो) के साथ प्रथम विस्तारण हैं। | |||
## संरचना गवाक्ष (विंडो) 3*3 आव्यूह और संवलन है | |||
##लूप के लिए पंक्ति श्रेणी से गवाक्ष (विंडो) के साथ न्यूनतम मान निकालें [2 ~ छवि ऊंचाई - 1] स्तंभ श्रेणी के साथ [2 ~ छवि चौड़ाई - 1] | |||
#न्यूनतम मान को शून्य आव्यूह में भरें और एक नई छवि संचित करें | |||
##सीमा के लिए, इसमें अभी भी सुधार किया जा सकता है। चूंकि विधि में, सीमा की उपेक्षा की जाती है। सीमाओं से निपटने के लिए पैडिंग तत्वों का उपयोग किया जाता है। | |||
फिर अपक्षरण (विस्तारण छवि को निविष्ट के रूप में लें) | |||
# मूल छवि के समान आकार का शून्य आव्यूह बनाएं। | |||
# संरचनात्मक गवाक्ष (विंडो) के साथ अपक्षरण। | |||
## संरचना गवाक्ष (विंडो) 3*3 आव्यूह और संवलन है | |||
##लूप के लिए पंक्ति श्रेणी से गवाक्ष (विंडो) के साथ अधिकतम मान निकालें [2 ~ छवि ऊंचाई - 1] स्तंभ श्रेणी के साथ [2 ~ छवि चौड़ाई - 1] | |||
# अधिकतम मान को शून्य आव्यूह में भरें और एक नई छवि संचित करें | |||
## सीमा के लिए, इसमें अभी भी सुधार किया जा सकता है। चूंकि विधि में सीमा की उपेक्षा की जाती है। सीमाओं से निपटने के लिए पैडिंग तत्वों को लागू किया जाता है। | |||
# परिणाम उपरोक्त तालिका के अनुसार हैं | |||
== अनुप्रयोग == | == अनुप्रयोग == | ||
{{further|Digital imaging|Applications of computer vision}} | {{further|Digital imaging|Applications of computer vision}} | ||
=== डिजिटल कैमरा छवि === | |||
=== डिजिटल कैमरा | डिजिटल कैमरों में सामान्यतः विशेष डिजिटल छवि प्रसंस्करण हार्डवेयर शामिल हैं - या तो अनुरागी चिप या अन्य चिप पर अतिरिक्त परिपथिकी (सर्किटरी) - अपने छवि संवेदक (सेंसर) से मूल एवं प्रारम्भिक डेटा को मानक छवि संचिका (फ़ाइल) प्रारूप में रंग-सुधारित छवि में परिवर्तित करने के लिए हैं। अतिरिक्त स्थिति प्रसंस्करण तकनीक अधिक स्वाभाविक रूप से दिखने वाली छवियों को बनाने के लिए कोर तीक्षणता (एज शार्पनेस) या रंग संतृप्ति को बढ़ाती है। | ||
डिजिटल कैमरों में | |||
=== फिल्म === | === फिल्म === | ||
वेस्टवर्ल्ड (1973) एंड्रॉइड के दृष्टिकोण को | वेस्टवर्ल्ड (1973) पहली वैशिष्टय (फीचर) फिल्म थी जिसने डिजिटल छवि प्रसंस्करण से लेकर उन्मत्त (पिक्सललेट) छायाचित्रण तक एंड्रॉइड के दृष्टिकोण को अनुकारित करने के लिए उपयोग किया गया।<ref>[http://www.beanblossom.in.us/larryy/cgi.html A Brief, Early History of Computer Graphics in Film] {{webarchive |url=https://web.archive.org/web/20120717074134/http://www.beanblossom.in.us/larryy/cgi.html |date=17 July 2012 }}, [[Larry Yaeger]], 16 August 2002 (last update), retrieved 24 March 2010</ref> छवि प्रसंस्करण का उपयोग क्रोमा कुंजी प्रभाव (क्रोमा कि इफ़ेक्ट) उत्पन्न करने के लिए भी किया जाता है जो अभिनेताओं की पृष्ठभूमि को प्राकृतिक या कलात्मक दृश्यों से बदल देता है। | ||
=== | === मुखाकृति परिचयन === | ||
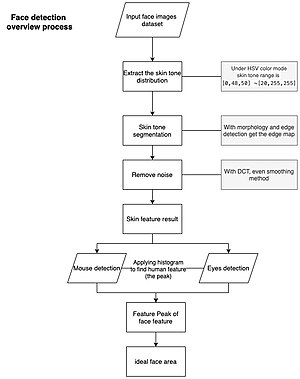
[[File:Face detection process V1.jpg|thumb|चेहरे का पता लगाने की प्रक्रिया]] | [[File:Face detection process V1.jpg|thumb|चेहरे का पता लगाने की प्रक्रिया]] | ||
मुखाकृति परिचयन गणितीय आकृति विज्ञान, असतत कोज्या संक्रियाके साथ कार्यान्वित किया जाता है जिसे सामान्यतः DCT और क्षैतिज प्रक्षेपण (गणित) कहा जाता है। | |||
==== विशेष गुण-आधारित विधि के साथ सामान्य विधि ==== | |||
विशेष गुण-आधारित विधि मुखाकृति परिचयन के लिए त्वचा की टोन, कोर पहचान, चेहरे का आकार और चेहरे की विशेषता (जैसे आंखें, मुंह, आदि) का उपयोग किया जाता है। त्वचा की टोन, चेहरे का आकार, और सभी अद्वितीय तत्व जो केवल मानव चेहरे के पास हैं, उन्हें विशेषताओं के रूप में वर्णित किया जा सकता है। | |||
चेहरे का | ==== प्रक्रिया स्पष्टीकरण ==== | ||
# चेहरे की छवियों के एक बैच को देखते हुए, सबसे पहले, चेहरे की छवियों का प्रतिदर्शी लेकर त्वचा की टोन परिसर (रेंज) निकालें। त्वचा की टोन परिसर (रेंज) केवल त्वचा फिल्टर है। | |||
## त्वचा की टोन निकालने के की स्थिति में छवियों की तुलना करने के लिए संरचनात्मक समानता सूचकांक माप (SSIM) लगाया जा सकता है। | |||
## सामान्य रूप से, HSV या RGB रंग स्थान त्वचा फ़िल्टर के लिए उपयुक्त होते हैं। उदहारण HSV प्रणाली, त्वचा की टोन परिसर (रेंज) [0,48,50] ~ [20,255,255] है | |||
# त्वचा की टोन के साथ छवियों को फ़िल्टर करने के बाद, चेहरे का कोर प्राप्त करने के लिए, चटकीलेपन को दूर करने और अनुपस्थित त्वचा क्षेत्रों को भरने के लिए आकृति विज्ञान और DCT का उपयोग किया जाता है। | |||
## अनुपस्थित त्वचा को भरने के लिए प्रारंभिक विधि या समापन विधि का उपयोग किया जा सकता है। | |||
## DCT त्वचा की टोन जैसी वस्तुओं से बचने के लिए है। चूंकि मानव चेहरों की संव्यूति (टेक्सचर) हमेशा उच्च होते है। | |||
## चेहरे का कोर प्राप्त करने के लिए सोबेल ऑपरेटर या अन्य ऑपरेटरों का उपयोग किया जाता है। | |||
# आंखों जैसी मानवीय विशेषताओं को स्थापित करने के लिए, प्रक्षेपण का उपयोग करके और प्रक्षेपण के आयतचित्र (हिस्टोग्राम) के अधिकतम मान ज्ञात करते है जिससे माउस, बाल और होंठ जैसी विशेष गुण प्राप्त करने में मदद करता है। | |||
## प्रक्षेपण केवल उच्च आवृत्ति को देखने के लिए छवि को प्रक्षेपित करता है जो सामान्यतः विशेष गुण की स्थिति है। | |||
=== छवि कोटि पद्धति में संशोधन === | |||
छवि कोटि कैमरा कंपन से प्रभावित हो सकती है, अति प्रभावाधीन (ओवर-एक्सपोज़र), ग्रे स्तर के वितरण को बहुत केंद्रीकृत, और चटकीला आदि से प्रभावित किया जा सकता है, उदाहरण के लिए, चटकीले होने की समस्या को चौरसाई (स्मूथिंग) विधि द्वारा ठीक किया जा सकता है जबकि ग्रे स्तर वितरण समस्या को आयतचित्र (हिस्टोग्राम) समीकरण द्वारा संशोधित किया जा सकता है। | |||
=== | ==== चौरसाई (स्मूथिंग) विधि ==== | ||
चित्रण में, अगर कुछ अनैच्छिक रंग है, तो अनैच्छिक रंग के आसपास कुछ रंग लेना और उनका औसत लिया जाता है। यह चौरसाई (स्मूथिंग) विधि के उपयोग का आसान तरीका है। | |||
चौरसाई (स्मूथिंग) विधि को आवरण और संवलन के साथ परिपालित किया जा सकता है। उदाहरण के लिए नीचे दी गई छोटी छवि और आवरण देखें। | |||
छवि<math> | |||
<math> | |||
\begin{bmatrix} | \begin{bmatrix} | ||
2 & 5 & 6 & 5\\ | 2 & 5 & 6 & 5\\ | ||
| Line 489: | Line 507: | ||
7 & 3 & 2 & 2 | 7 & 3 & 2 & 2 | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math>है। | ||
आवरण<math> | |||
\begin{bmatrix} | \begin{bmatrix} | ||
1/9 & 1/9 & 1/9 \\ | 1/9 & 1/9 & 1/9 \\ | ||
| Line 496: | Line 515: | ||
1/9 & 1/9 & 1/9 | 1/9 & 1/9 & 1/9 | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math>है। | ||
<math> | संवलन और चौरसाई (स्मूथिंग) के बाद, छवि<math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
2 & 5 & 6 & 5\\ | 2 & 5 & 6 & 5\\ | ||
| Line 505: | Line 524: | ||
7 & 3 & 2 & 2 | 7 & 3 & 2 & 2 | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math>है। | ||
छवियों का अवलोकन [1, 1], छवि [1, 2], छवि [2, 1], और छवि [2, 2]। | छवियों का अवलोकन [1, 1], छवि [1, 2], छवि [2, 1], और छवि [2, 2]। | ||
मूल छवि पिक्सेल 1, 4, 28, 30 है। मास्क को | |||
मूल छवि पिक्सेल 1, 4, 28, 30 है। मास्क को चिकना करने के बाद, पिक्सेल क्रमशः 9, 10, 9, 9 हो जाता है। | |||
नई छवि [1, 1] = <math>\tfrac{1}{9}</math> * (छवि [0,0]+छवि [0,1]+छवि [0,2]+छवि [1,0]+छवि [1,1]+छवि [1,2]+छवि [2,0]+छवि [2,1]+छवि [2,2]) | नई छवि [1, 1] = <math>\tfrac{1}{9}</math> * (छवि [0,0]+छवि [0,1]+छवि [0,2]+छवि [1,0]+छवि [1,1]+छवि [1,2]+छवि [2,0]+छवि [2,1]+छवि [2,2]) | ||
नई छवि [1, 1] = | नई छवि [1, 1] = फलक (<math>\tfrac{1}{9}</math> * (2+5+6+3+1+4+1+28+30)) = 9 | ||
नई छवि [1, 2] = | नई छवि [1, 2] = फलक (<math>\tfrac{1}{9}</math> * (5+6+5+1+4+6+28+30+2)) = 10 | ||
नई छवि [2, 1] = | नई छवि [2, 1] = फलक (<math>\tfrac{1}{9}</math> * (3+1+4+1+28+30+73+3+2)) = 9 | ||
नई छवि [2, 2] = | नई छवि [2, 2] = फलक (<math>\tfrac{1}{9}</math> * (1+4+6+28+30+2+3+2+2)) = 9 | ||
==== ग्रे स्तर आयतचित्र (हिस्टोग्राम) विधि ==== | ==== ग्रे स्तर आयतचित्र (हिस्टोग्राम) विधि ==== | ||
| Line 542: | Line 564: | ||
|- | |- | ||
| चौरसाई (स्मूथिंग) विधि | | चौरसाई (स्मूथिंग) विधि | ||
| | | Matlab से शोर (कोलाहल), लवण तथा ऊषण 0.01 पैरामीटर के साथ चटकीली छवि बनाने के लिए मूल छवि को जोड़ा जाता है। | ||
| [[File:Helmet with noise.jpg|thumb|]] | | [[File:Helmet with noise.jpg|thumb|]] | ||
| | | | ||
| Line 570: | Line 592: | ||
== यह भी देखें == | == यह भी देखें == | ||
{{cmn| | {{cmn| | ||
* [[ | * [[डिजिटल छवि चित्रण]] | ||
* [[ | * [[संगणक (कंप्यूटर) ग्राफिक्स]] | ||
* [[ | * [[संगणक (कंप्यूटर) स्वप्न]] | ||
* [[CVIPtools]] | * [[CVIPtools]] | ||
* [[ | * [[अंकीयकरण]] | ||
* [[ | * [[फोरियर रूपांतरण]] | ||
* [[ | * [[मुक्त परिसीमा प्रतिबंध]] | ||
* [[GPGPU]] | * [[GPGPU]] | ||
* [[ | * [[समाकृति निस्पंदन (होमोमोर्फिक फ़िल्टरिंग)]] | ||
* [[ | * [[छवि विश्लेषण]] | ||
* [[IEEE | * [[IEEE सुधिरस परिवहन व्यवस्था वर्ग (इंटेलिजेंट ट्रांसपोर्ट सिस्टम सोसाइटी)]] | ||
* [[ | * [[न्यूनतम वर्ग वर्णक्रमीय विश्लेषण]] | ||
* [[ | * [[बहुविमीय तंत्र ]] | ||
* [[ | * [[शिथिलन लेबलिंग]] | ||
* [[ | * [[रिमोट संवेदी सॉफ्टवेयर]] | ||
* [[ | * [[मानक परीक्षण चित्र]] | ||
* [[ | * [[सुपर रिजल्यूशन]] | ||
* [[ | * [[कुल भिन्नता निरूपण]] | ||
* [[ | * [[मशीन दृष्टि]] | ||
* [[ | * [[परिबद्ध विचरण]] | ||
* [[ | * [[सूक्ष्मविकिरणमापी]] | ||
}} | }} | ||
| Line 644: | Line 666: | ||
{{Authority control}} | {{Authority control}} | ||
{{DEFAULTSORT:Digital image processing}} | {{DEFAULTSORT:Digital image processing}}] | ||
[[Category: Machine Translated Page]] | [[Category:AC with 0 elements|Digital image processing]] | ||
[[Category:All articles containing potentially dated statements|Digital image processing]] | |||
[[Category:Articles containing potentially dated statements from 2015|Digital image processing]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page|Digital image processing]] | |||
[[Category:Articles with invalid date parameter in template|Digital image processing]] | |||
[[Category:Articles with short description|Digital image processing]] | |||
[[Category:CS1|Digital image processing]] | |||
[[Category:CS1 errors|Digital image processing]] | |||
[[Category:CS1 maint|Digital image processing]] | |||
[[Category:Collapse templates|Digital image processing]] | |||
[[Category:Lua-based templates|Digital image processing]] | |||
[[Category:Machine Translated Page|Digital image processing]] | |||
[[Category:Multi-column templates|Digital image processing]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Digital image processing]] | |||
[[Category:Pages using div col with small parameter|Digital image processing]] | |||
[[Category:Pages with reference errors|Digital image processing]] | |||
[[Category:Pages with script errors|Digital image processing]] | |||
[[Category:Short description with empty Wikidata description|Digital image processing]] | |||
[[Category:Sidebars with styles needing conversion|Digital image processing]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Digital image processing]] | |||
[[Category:Templates generating microformats|Digital image processing]] | |||
[[Category:Templates that add a tracking category|Digital image processing]] | |||
[[Category:Templates that are not mobile friendly|Digital image processing]] | |||
[[Category:Templates that generate short descriptions|Digital image processing]] | |||
[[Category:Templates used by AutoWikiBrowser|Cite web]] | |||
[[Category:Templates using TemplateData|Digital image processing]] | |||
[[Category:Templates using under-protected Lua modules|Digital image processing]] | |||
[[Category:Webarchive template wayback links|Digital image processing]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates|Digital image processing]] | |||
[[Category:कंप्यूटर विजन|Digital image processing]] | |||
[[Category:छवि प्रसंस्करण|Digital image processing]] | |||
[[Category:डिजिटल इमेजिंग|Digital image processing]] | |||
[[Category:१ ९ ६० के दशक में कंप्यूटर से संबंधित परिचय|Digital image processing]] | |||
Latest revision as of 15:40, 11 August 2023
डिजिटल छवि प्रसंस्करण किसी कलन विधि (एल्गोरिदम) के माध्यम से डिजिटल छवियों को संसाधित करने के लिए डिजिटल संगणक (कंप्यूटर) का उपयोग है।[1][2] डिजिटल एकल प्रसंस्करण के उपश्रेणी या क्षेत्र के रूप में, डिजिटल छवि प्रसंस्करण के समधर्मी (एनालॉग) छवि प्रसंस्करण पर कई फायदे हैं। यह निविष्टि डेटा पर कलन विधि (एल्गोरिदम) की विस्तृत श्रृंखला को उपयोजित करता है और प्रसंस्करण के दौरान शोर (कोलाहल) के निर्माण और विरूपण जैसी समस्याओं का परिवर्जन कर सकता है। चूंकि छवियों को दो विमाओ (शायद अधिक) पर निरूपित किया गया है, इसलिए डिजिटल छवि प्रसंस्करण को बहुविमीय प्रणालियों के रूप में प्रतिदर्श किया जा सकता है। डिजिटल छवि प्रसंस्करण का निर्माण और विकास मुख्य रूप से तीन कारकों से प्रभावित होता है, संगणक (कंप्यूटर) का विकास, गणित का विकास (विशेषकर असतत गणित सिद्धांत का निर्माण और सुधार), पर्यावरण, कृषि, सैन्य, उद्योग और चिकित्सा विज्ञान में अनुप्रयोगों की एक विस्तृत श्रृंखला की आवश्यकता में वृद्धि।
इतिहास
1960 के दशक में, डिजिटल छवि प्रसंस्करण की कई तकनीकें, या जिन्हें प्रायः डिजिटल चित्रण प्रसंस्करण कहा जाता है, बेल प्रयोगशाला, जेट प्रोपल्शन (प्रणोदन) प्रयोगशाला, मैसाचुसेट्स प्राद्योगिकी संस्थान, मैरीलैंड विश्वविद्यालय और कुछ अन्य शोध सुविधाएं उपग्रह बिंबावली (सैटेलाइट इमेजरी), मानक तंत्रिका-फोटो संक्रिया(वायर-फोटो स्टैण्डर्ड कन्वर्शन), मेडिकल प्रतिबिंबन, वीडियोफोन, संप्रतीक अभिज्ञान (करैक्टर रिकग्निशन), और छायाचित्र वर्धन के लिए अनुप्रयोगों के साथ विकसित की गई।[3] प्रारंभिक छवि प्रसंस्करण का उद्देश्य छवि की गुणवत्ता में सुधार तथा मनुष्यों के लिए लोगों के दृश्य प्रभाव में सुधार करना है। छवि प्रसंस्करण में, निविष्ट एक निम्न-कोटि वाली छवि होती है, और निर्गत उच्च कोटि वाली छवि प्राप्त होती है। सामान्य छवि प्रसंस्करण में छवि वर्धन, प्रत्यावर्तन, संकेतन और संपीड़न होता है। पहला सफल अनुप्रयोग अमेरिकन जेट प्रणोदन (प्रोपल्शन) प्रयोगशाला (JPL) था। उन्होंने सूर्य की स्थिति और चंद्रमा के वातावरण को ध्यान में रखते हुए 1964 में अन्तरिक्ष संसूचक रेज़र 7 द्वारा वापस भेजी गई हजारों चंद्र तस्वीरों पर छवि प्रसंस्करण तकनीकों जैसे कि ज्यामितीय सुधार, उन्नयन परिवर्तन, चटकीलापन हटाने आदि का उपयोग किया। संगणक (कंप्यूटर) द्वारा चंद्रमा की सतह के नक्शे की सफल मैपिंग का प्रभाव एक बड़ी सफलता रही है। बाद में, अंतरिक्ष यान द्वारा वापस भेजी गई लगभग 100,000 तस्वीरों पर अधिक जटिल छवि प्रसंस्करण का प्रदर्शन किया गया, ताकि स्थलाकृतिक मानचित्र, रंगीन मानचित्र और चंद्रमा का विशालदर्शी चित्र वर्ण प्राप्त किया जा सके, जिसने असाधारण परिणाम हासिल किए और चांद पर मानव के उतरने की ठोस नींव रखी। <रेफ नाम =: 1>Gonzalez, Rafael C. (2008). Digital image processing. Woods, Richard E. (Richard Eugene), 1954- (3rd ed.). Upper Saddle River, N.J.: Prentice Hall. pp. 23–28. ISBN 9780131687288. OCLC 137312858.</ref>
हालाँकि, उस युग के संगणक (कंप्यूटिंग) उपकरणों के साथ प्रसंस्करण की लागत काफी अधिक थी। यह 1970 के दशक में बदल गया, जब डिजिटल छवि प्रसंस्करण सस्ते संगणक (कंप्यूटर) के रूप में आ गई और उपयुक्त हार्डवेयर उपलब्ध हो गया। इससे छवियों को वास्तविक समय में संसाधित किया जाता है, कुछ निष्ठित समस्याओं जैसे कि दूरदर्शन (टेलीविजन) मानकों के संक्रिया के लिए। जैसे-जैसे सामान्य-प्रयोजन वाले संगणक (कंप्यूटर) तीव्रता से कार्य करने लगे, उन्होंने सबसे विशिष्ट और संगणक (कंप्यूटर)-गहन संचालन को छोड़कर सभी के लिए उपयुक्त हार्डवेयर की भूमिका निभानी शुरू कर दी। 2000 के दशक में उपलब्ध तीव्रता से कार्य करने वाला संगणक (कंप्यूटर) और एकल संसाधित्र (प्रोसेसर) के साथ, डिजिटल छवि प्रसंस्करण छवि प्रसंस्करण का सबसे सामान्य रूप बन गया है, और सामान्यतः छवि प्रसंस्करण में इसका उपयोग किया जाता है क्योंकि यह न केवल सबसे बहुमुखी तरीका है, बल्कि सबसे सस्ता भी है।
छवि संवेदक (सेंसर)
आधुनिक छवि संवेदक (सेंसर) का आधार धातु आक्साइड अर्धचालक (MOS) तकनीक है,[4] जो 1959 में बेल प्रयोगशाला में मोहम्मद एम. अटाला और डॉन कहंग द्वारा MOSFET (MOS क्षेत्र प्रभावी ट्रांजिस्टर (फील्ड-इफेक्ट ट्रांजिस्टर)) के आविष्कार से उत्पन्न की गई।[5] इससे डिजिटल अर्धचालक छवि संवेदक (सेंसर) का विकास हुआ, जिसमें आवेश युग्मित युक्ति (CCD) और बाद में CMOS संवेदक (सेंसर) शामिल हैं।[4]
आवेश युग्मित युक्ति का आविष्कार विलार्ड एस. बॉयल और जॉर्ज ई. स्मिथ ने 1969 में बेल प्रयोगशाला में किया।[6] MOS तकनीक पर शोध करते समय, उन्होंने महसूस किया कि विद्युत आवेश चुंबकीय बुद्बुद्द स्मृति का सादृश्य है और इसे छोटे से MOS संधारित्र पर संग्रहीत किया जा सकता है। चूंकि MOS संधारित्र की एक श्रृंखला को एक पंक्ति में बनाना काफी सरल होता है, इसलिए उन्होंने उनमे उपयुक्त वोल्टेज लगाया गया ताकि आवेश को एक से दूसरे तक ले जाया जा सके।[4] CCD एक अर्धचालक परिपथ है जिसका उपयोग बाद में दूरदर्शन (टेलीविजन) प्रसारण के लिए पहले डिजिटल वीडियो कैमरों में किया गया।[7]
NMOS एक्टिव-पिक्सेल संवेदक (सेंसर) (APS) का आविष्कार 1980 के दशक के मध्य में जापान में ओलंपस द्वारा किया गया था। यह MOS अर्धचालक युक्ति संरचना में अग्रिमों द्वारा सक्षम किया गया, जिसमें MOSFET प्रवर्धन छोटे माइक्रोन और फिर उप-माइक्रोन स्तर तक पहुंच गई।[8][9] NMOS APS को 1985 में ओलंपस में त्सुतोमु नाकामुरा की टीम द्वारा बनाया गया।[10] CMOS एक्टिव-पिक्सेल संवेदक (सेंसर) (CMOS संवेदक (सेंसर)) को बाद में एरिक फॉसम की टीम द्वारा 1993 में नासा जेट प्रणोदन (प्रोपल्शन) प्रयोगशाला में विकसित किया गया था।[11] 2007 तक, CMOS संवेदक (सेंसर) की बिक्री ने CCD संवेदक (सेंसर) से अधिक बिक्री की।[12]
छवि संपीडन
डिजिटल छवि संपीडन दूरदर्शन (टेक्नोलॉजी) में महत्वपूर्ण विकास असतत कोज्या रूपांतरण (DCT) है, जो नासिर अहमद द्वारा पहली बार 1972 में प्रस्तावित एक हानिपूर्ण संपीड़न तकनीक थी।[13] DCT संपीड़न JPEG के लिए आधार बन गया, जिसे 1992 में संयुक्त छायाचित्रित (फोटोग्राफिक) विशेषज्ञों के समूह द्वारा प्रस्तुत किया गया।[14] JPEG छवियों को बहुत छोटे फ़ाइल आकारों में संकुचित करता है, और इंटरनेट पर सबसे व्यापक रूप से उपयोग की जाने वाली छवि फ़ाइल प्रारूप बन गया है।[15] इसका अत्यधिक कुशल DCT संपीड़न कलन विधि (एल्गोरिथ्म) डिजिटल छवियों और डिजिटल तस्वीरों के व्यापक प्रसार के लिए काफी हद तक जिम्मेदार था,[16] as of 2015[update] तक हर दिन कई अरब JPEG छवियों का उत्पादन किया गया।[17]
डिजिटल संकेत संसाधित्र (प्रोसेसर) (DSP)
1970 के दशक में MOS तकनीक को व्यापक रूप से अपनाने से इलेक्ट्रॉनिक संकेत प्रसंस्करण में क्रांति आई।[18] MOS समाकलित (इंटीग्रेटेड) परिपथ तकनीक 1970 के दशक की शुरुआत में पहले एकल-चिप सूक्ष्म संसाधित्र (माइक्रोप्रोसेसर्स) और माइक्रो नियंत्रक (माइक्रोकंट्रोलर्स) के लिए आधार है,[19] और फिर 1970 के दशक के अंत में पहला एकल-चिप डिजिटल संकेत संसाधित्र (प्रोसेसर) (DSP) चिप।[20][21] DSP चिप तब से डिजिटल छवि प्रसंस्करण में व्यापक रूप से उपयोग किया गया।[20]
असतत कोज्या रूपांतरण (DCT) छवि संपीडन कलन विधि (एल्गोरिदम) को DSP चिप में व्यापक रूप से लागू किया गया है, जिसमें कई कंपनियां DCT प्रौद्योगिकी के आधार पर DSP चिप विकसित करती हैं। DCTs व्यापक रूप से एन्कोडिंग, डिकोडिंग, वीडियो कोडिंग, श्रव्य कोडिंग, बहुभाजन (मल्टीप्लेक्सिंग), नियंत्रण संकेत (कंट्रोल सिग्नल्स), संकेत (सिग्नल्स), समधर्मी (एनालॉग)-से-डिजिटल रूपांतरण, आरूपण ज्योतिर्मयता (फॉर्मेटिंग ल्यूमिनेंस) और रंग अंतर, और रंग प्रारूप जैसे YUV444 और YUV411 के लिए व्यापक रूप से उपयोग किया जाता है। DCT का उपयोग एन्कोडिंग संचालन के लिए भी किया जाता है जैसे कि गति अनुमान, गति प्रतिकर, अंतर-फ्रेम पूर्वाकलन, परिमाणीकरण, प्रात्यक्षिक भार, एन्ट्रापी एन्कोडिंग, चर (वेरिएबल) एन्कोडिंग, और गति सदिश, और विभिन्न रंग प्रारूपों के बीच विपरीत संचालन (YIQ, YUV और RGB) प्रदर्शनी (डिस्प्ले) प्रयोजन के लिए होते है। DCT का उपयोग सामान्यतः उच्च स्पष्टता दूरदर्शन (हाई-डेफिनिशन टेलीविज़न) (HDTV) एनकोडर/डिकोडर चिप के लिए भी किया जाता है।[22]
चिकित्सीय प्रतिबिंबन (मेडिकल इमेजिंग)
1972 में, ब्रिटिश कंपनी EMI हाउसफील्ड के अभियांत्रिक ने मस्तष्क रोगनिदान के लिए एक्स-रे अभिकलित (कंप्यूटेड) टोमोग्राफी उपकरण का आविष्कार किया, जिसे समान्यतः CT (संगणक (कंप्यूटर) टोमोग्राफी) कहा जाता है। CT केन्द्रक (न्यूक्लियस) विधि मानव मस्तष्क के खंड के प्रक्षेपण पर आधारित है और संगणक (कंप्यूटर) द्वारा क्रॉस-अनुभागीय छवि के पुनर्निर्माण के लिए संसाधित की जाती है, जिसे छवि पुनर्निर्माण कहा जाता है। 1975 में, EMI ने सफलतापूर्वक पूरे शरीर के लिए एक CT उपकरण विकसित किया, जिसने मानव शरीर के विभिन्न हिस्सों की एक स्पष्ट टोमोग्राफिक छवि प्राप्त की। 1979 में, इस रोगनिदान तकनीक ने नोबेल पुरस्कार जीता। <रेफरी नाम =: 1 /> चिकित्सा अनुप्रयोगों के लिए डिजिटल छवि प्रसंस्करण तकनीक को 1994 में अंतरिक्ष अनुसंधान अंतरिक्ष प्रौद्योगिकी हॉल ऑफ फ़ेम में शामिल किया गया।[23]
कार्य
डिजिटल छवि प्रसंस्करण बहुत अधिक जटिल कलन विधि (एल्गोरिदम) के उपयोग की अनुमति देता है, और इसलिए, सरल कार्यों में अधिक परिष्कृत प्रदर्शन और उन तरीकों के कार्यान्वयन का परिपालन कर सकता है जो समधर्मी (एनालॉग) माध्यमों से असंभव होगा।
विशेष रूप से, डिजिटल छवि प्रसंस्करण का एक ठोस अनुप्रयोग है, और एक प्रायोगिक तकनीक पर आधारित है:
- वर्गीकरण
- विशेषता निकर्ष
- बहु-स्तरीय संकेत विश्लेषण
- अभिरचना (पैटर्न) पहचान
- प्रक्षेपण
डिजिटल छवि प्रसंस्करण में उपयोग की जाने वाली कुछ तकनीकों में शामिल हैं:
- विषमदैशिक विसरण
- अप्रत्यक्ष मार्कोव मॉडल
- छवि संशोधन
- छवि बहाली (प्रत्यावर्तन)
- स्वतंत्र घटक विश्लेषण
- रैखिक फ़िल्टरिंग
- तंत्रिका - तंत्र
- आंशिकअवकल समीकरण
- पिक्सेलेशन
- अभिलक्षण (फीचर) सुमेलन का उल्लेख
- प्रमुख घटक विश्लेषण
- स्व-आयोजन मानचित्र
- तरंगिका
डिजिटल छवि परिवर्तन
फ़िल्टरिंग
डिजिटल फिल्टर का उपयोग डिजिटल छवियों को धुंधला और तेज करने के लिए किया जाता है। फ़िल्टरिंग द्वारा किया जा सकता है:
- स्थानिक कार्यक्षेत्र में विशेष रूप से बनाए गए कर्नेल (फ़िल्टर सरणी) के साथ संवलन <रेफ नाम =: 0>Zhang, M. Z.; Livingston, A. R.; Asari, V. K. (2008). "A High Performance Architecture for Implementation of 2-D Convolution with Quadrant Symmetric Kernels". International Journal of Computers and Applications. 30 (4): 298–308. doi:10.1080/1206212x.2008.11441909. S2CID 57289814.</ref>
- आवृत्ति (फॉरिएर) कार्यक्षेत्र में विशिष्ट आवृत्ति क्षेत्रों का आवरण करता है
निम्नलिखित उदाहरण दोनों विधियों को दिखाते हैं: <रेफ नाम = गोंजालेज 2008>Gonzalez, Rafael (2008). Digital Image Processing, 3rd. Pearson Hall. ISBN 9780131687288.</ref>
| फ़िल्टर का प्रकार | आवरण | उदाहरण |
|---|---|---|
| वास्तविक छवि | File:Affine Transformation Original Checkerboard.jpg | |
| स्थानिक निम्न पारक | File:Spatial Mean Filter Checkerboard.png | |
| स्थानिक उच्च पारक | File:Spatial Laplacian Filter Checkerboard.png | |
| फॉरिएर निरूपण | सूडो-कोड:
छवि = शतरंज फलक F = छवि का फोरिएर रूपांतरण छवि: लघुगणक(1+निरपेक्ष मान(F)) |
File:Fourier Space Checkerboard.png |
| फॉरिएर निम्न पारक | 
|

|
| फॉरिएर उच्च पारक | 
|

|
फॉरिएर कार्यक्षेत्र फ़िल्टरिंग में छवि पैडिंग
छवियों को सामान्यतः फॉरिएर स्पेस में बदलने से पहले स्थूल (पैडेड) किया जाता है, नीचे दिए गए उच्च पारक (हाईपास) फ़िल्टर की गई छवियां विभिन्न पैडिंग तकनीकों के परिणामों को दर्शाती हैं।
| शून्य स्थूल (पैडेड) | पुनरावर्ती कोर स्थूल (पैडेड) |
|---|---|

|

|
ध्यान दें कि पुनरावर्ती कोर वाले पैडिंग की तुलना में शून्य स्थूल (पैडेड) होने पर उच्च पारक (हाईपास) फ़िल्टर अतिरिक्त कोर को दिखाता है।
फ़िल्टरिंग कोड उदाहरण
स्थानिक कार्यक्षेत्र उच्च पारक (हाईपास) फ़िल्टरिंग के लिए MATLAB उदाहरण है।
img=checkerboard(20); % generate checkerboard
% ************************** SPATIAL DOMAIN ***************************
klaplace=[0 -1 0; -1 5 -1; 0 -1 0]; % Laplacian filter kernel
X=conv2(img,klaplace); % convolve test img with
% 3x3 Laplacian kernel
figure()
imshow(X,[]) % show Laplacian filtered
title('Laplacian Edge Detection')
सजातीय संक्रिया
सजातीय संक्रिया पैमाने, घूर्णन, स्थानांतरण, दर्पण और अपरूपण सहित मूलभूत छवि परिवर्तनों को सक्षम करते हैं जैसा कि निम्नलिखित उदाहरणों में दिखाया गया है।
| संक्रिया | सजातीय आव्यूह | उदाहरण |
|---|---|---|
| सर्वसमिका | 
| |
| परावर्तन | 
| |
| पैमाना | 
| |
| घूर्णन |  जहाँ θ = π/6 =30° जहाँ θ = π/6 =30°
| |
| अपरूपण | 
|
छवि के लिए सजातीय आव्यूह के उपयोग के लिए, छवि को आव्यूह में बदल दिया जाता है जिसमें प्रत्येक प्रविष्टि उस स्थान पर पिक्सेल तीव्रता के सामान होती है। फिर प्रत्येक पिक्सेल के स्थान को सदिश के रूप में दर्शाया जाता है जो छवि में उस पिक्सेल के निर्देशांक को दर्शाता है, [x, y], जहां x और y छवि आव्यूह में पिक्सेल की पंक्ति और स्तंभ हैं। यह निर्देशांक सजातीय-संक्रिया आव्यूह से गुणा करते है, जो यह स्थिति देता है कि निष्पाद (आउटपुट) छवि में पिक्सेल मान की प्रतिलिपि बनाई जाती है।
हालांकि, उन रूपांतरणों की अनुमति देने के लिए जिन्हें प्रतिश्रवणिक (ट्रांसलेशन) रूपांतरणों की आवश्यकता होती है, त्रि विमीय सजातीय निर्देशांक की आवश्यकता होती है। तीसरी विमा सामान्यतः अशून्य स्थिरांक के लिए समुच्चय होता है, सामान्यतः 1, ताकि नया निर्देशांक [x, y, 1] हो। यह निर्देशांक सदिश को 3 बटा 3 आव्यूह से गुणा करने की अनुमति देता है, जिससे अनुवाद बदलाव सक्षम होते हैं। तो तीसरी विमा, जो स्थिरांक 1 है, स्थानान्तरण की अनुमति देता है।
चूंकि आव्यूह गुणन साहचर्य है, इसलिए कई सजातीय रूपांतरणों को एक ही सजातीय संक्रियामें जोड़ा जा सकता है, ताकि रूपांतरण किए जाने के क्रम में प्रत्येक विशिष्ट संक्रिया के आव्यूह को गुणा किया जा सके। इसका परिणाम एक एकल आव्यूह होता है, जब एक सदिश बिंदु पर लागू किया जाता है, तो वह परिणाम प्राप्त होता है जो अनुक्रम में सदिश [x, y, 1] पर किए गए सभी विशिष्ट परिवर्तनों के समान होता है। इस प्रकार सजातीय संक्रिया आव्यूह के अनुक्रम को एकल सजातीय संक्रिया आव्यूह में घटाया जा सकता है।
उदाहरण के लिए, द्वी विमीय निर्देशांक केवल मूल (0, 0) के चारों ओर में घूर्णन की अनुमति देते हैं। लेकिन त्रि विमीय सजातीय निर्देशांक का उपयोग पहले किसी भी बिंदु को (0, 0) में स्थानान्तरित करने के लिए किया जा सकता है, फिर घूर्णन किया जा सकता है, और अंत में मूल बिंदु (0, 0) का मूल बिंदु (पहले स्थानांतरण के विपरीत) में स्थानांतरण किया जा सकता है। इन 3 सजातीय परिवर्तनों को एकल आव्यूह में जोड़ा जा सकता है, इस प्रकार छवि में किसी भी बिंदु के चारों ओर घूर्णन करता है।[24]
छवि आकृति विज्ञान के साथ डेनोइसिंग
गणितीय आकृति विज्ञान छवियों को निरूपित करने के लिए उपयुक्त है। गणितीय आकृति विज्ञान में संरचना तत्व महत्वपूर्ण हैं।
निम्नलिखित उदाहरण संरचना तत्वों के बारे में हैं। डेनोइसे फलन, I के रूप में छवि, और B के रूप में संरचना तत्व को नीचे और तालिका के रूप में दिखाया गया है।
उदहारण के लिए
विस्तारण को परिभाषित करें (i, b) (i, j) = । माना विस्तारण (i, b) = d (i, b)
D(i ', b) (1,1) =
अपक्षरण को परिभाषित करें (i, b) (i, j) = । माना अपक्षरण (i, b) = e (i, b)
E(i ', b) (1,1) =
विस्तारण के बाद अपक्षरण के बाद
अभिमुख विधि केवल पहला अपक्षरण है, और फिर विस्तारण होता है जबकि संवरण विधि इसके विपरीत है। वास्तव में, D(i, b) और E(i, b) को संवलन द्वारा कार्यान्वित किया जा सकता है
| संरचना तत्व | आवरण | कोड | उदाहरण |
|---|---|---|---|
| वास्तविक छवि | नहीं | मूल छवि पढ़ने के लिए Matlab का प्रयोग करें
original = imread('scene.jpg');
image = rgb2gray(original);
[r, c, channel] = size(image);
se = logical([1 1 1 ; 1 1 1 ; 1 1 1]);
[p, q] = size(se);
halfH = floor(p/2);
halfW = floor(q/2);
time = 3; % denoising 3 times with all method
|
|
| विस्तारण | विस्तारण के लिए Matlab का प्रयोग करें
imwrite(image, "scene_dil.jpg")
extractmax = zeros(size(image), class(image));
for i = 1 : time
dil_image = imread('scene_dil.jpg');
for col = (halfW + 1): (c - halfW)
for row = (halfH + 1) : (r - halfH)
dpointD = row - halfH;
dpointU = row + halfH;
dpointL = col - halfW;
dpointR = col + halfW;
dneighbor = dil_image(dpointD:dpointU, dpointL:dpointR);
filter = dneighbor(se);
extractmax(row, col) = max(filter);
end
end
imwrite(extractmax, "scene_dil.jpg");
end
|
||
| अपक्षरण | अपक्षरण के लिए Matlab का प्रयोग करें
imwrite(image, 'scene_ero.jpg');
extractmin = zeros(size(image), class(image));
for i = 1: time
ero_image = imread('scene_ero.jpg');
for col = (halfW + 1): (c - halfW)
for row = (halfH +1): (r -halfH)
pointDown = row-halfH;
pointUp = row+halfH;
pointLeft = col-halfW;
pointRight = col+halfW;
neighbor = ero_image(pointDown:pointUp,pointLeft:pointRight);
filter = neighbor(se);
extractmin(row, col) = min(filter);
end
end
imwrite(extractmin, "scene_ero.jpg");
end
|
||
| अभिमुख | अभिमुख के लिए Matlab का प्रयोग करें
imwrite(extractmin, "scene_opening.jpg")
extractopen = zeros(size(image), class(image));
for i = 1 : time
dil_image = imread('scene_opening.jpg');
for col = (halfW + 1): (c - halfW)
for row = (halfH + 1) : (r - halfH)
dpointD = row - halfH;
dpointU = row + halfH;
dpointL = col - halfW;
dpointR = col + halfW;
dneighbor = dil_image(dpointD:dpointU, dpointL:dpointR);
filter = dneighbor(se);
extractopen(row, col) = max(filter);
end
end
imwrite(extractopen, "scene_opening.jpg");
end
|
||
| निष्कर्ष | निष्कर्ष के लिए Matlab का प्रयोग करें
imwrite(extractmax, "scene_closing.jpg")
extractclose = zeros(size(image), class(image));
for i = 1 : time
ero_image = imread('scene_closing.jpg');
for col = (halfW + 1): (c - halfW)
for row = (halfH + 1) : (r - halfH)
dpointD = row - halfH;
dpointU = row + halfH;
dpointL = col - halfW;
dpointR = col + halfW;
dneighbor = ero_image(dpointD:dpointU, dpointL:dpointR);
filter = dneighbor(se);
extractclose(row, col) = min(filter);
end
end
imwrite(extractclose, "scene_closing.jpg");
end
|
छवि के लिए डेनोइसिंग विधि के उपयोग के लिए, छवि को ग्रे स्केल में परिवर्तित कर दिया जाता है। डेनोइसिंग विधि वाला आवरण तार्किक मैट्रिक्स है। डेनोइसिंग विधियां चित्र के केंद्र से आधी ऊंचाई, आधी चौड़ाई से शुरू होती हैं, और पंक्ति संख्या, स्तंभ संख्या की छवि सीमा के साथ समाप्त होती हैं। सीमा के साथ मूल छवि में सहवासी (नेबर) अवरोध (ब्लॉक) [केंद्र के नीचे का बिंदु: ऊपर का बिंदु, केंद्र के बाईं ओर का बिंदु: केंद्र के दाईं ओर का बिंदु] है। संवलन सहवासी (नेबर) और संरचना तत्व और फिर केंद्र को न्यूनतम सहवासी (नेबर) से बदलें।।
उदाहरण के लिए संवरण विधि लें।
प्रथम विस्तारण
- छवि पढ़ें और इसे Matlab के साथ ग्रेस्केल में बदलें।
- छवि की माप प्राप्त करें। प्रत्युत्तर (रिटर्न) मान पंक्ति संख्याएँ और स्तंभ संख्याएँ सीमाओ का बाद में उपयोग किया जाता है।
- संरचना तत्व आपके विस्तारण या अपक्षरण फलन पर निर्भर करते हैं। पिक्सेल के सहवासी (नेबर) का न्यूनतम अपक्षरण विधि की ओर अग्रसित है और अधिकतम सहवासी (नेबर) विस्तारण विधि की ओर अग्रसित है।
- विस्तारण, अपक्षरण और संवरण के लिए समय निर्धारित करें।
- मूल छवि के समान आकार का शून्य आव्यूह बनाएं।
- संरचना गवाक्ष (विंडो) के साथ प्रथम विस्तारण हैं।
- संरचना गवाक्ष (विंडो) 3*3 आव्यूह और संवलन है
- लूप के लिए पंक्ति श्रेणी से गवाक्ष (विंडो) के साथ न्यूनतम मान निकालें [2 ~ छवि ऊंचाई - 1] स्तंभ श्रेणी के साथ [2 ~ छवि चौड़ाई - 1]
- न्यूनतम मान को शून्य आव्यूह में भरें और एक नई छवि संचित करें
- सीमा के लिए, इसमें अभी भी सुधार किया जा सकता है। चूंकि विधि में, सीमा की उपेक्षा की जाती है। सीमाओं से निपटने के लिए पैडिंग तत्वों का उपयोग किया जाता है।
फिर अपक्षरण (विस्तारण छवि को निविष्ट के रूप में लें)
- मूल छवि के समान आकार का शून्य आव्यूह बनाएं।
- संरचनात्मक गवाक्ष (विंडो) के साथ अपक्षरण।
- संरचना गवाक्ष (विंडो) 3*3 आव्यूह और संवलन है
- लूप के लिए पंक्ति श्रेणी से गवाक्ष (विंडो) के साथ अधिकतम मान निकालें [2 ~ छवि ऊंचाई - 1] स्तंभ श्रेणी के साथ [2 ~ छवि चौड़ाई - 1]
- अधिकतम मान को शून्य आव्यूह में भरें और एक नई छवि संचित करें
- सीमा के लिए, इसमें अभी भी सुधार किया जा सकता है। चूंकि विधि में सीमा की उपेक्षा की जाती है। सीमाओं से निपटने के लिए पैडिंग तत्वों को लागू किया जाता है।
- परिणाम उपरोक्त तालिका के अनुसार हैं
अनुप्रयोग
डिजिटल कैमरा छवि
डिजिटल कैमरों में सामान्यतः विशेष डिजिटल छवि प्रसंस्करण हार्डवेयर शामिल हैं - या तो अनुरागी चिप या अन्य चिप पर अतिरिक्त परिपथिकी (सर्किटरी) - अपने छवि संवेदक (सेंसर) से मूल एवं प्रारम्भिक डेटा को मानक छवि संचिका (फ़ाइल) प्रारूप में रंग-सुधारित छवि में परिवर्तित करने के लिए हैं। अतिरिक्त स्थिति प्रसंस्करण तकनीक अधिक स्वाभाविक रूप से दिखने वाली छवियों को बनाने के लिए कोर तीक्षणता (एज शार्पनेस) या रंग संतृप्ति को बढ़ाती है।
फिल्म
वेस्टवर्ल्ड (1973) पहली वैशिष्टय (फीचर) फिल्म थी जिसने डिजिटल छवि प्रसंस्करण से लेकर उन्मत्त (पिक्सललेट) छायाचित्रण तक एंड्रॉइड के दृष्टिकोण को अनुकारित करने के लिए उपयोग किया गया।[25] छवि प्रसंस्करण का उपयोग क्रोमा कुंजी प्रभाव (क्रोमा कि इफ़ेक्ट) उत्पन्न करने के लिए भी किया जाता है जो अभिनेताओं की पृष्ठभूमि को प्राकृतिक या कलात्मक दृश्यों से बदल देता है।
मुखाकृति परिचयन
मुखाकृति परिचयन गणितीय आकृति विज्ञान, असतत कोज्या संक्रियाके साथ कार्यान्वित किया जाता है जिसे सामान्यतः DCT और क्षैतिज प्रक्षेपण (गणित) कहा जाता है।
विशेष गुण-आधारित विधि के साथ सामान्य विधि
विशेष गुण-आधारित विधि मुखाकृति परिचयन के लिए त्वचा की टोन, कोर पहचान, चेहरे का आकार और चेहरे की विशेषता (जैसे आंखें, मुंह, आदि) का उपयोग किया जाता है। त्वचा की टोन, चेहरे का आकार, और सभी अद्वितीय तत्व जो केवल मानव चेहरे के पास हैं, उन्हें विशेषताओं के रूप में वर्णित किया जा सकता है।
प्रक्रिया स्पष्टीकरण
- चेहरे की छवियों के एक बैच को देखते हुए, सबसे पहले, चेहरे की छवियों का प्रतिदर्शी लेकर त्वचा की टोन परिसर (रेंज) निकालें। त्वचा की टोन परिसर (रेंज) केवल त्वचा फिल्टर है।
- त्वचा की टोन निकालने के की स्थिति में छवियों की तुलना करने के लिए संरचनात्मक समानता सूचकांक माप (SSIM) लगाया जा सकता है।
- सामान्य रूप से, HSV या RGB रंग स्थान त्वचा फ़िल्टर के लिए उपयुक्त होते हैं। उदहारण HSV प्रणाली, त्वचा की टोन परिसर (रेंज) [0,48,50] ~ [20,255,255] है
- त्वचा की टोन के साथ छवियों को फ़िल्टर करने के बाद, चेहरे का कोर प्राप्त करने के लिए, चटकीलेपन को दूर करने और अनुपस्थित त्वचा क्षेत्रों को भरने के लिए आकृति विज्ञान और DCT का उपयोग किया जाता है।
- अनुपस्थित त्वचा को भरने के लिए प्रारंभिक विधि या समापन विधि का उपयोग किया जा सकता है।
- DCT त्वचा की टोन जैसी वस्तुओं से बचने के लिए है। चूंकि मानव चेहरों की संव्यूति (टेक्सचर) हमेशा उच्च होते है।
- चेहरे का कोर प्राप्त करने के लिए सोबेल ऑपरेटर या अन्य ऑपरेटरों का उपयोग किया जाता है।
- आंखों जैसी मानवीय विशेषताओं को स्थापित करने के लिए, प्रक्षेपण का उपयोग करके और प्रक्षेपण के आयतचित्र (हिस्टोग्राम) के अधिकतम मान ज्ञात करते है जिससे माउस, बाल और होंठ जैसी विशेष गुण प्राप्त करने में मदद करता है।
- प्रक्षेपण केवल उच्च आवृत्ति को देखने के लिए छवि को प्रक्षेपित करता है जो सामान्यतः विशेष गुण की स्थिति है।
छवि कोटि पद्धति में संशोधन
छवि कोटि कैमरा कंपन से प्रभावित हो सकती है, अति प्रभावाधीन (ओवर-एक्सपोज़र), ग्रे स्तर के वितरण को बहुत केंद्रीकृत, और चटकीला आदि से प्रभावित किया जा सकता है, उदाहरण के लिए, चटकीले होने की समस्या को चौरसाई (स्मूथिंग) विधि द्वारा ठीक किया जा सकता है जबकि ग्रे स्तर वितरण समस्या को आयतचित्र (हिस्टोग्राम) समीकरण द्वारा संशोधित किया जा सकता है।
चौरसाई (स्मूथिंग) विधि
चित्रण में, अगर कुछ अनैच्छिक रंग है, तो अनैच्छिक रंग के आसपास कुछ रंग लेना और उनका औसत लिया जाता है। यह चौरसाई (स्मूथिंग) विधि के उपयोग का आसान तरीका है।
चौरसाई (स्मूथिंग) विधि को आवरण और संवलन के साथ परिपालित किया जा सकता है। उदाहरण के लिए नीचे दी गई छोटी छवि और आवरण देखें।
छविहै।
आवरणहै।
संवलन और चौरसाई (स्मूथिंग) के बाद, छविहै।
छवियों का अवलोकन [1, 1], छवि [1, 2], छवि [2, 1], और छवि [2, 2]।
मूल छवि पिक्सेल 1, 4, 28, 30 है। मास्क को चिकना करने के बाद, पिक्सेल क्रमशः 9, 10, 9, 9 हो जाता है।
नई छवि [1, 1] = * (छवि [0,0]+छवि [0,1]+छवि [0,2]+छवि [1,0]+छवि [1,1]+छवि [1,2]+छवि [2,0]+छवि [2,1]+छवि [2,2])
नई छवि [1, 1] = फलक ( * (2+5+6+3+1+4+1+28+30)) = 9
नई छवि [1, 2] = फलक ( * (5+6+5+1+4+6+28+30+2)) = 10
नई छवि [2, 1] = फलक ( * (3+1+4+1+28+30+73+3+2)) = 9
नई छवि [2, 2] = फलक ( * (1+4+6+28+30+2+3+2+2)) = 9
ग्रे स्तर आयतचित्र (हिस्टोग्राम) विधि
सामान्यतः, नीचे दी गई छवि से ग्रे स्तर का आयतचित्र (हिस्टोग्राम) दिया जाता है। छवि से समान वितरण के लिए आयतचित्र (हिस्टोग्राम) को बदलना सामान्यतः हम आयतचित्र (हिस्टोग्राम) समकरण कहते हैं।
असतत समय में, ग्रे स्तर आयतचित्र (हिस्टोग्राम) का क्षेत्र है (चित्र 1 देखें) जबकि समान वितरण का क्षेत्रफल है (चित्र 2 देखें)। यह स्पष्ट है कि क्षेत्र नहीं बदलेगा, इसलिए ।
समान वितरण से, की प्रायिकता है जब
निरंतर समय में, समीकरण है।
इसके अलावा, किसी फलन की परिभाषा के आधार पर, ग्रे स्तर आयतचित्र (हिस्टोग्राम) विधि फलन प्राप्त करने जैसा है, यह f(p) = q को संतुष्ट करता है।
| परिष्करण (संशोधन) विधि | समस्या | परिष्करण (संशोधन) से पहले | प्रक्रिया | परिष्करण (संशोधन) के बाद |
|---|---|---|---|---|
| चौरसाई (स्मूथिंग) विधि | Matlab से शोर (कोलाहल), लवण तथा ऊषण 0.01 पैरामीटर के साथ चटकीली छवि बनाने के लिए मूल छवि को जोड़ा जाता है। |
|
||
| आयतचित्र
(हिस्टोग्राम) समकरण |
ग्रे स्तर का वितरण भी केंद्रीकृत है। | आयतचित्र (हिस्टोग्राम) समीकरण का संदर्भ लें |
यह भी देखें
- डिजिटल छवि चित्रण
- संगणक (कंप्यूटर) ग्राफिक्स
- संगणक (कंप्यूटर) स्वप्न
- CVIPtools
- अंकीयकरण
- फोरियर रूपांतरण
- मुक्त परिसीमा प्रतिबंध
- GPGPU
- समाकृति निस्पंदन (होमोमोर्फिक फ़िल्टरिंग)
- छवि विश्लेषण
- IEEE सुधिरस परिवहन व्यवस्था वर्ग (इंटेलिजेंट ट्रांसपोर्ट सिस्टम सोसाइटी)
- न्यूनतम वर्ग वर्णक्रमीय विश्लेषण
- बहुविमीय तंत्र
- शिथिलन लेबलिंग
- रिमोट संवेदी सॉफ्टवेयर
- मानक परीक्षण चित्र
- सुपर रिजल्यूशन
- कुल भिन्नता निरूपण
- मशीन दृष्टि
- परिबद्ध विचरण
- सूक्ष्मविकिरणमापी
संदर्भ
- ↑ Chakravorty, Pragnan (2018). "What is a Signal? [Lecture Notes]". IEEE Signal Processing Magazine. 35 (5): 175–177. Bibcode:2018ISPM...35..175C. doi:10.1109/MSP.2018.2832195. S2CID 52164353.
- ↑ Gonzalez, Rafael (2018). Digital image processing. New York, NY: Pearson. ISBN 978-0-13-335672-4. OCLC 966609831.
- ↑ Azriel Rosenfeld, Picture Processing by Computer, New York: Academic Press, 1969
- ↑ 4.0 4.1 4.2 Williams, J. B. (2017). The Electronics Revolution: Inventing the Future. Springer. pp. 245–8. ISBN 9783319490885.
- ↑ "1960: Metal Oxide Semiconductor (MOS) Transistor Demonstrated". The Silicon Engine. Computer History Museum. Archived from the original on 3 October 2019. Retrieved 31 August 2019.
- ↑ James R. Janesick (2001). Scientific charge-coupled devices. SPIE Press. pp. 3–4. ISBN 978-0-8194-3698-6.
- ↑ Boyle, William S; Smith, George E. (1970). "Charge Coupled Semiconductor Devices". Bell Syst. Tech. J. 49 (4): 587–593. doi:10.1002/j.1538-7305.1970.tb01790.x.
- ↑ Fossum, Eric R. (12 July 1993). "Active pixel sensors: Are CCDS dinosaurs?". In Blouke, Morley M. (ed.). Charge-Coupled Devices and Solid State Optical Sensors III. Proceedings of the SPIE. Vol. 1900. pp. 2–14. Bibcode:1993SPIE.1900....2F. CiteSeerX 10.1.1.408.6558. doi:10.1117/12.148585. S2CID 10556755.
- ↑ Fossum, Eric R. (2007). "Active Pixel Sensors". S2CID 18831792.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Matsumoto, Kazuya; et al. (1985). "A new MOS phototransistor operating in a non-destructive readout mode". Japanese Journal of Applied Physics. 24 (5A): L323. Bibcode:1985JaJAP..24L.323M. doi:10.1143/JJAP.24.L323.
- ↑ Fossum, Eric R.; Hondongwa, D. B. (2014). "A Review of the Pinned Photodiode for CCD and CMOS Image Sensors". IEEE Journal of the Electron Devices Society. 2 (3): 33–43. doi:10.1109/JEDS.2014.2306412.
- ↑ "CMOS Image Sensor Sales Stay on Record-Breaking Pace". IC Insights. 8 May 2018. Archived from the original on 21 June 2019. Retrieved 6 October 2019.
- ↑ Ahmed, Nasir (January 1991). "How I Came Up With the Discrete Cosine Transform". Digital Signal Processing. 1 (1): 4–5. doi:10.1016/1051-2004(91)90086-Z. Archived from the original on 10 June 2016. Retrieved 10 October 2019.
- ↑ "T.81 – DIGITAL COMPRESSION AND CODING OF CONTINUOUS-TONE STILL IMAGES – REQUIREMENTS AND GUIDELINES" (PDF). CCITT. September 1992. Archived (PDF) from the original on 17 July 2019. Retrieved 12 July 2019.
- ↑ "The JPEG image format explained". BT.com. BT Group. 31 May 2018. Archived from the original on 5 August 2019. Retrieved 5 August 2019.
- ↑ "What Is a JPEG? The Invisible Object You See Every Day". The Atlantic. 24 September 2013. Archived from the original on 9 October 2019. Retrieved 13 September 2019.
- ↑ Baraniuk, Chris (15 October 2015). "Copy protections could come to JPEGs". BBC News. Archived from the original on 9 October 2019. Retrieved 13 September 2019.
- ↑ Grant, Duncan Andrew; Gowar, John (1989). Power MOSFETS: theory and applications. Wiley. p. 1. ISBN 9780471828679.
The metal-oxide-semiconductor field-effect transistor (MOSFET) is the most commonly used active device in the very large-scale integration of digital integrated circuits (VLSI). During the 1970s these components revolutionized electronic signal processing, control systems and computers.
- ↑ Shirriff, Ken (30 August 2016). "The Surprising Story of the First Microprocessors". IEEE Spectrum. Institute of Electrical and Electronics Engineers. 53 (9): 48–54. doi:10.1109/MSPEC.2016.7551353. S2CID 32003640. Archived from the original on 13 October 2019. Retrieved 13 October 2019.
- ↑ 20.0 20.1 "1979: Single Chip Digital Signal Processor Introduced". The Silicon Engine. Computer History Museum. Archived from the original on 3 October 2019. Retrieved 14 October 2019.
- ↑ Taranovich, Steve (27 August 2012). "30 years of DSP: From a child's toy to 4G and beyond". EDN. Archived from the original on 14 October 2019. Retrieved 14 October 2019.
- ↑ Stanković, Radomir S.; Astola, Jaakko T. (2012). "Reminiscences of the Early Work in DCT: Interview with K.R. Rao" (PDF). Reprints from the Early Days of Information Sciences. 60. Archived (PDF) from the original on 13 October 2019. Retrieved 13 October 2019.
- ↑ "Space Technology Hall of Fame:Inducted Technologies/1994". Space Foundation. 1994. Archived from the original on 4 July 2011. Retrieved 7 January 2010.
- ↑ House, Keyser (6 December 2016). Affine Transformations (PDF). ISBN 9781482234602. Archived (PDF) from the original on 30 August 2017. Retrieved 26 March 2019.
{{cite book}}:|website=ignored (help) - ↑ A Brief, Early History of Computer Graphics in Film Archived 17 July 2012 at the Wayback Machine, Larry Yaeger, 16 August 2002 (last update), retrieved 24 March 2010
अग्रिम पठन
- Solomon, C.J.; Breckon, T.P. (2010). Fundamentals of Digital Image Processing: A Practical Approach with Examples in Matlab. Wiley-Blackwell. doi:10.1002/9780470689776. ISBN 978-0470844731.
- Wilhelm Burger; Mark J. Burge (2007). Digital Image Processing: An Algorithmic Approach Using Java. Springer. ISBN 978-1-84628-379-6.
- R. Fisher; K Dawson-Howe; A. Fitzgibbon; C. Robertson; E. Trucco (2005). Dictionary of Computer Vision and Image Processing. John Wiley. ISBN 978-0-470-01526-1.
- Rafael C. Gonzalez; Richard E. Woods; Steven L. Eddins (2004). Digital Image Processing using MATLAB. Pearson Education. ISBN 978-81-7758-898-9.
- Tim Morris (2004). Computer Vision and Image Processing. Palgrave Macmillan. ISBN 978-0-333-99451-1.
- Tyagi Vipin (2018). Understanding Digital Image Processing. Taylor and Francis CRC Press. ISBN 978-11-3856-6842.
- Milan Sonka; Vaclav Hlavac; Roger Boyle (1999). Image Processing, Analysis, and Machine Vision. PWS Publishing. ISBN 978-0-534-95393-5.
- Rafael C. Gonzalez (2008). Digital Image Processing. Prentice Hall. ISBN 9780131687288
बाहरी संबंध
- Lectures on Image Processing, by Alan Peters. Vanderbilt University. Updated 7 January 2016.
- Processing digital images with computer algorithms
]