फीचर चयन: Difference between revisions
No edit summary |
No edit summary |
||
| (15 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Procedure in machine learning and statistics}} | {{short description|Procedure in machine learning and statistics}} | ||
{{machine learning bar}} | {{machine learning bar}} | ||
[[ यंत्र अधिगम | | [[ यंत्र अधिगम | मशीन लर्निंग]] और सांख्यिकी में, '''फीचर''' '''सिलेक्शन''' होता हैं, जिसे वैरिएबल सिलेक्शन , विशेषता सिलेक्शन या वैरिएबल सबसेट सिलेक्शन के रूप में भी जाना जाता है | यह मॉडल निर्माण में उपयोग के लिए प्रासंगिक [[ फ़ीचर (मशीन लर्निंग) |फीचर (मशीन लर्निंग)]] (वेरिएबल , प्रडिक्टर) के सबसेट का सिलेक्शन करने की प्रक्रिया है। फीचर सिलेक्शन तकनीकों का उपयोग अनेक कारणों से किया जाता है | | ||
:* शोधकर्ताओं/उपयोगकर्ताओं द्वारा व्याख्या करना | :* शोधकर्ताओं/उपयोगकर्ताओं द्वारा व्याख्या करना और उसको सरल बनाने के लिए मॉडलों का सरलीकरण,<ref name="islr">{{cite book |author1=Gareth James |author2=Daniela Witten |author3=Trevor Hastie |author4=Robert Tibshirani |title=सांख्यिकीय शिक्षा का एक परिचय|publisher=Springer |year=2013 |url=http://www-bcf.usc.edu/~gareth/ISL/ |page=204}}</ref> | ||
:* कम प्रशिक्षण | :* कम समय में प्रशिक्षण,<ref>{{Citation|last1=Brank|first1=Janez|title=Feature Selection|date=2011|url=http://link.springer.com/10.1007/978-0-387-30164-8_306|encyclopedia=Encyclopedia of Machine Learning|pages=402–406|editor-last=Sammut|editor-first=Claude|place=Boston, MA|publisher=Springer US|language=en|doi=10.1007/978-0-387-30164-8_306|isbn=978-0-387-30768-8|access-date=2021-07-13|last2=Mladenić|first2=Dunja|last3=Grobelnik|first3=Marko|last4=Liu|first4=Huan|last5=Mladenić|first5=Dunja|last6=Flach|first6=Peter A.|last7=Garriga|first7=Gemma C.|last8=Toivonen|first8=Hannu|last9=Toivonen|first9=Hannu|editor2-last=Webb|editor2-first=Geoffrey I.}}</ref> | ||
:* आयामीता के | :* आयामीता के कर्स से बचने के लिए,<ref>{{Cite journal|last=Kramer|first=Mark A.|date=1991|title=ऑटोएसोसिएटिव न्यूरल नेटवर्क का उपयोग करके नॉनलाइनियर प्रमुख घटक विश्लेषण|url=https://aiche.onlinelibrary.wiley.com/doi/abs/10.1002/aic.690370209|journal=AIChE Journal|language=en|volume=37|issue=2|pages=233–243|doi=10.1002/aic.690370209|issn=1547-5905}}</ref> | ||
:*लर्निंग मॉडल क्लास के साथ डेटा की अनुकूलता में सुधार,<ref>{{Cite journal|last1=Kratsios|first1=Anastasis|last2=Hyndman|first2=Cody|date=2021|title=NEU: A Meta-Algorithm for Universal UAP-Invariant Feature Representation|url=http://jmlr.org/papers/v22/18-803.html|journal=Journal of Machine Learning Research|volume=22|issue=92|pages=1–51|issn=1533-7928}}</ref> | :*लर्निंग मॉडल क्लास के साथ डेटा की अनुकूलता में सुधार,<ref>{{Cite journal|last1=Kratsios|first1=Anastasis|last2=Hyndman|first2=Cody|date=2021|title=NEU: A Meta-Algorithm for Universal UAP-Invariant Feature Representation|url=http://jmlr.org/papers/v22/18-803.html|journal=Journal of Machine Learning Research|volume=22|issue=92|pages=1–51|issn=1533-7928}}</ref> | ||
:*इनपुट | :*इनपुट स्थान में उपस्थित अंतर्निहित [[सममित स्थान]] को एनकोड करें। <ref>{{Cite book|last1=Persello|first1=Claudio|last2=Bruzzone|first2=Lorenzo|title=2014 IEEE Geoscience and Remote Sensing Symposium |chapter=Relevant and invariant feature selection of hyperspectral images for domain generalization |date=July 2014|chapter-url=http://dx.doi.org/10.1109/igarss.2014.6947252|pages=3562–3565|publisher=IEEE|doi=10.1109/igarss.2014.6947252|isbn=978-1-4799-5775-0|s2cid=8368258|url=https://ris.utwente.nl/ws/files/122945513/Persello2014relevant.pdf }}</ref><ref>{{Cite journal|last1=Hinkle|first1=Jacob|last2=Muralidharan|first2=Prasanna|last3=Fletcher|first3=P. Thomas|last4=Joshi|first4=Sarang|date=2012|editor-last=Fitzgibbon|editor-first=Andrew|editor2-last=Lazebnik|editor2-first=Svetlana|editor3-last=Perona|editor3-first=Pietro|editor4-last=Sato|editor4-first=Yoichi|editor5-last=Schmid|editor5-first=Cordelia|title=रीमैनियन मैनिफोल्ड्स पर बहुपद प्रतिगमन|url=https://link.springer.com/chapter/10.1007/978-3-642-33712-3_1|journal=Computer Vision – ECCV 2012|series=Lecture Notes in Computer Science|volume=7574|language=en|location=Berlin, Heidelberg|publisher=Springer|pages=1–14|doi=10.1007/978-3-642-33712-3_1|isbn=978-3-642-33712-3|arxiv=1201.2395|s2cid=8849753}}</ref><ref>{{Cite journal|last=Yarotsky|first=Dmitry|date=2021-04-30|title=तंत्रिका नेटवर्क द्वारा अपरिवर्तनीय मानचित्रों का सार्वभौमिक अनुमान|url=https://doi.org/10.1007/s00365-021-09546-1|journal=Constructive Approximation|volume=55 |pages=407–474 |language=en|doi=10.1007/s00365-021-09546-1|issn=1432-0940|arxiv=1804.10306|s2cid=13745401}}</ref><ref>{{Cite journal|last1=Hauberg|first1=Søren|last2=Lauze|first2=François|last3=Pedersen|first3=Kim Steenstrup|date=2013-05-01|title=रीमैनियन मैनिफ़ोल्ड्स पर असुगंधित कल्मन फ़िल्टरिंग|url=https://doi.org/10.1007/s10851-012-0372-9|journal=Journal of Mathematical Imaging and Vision|language=en|volume=46|issue=1|pages=103–120|doi=10.1007/s10851-012-0372-9|s2cid=8501814|issn=1573-7683}}</ref> | ||
फीचर | फीचर सिलेक्शन तकनीक का उपयोग करते समय केंद्रीय आधार यह है कि डेटा में कुछ विशेषताएं सम्मिलित हैं जो तब अनावश्यक हैं या अप्रासंगिक हैं, और इस प्रकार सूचना को अधिक हानि के अतिरिक्त उन्हें हटाया जा सकता है। <ref name="Bermingham-prolog">{{cite journal|last1=Kratsios|first1=Anastasis|last2=Hyndman|first2=Cody|date=June 8, 2021|title=NEU: A Meta-Algorithm for Universal UAP-Invariant Feature Representation|url=https://jmlr.org/papers/v22/18-803.html|journal=[[Journal of Machine Learning Research]]|volume=22|page=10312|doi=10.1038/srep10312 |pmid=25988841 |pmc=4437376 |bibcode=2015NatSR...510312B}}</ref> यह निरर्थक और अप्रासंगिक दो भिन्न-भिन्न धारणाएँ होती हैं, क्योंकि प्रासंगिक विशेषता किसी अन्य प्रासंगिक विशेषता की उपस्थिति में निरर्थक हो सकती है जिसके साथ यह दृढ़ता से सहसंबद्ध होता है।{{r|guyon-intro}} | ||
फीचर सिलेक्शन तकनीकों को फीचर निष्कर्षण से भिन्न किया जाना चाहिए। <ref>{{cite journal | |||
|last=Sarangi|first=Susanta |author2=Sahidullah, Md |author3=Saha, Goutam | |last=Sarangi|first=Susanta |author2=Sahidullah, Md |author3=Saha, Goutam | ||
|title=Optimization of data-driven filterbank for automatic speaker verification | |title=Optimization of data-driven filterbank for automatic speaker verification | ||
|journal=Digital Signal Processing |date=September 2020 |volume=104 | |journal=Digital Signal Processing |date=September 2020 |volume=104 | ||
|page=102795 |doi= 10.1016/j.dsp.2020.102795|arxiv=2007.10729|s2cid=220665533 }}</ref> | |page=102795 |doi= 10.1016/j.dsp.2020.102795|arxiv=2007.10729|s2cid=220665533 }}</ref> फीचर निष्कर्षण मूल फीचर्स के कार्यों से नई सुविधाएँ बनाता है, जबकि फीचर सिलेक्शन फीचर्स का सबसेट लौटाता है। फीचर सिलेक्शन तकनीकों का उपयोग अधिकांशतः उन डोमेन में किया जाता है जहाँ अनेक सुविधाएँ और तुलनात्मक रूप से प्रतिरुप (या डेटा बिंदु) होते हैं। फीचर सिलेक्शन के अनुप्रयोग के लिए आदर्श स्तिथियों में [[स्टाइलोमेट्री]] और [[डीएनए माइक्रोएरे]] डेटा का विश्लेषण सम्मिलित होता है, जहां अनेक हजारों विशेषताएं होती हैं, और इसमें कुछ दशको से सैकड़ों प्रतिरुप हैं। | ||
==परिचय== | ==परिचय== | ||
फीचर सिलेक्शन एल्गोरिथ्म को नए फीचर सबसेट के प्रस्ताव के लिए खोज तकनीक के संयोजन के रूप में देखा जा सकता है | इसके साथ ही मूल्यांकन उपाय जो विभिन्न फीचर सबसेट को स्कोर करता है। यह सबसे सरल एल्गोरिदम फीचर्स के प्रत्येक संभावित उपसमूह का परीक्षण करना है जो त्रुटि दर को कम करता है। यह स्थान की विस्तृत खोज है, और यह लघु से लघु फीचर सेट को छोड़कर सभी के लिए कम्प्यूटेशनल रूप से कठिन है। मूल्यांकन मेट्रिक का चुनाव एल्गोरिदम को अधिक रूप से प्रभावित करता है, और यह मूल्यांकन मेट्रिक्स होता हैं जो फीचर सिलेक्शन एल्गोरिदम की तीन मुख्य श्रेणियों के मध्य अंतर करते हैं | इसमें रैपर, फिल्टर और एम्बेडेड विधियां होती हैं। <ref name="guyon-intro">{{cite journal |title=वेरिएबल और फ़ीचर चयन का एक परिचय|first1=Isabelle |last1=Guyon |first2=André |last2=Elisseeff |journal=[[Journal of Machine Learning Research|JMLR]] |volume=3 |year=2003 |url=http://jmlr.csail.mit.edu/papers/v3/guyon03a.html}}</ref> | |||
* रैपर विधियाँ फीचर | * रैपर विधियाँ फीचर सबसेट को स्कोर करने के लिए पूर्वानुमानित मॉडल का उपयोग करती हैं। प्रत्येक नए सबसेट का उपयोग मॉडल को प्रशिक्षित करने के लिए किया जाता है, जिसका परीक्षण होल्ड-आउट सेट पर किया जाता है। उस होल्ड-आउट सेट (मॉडल की त्रुटि दर) पर की गई त्रुटियों की संख्या की गणना करने से उस सबसेट के लिए स्कोर मिलता है। चूँकि रैपर विधियाँ प्रत्येक सबसेट के लिए नए मॉडल को प्रशिक्षित करती हैं, वह कम्प्यूटेशनल रूप से बहुत गहन होती हैं, किन्तु सामान्यतः यह उस विशेष प्रकार के मॉडल या विशिष्ट समस्या के लिए सबसे अच्छा प्रदर्शन करने वाला फीचर सेट प्रदान करती हैं। | ||
* फ़िल्टर विधियाँ फीचर | * फ़िल्टर विधियाँ फीचर सबसेट को स्कोर करने के लिए त्रुटि दर के अतिरिक्त प्रॉक्सी माप का उपयोग करती हैं। फीचर सेट की उपयोगिता को ध्यान में रखते हुए, गणना करने में तीव्र होने के लिए इस उपाय को चुना गया है। सामान्य उपायों में [[आपसी जानकारी|म्यूच्यूअल इनफार्मेशन]] सम्मिलित होती है,<ref name="guyon-intro"/> यह पॉइंटवाइस म्यूच्यूअल इनफार्मेशन हैं ,<ref name="textcat"/> [[पियर्सन उत्पाद-क्षण सहसंबंध गुणांक|पियर्सन प्रोडक्ट-मोमेंट कॉरर्लशन कॉएफिसिएंट]], [[राहत (सुविधा चयन)|रिलीफ (फीचर सिलेक्शन )]] | रिलीफ-बेस्ड एल्गोरिदम हैं,<ref>{{Cite journal|last1=Urbanowicz|first1=Ryan J.|last2=Meeker|first2=Melissa|last3=LaCava|first3=William|last4=Olson|first4=Randal S.|last5=Moore|first5=Jason H.|title=Relief-Based Feature Selection: Introduction and Review|journal=Journal of Biomedical Informatics|volume=85|pages=189–203|arxiv=1711.08421|pmid=30031057|pmc=6299836|year=2018|doi=10.1016/j.jbi.2018.07.014}}</ref> और अंतर/अंतर क्लास दूरी या प्रत्येक वर्ग/फीचर संयोजन के लिए [[सांख्यिकीय परिकल्पना परीक्षण]] के स्कोर सम्मिलित हैं। <ref name="textcat">{{cite conference |last1=Yang |first1=Yiming |first2=Jan O. |last2=Pedersen |title=पाठ वर्गीकरण में फीचर चयन पर एक तुलनात्मक अध्ययन|conference=ICML |year=1997|url=http://www.surdeanu.info/mihai/teaching/ista555-spring15/readings/yang97comparative.pdf}}</ref><ref>{{cite journal |last1=Forman |first1=George |title=पाठ वर्गीकरण के लिए फीचर चयन मेट्रिक्स का एक व्यापक अनुभवजन्य अध्ययन|journal=Journal of Machine Learning Research |volume=3 |year=2003 |pages=1289–1305|url=http://www.jmlr.org/papers/volume3/forman03a/forman03a.pdf}}</ref> फ़िल्टर सामान्यतः रैपर्स की तुलना में कम कम्प्यूटेशनल रूप से गहन होते हैं, किन्तु वह फीचर सेट का उत्पादन करते हैं जो विशिष्ट प्रकार के पूर्वानुमानित मॉडल के अनुरूप नहीं होता है। <ref>{{cite journal|author1=Yishi Zhang|author2=Shujuan Li|author3=Teng Wang|author4=Zigang Zhang|title=अलग-अलग वर्गों के लिए विचलन-आधारित सुविधा चयन|journal=Neurocomputing|date=2013|volume=101|issue=4|pages=32–42|doi=10.1016/j.neucom.2012.06.036}}</ref> ट्यूनिंग की इस कमी का अर्थ है कि फ़िल्टर से सेट किया गया फीचर रैपर से सेट की तुलना में अधिक सामान्य है, सामान्यतः रैपर की तुलना में कम पूर्वानुमान प्रदर्शन देता है। चूँकि फीचर सेट में पूर्वानुमान मॉडल की धारणाएँ सम्मिलित नहीं हैं, और इसलिए यह फीचर्स के मध्य संबंधों को प्रदर्शित करने के लिए अधिक उपयोगी है। अनेक फ़िल्टर स्पष्ट सर्वोत्तम फीचर सबसेट के अतिरिक्त फीचर रैंकिंग प्रदान करते हैं, और रैंकिंग में कट-ऑफ पॉइंट क्रॉस-वैलिडेशन (सांख्यिकी) या क्रॉस-वैलिडेशन के माध्यम से चुना जाता है। फ़िल्टर विधियों का उपयोग रैपर विधियों के लिए प्रीप्रोसेसिंग चरण के रूप में भी किया गया है, जिससे बड़ी समस्याओं पर रैपर का उपयोग किया जा सकता है। अन्य लोकप्रिय दृष्टिकोण रिकर्सिव फीचर एलिमिनेशन एल्गोरिदम है, <ref>{{cite journal|author1=Guyon I.|author2=Weston J.|author3=Barnhill S.|author4=Vapnik V.|title=सपोर्ट वेक्टर मशीनों का उपयोग करके कैंसर वर्गीकरण के लिए जीन चयन|journal=Machine Learning|date=2002|volume=46|issue=1–3|pages=389–422|doi=10.1023/A:1012487302797|doi-access=free}}</ref> सामान्यतः मॉडल का निरंतर निर्माण करने और कम वजन वाले फीचर्स को हटाने के लिए [[ समर्थन वेक्टर मशीन |सपोर्ट वेक्टर मशीन]] के साथ उपयोग किया जाता है। | ||
* एंबेडेड विधियां तकनीकों का समूह है जो मॉडल निर्माण प्रक्रिया के | * एंबेडेड विधियां तकनीकों का समूह होती है जो मॉडल निर्माण प्रक्रिया के भागों के रूप में फीचर सिलेक्शन करती है। इस दृष्टिकोण का उदाहरण रेखीय मॉडल के निर्माण के लिए लासो (सांख्यिकी) विधि होती है, जो प्रतिगमन गुणांक को L1 दंड के साथ दंडित करता है, उनमें से अनेक को शून्य तक संकुचित कर देता है। कोई भी विशेषता जिसमें गैर-शून्य प्रतिगमन गुणांक है, उसे लैस्सो एल्गोरिथ्म द्वारा 'सिलेक्शन' किया जाता है। लैस्सो में सुधारों में बोलासो सम्मिलित है जो प्रतिरूपों को बूटस्ट्रैप करता है | <ref name=Bolasso>{{Cite book|last1=Bach|first1=Francis R|title=Bolasso: model consistent lasso estimation through the bootstrap|journal=Proceedings of the 25th International Conference on Machine Learning|date=2008|pages=33–40|doi=10.1145/1390156.1390161|isbn=9781605582054|s2cid=609778}}</ref> [[इलास्टिक नेट नियमितीकरण]], जो लैस्सो के L1 दंड को [[ रिज प्रतिगमन |रिज रिग्रेशन]] के L2 दंड के साथ जोड़ता है | और फ़ीआलेक्ट जो प्रतिगमन गुणांक के संयुक्त विश्लेषण के आधार पर सभी विशेषताओं को स्कोर करता है। <ref name=FeaLect>{{cite journal|last1=Zare|first1=Habil|title=लिंफोमा निदान के अनुप्रयोग के साथ लैस्सो के संयुक्त विश्लेषण के आधार पर सुविधाओं की प्रासंगिकता का स्कोरिंग|journal=BMC Genomics|date=2013|volume=14|issue=Suppl 1 |pages=S14|doi=10.1186/1471-2164-14-S1-S14|pmid=23369194|pmc=3549810}}</ref> एईएफएस आगे लैस्सो को ऑटोएन्कोडर्स के साथ नॉनलाइनियर परिदृश्य तक विस्तारित करता है। <ref>{{cite conference |author1=Kai Han|author2=Yunhe Wang|author3=Chao Zhang|author4=Chao Li|author5=Chao Xu|title=ऑटोएन्कोडर ने बिना पर्यवेक्षित सुविधा चयन को प्रेरित किया|conference=IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) |year=2018}}</ref> कम्प्यूटेशनल सम्मिश्रता के संदर्भ में यह दृष्टिकोण फिल्टर और रैपर के मध्य होते हैं। | ||
पारंपरिक [[प्रतिगमन विश्लेषण]] में, फीचर | पारंपरिक [[प्रतिगमन विश्लेषण]] में, फीचर सिलेक्शन का सबसे लोकप्रिय रूप [[चरणबद्ध प्रतिगमन|'''वेरिएबल स्टेपवाइज रिग्रेशन''']] है, जो रैपर तकनीक होती है। यह [[लालची एल्गोरिदम|ग्रीडी एल्गोरिदम]] है जो प्रत्येक समय में सबसे अच्छी फीचर जोड़ता है | और (सबसे व्यर्थ फीचर को हटा देता है)। मुख्य नियंत्रण उद्देश्य यह तय करना है कि एल्गोरिदम को कब रोकना है। मशीन लर्निंग में, यह सामान्यतः क्रॉस-वैलिडेशन (सांख्यिकी)|क्रॉस-वैलिडेशन द्वारा किया जाता है। आँकड़ों में, कुछ मानदंड अनुकूलित किए गए हैं। इससे श्रंखला बनाने की अंतर्निहित समस्या उत्पन्न होती है। इससे अधिक शक्तिशाली विधियों का अनुमान लगाया गया है, जैसे शाखा में बाउंड और पीसवाइस लीनियर नेटवर्क होते हैं। | ||
== | ==सबसेट सिलेक्शन == | ||
सबसेट सिलेक्शन उपयुक्तता के लिए समूह के रूप में फीचर्स के सबसेट का मूल्यांकन करता है। सबसेट [[खोज एल्गोरिथ्म|सर्च एल्गोरिथ्म]] को रैपर, फिल्टर और एम्बेडेड विधियों में विभाजित किया जा सकता है। रैपर्स संभावित फीचर्स के स्थान के माध्यम से खोज करने के लिए खोज एल्गोरिदम का उपयोग करते हैं और सबसेट पर मॉडल चलाकर प्रत्येक सबसेट का मूल्यांकन करते हैं। रैपर कम्प्यूटेशनल रूप से मूल्यवान हो सकते हैं और मॉडल में अधिक फिट होने पर कठिन परिस्थिति हो सकती है। खोज दृष्टिकोण में फ़िल्टर रैपर के समान होते हैं, किन्तु यह किसी मॉडल के विरुद्ध मूल्यांकन करने के अतिरिक्त, सरल फ़िल्टर का मूल्यांकन किया जाता है। एंबेडेड तकनीकें मॉडल में अंतर्निहित और विशिष्ट होती हैं। | |||
अनेक लोकप्रिय खोज दृष्टिकोण | अनेक लोकप्रिय खोज दृष्टिकोण ग्रीडी एल्गोरिदम [[पहाड़ी की चढ़ाई|हिल क्लिंबिंग]] का उपयोग करते हैं, जो फीचर्स के उम्मीदवार उपसमूह का पुनरावृत्तीय मूल्यांकन करता है, फिर उपसमूह को संशोधित करता है और मूल्यांकन करता है कि क्या नया उपसमूह पुराने की तुलना में सही है। सबसेट के मूल्यांकन के लिए स्कोरिंग मीट्रिक (गणित) की आवश्यकता होती है जो फीचर्स के उपसमूह को ग्रेड करती है। व्यापक खोज सामान्यतः अव्यावहारिक होती है, इसलिए कुछ कार्यान्वयनकर्ता (या ऑपरेटर) परिभाषित स्टॉपिंग बिंदु पर होते हैं, उस बिंदु तक खोजे गए उच्चतम स्कोर वाले फीचर्स के सबसेट को संतबषजनक फीचर सबसेट के रूप में चुना जाता है। इसको रोकने का मानदंड एल्गोरिथम के अनुसार भिन्न होता है | इस प्रकार यह संभावित मानदंडों में सम्मिलित हैं | सबसेट स्कोर सीमा से अधिक होता है | कार्य का अधिकतम अनुमत रन टाइम सरपास्ड हो गया है | | ||
वैकल्पिक खोज-आधारित तकनीकें [[लक्षित प्रक्षेपण खोज]] पर आधारित होती हैं जो उच्च स्कोर वाले डेटा के निम्न-आयामी अनुमानों का पता लगाती हैं | वैकल्पिक खोज-आधारित तकनीकें [[लक्षित प्रक्षेपण खोज]] पर आधारित होती हैं जो उच्च स्कोर वाले डेटा के निम्न-आयामी अनुमानों का पता लगाती हैं | फिर उन विशेषताओं का सिलेक्शन किया जाता है जिनके निचले-आयामी स्थान में सबसे बड़े प्रक्षेपण होते हैं। | ||
खोज दृष्टिकोण में | खोज दृष्टिकोण में सम्मिलित हैं | | ||
* | *एक्सहॉस्टइव <ref>{{cite arXiv |last1=Hazimeh |first1=Hussein| last2=Mazumder |first2=Rahul |last3=Saab |first3=Ali |eprint=2004.06152 |title=Sparse Regression at Scale: Branch-and-Bound rooted in First-Order Optimization |class= stat.CO|date=2020}}</ref> | ||
* | * बेस्ट फर्स्ट | ||
* [[तैयार किए हुयी धातु पे पानी चढाने की कला]] | * [[तैयार किए हुयी धातु पे पानी चढाने की कला|सिम्युलेटेड एनीलिंग]] | ||
* [[जेनेटिक एल्गोरिद्म]]<ref>{{Cite journal|last1=Soufan|first1=Othman|last2=Kleftogiannis|first2=Dimitrios|last3=Kalnis|first3=Panos|last4=Bajic|first4=Vladimir B.|date=2015-02-26|title=DWFS: A Wrapper Feature Selection Tool Based on a Parallel Genetic Algorithm|journal=PLOS ONE|language=en|volume=10|issue=2|pages=e0117988|doi=10.1371/journal.pone.0117988|pmid=25719748|pmc=4342225|issn=1932-6203|bibcode=2015PLoSO..1017988S|doi-access=free}}</ref> | * [[जेनेटिक एल्गोरिद्म|जेनेटिक एल्गोरिदम]] <ref>{{Cite journal|last1=Soufan|first1=Othman|last2=Kleftogiannis|first2=Dimitrios|last3=Kalnis|first3=Panos|last4=Bajic|first4=Vladimir B.|date=2015-02-26|title=DWFS: A Wrapper Feature Selection Tool Based on a Parallel Genetic Algorithm|journal=PLOS ONE|language=en|volume=10|issue=2|pages=e0117988|doi=10.1371/journal.pone.0117988|pmid=25719748|pmc=4342225|issn=1932-6203|bibcode=2015PLoSO..1017988S|doi-access=free}}</ref> | ||
* | * ग्रीडी फॉरवर्ड सिलेक्शन <ref>{{cite journal|last1=Figueroa|first1=Alejandro|title=वेब क्वेरी के पीछे उपयोगकर्ता के इरादे को पहचानने के लिए प्रभावी सुविधाओं की खोज करना|journal=Computers in Industry|date=2015|volume=68|pages=162–169|url=https://www.researchgate.net/publication/271911317|doi=10.1016/j.compind.2015.01.005}}</ref><ref>{{cite conference |last=Figueroa|first=Alejandro |author2=Guenter Neumann |url=https://www.researchgate.net/publication/259174469 |title=सामुदायिक प्रश्न उत्तर के लिए क्वेरी लॉग से प्रभावी पैराफ्रेज़ को रैंक करना सीखना|conference= AAAI |year=2013}}</ref><ref>{{cite journal|last=Figueroa|first=Alejandro |author2=Guenter Neumann|title=सामुदायिक प्रश्न उत्तर में प्रभावी पैराग्राफों की रैंकिंग के लिए श्रेणी-विशिष्ट मॉडल|journal=Expert Systems with Applications|date=2014|volume=41|issue=10 |pages=4730–4742|url=https://www.researchgate.net/publication/260519271|doi=10.1016/j.eswa.2014.02.004|hdl=10533/196878|hdl-access=free}}</ref> | ||
* | * ग्रीडी बैकवर्ड एलिमिनेशन | ||
* [[कण झुंड अनुकूलन]]<ref name="sciencedirect.com">{{cite journal|last1=Zhang|first1=Y.|last2=Wang|first2=S.|last3=Phillips|first3=P.|title=स्पैम डिटेक्शन पर लागू डिसीजन ट्री का उपयोग करके फ़ीचर चयन के लिए म्यूटेशन ऑपरेटर के साथ बाइनरी पीएसओ|journal=Knowledge-Based Systems|date=2014|volume=64|pages=22–31|doi=10.1016/j.knosys.2014.03.015}}</ref> | * [[कण झुंड अनुकूलन|पार्टिकल स्वार्म ऑप्टिमाइजेशन]] <ref name="sciencedirect.com">{{cite journal|last1=Zhang|first1=Y.|last2=Wang|first2=S.|last3=Phillips|first3=P.|title=स्पैम डिटेक्शन पर लागू डिसीजन ट्री का उपयोग करके फ़ीचर चयन के लिए म्यूटेशन ऑपरेटर के साथ बाइनरी पीएसओ|journal=Knowledge-Based Systems|date=2014|volume=64|pages=22–31|doi=10.1016/j.knosys.2014.03.015}}</ref> | ||
* | * टार्गेटेड प्रोजेक्शन परसूट | ||
* | * स्कैटर सर्च <ref>F.C. Garcia-Lopez, M. Garcia-Torres, B. Melian, J.A. Moreno-Perez, J.M. Moreno-Vega. [https://pdfs.semanticscholar.org/ea5d/770e97b9330032e8713b0c105b523750a7c3.pdf Solving feature subset selection problem by a Parallel Scatter Search], ''European Journal of Operational Research'', vol. 169, no. 2, pp. 477–489, 2006. | ||
</ref><ref>{{Cite book|chapter-url=https://dl.acm.org/doi/abs/10.1145/3449726.3459481|doi = 10.1145/3449726.3459481|chapter = Scatter search for high-dimensional feature selection using feature grouping|title = आनुवंशिक और विकासवादी संगणना सम्मेलन साथी की कार्यवाही|year = 2021|last1 = García-Torres|first1 = Miguel|last2 = Gómez-Vela|first2 = Francisco|last3 = Divina|first3 = Federico|last4 = Pinto-Roa|first4 = Diego P.|last5 = Noguera|first5 = José Luis Vázquez|last6 = Román|first6 = Julio C. Mello|pages = 149–150|isbn = 9781450383516|s2cid = 235770316}}</ref> | </ref><ref>{{Cite book|chapter-url=https://dl.acm.org/doi/abs/10.1145/3449726.3459481|doi = 10.1145/3449726.3459481|chapter = Scatter search for high-dimensional feature selection using feature grouping|title = आनुवंशिक और विकासवादी संगणना सम्मेलन साथी की कार्यवाही|year = 2021|last1 = García-Torres|first1 = Miguel|last2 = Gómez-Vela|first2 = Francisco|last3 = Divina|first3 = Federico|last4 = Pinto-Roa|first4 = Diego P.|last5 = Noguera|first5 = José Luis Vázquez|last6 = Román|first6 = Julio C. Mello|pages = 149–150|isbn = 9781450383516|s2cid = 235770316}}</ref> | ||
* [[परिवर्तनीय पड़ोस खोज]]<ref>F.C. Garcia-Lopez, M. Garcia-Torres, B. Melian, J.A. Moreno-Perez, J.M. Moreno-Vega. [https://web.archive.org/web/20190830132140/https://pdfs.semanticscholar.org/9428/2985d2c2ea4eb9f49846bedc12003a47db49.pdf Solving Feature Subset Selection Problem by a Hybrid Metaheuristic]. In ''First International Workshop on Hybrid Metaheuristics'', pp. 59–68, 2004.</ref><ref>M. Garcia-Torres, F. Gomez-Vela, B. Melian, J.M. Moreno-Vega. [https://www.researchgate.net/profile/Miguel_Garcia_Torres/publication/229763203_Parallel_Scatter_Search/links/5b2788a00f7e9be8bdaeb0d0/Parallel-Scatter-Search.pdf High-dimensional feature selection via feature grouping: A Variable Neighborhood Search approach], ''Information Sciences'', vol. 326, pp. 102-118, 2016.</ref> | * [[परिवर्तनीय पड़ोस खोज|वेरिएबल नेबरहुड सर्च]] <ref>F.C. Garcia-Lopez, M. Garcia-Torres, B. Melian, J.A. Moreno-Perez, J.M. Moreno-Vega. [https://web.archive.org/web/20190830132140/https://pdfs.semanticscholar.org/9428/2985d2c2ea4eb9f49846bedc12003a47db49.pdf Solving Feature Subset Selection Problem by a Hybrid Metaheuristic]. In ''First International Workshop on Hybrid Metaheuristics'', pp. 59–68, 2004.</ref><ref>M. Garcia-Torres, F. Gomez-Vela, B. Melian, J.M. Moreno-Vega. [https://www.researchgate.net/profile/Miguel_Garcia_Torres/publication/229763203_Parallel_Scatter_Search/links/5b2788a00f7e9be8bdaeb0d0/Parallel-Scatter-Search.pdf High-dimensional feature selection via feature grouping: A Variable Neighborhood Search approach], ''Information Sciences'', vol. 326, pp. 102-118, 2016.</ref> | ||
वर्गीकरण समस्याओं के लिए दो लोकप्रिय फ़िल्टर मेट्रिक्स सहसंबंध और पारस्परिक | वर्गीकरण समस्याओं के लिए दो लोकप्रिय फ़िल्टर मेट्रिक्स सहसंबंध और पारस्परिक सूचना हैं,चूंकि गणितीय अर्थ में कोई भी वास्तविक मीट्रिक (गणित) या 'दूरी माप' नहीं है, क्योंकि वह त्रिकोण असमानता का पालन करने में विफल रहते हैं और इस प्रकार किसी भी वास्तविक 'दूरी' की गणना नहीं करते हैं - उन्हें 'स्कोर' के रूप में माना जाना चाहिए। इन अंकों की गणना उम्मीदवार फीचर (या फीचर्स के सेट) और वांछित आउटपुट श्रेणी के मध्य की जाती है। चूँकि, यह ऐसे सत्य मेट्रिक्स होते हैं जो पारस्परिक सूचना का सरल कार्य करते हैं <ref>{{Cite journal|arxiv=q-bio/0311039|last1=Kraskov|first1=Alexander|title=पारस्परिक सूचना पर आधारित पदानुक्रमित क्लस्टरिंग|last2=Stögbauer|first2=Harald|last3=Andrzejak|first3=Ralph G|last4=Grassberger|first4=Peter|year=2003|bibcode=2003q.bio....11039K}}</ref> तथा म्यूच्यूअल इनफार्मेशन या मीट्रिक देखें। | ||
अन्य उपलब्ध फ़िल्टर मेट्रिक्स में | अन्य उपलब्ध फ़िल्टर मेट्रिक्स में सम्मिलित हैं | | ||
* वर्ग पृथक्करण | * वर्ग पृथक्करण | ||
| Line 52: | Line 52: | ||
** संभाव्य दूरी | ** संभाव्य दूरी | ||
** [[एन्ट्रॉपी (सूचना सिद्धांत)]] | ** [[एन्ट्रॉपी (सूचना सिद्धांत)]] | ||
* संगति-आधारित | * संगति-आधारित फीचर सिलेक्शन | ||
* सहसंबंध-आधारित | * सहसंबंध-आधारित फीचर सिलेक्शन | ||
==अधिकतम मानदंड== | |||
अधिकतमत मानदंड का चुनाव कठिन होता है क्योंकि फीचर सिलेक्शन कार्य में अनेक उद्देश्य होते हैं। अनेक सामान्य मानदंडों में स्पष्टता की माप सम्मिलित होता है, जिसे सिलेक्शन फीचर्स की संख्या द्वारा दंडित किया जाता है। उदाहरणों में अकाइक सूचना मानदंड (एआईसी) और मैलोज़ C<sub>p</sub> सम्मिलित हैं | जिनमें प्रत्येक अतिरिक्त फीचर के लिए 2 का दंड है। यह एआईसी [[सूचना सिद्धांत]] पर आधारित है, और प्रभावी रूप से [[अधिकतम एन्ट्रापी सिद्धांत|मैक्सिमम एन्ट्रापी सिद्धांत]] के माध्यम से प्राप्त होता है। <ref>{{Citation | first=H. |last=Akaike |author-link=Hirotugu Akaike | contribution = Prediction and entropy | pages=1–24 | title= A Celebration of Statistics | editor1-first= A. C. | editor1-last= Atkinson | editor2-first= S. E. | editor2-last= Fienberg | editor2-link= Stephen Fienberg | year = 1985 | publisher= Springer|url=https://apps.dtic.mil/dtic/tr/fulltext/u2/a120956.pdf|archive-url=https://web.archive.org/web/20190830132141/https://apps.dtic.mil/dtic/tr/fulltext/u2/a120956.pdf|url-status=live|archive-date=August 30, 2019}}.</ref><ref>{{Citation |last1=Burnham |first1=K. P. |last2=Anderson |first2=D. R. |year=2002 |title=Model Selection and Multimodel Inference: A practical information-theoretic approach |edition=2nd |publisher= [[Springer-Verlag]] |url=https://books.google.com/books?id=fT1Iu-h6E-oC|isbn=9780387953649 }}.</ref> | |||
अन्य मानदंड [[बायेसियन सूचना मानदंड]] (बीआईसी) हैं, जो प्रत्येक जोड़े गए फीचर के लिए <math>\sqrt{\log{n}}</math> के दंड का उपयोग करता है, [[न्यूनतम विवरण लंबाई]] (एमडीएल) जो असम्बद्ध रूप से <math>\sqrt{\log{n}}</math> का उपयोग करता है, [[बोनफेरोनी सुधार]] / आरआईसी जो <math>\sqrt{2\log{p}}</math> का उपयोग करता है, अधिकतम निर्भरता फीचर सिलेक्शन , और विभिन्न प्रकार के नए मानदंड जो [[झूठी खोज दर|फाल्स डिस्कवर रेट]] (एफडीआर) से प्रेरित हैं, जो <math>\sqrt{2\log{\frac{p}{q}}}</math> के समीप कुछ का उपयोग करते हैं। फीचर्स के सबसे प्रासंगिक उपसमूह का सिलेक्शन करने के लिए अधिकतम [[एन्ट्रापी दर]] मानदंड का भी उपयोग किया जा सकता है। <ref>{{cite journal |last1=Einicke |first1=G. A. |title=दौड़ने के दौरान घुटने और टखने की गतिशीलता में परिवर्तन को वर्गीकृत करने के लिए सुविधाओं का अधिकतम-एंट्रॉपी दर चयन|journal=IEEE Journal of Biomedical and Health Informatics |volume=28 |issue=4 |pages=1097–1103 |year=2018 |doi= 10.1109/JBHI.2017.2711487 |pmid=29969403 |s2cid=49555941 }}</ref> | |||
==संरचना सीखना== | ==संरचना सीखना== | ||
फ़िल्टर | फ़िल्टर फीचर सिलेक्शन अधिक सामान्य प्रतिमान का विशिष्ट स्थिति है जिसे [[संरचित भविष्यवाणी|संरचित]] पूर्वानुमान कहा जाता है। फीचर सिलेक्शन विशिष्ट लक्ष्य वेरिएबल के लिए प्रासंगिक फीचर सेट खोजता है जबकि संरचना शिक्षण सभी वेरिएबल के मध्य संबंधों को खोजता है, सामान्यतः इन सम्बन्धो को ग्राफ के रूप में व्यक्त करता हैं। यह सबसे सामान्य संरचना सीखने वाले एल्गोरिदम मानते हैं कि डेटा [[बायेसियन नेटवर्क]] द्वारा उत्पन्न होता है, और इसलिए संरचना [[निर्देशित ग्राफ|निर्देशित]] ग्राफिकल [[ चित्रमय मॉडल |मॉडल]] है। फ़िल्टर फीचर सिलेक्शन समस्या का अधिकतम समाधान लक्ष्य नोड का [[मार्कोव कंबल|मार्कोव ब्लंकेट]] है, और बायेसियन नेटवर्क में, प्रत्येक नोड के लिए अद्वितीय मार्कोव ब्लंकेट है। <ref>{{cite journal|last1=Aliferis|first1=Constantin|title=Local causal and markov blanket induction for causal discovery and feature selection for classification part I: Algorithms and empirical evaluation|journal=Journal of Machine Learning Research|date=2010|volume=11|pages=171–234|url=http://jmlr.org/papers/volume11/aliferis10a/aliferis10a.pdf}}</ref> | ||
==सूचना सिद्धांत आधारित फीचर सिलेक्शन तंत्र== | |||
चारों ओर विभिन्न फीचर सिलेक्शन तंत्र हैं जो विभिन्न फीचर्स को स्कोर करने के लिए पारस्परिक सूचना का उपयोग करते हैं। वह सामान्यतः सभी समान एल्गोरिदम का उपयोग करते हैं | | |||
#सभी फीचर्स (<math> f_{i} \in F </math>) और लक्ष्य वर्ग ({{mvar|c }}) के मध्य स्कोर के रूप में पारस्परिक सूचना की गणना करें | |||
# सबसे बड़े स्कोर वाली फीचर का सिलेक्शन करें (उदाहरण के लिए . <math>\underset{f_{i} \in F}\operatorname{argmax}(I(f_{i},c))</math>) और इसे सिलेक्शन फीचर्स ({{mvar|S }}) के सेट में जोड़ें | |||
# उस स्कोर की गणना करें जो पारस्परिक सूचना से प्राप्त किया जा सकता है | |||
# सबसे बड़े स्कोर वाली फीचर का सिलेक्शन करें और इसे सिलेक्शन फीचर्स के सेट में जोड़ें (उदाहरण के लिए) <math>\underset{f_{i} \in F}\operatorname{argmax}(I_{derived}(f_{i},c))</math>) | |||
# 3. और 4. को तब तक दोहराएँ जब तक कि निश्चित संख्या में फीचर्स का सिलेक्शन न हो जाए (उदाहरण के लिए) <math>|S|=l</math>) | |||
सबसे सरल दृष्टिकोण म्यूच्यूअल इनफार्मेशन को व्युत्पन्न स्कोर के रूप में उपयोग करता है।<ref name="Brown">{{cite journal |last1=Brown |first1=Gavin |last2=Pocock |first2=Adam |last3=Zhao |first3=Ming-Jie |last4=Luján |first4=Mikel |title=Conditional Likelihood Maximisation: A Unifying Framework for Information Theoretic Feature Selection |journal= [[Journal of Machine Learning Research]] |date=2012 |volume=13 |pages=27–66 |url=http://dl.acm.org/citation.cfm?id=2188385.2188387}}[http://www.jmlr.org/papers/volume13/brown12a/brown12a.pdf]</ref> | |||
चूँकि, भिन्न-भिन्न दृष्टिकोण हैं, जो फीचर्स के मध्य रिडंडेंसीय को कम करने का प्रयास करते हैं। | |||
===न्यूनतम- | ===न्यूनतम-रिडंडेंसीय-अधिकतम-प्रासंगिकता (एमआरएमआर) फीचर सिलेक्शन === | ||
पेंग एट अल.<ref>{{cite journal |last1=Peng |first1=H. C. |last2=Long |first2=F. |last3=Ding |first3=C. |title=Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy |journal= [[IEEE Transactions on Pattern Analysis and Machine Intelligence]] |volume=27 |issue=8 |pages=1226–1238 |year=2005 |doi=10.1109/TPAMI.2005.159 |pmid=16119262|citeseerx=10.1.1.63.5765 |s2cid=206764015 }} [http://home.penglab.com/proj/mRMR/index.htm Program]</ref> | पेंग एट अल.<ref>{{cite journal |last1=Peng |first1=H. C. |last2=Long |first2=F. |last3=Ding |first3=C. |title=Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy |journal= [[IEEE Transactions on Pattern Analysis and Machine Intelligence]] |volume=27 |issue=8 |pages=1226–1238 |year=2005 |doi=10.1109/TPAMI.2005.159 |pmid=16119262|citeseerx=10.1.1.63.5765 |s2cid=206764015 }} [http://home.penglab.com/proj/mRMR/index.htm Program]</ref> फीचर सिलेक्शन विधि प्रस्तावित की गई जो फीचर्स का सिलेक्शन करने के लिए पारस्परिक सूचना , सहसंबंध, या दूरी/समानता स्कोर का उपयोग कर सकती है। इसका उद्देश्य अन्य सिलेक्शन फीचर्स की उपस्थिति में किसी फीचर की प्रासंगिकता को उसके रिडंडेंसीय द्वारा दंडित करना है। क्लास {{mvar|c }} के लिए फीचर सम्मुचय {{mvar|S }} की प्रासंगिकता को व्यक्तिगत फीचर {{math|''f<sub>i</sub>'' }} और क्लास {{mvar|c }} के मध्य सभी पारस्परिक सूचना मानों के औसत मान से द्वारा परिभाषित किया गया है | | ||
:<math> D(S,c) = \frac{1}{|S|}\sum_{f_{i}\in S}I(f_{i};c) </math>. | :<math> D(S,c) = \frac{1}{|S|}\sum_{f_{i}\in S}I(f_{i};c) </math>. | ||
समुच्चय में सभी | समुच्चय में सभी फीचर्स का रिडंडेंसीय {{mvar|S }} फीचर के मध्य सभी पारस्परिक सूचना मानों का औसत मान {{math|''f<sub>i</sub>'' }} और फीचर {{math|''f<sub>j</sub>'' }} है | | ||
:<math> R(S) = \frac{1}{|S|^{2}}\sum_{f_{i},f_{j}\in S}I(f_{i};f_{j})</math> | :<math> R(S) = \frac{1}{|S|^{2}}\sum_{f_{i},f_{j}\in S}I(f_{i};f_{j})</math> | ||
| Line 90: | Line 93: | ||
\left[\frac{1}{|S|}\sum_{f_{i}\in S}I(f_{i};c) - | \left[\frac{1}{|S|}\sum_{f_{i}\in S}I(f_{i};c) - | ||
\frac{1}{|S|^{2}}\sum_{f_{i},f_{j}\in S}I(f_{i};f_{j})\right].</math> | \frac{1}{|S|^{2}}\sum_{f_{i},f_{j}\in S}I(f_{i};f_{j})\right].</math> | ||
मान लीजिए कि | मान लीजिए कि {{mvar|n }} पूर्ण-समुच्चय सुविधाएँ हैं। मान लीजिए {{math|''x<sub>i</sub>''}} फीचर {{math|''f<sub>i</sub>''}} के लिए सेट सदस्यता संकेतक फलन है, जिससे {{math|1=''x<sub>i</sub>''=1}} उपस्थिति को संकेत करे और {{math|1=''x<sub>i</sub>''=0}} वैश्विक स्तर पर अधिकतम फीचर सेट में फीचर {{math|''f<sub>i</sub>''}} की अनुपस्थिति को संकेत करे। मान लीजिए <math>c_i=I(f_i;c)</math> और <math>a_{ij}=I(f_i;f_j)</math> हैं। फिर उपरोक्त को अनुकूलन समस्या के रूप में लिखा जा सकता है | ||
:<math>\mathrm{mRMR}= \max_{x\in \{0,1\}^{n}} | :<math>\mathrm{mRMR}= \max_{x\in \{0,1\}^{n}} | ||
| Line 96: | Line 99: | ||
\frac{\sum^{n}_{i,j=1}a_{ij}x_{i}x_{j}} | \frac{\sum^{n}_{i,j=1}a_{ij}x_{i}x_{j}} | ||
{(\sum^{n}_{i=1}x_{i})^{2}}\right].</math> | {(\sum^{n}_{i=1}x_{i})^{2}}\right].</math> | ||
एमआरएमआर एल्गोरिदम सैद्धांतिक रूप से | एमआरएमआर एल्गोरिदम सैद्धांतिक रूप से अधिकतम-निर्भरता फीचर सिलेक्शन एल्गोरिदम का अनुमान होता है जो सिलेक्शन फीचर्स के संयुक्त वितरण और वर्गीकरण वेरिएबल के मध्य पारस्परिक सूचना को अधिकतम करता है। चूंकि एमआरएमआर बहुत लघु समस्याओं की श्रृंखला के साथ संयोजन अनुमान समस्या का अनुमान लगाता है, जिनमें से प्रत्येक में केवल दो वेरिएबल सम्मिलित होते हैं, इस प्रकार यह जोड़ीदार संयुक्त संभावनाओं का उपयोग करता है जो अधिक शक्तिशाली होते हैं। कुछ स्थितियों में एल्गोरिदम फीचर्स की उपयोगिता को कम समझ सकता है क्योंकि इसमें उन फीचर्स के मध्य इंटरैक्शन को मापने की कोई विधि नहीं है जो इसकी प्रासंगिकता को बढ़ा सकते हैं। इससे व्यर्थ प्रदर्शन हो सकता है <ref name="Brown" /> जब विशेषताएँ व्यक्तिगत रूप से व्यर्थ होती हैं, किन्तु संयुक्त होने पर यह उपयोगी होती हैं ( पैथोलॉजिकल स्थिति तब पायी जाती है जब वर्ग फीचर्स का समता कार्य होता है)। सामान्यतः एल्गोरिथ्म सैद्धांतिक रूप से अधिकतम-निर्भरता सिलेक्शन की तुलना में अधिक कुशल (आवश्यक डेटा की मात्रा के संदर्भ में) होता है, फिर भी कम जोड़ीदार रिडंडेंसीय के साथ फीचर सेट तैयार करता है। | ||
एमआरएमआर फ़िल्टर विधियों के बड़े वर्ग का उदाहरण है जो विभिन्न विधियों से प्रासंगिकता और रिडंडेंसीय के मध्य व्यापार करता है।<ref name="Brown"/><ref name="docs.google">Nguyen, H., Franke, K., Petrovic, S. (2010). "Towards a Generic Feature-Selection Measure for Intrusion Detection", In Proc. International Conference on Pattern Recognition (ICPR), Istanbul, Turkey. [https://www.researchgate.net/publication/220928649_Towards_a_Generic_Feature-Selection_Measure_for_Intrusion_Detection?ev=prf_pub]</ref> | |||
=== [[द्विघात प्रोग्रामिंग]] | === [[द्विघात प्रोग्रामिंग|क्वाद्रटिक प्रोग्रामिंग]] '''फीचर''' सिलेक्शन === | ||
एमआरएमआर | एमआरएमआर फीचर सिलेक्शन के लिए वृद्धिशील ग्रीडी रणनीति का विशिष्ट उदाहरण है | इसमें फीचर का सिलेक्शन हो जाने के पश्चात् होते हैं, इसके पश्चात् चरण में असिलेक्शन नहीं किया जा सकता है। जबकि एमआरएमआर को कुछ फीचर्स को कम करने के लिए फ्लोटिंग सर्च का उपयोग करके अनुकूलित किया जा सकता है, इसे वैश्विक द्विघात प्रोग्रामिंग अनुकूलन समस्या के रूप में निम्नानुसार पुन: तैयार किया जा सकता है | <ref name="QPFS">{{cite journal |first1=I. |last1=Rodriguez-Lujan |first2=R. |last2=Huerta |first3=C. |last3=Elkan |first4=C. |last4=Santa Cruz |title=द्विघात प्रोग्रामिंग सुविधा चयन|journal=[[Journal of Machine Learning Research|JMLR]] |volume=11 |pages=1491–1516 |year=2010 |url=http://jmlr.csail.mit.edu/papers/volume11/rodriguez-lujan10a/rodriguez-lujan10a.pdf}}</ref> | ||
:<math> | :<math> | ||
\mathrm{QPFS}: \min_\mathbf{x} \left\{ \alpha \mathbf{x}^T H \mathbf{x} - \mathbf{x}^T F\right\} \quad \mbox{s.t.} \ \sum_{i=1}^n x_i=1, x_i\geq 0 | \mathrm{QPFS}: \min_\mathbf{x} \left\{ \alpha \mathbf{x}^T H \mathbf{x} - \mathbf{x}^T F\right\} \quad \mbox{s.t.} \ \sum_{i=1}^n x_i=1, x_i\geq 0 | ||
</math> | </math> | ||
जहां <math>F_{n\times1}=[I(f_1;c),\ldots, I(f_n;c)]^T</math> फीचर प्रासंगिकता का वेक्टर है, यह मानते हुए कि कुल मिलाकर {{mvar|n }} फीचर हैं, तथा <math>H_{n\times n}=[I(f_i;f_j)]_{i,j=1\ldots n}</math> फीचर जोड़ीदार रिडंडेंसीय का आव्युह है, और <math>\mathbf{x}_{n\times 1}</math> सापेक्ष फीचर भार का प्रतिनिधित्व करता है। क्यूएफपीएस को द्विघात प्रोग्रामिंग के माध्यम से समाधान किया जाता है। वर्तमान में यह दिखाया गया है कि क्यूएफपीएस लघु एन्ट्रापी वाले फीचर्स के प्रति पक्षपाती है, <ref name="CMI" /> इसकी लिए इसे फीचर सेल्फ रिडंडेंसी टर्म <math>I(f_i;f_i)</math> को {{mvar|H }} के विकर्ण पर रखा गया है। | |||
=== | === नियमबद्ध पारस्परिक सूचना === | ||
पारस्परिक | पारस्परिक सूचना के लिए प्राप्त अन्य स्कोर नियमबद्ध प्रासंगिकता पर आधारित है <ref name="CMI">Nguyen X. Vinh, Jeffrey Chan, Simone Romano and James Bailey, "Effective Global Approaches for Mutual Information based Feature Selection". Proceedings of the 20th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD'14), August 24–27, New York City, 2014. "[http://people.eng.unimelb.edu.au/baileyj/papers/frp0038-Vinh.pdf]"</ref> | ||
:<math> | :<math> | ||
\mathrm{SPEC_{CMI}}: \max_{\mathbf{x}} \left\{\mathbf{x}^T Q \mathbf{x}\right\} \quad \mbox{s.t.}\ \|\mathbf{x}\|=1, x_i\geq 0 | \mathrm{SPEC_{CMI}}: \max_{\mathbf{x}} \left\{\mathbf{x}^T Q \mathbf{x}\right\} \quad \mbox{s.t.}\ \|\mathbf{x}\|=1, x_i\geq 0 | ||
</math> | </math> | ||
जहाँ <math>Q_{ii}=I(f_i;c)</math> और <math>Q_{ij}=(I(f_i;c|f_j)+I(f_j;c|f_i))/2, i\ne j</math>. | |||
{{math|SPEC<sub>CMI</sub>}} का लाभ यह है कि इसे केवल {{mvar|Q}} के प्रमुख आइजनवेक्टर को खोजकर समाधान किया जा सकता है, इस प्रकार यह बहुत स्केलेबल है। {{math|SPEC<sub>CMI</sub>}} दूसरे क्रम के फीचर इंटरैक्शन को भी संभालता है। | |||
===संयुक्त पारस्परिक | ===संयुक्त पारस्परिक सूचना === | ||
विभिन्न अंकों के अध्ययन में ब्राउन एट | विभिन्न अंकों के अध्ययन में ब्राउन एट अल और अन्य ने <ref name="Brown" /> [[संयुक्त पारस्परिक जानकारी|संयुक्त पारस्परिक]] सूचना की अनुशंसा की हैं | <ref>{{cite journal |last1=Yang |first1=Howard Hua |last2=Moody |first2=John |title=Data visualization and feature selection: New algorithms for nongaussian data |journal=Advances in Neural Information Processing Systems |date=2000 |pages=687–693 |url=https://papers.nips.cc/paper/1779-data-visualization-and-feature-selection-new-algorithms-for-nongaussian-data.pdf}}</ref> यह फीचर सिलेक्शन के लिए अच्छे स्कोर के रूप में होता हैं। स्कोर उस फीचर को खोजने का प्रयास करता है, जो रिडंडेंसीय से बचने के लिए पहले से सिलेक्शन फीचर्स में सबसे नई सूचना को जोड़ता है। यह स्कोर इस प्रकार तैयार किया गया है | ||
:<math> | :<math> | ||
| Line 128: | Line 129: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
स्कोर पहले से | स्कोर पहले से सिलेक्शन फीचर्स (<math> f_j \in S </math>) और जांच के अनुसार फीचर (<math>f_i</math>) के मध्य रिडंडेंसीय का अनुमान लगाने के लिए [[सशर्त पारस्परिक जानकारी|नियमबद्ध पारस्परिक]] सूचना और पारस्परिक सूचना का उपयोग करता है। | ||
==हिल्बर्ट-श्मिट स्वतंत्रता मानदंड लैस्सो आधारित | ==हिल्बर्ट-श्मिट स्वतंत्रता मानदंड लैस्सो आधारित फीचर सिलेक्शन == | ||
उच्च-आयामी और | उच्च-आयामी और लघु प्रतिरूप डेटा के लिए (उदाहरण के लिए, आयामीता > {{10^|5 }} और प्रतिरूपों की संख्या < {{10^|3}}) हैं, हिल्बर्ट-श्मिट इंडिपेंडेंस क्राइटेरियन लासो (एचएसआईसी लासो) उपयोगी है। <ref name="HSICLasso">{{cite journal |first1=M. |last1=Yamada |first2=W. |last2=Jitkrittum |first3=L. |last3=Sigal |first4=E. P. |last4=Xing |first5=M. |last5=Sugiyama |title=फ़ीचर-वार नॉन-लीनियर लैस्सो द्वारा उच्च-आयामी फ़ीचर चयन|journal=Neural Computation |volume=26 |issue=1 |pages=185–207 |year=2014 |doi=10.1162/NECO_a_00537 |pmid=24102126 |arxiv=1202.0515 |s2cid=2742785 }}</ref> एचएसआईसी लासो अनुकूलन समस्या इस प्रकार दी गई है | ||
:<math> | :<math> | ||
\mathrm{HSIC_{Lasso}}: \min_{\mathbf{x}} \frac{1}{2}\sum_{k,l = 1}^n x_k x_l {\mbox{HSIC}}(f_k,f_l) - \sum_{k = 1}^n x_k {\mbox{HSIC}}(f_k,c) + \lambda \|\mathbf{x}\|_1, \quad \mbox{s.t.} \ x_1,\ldots, x_n \geq 0, | \mathrm{HSIC_{Lasso}}: \min_{\mathbf{x}} \frac{1}{2}\sum_{k,l = 1}^n x_k x_l {\mbox{HSIC}}(f_k,f_l) - \sum_{k = 1}^n x_k {\mbox{HSIC}}(f_k,c) + \lambda \|\mathbf{x}\|_1, \quad \mbox{s.t.} \ x_1,\ldots, x_n \geq 0, | ||
</math> | </math> | ||
जहाँ <math>{\mbox{HSIC}}(f_k,c) =\mbox{tr}(\bar{\mathbf{K}}^{(k)} \bar{\mathbf{L}})</math> कर्नेल-आधारित स्वतंत्रता माप है जिसे (अनुभवजन्य) हिल्बर्ट-श्मिट स्वतंत्रता मानदंड (एचएसआईसी) <math>\mbox{tr}(\cdot)</math> कहा जाता है, | |||
[[ट्रेस (रैखिक बीजगणित)]] <math>\lambda</math> को दर्शाता है, नियमितीकरण <math>\bar{\mathbf{K}}^{(k)} = \mathbf{\Gamma} \mathbf{K}^{(k)} \mathbf{\Gamma}</math> पैरामीटर है, और <math>\bar{\mathbf{L}} = \mathbf{\Gamma} \mathbf{L} \mathbf{\Gamma}</math> इनपुट और आउटपुट केंद्रित [[ग्राम मैट्रिक्स|ग्राम आव्युह]] हैं, यह | |||
<math>K^{(k)}_{i,j} = K(u_{k,i},u_{k,j})</math> और <math>L_{i,j} = L(c_i,c_j)</math> ग्राम आव्युह होता हैं, यह <math>K(u,u')</math> और <math>L(c,c')</math> कर्नेल फलन हैं,और <math>\mathbf{\Gamma} = \mathbf{I}_m - \frac{1}{m}\mathbf{1}_m \mathbf{1}_m^T</math> केन्द्रित आव्युह <math>\mathbf{I}_m </math> होता है, यह {{mvar|m }}-आयामी पहचान आव्युह ({{mvar|m }}: प्रतिरूपों की संख्या), <math>\mathbf{1}_m </math> है और {{mvar|m }}-सभी के साथ आयामी वेक्टर, और <math>\|\cdot\|_{1}</math> <math>\ell_1</math>-मानदंड है। एचएसआईसी सदैव गैर-ऋणात्मक मान लेता है, और यदि शून्य है और केवल तभी जब दो यादृच्छिक वेरिएबल सांख्यिकीय रूप से स्वतंत्र होते हैं जब गाऊसी कर्नेल जैसे सार्वभौमिक पुनरुत्पादन कर्नेल का उपयोग किया जाता है। | |||
एचएसआईसी लैस्सो को इस प्रकार लिखा जा सकता है | |||
:<math> | :<math> | ||
\mathrm{HSIC_{Lasso}}: \min_{\mathbf{x}} \frac{1}{2}\left\|\bar{\mathbf{L}} - \sum_{k = 1}^{n} x_k \bar{\mathbf{K}}^{(k)} \right\|^2_{F} + \lambda \|\mathbf{x}\|_1, \quad \mbox{s.t.} \ x_1,\ldots,x_n \geq 0, | \mathrm{HSIC_{Lasso}}: \min_{\mathbf{x}} \frac{1}{2}\left\|\bar{\mathbf{L}} - \sum_{k = 1}^{n} x_k \bar{\mathbf{K}}^{(k)} \right\|^2_{F} + \lambda \|\mathbf{x}\|_1, \quad \mbox{s.t.} \ x_1,\ldots,x_n \geq 0, | ||
</math> | </math> | ||
जहाँ<math>\|\cdot\|_{F}</math> [[फ्रोबेनियस मानदंड]] है इसकी अनुकूलन समस्या लैस्सो समस्या है, और इस प्रकार इसे दोहरी [[संवर्धित लैग्रेंजियन विधि]] जैसे अत्याधुनिक लैस्सो सॉल्वर के साथ कुशलतापूर्वक समाधान किया जा सकता है। | |||
==सहसंबंध | ==सहसंबंध फीचर सिलेक्शन == | ||
सहसंबंध | सहसंबंध फीचर सिलेक्शन (सीएफएस) माप निम्नलिखित परिकल्पना के आधार पर फीचर्स के सबसेट का मूल्यांकन करता है | और अच्छे फीचर सबसेट में वर्गीकरण के साथ अत्यधिक सहसंबद्ध विशेषताएं होती हैं, फिर भी दूसरे से असंबद्ध होती हैं। <ref>{{cite thesis |first=M. |last=Hall |date=1999 |type=PhD thesis |url=https://www.cs.waikato.ac.nz/~mhall/thesis.pdf |title=मशीन लर्निंग के लिए सहसंबंध-आधारित फ़ीचर चयन|publisher=University of Waikato }}</ref><ref>{{cite book |last1=Senliol |first1=Baris |first2=Gokhan |last2=Gulgezen |first3=Lei |last3=Yu |first4=Zehra |last4=Cataltepe |title=2008 23rd International Symposium on Computer and Information Sciences |chapter=Fast Correlation Based Filter (FCBF) with a different search strategy |display-authors=1 |pages=1–4 |date=2008 |doi=10.1109/ISCIS.2008.4717949 |isbn=978-1-4244-2880-9 |s2cid=8398495 }}</ref> निम्नलिखित समीकरण k विशेषताओं से युक्त फीचर सबसेट S की योग्यता देता है | | ||
:<math> \mathrm{Merit}_{S_{k}} = \frac{k\overline{r_{cf}}}{\sqrt{k+k(k-1)\overline{r_{ff}}}}.</math> | :<math> \mathrm{Merit}_{S_{k}} = \frac{k\overline{r_{cf}}}{\sqrt{k+k(k-1)\overline{r_{ff}}}}.</math> | ||
यहाँ, <math> \overline{r_{cf}} </math> सभी | यहाँ, <math> \overline{r_{cf}} </math> सभी फीचर -वर्गीकरण सहसंबंधों का औसत मान है, और <math> \overline{r_{ff}} </math> सभी फीचर -फीचर सहसंबंधों का औसत मान है। सीएफएस मानदंड को इस प्रकार परिभाषित किया गया है | | ||
:<math>\mathrm{CFS} = \max_{S_k} | :<math>\mathrm{CFS} = \max_{S_k} | ||
| Line 157: | Line 162: | ||
+ r_{f_k f_{k-1} })}}\right].</math> | + r_{f_k f_{k-1} })}}\right].</math> | ||
<math>r_{cf_{i}}</math>और <math>r_{f_{i}f_{j}}</math> वेरिएबल को सहसंबंध के रूप में संदर्भित किया जाता है, किन्तु आवश्यक नहीं कि यह पियर्सन सहसंबंध गुणांक या स्पीयरमैन के ρ होते हैं। हॉल का शोध प्रबंध इनमें से किसी का भी उपयोग नहीं करता है,किंतु संबंधितता के तीन भिन्न-भिन्न मापों में हैं, उपायों, न्यूनतम विवरण लंबाई (एमडीएल), सममित अनिश्चितता का उपयोग करता है और यह रिलीफ (फीचर सिलेक्शन ) का भी उपयोग करता है। | |||
माना ''x<sub>i</sub>'' फीचर ''f<sub>i</sub>'' के लिए सेट सदस्यता संकेतक फलन होता हैं तब उपरोक्त को अनुकूलन समस्या के रूप में फिर से लिखा जा सकता है | |||
:<math>\mathrm{CFS} = \max_{x\in \{0,1\}^{n}} | :<math>\mathrm{CFS} = \max_{x\in \{0,1\}^{n}} | ||
\left[\frac{(\sum^{n}_{i=1}a_{i}x_{i})^{2}} | \left[\frac{(\sum^{n}_{i=1}a_{i}x_{i})^{2}} | ||
{\sum^{n}_{i=1}x_i + \sum_{i\neq j} 2b_{ij} x_i x_j }\right].</math> | {\sum^{n}_{i=1}x_i + \sum_{i\neq j} 2b_{ij} x_i x_j }\right].</math> | ||
उपरोक्त संयोजनात्मक समस्याएं, वास्तव में, मिश्रित 0-1 [[रैखिक प्रोग्रामिंग]] समस्याएं हैं जिन्हें शाखा-और-बाउंड एल्गोरिदम का उपयोग करके | उपरोक्त संयोजनात्मक समस्याएं, वास्तव में, मिश्रित 0-1 [[रैखिक प्रोग्रामिंग]] समस्याएं हैं | जिन्हें शाखा-और-बाउंड एल्गोरिदम का उपयोग करके समाधान किया जा सकता है। <ref>{{cite journal |first1=Hai |last1=Nguyen |first2=Katrin |last2=Franke |first3=Slobodan |last3=Petrovic |title=सुविधा चयन उपायों के एक वर्ग का अनुकूलन|journal=Proceedings of the NIPS 2009 Workshop on Discrete Optimization in Machine Learning: Submodularity, Sparsity & Polyhedra (DISCML) |location=Vancouver, Canada |date=December 2009 |url=https://www.researchgate.net/publication/231175763 }}</ref> | ||
== | ==डिसिजन ट्री== | ||
[[ निर्णय वृक्ष | | [[ निर्णय वृक्ष | डिसिजन ट्री]] या ट्री [[सामूहिक शिक्षा]] की विशेषताओं को निरर्थक दिखाया गया है। वर्तमान विधि जिसे नियमितीकृत ट्री कहा जाता है <ref name="DengRunger2012">H. Deng, G. Runger, "[https://arxiv.org/abs/1201.1587 Feature Selection via Regularized Trees]", Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), IEEE, 2012</ref> फीचर सबसेट सिलेक्शन के लिए उपयोग किया जा सकता है। नियमितीकृत ट्री वर्तमान नोड को विभाजित करने के लिए पूर्व ट्री नोड्स पर सिलेक्शन वेरिएबल के समान वेरिएबल का उपयोग करके दंडित करते हैं। नियमितीकृत ट्री को केवल ट्री मॉडल (या ट्री संयोजन मॉडल) बनाने की आवश्यकता होती है और इस प्रकार वह कम्प्यूटेशनल रूप से कुशल होते हैं। | ||
नियमितीकृत | नियमितीकृत ट्री स्वाभाविक रूप से संख्यात्मक और श्रेणीगत विशेषताओं, अंतःक्रियाओं और गैर-रैखिकताओं को संभालते हैं। वह विशेषता मापदंडो (इकाइयों) के लिए अपरिवर्तनीय हैं और यह आउटलेर्स के प्रति असंवेदनशील हैं, और इस प्रकार, [[सामान्यीकरण (सांख्यिकी)]] जैसे कम [[डेटा प्रीप्रोसेसिंग]] की आवश्यकता होती है। नियमित यादृच्छिक फॉरेस्ट (आरआरएफ)<ref name="RRF">[https://cran.r-project.org/web/packages/RRF/index.html RRF: Regularized Random Forest], [[R (programming language)|R]] package on [[CRAN (R programming language)|CRAN]]</ref> प्रकार का डिसिजन ट्री है। निर्देशित आरआरएफ उन्नत आरआरएफ होता है जो सामान्य यादृच्छिक फॉरेस्ट से महत्व स्कोर द्वारा निर्देशित होता है। | ||
==मेटाहेयुरिस्टिक्स विधियों पर अवलोकन== | ==मेटाहेयुरिस्टिक्स विधियों पर अवलोकन== | ||
[[मेटाह्यूरिस्टिक]] कठिन ( | [[मेटाह्यूरिस्टिक]] कठिन (सामान्यतः [[एनपी-कठोरता]] एनपी-हार्ड समस्या) अनुकूलन समस्याओं को समाधान करने के लिए समर्पित एल्गोरिदम का सामान्य विवरण है जिसके लिए कोई मौलिक समाधान विधियां नहीं हैं। सामान्यतः, मेटाह्यूरिस्टिक स्टोकेस्टिक एल्गोरिदम है जो वैश्विक अधिकतम तक पहुंचने की प्रवृत्ति रखता है। सरल स्थानीय खोज से लेकर सम्मिश्र वैश्विक खोज एल्गोरिदम तक अनेक मेटाह्यूरिस्टिक्स हैं। | ||
===मुख्य सिद्धांत=== | ===मुख्य सिद्धांत=== | ||
फीचर सिलेक्शन विधियों को सामान्यतः तीन वर्गों में प्रस्तुत किया जाता है, जो इस पर आधारित होता है कि वह सिलेक्शन एल्गोरिदम और मॉडल बिल्डिंग को कैसे जोड़ते हैं। | |||
====फ़िल्टर विधि==== | ====फ़िल्टर विधि==== | ||
[[File:Filter Methode.png|thumb|300px| | [[File:Filter Methode.png|thumb|300px|फीचर सिलेक्शन के लिए फ़िल्टर विधि]]फ़िल्टर प्रकार के विधियों मॉडल की चिंता किए बिना वेरिएबल का सिलेक्शन करते हैं। वह केवल पूर्वानुमान करने के लिए वेरिएबल के साथ सहसंबंध जैसी सामान्य विशेषताओं पर आधारित होते हैं। फ़िल्टर विधियाँ कम से कम आकर्षक वेरिएबल को दबा देती हैं। अन्य वेरिएबल वर्गीकरण या डेटा को वर्गीकृत करने या पूर्वानुमान करने के लिए उपयोग किए जाने वाले प्रतिगमन मॉडल का भाग होते हैं। यह विधियां समय की गणना करने में विशेष रूप से प्रभावी होती हैं और ओवरफिटिंग के लिए शक्तिशाली हैं। <ref name="ReferenceA">{{cite thesis |first=Julie |last=Hamon |title=Optimisation combinatoire pour la sélection de variables en régression en grande dimension: Application en génétique animale |url=https://tel.archives-ouvertes.fr/tel-00920205 |date=November 2013 |publisher=[[Lille University of Science and Technology]] |language=fr }}</ref> | ||
फ़िल्टर विधियाँ निरर्थक | फ़िल्टर विधियाँ निरर्थक वेरिएबल का सिलेक्शन करती हैं जब वह वेरिएबल के मध्य संबंधों पर विचार नहीं करते हैं। चूँकि, अधिक विस्तृत सुविधाएँ एक-दूसरे से अत्यधिक सहसंबंधित वेरिएबल को हटाकर इस समस्या को कम करने का प्रयास करती हैं, जैसे कि फास्ट सहसंबंध आधारित फ़िल्टर (एफसीबीएफ) एल्गोरिथ्म हैं। <ref>{{Cite journal |first1=Lei |last1=Yu |first2=Huan |last2=Liu |title=Feature selection for high-dimensional data: a fast correlation-based filter solution |journal=ICML'03: Proceedings of the Twentieth International Conference on International Conference on Machine Learning |date=August 2003 |pages=856–863 |url=https://www.aaai.org/Papers/ICML/2003/ICML03-111.pdf }}</ref> | ||
====रैपर विधि==== | ====रैपर विधि==== | ||
[[File:Feature selection Wrapper Method.png|thumb|300px| | [[File:Feature selection Wrapper Method.png|thumb|300px|फीचर सिलेक्शन के लिए रैपर विधि]]रैपर विधियां वेरिएबल्स के सबसेट का मूल्यांकन करती हैं जो फ़िल्टर दृष्टिकोण के विपरीत हैं, यह वेरिएबल्स के मध्य संभावित इंटरैक्शन का अनुमान लगाने की अनुमति देती हैं। <ref name="M. Phuong, Z pages 301-309">T. M. Phuong, Z. Lin et R. B. Altman. [http://htsnp.stanford.edu/FSFS/TaggingSNP.pdf Choosing SNPs using feature selection.] {{Webarchive|url=https://web.archive.org/web/20160913211229/http://htsnp.stanford.edu/FSFS/TaggingSNP.pdf |date=2016-09-13 }} Proceedings / IEEE Computational Systems Bioinformatics Conference, CSB. IEEE Computational Systems Bioinformatics Conference, pages 301-309, 2005. {{PMID|16447987}}.</ref> इन विधियों की दो मुख्य हानि हैं | ||
* अवलोकनों की संख्या अपर्याप्त होने पर ओवरफिटिंग का | * अवलोकनों की संख्या अपर्याप्त होने पर ओवरफिटिंग का विपत्ति बढ़ जाती है। | ||
* महत्वपूर्ण गणना समय | * जब महत्वपूर्ण गणना समय में वेरिएबल की संख्या बड़ी होती हैं। | ||
====एम्बेडेड विधि==== | ====एम्बेडेड विधि==== | ||
[[File:Feature selection Embedded Method.png|thumb|300px| | [[File:Feature selection Embedded Method.png|thumb|300px|फीचर सिलेक्शन के लिए एंबेडेड विधि]]एंबेडेड विधियों वर्तमान में प्रस्तावित किए गए हैं जो पूर्व दोनों विधियों के लाभों को संयोजित करने का प्रयास करते हैं। शिक्षण एल्गोरिदम अपनी स्वयं की परिवर्तनीय सिलेक्शन प्रक्रिया का लाभ उठाता है और फीचर सिलेक्शन और वर्गीकरण के साथ करता है, जैसे एफआरएमटी एल्गोरिदम हैं। <ref>{{cite journal |last1=Saghapour |first1=E. |last2=Kermani |first2=S. |last3=Sehhati |first3=M. |year=2017 |title=प्रोटिओमिक्स डेटा का उपयोग करके कैंसर के चरणों की भविष्यवाणी के लिए एक नवीन फीचर रैंकिंग पद्धति|journal=[[PLOS ONE]] |volume=12 |issue=9 |pages=e0184203 |doi=10.1371/journal.pone.0184203 |pmid=28934234 |pmc=5608217 |bibcode=2017PLoSO..1284203S |doi-access=free }}</ref> | ||
=== | ===फीचर सिलेक्शन मेटाह्यूरिस्टिक्स का अनुप्रयोग=== | ||
यह साहित्य में | यह साहित्य में वर्तमान में उपयोग किए गए फीचर सिलेक्शन मेटाह्यूरिस्टिक्स के अनुप्रयोग का सर्वेक्षण है। इस सर्वेक्षण को जे. हैमन ने अपनी 2013 की थीसिस में वास्तविक किया था। <ref name="ReferenceA"/> | ||
{| class="wikitable sortable" | {| class="wikitable sortable" | ||
| Line 202: | Line 207: | ||
! [[Evaluation function|मूल्यांकन कार्य]] !! संदर्भ | ! [[Evaluation function|मूल्यांकन कार्य]] !! संदर्भ | ||
|- | |- | ||
| [[Single-nucleotide polymorphism|एसएनपीएस]] || | | [[Single-nucleotide polymorphism|एसएनपीएस]] ||फीचर समानता का उपयोग करके फीचर सिलेक्शन | ||
| फ़िल्टर || || r<sup>2</sup> || फुओंग 2005<ref name="M. Phuong, Z pages 301-309"/> | | फ़िल्टर || || r<sup>2</sup> || फुओंग 2005<ref name="M. Phuong, Z pages 301-309"/> | ||
|- | |- | ||
| एसएनपीएस || [[Genetic algorithm|जेनेटिक एल्गोरिदम]] || डब्ल्यूरैपर || [[Decision tree learning| | | एसएनपीएस || [[Genetic algorithm|जेनेटिक एल्गोरिदम]] || डब्ल्यूरैपर || [[Decision tree learning|डिसिजन ट्री]] || वर्गीकरण स्पष्टता (10 गुना) || शाह 2004<ref>{{cite journal | last1 = Shah | first1 = S. C. | last2 = Kusiak | first2 = A. | year = 2004 | title = Data mining and genetic algorithm based gene/SNP selection | journal = Artificial Intelligence in Medicine | volume = 31 | issue = 3| pages = 183–196 | doi = 10.1016/j.artmed.2004.04.002 | pmid = 15302085 }}</ref> | ||
|- | |- | ||
| एसएनपीएस || [[Hill climbing|हिल क्लिंबिंग]] || फ़िल्टर + डब्ल्यूरैपर || [[Naive Bayes classifier|नाइव बायेसियन]] || वर्गों का पूर्वानुमानित अवशिष्ट योग || लांग 2007<ref>{{cite journal | last1 = Long | first1 = N. | last2 = Gianola | first2 = D. | last3 = Weigel | first3 = K. A | year = 2011 | title = Dimension reduction and variable selection for genomic selection: application to predicting milk yield in Holsteins | journal = Journal of Animal Breeding and Genetics | volume = 128 | issue = 4| pages = 247–257 | doi=10.1111/j.1439-0388.2011.00917.x| pmid = 21749471 }}</ref> | | एसएनपीएस || [[Hill climbing|हिल क्लिंबिंग]] || फ़िल्टर + डब्ल्यूरैपर || [[Naive Bayes classifier|नाइव बायेसियन]] || वर्गों का पूर्वानुमानित अवशिष्ट योग || लांग 2007<ref>{{cite journal | last1 = Long | first1 = N. | last2 = Gianola | first2 = D. | last3 = Weigel | first3 = K. A | year = 2011 | title = Dimension reduction and variable selection for genomic selection: application to predicting milk yield in Holsteins | journal = Journal of Animal Breeding and Genetics | volume = 128 | issue = 4| pages = 247–257 | doi=10.1111/j.1439-0388.2011.00917.x| pmid = 21749471 }}</ref> | ||
| Line 221: | Line 226: | ||
| जेनेटिक एल्गोरिदम || डब्ल्यूरैपर || बहुरेखीय प्रतिगमन, [[Partial least squares regression|आंशिक न्यूनतम वर्ग]]|| [[root-mean-square error|मूल-माध्य-वर्ग त्रुटि]] पूर्वानुमान का || ब्रॉडहर्स्ट एट अल. 1997<ref>{{cite journal |first1=D. |last1=Broadhurst |first2=R. |last2=Goodacre |first3=A. |last3=Jones |first4=J. J. |last4=Rowland |first5=D. B. |last5=Kell |title=Genetic algorithms as a method for variable selection in multiple linear regression and partial least squares regression, with applications to pyrolysis mass spectrometry |journal=Analytica Chimica Acta |volume=348 |issue=1–3 |pages=71–86 |year=1997 |doi=10.1016/S0003-2670(97)00065-2 }}</ref> | | जेनेटिक एल्गोरिदम || डब्ल्यूरैपर || बहुरेखीय प्रतिगमन, [[Partial least squares regression|आंशिक न्यूनतम वर्ग]]|| [[root-mean-square error|मूल-माध्य-वर्ग त्रुटि]] पूर्वानुमान का || ब्रॉडहर्स्ट एट अल. 1997<ref>{{cite journal |first1=D. |last1=Broadhurst |first2=R. |last2=Goodacre |first3=A. |last3=Jones |first4=J. J. |last4=Rowland |first5=D. B. |last5=Kell |title=Genetic algorithms as a method for variable selection in multiple linear regression and partial least squares regression, with applications to pyrolysis mass spectrometry |journal=Analytica Chimica Acta |volume=348 |issue=1–3 |pages=71–86 |year=1997 |doi=10.1016/S0003-2670(97)00065-2 }}</ref> | ||
|- | |- | ||
| स्पैम || [[Mutation (genetic algorithm)|बाइनरी पीएसओ + म्यूटेशन]] || डब्ल्यूरैपर || [[Decision tree| | | स्पैम || [[Mutation (genetic algorithm)|बाइनरी पीएसओ + म्यूटेशन]] || डब्ल्यूरैपर || [[Decision tree|डिसिजन ट्री]] || भारांकित निवेश || झांग 2014<ref name="sciencedirect.com"/> | ||
|- | |- | ||
| माइक्रोएरे || [[Tabu search|ताबू सर्च]] + [[Particle swarm optimization|पीएसओ]]|| डब्ल्यूरैपर || [[Support Vector Machine|सपोर्ट | | माइक्रोएरे || [[Tabu search|ताबू सर्च]] + [[Particle swarm optimization|पीएसओ]]|| डब्ल्यूरैपर || [[Support Vector Machine|सपोर्ट वेक्टर मशीन,]][[k-nearest neighbors algorithm|, K निकटतम नेबर]] || [[Euclidean Distance|यूक्लिडियन दूरी]] || चुआंग 2009<ref>{{cite journal | last1 = Chuang | first1 = L.-Y. | last2 = Yang | first2 = C.-H. | year = 2009 | title = Tabu search and binary particle swarm optimization for feature selection using microarray data | journal = Journal of Computational Biology | volume = 16 | issue = 12| pages = 1689–1703 | doi = 10.1089/cmb.2007.0211 | pmid = 20047491 }}</ref> | ||
|- | |- | ||
| माइक्रोएरे || पीएसओ + जेनेटिक एल्गोरिदम || डब्ल्यूरैपर || सपोर्ट | | माइक्रोएरे || पीएसओ + जेनेटिक एल्गोरिदम || डब्ल्यूरैपर || सपोर्ट वेक्टर मशीन || वर्गीकरण स्पष्टता (10 गुना) || अल्बा 2007<ref>E. Alba, J. Garia-Nieto, L. Jourdan et E.-G. Talbi. [http://neo.lcc.uma.es/presentacionesCongreso/JMcec2007.pdf Gene Selection in Cancer Classification using PSO-SVM and GA-SVM Hybrid Algorithms.] Congress on Evolutionary Computation, Singapor: Singapore (2007), 2007</ref> | ||
|- | |- | ||
| माइक्रोएरे || जेनेटिक एल्गोरिदम + [[Iterated local search|पुनरावर्ती स्थानीय खोज]]|| एम्बेडेड || सपोर्ट | | माइक्रोएरे || जेनेटिक एल्गोरिदम + [[Iterated local search|पुनरावर्ती स्थानीय खोज]]|| एम्बेडेड || सपोर्ट वेक्टर मशीन || वर्गीकरण स्पष्टता (10 गुना) || डुवाल 2009<ref name="B. Duval, J pages 201-208">B. Duval, J.-K. Hao et J. C. Hernandez Hernandez. [http://www.info.univ-angers.fr/pub/hao/papers/GECCO09.pdf A memetic algorithm for gene selection and molecular classification of an cancer.] In Proceedings of the 11th Annual conference on Genetic and evolutionary computation, GECCO '09, pages 201-208, New York, NY, USA, 2009. ACM.</ref> | ||
|- | |- | ||
| माइक्रोएरे || पुनरावर्ती स्थानीय खोज || डब्ल्यूरैपर || प्रतिगमन || [[Posterior probability|पश्च संभाव्यता]] || हंस 2007<ref>C. Hans, A. Dobra et M. West. [https://www.researchgate.net/profile/Adrian_Dobra/publication/228388856_Shotgun_Stochastic_Search_for_Large_p_Regression/links/02bfe5125185997d06000000.pdf Shotgun stochastic search for 'large p' regression]. Journal of the American Statistical Association, 2007.</ref> | | माइक्रोएरे || पुनरावर्ती स्थानीय खोज || डब्ल्यूरैपर || प्रतिगमन || [[Posterior probability|पश्च संभाव्यता]] || हंस 2007<ref>C. Hans, A. Dobra et M. West. [https://www.researchgate.net/profile/Adrian_Dobra/publication/228388856_Shotgun_Stochastic_Search_for_Large_p_Regression/links/02bfe5125185997d06000000.pdf Shotgun stochastic search for 'large p' regression]. Journal of the American Statistical Association, 2007.</ref> | ||
| Line 235: | Line 240: | ||
| माइक्रोएरे || [[Memetic algorithm|हाइब्रिड जेनेटिक एल्गोरिदम]] || डब्ल्यूरैपर || K निकटतम नेबर || वर्गीकरण स्पष्टता (लीव-वन-आउट क्रॉस-वैलिडेशन) || ओह 2004<ref>{{cite journal | last1 = Oh | first1 = I. S. | last2 = Moon | first2 = B. R. | year = 2004 | title = Hybrid genetic algorithms for feature selection | journal = [[IEEE Transactions on Pattern Analysis and Machine Intelligence]] | volume = 26 | issue = 11| pages = 1424–1437 | doi=10.1109/tpami.2004.105| pmid = 15521491 | citeseerx = 10.1.1.467.4179 }}</ref> | | माइक्रोएरे || [[Memetic algorithm|हाइब्रिड जेनेटिक एल्गोरिदम]] || डब्ल्यूरैपर || K निकटतम नेबर || वर्गीकरण स्पष्टता (लीव-वन-आउट क्रॉस-वैलिडेशन) || ओह 2004<ref>{{cite journal | last1 = Oh | first1 = I. S. | last2 = Moon | first2 = B. R. | year = 2004 | title = Hybrid genetic algorithms for feature selection | journal = [[IEEE Transactions on Pattern Analysis and Machine Intelligence]] | volume = 26 | issue = 11| pages = 1424–1437 | doi=10.1109/tpami.2004.105| pmid = 15521491 | citeseerx = 10.1.1.467.4179 }}</ref> | ||
|- | |- | ||
| माइक्रोएरे || जेनेटिक एल्गोरिदम || डब्ल्यूरैपर || सपोर्ट | | माइक्रोएरे || जेनेटिक एल्गोरिदम || डब्ल्यूरैपर || सपोर्ट वेक्टर मशीन || [[Sensitivity and specificity|सेंसिटिविटी और विशिष्टता]] || ज़ुआन 2011<ref>{{cite journal | last1 = Xuan | first1 = P. | last2 = Guo | first2 = M. Z. | last3 = Wang | first3 = J. | last4 = Liu | first4 = X. Y. | last5 = Liu | first5 = Y. | year = 2011 | title = Genetic algorithm-based efficient feature selection for classification of pre-miRNAs | journal = Genetics and Molecular Research | volume = 10 | issue = 2| pages = 588–603 | doi = 10.4238/vol10-2gmr969 | pmid = 21491369 | doi-access = free }}</ref> | ||
|- | |- | ||
| माइक्रोएरे || जेनेटिक एल्गोरिदम || डब्ल्यूरैपर || सभी युग्मित सपोर्ट | | माइक्रोएरे || जेनेटिक एल्गोरिदम || डब्ल्यूरैपर || सभी युग्मित सपोर्ट वेक्टर मशीन || वर्गीकरण स्पष्टता (लीव-वन-आउट क्रॉस-वैलिडेशन) || पेंग 2003<ref>{{cite journal | last1 = Peng | first1 = S. | year = 2003 | title = Molecular classification of cancer types from microarray data using the combination of genetic algorithms and support vector machines | journal = FEBS Letters | volume = 555 | issue = 2| pages = 358–362 | doi=10.1016/s0014-5793(03)01275-4| pmid = 14644442 | doi-access = free }}</ref> | ||
|- | |- | ||
| माइक्रोएरे || जेनेटिक एल्गोरिदम || एम्बेडेड || सपोर्ट | | माइक्रोएरे || जेनेटिक एल्गोरिदम || एम्बेडेड || सपोर्ट वेक्टर मशीन || वर्गीकरण स्पष्टता (10 गुना) || हर्नांडेज़ 2007<ref>{{cite book |first1=J. C. H. |last1=Hernandez |first2=B. |last2=Duval |first3=J.-K. |last3=Hao |chapter=A Genetic Embedded Approach for Gene Selection and Classification of Microarray Data |title=Evolutionary Computation,Machine Learning and Data Mining in Bioinformatics. EvoBIO 2007 |series=Lecture Notes in Computer Science |volume=4447 |pages=90–101 |location=Berlin |year=2007 |publisher=Springer Verlag |isbn=978-3-540-71782-9 |doi=10.1007/978-3-540-71783-6_9 }}</ref> | ||
|- | |- | ||
| माइक्रोएरे || जेनेटिक एल्गोरिदम || हाइब्रिड || सपोर्ट | | माइक्रोएरे || जेनेटिक एल्गोरिदम || हाइब्रिड || सपोर्ट वेक्टर मशीन || वर्गीकरण स्पष्टता (लीव-वन-आउट क्रॉस-वैलिडेशन) || ह्यूर्टा 2006<ref>{{cite book |first1=E. B. |last1=Huerta |first2=B. |last2=Duval |first3=J.-K. |last3=Hao |chapter=A Hybrid GA/SVM Approach for Gene Selection and Classification of Microarray Data |title=Applications of Evolutionary Computing. EvoWorkshops 2006 |series=Lecture Notes in Computer Science |volume=3907 |pages=34–44 |year=2006 |isbn=978-3-540-33237-4 |doi=10.1007/11732242_4 }}</ref> | ||
|- | |- | ||
| माइक्रोएरे || जेनेटिक एल्गोरिदम || || सपोर्ट | | माइक्रोएरे || जेनेटिक एल्गोरिदम || || सपोर्ट वेक्टर मशीन || वर्गीकरण स्पष्टता (10 गुना) || मुनि 2006<ref>{{cite journal |first1=D. P. |last1=Muni |first2=N. R. |last2=Pal |first3=J. |last3=Das |title=Genetic programming for simultaneous feature selection and classifier design |journal= IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics|volume=36 |issue=1 |pages=106–117 |year=2006 |doi=10.1109/TSMCB.2005.854499 |pmid=16468570 |s2cid=2073035 }}</ref> | ||
|- | |- | ||
| माइक्रोएरे || जेनेटिक एल्गोरिदम || डब्ल्यूरैपर || सपोर्ट | | माइक्रोएरे || जेनेटिक एल्गोरिदम || डब्ल्यूरैपर || सपोर्ट वेक्टर मशीन || एह-डायल, क्लंप || जॉर्डन 2005<ref>{{cite journal |first1=L. |last1=Jourdan |first2=C. |last2=Dhaenens |first3=E.-G. |last3=Talbi |title=Linkage disequilibrium study with a parallel adaptive GA |journal=[[International Journal of Foundations of Computer Science]] |year=2005 |volume=16 |issue=2 |pages=241–260 |doi=10.1142/S0129054105002978 }}</ref> | ||
|- | |- | ||
| [[Alzheimer's disease|अल्जाइमर रोग]] || [[Welch's t-test|वेल्च का टी-टेस्ट]] || फ़िल्टर || सपोर्ट | | [[Alzheimer's disease|अल्जाइमर रोग]] || [[Welch's t-test|वेल्च का टी-टेस्ट]] || फ़िल्टर || सपोर्ट वेक्टर मशीन || वर्गीकरण स्पष्टता (10 गुना) || झांग 2015<ref>{{cite journal|last1=Zhang|first1=Y.|last2=Dong|first2=Z.|last3=Phillips|first3=P.|last4=Wang|first4=S.|title=Detection of subjects and brain regions related to Alzheimer's disease using 3D MRI scans based on eigenbrain and machine learning|journal=Frontiers in Computational Neuroscience|date=2015|volume=9|page=66|doi=10.3389/fncom.2015.00066|pmid=26082713|pmc=4451357|doi-access=free}}</ref> | ||
|- | |- | ||
| [[Computer vision|कंप्यूटर विजन]] | | [[Computer vision|कंप्यूटर विजन]] | ||
|[https://it.mathworks.com/matlabcentral/fileexchange/56937-feature-selection-library अनंत | |[https://it.mathworks.com/matlabcentral/fileexchange/56937-feature-selection-library अनंत फीचर सिलेक्शन] | ||
|फ़िल्टर | |फ़िल्टर | ||
|स्वतंत्र | |स्वतंत्र | ||
| Line 257: | Line 262: | ||
|- | |- | ||
|माइक्रोएरेs | |माइक्रोएरेs | ||
|[https://it.mathworks.com/matlabcentral/fileexchange/56937-feature-selection-library | |[https://it.mathworks.com/matlabcentral/fileexchange/56937-feature-selection-library आइजेनवेक्टरसेंट्रलिटी एफएस] | ||
|फ़िल्टर | |फ़िल्टर | ||
|स्वतंत्र | |स्वतंत्र | ||
| Line 272: | Line 277: | ||
==लर्निंग एल्गोरिदम में अंतर्निहित | ==लर्निंग एल्गोरिदम में अंतर्निहित फीचर सिलेक्शन == | ||
कुछ शिक्षण एल्गोरिदम अपने समग्र संचालन के | कुछ शिक्षण एल्गोरिदम अपने समग्र संचालन के भागों के रूप में फीचर सिलेक्शन करते हैं। इसमे सम्मिलित है: | ||
* {{tmath|l_1}}-नियमितीकरण तकनीकें, जैसे विरल प्रतिगमन, लैस्सो, और {{tmath|l_1}}-एसवीएम | * {{tmath|l_1}}-नियमितीकरण तकनीकें, जैसे विरल प्रतिगमन, लैस्सो, और {{tmath|l_1}}-एसवीएम | ||
* | *डिसिजन ट्री,<ref name="DengRunger2012" /> जैसे आरआरएफ पैकेज में नियमित यादृच्छिक फॉरेस्ट प्रयुक्त किया गया <ref name="RRF" /> | ||
*[[निर्णय वृक्ष सीखना|डिसिजन ट्री]] <ref>R. Kohavi and G. John, "[https://ai.stanford.edu/~ronnyk/wrappersPrint.pdf Wrappers for feature subset selection]", ''[[Artificial Intelligence (journal)|Artificial intelligence]]'' 97.1-2 (1997): 273-324</ref> | |||
* [[मेमेटिक एल्गोरिदम]] | * [[मेमेटिक एल्गोरिदम]] | ||
* [[ यादृच्छिक बहुपद लॉगिट | | * [[ यादृच्छिक बहुपद लॉगिट | रैंडम मल्टीनोमियल लॉगिट]] (आरएमएनएल) | ||
* [[ऑटोएनकोडर]] | * [[ऑटोएनकोडर]] बॉटनेक-लेयर के साथ ऑटो-एनकोडिंग नेटवर्क | ||
* [[सबमॉड्यूलर सेट फ़ंक्शन|सबमॉड्यूलर | * [[सबमॉड्यूलर सेट फ़ंक्शन|सबमॉड्यूलर सेट फलन]] फीचर सिलेक्शन <ref>{{cite arXiv|eprint=1102.3975|last1=Das|first1=Abhimanyu|title=Submodular meets Spectral: Greedy Algorithms for Subset Selection, Sparse Approximation and Dictionary Selection|last2=Kempe|first2=David|class=stat.ML|year=2011}}</ref><ref>Liu et al., [http://melodi.ee.washington.edu/~bilmes/mypubs/liu-submodfeature2013-icassp.pdf Submodular feature selection for high-dimensional acoustic score spaces] {{Webarchive|url=https://web.archive.org/web/20151017122628/http://melodi.ee.washington.edu/~bilmes/mypubs/liu-submodfeature2013-icassp.pdf |date=2015-10-17 }}</ref><ref>Zheng et al., [http://papers.nips.cc/paper/5565-deep-convolutional-neural-network-for-image-deconvolution Submodular Attribute Selection for Action Recognition in Video] {{Webarchive|url=https://web.archive.org/web/20151118001059/http://papers.nips.cc/paper/5565-deep-convolutional-neural-network-for-image-deconvolution |date=2015-11-18 }}</ref> | ||
* स्थानीय शिक्षण आधारित | * स्थानीय शिक्षण आधारित फीचर सिलेक्शन हैं <ref>{{cite journal | last1 = Sun | first1 = Y. | last2 = Todorovic | first2 = S. | last3 = Goodison | first3 = S. | year = 2010 |title=उच्च-आयामी डेटा विश्लेषण के लिए स्थानीय-शिक्षण-आधारित सुविधा चयन| journal = [[IEEE Transactions on Pattern Analysis and Machine Intelligence]] | volume = 32 | issue = 9| pages = 1610–1626 | doi = 10.1109/tpami.2009.190 | pmc = 3445441 | pmid = 20634556 }}</ref> पारंपरिक विधियों की तुलना में, इसमें कोई अनुमानी खोज सम्मिलित नहीं है, यह सरलता से बहु-वर्ग की समस्याओं को संभाल सकता है, यह रैखिक और गैर-रेखीय दोनों समस्याओं के लिए कार्य करता है। यह शक्तिशाली सैद्धांतिक आधार द्वारा भी समर्थित है। संख्यात्मक प्रयोगों से पता चला है कि यह विधि के समीप-से-अधिकतम समाधान प्राप्त कर सकती है, तथापि डेटा में >1M अप्रासंगिक विशेषताएं होती हैं। | ||
* फीचर | * फीचर सिलेक्शन के आधार पर अनुशंसा प्रणाली और <ref>D.H. Wang, Y.C. Liang, D.Xu, X.Y. Feng, R.C. Guan(2018), "[https://www.sciencedirect.com/science/article/pii/S0950705118302107 A content-based recommender system for computer science publications]", ''[[Knowledge-Based Systems]]'', 157: 1-9</ref> फीचर सिलेक्शन विधियों को अनुशंसाकर्ता सिस्टम अनुसंधान में प्रस्तुत किया गया है। | ||
==यह भी देखें== | ==यह भी देखें== | ||
* [[क्लस्टर विश्लेषण]] | * [[क्लस्टर विश्लेषण|क्लस्टर एनालिसिस]] | ||
* [[डेटा खनन]] | * [[डेटा खनन|डेटा माइनिंग]] | ||
* [[आयामीता में कमी]] | * [[आयामीता में कमी]] | ||
* | * फ़ीचर एक्सट्रेक्शन | ||
* [[हाइपरपैरामीटर अनुकूलन]] | * [[हाइपरपैरामीटर अनुकूलन|हाइपरपैरामीटर ऑप्टिमाइजेशन]] | ||
* [[मॉडल चयन]] | * [[मॉडल चयन|मॉडल सिलेक्शन]] | ||
* | * रिलीफ (फ़ीचर सिलेक्शन) | ||
==संदर्भ== | ==संदर्भ== | ||
{{Reflist|30em}} | {{Reflist|30em}} | ||
==अग्रिम पठन== | ==अग्रिम पठन== | ||
| Line 302: | Line 307: | ||
* {{cite book | title= Feature Selection for Knowledge Discovery and Data Mining | author1-first= Huan | author1-last=Liu | author2-first= Hiroshi | author2-last= Motoda | year= 1998 | publisher= Springer |url=https://books.google.com/books?id=aaDbBwAAQBAJ | isbn=0-7923-8198-X }} | * {{cite book | title= Feature Selection for Knowledge Discovery and Data Mining | author1-first= Huan | author1-last=Liu | author2-first= Hiroshi | author2-last= Motoda | year= 1998 | publisher= Springer |url=https://books.google.com/books?id=aaDbBwAAQBAJ | isbn=0-7923-8198-X }} | ||
* {{cite journal |first1=Huan |last1=Liu |first2=Lei |last2=Yu |title=Toward Integrating Feature Selection Algorithms for Classification and Clustering |journal=IEEE Transactions on Knowledge and Data Engineering |volume=17 |issue=4 |year=2005 |pages=491–502 |doi=10.1109/TKDE.2005.66 |s2cid=1607600 }} | * {{cite journal |first1=Huan |last1=Liu |first2=Lei |last2=Yu |title=Toward Integrating Feature Selection Algorithms for Classification and Clustering |journal=IEEE Transactions on Knowledge and Data Engineering |volume=17 |issue=4 |year=2005 |pages=491–502 |doi=10.1109/TKDE.2005.66 |s2cid=1607600 }} | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
* [https://web.archive.org/web/20120511162342/http://featureselection.asu.edu/software.php Feature Selection Package, Arizona State University (Matlab Code)] | * [https://web.archive.org/web/20120511162342/http://featureselection.asu.edu/software.php Feature Selection Package, Arizona State University (Matlab Code)] | ||
| Line 310: | Line 313: | ||
* [http://home.penglab.com/proj/mRMR/index.htm Minimum-redundancy-maximum-relevance (mRMR) feature selection program] | * [http://home.penglab.com/proj/mRMR/index.htm Minimum-redundancy-maximum-relevance (mRMR) feature selection program] | ||
* [http://mloss.org/software/view/386/ FEAST] (Open source Feature Selection algorithms in C and MATLAB) | * [http://mloss.org/software/view/386/ FEAST] (Open source Feature Selection algorithms in C and MATLAB) | ||
[[Category: | [[Category:CS1 English-language sources (en)]] | ||
[[Category:CS1 errors]] | |||
[[Category:CS1 français-language sources (fr)]] | |||
[[Category:Created On 25/07/2023]] | [[Category:Created On 25/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Translated in Hindi]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:आयाम में कमी]] | |||
[[Category:मॉडल चयन]] | |||
Latest revision as of 11:18, 14 August 2023
| Part of a series on |
| Machine learning and data mining |
|---|
 |
मशीन लर्निंग और सांख्यिकी में, फीचर सिलेक्शन होता हैं, जिसे वैरिएबल सिलेक्शन , विशेषता सिलेक्शन या वैरिएबल सबसेट सिलेक्शन के रूप में भी जाना जाता है | यह मॉडल निर्माण में उपयोग के लिए प्रासंगिक फीचर (मशीन लर्निंग) (वेरिएबल , प्रडिक्टर) के सबसेट का सिलेक्शन करने की प्रक्रिया है। फीचर सिलेक्शन तकनीकों का उपयोग अनेक कारणों से किया जाता है |
फीचर सिलेक्शन तकनीक का उपयोग करते समय केंद्रीय आधार यह है कि डेटा में कुछ विशेषताएं सम्मिलित हैं जो तब अनावश्यक हैं या अप्रासंगिक हैं, और इस प्रकार सूचना को अधिक हानि के अतिरिक्त उन्हें हटाया जा सकता है। [9] यह निरर्थक और अप्रासंगिक दो भिन्न-भिन्न धारणाएँ होती हैं, क्योंकि प्रासंगिक विशेषता किसी अन्य प्रासंगिक विशेषता की उपस्थिति में निरर्थक हो सकती है जिसके साथ यह दृढ़ता से सहसंबद्ध होता है।[10]
फीचर सिलेक्शन तकनीकों को फीचर निष्कर्षण से भिन्न किया जाना चाहिए। [11] फीचर निष्कर्षण मूल फीचर्स के कार्यों से नई सुविधाएँ बनाता है, जबकि फीचर सिलेक्शन फीचर्स का सबसेट लौटाता है। फीचर सिलेक्शन तकनीकों का उपयोग अधिकांशतः उन डोमेन में किया जाता है जहाँ अनेक सुविधाएँ और तुलनात्मक रूप से प्रतिरुप (या डेटा बिंदु) होते हैं। फीचर सिलेक्शन के अनुप्रयोग के लिए आदर्श स्तिथियों में स्टाइलोमेट्री और डीएनए माइक्रोएरे डेटा का विश्लेषण सम्मिलित होता है, जहां अनेक हजारों विशेषताएं होती हैं, और इसमें कुछ दशको से सैकड़ों प्रतिरुप हैं।
परिचय
फीचर सिलेक्शन एल्गोरिथ्म को नए फीचर सबसेट के प्रस्ताव के लिए खोज तकनीक के संयोजन के रूप में देखा जा सकता है | इसके साथ ही मूल्यांकन उपाय जो विभिन्न फीचर सबसेट को स्कोर करता है। यह सबसे सरल एल्गोरिदम फीचर्स के प्रत्येक संभावित उपसमूह का परीक्षण करना है जो त्रुटि दर को कम करता है। यह स्थान की विस्तृत खोज है, और यह लघु से लघु फीचर सेट को छोड़कर सभी के लिए कम्प्यूटेशनल रूप से कठिन है। मूल्यांकन मेट्रिक का चुनाव एल्गोरिदम को अधिक रूप से प्रभावित करता है, और यह मूल्यांकन मेट्रिक्स होता हैं जो फीचर सिलेक्शन एल्गोरिदम की तीन मुख्य श्रेणियों के मध्य अंतर करते हैं | इसमें रैपर, फिल्टर और एम्बेडेड विधियां होती हैं। [10]
- रैपर विधियाँ फीचर सबसेट को स्कोर करने के लिए पूर्वानुमानित मॉडल का उपयोग करती हैं। प्रत्येक नए सबसेट का उपयोग मॉडल को प्रशिक्षित करने के लिए किया जाता है, जिसका परीक्षण होल्ड-आउट सेट पर किया जाता है। उस होल्ड-आउट सेट (मॉडल की त्रुटि दर) पर की गई त्रुटियों की संख्या की गणना करने से उस सबसेट के लिए स्कोर मिलता है। चूँकि रैपर विधियाँ प्रत्येक सबसेट के लिए नए मॉडल को प्रशिक्षित करती हैं, वह कम्प्यूटेशनल रूप से बहुत गहन होती हैं, किन्तु सामान्यतः यह उस विशेष प्रकार के मॉडल या विशिष्ट समस्या के लिए सबसे अच्छा प्रदर्शन करने वाला फीचर सेट प्रदान करती हैं।
- फ़िल्टर विधियाँ फीचर सबसेट को स्कोर करने के लिए त्रुटि दर के अतिरिक्त प्रॉक्सी माप का उपयोग करती हैं। फीचर सेट की उपयोगिता को ध्यान में रखते हुए, गणना करने में तीव्र होने के लिए इस उपाय को चुना गया है। सामान्य उपायों में म्यूच्यूअल इनफार्मेशन सम्मिलित होती है,[10] यह पॉइंटवाइस म्यूच्यूअल इनफार्मेशन हैं ,[12] पियर्सन प्रोडक्ट-मोमेंट कॉरर्लशन कॉएफिसिएंट, रिलीफ (फीचर सिलेक्शन ) | रिलीफ-बेस्ड एल्गोरिदम हैं,[13] और अंतर/अंतर क्लास दूरी या प्रत्येक वर्ग/फीचर संयोजन के लिए सांख्यिकीय परिकल्पना परीक्षण के स्कोर सम्मिलित हैं। [12][14] फ़िल्टर सामान्यतः रैपर्स की तुलना में कम कम्प्यूटेशनल रूप से गहन होते हैं, किन्तु वह फीचर सेट का उत्पादन करते हैं जो विशिष्ट प्रकार के पूर्वानुमानित मॉडल के अनुरूप नहीं होता है। [15] ट्यूनिंग की इस कमी का अर्थ है कि फ़िल्टर से सेट किया गया फीचर रैपर से सेट की तुलना में अधिक सामान्य है, सामान्यतः रैपर की तुलना में कम पूर्वानुमान प्रदर्शन देता है। चूँकि फीचर सेट में पूर्वानुमान मॉडल की धारणाएँ सम्मिलित नहीं हैं, और इसलिए यह फीचर्स के मध्य संबंधों को प्रदर्शित करने के लिए अधिक उपयोगी है। अनेक फ़िल्टर स्पष्ट सर्वोत्तम फीचर सबसेट के अतिरिक्त फीचर रैंकिंग प्रदान करते हैं, और रैंकिंग में कट-ऑफ पॉइंट क्रॉस-वैलिडेशन (सांख्यिकी) या क्रॉस-वैलिडेशन के माध्यम से चुना जाता है। फ़िल्टर विधियों का उपयोग रैपर विधियों के लिए प्रीप्रोसेसिंग चरण के रूप में भी किया गया है, जिससे बड़ी समस्याओं पर रैपर का उपयोग किया जा सकता है। अन्य लोकप्रिय दृष्टिकोण रिकर्सिव फीचर एलिमिनेशन एल्गोरिदम है, [16] सामान्यतः मॉडल का निरंतर निर्माण करने और कम वजन वाले फीचर्स को हटाने के लिए सपोर्ट वेक्टर मशीन के साथ उपयोग किया जाता है।
- एंबेडेड विधियां तकनीकों का समूह होती है जो मॉडल निर्माण प्रक्रिया के भागों के रूप में फीचर सिलेक्शन करती है। इस दृष्टिकोण का उदाहरण रेखीय मॉडल के निर्माण के लिए लासो (सांख्यिकी) विधि होती है, जो प्रतिगमन गुणांक को L1 दंड के साथ दंडित करता है, उनमें से अनेक को शून्य तक संकुचित कर देता है। कोई भी विशेषता जिसमें गैर-शून्य प्रतिगमन गुणांक है, उसे लैस्सो एल्गोरिथ्म द्वारा 'सिलेक्शन' किया जाता है। लैस्सो में सुधारों में बोलासो सम्मिलित है जो प्रतिरूपों को बूटस्ट्रैप करता है | [17] इलास्टिक नेट नियमितीकरण, जो लैस्सो के L1 दंड को रिज रिग्रेशन के L2 दंड के साथ जोड़ता है | और फ़ीआलेक्ट जो प्रतिगमन गुणांक के संयुक्त विश्लेषण के आधार पर सभी विशेषताओं को स्कोर करता है। [18] एईएफएस आगे लैस्सो को ऑटोएन्कोडर्स के साथ नॉनलाइनियर परिदृश्य तक विस्तारित करता है। [19] कम्प्यूटेशनल सम्मिश्रता के संदर्भ में यह दृष्टिकोण फिल्टर और रैपर के मध्य होते हैं।
पारंपरिक प्रतिगमन विश्लेषण में, फीचर सिलेक्शन का सबसे लोकप्रिय रूप वेरिएबल स्टेपवाइज रिग्रेशन है, जो रैपर तकनीक होती है। यह ग्रीडी एल्गोरिदम है जो प्रत्येक समय में सबसे अच्छी फीचर जोड़ता है | और (सबसे व्यर्थ फीचर को हटा देता है)। मुख्य नियंत्रण उद्देश्य यह तय करना है कि एल्गोरिदम को कब रोकना है। मशीन लर्निंग में, यह सामान्यतः क्रॉस-वैलिडेशन (सांख्यिकी)|क्रॉस-वैलिडेशन द्वारा किया जाता है। आँकड़ों में, कुछ मानदंड अनुकूलित किए गए हैं। इससे श्रंखला बनाने की अंतर्निहित समस्या उत्पन्न होती है। इससे अधिक शक्तिशाली विधियों का अनुमान लगाया गया है, जैसे शाखा में बाउंड और पीसवाइस लीनियर नेटवर्क होते हैं।
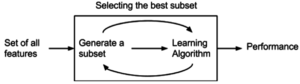
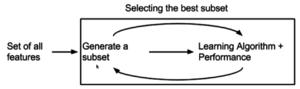
सबसेट सिलेक्शन
सबसेट सिलेक्शन उपयुक्तता के लिए समूह के रूप में फीचर्स के सबसेट का मूल्यांकन करता है। सबसेट सर्च एल्गोरिथ्म को रैपर, फिल्टर और एम्बेडेड विधियों में विभाजित किया जा सकता है। रैपर्स संभावित फीचर्स के स्थान के माध्यम से खोज करने के लिए खोज एल्गोरिदम का उपयोग करते हैं और सबसेट पर मॉडल चलाकर प्रत्येक सबसेट का मूल्यांकन करते हैं। रैपर कम्प्यूटेशनल रूप से मूल्यवान हो सकते हैं और मॉडल में अधिक फिट होने पर कठिन परिस्थिति हो सकती है। खोज दृष्टिकोण में फ़िल्टर रैपर के समान होते हैं, किन्तु यह किसी मॉडल के विरुद्ध मूल्यांकन करने के अतिरिक्त, सरल फ़िल्टर का मूल्यांकन किया जाता है। एंबेडेड तकनीकें मॉडल में अंतर्निहित और विशिष्ट होती हैं।
अनेक लोकप्रिय खोज दृष्टिकोण ग्रीडी एल्गोरिदम हिल क्लिंबिंग का उपयोग करते हैं, जो फीचर्स के उम्मीदवार उपसमूह का पुनरावृत्तीय मूल्यांकन करता है, फिर उपसमूह को संशोधित करता है और मूल्यांकन करता है कि क्या नया उपसमूह पुराने की तुलना में सही है। सबसेट के मूल्यांकन के लिए स्कोरिंग मीट्रिक (गणित) की आवश्यकता होती है जो फीचर्स के उपसमूह को ग्रेड करती है। व्यापक खोज सामान्यतः अव्यावहारिक होती है, इसलिए कुछ कार्यान्वयनकर्ता (या ऑपरेटर) परिभाषित स्टॉपिंग बिंदु पर होते हैं, उस बिंदु तक खोजे गए उच्चतम स्कोर वाले फीचर्स के सबसेट को संतबषजनक फीचर सबसेट के रूप में चुना जाता है। इसको रोकने का मानदंड एल्गोरिथम के अनुसार भिन्न होता है | इस प्रकार यह संभावित मानदंडों में सम्मिलित हैं | सबसेट स्कोर सीमा से अधिक होता है | कार्य का अधिकतम अनुमत रन टाइम सरपास्ड हो गया है |
वैकल्पिक खोज-आधारित तकनीकें लक्षित प्रक्षेपण खोज पर आधारित होती हैं जो उच्च स्कोर वाले डेटा के निम्न-आयामी अनुमानों का पता लगाती हैं | फिर उन विशेषताओं का सिलेक्शन किया जाता है जिनके निचले-आयामी स्थान में सबसे बड़े प्रक्षेपण होते हैं।
खोज दृष्टिकोण में सम्मिलित हैं |
- एक्सहॉस्टइव [20]
- बेस्ट फर्स्ट
- सिम्युलेटेड एनीलिंग
- जेनेटिक एल्गोरिदम [21]
- ग्रीडी फॉरवर्ड सिलेक्शन [22][23][24]
- ग्रीडी बैकवर्ड एलिमिनेशन
- पार्टिकल स्वार्म ऑप्टिमाइजेशन [25]
- टार्गेटेड प्रोजेक्शन परसूट
- स्कैटर सर्च [26][27]
- वेरिएबल नेबरहुड सर्च [28][29]
वर्गीकरण समस्याओं के लिए दो लोकप्रिय फ़िल्टर मेट्रिक्स सहसंबंध और पारस्परिक सूचना हैं,चूंकि गणितीय अर्थ में कोई भी वास्तविक मीट्रिक (गणित) या 'दूरी माप' नहीं है, क्योंकि वह त्रिकोण असमानता का पालन करने में विफल रहते हैं और इस प्रकार किसी भी वास्तविक 'दूरी' की गणना नहीं करते हैं - उन्हें 'स्कोर' के रूप में माना जाना चाहिए। इन अंकों की गणना उम्मीदवार फीचर (या फीचर्स के सेट) और वांछित आउटपुट श्रेणी के मध्य की जाती है। चूँकि, यह ऐसे सत्य मेट्रिक्स होते हैं जो पारस्परिक सूचना का सरल कार्य करते हैं [30] तथा म्यूच्यूअल इनफार्मेशन या मीट्रिक देखें।
अन्य उपलब्ध फ़िल्टर मेट्रिक्स में सम्मिलित हैं |
- वर्ग पृथक्करण
- त्रुटि संभावना
- अंतर-वर्ग दूरी
- संभाव्य दूरी
- एन्ट्रॉपी (सूचना सिद्धांत)
- संगति-आधारित फीचर सिलेक्शन
- सहसंबंध-आधारित फीचर सिलेक्शन
अधिकतम मानदंड
अधिकतमत मानदंड का चुनाव कठिन होता है क्योंकि फीचर सिलेक्शन कार्य में अनेक उद्देश्य होते हैं। अनेक सामान्य मानदंडों में स्पष्टता की माप सम्मिलित होता है, जिसे सिलेक्शन फीचर्स की संख्या द्वारा दंडित किया जाता है। उदाहरणों में अकाइक सूचना मानदंड (एआईसी) और मैलोज़ Cp सम्मिलित हैं | जिनमें प्रत्येक अतिरिक्त फीचर के लिए 2 का दंड है। यह एआईसी सूचना सिद्धांत पर आधारित है, और प्रभावी रूप से मैक्सिमम एन्ट्रापी सिद्धांत के माध्यम से प्राप्त होता है। [31][32]
अन्य मानदंड बायेसियन सूचना मानदंड (बीआईसी) हैं, जो प्रत्येक जोड़े गए फीचर के लिए के दंड का उपयोग करता है, न्यूनतम विवरण लंबाई (एमडीएल) जो असम्बद्ध रूप से का उपयोग करता है, बोनफेरोनी सुधार / आरआईसी जो का उपयोग करता है, अधिकतम निर्भरता फीचर सिलेक्शन , और विभिन्न प्रकार के नए मानदंड जो फाल्स डिस्कवर रेट (एफडीआर) से प्रेरित हैं, जो के समीप कुछ का उपयोग करते हैं। फीचर्स के सबसे प्रासंगिक उपसमूह का सिलेक्शन करने के लिए अधिकतम एन्ट्रापी दर मानदंड का भी उपयोग किया जा सकता है। [33]
संरचना सीखना
फ़िल्टर फीचर सिलेक्शन अधिक सामान्य प्रतिमान का विशिष्ट स्थिति है जिसे संरचित पूर्वानुमान कहा जाता है। फीचर सिलेक्शन विशिष्ट लक्ष्य वेरिएबल के लिए प्रासंगिक फीचर सेट खोजता है जबकि संरचना शिक्षण सभी वेरिएबल के मध्य संबंधों को खोजता है, सामान्यतः इन सम्बन्धो को ग्राफ के रूप में व्यक्त करता हैं। यह सबसे सामान्य संरचना सीखने वाले एल्गोरिदम मानते हैं कि डेटा बायेसियन नेटवर्क द्वारा उत्पन्न होता है, और इसलिए संरचना निर्देशित ग्राफिकल मॉडल है। फ़िल्टर फीचर सिलेक्शन समस्या का अधिकतम समाधान लक्ष्य नोड का मार्कोव ब्लंकेट है, और बायेसियन नेटवर्क में, प्रत्येक नोड के लिए अद्वितीय मार्कोव ब्लंकेट है। [34]
सूचना सिद्धांत आधारित फीचर सिलेक्शन तंत्र
चारों ओर विभिन्न फीचर सिलेक्शन तंत्र हैं जो विभिन्न फीचर्स को स्कोर करने के लिए पारस्परिक सूचना का उपयोग करते हैं। वह सामान्यतः सभी समान एल्गोरिदम का उपयोग करते हैं |
- सभी फीचर्स () और लक्ष्य वर्ग (c ) के मध्य स्कोर के रूप में पारस्परिक सूचना की गणना करें
- सबसे बड़े स्कोर वाली फीचर का सिलेक्शन करें (उदाहरण के लिए . ) और इसे सिलेक्शन फीचर्स (S ) के सेट में जोड़ें
- उस स्कोर की गणना करें जो पारस्परिक सूचना से प्राप्त किया जा सकता है
- सबसे बड़े स्कोर वाली फीचर का सिलेक्शन करें और इसे सिलेक्शन फीचर्स के सेट में जोड़ें (उदाहरण के लिए) )
- 3. और 4. को तब तक दोहराएँ जब तक कि निश्चित संख्या में फीचर्स का सिलेक्शन न हो जाए (उदाहरण के लिए) )
सबसे सरल दृष्टिकोण म्यूच्यूअल इनफार्मेशन को व्युत्पन्न स्कोर के रूप में उपयोग करता है।[35]
चूँकि, भिन्न-भिन्न दृष्टिकोण हैं, जो फीचर्स के मध्य रिडंडेंसीय को कम करने का प्रयास करते हैं।
न्यूनतम-रिडंडेंसीय-अधिकतम-प्रासंगिकता (एमआरएमआर) फीचर सिलेक्शन
पेंग एट अल.[36] फीचर सिलेक्शन विधि प्रस्तावित की गई जो फीचर्स का सिलेक्शन करने के लिए पारस्परिक सूचना , सहसंबंध, या दूरी/समानता स्कोर का उपयोग कर सकती है। इसका उद्देश्य अन्य सिलेक्शन फीचर्स की उपस्थिति में किसी फीचर की प्रासंगिकता को उसके रिडंडेंसीय द्वारा दंडित करना है। क्लास c के लिए फीचर सम्मुचय S की प्रासंगिकता को व्यक्तिगत फीचर fi और क्लास c के मध्य सभी पारस्परिक सूचना मानों के औसत मान से द्वारा परिभाषित किया गया है |
- .
समुच्चय में सभी फीचर्स का रिडंडेंसीय S फीचर के मध्य सभी पारस्परिक सूचना मानों का औसत मान fi और फीचर fj है |
एमआरएमआर मानदंड ऊपर दिए गए दो उपायों का संयोजन है और इसे निम्नानुसार परिभाषित किया गया है:
मान लीजिए कि n पूर्ण-समुच्चय सुविधाएँ हैं। मान लीजिए xi फीचर fi के लिए सेट सदस्यता संकेतक फलन है, जिससे xi=1 उपस्थिति को संकेत करे और xi=0 वैश्विक स्तर पर अधिकतम फीचर सेट में फीचर fi की अनुपस्थिति को संकेत करे। मान लीजिए और हैं। फिर उपरोक्त को अनुकूलन समस्या के रूप में लिखा जा सकता है
एमआरएमआर एल्गोरिदम सैद्धांतिक रूप से अधिकतम-निर्भरता फीचर सिलेक्शन एल्गोरिदम का अनुमान होता है जो सिलेक्शन फीचर्स के संयुक्त वितरण और वर्गीकरण वेरिएबल के मध्य पारस्परिक सूचना को अधिकतम करता है। चूंकि एमआरएमआर बहुत लघु समस्याओं की श्रृंखला के साथ संयोजन अनुमान समस्या का अनुमान लगाता है, जिनमें से प्रत्येक में केवल दो वेरिएबल सम्मिलित होते हैं, इस प्रकार यह जोड़ीदार संयुक्त संभावनाओं का उपयोग करता है जो अधिक शक्तिशाली होते हैं। कुछ स्थितियों में एल्गोरिदम फीचर्स की उपयोगिता को कम समझ सकता है क्योंकि इसमें उन फीचर्स के मध्य इंटरैक्शन को मापने की कोई विधि नहीं है जो इसकी प्रासंगिकता को बढ़ा सकते हैं। इससे व्यर्थ प्रदर्शन हो सकता है [35] जब विशेषताएँ व्यक्तिगत रूप से व्यर्थ होती हैं, किन्तु संयुक्त होने पर यह उपयोगी होती हैं ( पैथोलॉजिकल स्थिति तब पायी जाती है जब वर्ग फीचर्स का समता कार्य होता है)। सामान्यतः एल्गोरिथ्म सैद्धांतिक रूप से अधिकतम-निर्भरता सिलेक्शन की तुलना में अधिक कुशल (आवश्यक डेटा की मात्रा के संदर्भ में) होता है, फिर भी कम जोड़ीदार रिडंडेंसीय के साथ फीचर सेट तैयार करता है।
एमआरएमआर फ़िल्टर विधियों के बड़े वर्ग का उदाहरण है जो विभिन्न विधियों से प्रासंगिकता और रिडंडेंसीय के मध्य व्यापार करता है।[35][37]
क्वाद्रटिक प्रोग्रामिंग फीचर सिलेक्शन
एमआरएमआर फीचर सिलेक्शन के लिए वृद्धिशील ग्रीडी रणनीति का विशिष्ट उदाहरण है | इसमें फीचर का सिलेक्शन हो जाने के पश्चात् होते हैं, इसके पश्चात् चरण में असिलेक्शन नहीं किया जा सकता है। जबकि एमआरएमआर को कुछ फीचर्स को कम करने के लिए फ्लोटिंग सर्च का उपयोग करके अनुकूलित किया जा सकता है, इसे वैश्विक द्विघात प्रोग्रामिंग अनुकूलन समस्या के रूप में निम्नानुसार पुन: तैयार किया जा सकता है | [38]
जहां फीचर प्रासंगिकता का वेक्टर है, यह मानते हुए कि कुल मिलाकर n फीचर हैं, तथा फीचर जोड़ीदार रिडंडेंसीय का आव्युह है, और सापेक्ष फीचर भार का प्रतिनिधित्व करता है। क्यूएफपीएस को द्विघात प्रोग्रामिंग के माध्यम से समाधान किया जाता है। वर्तमान में यह दिखाया गया है कि क्यूएफपीएस लघु एन्ट्रापी वाले फीचर्स के प्रति पक्षपाती है, [39] इसकी लिए इसे फीचर सेल्फ रिडंडेंसी टर्म को H के विकर्ण पर रखा गया है।
नियमबद्ध पारस्परिक सूचना
पारस्परिक सूचना के लिए प्राप्त अन्य स्कोर नियमबद्ध प्रासंगिकता पर आधारित है [39]
जहाँ और .
SPECCMI का लाभ यह है कि इसे केवल Q के प्रमुख आइजनवेक्टर को खोजकर समाधान किया जा सकता है, इस प्रकार यह बहुत स्केलेबल है। SPECCMI दूसरे क्रम के फीचर इंटरैक्शन को भी संभालता है।
संयुक्त पारस्परिक सूचना
विभिन्न अंकों के अध्ययन में ब्राउन एट अल और अन्य ने [35] संयुक्त पारस्परिक सूचना की अनुशंसा की हैं | [40] यह फीचर सिलेक्शन के लिए अच्छे स्कोर के रूप में होता हैं। स्कोर उस फीचर को खोजने का प्रयास करता है, जो रिडंडेंसीय से बचने के लिए पहले से सिलेक्शन फीचर्स में सबसे नई सूचना को जोड़ता है। यह स्कोर इस प्रकार तैयार किया गया है
स्कोर पहले से सिलेक्शन फीचर्स () और जांच के अनुसार फीचर () के मध्य रिडंडेंसीय का अनुमान लगाने के लिए नियमबद्ध पारस्परिक सूचना और पारस्परिक सूचना का उपयोग करता है।
हिल्बर्ट-श्मिट स्वतंत्रता मानदंड लैस्सो आधारित फीचर सिलेक्शन
उच्च-आयामी और लघु प्रतिरूप डेटा के लिए (उदाहरण के लिए, आयामीता > 105 और प्रतिरूपों की संख्या < 103) हैं, हिल्बर्ट-श्मिट इंडिपेंडेंस क्राइटेरियन लासो (एचएसआईसी लासो) उपयोगी है। [41] एचएसआईसी लासो अनुकूलन समस्या इस प्रकार दी गई है
जहाँ कर्नेल-आधारित स्वतंत्रता माप है जिसे (अनुभवजन्य) हिल्बर्ट-श्मिट स्वतंत्रता मानदंड (एचएसआईसी) कहा जाता है,
ट्रेस (रैखिक बीजगणित) को दर्शाता है, नियमितीकरण पैरामीटर है, और इनपुट और आउटपुट केंद्रित ग्राम आव्युह हैं, यह
और ग्राम आव्युह होता हैं, यह और कर्नेल फलन हैं,और केन्द्रित आव्युह होता है, यह m -आयामी पहचान आव्युह (m : प्रतिरूपों की संख्या), है और m -सभी के साथ आयामी वेक्टर, और -मानदंड है। एचएसआईसी सदैव गैर-ऋणात्मक मान लेता है, और यदि शून्य है और केवल तभी जब दो यादृच्छिक वेरिएबल सांख्यिकीय रूप से स्वतंत्र होते हैं जब गाऊसी कर्नेल जैसे सार्वभौमिक पुनरुत्पादन कर्नेल का उपयोग किया जाता है।
एचएसआईसी लैस्सो को इस प्रकार लिखा जा सकता है
जहाँ फ्रोबेनियस मानदंड है इसकी अनुकूलन समस्या लैस्सो समस्या है, और इस प्रकार इसे दोहरी संवर्धित लैग्रेंजियन विधि जैसे अत्याधुनिक लैस्सो सॉल्वर के साथ कुशलतापूर्वक समाधान किया जा सकता है।
सहसंबंध फीचर सिलेक्शन
सहसंबंध फीचर सिलेक्शन (सीएफएस) माप निम्नलिखित परिकल्पना के आधार पर फीचर्स के सबसेट का मूल्यांकन करता है | और अच्छे फीचर सबसेट में वर्गीकरण के साथ अत्यधिक सहसंबद्ध विशेषताएं होती हैं, फिर भी दूसरे से असंबद्ध होती हैं। [42][43] निम्नलिखित समीकरण k विशेषताओं से युक्त फीचर सबसेट S की योग्यता देता है |
यहाँ, सभी फीचर -वर्गीकरण सहसंबंधों का औसत मान है, और सभी फीचर -फीचर सहसंबंधों का औसत मान है। सीएफएस मानदंड को इस प्रकार परिभाषित किया गया है |
और वेरिएबल को सहसंबंध के रूप में संदर्भित किया जाता है, किन्तु आवश्यक नहीं कि यह पियर्सन सहसंबंध गुणांक या स्पीयरमैन के ρ होते हैं। हॉल का शोध प्रबंध इनमें से किसी का भी उपयोग नहीं करता है,किंतु संबंधितता के तीन भिन्न-भिन्न मापों में हैं, उपायों, न्यूनतम विवरण लंबाई (एमडीएल), सममित अनिश्चितता का उपयोग करता है और यह रिलीफ (फीचर सिलेक्शन ) का भी उपयोग करता है।
माना xi फीचर fi के लिए सेट सदस्यता संकेतक फलन होता हैं तब उपरोक्त को अनुकूलन समस्या के रूप में फिर से लिखा जा सकता है
उपरोक्त संयोजनात्मक समस्याएं, वास्तव में, मिश्रित 0-1 रैखिक प्रोग्रामिंग समस्याएं हैं | जिन्हें शाखा-और-बाउंड एल्गोरिदम का उपयोग करके समाधान किया जा सकता है। [44]
डिसिजन ट्री
डिसिजन ट्री या ट्री सामूहिक शिक्षा की विशेषताओं को निरर्थक दिखाया गया है। वर्तमान विधि जिसे नियमितीकृत ट्री कहा जाता है [45] फीचर सबसेट सिलेक्शन के लिए उपयोग किया जा सकता है। नियमितीकृत ट्री वर्तमान नोड को विभाजित करने के लिए पूर्व ट्री नोड्स पर सिलेक्शन वेरिएबल के समान वेरिएबल का उपयोग करके दंडित करते हैं। नियमितीकृत ट्री को केवल ट्री मॉडल (या ट्री संयोजन मॉडल) बनाने की आवश्यकता होती है और इस प्रकार वह कम्प्यूटेशनल रूप से कुशल होते हैं।
नियमितीकृत ट्री स्वाभाविक रूप से संख्यात्मक और श्रेणीगत विशेषताओं, अंतःक्रियाओं और गैर-रैखिकताओं को संभालते हैं। वह विशेषता मापदंडो (इकाइयों) के लिए अपरिवर्तनीय हैं और यह आउटलेर्स के प्रति असंवेदनशील हैं, और इस प्रकार, सामान्यीकरण (सांख्यिकी) जैसे कम डेटा प्रीप्रोसेसिंग की आवश्यकता होती है। नियमित यादृच्छिक फॉरेस्ट (आरआरएफ)[46] प्रकार का डिसिजन ट्री है। निर्देशित आरआरएफ उन्नत आरआरएफ होता है जो सामान्य यादृच्छिक फॉरेस्ट से महत्व स्कोर द्वारा निर्देशित होता है।
मेटाहेयुरिस्टिक्स विधियों पर अवलोकन
मेटाह्यूरिस्टिक कठिन (सामान्यतः एनपी-कठोरता एनपी-हार्ड समस्या) अनुकूलन समस्याओं को समाधान करने के लिए समर्पित एल्गोरिदम का सामान्य विवरण है जिसके लिए कोई मौलिक समाधान विधियां नहीं हैं। सामान्यतः, मेटाह्यूरिस्टिक स्टोकेस्टिक एल्गोरिदम है जो वैश्विक अधिकतम तक पहुंचने की प्रवृत्ति रखता है। सरल स्थानीय खोज से लेकर सम्मिश्र वैश्विक खोज एल्गोरिदम तक अनेक मेटाह्यूरिस्टिक्स हैं।
मुख्य सिद्धांत
फीचर सिलेक्शन विधियों को सामान्यतः तीन वर्गों में प्रस्तुत किया जाता है, जो इस पर आधारित होता है कि वह सिलेक्शन एल्गोरिदम और मॉडल बिल्डिंग को कैसे जोड़ते हैं।
फ़िल्टर विधि
फ़िल्टर प्रकार के विधियों मॉडल की चिंता किए बिना वेरिएबल का सिलेक्शन करते हैं। वह केवल पूर्वानुमान करने के लिए वेरिएबल के साथ सहसंबंध जैसी सामान्य विशेषताओं पर आधारित होते हैं। फ़िल्टर विधियाँ कम से कम आकर्षक वेरिएबल को दबा देती हैं। अन्य वेरिएबल वर्गीकरण या डेटा को वर्गीकृत करने या पूर्वानुमान करने के लिए उपयोग किए जाने वाले प्रतिगमन मॉडल का भाग होते हैं। यह विधियां समय की गणना करने में विशेष रूप से प्रभावी होती हैं और ओवरफिटिंग के लिए शक्तिशाली हैं। [47]
फ़िल्टर विधियाँ निरर्थक वेरिएबल का सिलेक्शन करती हैं जब वह वेरिएबल के मध्य संबंधों पर विचार नहीं करते हैं। चूँकि, अधिक विस्तृत सुविधाएँ एक-दूसरे से अत्यधिक सहसंबंधित वेरिएबल को हटाकर इस समस्या को कम करने का प्रयास करती हैं, जैसे कि फास्ट सहसंबंध आधारित फ़िल्टर (एफसीबीएफ) एल्गोरिथ्म हैं। [48]
रैपर विधि
रैपर विधियां वेरिएबल्स के सबसेट का मूल्यांकन करती हैं जो फ़िल्टर दृष्टिकोण के विपरीत हैं, यह वेरिएबल्स के मध्य संभावित इंटरैक्शन का अनुमान लगाने की अनुमति देती हैं। [49] इन विधियों की दो मुख्य हानि हैं
- अवलोकनों की संख्या अपर्याप्त होने पर ओवरफिटिंग का विपत्ति बढ़ जाती है।
- जब महत्वपूर्ण गणना समय में वेरिएबल की संख्या बड़ी होती हैं।
एम्बेडेड विधि
एंबेडेड विधियों वर्तमान में प्रस्तावित किए गए हैं जो पूर्व दोनों विधियों के लाभों को संयोजित करने का प्रयास करते हैं। शिक्षण एल्गोरिदम अपनी स्वयं की परिवर्तनीय सिलेक्शन प्रक्रिया का लाभ उठाता है और फीचर सिलेक्शन और वर्गीकरण के साथ करता है, जैसे एफआरएमटी एल्गोरिदम हैं। [50]
फीचर सिलेक्शन मेटाह्यूरिस्टिक्स का अनुप्रयोग
यह साहित्य में वर्तमान में उपयोग किए गए फीचर सिलेक्शन मेटाह्यूरिस्टिक्स के अनुप्रयोग का सर्वेक्षण है। इस सर्वेक्षण को जे. हैमन ने अपनी 2013 की थीसिस में वास्तविक किया था। [47]
| Application | एल्गोरिदम | दृष्टिकोण | वर्गीकरणकर्ता | मूल्यांकन कार्य | संदर्भ |
|---|---|---|---|---|---|
| एसएनपीएस | फीचर समानता का उपयोग करके फीचर सिलेक्शन | फ़िल्टर | r2 | फुओंग 2005[49] | |
| एसएनपीएस | जेनेटिक एल्गोरिदम | डब्ल्यूरैपर | डिसिजन ट्री | वर्गीकरण स्पष्टता (10 गुना) | शाह 2004[51] |
| एसएनपीएस | हिल क्लिंबिंग | फ़िल्टर + डब्ल्यूरैपर | नाइव बायेसियन | वर्गों का पूर्वानुमानित अवशिष्ट योग | लांग 2007[52] |
| एसएनपीएस | सिम्युलेटेड एनीलिंग | नाइव बायेसियन | वर्गीकरण स्पष्टता (5 गुना) | उस्तुंकर 2011[53] | |
| सेगमेंट पैरोल | अंट कॉलोनी | डब्ल्यूरैपर | कृत्रिम नेचुरल नेटवर्क | एमएसई | अल-अनी 2005 |
| मार्केटिंग | सिम्युलेटेड एनीलिंग | डब्ल्यूरैपर | प्रतिगमन | एआईसी,, r2 | मेरि 2006[54] |
| इकॉनॉमिक्स | सिम्युलेटेड एनीलिंग, जेनेटिक एल्गोरिदम | डब्ल्यूरैपर | प्रतिगमन | बीआईसी | कपेतनियोस 2007[55] |
| वर्णक्रमीय द्रव्यमान | जेनेटिक एल्गोरिदम | डब्ल्यूरैपर | बहुरेखीय प्रतिगमन, आंशिक न्यूनतम वर्ग | मूल-माध्य-वर्ग त्रुटि पूर्वानुमान का | ब्रॉडहर्स्ट एट अल. 1997[56] |
| स्पैम | बाइनरी पीएसओ + म्यूटेशन | डब्ल्यूरैपर | डिसिजन ट्री | भारांकित निवेश | झांग 2014[25] |
| माइक्रोएरे | ताबू सर्च + पीएसओ | डब्ल्यूरैपर | सपोर्ट वेक्टर मशीन,, K निकटतम नेबर | यूक्लिडियन दूरी | चुआंग 2009[57] |
| माइक्रोएरे | पीएसओ + जेनेटिक एल्गोरिदम | डब्ल्यूरैपर | सपोर्ट वेक्टर मशीन | वर्गीकरण स्पष्टता (10 गुना) | अल्बा 2007[58] |
| माइक्रोएरे | जेनेटिक एल्गोरिदम + पुनरावर्ती स्थानीय खोज | एम्बेडेड | सपोर्ट वेक्टर मशीन | वर्गीकरण स्पष्टता (10 गुना) | डुवाल 2009[59] |
| माइक्रोएरे | पुनरावर्ती स्थानीय खोज | डब्ल्यूरैपर | प्रतिगमन | पश्च संभाव्यता | हंस 2007[60] |
| माइक्रोएरे | जेनेटिक एल्गोरिदम | डब्ल्यूरैपर | K निकटतम नेबर | वर्गीकरण स्पष्टता (लीव-वन-आउट क्रॉस-वैलिडेशन) | जिरापेच-उम्पई 2005[61] |
| माइक्रोएरे | हाइब्रिड जेनेटिक एल्गोरिदम | डब्ल्यूरैपर | K निकटतम नेबर | वर्गीकरण स्पष्टता (लीव-वन-आउट क्रॉस-वैलिडेशन) | ओह 2004[62] |
| माइक्रोएरे | जेनेटिक एल्गोरिदम | डब्ल्यूरैपर | सपोर्ट वेक्टर मशीन | सेंसिटिविटी और विशिष्टता | ज़ुआन 2011[63] |
| माइक्रोएरे | जेनेटिक एल्गोरिदम | डब्ल्यूरैपर | सभी युग्मित सपोर्ट वेक्टर मशीन | वर्गीकरण स्पष्टता (लीव-वन-आउट क्रॉस-वैलिडेशन) | पेंग 2003[64] |
| माइक्रोएरे | जेनेटिक एल्गोरिदम | एम्बेडेड | सपोर्ट वेक्टर मशीन | वर्गीकरण स्पष्टता (10 गुना) | हर्नांडेज़ 2007[65] |
| माइक्रोएरे | जेनेटिक एल्गोरिदम | हाइब्रिड | सपोर्ट वेक्टर मशीन | वर्गीकरण स्पष्टता (लीव-वन-आउट क्रॉस-वैलिडेशन) | ह्यूर्टा 2006[66] |
| माइक्रोएरे | जेनेटिक एल्गोरिदम | सपोर्ट वेक्टर मशीन | वर्गीकरण स्पष्टता (10 गुना) | मुनि 2006[67] | |
| माइक्रोएरे | जेनेटिक एल्गोरिदम | डब्ल्यूरैपर | सपोर्ट वेक्टर मशीन | एह-डायल, क्लंप | जॉर्डन 2005[68] |
| अल्जाइमर रोग | वेल्च का टी-टेस्ट | फ़िल्टर | सपोर्ट वेक्टर मशीन | वर्गीकरण स्पष्टता (10 गुना) | झांग 2015[69] |
| कंप्यूटर विजन | अनंत फीचर सिलेक्शन | फ़िल्टर | स्वतंत्र | औसत परिशुद्धता, आरओसी एयूसी | रोफ़ो 2015[70] |
| माइक्रोएरेs | आइजेनवेक्टरसेंट्रलिटी एफएस | फ़िल्टर | स्वतंत्र | औसत परिशुद्धता, स्पष्टता, आरओसी एयूसी | रोफ़ो और मेल्ज़ी 2016[71] |
| एक्सएमएल | सममितीय टाऊ (एसटी) | फ़िल्टर | संरचनात्मक सहयोगी वर्गीकरण | स्पष्टता, कवरेज | शाहरानी और हैडज़िक 2014 |
लर्निंग एल्गोरिदम में अंतर्निहित फीचर सिलेक्शन
कुछ शिक्षण एल्गोरिदम अपने समग्र संचालन के भागों के रूप में फीचर सिलेक्शन करते हैं। इसमे सम्मिलित है:
- -नियमितीकरण तकनीकें, जैसे विरल प्रतिगमन, लैस्सो, और -एसवीएम
- डिसिजन ट्री,[45] जैसे आरआरएफ पैकेज में नियमित यादृच्छिक फॉरेस्ट प्रयुक्त किया गया [46]
- डिसिजन ट्री [72]
- मेमेटिक एल्गोरिदम
- रैंडम मल्टीनोमियल लॉगिट (आरएमएनएल)
- ऑटोएनकोडर बॉटनेक-लेयर के साथ ऑटो-एनकोडिंग नेटवर्क
- सबमॉड्यूलर सेट फलन फीचर सिलेक्शन [73][74][75]
- स्थानीय शिक्षण आधारित फीचर सिलेक्शन हैं [76] पारंपरिक विधियों की तुलना में, इसमें कोई अनुमानी खोज सम्मिलित नहीं है, यह सरलता से बहु-वर्ग की समस्याओं को संभाल सकता है, यह रैखिक और गैर-रेखीय दोनों समस्याओं के लिए कार्य करता है। यह शक्तिशाली सैद्धांतिक आधार द्वारा भी समर्थित है। संख्यात्मक प्रयोगों से पता चला है कि यह विधि के समीप-से-अधिकतम समाधान प्राप्त कर सकती है, तथापि डेटा में >1M अप्रासंगिक विशेषताएं होती हैं।
- फीचर सिलेक्शन के आधार पर अनुशंसा प्रणाली और [77] फीचर सिलेक्शन विधियों को अनुशंसाकर्ता सिस्टम अनुसंधान में प्रस्तुत किया गया है।
यह भी देखें
- क्लस्टर एनालिसिस
- डेटा माइनिंग
- आयामीता में कमी
- फ़ीचर एक्सट्रेक्शन
- हाइपरपैरामीटर ऑप्टिमाइजेशन
- मॉडल सिलेक्शन
- रिलीफ (फ़ीचर सिलेक्शन)
संदर्भ
- ↑ Gareth James; Daniela Witten; Trevor Hastie; Robert Tibshirani (2013). सांख्यिकीय शिक्षा का एक परिचय. Springer. p. 204.
- ↑ Brank, Janez; Mladenić, Dunja; Grobelnik, Marko; Liu, Huan; Mladenić, Dunja; Flach, Peter A.; Garriga, Gemma C.; Toivonen, Hannu; Toivonen, Hannu (2011), "Feature Selection", in Sammut, Claude; Webb, Geoffrey I. (eds.), Encyclopedia of Machine Learning (in English), Boston, MA: Springer US, pp. 402–406, doi:10.1007/978-0-387-30164-8_306, ISBN 978-0-387-30768-8, retrieved 2021-07-13
- ↑ Kramer, Mark A. (1991). "ऑटोएसोसिएटिव न्यूरल नेटवर्क का उपयोग करके नॉनलाइनियर प्रमुख घटक विश्लेषण". AIChE Journal (in English). 37 (2): 233–243. doi:10.1002/aic.690370209. ISSN 1547-5905.
- ↑ Kratsios, Anastasis; Hyndman, Cody (2021). "NEU: A Meta-Algorithm for Universal UAP-Invariant Feature Representation". Journal of Machine Learning Research. 22 (92): 1–51. ISSN 1533-7928.
- ↑ Persello, Claudio; Bruzzone, Lorenzo (July 2014). "Relevant and invariant feature selection of hyperspectral images for domain generalization". 2014 IEEE Geoscience and Remote Sensing Symposium (PDF). IEEE. pp. 3562–3565. doi:10.1109/igarss.2014.6947252. ISBN 978-1-4799-5775-0. S2CID 8368258.
- ↑ Hinkle, Jacob; Muralidharan, Prasanna; Fletcher, P. Thomas; Joshi, Sarang (2012). Fitzgibbon, Andrew; Lazebnik, Svetlana; Perona, Pietro; Sato, Yoichi; Schmid, Cordelia (eds.). "रीमैनियन मैनिफोल्ड्स पर बहुपद प्रतिगमन". Computer Vision – ECCV 2012. Lecture Notes in Computer Science (in English). Berlin, Heidelberg: Springer. 7574: 1–14. arXiv:1201.2395. doi:10.1007/978-3-642-33712-3_1. ISBN 978-3-642-33712-3. S2CID 8849753.
- ↑ Yarotsky, Dmitry (2021-04-30). "तंत्रिका नेटवर्क द्वारा अपरिवर्तनीय मानचित्रों का सार्वभौमिक अनुमान". Constructive Approximation (in English). 55: 407–474. arXiv:1804.10306. doi:10.1007/s00365-021-09546-1. ISSN 1432-0940. S2CID 13745401.
- ↑ Hauberg, Søren; Lauze, François; Pedersen, Kim Steenstrup (2013-05-01). "रीमैनियन मैनिफ़ोल्ड्स पर असुगंधित कल्मन फ़िल्टरिंग". Journal of Mathematical Imaging and Vision (in English). 46 (1): 103–120. doi:10.1007/s10851-012-0372-9. ISSN 1573-7683. S2CID 8501814.
- ↑ Kratsios, Anastasis; Hyndman, Cody (June 8, 2021). "NEU: A Meta-Algorithm for Universal UAP-Invariant Feature Representation". Journal of Machine Learning Research. 22: 10312. Bibcode:2015NatSR...510312B. doi:10.1038/srep10312. PMC 4437376. PMID 25988841.
- ↑ 10.0 10.1 10.2 Guyon, Isabelle; Elisseeff, André (2003). "वेरिएबल और फ़ीचर चयन का एक परिचय". JMLR. 3.
- ↑ Sarangi, Susanta; Sahidullah, Md; Saha, Goutam (September 2020). "Optimization of data-driven filterbank for automatic speaker verification". Digital Signal Processing. 104: 102795. arXiv:2007.10729. doi:10.1016/j.dsp.2020.102795. S2CID 220665533.
- ↑ 12.0 12.1 Yang, Yiming; Pedersen, Jan O. (1997). पाठ वर्गीकरण में फीचर चयन पर एक तुलनात्मक अध्ययन (PDF). ICML.
- ↑ Urbanowicz, Ryan J.; Meeker, Melissa; LaCava, William; Olson, Randal S.; Moore, Jason H. (2018). "Relief-Based Feature Selection: Introduction and Review". Journal of Biomedical Informatics. 85: 189–203. arXiv:1711.08421. doi:10.1016/j.jbi.2018.07.014. PMC 6299836. PMID 30031057.
- ↑ Forman, George (2003). "पाठ वर्गीकरण के लिए फीचर चयन मेट्रिक्स का एक व्यापक अनुभवजन्य अध्ययन" (PDF). Journal of Machine Learning Research. 3: 1289–1305.
- ↑ Yishi Zhang; Shujuan Li; Teng Wang; Zigang Zhang (2013). "अलग-अलग वर्गों के लिए विचलन-आधारित सुविधा चयन". Neurocomputing. 101 (4): 32–42. doi:10.1016/j.neucom.2012.06.036.
- ↑ Guyon I.; Weston J.; Barnhill S.; Vapnik V. (2002). "सपोर्ट वेक्टर मशीनों का उपयोग करके कैंसर वर्गीकरण के लिए जीन चयन". Machine Learning. 46 (1–3): 389–422. doi:10.1023/A:1012487302797.
- ↑ Bach, Francis R (2008). Bolasso: model consistent lasso estimation through the bootstrap. pp. 33–40. doi:10.1145/1390156.1390161. ISBN 9781605582054. S2CID 609778.
{{cite book}}:|journal=ignored (help) - ↑ Zare, Habil (2013). "लिंफोमा निदान के अनुप्रयोग के साथ लैस्सो के संयुक्त विश्लेषण के आधार पर सुविधाओं की प्रासंगिकता का स्कोरिंग". BMC Genomics. 14 (Suppl 1): S14. doi:10.1186/1471-2164-14-S1-S14. PMC 3549810. PMID 23369194.
- ↑ Kai Han; Yunhe Wang; Chao Zhang; Chao Li; Chao Xu (2018). ऑटोएन्कोडर ने बिना पर्यवेक्षित सुविधा चयन को प्रेरित किया. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP).
- ↑ Hazimeh, Hussein; Mazumder, Rahul; Saab, Ali (2020). "Sparse Regression at Scale: Branch-and-Bound rooted in First-Order Optimization". arXiv:2004.06152 [stat.CO].
- ↑ Soufan, Othman; Kleftogiannis, Dimitrios; Kalnis, Panos; Bajic, Vladimir B. (2015-02-26). "DWFS: A Wrapper Feature Selection Tool Based on a Parallel Genetic Algorithm". PLOS ONE (in English). 10 (2): e0117988. Bibcode:2015PLoSO..1017988S. doi:10.1371/journal.pone.0117988. ISSN 1932-6203. PMC 4342225. PMID 25719748.
- ↑ Figueroa, Alejandro (2015). "वेब क्वेरी के पीछे उपयोगकर्ता के इरादे को पहचानने के लिए प्रभावी सुविधाओं की खोज करना". Computers in Industry. 68: 162–169. doi:10.1016/j.compind.2015.01.005.
- ↑ Figueroa, Alejandro; Guenter Neumann (2013). सामुदायिक प्रश्न उत्तर के लिए क्वेरी लॉग से प्रभावी पैराफ्रेज़ को रैंक करना सीखना. AAAI.
- ↑ Figueroa, Alejandro; Guenter Neumann (2014). "सामुदायिक प्रश्न उत्तर में प्रभावी पैराग्राफों की रैंकिंग के लिए श्रेणी-विशिष्ट मॉडल". Expert Systems with Applications. 41 (10): 4730–4742. doi:10.1016/j.eswa.2014.02.004. hdl:10533/196878.
- ↑ 25.0 25.1 Zhang, Y.; Wang, S.; Phillips, P. (2014). "स्पैम डिटेक्शन पर लागू डिसीजन ट्री का उपयोग करके फ़ीचर चयन के लिए म्यूटेशन ऑपरेटर के साथ बाइनरी पीएसओ". Knowledge-Based Systems. 64: 22–31. doi:10.1016/j.knosys.2014.03.015.
- ↑ F.C. Garcia-Lopez, M. Garcia-Torres, B. Melian, J.A. Moreno-Perez, J.M. Moreno-Vega. Solving feature subset selection problem by a Parallel Scatter Search, European Journal of Operational Research, vol. 169, no. 2, pp. 477–489, 2006.
- ↑ García-Torres, Miguel; Gómez-Vela, Francisco; Divina, Federico; Pinto-Roa, Diego P.; Noguera, José Luis Vázquez; Román, Julio C. Mello (2021). "Scatter search for high-dimensional feature selection using feature grouping". आनुवंशिक और विकासवादी संगणना सम्मेलन साथी की कार्यवाही. pp. 149–150. doi:10.1145/3449726.3459481. ISBN 9781450383516. S2CID 235770316.
- ↑ F.C. Garcia-Lopez, M. Garcia-Torres, B. Melian, J.A. Moreno-Perez, J.M. Moreno-Vega. Solving Feature Subset Selection Problem by a Hybrid Metaheuristic. In First International Workshop on Hybrid Metaheuristics, pp. 59–68, 2004.
- ↑ M. Garcia-Torres, F. Gomez-Vela, B. Melian, J.M. Moreno-Vega. High-dimensional feature selection via feature grouping: A Variable Neighborhood Search approach, Information Sciences, vol. 326, pp. 102-118, 2016.
- ↑ Kraskov, Alexander; Stögbauer, Harald; Andrzejak, Ralph G; Grassberger, Peter (2003). "पारस्परिक सूचना पर आधारित पदानुक्रमित क्लस्टरिंग". arXiv:q-bio/0311039. Bibcode:2003q.bio....11039K.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Akaike, H. (1985), "Prediction and entropy", in Atkinson, A. C.; Fienberg, S. E. (eds.), A Celebration of Statistics (PDF), Springer, pp. 1–24, archived (PDF) from the original on August 30, 2019.
- ↑ Burnham, K. P.; Anderson, D. R. (2002), Model Selection and Multimodel Inference: A practical information-theoretic approach (2nd ed.), Springer-Verlag, ISBN 9780387953649.
- ↑ Einicke, G. A. (2018). "दौड़ने के दौरान घुटने और टखने की गतिशीलता में परिवर्तन को वर्गीकृत करने के लिए सुविधाओं का अधिकतम-एंट्रॉपी दर चयन". IEEE Journal of Biomedical and Health Informatics. 28 (4): 1097–1103. doi:10.1109/JBHI.2017.2711487. PMID 29969403. S2CID 49555941.
- ↑ Aliferis, Constantin (2010). "Local causal and markov blanket induction for causal discovery and feature selection for classification part I: Algorithms and empirical evaluation" (PDF). Journal of Machine Learning Research. 11: 171–234.
- ↑ 35.0 35.1 35.2 35.3 Brown, Gavin; Pocock, Adam; Zhao, Ming-Jie; Luján, Mikel (2012). "Conditional Likelihood Maximisation: A Unifying Framework for Information Theoretic Feature Selection". Journal of Machine Learning Research. 13: 27–66.[1]
- ↑ Peng, H. C.; Long, F.; Ding, C. (2005). "Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy". IEEE Transactions on Pattern Analysis and Machine Intelligence. 27 (8): 1226–1238. CiteSeerX 10.1.1.63.5765. doi:10.1109/TPAMI.2005.159. PMID 16119262. S2CID 206764015. Program
- ↑ Nguyen, H., Franke, K., Petrovic, S. (2010). "Towards a Generic Feature-Selection Measure for Intrusion Detection", In Proc. International Conference on Pattern Recognition (ICPR), Istanbul, Turkey. [2]
- ↑ Rodriguez-Lujan, I.; Huerta, R.; Elkan, C.; Santa Cruz, C. (2010). "द्विघात प्रोग्रामिंग सुविधा चयन" (PDF). JMLR. 11: 1491–1516.
- ↑ 39.0 39.1 Nguyen X. Vinh, Jeffrey Chan, Simone Romano and James Bailey, "Effective Global Approaches for Mutual Information based Feature Selection". Proceedings of the 20th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD'14), August 24–27, New York City, 2014. "[3]"
- ↑ Yang, Howard Hua; Moody, John (2000). "Data visualization and feature selection: New algorithms for nongaussian data" (PDF). Advances in Neural Information Processing Systems: 687–693.
- ↑ Yamada, M.; Jitkrittum, W.; Sigal, L.; Xing, E. P.; Sugiyama, M. (2014). "फ़ीचर-वार नॉन-लीनियर लैस्सो द्वारा उच्च-आयामी फ़ीचर चयन". Neural Computation. 26 (1): 185–207. arXiv:1202.0515. doi:10.1162/NECO_a_00537. PMID 24102126. S2CID 2742785.
- ↑ Hall, M. (1999). मशीन लर्निंग के लिए सहसंबंध-आधारित फ़ीचर चयन (PDF) (PhD thesis). University of Waikato.
- ↑ Senliol, Baris; et al. (2008). "Fast Correlation Based Filter (FCBF) with a different search strategy". 2008 23rd International Symposium on Computer and Information Sciences. pp. 1–4. doi:10.1109/ISCIS.2008.4717949. ISBN 978-1-4244-2880-9. S2CID 8398495.
- ↑ Nguyen, Hai; Franke, Katrin; Petrovic, Slobodan (December 2009). "सुविधा चयन उपायों के एक वर्ग का अनुकूलन". Proceedings of the NIPS 2009 Workshop on Discrete Optimization in Machine Learning: Submodularity, Sparsity & Polyhedra (DISCML). Vancouver, Canada.
- ↑ 45.0 45.1 H. Deng, G. Runger, "Feature Selection via Regularized Trees", Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), IEEE, 2012
- ↑ 46.0 46.1 RRF: Regularized Random Forest, R package on CRAN
- ↑ 47.0 47.1 Hamon, Julie (November 2013). Optimisation combinatoire pour la sélection de variables en régression en grande dimension: Application en génétique animale (Thesis) (in français). Lille University of Science and Technology.
- ↑ Yu, Lei; Liu, Huan (August 2003). "Feature selection for high-dimensional data: a fast correlation-based filter solution" (PDF). ICML'03: Proceedings of the Twentieth International Conference on International Conference on Machine Learning: 856–863.
- ↑ 49.0 49.1 T. M. Phuong, Z. Lin et R. B. Altman. Choosing SNPs using feature selection. Archived 2016-09-13 at the Wayback Machine Proceedings / IEEE Computational Systems Bioinformatics Conference, CSB. IEEE Computational Systems Bioinformatics Conference, pages 301-309, 2005. PMID 16447987.
- ↑ Saghapour, E.; Kermani, S.; Sehhati, M. (2017). "प्रोटिओमिक्स डेटा का उपयोग करके कैंसर के चरणों की भविष्यवाणी के लिए एक नवीन फीचर रैंकिंग पद्धति". PLOS ONE. 12 (9): e0184203. Bibcode:2017PLoSO..1284203S. doi:10.1371/journal.pone.0184203. PMC 5608217. PMID 28934234.
- ↑ Shah, S. C.; Kusiak, A. (2004). "Data mining and genetic algorithm based gene/SNP selection". Artificial Intelligence in Medicine. 31 (3): 183–196. doi:10.1016/j.artmed.2004.04.002. PMID 15302085.
- ↑ Long, N.; Gianola, D.; Weigel, K. A (2011). "Dimension reduction and variable selection for genomic selection: application to predicting milk yield in Holsteins". Journal of Animal Breeding and Genetics. 128 (4): 247–257. doi:10.1111/j.1439-0388.2011.00917.x. PMID 21749471.
- ↑ Üstünkar, Gürkan; Özöğür-Akyüz, Süreyya; Weber, Gerhard W.; Friedrich, Christoph M.; Aydın Son, Yeşim (2012). "Selection of representative SNP sets for genome-wide association studies: A metaheuristic approach". Optimization Letters. 6 (6): 1207–1218. doi:10.1007/s11590-011-0419-7. S2CID 8075318.
- ↑ Meiri, R.; Zahavi, J. (2006). "Using simulated annealing to optimize the feature selection problem in marketing applications". European Journal of Operational Research. 171 (3): 842–858. doi:10.1016/j.ejor.2004.09.010.
- ↑ Kapetanios, G. (2007). "Variable Selection in Regression Models using Nonstandard Optimisation of Information Criteria". Computational Statistics & Data Analysis. 52 (1): 4–15. doi:10.1016/j.csda.2007.04.006.
- ↑ Broadhurst, D.; Goodacre, R.; Jones, A.; Rowland, J. J.; Kell, D. B. (1997). "Genetic algorithms as a method for variable selection in multiple linear regression and partial least squares regression, with applications to pyrolysis mass spectrometry". Analytica Chimica Acta. 348 (1–3): 71–86. doi:10.1016/S0003-2670(97)00065-2.
- ↑ Chuang, L.-Y.; Yang, C.-H. (2009). "Tabu search and binary particle swarm optimization for feature selection using microarray data". Journal of Computational Biology. 16 (12): 1689–1703. doi:10.1089/cmb.2007.0211. PMID 20047491.
- ↑ E. Alba, J. Garia-Nieto, L. Jourdan et E.-G. Talbi. Gene Selection in Cancer Classification using PSO-SVM and GA-SVM Hybrid Algorithms. Congress on Evolutionary Computation, Singapor: Singapore (2007), 2007
- ↑ B. Duval, J.-K. Hao et J. C. Hernandez Hernandez. A memetic algorithm for gene selection and molecular classification of an cancer. In Proceedings of the 11th Annual conference on Genetic and evolutionary computation, GECCO '09, pages 201-208, New York, NY, USA, 2009. ACM.
- ↑ C. Hans, A. Dobra et M. West. Shotgun stochastic search for 'large p' regression. Journal of the American Statistical Association, 2007.
- ↑ Aitken, S. (2005). "Feature selection and classification for microarray data analysis: Evolutionary methods for identifying predictive genes". BMC Bioinformatics. 6 (1): 148. doi:10.1186/1471-2105-6-148. PMC 1181625. PMID 15958165.
- ↑ Oh, I. S.; Moon, B. R. (2004). "Hybrid genetic algorithms for feature selection". IEEE Transactions on Pattern Analysis and Machine Intelligence. 26 (11): 1424–1437. CiteSeerX 10.1.1.467.4179. doi:10.1109/tpami.2004.105. PMID 15521491.
- ↑ Xuan, P.; Guo, M. Z.; Wang, J.; Liu, X. Y.; Liu, Y. (2011). "Genetic algorithm-based efficient feature selection for classification of pre-miRNAs". Genetics and Molecular Research. 10 (2): 588–603. doi:10.4238/vol10-2gmr969. PMID 21491369.
- ↑ Peng, S. (2003). "Molecular classification of cancer types from microarray data using the combination of genetic algorithms and support vector machines". FEBS Letters. 555 (2): 358–362. doi:10.1016/s0014-5793(03)01275-4. PMID 14644442.
- ↑ Hernandez, J. C. H.; Duval, B.; Hao, J.-K. (2007). "A Genetic Embedded Approach for Gene Selection and Classification of Microarray Data". Evolutionary Computation,Machine Learning and Data Mining in Bioinformatics. EvoBIO 2007. Lecture Notes in Computer Science. Vol. 4447. Berlin: Springer Verlag. pp. 90–101. doi:10.1007/978-3-540-71783-6_9. ISBN 978-3-540-71782-9.
- ↑ Huerta, E. B.; Duval, B.; Hao, J.-K. (2006). "A Hybrid GA/SVM Approach for Gene Selection and Classification of Microarray Data". Applications of Evolutionary Computing. EvoWorkshops 2006. Lecture Notes in Computer Science. Vol. 3907. pp. 34–44. doi:10.1007/11732242_4. ISBN 978-3-540-33237-4.
- ↑ Muni, D. P.; Pal, N. R.; Das, J. (2006). "Genetic programming for simultaneous feature selection and classifier design". IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics. 36 (1): 106–117. doi:10.1109/TSMCB.2005.854499. PMID 16468570. S2CID 2073035.
- ↑ Jourdan, L.; Dhaenens, C.; Talbi, E.-G. (2005). "Linkage disequilibrium study with a parallel adaptive GA". International Journal of Foundations of Computer Science. 16 (2): 241–260. doi:10.1142/S0129054105002978.
- ↑ Zhang, Y.; Dong, Z.; Phillips, P.; Wang, S. (2015). "Detection of subjects and brain regions related to Alzheimer's disease using 3D MRI scans based on eigenbrain and machine learning". Frontiers in Computational Neuroscience. 9: 66. doi:10.3389/fncom.2015.00066. PMC 4451357. PMID 26082713.
- ↑ Roffo, G.; Melzi, S.; Cristani, M. (2015-12-01). "Infinite Feature Selection". 2015 IEEE International Conference on Computer Vision (ICCV). pp. 4202–4210. doi:10.1109/ICCV.2015.478. ISBN 978-1-4673-8391-2. S2CID 3223980.
- ↑ Roffo, Giorgio; Melzi, Simone (September 2016). "Features Selection via Eigenvector Centrality" (PDF). NFmcp2016. Retrieved 12 November 2016.
- ↑ R. Kohavi and G. John, "Wrappers for feature subset selection", Artificial intelligence 97.1-2 (1997): 273-324
- ↑ Das, Abhimanyu; Kempe, David (2011). "Submodular meets Spectral: Greedy Algorithms for Subset Selection, Sparse Approximation and Dictionary Selection". arXiv:1102.3975 [stat.ML].
- ↑ Liu et al., Submodular feature selection for high-dimensional acoustic score spaces Archived 2015-10-17 at the Wayback Machine
- ↑ Zheng et al., Submodular Attribute Selection for Action Recognition in Video Archived 2015-11-18 at the Wayback Machine
- ↑ Sun, Y.; Todorovic, S.; Goodison, S. (2010). "उच्च-आयामी डेटा विश्लेषण के लिए स्थानीय-शिक्षण-आधारित सुविधा चयन". IEEE Transactions on Pattern Analysis and Machine Intelligence. 32 (9): 1610–1626. doi:10.1109/tpami.2009.190. PMC 3445441. PMID 20634556.
- ↑ D.H. Wang, Y.C. Liang, D.Xu, X.Y. Feng, R.C. Guan(2018), "A content-based recommender system for computer science publications", Knowledge-Based Systems, 157: 1-9
अग्रिम पठन
- Guyon, Isabelle; Elisseeff, Andre (2003). "An Introduction to Variable and Feature Selection". Journal of Machine Learning Research. 3: 1157–1182.
- Harrell, F. (2001). Regression Modeling Strategies. Springer. ISBN 0-387-95232-2.
- Liu, Huan; Motoda, Hiroshi (1998). Feature Selection for Knowledge Discovery and Data Mining. Springer. ISBN 0-7923-8198-X.
- Liu, Huan; Yu, Lei (2005). "Toward Integrating Feature Selection Algorithms for Classification and Clustering". IEEE Transactions on Knowledge and Data Engineering. 17 (4): 491–502. doi:10.1109/TKDE.2005.66. S2CID 1607600.
बाहरी संबंध
- Feature Selection Package, Arizona State University (Matlab Code)
- NIPS challenge 2003 (see also NIPS)
- Naive Bayes implementation with feature selection in Visual Basic (includes executable and source code)
- Minimum-redundancy-maximum-relevance (mRMR) feature selection program
- FEAST (Open source Feature Selection algorithms in C and MATLAB)