फ़्रिक्वेंसी मॉड्यूलेशन संश्लेषण: Difference between revisions
No edit summary |
No edit summary |
||
| (17 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Form of sound synthesis}} | {{short description|Form of sound synthesis}} | ||
{|style="float:right;width:400px;text-align:center;" <!-- class="wikitable" --> | {|style="float:right;width:400px;text-align:center;" <!-- class="wikitable" --> | ||
|+ '''2 | |+ '''2 संचालक का उपयोग करके एफएम संश्लेषण''' | ||
|- | |- | ||
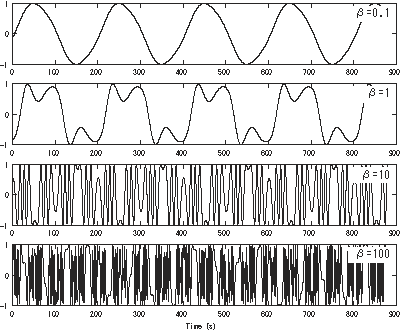
|style="line-height:1.8ex;text-align:left;"|<small>[[Image:2op FM (large font).svg|left|200px]] एक 220 हर्ट्ज वाहक टोन एफसी,[[frequency modulation#Modulation index| | |style="line-height:1.8ex;text-align:left;"|<small>[[Image:2op FM (large font).svg|left|200px]] एक 220 हर्ट्ज वाहक टोन एफसी,[[frequency modulation#Modulation index|आवृति मॉड्यूलेशन इंडेक्स]],β के विभिन्न विकल्पों के साथ, 440 हर्ट्ज मॉड्यूलेटिंग टोन एफएम द्वारा मॉड्यूलेटेड है। समय डोमेन संकेत ऊपर चित्रित किए गए हैं, और संबंधित स्पेक्ट्रा नीचे दिखाए गए हैं ([[decibel|डीबी]] में वर्णक्रम आयाम).।</small> | ||
|- | |- | ||
| | | | ||
| Line 13: | Line 13: | ||
[[Image:frequencymodulationdemo-fd.png]] | [[Image:frequencymodulationdemo-fd.png]] | ||
|} | |} | ||
[[आवृति का उतार - चढ़ाव|आवृत्ति मॉड्यूलेशन]] संश्लेषण (या एफएम संश्लेषण) ध्वनि संश्लेषण का एक रूप है जिसके | '''[[आवृति का उतार - चढ़ाव|आवृत्ति मॉड्यूलेशन]] संश्लेषण''' (या '''एफएम संश्लेषण)''' ध्वनि संश्लेषण का एक ऐसा रूप है जिसके अनुसार एक मॉड्यूलर के साथ इसकी आवृत्ति को मॉड्यूलेट करके [[तरंग]] की आवृत्ति को परिवर्तित कर दिया जाता है। एक दोलक की ([[तात्कालिक आवृत्ति|तात्कालिक]]) आवृत्ति को मॉड्यूलेटिंग संकेत के [[आयाम]] के अनुसार परिवर्तित कर दिया जाता है।<ref>{{harvnb|Dodge|Jerse|1997|p=115}}</ref> | ||
एफएम संश्लेषण [[ लयबद्ध | | एफएम संश्लेषण [[ लयबद्ध |संनादी]] और [[असंगति|असंनादी]] दोनों ध्वनियाँ बना सकता है। संनादी ध्वनियों को संश्लेषित करने के लिए, मॉड्यूलेटिंग संकेत का मूल वाहक संकेत के साथ संनादी संबंध होना चाहिए। जैसे-जैसे आवृत्ति मॉड्यूलेशन की मात्रा बढ़ती है, ध्वनि उत्तरोत्तर जटिल होती जाती है। वाहक संकेत (अर्थात असंनादी) के गैर-पूर्णांक गुणकों वाली आवृत्तियों वाले मॉड्यूलेटर के उपयोग के माध्यम से, असंनादी घंटी-जैसे और परिताड़न स्पेक्ट्रा बनाया जा सकता है। | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
समधर्मी [[थरथरानवाला|दोलक]] का उपयोग करके एफएम संश्लेषण के परिणामस्वरूप | समधर्मी [[थरथरानवाला|दोलक]] का उपयोग करके एफएम संश्लेषण के परिणामस्वरूप तारत्व अस्थिरता हो सकती है।<ref>{{Cite book |last1=McGuire |first1=Sam |url=https://books.google.com/books?id=S90NEAAAQBAJ&dq=analog+fm+synthesis+unstable&pg=SA3-PA11 |title=डिजिटल आर्केस्ट्रा की कला|last2=Matějů |first2=Zbyněk |date=2020-12-28 |publisher=CRC Press |isbn=978-1-000-28699-1 |language=en}}</ref> यद्यपि, एफएम संश्लेषण को डिजिटल रूप से भी प्रयुक्त किया जा सकता है, जो अधिक स्थिर है और मानक अभ्यास बन गया है। डिजिटल एफएम संश्लेषण (तात्कालिक आवृत्ति के समय एकीकरण का उपयोग करके [[चरण मॉड्यूलेशन]] के बराबर) 1974 की प्रारंभ में कई संगीत वाद्ययंत्रों का आधार था। 1980 में यामाहा जीएस-1 को व्यावसायिक रूप से जारी करने से पहले, यामाहा ने एफएम संश्लेषण पर आधारित पहला प्रोटोटाइप [[डिजिटल सिंथेसाइज़र|डिजिटल संश्लेषण]]<ref name=yamaha2014/> 1974 में बनाया था।<ref name="roads"/> 1978 में [[न्यू इंग्लैंड डिजिटल]] कॉर्पोरेशन द्वारा निर्मित [[सिंक्लेवियर]] में एक डिजिटल एफएम संश्लेषण सम्मिलित था, जो यामाहा से लाइसेंस प्राप्त एफएम संश्लेषण कलन विधि का उपयोग करता था।<ref name=mixmag2006>{{cite journal | title = 1978 New England Digital Synclavier | url = http://www.mixonline.com/news/news-products/1978-new-england-digital-synclavier/383609 | date = September 1, 2006 | journal = Mix | publisher = Penton Media}}</ref> 1983 में जारी यामाहा के अभूतपूर्व डीएक्स7 संश्लेषण ने 1980 के दशक के मध्य में एफएम को संश्लेषण के क्षेत्र में सबसे आगे ला दिया। | ||
=== मनोरंजन का उपयोग: पीसी, आर्केड, गेम कंसोल और मोबाइल फोन पर एफएम ध्वनि क्लिप === | === मनोरंजन का उपयोग: पीसी, आर्केड, गेम कंसोल और मोबाइल फोन पर एफएम ध्वनि क्लिप === | ||
नब्बे के दशक के मध्य तक एफएम संश्लेषण भी गेम और सॉफ्टवेयर के लिए सामान्य सेटिंग बन | नब्बे के दशक के मध्य तक एफएम संश्लेषण भी गेम और सॉफ्टवेयर के लिए सामान्य सेटिंग बन गयी। [[आईबीएम पीसी संगत]] प्रणाली के लिए, एडलिब और [[ ध्वनि फाड़ने वाला |ध्वनि स्फोटकर्ता]] जैसे साउंड कार्ड ने [[यामाहा कॉर्पोरेशन]] [[यामाहा YM3812|ओपीएल2]] और ओपीएल3 जैसे यामाहा चिप को लोकप्रिय बनाया। अन्य कंप्यूटर जैसे शार्प [[X68000|एक्स68000]] और [[MSX|एमSएक्स]] ([[यामाहा CX5M|यामाहा सीएक्स5एम]]) [[यामाहा YM2151|यामाहा वाईएम2151]] साउंड चिप का उपयोग करते हैं (जो सामान्यतः नब्बे के दशक के मध्य तक आर्केड मशीनों के लिए भी उपयोग किया जाता था), और [[NEC|एनइसी]] [[PC-88|पीसी -88]] और [[PC-98|पीसी -98]] कंप्यूटर [[यामाहा YM2203|यामाहा वाईएम2203]] और [[OPNA|ओपीएनए]] का उपयोग करते हैं। आर्केड प्रणाली और गेम कंसोल के लिए, [[ओपीएनबी]] का उपयोग [[ कौशल |टैटो]] के आर्केड बोर्डों में मुख्य मूलभूत ध्वनि जनित्र बोर्ड के रूप में किया गया था और विशेष रूप से [[एसएनके]] के [[नियो जियो]] आर्केड (एमवीएस) और होम कंसोल (एईएस) मशीनों में उपयोग किया गया था। ओपीएनबी के एक संस्करण का उपयोग [[सिस्टम्स से टैटो|प्रणाली से टैटो]] में किया गया था। संबंधित [[OPN2|ओपीएन2]] का उपयोग [[सेगा]] मेगा ड्राइव (जेनेसिस) और [[ द्रोह |द्रोह]] के [[एफएम टाउन्स मार्टी]] में इसके ध्वनि जनित्र चिप में से एक के रूप में किया गया था। 2000 के दशक के समय, एफएम संश्लेषण का उपयोग रिंगटोन और अन्य ध्वनियों को चलाने के लिए फोन की एक विस्तृत श्रृंखला पर भी किया गया था, सामान्यतः [[एसएमएएफ]] प्रारूप में उपयोग किया गया था। | ||
==इतिहास== | ==इतिहास== | ||
=== [[डॉन बुचला]] (1960 के दशक के मध्य) === | === [[डॉन बुचला]] (1960 के दशक के मध्य) === | ||
चाउनिंग के पेटेंट से पहले, डॉन बुचला ने 1960 के दशक के मध्य में अपने उपकरणों पर एफएम | चाउनिंग के पेटेंट से पहले, डॉन बुचला ने 1960 के दशक के मध्य में अपने उपकरणों पर एफएम प्रयुक्त किया था। उनके 158, 258 और 259 दोहरे दोलक मॉड्यूल में एक विशिष्ट एफएम नियंत्रण वोल्टता इनपुट था,<ref name="buchla100"> | ||
{{cite book | {{cite book | ||
| author = Dr. Hubert Howe<!-- (Queens College, NY) --> | | author = Dr. Hubert Howe<!-- (Queens College, NY) --> | ||
| Line 36: | Line 36: | ||
| quote = ''At this point we may consider various additional signal modifications that we may wish to make to the series of tones produced by the above example. For instance, if we would like to add frequency modulation to the tones, it is necessary to patch another audio signal into the jack connected by a line to the middle dial on the Model 158 Dual Sine-Sawtooth Oscillator. ...'' | | quote = ''At this point we may consider various additional signal modifications that we may wish to make to the series of tones produced by the above example. For instance, if we would like to add frequency modulation to the tones, it is necessary to patch another audio signal into the jack connected by a line to the middle dial on the Model 158 Dual Sine-Sawtooth Oscillator. ...'' | ||
}} | }} | ||
</ref> और मॉडल 208 ( | </ref> और मॉडल 208 (संगीत ईज़ल) में एक मॉड्यूलेशन दोलक दृढ-तारित था जो एफएम के साथ-साथ प्राथमिक दोलक के एएम की अनुमति देता था।<ref name="buchla music easel"> | ||
{{cite book | {{cite book | ||
| author = Atten Strange | | author = Atten Strange | ||
| Line 44: | Line 44: | ||
| publication-date = 1974 | | publication-date = 1974 | ||
}} | }} | ||
</ref> इन | </ref> इन प्रारंभिक अनुप्रयोगों में समधर्मी दोलक का उपयोग किया गया था, और इस क्षमता का अनुसरण मिनिमोग और [[एआरपी ओडिसी]] सहित अन्य मॉड्यूलर संश्लेषण और पोर्टेबल संश्लेषण द्वारा भी किया गया था। | ||
=== जॉन चाउनिंग (1960 के अंत से 1970 के दशक तक) === | === जॉन चाउनिंग (1960 के अंत से 1970 के दशक तक) === | ||
[[File:Chowning.jpg|thumb|डिजिटल | [[File:Chowning.jpg|thumb|डिजिटल आवृति मॉड्यूलेशन संश्लेषण [[जॉन चाउनिंग]] द्वारा विकसित किया गया था]]20वीं शताब्दी के मध्य तक, ध्वनि प्रसारित करने का एक साधन, आवृति मॉड्यूलेशन (एफएम) को दशकों से समझा जा रहा था और इसका उपयोग [[एफएम प्रसारण|रेडियो प्रसारण]] प्रसारित करने के लिए किया जा रहा था। एफएम संश्लेषण का विकास 1967 में कैलिफोर्निया के स्टैनफोर्ड विश्वविद्यालय में जॉन चाउनिंग द्वारा किया गया था, जो एनालॉग संश्लेषण से भिन्न ध्वनियाँ बनाने की प्रयास कर रहे थे। उनके एल्गोरिदम को 1973 में जापानी कंपनी यामाहा को लाइसेंस दिया गया था।<ref name="yamaha2014">{{cite web |ref={{sfnref|Yamaha|2014}} | title = [Chapter 2] FM Tone Generators and the Dawn of Home Music Production | url = http://usa.yamaha.com/products/music-production/synthesizers/synth_40th/history/chapter02/ | archive-url= https://web.archive.org/web/20170511080846/http://usa.yamaha.com/products/music-production/synthesizers/synth_40th/history/chapter02/ | archive-date=2017-05-11 | work = Yamaha Synth 40th Anniversary - History | year = 2014 | publisher = Yamaha Corporation}}</ref> यामाहा (यूएस पेटेंट 4018121 अप्रैल 1977<ref name="uspto">{{cite web|url=http://patft.uspto.gov/netacgi/nph-Parser?patentnumber=4018121|publisher=patft.uspto.gov|title=U.S. Patent 4018121 Apr 1977|access-date=2017-04-30}}</ref> या यूएस पेटेंट 4,018,121) द्वारा व्यावसायीकरण किया गया कार्यान्वयन वस्तुतः चरण मॉड्यूलेशन पर आधारित है,<ref name="patent">{{cite web|url=https://patents.google.com/patent/US4018121A/en=|title=Patent US4018121 - Method of synthesizing a musical sound - Google Patents |access-date=2017-04-30}}</ref> किन्तु परिणाम गणितीय रूप से समकक्ष होते हैं क्योंकि दोनों अनिवार्य रूप से चतुर्भुज आयाम मॉड्यूलेशन का एक विशेष स्थिति है<ref> | ||
{{cite web | {{cite web | ||
|author = Rob Hordijk | |author = Rob Hordijk | ||
| Line 62: | Line 62: | ||
==== यामाहा द्वारा विस्तार ==== | ==== यामाहा द्वारा विस्तार ==== | ||
यामाहा के इंजीनियरों ने वाणिज्यिक डिजिटल | यामाहा के इंजीनियरों ने वाणिज्यिक डिजिटल संश्लेषक में उपयोग के लिए चाउनिंग के एल्गोरिदम को अपनाना प्रारम्भ कर दिया, जिसमें आवृत्ति मॉड्यूलेशन के समय एनालॉग सिस्टम में सामान्य रूप से होने वाली विकृति से बचने के लिए "कुंजी मापन" विधि जैसे सुधार सम्मिलित किए गए, यद्यपि यामाहा को अपने एफएम डिजिटल संश्लेषक जारी करने में कई वर्ष लगेंगे।<ref name="holmes_257-8">{{cite book|title=इलेक्ट्रॉनिक और प्रायोगिक संगीत: प्रौद्योगिकी, संगीत और संस्कृति|first=Thom|last=Holmes|edition=3rd|publisher=[[Taylor & Francis]]|year=2008|isbn=978-0-415-95781-6|chapter=Early Computer Music|pages=257–8|chapter-url=https://books.google.com/books?id=hCthQ-bec-QC&pg=PA257|access-date=2011-06-04}}</ref> 1970 के दशक में, यामाहा को कंपनी के पूर्व नाम "निप्पॉन गक्की सेइज़ो काबुशिकी कैशा" के अनुसार कई पेटेंट दिए गए, जिससे चाउनिंग का कार्य विकसित हुआ।<ref name="patent" /> यामाहा ने 1974 में पहला प्रोटोटाइप एफएम डिजिटल संश्लेषण बनाया।<ref name="yamaha2014" /> यामाहा ने अंततः 1980 में जारी पहले एफएम डिजिटल संश्लेषण, यामाहा जीएस-1 के साथ एफएम संश्लेषण विधि का व्यावसायीकरण किया।<ref name="roads">{{cite book|title=कंप्यूटर संगीत ट्यूटोरियल|author=Curtis Roads|publisher=[[MIT Press]]|year=1996|isbn=0-262-68082-3|page=226|url=https://books.google.com/books?id=nZ-TetwzVcIC&pg=PA226|access-date=2011-06-05}}</ref> | ||
[[File:YAMAHA DX7.jpg|thumb|एफएम डिजिटल | [[File:YAMAHA DX7.jpg|thumb|एफएम डिजिटल संश्लेषण यामाहा डीएक्स7 (1983)]]एफएम संश्लेषण डिजिटल संश्लेषण की कुछ प्रारंभिक पीढ़ियों का आधार था, विशेष रूप से यामाहा से, साथ ही यामाहा से लाइसेंस के अनुसार न्यू इंग्लैंड डिजिटल कॉर्पोरेशन।<ref name="mixmag2006"/> 1983 में रिलीज़ हुआ यामाहा का डीएक्स7 संश्लेषण, 1980 के दशक में सर्वव्यापी था। यामाहा के कई अन्य मॉडल उस दशक के समय एफएम संश्लेषण की विविधता और विकास प्रदान करते हैं।<ref name="SoS80s">{{cite web|url=http://www.soundonsound.com/sos/sep01/articles/retrofmpt2.asp|title=Sounds of the '80s Part 2: The Yamaha DX1 & Its Successors (Retro)|author=Gordon Reid|date=September 2001|work=Sound on Sound|archive-url=https://web.archive.org/web/20110917223333/http://www.soundonsound.com/sos/sep01/articles/retrofmpt2.asp|archive-date=17 September 2011|access-date=2011-06-29|df=dmy}}</ref> | ||
यामाहा ने 1970 के दशक में एफएम के अपने हार्डवेयर कार्यान्वयन का पेटेंट कराया था,<ref name="patent"/> 1990 के दशक के मध्य तक इसे एफएम प्रौद्योगिकी के बाजार पर लगभग एकाधिकार | यामाहा ने 1970 के दशक में एफएम के अपने हार्डवेयर कार्यान्वयन का पेटेंट कराया था,<ref name="patent"/> 1990 के दशक के मध्य तक इसे एफएम प्रौद्योगिकी के बाजार पर लगभग एकाधिकार को जारी रखने की अनुमति दी गई। | ||
==== [[कैसियो]] द्वारा संबंधित विकास ==== | ==== [[कैसियो]] द्वारा संबंधित विकास ==== | ||
कैसियो ने [[चरण विरूपण संश्लेषण]] नामक संश्लेषण का एक संबंधित रूप विकसित किया, जिसका उपयोग इसके [[कैसियो सीजेड सिंथेसाइज़र]] में किया जाता है। इसमें | कैसियो ने [[चरण विरूपण संश्लेषण|चरण विरूपण]] संश्लेषण नामक संश्लेषण का एक संबंधित रूप विकसित किया, जिसका उपयोग इसके [[कैसियो सीजेड सिंथेसाइज़र|कैसियो सीजेड]] संश्लेषण में किया जाता है। इसमें डीएक्स श्रृंखला के समान (किन्तु थोड़ा अलग विधि से प्राप्त) ध्वनि गुणवत्ता थी। | ||
=== 1990 का दशक === | === 1990 का दशक === | ||
==== पेटेंट की समाप्ति के बाद लोकप्रियता ==== | ==== पेटेंट की समाप्ति के बाद लोकप्रियता ==== | ||
1995 में स्टैनफोर्ड यूनिवर्सिटी एफएम पेटेंट की समाप्ति के साथ, डिजिटल एफएम संश्लेषण अब अन्य निर्माताओं द्वारा स्वतंत्र रूप से | 1995 में स्टैनफोर्ड यूनिवर्सिटी एफएम पेटेंट की समाप्ति के साथ, डिजिटल एफएम संश्लेषण अब अन्य निर्माताओं द्वारा स्वतंत्र रूप से प्रयुक्त किया जा सकता है। एफएम विश्लेषण पेटेंट ने समाप्त होने से पहले स्टैनफोर्ड को 20 मिलियन डॉलर दिलाए, जिससे यह (1994 में) "स्टैनफोर्ड के इतिहास में दूसरा सबसे आकर्षक लाइसेंसिंग समझौता" बन गया।<ref>Stanford University News Service (06/07/94), [http://news.stanford.edu/pr/94/940607Arc4222.html Music synthesis approaches sound quality of real instruments]</ref> एफएम आज अधिकतर सॉफ्टवेयर-आधारित सिंथ में पाया जाता है जैसे कि[[ देशी उपकरण | प्राकृतिक उपकरण]] द्वारा एफएम8 या [[ छवि लाइन |प्रतिरूप पंक्ति]] द्वारा [[ अस्पष्ट |अस्पष्ट]], किन्तु इसे कुछ आधुनिक डिजिटल संश्लेषण के संश्लेषण भंडार में भी सम्मिलित किया गया है, जो सामान्यतः संश्लेषण के अन्य विधियों के साथ एक विकल्प के रूप में सह-अस्तित्व में है, [[घटाव संश्लेषण|वियोज्य संश्लेषण]], प्रतिदर्श-आधारित विश्लेषण, [[ योगात्मक संश्लेषण |योगात्मक]] संश्लेषण और अन्य विधि के साथ विकल्प के रूप में उपयोग किया जाता है। ऐसे हार्डवेयर सिंथ में एफएम की जटिलता की मात्रा साधारण 2-संचालक एफएम से लेकर [[कोर्ग क्रोनोस]] और [[एलेसिस फ्यूजन]] के अत्यधिक नम्य 6-संचालक इंजन तक, बड़े पैमाने पर मॉड्यूलर इंजन में एफएम के निर्माण तक भिन्न हो सकती है जैसे कि [[कुर्ज़वील म्यूजिक सिस्टम|कुर्ज़वील संगीत प्रणाली]] द्वारा नवीनतम संश्लेषण में उपयोग किया जाता है। | ||
==== रीयलटाइम संवलन और मॉड्यूलेशन (एएफएम + प्रतिदर्श) और फॉर्मेंट शेपिंग विश्लेषण ==== | |||
यामाहा एसवाई99 और [[यामाहा FS1R|यामाहा एफएस1आर]] की रिलीज़ के बाद विशेष रूप से उनकी एफएम क्षमताओं के लिए विपणन किए गए नवीन हार्डवेयर सिंथ बाजार से लुप्त हो गए<ref name=YamahaSY99>{{cite web |title=Yamaha SY99 spec |url=https://jp.yamaha.com/products/music_production/synthesizers/sy99/specs.html |language=Japanese |website=[[Yamaha Corporation]]}}</ref><ref name=SOS1998>{{cite magazine |first1=Debbie |last1=Poyser |first2=Derek |last2=Johnson |date=1998 |title=Yamaha FS1R - FM Synthesis / Formant-shaping Tone Generator |url=https://www.soundonsound.com/reviews/yamaha-fs1r |magazine=[[Sound on Sound]] |issue=December 1998}}</ref> और यहां तक कि उन्होंने क्रमशः प्रतिदर्श-आधारित संश्लेषण और फॉर्मेंट संश्लेषण के समकक्षों के रूप में अपनी अत्यधिक शक्तिशाली एफएम क्षमताओं का विपणन किया। यद्यपि, ठीक रूप से विकसित एफएम संश्लेषण विकल्प क्लैविया, एलेसिस फ्यूजन रेंज, कॉर्ग ओएसिस और क्रोनोस और मॉडर एनएफ -1 द्वारा निर्मित नॉर्ड लीड सिंथ की एक विशेषता है। विभिन्न अन्य संश्लेषण अपने मुख्य इंजनों के पूरक के लिए सीमित एफएम क्षमताएँ प्रदान करते हैं। | |||
बहु वर्णक्रम तरंग रूपों के साथ 8 एफएम संचालक के समूह का संयोजन 1999 में यामाहा द्वारा एफएस1आर में प्रारंभिक हुआ। एफएस1आर में 16 संचालक, 8 मानक एफएम संचालक और 8 अतिरिक्त संचालक थे जो ध्वनि स्रोत के रूप में दोलक के अतिरिक्त ध्वनि स्रोत का उपयोग करते थे। ट्यून करने योग्य ध्वनि स्रोतों को जोड़कर एफएस1आर मानव ध्वनि और पवन उपकरण में उत्पन्न ध्वनियों को मॉडल कर सकता है, साथ ही पर्क्यूशन उपकरण ध्वनियां भी बना सकता है। एफएस1आर में एक अतिरिक्त तरंग रूप भी सम्मिलित है जिसे फॉर्मेंट तरंग रूप कहा जाता है। फॉर्मेंट का उपयोग सेलो, वायलिन, ध्वनिक गिटार, बैसून, अंग्रेजी हॉर्न, या मानव ध्वनि जैसे हॉर्न वाले शारीरिक वाद्ययंत्रों की ध्वनियों को मॉडल करने के लिए किया जा सकता है। फॉर्मेंट कई पीतल के उपकरणों के सन्नादी वर्णक्रम में भी पाए जा सकते हैं।<ref name="zollinger2016" /> | |||
=== 2000-वर्तमान === | === 2000-वर्तमान === | ||
==== परिवर्तनीय चरण मॉड्यूलेशन, एफएम-एक्स संश्लेषण, परिवर्तित एफएम, आदि ==== | ==== परिवर्तनीय चरण मॉड्यूलेशन, एफएम-एक्स संश्लेषण, परिवर्तित एफएम, आदि ==== | ||
2016 में, [[कोर्ग]] ने | 2016 में, [[कोर्ग|कॉर्ग]] ने संहत, प्रभावकारी डेस्कटॉप मॉड्यूल की कॉर्ग [[ उलट |वोल्का]] श्रृंखला का एक, 3-वॉयस, 6 संचालक एफएम पुनरावृत्ति, कॉर्ग वोल्का एफएम जारी किया।<ref>[https://www.korg.com/us/products/dj/volca_fm/ Volca FM product page]</ref> और यामाहा ने मोंटाज जारी किया, जो 128-वॉयस प्रतिदर्श-आधारित इंजन को 128-वॉयस एफएम इंजन के साथ जोड़ता है। एफएम के इस पुनरावृत्ति को एफएम-एक्स कहा जाता है, और इसमें 8 संचालक सम्मिलित हैं; प्रत्येक संचालक के निकट कई मूलभूत तरंग रूपों का विकल्प होता है, किन्तु प्रत्येक तरंग रूप में उसके वर्णक्रम को समायोजित करने के लिए कई पैरामीटर होते हैं।<ref>[https://usa.yamaha.com/products/music_production/synthesizers/montage/features.html#product-tabs Yamaha Montage Product Features Page]</ref> यामाहा मोंटाज के बाद 2018 में अधिक प्रभावकारी यामाहा एमओडीएक्स आया, जिसमें 128-वॉयस प्रतिदर्श-आधारित इंजन के अतिरिक्त 64-वॉयस, 8 संचालक एफएम-एक्स संरचना था।<ref>[https://usa.yamaha.com/products/music_production/synthesizers/modx/features.html#product-tabs Yamaha MODX Product Features Page]</ref> इलेक्ट्रॉन ने 2018 में डिजिटोन, एक 8-वॉयस, 4 संचालक एफएम सिंथ लॉन्च किया, जिसमें इलेक्ट्रॉन का प्रसिद्ध अनुक्रम इंजन सम्मिलित है।<ref>[https://www.elektron.se/products/digitone/ Digitone product page]</ref> | ||
एफएम-एक्स विश्लेषण को 2016 में यामाहा मोंटेज संश्लेषण के साथ प्रस्तुत किया गया था। एफएम-एक्स 8 संचालक का उपयोग करता है। प्रत्येक एफएम-एक्स संचालक के निकट चुनने के लिए बहु वर्णक्रम तरंग रूपों का एक समूह होता है, जिसका अर्थ है कि प्रत्येक एफएम-एक्स संचालक 3 या 4 डीएक्स7 एफएम संचालक के समावेश के बराबर हो सकता है। चयन योग्य तरंग रूपों की सूची में ज्या तरंगें, All1 और All2 तरंग रूप, ओड1 और ओड2 तरंग रूप, और आरइएस 1 और आरइएस 2 तरंग रूप सम्मिलित हैं। ज्या तरंग चयन डीएक्स7 तरंग रूपों के समान ही कार्य करता है। All1 और All2 तरंग रूप एक सॉ-दंतिका तरंग रूप हैं। ओड1 और ओड 2 तरंग रूप स्पन्द या वर्ग तरंगें हैं। इन दो प्रकार के तरंग रूपों का उपयोग अधिकांश उपकरणों के सन्नादी वर्णक्रम के निचले भाग में मूलभूत सन्नादी शीर्ष को मॉडल करने के लिए किया जा सकता है। आरइएस 1 और आरइएस 2 तरंग रूप वर्णक्रमीय शिखर को एक विशिष्ट सन्नादी तक ले जाते हैं और इसका उपयोग किसी उपकरण के वर्णक्रम में आगे सन्नादी के त्रिकोणीय या गोलाकार समूहों को मॉडल करने के लिए किया जा सकता है। All1 या ओड1 तरंग रूप को कई आरइएस 1 (या आरइएस 2) तरंग रूपों के साथ संयोजित करना (और उनके आयामों को समायोजित करना) किसी उपकरण या ध्वनि के सन्नादी वर्णक्रम को मॉडल कर सकता है।<ref name="zollinger2016">{{Cite web|url=http://javelinart.com/FM_Synthesis_of_Real_Instruments.pdf |archive-url=https://web.archive.org/web/20170925230705/http://javelinart.com/FM_Synthesis_of_Real_Instruments.pdf |archive-date=2017-09-25 |url-status=live|title=FM_Synthesis_of_Real_Instruments|last=Zollinger|first=W. Thor|date=Dec 2017}}</ref> | |||
== वर्णक्रमीय विश्लेषण == | == वर्णक्रमीय विश्लेषण == | ||
एफएम संश्लेषण के कई रूप हैं, जिनमें | एफएम संश्लेषण के कई रूप हैं, जिनमें सम्मिलित हैं: | ||
*विभिन्न | *विभिन्न संचालक व्यवस्थाएं (यामाहा शब्दावली में एफएम एल्गोरिदम के रूप में जानी जाती हैं) | ||
**2 | **2 संचालक | ||
**सीरियल एफएम (एकाधिक चरण) | **सीरियल एफएम (एकाधिक चरण) | ||
**समानांतर एफएम (एकाधिक मॉड्यूलेटर, एकाधिक-वाहक), | **समानांतर एफएम (एकाधिक मॉड्यूलेटर, एकाधिक-वाहक), | ||
**उनका मिश्रण | **उनका मिश्रण | ||
* | *संचालक की विभिन्न तरंगें | ||
** | **ज्यावक्रीय तरंगरूप | ||
**अन्य तरंगरूप | **अन्य तरंगरूप | ||
*अतिरिक्त मॉड्यूलेशन | *अतिरिक्त मॉड्यूलेशन | ||
**रैखिक एफएम | **रैखिक एफएम | ||
** | **चरघातांकी एफएम (समधर्मी संश्लेषण के सीवी/अक्टूबर इंटरफ़ेस के लिए प्रति-लघुगणक रूपांतरण से पहले) | ||
**एफएम के साथ [[थरथरानवाला सिंक]] | **एफएम के साथ [[थरथरानवाला सिंक]] | ||
इत्यादि | |||
इन विविधताओं के मूल के रूप में, हम निम्नलिखित पर 2 | इन विविधताओं के मूल के रूप में, हम निम्नलिखित पर 2 संचालक (दो ज्यावक्रीय संचालक का उपयोग करके रैखिक एफएम संश्लेषण) के वर्णक्रम का विश्लेषण करते हैं। | ||
=== 2 | === 2 संचालक === | ||
एक मॉड्यूलेटर के साथ एफएम संश्लेषण द्वारा उत्पन्न | एक मॉड्यूलेटर के साथ एफएम संश्लेषण द्वारा उत्पन्न वर्णक्रम निम्नानुसार व्यक्त किया गया है:<ref>{{harvnb|Chowning|1973|pp=1–2}}</ref><ref> | ||
{{cite web | {{cite web | ||
| last = Doering | first = Ed | | last = Doering | first = Ed | ||
| Line 112: | Line 111: | ||
| access-date = 2013-04-11 | | access-date = 2013-04-11 | ||
}}</ref> | }}</ref> | ||
मॉड्यूलेशन | |||
मॉड्यूलेशन संकेत के लिए <math>m(t) = B\,\sin(\omega_m t)\,</math>, वाहक संकेत है:<ref group="note">Note that modulation signal <math>m(t)</math> as [[instantaneous frequency]] is converted to the [[phase (waves)|phase]] of carrier signal <math>FM(t)</math>, by time integral between <math>[0, t]</math>.</ref> | |||
:<math>\begin{align} | :<math>\begin{align} | ||
FM(t) & \ =\ A\,\sin\left(\,\int_0^t \left(\omega_c + B\,\sin(\omega_m\,\tau)\right)d\tau\right) \\ | FM(t) & \ =\ A\,\sin\left(\,\int_0^t \left(\omega_c + B\,\sin(\omega_m\,\tau)\right)d\tau\right) \\ | ||
| Line 118: | Line 118: | ||
& \ =\ A\,\sin\left(\omega_c\,t + \frac{B}{\omega_m}\left(\sin(\omega_m\,t - \pi/2) + 1\right)\right) \\ | & \ =\ A\,\sin\left(\omega_c\,t + \frac{B}{\omega_m}\left(\sin(\omega_m\,t - \pi/2) + 1\right)\right) \\ | ||
\end{align}</math> | \end{align}</math> | ||
यदि | यदि हम वाहक <math>\phi_c = B/\omega_m\,</math> और मॉड्यूलेटर <math>\phi_m = - \pi/2\,</math> पर स्थिर चरण प्रतिबन्धों को अनदेखा कर दें, तो अंततः हमें निम्नलिखित अभिव्यक्ति मिलेगी, जैसा कि {{harvnb|चाउनिंग|1973}} और {{harvnb|रोअड्स|1996|p=[https://books.google.com/books?id=nZ-TetwzVcIC&&pg=PA232 232]}}: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
FM(t) & \ \approx\ A\,\sin\left(\omega_c\,t + \beta\,\sin(\omega_m\,t)\right) \\ | FM(t) & \ \approx\ A\,\sin\left(\omega_c\,t + \beta\,\sin(\omega_m\,t)\right) \\ | ||
| Line 125: | Line 125: | ||
& \ =\ A\sum_{n=-\infty}^{\infty} J_n(\beta)\,\sin((\omega_c+n\,\omega_m)\,t) | & \ =\ A\sum_{n=-\infty}^{\infty} J_n(\beta)\,\sin((\omega_c+n\,\omega_m)\,t) | ||
\end{align}</math> | \end{align}</math> | ||
है, जहाँ <math>\omega_c\,,\,\omega_m\,</math> वाहक और मॉड्यूलेटर की [[कोणीय आवृत्ति|कोणीय आवृत्तियां]] (<math>\,\omega = 2\pi f\,</math>) हैं, आवृत्ति मॉड्यूलेशन मॉड्यूलेशन सूचकांक है, और आयाम <math>\beta = B / \omega_m\,</math> <math>J_n(\beta)\,</math> क्रमशः पहले जैसे का <math>n\,</math>-वां बेसेल फलन है।<ref group="note">The above expression is transformed using [[List of trigonometric identities#Angle sum and difference identities|trigonometric addition formulas]] | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\sin(x \pm y) &= \sin x \cos y \pm \cos x \sin y | \sin(x \pm y) &= \sin x \cos y \pm \cos x \sin y | ||
| Line 152: | Line 152: | ||
& \ =\ \sum_{n=-\infty}^{\infty} J_n(\beta)\,\sin(\theta_c + n\theta_m)\qquad(\because\ J_{-n}(x) = (-1)^n J_{n}(x)) | & \ =\ \sum_{n=-\infty}^{\infty} J_n(\beta)\,\sin(\theta_c + n\theta_m)\qquad(\because\ J_{-n}(x) = (-1)^n J_{n}(x)) | ||
\end{align}</math></ref> | \end{align}</math></ref> | ||
==यह भी देखें== | ==यह भी देखें== | ||
*योगात्मक संश्लेषण | *योगात्मक संश्लेषण | ||
*[[ चिप धुन ]] | *[[ चिप धुन |चिपट्यून]] | ||
*डिजिटल | *डिजिटल संश्लेषण | ||
*[[इलेक्ट्रॉनिक संगीत]] | *[[इलेक्ट्रॉनिक संगीत]] | ||
*[[अच्छा पत्रक]] | *[[अच्छा पत्रक|साउंड कार्ड]] | ||
*[[ध्वनि चिप]] | *[[ध्वनि चिप]] | ||
*[[वीडियो गेम संगीत]] | *[[वीडियो गेम संगीत]] | ||
==संदर्भ== | ==संदर्भ== | ||
=== फ़ुटनोट === | === फ़ुटनोट === | ||
{{reflist|group=note}} | {{reflist|group=note}} | ||
| Line 173: | Line 167: | ||
===उद्धरण=== | ===उद्धरण=== | ||
{{reflist}} | {{reflist}} | ||
===ग्रन्थसूची=== | ===ग्रन्थसूची=== | ||
| Line 211: | Line 204: | ||
}} | }} | ||
{{div col end}} | {{div col end}} | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
| Line 219: | Line 211: | ||
* [http://www.soundonsound.com/sos/may00/articles/synth.htm Synth Secrets, Part 13: More On Frequency Modulation], by Gordon Reid | * [http://www.soundonsound.com/sos/may00/articles/synth.htm Synth Secrets, Part 13: More On Frequency Modulation], by Gordon Reid | ||
* [http://www.soundonsound.com/sos/1997_articles/sep97/synthschool3.html Paul Wiffens Synth School: Part 3] | * [http://www.soundonsound.com/sos/1997_articles/sep97/synthschool3.html Paul Wiffens Synth School: Part 3] | ||
* [http://yala.freeservers.com/2fmsynth.htm#2Mod F.M. Synthesis including | * [http://yala.freeservers.com/2fmsynth.htm#2Mod F.M. Synthesis including compleएक्स operator analysis] [http://sites.google.com/view/yala-music1/fm-synthesis mirror site of F.M. Synthesis, 2019] | ||
{{Sound synthesis types}} | {{Sound synthesis types}} | ||
[[Category: | [[Category:CS1 English-language sources (en)]] | ||
[[Category:CS1 maint]] | |||
[[Category:Citation Style 1 templates|M]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 25/07/2023]] | [[Category:Created On 25/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates based on the Citation/CS1 Lua module]] | |||
[[Category:Templates generating COinS|Cite magazine]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:ध्वनि संश्लेषण के प्रकार]] | |||
Latest revision as of 11:20, 14 August 2023
| एक 220 हर्ट्ज वाहक टोन एफसी,आवृति मॉड्यूलेशन इंडेक्स,β के विभिन्न विकल्पों के साथ, 440 हर्ट्ज मॉड्यूलेटिंग टोन एफएम द्वारा मॉड्यूलेटेड है। समय डोमेन संकेत ऊपर चित्रित किए गए हैं, और संबंधित स्पेक्ट्रा नीचे दिखाए गए हैं (डीबी में वर्णक्रम आयाम).। |
|
|
आवृत्ति मॉड्यूलेशन संश्लेषण (या एफएम संश्लेषण) ध्वनि संश्लेषण का एक ऐसा रूप है जिसके अनुसार एक मॉड्यूलर के साथ इसकी आवृत्ति को मॉड्यूलेट करके तरंग की आवृत्ति को परिवर्तित कर दिया जाता है। एक दोलक की (तात्कालिक) आवृत्ति को मॉड्यूलेटिंग संकेत के आयाम के अनुसार परिवर्तित कर दिया जाता है।[1]
एफएम संश्लेषण संनादी और असंनादी दोनों ध्वनियाँ बना सकता है। संनादी ध्वनियों को संश्लेषित करने के लिए, मॉड्यूलेटिंग संकेत का मूल वाहक संकेत के साथ संनादी संबंध होना चाहिए। जैसे-जैसे आवृत्ति मॉड्यूलेशन की मात्रा बढ़ती है, ध्वनि उत्तरोत्तर जटिल होती जाती है। वाहक संकेत (अर्थात असंनादी) के गैर-पूर्णांक गुणकों वाली आवृत्तियों वाले मॉड्यूलेटर के उपयोग के माध्यम से, असंनादी घंटी-जैसे और परिताड़न स्पेक्ट्रा बनाया जा सकता है।
अनुप्रयोग
समधर्मी दोलक का उपयोग करके एफएम संश्लेषण के परिणामस्वरूप तारत्व अस्थिरता हो सकती है।[2] यद्यपि, एफएम संश्लेषण को डिजिटल रूप से भी प्रयुक्त किया जा सकता है, जो अधिक स्थिर है और मानक अभ्यास बन गया है। डिजिटल एफएम संश्लेषण (तात्कालिक आवृत्ति के समय एकीकरण का उपयोग करके चरण मॉड्यूलेशन के बराबर) 1974 की प्रारंभ में कई संगीत वाद्ययंत्रों का आधार था। 1980 में यामाहा जीएस-1 को व्यावसायिक रूप से जारी करने से पहले, यामाहा ने एफएम संश्लेषण पर आधारित पहला प्रोटोटाइप डिजिटल संश्लेषण[3] 1974 में बनाया था।[4] 1978 में न्यू इंग्लैंड डिजिटल कॉर्पोरेशन द्वारा निर्मित सिंक्लेवियर में एक डिजिटल एफएम संश्लेषण सम्मिलित था, जो यामाहा से लाइसेंस प्राप्त एफएम संश्लेषण कलन विधि का उपयोग करता था।[5] 1983 में जारी यामाहा के अभूतपूर्व डीएक्स7 संश्लेषण ने 1980 के दशक के मध्य में एफएम को संश्लेषण के क्षेत्र में सबसे आगे ला दिया।
मनोरंजन का उपयोग: पीसी, आर्केड, गेम कंसोल और मोबाइल फोन पर एफएम ध्वनि क्लिप
नब्बे के दशक के मध्य तक एफएम संश्लेषण भी गेम और सॉफ्टवेयर के लिए सामान्य सेटिंग बन गयी। आईबीएम पीसी संगत प्रणाली के लिए, एडलिब और ध्वनि स्फोटकर्ता जैसे साउंड कार्ड ने यामाहा कॉर्पोरेशन ओपीएल2 और ओपीएल3 जैसे यामाहा चिप को लोकप्रिय बनाया। अन्य कंप्यूटर जैसे शार्प एक्स68000 और एमSएक्स (यामाहा सीएक्स5एम) यामाहा वाईएम2151 साउंड चिप का उपयोग करते हैं (जो सामान्यतः नब्बे के दशक के मध्य तक आर्केड मशीनों के लिए भी उपयोग किया जाता था), और एनइसी पीसी -88 और पीसी -98 कंप्यूटर यामाहा वाईएम2203 और ओपीएनए का उपयोग करते हैं। आर्केड प्रणाली और गेम कंसोल के लिए, ओपीएनबी का उपयोग टैटो के आर्केड बोर्डों में मुख्य मूलभूत ध्वनि जनित्र बोर्ड के रूप में किया गया था और विशेष रूप से एसएनके के नियो जियो आर्केड (एमवीएस) और होम कंसोल (एईएस) मशीनों में उपयोग किया गया था। ओपीएनबी के एक संस्करण का उपयोग प्रणाली से टैटो में किया गया था। संबंधित ओपीएन2 का उपयोग सेगा मेगा ड्राइव (जेनेसिस) और द्रोह के एफएम टाउन्स मार्टी में इसके ध्वनि जनित्र चिप में से एक के रूप में किया गया था। 2000 के दशक के समय, एफएम संश्लेषण का उपयोग रिंगटोन और अन्य ध्वनियों को चलाने के लिए फोन की एक विस्तृत श्रृंखला पर भी किया गया था, सामान्यतः एसएमएएफ प्रारूप में उपयोग किया गया था।
इतिहास
डॉन बुचला (1960 के दशक के मध्य)
चाउनिंग के पेटेंट से पहले, डॉन बुचला ने 1960 के दशक के मध्य में अपने उपकरणों पर एफएम प्रयुक्त किया था। उनके 158, 258 और 259 दोहरे दोलक मॉड्यूल में एक विशिष्ट एफएम नियंत्रण वोल्टता इनपुट था,[6] और मॉडल 208 (संगीत ईज़ल) में एक मॉड्यूलेशन दोलक दृढ-तारित था जो एफएम के साथ-साथ प्राथमिक दोलक के एएम की अनुमति देता था।[7] इन प्रारंभिक अनुप्रयोगों में समधर्मी दोलक का उपयोग किया गया था, और इस क्षमता का अनुसरण मिनिमोग और एआरपी ओडिसी सहित अन्य मॉड्यूलर संश्लेषण और पोर्टेबल संश्लेषण द्वारा भी किया गया था।
जॉन चाउनिंग (1960 के अंत से 1970 के दशक तक)

20वीं शताब्दी के मध्य तक, ध्वनि प्रसारित करने का एक साधन, आवृति मॉड्यूलेशन (एफएम) को दशकों से समझा जा रहा था और इसका उपयोग रेडियो प्रसारण प्रसारित करने के लिए किया जा रहा था। एफएम संश्लेषण का विकास 1967 में कैलिफोर्निया के स्टैनफोर्ड विश्वविद्यालय में जॉन चाउनिंग द्वारा किया गया था, जो एनालॉग संश्लेषण से भिन्न ध्वनियाँ बनाने की प्रयास कर रहे थे। उनके एल्गोरिदम को 1973 में जापानी कंपनी यामाहा को लाइसेंस दिया गया था।[3] यामाहा (यूएस पेटेंट 4018121 अप्रैल 1977[8] या यूएस पेटेंट 4,018,121) द्वारा व्यावसायीकरण किया गया कार्यान्वयन वस्तुतः चरण मॉड्यूलेशन पर आधारित है,[9] किन्तु परिणाम गणितीय रूप से समकक्ष होते हैं क्योंकि दोनों अनिवार्य रूप से चतुर्भुज आयाम मॉड्यूलेशन का एक विशेष स्थिति है[10]
1970-1980
यामाहा द्वारा विस्तार
यामाहा के इंजीनियरों ने वाणिज्यिक डिजिटल संश्लेषक में उपयोग के लिए चाउनिंग के एल्गोरिदम को अपनाना प्रारम्भ कर दिया, जिसमें आवृत्ति मॉड्यूलेशन के समय एनालॉग सिस्टम में सामान्य रूप से होने वाली विकृति से बचने के लिए "कुंजी मापन" विधि जैसे सुधार सम्मिलित किए गए, यद्यपि यामाहा को अपने एफएम डिजिटल संश्लेषक जारी करने में कई वर्ष लगेंगे।[11] 1970 के दशक में, यामाहा को कंपनी के पूर्व नाम "निप्पॉन गक्की सेइज़ो काबुशिकी कैशा" के अनुसार कई पेटेंट दिए गए, जिससे चाउनिंग का कार्य विकसित हुआ।[9] यामाहा ने 1974 में पहला प्रोटोटाइप एफएम डिजिटल संश्लेषण बनाया।[3] यामाहा ने अंततः 1980 में जारी पहले एफएम डिजिटल संश्लेषण, यामाहा जीएस-1 के साथ एफएम संश्लेषण विधि का व्यावसायीकरण किया।[4]
एफएम संश्लेषण डिजिटल संश्लेषण की कुछ प्रारंभिक पीढ़ियों का आधार था, विशेष रूप से यामाहा से, साथ ही यामाहा से लाइसेंस के अनुसार न्यू इंग्लैंड डिजिटल कॉर्पोरेशन।[5] 1983 में रिलीज़ हुआ यामाहा का डीएक्स7 संश्लेषण, 1980 के दशक में सर्वव्यापी था। यामाहा के कई अन्य मॉडल उस दशक के समय एफएम संश्लेषण की विविधता और विकास प्रदान करते हैं।[12]
यामाहा ने 1970 के दशक में एफएम के अपने हार्डवेयर कार्यान्वयन का पेटेंट कराया था,[9] 1990 के दशक के मध्य तक इसे एफएम प्रौद्योगिकी के बाजार पर लगभग एकाधिकार को जारी रखने की अनुमति दी गई।
कैसियो द्वारा संबंधित विकास
कैसियो ने चरण विरूपण संश्लेषण नामक संश्लेषण का एक संबंधित रूप विकसित किया, जिसका उपयोग इसके कैसियो सीजेड संश्लेषण में किया जाता है। इसमें डीएक्स श्रृंखला के समान (किन्तु थोड़ा अलग विधि से प्राप्त) ध्वनि गुणवत्ता थी।
1990 का दशक
पेटेंट की समाप्ति के बाद लोकप्रियता
1995 में स्टैनफोर्ड यूनिवर्सिटी एफएम पेटेंट की समाप्ति के साथ, डिजिटल एफएम संश्लेषण अब अन्य निर्माताओं द्वारा स्वतंत्र रूप से प्रयुक्त किया जा सकता है। एफएम विश्लेषण पेटेंट ने समाप्त होने से पहले स्टैनफोर्ड को 20 मिलियन डॉलर दिलाए, जिससे यह (1994 में) "स्टैनफोर्ड के इतिहास में दूसरा सबसे आकर्षक लाइसेंसिंग समझौता" बन गया।[13] एफएम आज अधिकतर सॉफ्टवेयर-आधारित सिंथ में पाया जाता है जैसे कि प्राकृतिक उपकरण द्वारा एफएम8 या प्रतिरूप पंक्ति द्वारा अस्पष्ट, किन्तु इसे कुछ आधुनिक डिजिटल संश्लेषण के संश्लेषण भंडार में भी सम्मिलित किया गया है, जो सामान्यतः संश्लेषण के अन्य विधियों के साथ एक विकल्प के रूप में सह-अस्तित्व में है, वियोज्य संश्लेषण, प्रतिदर्श-आधारित विश्लेषण, योगात्मक संश्लेषण और अन्य विधि के साथ विकल्प के रूप में उपयोग किया जाता है। ऐसे हार्डवेयर सिंथ में एफएम की जटिलता की मात्रा साधारण 2-संचालक एफएम से लेकर कोर्ग क्रोनोस और एलेसिस फ्यूजन के अत्यधिक नम्य 6-संचालक इंजन तक, बड़े पैमाने पर मॉड्यूलर इंजन में एफएम के निर्माण तक भिन्न हो सकती है जैसे कि कुर्ज़वील संगीत प्रणाली द्वारा नवीनतम संश्लेषण में उपयोग किया जाता है।
रीयलटाइम संवलन और मॉड्यूलेशन (एएफएम + प्रतिदर्श) और फॉर्मेंट शेपिंग विश्लेषण
यामाहा एसवाई99 और यामाहा एफएस1आर की रिलीज़ के बाद विशेष रूप से उनकी एफएम क्षमताओं के लिए विपणन किए गए नवीन हार्डवेयर सिंथ बाजार से लुप्त हो गए[14][15] और यहां तक कि उन्होंने क्रमशः प्रतिदर्श-आधारित संश्लेषण और फॉर्मेंट संश्लेषण के समकक्षों के रूप में अपनी अत्यधिक शक्तिशाली एफएम क्षमताओं का विपणन किया। यद्यपि, ठीक रूप से विकसित एफएम संश्लेषण विकल्प क्लैविया, एलेसिस फ्यूजन रेंज, कॉर्ग ओएसिस और क्रोनोस और मॉडर एनएफ -1 द्वारा निर्मित नॉर्ड लीड सिंथ की एक विशेषता है। विभिन्न अन्य संश्लेषण अपने मुख्य इंजनों के पूरक के लिए सीमित एफएम क्षमताएँ प्रदान करते हैं।
बहु वर्णक्रम तरंग रूपों के साथ 8 एफएम संचालक के समूह का संयोजन 1999 में यामाहा द्वारा एफएस1आर में प्रारंभिक हुआ। एफएस1आर में 16 संचालक, 8 मानक एफएम संचालक और 8 अतिरिक्त संचालक थे जो ध्वनि स्रोत के रूप में दोलक के अतिरिक्त ध्वनि स्रोत का उपयोग करते थे। ट्यून करने योग्य ध्वनि स्रोतों को जोड़कर एफएस1आर मानव ध्वनि और पवन उपकरण में उत्पन्न ध्वनियों को मॉडल कर सकता है, साथ ही पर्क्यूशन उपकरण ध्वनियां भी बना सकता है। एफएस1आर में एक अतिरिक्त तरंग रूप भी सम्मिलित है जिसे फॉर्मेंट तरंग रूप कहा जाता है। फॉर्मेंट का उपयोग सेलो, वायलिन, ध्वनिक गिटार, बैसून, अंग्रेजी हॉर्न, या मानव ध्वनि जैसे हॉर्न वाले शारीरिक वाद्ययंत्रों की ध्वनियों को मॉडल करने के लिए किया जा सकता है। फॉर्मेंट कई पीतल के उपकरणों के सन्नादी वर्णक्रम में भी पाए जा सकते हैं।[16]
2000-वर्तमान
परिवर्तनीय चरण मॉड्यूलेशन, एफएम-एक्स संश्लेषण, परिवर्तित एफएम, आदि
2016 में, कॉर्ग ने संहत, प्रभावकारी डेस्कटॉप मॉड्यूल की कॉर्ग वोल्का श्रृंखला का एक, 3-वॉयस, 6 संचालक एफएम पुनरावृत्ति, कॉर्ग वोल्का एफएम जारी किया।[17] और यामाहा ने मोंटाज जारी किया, जो 128-वॉयस प्रतिदर्श-आधारित इंजन को 128-वॉयस एफएम इंजन के साथ जोड़ता है। एफएम के इस पुनरावृत्ति को एफएम-एक्स कहा जाता है, और इसमें 8 संचालक सम्मिलित हैं; प्रत्येक संचालक के निकट कई मूलभूत तरंग रूपों का विकल्प होता है, किन्तु प्रत्येक तरंग रूप में उसके वर्णक्रम को समायोजित करने के लिए कई पैरामीटर होते हैं।[18] यामाहा मोंटाज के बाद 2018 में अधिक प्रभावकारी यामाहा एमओडीएक्स आया, जिसमें 128-वॉयस प्रतिदर्श-आधारित इंजन के अतिरिक्त 64-वॉयस, 8 संचालक एफएम-एक्स संरचना था।[19] इलेक्ट्रॉन ने 2018 में डिजिटोन, एक 8-वॉयस, 4 संचालक एफएम सिंथ लॉन्च किया, जिसमें इलेक्ट्रॉन का प्रसिद्ध अनुक्रम इंजन सम्मिलित है।[20]
एफएम-एक्स विश्लेषण को 2016 में यामाहा मोंटेज संश्लेषण के साथ प्रस्तुत किया गया था। एफएम-एक्स 8 संचालक का उपयोग करता है। प्रत्येक एफएम-एक्स संचालक के निकट चुनने के लिए बहु वर्णक्रम तरंग रूपों का एक समूह होता है, जिसका अर्थ है कि प्रत्येक एफएम-एक्स संचालक 3 या 4 डीएक्स7 एफएम संचालक के समावेश के बराबर हो सकता है। चयन योग्य तरंग रूपों की सूची में ज्या तरंगें, All1 और All2 तरंग रूप, ओड1 और ओड2 तरंग रूप, और आरइएस 1 और आरइएस 2 तरंग रूप सम्मिलित हैं। ज्या तरंग चयन डीएक्स7 तरंग रूपों के समान ही कार्य करता है। All1 और All2 तरंग रूप एक सॉ-दंतिका तरंग रूप हैं। ओड1 और ओड 2 तरंग रूप स्पन्द या वर्ग तरंगें हैं। इन दो प्रकार के तरंग रूपों का उपयोग अधिकांश उपकरणों के सन्नादी वर्णक्रम के निचले भाग में मूलभूत सन्नादी शीर्ष को मॉडल करने के लिए किया जा सकता है। आरइएस 1 और आरइएस 2 तरंग रूप वर्णक्रमीय शिखर को एक विशिष्ट सन्नादी तक ले जाते हैं और इसका उपयोग किसी उपकरण के वर्णक्रम में आगे सन्नादी के त्रिकोणीय या गोलाकार समूहों को मॉडल करने के लिए किया जा सकता है। All1 या ओड1 तरंग रूप को कई आरइएस 1 (या आरइएस 2) तरंग रूपों के साथ संयोजित करना (और उनके आयामों को समायोजित करना) किसी उपकरण या ध्वनि के सन्नादी वर्णक्रम को मॉडल कर सकता है।[16]
वर्णक्रमीय विश्लेषण
एफएम संश्लेषण के कई रूप हैं, जिनमें सम्मिलित हैं:
- विभिन्न संचालक व्यवस्थाएं (यामाहा शब्दावली में एफएम एल्गोरिदम के रूप में जानी जाती हैं)
- 2 संचालक
- सीरियल एफएम (एकाधिक चरण)
- समानांतर एफएम (एकाधिक मॉड्यूलेटर, एकाधिक-वाहक),
- उनका मिश्रण
- संचालक की विभिन्न तरंगें
- ज्यावक्रीय तरंगरूप
- अन्य तरंगरूप
- अतिरिक्त मॉड्यूलेशन
- रैखिक एफएम
- चरघातांकी एफएम (समधर्मी संश्लेषण के सीवी/अक्टूबर इंटरफ़ेस के लिए प्रति-लघुगणक रूपांतरण से पहले)
- एफएम के साथ थरथरानवाला सिंक
इत्यादि
इन विविधताओं के मूल के रूप में, हम निम्नलिखित पर 2 संचालक (दो ज्यावक्रीय संचालक का उपयोग करके रैखिक एफएम संश्लेषण) के वर्णक्रम का विश्लेषण करते हैं।
2 संचालक
एक मॉड्यूलेटर के साथ एफएम संश्लेषण द्वारा उत्पन्न वर्णक्रम निम्नानुसार व्यक्त किया गया है:[21][22]
मॉड्यूलेशन संकेत के लिए , वाहक संकेत है:[note 1]
यदि हम वाहक और मॉड्यूलेटर पर स्थिर चरण प्रतिबन्धों को अनदेखा कर दें, तो अंततः हमें निम्नलिखित अभिव्यक्ति मिलेगी, जैसा कि चाउनिंग 1973 और रोअड्स 1996, p. 232:
है, जहाँ वाहक और मॉड्यूलेटर की कोणीय आवृत्तियां () हैं, आवृत्ति मॉड्यूलेशन मॉड्यूलेशन सूचकांक है, और आयाम क्रमशः पहले जैसे का -वां बेसेल फलन है।[note 2]
यह भी देखें
- योगात्मक संश्लेषण
- चिपट्यून
- डिजिटल संश्लेषण
- इलेक्ट्रॉनिक संगीत
- साउंड कार्ड
- ध्वनि चिप
- वीडियो गेम संगीत
संदर्भ
फ़ुटनोट
- ↑ Note that modulation signal as instantaneous frequency is converted to the phase of carrier signal , by time integral between .
- ↑ The above expression is transformed using trigonometric addition formulas
- (Source: Kreh 2012)
उद्धरण
- ↑ Dodge & Jerse 1997, p. 115
- ↑ McGuire, Sam; Matějů, Zbyněk (2020-12-28). डिजिटल आर्केस्ट्रा की कला (in English). CRC Press. ISBN 978-1-000-28699-1.
- ↑ 3.0 3.1 3.2 "[Chapter 2] FM Tone Generators and the Dawn of Home Music Production". Yamaha Synth 40th Anniversary - History. Yamaha Corporation. 2014. Archived from the original on 2017-05-11.
- ↑ 4.0 4.1 Curtis Roads (1996). कंप्यूटर संगीत ट्यूटोरियल. MIT Press. p. 226. ISBN 0-262-68082-3. Retrieved 2011-06-05.
- ↑ 5.0 5.1 "1978 New England Digital Synclavier". Mix. Penton Media. September 1, 2006.
- ↑
Dr. Hubert Howe (1960s). Buchla Electronic Music System: Users Manual written for CBS Musical Instruments (Buchla 100 Owner's Manual). Educational Research Department, CBS Musical Instruments, Columbia Broadcasting System. p. 7.
At this point we may consider various additional signal modifications that we may wish to make to the series of tones produced by the above example. For instance, if we would like to add frequency modulation to the tones, it is necessary to patch another audio signal into the jack connected by a line to the middle dial on the Model 158 Dual Sine-Sawtooth Oscillator. ...
- ↑ Atten Strange (1974). Programming and Metaprogramming in the Electro-Organism - An Operating Directive for the Music Easel. Buchla and Associates.
- ↑ "U.S. Patent 4018121 Apr 1977". patft.uspto.gov. Retrieved 2017-04-30.
- ↑ 9.0 9.1 9.2 "Patent US4018121 - Method of synthesizing a musical sound - Google Patents". Retrieved 2017-04-30.
- ↑ Rob Hordijk. "FM synthesis on Modular". Nord Modular & Micro Modular V3.03 tips & tricks. Clavia DMI AB. Archived from the original on 2007-04-07. Retrieved 2013-03-23.
- ↑ Holmes, Thom (2008). "Early Computer Music". इलेक्ट्रॉनिक और प्रायोगिक संगीत: प्रौद्योगिकी, संगीत और संस्कृति (3rd ed.). Taylor & Francis. pp. 257–8. ISBN 978-0-415-95781-6. Retrieved 2011-06-04.
- ↑ Gordon Reid (September 2001). "Sounds of the '80s Part 2: The Yamaha DX1 & Its Successors (Retro)". Sound on Sound. Archived from the original on 17 September 2011. Retrieved 2011-06-29.
- ↑ Stanford University News Service (06/07/94), Music synthesis approaches sound quality of real instruments
- ↑ "Yamaha SY99 spec". Yamaha Corporation (in Japanese).
{{cite web}}: CS1 maint: unrecognized language (link) - ↑ Poyser, Debbie; Johnson, Derek (1998). "Yamaha FS1R - FM Synthesis / Formant-shaping Tone Generator". Sound on Sound. No. December 1998.
- ↑ 16.0 16.1 Zollinger, W. Thor (Dec 2017). "FM_Synthesis_of_Real_Instruments" (PDF). Archived (PDF) from the original on 2017-09-25.
- ↑ Volca FM product page
- ↑ Yamaha Montage Product Features Page
- ↑ Yamaha MODX Product Features Page
- ↑ Digitone product page
- ↑ Chowning 1973, pp. 1–2
- ↑ Doering, Ed. "Frequency Modulation Mathematics". Retrieved 2013-04-11.
ग्रन्थसूची
- Chowning, J. (1973). "The Synthesis of Complex Audio Spectra by Means of Frequency Modulation" (PDF). Journal of the Audio Engineering Society. 21 (7).
- Chowning, John; Bristow, David (1986). FM Theory & Applications - By Musicians For Musicians. Tokyo: Yamaha. ISBN 4-636-17482-8.
- Dodge, Charles; Jerse, Thomas A. (1997). Computer Music: Synthesis, Composition and Performance. New York: Schirmer Books. ISBN 0-02-864682-7.
- Kreh, Martin (2012), "Bessel Functions" (PDF), The Pennsylvania State University, pp. 5–6, archived from the original (PDF) on 2017-11-18, retrieved 2014-08-22
- Roads, Curtis (1996). The Computer Music Tutorial. MIT Press. ISBN 978-0-262-68082-0.
बाहरी संबंध
- An Introduction To FM, by Bill Schottstaedt
- FM tutorial
- Synth Secrets, Part 12: An Introduction To Frequency Modulation, by Gordon Reid
- Synth Secrets, Part 13: More On Frequency Modulation, by Gordon Reid
- Paul Wiffens Synth School: Part 3
- F.M. Synthesis including compleएक्स operator analysis mirror site of F.M. Synthesis, 2019