मैली मशीन: Difference between revisions
(Created page with "{{Short description|Machine whose output is determined by its state and inputs}} गणना के सिद्धांत में, मीली मशीन एक प...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Machine whose output is determined by its state and inputs}} | {{Short description|Machine whose output is determined by its state and inputs}} | ||
थ्योरी ऑफ़ कम्प्यूटेशन में, '''मैली मशीन''' एक फाईनाईट-स्टेट मशीन है जिसकी आउटपुट वैल्यू इसकी वर्तमान स्टेट (कंप्यूटर विज्ञान) और वर्तमान इनपुट दोनों द्वारा निर्धारित की जाती है। यह [[मूर मशीन]] के कंट्रास्ट है, जिसका आउटपुट वैल्यू पूरी तरह से इसकी करंट स्टेट से निर्धारित होता है। मेयली मशीन एक डेटर्मीनिस्टिक फाईनाईट-स्टेट ट्रान्सडूसर है: प्रत्येक स्टेट और इनपुट के लिए, अधिकतम एक ट्रांजीशन पॉसिबल है। | |||
==इतिहास== | ==इतिहास== | ||
मीली मशीन का नाम जॉर्ज एच. मीली के नाम पर रखा गया है, जिन्होंने 1955 के पेपर, ए मेथड फॉर सिंथेसाइजिंग सीक्वेंशियल सर्किट्स में इस | मीली मशीन का नाम जॉर्ज एच. मीली के नाम पर रखा गया है, जिन्होंने 1955 के पेपर, ए मेथड फॉर सिंथेसाइजिंग सीक्वेंशियल सर्किट्स में इस कांसेप्ट को प्रेजेंट किया था। <ref>{{cite journal| last=Mealy| first=George H.| title=अनुक्रमिक सर्किट को संश्लेषित करने की एक विधि| journal=Bell System Technical Journal| volume=34| pages=1045–1079|date=September 1955| issue=5| doi=10.1002/j.1538-7305.1955.tb03788.x}}</ref> | ||
==औपचारिक परिभाषा== | ==औपचारिक परिभाषा== | ||
मीली मशीन एक | मीली मशीन एक 6-टुपल <math>(S, S_0, \Sigma, \Lambda, T, G)</math> है निम्नलिखित से मिलकर: | ||
* | * स्टेट का एक फाईनाईट सेट (कंप्यूटर विज्ञान) <math>S</math> | ||
* एक | * एक स्टार्ट स्टेट (जिसे आरंभिक अवस्था भी कहा जाता है) <math>S_0</math> जो कि एक एलिमेंट <math>S</math> है | ||
* एक | * एक फाईनाईट सेट जिसे इनपुट [[वर्णमाला (कंप्यूटर विज्ञान)|अल्फाबेट (कंप्यूटर विज्ञान)]] <math>\Sigma</math> कहा जाता है | ||
* एक | * एक फाईनाईट सेट जिसे आउटपुट अल्फाबेट <math>\Lambda</math> (कंप्यूटर विज्ञान) कहा जाता है | ||
* एक | * एक ट्रांजीशन फंक्शन (गणित) <math>T : S \times \Sigma \rightarrow S</math> एक स्टेट के पेअर और एक इनपुट सिंबल को करेस्पोंडिंग अगले स्टेट में मैप करना। | ||
* एक आउटपुट फ़ंक्शन <math>G : S \times \Sigma \rightarrow \Lambda</math> एक | * एक आउटपुट फ़ंक्शन <math>G : S \times \Sigma \rightarrow \Lambda</math> एक स्टेट और एक इनपुट सिंबल के पेअर को करेस्पोंडिंग आउटपुट सिंबल में मैप करना। | ||
कुछ फॉर्मूलेशन में, | कुछ फॉर्मूलेशन में, ट्रांजीशन और आउटपुट फ़ंक्शन को एक ही फ़ंक्शन में संयोजित किया जाता है <math>T : S \times \Sigma \rightarrow S \times \Lambda</math>। | ||
==मीली मशीनों और मूर मशीनों की तुलना== | ==मीली मशीनों और मूर मशीनों की तुलना== | ||
# मीली मशीनों में कम | # मीली मशीनों में कम स्टेट होती हैं: | ||
#* आर्क्स पर अलग-अलग आउटपुट (n<sup>2</sup>) | #* आर्क्स पर अलग-अलग आउटपुट (n<sup>2</sup>) स्टेटों के स्थान पर (एन)। | ||
# मूर मशीनों का उपयोग करना अधिक सुरक्षित है: | # मूर मशीनों का उपयोग करना अधिक सुरक्षित है: | ||
#* आउटपुट | #* आउटपुट क्लॉक एज पर बदलते हैं (हमेशा एक चक्र बाद में)। | ||
#* मेयली मशीनों में, इनपुट | #* मेयली मशीनों में, इनपुट चेंज के कारण लॉजिक होते ही आउटपुट में बदलाव हो सकता है - जब दो मशीनें आपस में जुड़ी होती हैं तो एक बड़ी समस्या होती है - यदि कोई सावधान नहीं है तो एसिंक्रोनस फीडबैक हो सकता है। | ||
# मीली मशीनें इनपुट पर तेजी से प्रतिक्रिया करती हैं: | # मीली मशीनें इनपुट पर तेजी से प्रतिक्रिया करती हैं: | ||
#* एक ही चक्र में प्रतिक्रिया करें—उन्हें घड़ी का इंतज़ार करने की ज़रूरत नहीं है। | #* एक ही चक्र में प्रतिक्रिया करें—उन्हें घड़ी का इंतज़ार करने की ज़रूरत नहीं है। | ||
#* मूर मशीनों में, स्थिति को आउटपुट में डिकोड करने के लिए अधिक | #* मूर मशीनों में, स्थिति को आउटपुट में डिकोड करने के लिए अधिक लॉजिक की आवश्यकता हो सकती है - क्लॉक एज के बाद अधिक गेट विलंब। | ||
==आरेख== | ==आरेख== | ||
मीली मशीन के लिए [[राज्य आरेख]] प्रत्येक | '''मीली मशीन के लिए''' [[राज्य आरेख|स्टेट आरेख]] प्रत्येक ट्रांजीशन किनारे के साथ एक आउटपुट वैल्यू को जोड़ता है, मूर मशीन के लिए स्टेट आरेख के विपरीत, जो प्रत्येक स्टेट के साथ एक आउटपुट वैल्यू को जोड़ता है। | ||
जब इनपुट और आउटपुट अल्फाबेट दोनों हों {{math|Σ}}, कोई माइली ऑटोमेटा से हेलिक्स [[निर्देशित ग्राफ]] भी जोड़ सकता है | जब इनपुट और आउटपुट अल्फाबेट दोनों हों {{math|Σ}}, कोई माइली ऑटोमेटा से हेलिक्स [[निर्देशित ग्राफ]] भी जोड़ सकता है {{math|(''S'' × Σ, (''x'', ''i'') → (''T''(''x'', ''i''), ''G''(''x'', ''i'')))}}.<ref>Akhavi et al (2012)</ref> इस ग्राफ़ में शीर्षों के रूप में स्टेट और अक्षरों के पेअर हैं, प्रत्येक नोड आउट-डिग्री एक का है, और का उत्तराधिकारी है {{math|(''x'', ''i'')}} ऑटोमेटा की अगली स्थिति है और वह अक्षर है जो ऑटोमेटा आउटपुट होता है जब यह स्थापित होता है {{math|''x''}} और यह पत्र पढ़ता है {{math|''i''}}. यदि ऑटोमेटन द्विप्रतिवर्ती है तो यह ग्राफ असंयुक्त चक्रों का एक संघ है{{definition needed|date=September 2018}}. | ||
==उदाहरण== | ==उदाहरण== | ||
===सरल === | ===सरल === | ||
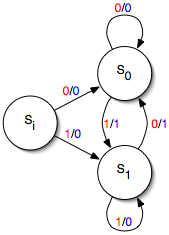
[[File:Mealy.png|thumb|169px|एक इनपुट और एक आउटपुट वाली एक साधारण मीली मशीन का आरेख बताएं। (प्रत्येक इनपुट मान के लिए आउटपुट 1, यदि वर्तमान इनपुट मान पिछले से भिन्न है, या अन्यथा 0।)]]एक साधारण मीली मशीन में एक इनपुट और एक आउटपुट होता है। प्रत्येक | [[File:Mealy.png|thumb|169px|एक इनपुट और एक आउटपुट वाली एक साधारण मीली मशीन का आरेख बताएं। (प्रत्येक इनपुट मान के लिए आउटपुट 1, यदि वर्तमान इनपुट मान पिछले से भिन्न है, या अन्यथा 0।)]]एक साधारण मीली मशीन में एक इनपुट और एक आउटपुट होता है। प्रत्येक ट्रांजीशन किनारे को इनपुट के मूल्य (लाल रंग में दिखाया गया है) और आउटपुट के मूल्य (नीले रंग में दिखाया गया है) के साथ लेबल किया गया है। मशीन स्टेट में शुरू होती है {{math|''S''<sub>i</sub>}}. (इस उदाहरण में, आउटपुट दो सबसे हाल के इनपुट मानों का अनन्य या | अनन्य-या है; इस प्रकार, मशीन एक एज डिटेक्टर लागू करती है, हर बार इनपुट फ्लिप होने पर 1 और अन्यथा 0 आउटपुट करती है।) | ||
=== जटिल === | === जटिल === | ||
| Line 41: | Line 41: | ||
==अनुप्रयोग== | ==अनुप्रयोग== | ||
मीली मशीनें सिफर मशीनों के लिए एक प्रारंभिक गणितीय मॉडल प्रदान करती हैं। उदाहरण के लिए, [[लैटिन वर्णमाला]] के इनपुट और आउटपुट | मीली मशीनें सिफर मशीनों के लिए एक प्रारंभिक गणितीय मॉडल प्रदान करती हैं। उदाहरण के लिए, [[लैटिन वर्णमाला|लैटिन अल्फाबेट]] के इनपुट और आउटपुट अल्फाबेट को ध्यान में रखते हुए, एक मेयली मशीन डिज़ाइन की जा सकती है जो अक्षरों की एक स्ट्रिंग (इनपुट का एक अनुक्रम) को एक सिफर स्ट्रिंग (आउटपुट का एक अनुक्रम) में संसाधित कर सकती है। हालाँकि, हालांकि [[ पहेली मशीन ]] का वर्णन करने के लिए मीली मॉडल का उपयोग किया जा सकता है, जटिल सिफरिंग मशीनों को डिजाइन करने के व्यवहार्य साधन प्रदान करने के लिए स्टेट आरेख बहुत जटिल होगा। | ||
मूर/मीली मशीनें [[नियतात्मक परिमित ऑटोमेटन]] हैं जिनका घड़ी की किसी भी टिक पर भी आउटपुट होता है। आधुनिक सीपीयू, कंप्यूटर, सेल फोन, डिजिटल घड़ियां और बुनियादी इलेक्ट्रॉनिक उपकरणों/मशीनों में इसे नियंत्रित करने के लिए कुछ प्रकार की परिमित | मूर/मीली मशीनें [[नियतात्मक परिमित ऑटोमेटन]] हैं जिनका घड़ी की किसी भी टिक पर भी आउटपुट होता है। आधुनिक सीपीयू, कंप्यूटर, सेल फोन, डिजिटल घड़ियां और बुनियादी इलेक्ट्रॉनिक उपकरणों/मशीनों में इसे नियंत्रित करने के लिए कुछ प्रकार की परिमित स्टेट मशीन होती है। | ||
सरल सॉफ़्टवेयर सिस्टम, विशेष रूप से वे जिन्हें [[नियमित अभिव्यक्ति]]यों का उपयोग करके दर्शाया जा सकता है, को परिमित | सरल सॉफ़्टवेयर सिस्टम, विशेष रूप से वे जिन्हें [[नियमित अभिव्यक्ति]]यों का उपयोग करके दर्शाया जा सकता है, को परिमित स्टेट मशीनों के रूप में मॉडल किया जा सकता है। ऐसी कई सरल प्रणालियाँ हैं, जैसे वेंडिंग मशीन या बुनियादी इलेक्ट्रॉनिक्स। | ||
दो परिमित | दो परिमित स्टेट मशीनों के प्रतिच्छेदन का पता लगाकर, कोई बहुत ही सरल तरीके से समवर्ती प्रणालियों को डिज़ाइन कर सकता है जो उदाहरण के लिए संदेशों का आदान-प्रदान करते हैं। उदाहरण के लिए, ट्रैफ़िक लाइट एक ऐसी प्रणाली है जिसमें कई उपप्रणालियाँ शामिल होती हैं, जैसे कि विभिन्न ट्रैफ़िक लाइटें, जो एक साथ काम करती हैं। | ||
अनुप्रयोगों के कुछ उदाहरण: | अनुप्रयोगों के कुछ उदाहरण: | ||
| Line 60: | Line 60: | ||
* [[सिंक्रोनस सर्किट]] | * [[सिंक्रोनस सर्किट]] | ||
* मूर मशीन | * मूर मशीन | ||
* [[एल्गोरिथम राज्य मशीन]] | * [[एल्गोरिथम राज्य मशीन|एल्गोरिथम स्टेट मशीन]] | ||
* [[रिचर्ड्स नियंत्रक]] | * [[रिचर्ड्स नियंत्रक]] | ||
Revision as of 03:25, 2 August 2023
थ्योरी ऑफ़ कम्प्यूटेशन में, मैली मशीन एक फाईनाईट-स्टेट मशीन है जिसकी आउटपुट वैल्यू इसकी वर्तमान स्टेट (कंप्यूटर विज्ञान) और वर्तमान इनपुट दोनों द्वारा निर्धारित की जाती है। यह मूर मशीन के कंट्रास्ट है, जिसका आउटपुट वैल्यू पूरी तरह से इसकी करंट स्टेट से निर्धारित होता है। मेयली मशीन एक डेटर्मीनिस्टिक फाईनाईट-स्टेट ट्रान्सडूसर है: प्रत्येक स्टेट और इनपुट के लिए, अधिकतम एक ट्रांजीशन पॉसिबल है।
इतिहास
मीली मशीन का नाम जॉर्ज एच. मीली के नाम पर रखा गया है, जिन्होंने 1955 के पेपर, ए मेथड फॉर सिंथेसाइजिंग सीक्वेंशियल सर्किट्स में इस कांसेप्ट को प्रेजेंट किया था। [1]
औपचारिक परिभाषा
मीली मशीन एक 6-टुपल है निम्नलिखित से मिलकर:
- स्टेट का एक फाईनाईट सेट (कंप्यूटर विज्ञान)
- एक स्टार्ट स्टेट (जिसे आरंभिक अवस्था भी कहा जाता है) जो कि एक एलिमेंट है
- एक फाईनाईट सेट जिसे इनपुट अल्फाबेट (कंप्यूटर विज्ञान) कहा जाता है
- एक फाईनाईट सेट जिसे आउटपुट अल्फाबेट (कंप्यूटर विज्ञान) कहा जाता है
- एक ट्रांजीशन फंक्शन (गणित) एक स्टेट के पेअर और एक इनपुट सिंबल को करेस्पोंडिंग अगले स्टेट में मैप करना।
- एक आउटपुट फ़ंक्शन एक स्टेट और एक इनपुट सिंबल के पेअर को करेस्पोंडिंग आउटपुट सिंबल में मैप करना।
कुछ फॉर्मूलेशन में, ट्रांजीशन और आउटपुट फ़ंक्शन को एक ही फ़ंक्शन में संयोजित किया जाता है ।
मीली मशीनों और मूर मशीनों की तुलना
- मीली मशीनों में कम स्टेट होती हैं:
- आर्क्स पर अलग-अलग आउटपुट (n2) स्टेटों के स्थान पर (एन)।
- मूर मशीनों का उपयोग करना अधिक सुरक्षित है:
- आउटपुट क्लॉक एज पर बदलते हैं (हमेशा एक चक्र बाद में)।
- मेयली मशीनों में, इनपुट चेंज के कारण लॉजिक होते ही आउटपुट में बदलाव हो सकता है - जब दो मशीनें आपस में जुड़ी होती हैं तो एक बड़ी समस्या होती है - यदि कोई सावधान नहीं है तो एसिंक्रोनस फीडबैक हो सकता है।
- मीली मशीनें इनपुट पर तेजी से प्रतिक्रिया करती हैं:
- एक ही चक्र में प्रतिक्रिया करें—उन्हें घड़ी का इंतज़ार करने की ज़रूरत नहीं है।
- मूर मशीनों में, स्थिति को आउटपुट में डिकोड करने के लिए अधिक लॉजिक की आवश्यकता हो सकती है - क्लॉक एज के बाद अधिक गेट विलंब।
आरेख
मीली मशीन के लिए स्टेट आरेख प्रत्येक ट्रांजीशन किनारे के साथ एक आउटपुट वैल्यू को जोड़ता है, मूर मशीन के लिए स्टेट आरेख के विपरीत, जो प्रत्येक स्टेट के साथ एक आउटपुट वैल्यू को जोड़ता है।
जब इनपुट और आउटपुट अल्फाबेट दोनों हों Σ, कोई माइली ऑटोमेटा से हेलिक्स निर्देशित ग्राफ भी जोड़ सकता है (S × Σ, (x, i) → (T(x, i), G(x, i))).[2] इस ग्राफ़ में शीर्षों के रूप में स्टेट और अक्षरों के पेअर हैं, प्रत्येक नोड आउट-डिग्री एक का है, और का उत्तराधिकारी है (x, i) ऑटोमेटा की अगली स्थिति है और वह अक्षर है जो ऑटोमेटा आउटपुट होता है जब यह स्थापित होता है x और यह पत्र पढ़ता है i. यदि ऑटोमेटन द्विप्रतिवर्ती है तो यह ग्राफ असंयुक्त चक्रों का एक संघ है[definition needed].
उदाहरण
सरल
एक साधारण मीली मशीन में एक इनपुट और एक आउटपुट होता है। प्रत्येक ट्रांजीशन किनारे को इनपुट के मूल्य (लाल रंग में दिखाया गया है) और आउटपुट के मूल्य (नीले रंग में दिखाया गया है) के साथ लेबल किया गया है। मशीन स्टेट में शुरू होती है Si. (इस उदाहरण में, आउटपुट दो सबसे हाल के इनपुट मानों का अनन्य या | अनन्य-या है; इस प्रकार, मशीन एक एज डिटेक्टर लागू करती है, हर बार इनपुट फ्लिप होने पर 1 और अन्यथा 0 आउटपुट करती है।)
जटिल
अधिक जटिल मीली मशीनों में कई इनपुट के साथ-साथ कई आउटपुट भी हो सकते हैं।
अनुप्रयोग
मीली मशीनें सिफर मशीनों के लिए एक प्रारंभिक गणितीय मॉडल प्रदान करती हैं। उदाहरण के लिए, लैटिन अल्फाबेट के इनपुट और आउटपुट अल्फाबेट को ध्यान में रखते हुए, एक मेयली मशीन डिज़ाइन की जा सकती है जो अक्षरों की एक स्ट्रिंग (इनपुट का एक अनुक्रम) को एक सिफर स्ट्रिंग (आउटपुट का एक अनुक्रम) में संसाधित कर सकती है। हालाँकि, हालांकि पहेली मशीन का वर्णन करने के लिए मीली मॉडल का उपयोग किया जा सकता है, जटिल सिफरिंग मशीनों को डिजाइन करने के व्यवहार्य साधन प्रदान करने के लिए स्टेट आरेख बहुत जटिल होगा।
मूर/मीली मशीनें नियतात्मक परिमित ऑटोमेटन हैं जिनका घड़ी की किसी भी टिक पर भी आउटपुट होता है। आधुनिक सीपीयू, कंप्यूटर, सेल फोन, डिजिटल घड़ियां और बुनियादी इलेक्ट्रॉनिक उपकरणों/मशीनों में इसे नियंत्रित करने के लिए कुछ प्रकार की परिमित स्टेट मशीन होती है।
सरल सॉफ़्टवेयर सिस्टम, विशेष रूप से वे जिन्हें नियमित अभिव्यक्तियों का उपयोग करके दर्शाया जा सकता है, को परिमित स्टेट मशीनों के रूप में मॉडल किया जा सकता है। ऐसी कई सरल प्रणालियाँ हैं, जैसे वेंडिंग मशीन या बुनियादी इलेक्ट्रॉनिक्स।
दो परिमित स्टेट मशीनों के प्रतिच्छेदन का पता लगाकर, कोई बहुत ही सरल तरीके से समवर्ती प्रणालियों को डिज़ाइन कर सकता है जो उदाहरण के लिए संदेशों का आदान-प्रदान करते हैं। उदाहरण के लिए, ट्रैफ़िक लाइट एक ऐसी प्रणाली है जिसमें कई उपप्रणालियाँ शामिल होती हैं, जैसे कि विभिन्न ट्रैफ़िक लाइटें, जो एक साथ काम करती हैं।
अनुप्रयोगों के कुछ उदाहरण:
- संख्या वर्गीकरण
- टाइमर के साथ देखें
- व्यापारिक मशीन
- ट्रैफिक - लाइट
- बारकोड स्कैनर
- गैस पंप
यह भी देखें
फ़ुटनोट
- ↑ Mealy, George H. (September 1955). "अनुक्रमिक सर्किट को संश्लेषित करने की एक विधि". Bell System Technical Journal. 34 (5): 1045–1079. doi:10.1002/j.1538-7305.1955.tb03788.x.
- ↑ Akhavi et al (2012)
संदर्भ
- Mealy, George H. (1955). A Method for Synthesizing Sequential Circuits. Bell System Technical Journal. pp. 1045–1079.
- Holcombe, W.M.L. (1982). Algebraic automata theory. Cambridge Studies in Advanced Mathematics. Vol. 1. Cambridge University Press. ISBN 0-521-60492-3. Zbl 0489.68046.
- Roth, Charles H., Jr. (2004). Fundamentals of Logic Design. Thomson-Engineering. pp. 364–367. ISBN 0-534-37804-8.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Akhavi, Ali; Klimann, Ines; Lombardy, Sylvain; Mairesse, Jean; Picantin, Matthieu (2012). "On the finiteness problem for automaton (semi)groups". International Journal of Algebra and Computation. 22 (6). arXiv:1105.4725. Bibcode:2011arXiv1105.4725A. doi:10.1142/S021819671250052X. S2CID 47518684. Zbl 1280.20038.
बाहरी संबंध
 Media related to मैली मशीन at Wikimedia Commons
Media related to मैली मशीन at Wikimedia Commons