डिवाइड-और-कॉन्कर आइजेनवैल्यू एल्गोरिदम: Difference between revisions
(Created page with "फूट डालो और जीतो eigenvalue एल्गोरिदम हर्मिटियन मैट्रिक्स या वास्तव...") |
No edit summary |
||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
'''विभाजन-और-कॉन्कर [[eigenvalue|अभिलक्षणिक मान]] एल्गोरिदम''' [[हर्मिटियन मैट्रिक्स|हर्मिटियन]] या [[वास्तविक संख्या|वास्तविक]] [[सममित मैट्रिक्स]] के लिए अभिलक्षणिक मान एल्गोरिदम का एक वर्ग है जो हाल ही में (लगभग 1990 के दशक में) [[क्यूआर एल्गोरिदम|क्यूआर (QR) एल्गोरिदम]] जैसे अधिक पारंपरिक एल्गोरिदम के साथ [[संख्यात्मक स्थिरता|स्थिरता]] और [[कम्प्यूटेशनल जटिलता सिद्धांत|दक्षता]] की स्थिति में प्रतिस्पर्धी बन गया है। इन एल्गोरिदम के पीछे मूल अवधारणा [[कंप्यूटर विज्ञान]] से विभाजन और कॉन्कर दृष्टिकोण है। अभिलक्षणिक मान प्रश्न को लगभग आधे आकार के दो प्रश्नों में विभाजित किया जाता है, इनमें से प्रत्येक को [[ प्रत्यावर्तन |पुनरावर्ती]] रूप से हल किया जाता है, और मूल प्रश्न के अभिलक्षणिक मानों की गणना इन छोटे प्रश्नों के परिणामों से की जाती है। | |||
यहां हम | यहां हम विभाजन और कॉन्कर एल्गोरिदम का सबसे सरल संस्करण प्रस्तुत करते हैं, जो मूल रूप से 1981 में क्यूपेन द्वारा प्रस्तावित एल्गोरिदम के समान है। इस लेख के क्षेत्र से बाहर उपस्थित कई विवरण छोड़ दिए जाएंगे हालाँकि, इन विवरणों पर विचार किए बिना, एल्गोरिथ्म पूरी तरह से स्थिर नहीं है। | ||
==पृष्ठभूमि== | ==पृष्ठभूमि== | ||
हर्मिटियन मैट्रिक्स के लिए अधिकांश | हर्मिटियन मैट्रिक्स के लिए अधिकांश अभिलक्षणिक मान एल्गोरिदम की तरह, विभाजन-और-कॉन्कर [[त्रिविकर्णीय मैट्रिक्स|त्रिविकर्णी]] रूप में कमी के साथ प्रारम्भ होते है। <math>m \times m</math> मैट्रिक्स के लिए, इसके लिए मानक विधि, [[ गृहस्थ प्रतिबिंब |हाउसहोल्डर परावर्तन]] के माध्यम से, <math>\frac{4}{3}m^{3}</math> प्लवी बिंदु संचालन लेती है, या <math>\frac{8}{3}m^{3}</math> यदि [[eigenvector|अभिलक्षणिक सदिशों]] की भी आवश्यकता होती है। अन्य एल्गोरिदम हैं, जैसे कि अर्नोल्डी पुनरावृत्ति, जो मैट्रिक्स के कुछ वर्गों के लिए बेहतर प्रदर्शन कर सकते हैं हम यहां इस पर आगे विचार नहीं करेंगे। कुछ स्थितियों में, अभिलक्षणिक मान प्रश्न को छोटे प्रश्नों में विभाजित करना संभव है। ब्लॉक विकर्ण मैट्रिक्स पर विचार करें | ||
कुछ | |||
:<math>T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix}.</math> | :<math>T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix}.</math> | ||
<math>T</math> के अभिलक्षणिक मानों और अभिलक्षणिक सदिशों केवल <math>T_{1}</math> और <math>T_{2}</math> के समान हैं, और इन दो छोटे प्रश्नों को हल करना मूल प्रश्न को एक साथ हल करने की तुलना में लगभग सदैव तीव्र होगा। इस तकनीक का उपयोग कई अभिलक्षणिक मान एल्गोरिदम की दक्षता में सुधार करने के लिए किया जा सकता है, लेकिन इसके विभाजन-और-कॉन्कर के लिए विशेष महत्व है। | |||
इस | इस लेख के शेष भाग के लिए, हम मान लेंगे कि विभाजन-और-कॉन्कर एल्गोरिथ्म का इनपुट <math>m \times m</math> वास्तविक सममित त्रिविकर्णी मैट्रिक्स <math>T</math> है। हालाँकि हर्मिटियन मैट्रिक्स के लिए एल्गोरिदम को संशोधित किया जा सकता है, हम यहां विवरण नहीं देते हैं। | ||
==विभाजन== | ==विभाजन== | ||
विभाजन-और-कॉन्कर एल्गोरिथ्म का ''विभाजन'' भाग इस प्रतिफलन से आता है कि त्रिविकर्णी मैट्रिक्स "लगभग" ब्लॉक विकर्ण है। | |||
:[[Image:Almost block diagonal.png]] | |||
:[[Image:Almost block diagonal.png]]सबमैट्रिक्स | :सबमैट्रिक्स <math>T_{1}</math> का आकार हम <math>n \times n</math> कहेंगे, और फिर <math>T_{2}</math> <math>(m - n) \times (m - n)</math> है। ध्यान दें कि <math>T</math> के लगभग ब्लॉक विकर्ण होने की टिप्पणी सत्य है, चाहे <math>n</math> को कैसे भी चुना जाए (अर्थात, मैट्रिक्स को विघटित करने के कई तरीके हैं)। हालाँकि, दक्षता के दृष्टिकोण से, <math>n \approx m/2</math> चुनना उचित है। | ||
:हम <math>T</math> को एक ब्लॉक विकर्ण मैट्रिक्स के साथ-साथ [[रैंक (रैखिक बीजगणित)|रैंक]]-1 सुधार के रूप में लिखते हैं- | |||
:[[Image:Block diagonal plus correction.png]] | |||
:<math>T_{1}</math> और <math>\hat{T}_{1}</math> के बीच एकमात्र अंतर यह है कि <math>\hat{T}_{1}</math> में निचली दाईं ओर की प्रविष्टि <math>t_{nn}</math> को <math>t_{nn} - \beta</math> से बदल दिया गया है और इसी तरह, <math>\hat{T}_{2}</math> में ऊपरी बाईं ओर की प्रविष्टि <math>t_{n+1,n+1}</math> को <math>t_{n+1,n+1} - \beta</math> से बदल दिया गया है। | |||
:[[Image:Block diagonal plus correction.png]] | :विभाजन चरण का शेष भाग <math>\hat{T}_{1}</math>और <math>\hat{T}_{2}</math> के अभिलक्षणिक मानों (और यदि वांछित हो तो अभिलक्षणिक सदिशों) को हल करना है, अर्थात [[विकर्णीय मैट्रिक्स|विकर्णन]] <math>\hat{T}_{1} = Q_{1} D_{1} Q_{1}^{T}</math> और <math>\hat{T}_{2} = Q_{2} D_{2} Q_{2}^{T}</math> खोजना है। इसे विभाजन-और-कॉन्कर एल्गोरिदम में पुनरावर्ती निर्देश के साथ पूरा किया जा सकता है, हालांकि व्यावहारिक कार्यान्वयन प्रायः छोटे पर्याप्त सबमैट्रिसेस के लिए क्यूआर एल्गोरिदम पर स्विच करते हैं। | ||
==कॉन्कर== | |||
एल्गोरिथम का कॉन्कर भाग अबोधगम्य भाग है। ऊपर परिकलित उपमैट्रिक्स के विकर्णीकरण को देखते हुए, हम मूल मैट्रिक्स का विकर्णीकरण कैसे ज्ञात कर सकते हैं? | |||
सबसे पहले, <math>z^{T} = (q_{1}^{T},q_{2}^{T})</math> को परिभाषित करें, जहां <math>q_{1}^{T}</math> <math>Q_{1}</math> की अंतिम पंक्ति है और <math>q_{2}^{T}</math> <math>Q_{2}</math> की पहली पंक्ति है। यह दर्शाना अब प्राथमिक है | |||
:<math>T = \begin{bmatrix} Q_{1} & \\ & Q_{2} \end{bmatrix} \left( \begin{bmatrix} D_{1} & \\ & D_{2} \end{bmatrix} + \beta z z^{T} \right) \begin{bmatrix} Q_{1}^{T} & \\ & Q_{2}^{T} \end{bmatrix}</math> | |||
शेष कार्य को विकर्ण मैट्रिक्स के अभिलक्षणिक मानों के साथ-साथ रैंक-एक सुधार को खोजने के लिए कम कर दिया गया है। यह कैसे करना है यह दिखाने से पहले, आइए अंकन को सरल बनाएं। हम मैट्रिक्स <math>D + w w^{T}</math> के अभिलक्षणिक मानों की खोज कर रहे हैं, जहां <math>D</math> अलग-अलग प्रविष्टियों के साथ विकर्ण है और <math>w</math> गैर-शून्य प्रविष्टियों वाला कोई सदिश है। | |||
शून्य प्रविष्टि की स्थिति सरल है, क्योंकि यदि w<sub>i</sub> शून्य है, (<math>e_i</math>,d<sub>i</sub>) <math>D + w w^{T}</math> का अभिलक्षणिक युग्म (<math>e_i</math> मानक आधार पर है) है क्योंकि | |||
<math>(D + w w^{T})e_i = De_i = d_i e_i</math>। | |||
<math>(D + w w^{T})e_i = De_i = d_i e_i</math> | |||
यदि <math>\lambda</math> एक अभिलक्षणिक मान है, तो हमारे पास है- | |||
:<math>(D + w w^{T})q = \lambda q</math> | :<math>(D + w w^{T})q = \lambda q</math> | ||
जहां <math>q</math> संगत अभिलक्षणिक सदिश है। अब | |||
:<math>(D - \lambda I)q + w(w^{T}q) = 0</math> | :<math>(D - \lambda I)q + w(w^{T}q) = 0</math> | ||
:<math>q + (D - \lambda I)^{-1} w(w^{T}q) = 0</math> | :<math>q + (D - \lambda I)^{-1} w(w^{T}q) = 0</math> | ||
:<math>w^{T}q + w^{T}(D - \lambda I)^{-1} w(w^{T}q) = 0</math> | :<math>w^{T}q + w^{T}(D - \lambda I)^{-1} w(w^{T}q) = 0</math> | ||
ध्यान रखें कि <math>w^{T}q</math> एक शून्येतर अदिश राशि | ध्यान रखें कि <math>w^{T}q</math> एक शून्येतर अदिश राशि है। न तो <math>w</math> और न ही <math>q</math> शून्य हैं। यदि <math>w^{T}q</math> शून्य होता, तो <math>q</math> <math>(D + w w^{T})q = \lambda q</math> द्वारा <math>D</math> का अभिलक्षणिक सदिश होता है। यदि ऐसा होता, तो <math>q</math> में केवल एक गैर-शून्य स्थिति होती क्योंकि <math>D</math> अलग विकर्ण है और इस प्रकार आंतरिक गुणनफल <math>w^{T}q</math> अंततः शून्य नहीं हो सकता। इसलिए, हमारे पास है- | ||
:<math>1 + w^{T}(D - \lambda I)^{-1} w = 0</math> | :<math>1 + w^{T}(D - \lambda I)^{-1} w = 0</math> | ||
या अदिश समीकरण के रूप में लिखा गया है, | या अदिश समीकरण के रूप में लिखा गया है, | ||
:<math>1 + \sum_{j=1}^{m} \frac{w_{j}^{2}}{d_{j} - \lambda} = 0.</math> | :<math>1 + \sum_{j=1}^{m} \frac{w_{j}^{2}}{d_{j} - \lambda} = 0.</math> | ||
इस समीकरण को | इस समीकरण को ''दीर्घकालिक समीकरण'' के नाम से जाना जाता है। इसलिए प्रश्न को इस समीकरण के बाईं ओर द्वारा परिभाषित तर्कसंगत फलन के रूट्स को खोजने तक सीमित कर दिया गया है। | ||
सभी सामान्य | सभी सामान्य अभिलक्षणिक मान एल्गोरिदम पुनरावृत्त होने चाहिए, और विभाजन-और-कॉन्कर एल्गोरिदम अलग नहीं है। [[अरेखीय]] दीर्घकालिक समीकरण को हल करने के लिए पुनरावृत्तीय तकनीक की आवश्यकता होती है, जैसे न्यूटन-रेफसन विधि। हालाँकि, प्रत्येक रूट को [[ बिग ओ अंकन |O]](1) पुनरावृत्तियों में पाया जा सकता है, जिनमें से प्रत्येक को <math>\Theta(m)</math> फ़्लॉप्स (<math>m</math>-डिग्री तर्कसंगत फलन के लिए) की आवश्यकता होती है, जिससे इस एल्गोरिदम के पुनरावृत्त भाग की लागत <math>\Theta(m^{2})</math> हो जाती है। | ||
==विश्लेषण== | ==विश्लेषण== | ||
जैसा कि | जैसा कि विभाजन और कॉन्कर एल्गोरिदम के लिए सामान्य है, हम कार्यावधि का विश्लेषण करने के लिए विभाजन-और-कॉन्कर पुनरावृत्ति के लिए [[मास्टर प्रमेय (एल्गोरिदम का विश्लेषण)|मास्टर प्रमेय]] का उपयोग करेंगे। | ||
याद रखें कि ऊपर हमने कहा है कि हम <math>n \approx m/2</math> चुनते हैं। हम [[पुनरावृत्ति संबंध]] लिख सकते हैं- | |||
:<math>T(m) = 2 \times T\left(\frac{m}{2}\right) + \Theta(m^{2})</math> | :<math>T(m) = 2 \times T\left(\frac{m}{2}\right) + \Theta(m^{2})</math> | ||
मास्टर प्रमेय के अंकन में, <math>a = b = 2</math> और इस | मास्टर प्रमेय के अंकन में, <math>a = b = 2</math> और इस प्रकार <math>\log_{b} a = 1</math>। स्पष्ट रूप से, <math>\Theta(m^{2}) = \Omega(m^{1})</math>, तो हमारे पास है | ||
:<math>T(m) = \Theta(m^{2})</math> | :<math>T(m) = \Theta(m^{2})</math> | ||
याद रखें कि ऊपर हमने बताया था कि हर्मिटियन मैट्रिक्स को त्रिविकर्ण रूप में कम | याद रखें कि ऊपर हमने बताया था कि हर्मिटियन मैट्रिक्स को त्रिविकर्ण रूप में कम करने में <math>\frac{4}{3}m^{3}</math> फ्लॉप्स लगते हैं। यह विभाजन-और-कॉन्कर भाग की कार्यावधि को कम कर देती है, और इस बिंदु पर यह स्पष्ट नहीं है कि विभाजन-और-कॉन्कर एल्गोरिथ्म क्यूआर एल्गोरिथ्म (जो त्रिविकर्ण मैट्रिक्स के लिए <math>\Theta(m^{2})</math> फ्लॉप्स भी लेता है) पर क्या लाभ प्रदान करता है। | ||
विभाजन-और-कॉन्कर का लाभ तब मिलता है जब अभिलक्षणिक सदिश की भी आवश्यकता होती है। यदि यह स्थिति है, तो त्रिविकर्ण रूप में कमी में <math>\frac{8}{3}m^{3}</math> लगता है, लेकिन एल्गोरिथ्म का दूसरा भाग <math>\Theta(m^{3})</math> भी लेता है। उचित लक्ष्य परिशुद्धता वाले क्यूआर एल्गोरिदम के लिए, यह <math>\approx 6 m^{3}</math> है, जबकि विभाजन-और-कॉन्कर के लिए यह <math>\approx \frac{4}{3}m^{3}</math> है। इस सुधार का कारण यह है कि विभाजन-और-कॉन्कर में, एल्गोरिदम का <math>\Theta(m^{3})</math> भाग (<math>Q</math> मैट्रिसेस को गुणा करना) पुनरावृत्ति से अलग है, जबकि क्यूआर में, यह प्रत्येक पुनरावृत्त चरण में होना चाहिए। कमी के लिए <math>\frac{8}{3}m^{3}</math> फ्लॉप्स को जोड़ने पर, कुल सुधार <math>\approx 9 m^{3}</math> से <math>\approx 4 m^{3}</math> फ्लॉप्स तक होता है। | |||
विभाजन-और-कॉन्कर एल्गोरिदम के व्यावहारिक उपयोग से पता चला है कि अधिकांश यथार्थवादी अभिलक्षणिक मान प्रश्नों में, एल्गोरिदम वास्तव में इससे बेहतर काम करता है। इसका कारण यह है कि प्रायः मैट्रिक्स <math>Q</math> और सदिश <math>z</math> संख्यात्मक रूप से अपर्याप्त होते हैं, जिसका अर्थ है कि उनके पास [[तैरनेवाला स्थल|प्लवी बिंदु]] परिशुद्धता से छोटे मानों के साथ कई प्रविष्टियाँ हैं, जो संख्यात्मक अपस्फीति की अनुमति देती हैं, अर्थात प्रश्न को अयुग्मित उप-प्रश्नों में तोड़ देती हैं। | |||
== | ==भिन्नरूप और कार्यान्वयन== | ||
यहां प्रस्तुत एल्गोरिदम सबसे सरल संस्करण है। कई व्यावहारिक कार्यान्वयन में, स्थिरता की गारंटी के लिए अधिक जटिल रैंक-1 सुधारों का उपयोग किया जाता है | यहां प्रस्तुत एल्गोरिदम सबसे सरल संस्करण है। कई व्यावहारिक कार्यान्वयन में, स्थिरता की गारंटी के लिए अधिक जटिल रैंक-1 सुधारों का उपयोग किया जाता है कुछ भिन्नरूप रैंक-2 सुधारों का भी उपयोग करते हैं।{{Citation needed|date=September 2011}} | ||
तर्कसंगत कार्यों के लिए विशेष रूट-खोज तकनीकें | तर्कसंगत कार्यों के लिए विशेष रूट-खोज तकनीकें उपस्थित हैं जो प्रदर्शन और स्थिरता दोनों की स्थिति में न्यूटन-रेफसन विधि से बेहतर कर सकती हैं। इनका उपयोग विभाजन-और-कॉन्कर एल्गोरिथ्म के पुनरावृत्त भाग को बेहतर बनाने के लिए किया जा सकता है। | ||
विभाजन-और-कॉन्कर एल्गोरिथ्म आसानी से [[समानांतर एल्गोरिदम|समानांतर]] है, और [[LAPACK|एलएपीएसीके (LAPACK)]] जैसे रैखिक बीजगणित कंप्यूटिंग पैकेज में उच्च गुणवत्ता वाले समानांतर कार्यान्वयन सम्मिलित हैं। | |||
==संदर्भ== | ==संदर्भ== | ||
| Line 82: | Line 82: | ||
{{Numerical linear algebra}} | {{Numerical linear algebra}} | ||
[[Category: | [[Category:All articles with unsourced statements]] | ||
[[Category:Articles with unsourced statements from September 2011]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 24/07/2023]] | [[Category:Created On 24/07/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:फूट डालो और जीतो एल्गोरिदम]] | |||
[[Category:संख्यात्मक रैखिक बीजगणित]] | |||
Latest revision as of 14:47, 17 August 2023
विभाजन-और-कॉन्कर अभिलक्षणिक मान एल्गोरिदम हर्मिटियन या वास्तविक सममित मैट्रिक्स के लिए अभिलक्षणिक मान एल्गोरिदम का एक वर्ग है जो हाल ही में (लगभग 1990 के दशक में) क्यूआर (QR) एल्गोरिदम जैसे अधिक पारंपरिक एल्गोरिदम के साथ स्थिरता और दक्षता की स्थिति में प्रतिस्पर्धी बन गया है। इन एल्गोरिदम के पीछे मूल अवधारणा कंप्यूटर विज्ञान से विभाजन और कॉन्कर दृष्टिकोण है। अभिलक्षणिक मान प्रश्न को लगभग आधे आकार के दो प्रश्नों में विभाजित किया जाता है, इनमें से प्रत्येक को पुनरावर्ती रूप से हल किया जाता है, और मूल प्रश्न के अभिलक्षणिक मानों की गणना इन छोटे प्रश्नों के परिणामों से की जाती है।
यहां हम विभाजन और कॉन्कर एल्गोरिदम का सबसे सरल संस्करण प्रस्तुत करते हैं, जो मूल रूप से 1981 में क्यूपेन द्वारा प्रस्तावित एल्गोरिदम के समान है। इस लेख के क्षेत्र से बाहर उपस्थित कई विवरण छोड़ दिए जाएंगे हालाँकि, इन विवरणों पर विचार किए बिना, एल्गोरिथ्म पूरी तरह से स्थिर नहीं है।
पृष्ठभूमि
हर्मिटियन मैट्रिक्स के लिए अधिकांश अभिलक्षणिक मान एल्गोरिदम की तरह, विभाजन-और-कॉन्कर त्रिविकर्णी रूप में कमी के साथ प्रारम्भ होते है। मैट्रिक्स के लिए, इसके लिए मानक विधि, हाउसहोल्डर परावर्तन के माध्यम से, प्लवी बिंदु संचालन लेती है, या यदि अभिलक्षणिक सदिशों की भी आवश्यकता होती है। अन्य एल्गोरिदम हैं, जैसे कि अर्नोल्डी पुनरावृत्ति, जो मैट्रिक्स के कुछ वर्गों के लिए बेहतर प्रदर्शन कर सकते हैं हम यहां इस पर आगे विचार नहीं करेंगे। कुछ स्थितियों में, अभिलक्षणिक मान प्रश्न को छोटे प्रश्नों में विभाजित करना संभव है। ब्लॉक विकर्ण मैट्रिक्स पर विचार करें
के अभिलक्षणिक मानों और अभिलक्षणिक सदिशों केवल और के समान हैं, और इन दो छोटे प्रश्नों को हल करना मूल प्रश्न को एक साथ हल करने की तुलना में लगभग सदैव तीव्र होगा। इस तकनीक का उपयोग कई अभिलक्षणिक मान एल्गोरिदम की दक्षता में सुधार करने के लिए किया जा सकता है, लेकिन इसके विभाजन-और-कॉन्कर के लिए विशेष महत्व है।
इस लेख के शेष भाग के लिए, हम मान लेंगे कि विभाजन-और-कॉन्कर एल्गोरिथ्म का इनपुट वास्तविक सममित त्रिविकर्णी मैट्रिक्स है। हालाँकि हर्मिटियन मैट्रिक्स के लिए एल्गोरिदम को संशोधित किया जा सकता है, हम यहां विवरण नहीं देते हैं।
विभाजन
विभाजन-और-कॉन्कर एल्गोरिथ्म का विभाजन भाग इस प्रतिफलन से आता है कि त्रिविकर्णी मैट्रिक्स "लगभग" ब्लॉक विकर्ण है।
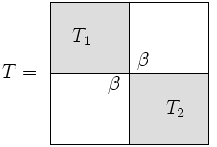
- सबमैट्रिक्स का आकार हम कहेंगे, और फिर है। ध्यान दें कि के लगभग ब्लॉक विकर्ण होने की टिप्पणी सत्य है, चाहे को कैसे भी चुना जाए (अर्थात, मैट्रिक्स को विघटित करने के कई तरीके हैं)। हालाँकि, दक्षता के दृष्टिकोण से, चुनना उचित है।
- हम को एक ब्लॉक विकर्ण मैट्रिक्स के साथ-साथ रैंक-1 सुधार के रूप में लिखते हैं-
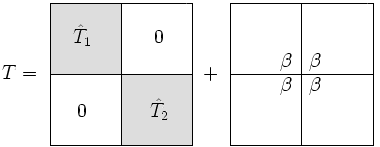
- और के बीच एकमात्र अंतर यह है कि में निचली दाईं ओर की प्रविष्टि को से बदल दिया गया है और इसी तरह, में ऊपरी बाईं ओर की प्रविष्टि को से बदल दिया गया है।
- विभाजन चरण का शेष भाग और के अभिलक्षणिक मानों (और यदि वांछित हो तो अभिलक्षणिक सदिशों) को हल करना है, अर्थात विकर्णन और खोजना है। इसे विभाजन-और-कॉन्कर एल्गोरिदम में पुनरावर्ती निर्देश के साथ पूरा किया जा सकता है, हालांकि व्यावहारिक कार्यान्वयन प्रायः छोटे पर्याप्त सबमैट्रिसेस के लिए क्यूआर एल्गोरिदम पर स्विच करते हैं।
कॉन्कर
एल्गोरिथम का कॉन्कर भाग अबोधगम्य भाग है। ऊपर परिकलित उपमैट्रिक्स के विकर्णीकरण को देखते हुए, हम मूल मैट्रिक्स का विकर्णीकरण कैसे ज्ञात कर सकते हैं?
सबसे पहले, को परिभाषित करें, जहां की अंतिम पंक्ति है और की पहली पंक्ति है। यह दर्शाना अब प्राथमिक है
शेष कार्य को विकर्ण मैट्रिक्स के अभिलक्षणिक मानों के साथ-साथ रैंक-एक सुधार को खोजने के लिए कम कर दिया गया है। यह कैसे करना है यह दिखाने से पहले, आइए अंकन को सरल बनाएं। हम मैट्रिक्स के अभिलक्षणिक मानों की खोज कर रहे हैं, जहां अलग-अलग प्रविष्टियों के साथ विकर्ण है और गैर-शून्य प्रविष्टियों वाला कोई सदिश है।
शून्य प्रविष्टि की स्थिति सरल है, क्योंकि यदि wi शून्य है, (,di) का अभिलक्षणिक युग्म ( मानक आधार पर है) है क्योंकि
।
यदि एक अभिलक्षणिक मान है, तो हमारे पास है-
जहां संगत अभिलक्षणिक सदिश है। अब
ध्यान रखें कि एक शून्येतर अदिश राशि है। न तो और न ही शून्य हैं। यदि शून्य होता, तो द्वारा का अभिलक्षणिक सदिश होता है। यदि ऐसा होता, तो में केवल एक गैर-शून्य स्थिति होती क्योंकि अलग विकर्ण है और इस प्रकार आंतरिक गुणनफल अंततः शून्य नहीं हो सकता। इसलिए, हमारे पास है-
या अदिश समीकरण के रूप में लिखा गया है,
इस समीकरण को दीर्घकालिक समीकरण के नाम से जाना जाता है। इसलिए प्रश्न को इस समीकरण के बाईं ओर द्वारा परिभाषित तर्कसंगत फलन के रूट्स को खोजने तक सीमित कर दिया गया है।
सभी सामान्य अभिलक्षणिक मान एल्गोरिदम पुनरावृत्त होने चाहिए, और विभाजन-और-कॉन्कर एल्गोरिदम अलग नहीं है। अरेखीय दीर्घकालिक समीकरण को हल करने के लिए पुनरावृत्तीय तकनीक की आवश्यकता होती है, जैसे न्यूटन-रेफसन विधि। हालाँकि, प्रत्येक रूट को O(1) पुनरावृत्तियों में पाया जा सकता है, जिनमें से प्रत्येक को फ़्लॉप्स (-डिग्री तर्कसंगत फलन के लिए) की आवश्यकता होती है, जिससे इस एल्गोरिदम के पुनरावृत्त भाग की लागत हो जाती है।
विश्लेषण
जैसा कि विभाजन और कॉन्कर एल्गोरिदम के लिए सामान्य है, हम कार्यावधि का विश्लेषण करने के लिए विभाजन-और-कॉन्कर पुनरावृत्ति के लिए मास्टर प्रमेय का उपयोग करेंगे।
याद रखें कि ऊपर हमने कहा है कि हम चुनते हैं। हम पुनरावृत्ति संबंध लिख सकते हैं-
मास्टर प्रमेय के अंकन में, और इस प्रकार । स्पष्ट रूप से, , तो हमारे पास है
याद रखें कि ऊपर हमने बताया था कि हर्मिटियन मैट्रिक्स को त्रिविकर्ण रूप में कम करने में फ्लॉप्स लगते हैं। यह विभाजन-और-कॉन्कर भाग की कार्यावधि को कम कर देती है, और इस बिंदु पर यह स्पष्ट नहीं है कि विभाजन-और-कॉन्कर एल्गोरिथ्म क्यूआर एल्गोरिथ्म (जो त्रिविकर्ण मैट्रिक्स के लिए फ्लॉप्स भी लेता है) पर क्या लाभ प्रदान करता है।
विभाजन-और-कॉन्कर का लाभ तब मिलता है जब अभिलक्षणिक सदिश की भी आवश्यकता होती है। यदि यह स्थिति है, तो त्रिविकर्ण रूप में कमी में लगता है, लेकिन एल्गोरिथ्म का दूसरा भाग भी लेता है। उचित लक्ष्य परिशुद्धता वाले क्यूआर एल्गोरिदम के लिए, यह है, जबकि विभाजन-और-कॉन्कर के लिए यह है। इस सुधार का कारण यह है कि विभाजन-और-कॉन्कर में, एल्गोरिदम का भाग ( मैट्रिसेस को गुणा करना) पुनरावृत्ति से अलग है, जबकि क्यूआर में, यह प्रत्येक पुनरावृत्त चरण में होना चाहिए। कमी के लिए फ्लॉप्स को जोड़ने पर, कुल सुधार से फ्लॉप्स तक होता है।
विभाजन-और-कॉन्कर एल्गोरिदम के व्यावहारिक उपयोग से पता चला है कि अधिकांश यथार्थवादी अभिलक्षणिक मान प्रश्नों में, एल्गोरिदम वास्तव में इससे बेहतर काम करता है। इसका कारण यह है कि प्रायः मैट्रिक्स और सदिश संख्यात्मक रूप से अपर्याप्त होते हैं, जिसका अर्थ है कि उनके पास प्लवी बिंदु परिशुद्धता से छोटे मानों के साथ कई प्रविष्टियाँ हैं, जो संख्यात्मक अपस्फीति की अनुमति देती हैं, अर्थात प्रश्न को अयुग्मित उप-प्रश्नों में तोड़ देती हैं।
भिन्नरूप और कार्यान्वयन
यहां प्रस्तुत एल्गोरिदम सबसे सरल संस्करण है। कई व्यावहारिक कार्यान्वयन में, स्थिरता की गारंटी के लिए अधिक जटिल रैंक-1 सुधारों का उपयोग किया जाता है कुछ भिन्नरूप रैंक-2 सुधारों का भी उपयोग करते हैं।[citation needed]
तर्कसंगत कार्यों के लिए विशेष रूट-खोज तकनीकें उपस्थित हैं जो प्रदर्शन और स्थिरता दोनों की स्थिति में न्यूटन-रेफसन विधि से बेहतर कर सकती हैं। इनका उपयोग विभाजन-और-कॉन्कर एल्गोरिथ्म के पुनरावृत्त भाग को बेहतर बनाने के लिए किया जा सकता है।
विभाजन-और-कॉन्कर एल्गोरिथ्म आसानी से समानांतर है, और एलएपीएसीके (LAPACK) जैसे रैखिक बीजगणित कंप्यूटिंग पैकेज में उच्च गुणवत्ता वाले समानांतर कार्यान्वयन सम्मिलित हैं।
संदर्भ
- Demmel, James W. (1997), Applied Numerical Linear Algebra, Philadelphia, PA: Society for Industrial and Applied Mathematics, ISBN 0-89871-389-7, MR 1463942.
- Cuppen, J.J.M. (1981). "A Divide and Conquer Method for the Symmetric Tridiagonal Eigenproblem". Numerische Mathematik. 36 (2): 177–195. doi:10.1007/BF01396757. S2CID 120504744.