द्रव गतिकी में सीमा की स्थितियाँ: Difference between revisions
(Created page with "{{details|Boundary conditions in computational fluid dynamics}} द्रव गतिकी में सीमा स्थितियाँ कम्प्यूटेश...") |
No edit summary |
||
| Line 2: | Line 2: | ||
द्रव गतिकी में सीमा स्थितियाँ कम्प्यूटेशनल द्रव गतिकी में [[सीमा मूल्य समस्या]]ओं के लिए बाधाओं का समूह हैं। इन सीमा स्थितियों में इनलेट सीमा स्थितियां, आउटलेट सीमा स्थितियां, दीवार सीमा स्थितियां, निरंतर दबाव सीमा स्थितियां, अक्षमिति सीमा स्थितियां, सममित सीमा स्थितियां और आवधिक या चक्रीय सीमा स्थितियां शामिल हैं। | द्रव गतिकी में सीमा स्थितियाँ कम्प्यूटेशनल द्रव गतिकी में [[सीमा मूल्य समस्या]]ओं के लिए बाधाओं का समूह हैं। इन सीमा स्थितियों में इनलेट सीमा स्थितियां, आउटलेट सीमा स्थितियां, दीवार सीमा स्थितियां, निरंतर दबाव सीमा स्थितियां, अक्षमिति सीमा स्थितियां, सममित सीमा स्थितियां और आवधिक या चक्रीय सीमा स्थितियां शामिल हैं। | ||
[[क्षणिक अवस्था (रासायनिक इंजीनियरिंग)]] समस्याओं के लिए | [[क्षणिक अवस्था (रासायनिक इंजीनियरिंग)]] समस्याओं के लिए और चीज़ की आवश्यकता होती है, यानी प्रारंभिक स्थितियाँ जहाँ प्रवाह चर के प्रारंभिक मान प्रवाह डोमेन में नोड्स पर निर्दिष्ट होते हैं।<ref name="Versteeg1995">{{cite book|author1=Henk Kaarle Versteeg|author2=Weeratunge Malalasekera|title=An Introduction to Computational Fluid Dynamics: The Finite Volume Method|year=1995|publisher=Longman Scientific & Technical|pages=192–206|isbn=0-582-21884-5}}</ref> सीएफडी में विभिन्न स्थितियों और उद्देश्यों के लिए विभिन्न प्रकार की सीमा शर्तों का उपयोग किया जाता है और उनकी चर्चा इस प्रकार की जाती है। | ||
==इनलेट सीमा शर्तें == | ==इनलेट सीमा शर्तें == | ||
[[File:Inlet Boundary Condition.jpg|thumb|एक पाइप में इनलेट प्रवाह वेग दिखा रहा है|200px]][[ प्रवेश ]] सीमा स्थितियों में, सभी प्रवाह चर (अनुसंधान) के वितरण को इनलेट सीमाओं पर मुख्य रूप से [[प्रवाह वेग]] पर निर्दिष्ट करने की आवश्यकता होती है।<ref name="Versteeg1995"/>इस प्रकार की सीमा स्थितियाँ सामान्य हैं और अधिकतर निर्दिष्ट की जाती हैं जहाँ इनलेट प्रवाह वेग ज्ञात होता है। | [[File:Inlet Boundary Condition.jpg|thumb|एक पाइप में इनलेट प्रवाह वेग दिखा रहा है|200px]][[ प्रवेश | प्रवेश]] सीमा स्थितियों में, सभी प्रवाह चर (अनुसंधान) के वितरण को इनलेट सीमाओं पर मुख्य रूप से [[प्रवाह वेग]] पर निर्दिष्ट करने की आवश्यकता होती है।<ref name="Versteeg1995"/> इस प्रकार की सीमा स्थितियाँ सामान्य हैं और अधिकतर निर्दिष्ट की जाती हैं जहाँ इनलेट प्रवाह वेग ज्ञात होता है। | ||
==आउटलेट सीमा स्थिति== | ==आउटलेट सीमा स्थिति== | ||
[[File:Outlet Boundary Condition.jpg|thumb|एक पाइप में आउटलेट प्रवाह वेग दिखा रहा है|200px]]आउटलेट सीमा स्थितियों में, सभी प्रवाह चर (अनुसंधान) के वितरण को निर्दिष्ट करने की आवश्यकता है, मुख्य रूप से प्रवाह वेग। इसे इनलेट सीमा स्थिति के संयोजन के रूप में सोचा जा सकता है। इस प्रकार की सीमा स्थितियाँ आम हैं और अधिकतर वहीं निर्दिष्ट की जाती हैं जहां आउटलेट वेग ज्ञात होता है।<ref name="Versteeg1995"/> | [[File:Outlet Boundary Condition.jpg|thumb|एक पाइप में आउटलेट प्रवाह वेग दिखा रहा है|200px]]आउटलेट सीमा स्थितियों में, सभी प्रवाह चर (अनुसंधान) के वितरण को निर्दिष्ट करने की आवश्यकता है, मुख्य रूप से प्रवाह वेग। इसे इनलेट सीमा स्थिति के संयोजन के रूप में सोचा जा सकता है। इस प्रकार की सीमा स्थितियाँ आम हैं और अधिकतर वहीं निर्दिष्ट की जाती हैं जहां आउटलेट वेग ज्ञात होता है।<ref name="Versteeg1995"/> | ||
प्रवाह | प्रवाह [[ प्रवाह कंडीशनिंग |प्रवाह कंडीशनिंग]] प्राप्त करता है जहां ज्यामितीय गड़बड़ी से दूर आउटलेट का चयन करने पर प्रवाह दिशा में कोई परिवर्तन नहीं होता है। ऐसे क्षेत्र में, आउटलेट की रूपरेखा तैयार की जा सकती है और [[दबाव]] को छोड़कर सभी चर के ढाल को प्रवाह दिशा में शून्य के बराबर किया जा सकता है। | ||
==नो-स्लिप सीमा शर्त== | ==नो-स्लिप सीमा शर्त== | ||
[[File:Wall Boundary Condition.jpg|thumb|दीवार की सीमा स्थिति दिखा रहा है|200px]][[पाइप प्रवाह]] की समस्याओं में सामने आने वाली सबसे आम सीमा नाली की दीवार है। उपयुक्त आवश्यकता को [[नो-स्लिप स्थिति]] | नो-स्लिप सीमा स्थिति कहा जाता है, जिसमें वेग का सामान्य घटक शून्य पर तय किया जाता है, और स्पर्शरेखा घटक को दीवार के वेग के बराबर सेट किया जाता है।<ref name="Versteeg1995"/>यह अंतर्ज्ञान के विपरीत हो सकता है, लेकिन प्रयोग और सिद्धांत दोनों में नो-स्लिप स्थिति दृढ़ता से स्थापित की गई है, हालांकि दशकों के विवाद और बहस के बाद ही।<ref>{{Cite journal | last1=Prabhakara|first1=Sandeep|last2=Deshpande|first2=M. D. | date=2004-04-01|title=द्रव यांत्रिकी में नो-स्लिप सीमा स्थिति| journal=Resonance | language=en | volume=9|issue=4 | pages=50–60|doi=10.1007/BF02834856|s2cid=124269972|issn=0973-712X}}</ref> | [[File:Wall Boundary Condition.jpg|thumb|दीवार की सीमा स्थिति दिखा रहा है|200px]][[पाइप प्रवाह]] की समस्याओं में सामने आने वाली सबसे आम सीमा नाली की दीवार है। उपयुक्त आवश्यकता को [[नो-स्लिप स्थिति]] | नो-स्लिप सीमा स्थिति कहा जाता है, जिसमें वेग का सामान्य घटक शून्य पर तय किया जाता है, और स्पर्शरेखा घटक को दीवार के वेग के बराबर सेट किया जाता है।<ref name="Versteeg1995"/> यह अंतर्ज्ञान के विपरीत हो सकता है, लेकिन प्रयोग और सिद्धांत दोनों में नो-स्लिप स्थिति दृढ़ता से स्थापित की गई है, हालांकि दशकों के विवाद और बहस के बाद ही।<ref>{{Cite journal | last1=Prabhakara|first1=Sandeep|last2=Deshpande|first2=M. D. | date=2004-04-01|title=द्रव यांत्रिकी में नो-स्लिप सीमा स्थिति| journal=Resonance | language=en | volume=9|issue=4 | pages=50–60|doi=10.1007/BF02834856|s2cid=124269972|issn=0973-712X}}</ref> | ||
<math display="block">V_\text{normal} = 0</math> | <math display="block">V_\text{normal} = 0</math> | ||
<math display="block">V_\text{tangential} = V_\text{wall}</math> | <math display="block">V_\text{tangential} = V_\text{wall}</math> | ||
| Line 21: | Line 21: | ||
==निरंतर दबाव सीमा की स्थिति== | ==निरंतर दबाव सीमा की स्थिति== | ||
[[File:Pressure Boundary Condition.jpg|thumb|निरंतर दबाव सीमा स्थिति दिखा रहा है|200px]]इस प्रकार की सीमा स्थिति का उपयोग वहां किया जाता है जहां दबाव के सीमा मान ज्ञात होते हैं और प्रवाह वितरण का सटीक विवरण अज्ञात होता है। इसमें मुख्य रूप से दबाव इनलेट और आउटलेट की स्थिति शामिल है। इस सीमा स्थिति का उपयोग करने वाले विशिष्ट उदाहरणों में उछाल संचालित प्रवाह, एकाधिक आउटलेट के साथ आंतरिक प्रवाह, मुक्त सतह प्रवाह और वस्तुओं के चारों ओर बाहरी प्रवाह शामिल हैं।<ref name="Versteeg1995"/> | [[File:Pressure Boundary Condition.jpg|thumb|निरंतर दबाव सीमा स्थिति दिखा रहा है|200px]]इस प्रकार की सीमा स्थिति का उपयोग वहां किया जाता है जहां दबाव के सीमा मान ज्ञात होते हैं और प्रवाह वितरण का सटीक विवरण अज्ञात होता है। इसमें मुख्य रूप से दबाव इनलेट और आउटलेट की स्थिति शामिल है। इस सीमा स्थिति का उपयोग करने वाले विशिष्ट उदाहरणों में उछाल संचालित प्रवाह, एकाधिक आउटलेट के साथ आंतरिक प्रवाह, मुक्त सतह प्रवाह और वस्तुओं के चारों ओर बाहरी प्रवाह शामिल हैं।<ref name="Versteeg1995"/> उदाहरण [[वायुमंडल]] में प्रवाह आउटलेट है जहां दबाव वायुमंडलीय है। | ||
==अक्षसममितीय सीमा शर्तें== | ==अक्षसममितीय सीमा शर्तें== | ||
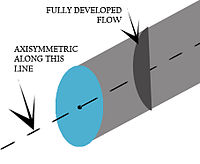
[[File:Axisymmetric Boundary Condition.jpg|thumb|अक्षसममितीय सीमा स्थिति दिखा रहा है|200px]]इस सीमा स्थिति में, मॉडल मुख्य अक्ष के संबंध में [[अक्षसममिति]] है जैसे कि | [[File:Axisymmetric Boundary Condition.jpg|thumb|अक्षसममितीय सीमा स्थिति दिखा रहा है|200px]]इस सीमा स्थिति में, मॉडल मुख्य अक्ष के संबंध में [[अक्षसममिति]] है जैसे कि विशेष आर = आर, सभी θs और प्रत्येक z = Z-स्लाइस पर, प्रत्येक प्रवाह चर का समान मूल्य होता है।<ref>{{cite web | url =http://tarpoff.com/engineering/cyclic_symmetric_BCs.doc | title = चक्रीय सममित बीसी| accessdate = 2015-08-09}}</ref> अच्छा उदाहरण गोलाकार पाइप में प्रवाह है जहां प्रवाह और पाइप अक्ष मेल खाते हैं। | ||
<br/> | <br/> | ||
| Line 32: | Line 32: | ||
==सममित सीमा स्थिति== | ==सममित सीमा स्थिति== | ||
[[File:Symmetric Boundary Condition.jpg|thumb|सममित सीमा स्थिति दिखा रहा है|200px]]इस सीमा स्थिति में, यह माना जाता है कि सीमा के दोनों किनारों पर समान भौतिक प्रक्रियाएं मौजूद हैं।<ref>{{cite web |url =http://tarpoff.com/engineering/cyclic_symmetric_BCs.doc | title = चक्रीय सममित बीसी| accessdate = 2013-10-10}}</ref> सभी चरों का सीमा से समान दूरी पर समान मान और ग्रेडिएंट होते हैं। यह | [[File:Symmetric Boundary Condition.jpg|thumb|सममित सीमा स्थिति दिखा रहा है|200px]]इस सीमा स्थिति में, यह माना जाता है कि सीमा के दोनों किनारों पर समान भौतिक प्रक्रियाएं मौजूद हैं।<ref>{{cite web |url =http://tarpoff.com/engineering/cyclic_symmetric_BCs.doc | title = चक्रीय सममित बीसी| accessdate = 2013-10-10}}</ref> सभी चरों का सीमा से समान दूरी पर समान मान और ग्रेडिएंट होते हैं। यह दर्पण के रूप में कार्य करता है जो दूसरी ओर सभी प्रवाह वितरण को दर्शाता है।<ref>{{cite web |url =http://www-ssc.igpp.ucla.edu/personnel/russell/ESS265/Ch10/ylwang/node28.html|title = Symmetric boundary condition}}</ref> | ||
[[सममित]] सीमा पर स्थितियाँ सीमा के पार कोई द्रव्यमान प्रवाह दर नहीं हैं और सीमा के पार कोई अदिश प्रवाह नहीं है। | [[सममित]] सीमा पर स्थितियाँ सीमा के पार कोई द्रव्यमान प्रवाह दर नहीं हैं और सीमा के पार कोई अदिश प्रवाह नहीं है। | ||
एक अच्छा उदाहरण प्रवाह में | एक अच्छा उदाहरण प्रवाह में सममित बाधा के साथ पाइप प्रवाह का है। बाधा ऊपरी प्रवाह और निचले प्रवाह को प्रतिबिंबित प्रवाह के रूप में विभाजित करती है। | ||
==आवधिक या चक्रीय सीमा स्थिति== | ==आवधिक या चक्रीय सीमा स्थिति== | ||
[[File:Cyclic-Pump Impeller.JPG|thumb|चक्रीय सीमा स्थिति दर्शाने वाला | [[File:Cyclic-Pump Impeller.JPG|thumb|चक्रीय सीमा स्थिति दर्शाने वाला चौथाई|200px]]एक समस्या में अलग प्रकार की [[समरूपता]] से आवधिक फ़ंक्शन या टर्न (ज्यामिति) सीमा स्थिति उत्पन्न होती है। यदि किसी घटक में प्रवाह वितरण में दो बार से अधिक दोहराया गया पैटर्न है, तो इस प्रकार सममित सीमा स्थिति के लिए आवश्यक दर्पण छवि आवश्यकताओं का उल्लंघन होता है। अच्छा उदाहरण स्वेप्ट वेन पंप (चित्र) होगा।<ref>{{cite web |url = http://tarpoff.com/engineering/cyclic_symmetric_BCs.doc | title = चक्रीय सममित बीसी| accessdate = 2013-10-10}}</ref> जहां चिह्नित क्षेत्र को आर-थीटा निर्देशांक में चार बार दोहराया जाता है। चक्रीय-सममित क्षेत्रों में समान प्रवाह चर और वितरण होना चाहिए और प्रत्येक Z-स्लाइस में इसे संतुष्ट करना चाहिए।<ref name="Versteeg1995"/> | ||
==यह भी देखें== | ==यह भी देखें== | ||
{{Commons category|Boundary conditions in computational fluid dynamics}} | {{Commons category|Boundary conditions in computational fluid dynamics}} | ||
Revision as of 19:52, 9 August 2023
द्रव गतिकी में सीमा स्थितियाँ कम्प्यूटेशनल द्रव गतिकी में सीमा मूल्य समस्याओं के लिए बाधाओं का समूह हैं। इन सीमा स्थितियों में इनलेट सीमा स्थितियां, आउटलेट सीमा स्थितियां, दीवार सीमा स्थितियां, निरंतर दबाव सीमा स्थितियां, अक्षमिति सीमा स्थितियां, सममित सीमा स्थितियां और आवधिक या चक्रीय सीमा स्थितियां शामिल हैं।
क्षणिक अवस्था (रासायनिक इंजीनियरिंग) समस्याओं के लिए और चीज़ की आवश्यकता होती है, यानी प्रारंभिक स्थितियाँ जहाँ प्रवाह चर के प्रारंभिक मान प्रवाह डोमेन में नोड्स पर निर्दिष्ट होते हैं।[1] सीएफडी में विभिन्न स्थितियों और उद्देश्यों के लिए विभिन्न प्रकार की सीमा शर्तों का उपयोग किया जाता है और उनकी चर्चा इस प्रकार की जाती है।
इनलेट सीमा शर्तें
प्रवेश सीमा स्थितियों में, सभी प्रवाह चर (अनुसंधान) के वितरण को इनलेट सीमाओं पर मुख्य रूप से प्रवाह वेग पर निर्दिष्ट करने की आवश्यकता होती है।[1] इस प्रकार की सीमा स्थितियाँ सामान्य हैं और अधिकतर निर्दिष्ट की जाती हैं जहाँ इनलेट प्रवाह वेग ज्ञात होता है।
आउटलेट सीमा स्थिति
आउटलेट सीमा स्थितियों में, सभी प्रवाह चर (अनुसंधान) के वितरण को निर्दिष्ट करने की आवश्यकता है, मुख्य रूप से प्रवाह वेग। इसे इनलेट सीमा स्थिति के संयोजन के रूप में सोचा जा सकता है। इस प्रकार की सीमा स्थितियाँ आम हैं और अधिकतर वहीं निर्दिष्ट की जाती हैं जहां आउटलेट वेग ज्ञात होता है।[1]
प्रवाह प्रवाह कंडीशनिंग प्राप्त करता है जहां ज्यामितीय गड़बड़ी से दूर आउटलेट का चयन करने पर प्रवाह दिशा में कोई परिवर्तन नहीं होता है। ऐसे क्षेत्र में, आउटलेट की रूपरेखा तैयार की जा सकती है और दबाव को छोड़कर सभी चर के ढाल को प्रवाह दिशा में शून्य के बराबर किया जा सकता है।
नो-स्लिप सीमा शर्त
पाइप प्रवाह की समस्याओं में सामने आने वाली सबसे आम सीमा नाली की दीवार है। उपयुक्त आवश्यकता को नो-स्लिप स्थिति | नो-स्लिप सीमा स्थिति कहा जाता है, जिसमें वेग का सामान्य घटक शून्य पर तय किया जाता है, और स्पर्शरेखा घटक को दीवार के वेग के बराबर सेट किया जाता है।[1] यह अंतर्ज्ञान के विपरीत हो सकता है, लेकिन प्रयोग और सिद्धांत दोनों में नो-स्लिप स्थिति दृढ़ता से स्थापित की गई है, हालांकि दशकों के विवाद और बहस के बाद ही।[2]
निरंतर दबाव सीमा की स्थिति
इस प्रकार की सीमा स्थिति का उपयोग वहां किया जाता है जहां दबाव के सीमा मान ज्ञात होते हैं और प्रवाह वितरण का सटीक विवरण अज्ञात होता है। इसमें मुख्य रूप से दबाव इनलेट और आउटलेट की स्थिति शामिल है। इस सीमा स्थिति का उपयोग करने वाले विशिष्ट उदाहरणों में उछाल संचालित प्रवाह, एकाधिक आउटलेट के साथ आंतरिक प्रवाह, मुक्त सतह प्रवाह और वस्तुओं के चारों ओर बाहरी प्रवाह शामिल हैं।[1] उदाहरण वायुमंडल में प्रवाह आउटलेट है जहां दबाव वायुमंडलीय है।
अक्षसममितीय सीमा शर्तें
इस सीमा स्थिति में, मॉडल मुख्य अक्ष के संबंध में अक्षसममिति है जैसे कि विशेष आर = आर, सभी θs और प्रत्येक z = Z-स्लाइस पर, प्रत्येक प्रवाह चर का समान मूल्य होता है।[3] अच्छा उदाहरण गोलाकार पाइप में प्रवाह है जहां प्रवाह और पाइप अक्ष मेल खाते हैं।
सममित सीमा स्थिति
इस सीमा स्थिति में, यह माना जाता है कि सीमा के दोनों किनारों पर समान भौतिक प्रक्रियाएं मौजूद हैं।[4] सभी चरों का सीमा से समान दूरी पर समान मान और ग्रेडिएंट होते हैं। यह दर्पण के रूप में कार्य करता है जो दूसरी ओर सभी प्रवाह वितरण को दर्शाता है।[5]
सममित सीमा पर स्थितियाँ सीमा के पार कोई द्रव्यमान प्रवाह दर नहीं हैं और सीमा के पार कोई अदिश प्रवाह नहीं है।
एक अच्छा उदाहरण प्रवाह में सममित बाधा के साथ पाइप प्रवाह का है। बाधा ऊपरी प्रवाह और निचले प्रवाह को प्रतिबिंबित प्रवाह के रूप में विभाजित करती है।
आवधिक या चक्रीय सीमा स्थिति
एक समस्या में अलग प्रकार की समरूपता से आवधिक फ़ंक्शन या टर्न (ज्यामिति) सीमा स्थिति उत्पन्न होती है। यदि किसी घटक में प्रवाह वितरण में दो बार से अधिक दोहराया गया पैटर्न है, तो इस प्रकार सममित सीमा स्थिति के लिए आवश्यक दर्पण छवि आवश्यकताओं का उल्लंघन होता है। अच्छा उदाहरण स्वेप्ट वेन पंप (चित्र) होगा।[6] जहां चिह्नित क्षेत्र को आर-थीटा निर्देशांक में चार बार दोहराया जाता है। चक्रीय-सममित क्षेत्रों में समान प्रवाह चर और वितरण होना चाहिए और प्रत्येक Z-स्लाइस में इसे संतुष्ट करना चाहिए।[1]
यह भी देखें
- प्रवाह कंडीशनिंग
- प्रारंभिक मूल्य समस्या
टिप्पणियाँ
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Henk Kaarle Versteeg; Weeratunge Malalasekera (1995). An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Longman Scientific & Technical. pp. 192–206. ISBN 0-582-21884-5.
- ↑ Prabhakara, Sandeep; Deshpande, M. D. (2004-04-01). "द्रव यांत्रिकी में नो-स्लिप सीमा स्थिति". Resonance (in English). 9 (4): 50–60. doi:10.1007/BF02834856. ISSN 0973-712X. S2CID 124269972.
- ↑ "चक्रीय सममित बीसी". Retrieved 2015-08-09.
- ↑ "चक्रीय सममित बीसी". Retrieved 2013-10-10.
- ↑ "Symmetric boundary condition".
- ↑ "चक्रीय सममित बीसी". Retrieved 2013-10-10.
संदर्भ
- Versteeg (1995). "Chapter 9". An Introduction to Computational Fluid Dynamics The Finite Volume Method, 2/e. Longman Scientific & Technical. pp. 192–206. ISBN 0-582-21884-5.