बहिर्वेशन (एक्सट्रपलेशन): Difference between revisions

From Vigyanwiki
No edit summary
No edit summary
Line 26: Line 26:
=== शांकव===
=== शांकव===


ज्ञात डेटा के अंत के पास पाँच बिंदुओं का उपयोग करके एक [[शंकु खंड]] बनाया जा सकता है। यदि बनाया गया शंकु खंड एक दीर्घवृत्त या वृत्त है, तो बहिर्वेशित होने पर यह वापस लूप करेगा और स्वयं से जुड़ जाएगा। एक एक्सट्रपलेटेड [[परवलय]] या [[ अतिशयोक्ति |अतिशयोक्ति]] स्वं को फिर से सम्मिलित नहीं करेगा, किंतु x-अक्ष के सापेक्ष वापस आ सकता है। इस प्रकार का एक्सट्रपलेशन एक शांकव खंड टेम्पलेट (कागज पर) या एक कंप्यूटर के साथ किया जा सकता है।
ज्ञात डेटा के अंत के पास पाँच बिंदुओं का उपयोग करके एक [[शंकु खंड]] बनाया जा सकता है। यदि बनाया गया शंकु खंड एक दीर्घवृत्त या वृत्त है, तो बहिर्वेशित होने पर यह वापस लूप करेगा और स्वयं से जुड़ जाएगा। एक एक्सट्रपलेटेड [[परवलय]] या [[ अतिशयोक्ति |अतिशयोक्ति]] स्वं को फिर से सम्मिलित नहीं करेगा, किंतु x-अक्ष के सापेक्ष वापस आ सकता है। इस प्रकार का एक्सट्रपलेशन एक शांकव खंड टेम्पलेट (पेपर पर) या एक कंप्यूटर के साथ किया जा सकता है।


=== फ्रेंच वक्र ===
=== फ्रेंच वक्र ===
Line 61: Line 61:
सम्मिश्र समय श्रृंखला के संदर्भ में, कुछ विशेषज्ञों ने पता लगाया है कि एक्सट्रपलेशन अधिक स्पष्ट होता है जब कारण बलों के अपघटन के माध्यम से किया जाता है।<ref>{{cite web|url= http://www.forecastingprinciples.com/paperpdf/Decomposition%20by%20Causal%20Forces.pdf | title = Decomposition by Causal Forces: A Procedure for Forecasting Complex Time Series |author1=J. Scott Armstrong |author2=Fred Collopy |author3=J. Thomas Yokum | year = 2004}}</ref>
सम्मिश्र समय श्रृंखला के संदर्भ में, कुछ विशेषज्ञों ने पता लगाया है कि एक्सट्रपलेशन अधिक स्पष्ट होता है जब कारण बलों के अपघटन के माध्यम से किया जाता है।<ref>{{cite web|url= http://www.forecastingprinciples.com/paperpdf/Decomposition%20by%20Causal%20Forces.pdf | title = Decomposition by Causal Forces: A Procedure for Forecasting Complex Time Series |author1=J. Scott Armstrong |author2=Fred Collopy |author3=J. Thomas Yokum | year = 2004}}</ref>


फ़ंक्शन के बारे में उचित धारणाओं के लिए भी, एक्सट्रपलेशन फ़ंक्शन से गंभीर रूप से भिन्न हो सकता है। उत्कृष्ट उदाहरण पाप (x) और संबंधित त्रिकोणमितीय कार्यों का छोटा शक्ति श्रृंखला प्रतिनिधित्व है। उदाहरण के लिए, केवल x = 0 के पास से डेटा लेकर, हम अनुमान लगा सकते हैं कि फ़ंक्शन sin(x) ~ x के रूप में व्यवहार करता है। x = 0 के निकट में, यह एक उत्कृष्ट अनुमान है। x = 0 से दूर चूँकि, एक्सट्रपलेशन इच्छित रूप से x-अक्ष से दूर चला जाता है जबकि sin(x) [[अंतराल (गणित)]] में रहता है [−1,1]। अथार्त बिना सीमा के त्रुटि बढ़ जाती है।
फ़ंक्शन के बारे में उचित धारणाओं के लिए भी, एक्सट्रपलेशन फ़ंक्शन से गंभीर रूप से भिन्न हो सकता है। उत्कृष्ट उदाहरण पाप (x) और संबंधित त्रिकोणमितीय कार्यों का छोटा शक्ति श्रृंखला प्रतिनिधित्व है। उदाहरण के लिए, केवल x = 0 के पास से डेटा लेकर, हम अनुमान लगा सकते हैं कि फ़ंक्शन sin(x) ~ x के रूप में व्यवहार करता है। x = 0 के निकट में, यह एक उत्कृष्ट अनुमान है। x = 0 से दूर चूँकि, एक्सट्रपलेशन इच्छित रूप से x-अक्ष से दूर चला जाता है जबकि sin(x) [[अंतराल (गणित)]] में रहता है [−1,1] अथार्त बिना सीमा के त्रुटि बढ़ जाती है।


x = 0 के आस-पास पाप (x) की शक्ति श्रृंखला में अधिक शब्द लेने से x = 0 के पास एक बड़े अंतराल पर उत्तम समझौता होगा, किंतु एक्सट्रपलेशन का उत्पादन होगा जो अंततः रैखिक सन्निकटन की तुलना में x -अक्ष से भी तेजी से दूर हो जाएगा।
x = 0 के आस-पास पाप (x) की शक्ति श्रृंखला में अधिक शब्द लेने से x = 0 के पास एक बड़े अंतराल पर उत्तम समझौता होगा, किंतु एक्सट्रपलेशन का उत्पादन होगा जो अंततः रैखिक सन्निकटन की तुलना में x -अक्ष से भी तेजी से दूर हो जाएगा।
Line 69: Line 69:
== सम्मिश्र तल में                                                                                            ==
== सम्मिश्र तल में                                                                                            ==


सम्मिश्र विश्लेषण में, एक्सट्रपलेशन की समस्या को वेरिएबल <math>\hat{z} = 1/z</math> के परिवर्तन से इंटरपोलेशन समस्या में परिवर्तित किया जा सकता है। यह परिवर्तन यूनिट सर्कल के अंदर सम्मिश्र तल के भाग को यूनिट सर्कल के बाहर सम्मिश्र तल के भाग के साथ आदान-प्रदान करता है। विशेष रूप से, अनंत पर संघनन बिंदु को मूल बिंदु पर मैप किया जाता है और इसके विपरीत। चूँकि इस परिवर्तन के साथ सावधानी रखनी चाहिए, क्योंकि मूल फ़ंक्शन में "विशेषताएं" हो सकती हैं, उदाहरण के लिए ध्रुव और अन्य विलक्षणताएं, अनंत पर जो नमूना किए गए डेटा से स्पष्ट नहीं थीं।
सम्मिश्र विश्लेषण में, एक्सट्रपलेशन की समस्या को वेरिएबल <math>\hat{z} = 1/z</math> के परिवर्तन से इंटरपोलेशन समस्या में परिवर्तित किया जा सकता है। यह परिवर्तन यूनिट सर्कल के अंदर सम्मिश्र तल के भाग को यूनिट सर्कल के बाहर सम्मिश्र तल के भाग के साथ आदान-प्रदान करता है। विशेष रूप से, अनंत पर संघनन बिंदु को मूल बिंदु पर मैप किया जाता है और इसके विपरीत। चूँकि इस परिवर्तन के साथ सावधानी रखनी चाहिए, क्योंकि मूल फ़ंक्शन में "विशेषताएं" हो सकती हैं, उदाहरण के लिए ध्रुव और अन्य विलक्षणताएं, अनंत पर जो प्रतिरूप किए गए डेटा से स्पष्ट नहीं थीं।


एक्सट्रपलेशन की एक और समस्या [[विश्लेषणात्मक निरंतरता]] की समस्या से शिथिल रूप से संबंधित है, जहां (समान्यत:) एक फ़ंक्शन (गणित) की एक शक्ति श्रृंखला का प्रतिनिधित्व एक फ़ंक्शन की सीमा के अपने बिंदुओं में से एक पर एक बड़े त्रिज्या के साथ एक शक्ति श्रृंखला का उत्पादन करने के लिए विस्तारित होता है। अभिसरण वास्तव में, एक छोटे क्षेत्र से डेटा का एक सेट एक बड़े क्षेत्र पर एक फ़ंक्शन को एक्सट्रपलेशन करने के लिए उप[[योग]] किया जाता है।
एक्सट्रपलेशन की एक और समस्या [[विश्लेषणात्मक निरंतरता]] की समस्या से शिथिल रूप से संबंधित है, जहां (समान्यत:) एक फ़ंक्शन (गणित) की एक शक्ति श्रृंखला का प्रतिनिधित्व एक फ़ंक्शन की सीमा के अपने बिंदुओं में से एक पर एक बड़े त्रिज्या के साथ एक शक्ति श्रृंखला का उत्पादन करने के लिए विस्तारित होता है। अभिसरण वास्तव में, एक छोटे क्षेत्र से डेटा का एक सेट एक बड़े क्षेत्र पर एक फ़ंक्शन को एक्सट्रपलेशन करने के लिए उप[[योग]] किया जाता है।
Line 75: Line 75:
फिर से, विश्लेषणात्मक निरंतरता को फ़ंक्शन (गणित) सुविधाओं द्वारा विफल किया जा सकता है जो प्रारंभिक डेटा से स्पष्ट नहीं थे।
फिर से, विश्लेषणात्मक निरंतरता को फ़ंक्शन (गणित) सुविधाओं द्वारा विफल किया जा सकता है जो प्रारंभिक डेटा से स्पष्ट नहीं थे।


इसके अतिरिक्त , कोई [[अनुक्रम परिवर्तन]] का उपयोग कर सकता है जैसे पाडे सन्निकटन और [[लेविन-प्रकार अनुक्रम परिवर्तन]] एक्सट्रपलेशन विधियों के रूप में जो शक्ति श्रृंखला के योग का नेतृत्व करते हैं जो अभिसरण के मूल त्रिज्या के बाहर भिन्न होते हैं। इस स्थिति में, अधिकांशतः तर्कसंगत सन्निकटन प्राप्त होता है
इसके अतिरिक्त , कोई [[अनुक्रम परिवर्तन]] का उपयोग कर सकता है जैसे पाडे सन्निकटन और [[लेविन-प्रकार अनुक्रम परिवर्तन]] एक्सट्रपलेशन विधियों के रूप में जो शक्ति श्रृंखला के योग का नेतृत्व करते हैं जो अभिसरण के मूल त्रिज्या के बाहर भिन्न होते हैं। इस स्थिति में, अधिकांशतः तर्कसंगत सन्निकटन प्राप्त होता है।
।


== तेज़ ==
== तेज़ ==
Line 99: Line 98:
  }}</ref>
  }}</ref>
== एक्सट्रपलेशन युक्ति ==
== एक्सट्रपलेशन युक्ति ==
एक्सट्रपलेशन युक्ति अनौपचारिक और बिना परिमाण के युक्ति होते हैं जो इस बात पर जोर देते हैं कि मूल्यों की सीमा से परे कुछ संभवतः सत्य है जिसके लिए इसे सत्य माना जाता है। उदाहरण के लिए, हम आवर्धक चश्मे के माध्यम से जो देखते हैं उसकी वास्तविकता में विश्वास करते हैं क्योंकि यह उस चीज़ से सहमत होता है जिसे हम नग्न आंखों से देखते हैं किंतु यह उससे आगे तक फैली हुई है; हम उस पर विश्वास करते हैं जो हम प्रकाश सूक्ष्मदर्शी के माध्यम से देखते हैं क्योंकि यह आवर्धक चश्मे के माध्यम से हम जो देखते हैं उससे सहमत होते हैं किंतु इससे आगे बढ़ते हैं; और इसी तरह इलेक्ट्रॉन सूक्ष्मदर्शी के लिए। जीव विज्ञान में इस तरह के युक्ति का व्यापक रूप से उपयोग जानवरों के अध्ययन से लेकर मनुष्यों तक और पायलट अध्ययन से व्यापक जनसंख्या तक करने के लिए किया जाता है।<ref>{{cite book |last=Steel |first=Daniel |date=2007 |title=Across the Boundaries: Extrapolation in Biology and Social Science |url=https://oxford.universitypressscholarship.com/view/10.1093/acprof:oso/9780195331448.001.0001/acprof-9780195331448 |location=Oxford |publisher=Oxford University Press |page= |isbn=9780195331448}}</ref>
एक्सट्रपलेशन युक्ति अनौपचारिक और बिना परिमाण के युक्ति होते हैं जो इस बात पर बल देते हैं कि मूल्यों की सीमा से परे कुछ संभवतः सत्य है जिसके लिए इसे सत्य माना जाता है। उदाहरण के लिए, हम आवर्धक चश्मे के माध्यम से जो देखते हैं उसकी वास्तविकता में विश्वास करते हैं क्योंकि यह उस चीज़ से सहमत होता है जिसे हम नग्न आंखों से देखते हैं किंतु यह उससे आगे तक फैली हुई है; हम उस पर विश्वास करते हैं जो हम प्रकाश सूक्ष्मदर्शी के माध्यम से देखते हैं क्योंकि यह आवर्धक चश्मे के माध्यम से हम जो देखते हैं उससे सहमत होते हैं किंतु इससे आगे बढ़ते हैं; और इसी तरह इलेक्ट्रॉन सूक्ष्मदर्शी के लिए। जीव विज्ञान में इस तरह के युक्ति का व्यापक रूप से उपयोग जानवरों के अध्ययन से लेकर मनुष्यों तक और पायलट अध्ययन से व्यापक जनसंख्या तक करने के लिए किया जाता है।<ref>{{cite book |last=Steel |first=Daniel |date=2007 |title=Across the Boundaries: Extrapolation in Biology and Social Science |url=https://oxford.universitypressscholarship.com/view/10.1093/acprof:oso/9780195331448.001.0001/acprof-9780195331448 |location=Oxford |publisher=Oxford University Press |page= |isbn=9780195331448}}</ref>


स्लिपरी स्लोप के युक्ति की तरह, एक्सट्रपलेशन के युक्ति ऐसे कारकों के आधार पर प्रबल या दुर्बल हो सकते हैं कि एक्सट्रपलेशन ज्ञात सीमा से कितनी दूर है।<ref>{{cite journal |last1=Franklin |first1=James |authorlink=James Franklin (philosopher) |date=2013 |title=तर्क जिनकी ताकत निरंतर भिन्नता पर निर्भर करती है|url=http://ojs.uwindsor.ca/ojs/leddy/index.php/informal_logic/article/view/3610/3000 |journal=Journal of Informal Logic |volume=33 |issue=1 |pages=33–56 |doi=10.22329/il.v33i1.3610 |access-date=29 June 2021}}</ref>
स्लिपरी स्लोप के युक्ति की तरह, एक्सट्रपलेशन के युक्ति ऐसे कारकों के आधार पर प्रबल या दुर्बल हो सकते हैं कि एक्सट्रपलेशन ज्ञात सीमा से कितनी दूर है।<ref>{{cite journal |last1=Franklin |first1=James |authorlink=James Franklin (philosopher) |date=2013 |title=तर्क जिनकी ताकत निरंतर भिन्नता पर निर्भर करती है|url=http://ojs.uwindsor.ca/ojs/leddy/index.php/informal_logic/article/view/3610/3000 |journal=Journal of Informal Logic |volume=33 |issue=1 |pages=33–56 |doi=10.22329/il.v33i1.3610 |access-date=29 June 2021}}</ref>
== यह भी देखें ==
== यह भी देखें ==
{{Wiktionary|extrapolation}}
{{Wiktionary|extrapolation}}
Line 123: Line 119:
==टिप्पणियाँ                                                                                                                    ==
==टिप्पणियाँ                                                                                                                    ==
{{reflist}}
{{reflist}}
==संदर्भ==
==संदर्भ==
*''Extrapolation Methods. Theory and Practice'' by C. Brezinski and [[Michela Redivo-Zaglia|M. Redivo Zaglia]], North-Holland, 1991.
*''Extrapolation Methods. Theory and Practice'' by C. Brezinski and [[Michela Redivo-Zaglia|M. Redivo Zaglia]], North-Holland, 1991.

Revision as of 16:03, 30 July 2023

For काल्पनिक कथा का जर्नल, see एक्सट्रपलेशन (पत्रिका). For जॉन मैकलॉघलिन एल्बम, see एक्सट्रपलेशन (एल्बम). For एप्पल टीवी+ सीरीज, see एक्सट्रपलेशन (टीवी श्रृंखला).

गणित में, एक्सट्रपलेशन एक प्रकार का अनुमान है, मूल अवलोकन सीमा से परे, एक वेरिएबल के मान का दूसरे वेरिएबल के साथ संबंध के आधार पर यह प्रक्षेप के समान है, जो ज्ञात अवलोकनों के बीच अनुमान उत्पन्न करता है, किंतु एक्सट्रपलेशन अधिक अनिश्चितता और अर्थहीन परिणाम उत्पन्न करने के उच्च विपत्ति के अधीन है। एक्सट्रपलेशन का अर्थ किसी विक्ट का विस्तार भी हो सकता है: विधि, यह मानते हुए कि समान विधियाँ प्रयुक्त होंगी। एक्सट्रपलेशन मानव अनुभव पर भी प्रयुक्त हो सकता है, ज्ञात अनुभव को किसी ऐसे क्षेत्र में प्रोजेक्ट, विस्तार, या विस्तारित करने के लिए प्रयुक्त हो सकता है जो अज्ञात या पहले से अनुभवी नहीं है जिससे अज्ञात के ज्ञान (समान्यत: अनुमानित) पर पहुंच सकता है।[1] (उदाहरण के लिए एक चालक गाड़ी चलाते समय अपनी दृष्टि से परे सड़क की स्थिति का अनुमान लगाता है)। एक्सट्रपलेशन विधि को आंतरिक पुनर्निर्माण समस्या में प्रयुक्त किया जा सकता है।

एक्सट्रपलेशन समस्या का उदाहरण चित्रण, जिसमें लाल डेटा बिंदुओं को देखते हुए पर नीले बॉक्स में एक सार्थक मान निर्दिष्ट करना सम्मिलित है

विधि

किस एक्सट्रपलेशन पद्धति को प्रयुक्त करने के लिए एक ध्वनि विकल्प उपस्थित डेटा बिंदुओं को बनाने वाली प्रक्रिया के प्राथमिक ज्ञान पर निर्भर करता है। कुछ विशेषज्ञों ने एक्सट्रपलेशन विधियों के मूल्यांकन में कारणात्मक शक्तियों के उपयोग का प्रस्ताव दिया है।[2] महत्वपूर्ण प्रश्न हैं, उदाहरण के लिए, यदि डेटा को निरंतर, सुचारू, संभवतः आवधिक आदि माना जा सकता है।

रैखिक

रैखिक एक्सट्रपलेशन का अर्थ है ज्ञात डेटा के अंत में एक स्पर्श रेखा बनाना और उस सीमा से परे इसका विस्तार करना है। रैखिक एक्सट्रपलेशन केवल अच्छे परिणाम प्रदान करेगा जब इसका उपयोग लगभग रैखिक फ़ंक्शन के ग्राफ़ को विस्तारित करने के लिए किया जाता है या ज्ञात डेटा से बहुत दूर नहीं होता है।

यदि एक्सट्रपलेशन किए जाने वाले बिंदु के निकटतम दो डेटा बिंदु और हैं, तो रैखिक एक्सट्रपलेशन फ़ंक्शन देता है:

(जो रैखिक इंटरपोलेशन के समान है यदि ). सम्मिलित किए जाने के लिए चुने गए डेटा बिंदुओं पर प्रतिगमन विश्लेषण जैसी तकनीकों द्वारा, दो से अधिक बिंदुओं को सम्मिलित करना और रैखिक इंटरपोलेंट के स्लोप का औसत सम्मिलित करना संभव है। यह रैखिक पूर्वानुमान के समान है।

बहुपद

अनुक्रम 1,2,3 का लैग्रेंज एक्सट्रपलेशन। 4 से एक्सट्रपलेशन न्यूनतम डिग्री के बहुपद की ओर जाता है (cyan पंक्ति)।

एक बहुपद वक्र पूरे ज्ञात डेटा के माध्यम से या अंत के पास (रैखिक एक्सट्रपलेशन के लिए दो बिंदु, द्विघात एक्सट्रपलेशन के लिए तीन बिंदु, आदि) बनाया जा सकता है। परिणामी वक्र को तब ज्ञात डेटा के अंत से आगे बढ़ाया जा सकता है। बहुपद एक्सट्रपलेशन समान्यत: लैग्रेंज इंटरपोलेशन के माध्यम से या डेटा को फिट करने वाली न्यूटन श्रृंखला बनाने के लिए परिमित अंतरों की न्यूटन की विधि का उपयोग करके किया जाता है। परिणामी बहुपद का उपयोग डेटा को एक्सट्रपलेशन करने के लिए किया जा सकता है।

उच्च-क्रम बहुपद एक्सट्रपलेशन का उपयोग उचित देखभाल के साथ किया जाना चाहिए। ऊपर दिए गए आंकड़े में डेटा सेट और समस्या के उदाहरण के लिए, ऑर्डर 1 (रैखिक एक्सट्रपलेशन) से ऊपर कुछ भी संभवतः अनुपयोगी मान उत्पन्न करेगा; बहिर्वेशित मूल्य का एक त्रुटि अनुमान बहुपद बहिर्वेशन की डिग्री के साथ बढ़ेगा। यह रूंज की घटना से संबंधित है।

शांकव

ज्ञात डेटा के अंत के पास पाँच बिंदुओं का उपयोग करके एक शंकु खंड बनाया जा सकता है। यदि बनाया गया शंकु खंड एक दीर्घवृत्त या वृत्त है, तो बहिर्वेशित होने पर यह वापस लूप करेगा और स्वयं से जुड़ जाएगा। एक एक्सट्रपलेटेड परवलय या अतिशयोक्ति स्वं को फिर से सम्मिलित नहीं करेगा, किंतु x-अक्ष के सापेक्ष वापस आ सकता है। इस प्रकार का एक्सट्रपलेशन एक शांकव खंड टेम्पलेट (पेपर पर) या एक कंप्यूटर के साथ किया जा सकता है।

फ्रेंच वक्र

फ़्रांसीसी वक्र एक्सट्रपलेशन किसी भी वितरण के लिए उपयुक्त एक विधि है जिसमें घातीय होने की प्रवृत्ति होती है, किंतु त्वरण या मंदी के कारकों के साथ[3] 1987 से यूके में एचआईवी/एड्स के विकास के पूर्वानुमान अनुमान प्रदान करने और कई वर्षों से यूके में वेरिएंट सीजेडी में इस पद्धति का सफलतापूर्वक उपयोग किया गया है। एक अन्य अध्ययन से पता चला है कि एक्सट्रपलेशन पूर्वानुमान परिणामों की समान गुणवत्ता को अधिक सम्मिश्र पूर्वानुमान रणनीतियों के रूप में उत्पन्न कर सकता है।[4]


त्रुटि पूर्वानुमान के साथ ज्यामितीय एक्सट्रपलेशन

अनुक्रम के 3 बिंदुओं और क्षण या सूचकांक के साथ बनाया जा सकता है, इस प्रकार के एक्सट्रपलेशन में ज्ञात श्रृंखला डेटाबेस (ओईआईएस) के बड़े प्रतिशत में पूर्वानुमान में 100% स्पष्टता होती है।[5]

त्रुटि पूर्वानुमान के साथ एक्सट्रपलेशन का उदाहरण:

क्रम = [1,2,3,5]

f1(x,y) = (x) / y

d1 = f1 (3,2)

d2 = f1 (5,3)

m = अंतिम क्रम (5)

n = अंतिम $ अंतिम क्रम

एफएनओएस (m,n,d1,d2) = राउंड ( ( ( n * d1 ) - m ) + ( m * d2 ) )

राउंड $ ((3*1.66)-5) + (5*1.6) = 8

गुणवत्ता

समान्यत:, एक्सट्रपलेशन की एक विशेष विधि की गुणवत्ता विधि द्वारा किए गए कार्य के बारे में धारणाओं से सीमित होती है। यदि विधि मानती है कि डेटा सुचारू है, तो एक गैर-सुचारू कार्य को व्यर्थ विधि से एक्सट्रपलेशन किया जाएगा।

सम्मिश्र समय श्रृंखला के संदर्भ में, कुछ विशेषज्ञों ने पता लगाया है कि एक्सट्रपलेशन अधिक स्पष्ट होता है जब कारण बलों के अपघटन के माध्यम से किया जाता है।[6]

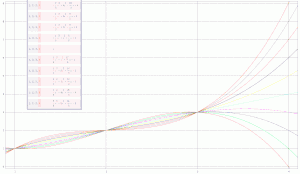
फ़ंक्शन के बारे में उचित धारणाओं के लिए भी, एक्सट्रपलेशन फ़ंक्शन से गंभीर रूप से भिन्न हो सकता है। उत्कृष्ट उदाहरण पाप (x) और संबंधित त्रिकोणमितीय कार्यों का छोटा शक्ति श्रृंखला प्रतिनिधित्व है। उदाहरण के लिए, केवल x = 0 के पास से डेटा लेकर, हम अनुमान लगा सकते हैं कि फ़ंक्शन sin(x) ~ x के रूप में व्यवहार करता है। x = 0 के निकट में, यह एक उत्कृष्ट अनुमान है। x = 0 से दूर चूँकि, एक्सट्रपलेशन इच्छित रूप से x-अक्ष से दूर चला जाता है जबकि sin(x) अंतराल (गणित) में रहता है [−1,1] अथार्त बिना सीमा के त्रुटि बढ़ जाती है।

x = 0 के आस-पास पाप (x) की शक्ति श्रृंखला में अधिक शब्द लेने से x = 0 के पास एक बड़े अंतराल पर उत्तम समझौता होगा, किंतु एक्सट्रपलेशन का उत्पादन होगा जो अंततः रैखिक सन्निकटन की तुलना में x -अक्ष से भी तेजी से दूर हो जाएगा।

यह विचलन एक्सट्रपलेशन विधियों की एक विशिष्ट संपत्ति है और केवल तभी बाधित होता है जब एक्सट्रपलेशन विधि (अनजाने में या जानबूझकर अतिरिक्त जानकारी के कारण) द्वारा ग्रहण किए गए कार्यात्मक रूप एक्सट्रपलेशन किए जा रहे है जो की फ़ंक्शन की प्रकृति का स्पष्ट रूप से प्रतिनिधित्व करते हैं। विशेष समस्याओं के लिए, यह अतिरिक्त जानकारी उपलब्ध हो सकती है, किंतु सामान्य स्थिति में, संभावित व्यवहार के एक व्यावहारिक रूप से छोटे सेट के साथ सभी संभावित कार्य व्यवहारों को संतुष्ट करना असंभव है।

सम्मिश्र तल में

सम्मिश्र विश्लेषण में, एक्सट्रपलेशन की समस्या को वेरिएबल के परिवर्तन से इंटरपोलेशन समस्या में परिवर्तित किया जा सकता है। यह परिवर्तन यूनिट सर्कल के अंदर सम्मिश्र तल के भाग को यूनिट सर्कल के बाहर सम्मिश्र तल के भाग के साथ आदान-प्रदान करता है। विशेष रूप से, अनंत पर संघनन बिंदु को मूल बिंदु पर मैप किया जाता है और इसके विपरीत। चूँकि इस परिवर्तन के साथ सावधानी रखनी चाहिए, क्योंकि मूल फ़ंक्शन में "विशेषताएं" हो सकती हैं, उदाहरण के लिए ध्रुव और अन्य विलक्षणताएं, अनंत पर जो प्रतिरूप किए गए डेटा से स्पष्ट नहीं थीं।

एक्सट्रपलेशन की एक और समस्या विश्लेषणात्मक निरंतरता की समस्या से शिथिल रूप से संबंधित है, जहां (समान्यत:) एक फ़ंक्शन (गणित) की एक शक्ति श्रृंखला का प्रतिनिधित्व एक फ़ंक्शन की सीमा के अपने बिंदुओं में से एक पर एक बड़े त्रिज्या के साथ एक शक्ति श्रृंखला का उत्पादन करने के लिए विस्तारित होता है। अभिसरण वास्तव में, एक छोटे क्षेत्र से डेटा का एक सेट एक बड़े क्षेत्र पर एक फ़ंक्शन को एक्सट्रपलेशन करने के लिए उपयोग किया जाता है।

फिर से, विश्लेषणात्मक निरंतरता को फ़ंक्शन (गणित) सुविधाओं द्वारा विफल किया जा सकता है जो प्रारंभिक डेटा से स्पष्ट नहीं थे।

इसके अतिरिक्त , कोई अनुक्रम परिवर्तन का उपयोग कर सकता है जैसे पाडे सन्निकटन और लेविन-प्रकार अनुक्रम परिवर्तन एक्सट्रपलेशन विधियों के रूप में जो शक्ति श्रृंखला के योग का नेतृत्व करते हैं जो अभिसरण के मूल त्रिज्या के बाहर भिन्न होते हैं। इस स्थिति में, अधिकांशतः तर्कसंगत सन्निकटन प्राप्त होता है।

तेज़

एक्सट्रपोलेटेड डेटा अधिकांशतः कर्नेल फ़ंक्शन में परिवर्तित हो जाता है। डेटा को एक्सट्रपोलेशन के बाद, डेटा का आकार N गुना बढ़ जाता है, यहाँ N लगभग 2-3 है। यदि इस डेटा को किसी ज्ञात कर्नेल फ़ंक्शन में परिवर्तित करने की आवश्यकता है, तो संख्यात्मक गणना तेजी से फूरियर ट्रांसफॉर्म (एफएफटी) के साथ भी N log(N) गुना बढ़ जाएगी। एक एल्गोरिदम उपस्थित है, यह विश्लेषणात्मक रूप से एक्सट्रपलेटेड डेटा के हिस्से से योगदान की गणना करता है। मूल कनवल्शन गणना की तुलना में गणना समय को छोड़ा जा सकता है। इसलिए इस एल्गोरिदम के साथ एक्सट्रपोलेटेड डेटा का उपयोग करके कनवल्शन की गणना लगभग नहीं बढ़ाई जाती है। इसे तीव्र एक्सट्रपलेशन कहा जाता है। तेज़ एक्सट्रपलेशन को सीटी छवि पुनर्निर्माण के लिए प्रयुक्त किया गया है।[7]

एक्सट्रपलेशन युक्ति

एक्सट्रपलेशन युक्ति अनौपचारिक और बिना परिमाण के युक्ति होते हैं जो इस बात पर बल देते हैं कि मूल्यों की सीमा से परे कुछ संभवतः सत्य है जिसके लिए इसे सत्य माना जाता है। उदाहरण के लिए, हम आवर्धक चश्मे के माध्यम से जो देखते हैं उसकी वास्तविकता में विश्वास करते हैं क्योंकि यह उस चीज़ से सहमत होता है जिसे हम नग्न आंखों से देखते हैं किंतु यह उससे आगे तक फैली हुई है; हम उस पर विश्वास करते हैं जो हम प्रकाश सूक्ष्मदर्शी के माध्यम से देखते हैं क्योंकि यह आवर्धक चश्मे के माध्यम से हम जो देखते हैं उससे सहमत होते हैं किंतु इससे आगे बढ़ते हैं; और इसी तरह इलेक्ट्रॉन सूक्ष्मदर्शी के लिए। जीव विज्ञान में इस तरह के युक्ति का व्यापक रूप से उपयोग जानवरों के अध्ययन से लेकर मनुष्यों तक और पायलट अध्ययन से व्यापक जनसंख्या तक करने के लिए किया जाता है।[8]

स्लिपरी स्लोप के युक्ति की तरह, एक्सट्रपलेशन के युक्ति ऐसे कारकों के आधार पर प्रबल या दुर्बल हो सकते हैं कि एक्सट्रपलेशन ज्ञात सीमा से कितनी दूर है।[9]

यह भी देखें

Look up extrapolation in Wiktionary, the free dictionary.

टिप्पणियाँ

  1. ↑ Extrapolation, entry at Merriam–Webster
  2. ↑ J. Scott Armstrong; Fred Collopy (1993). "Causal Forces: Structuring Knowledge for Time-series Extrapolation". Journal of Forecasting. 12 (2): 103–115. CiteSeerX 10.1.1.42.40. doi:10.1002/for.3980120205. S2CID 3233162. Retrieved 2012-01-10.
  3. ↑ AIDSCJDUK.info Main Index
  4. ↑ J. Scott Armstrong (1984). "Forecasting by Extrapolation: Conclusions from Twenty-Five Years of Research". Interfaces. 14 (6): 52–66. CiteSeerX 10.1.1.715.6481. doi:10.1287/inte.14.6.52. S2CID 5805521. Retrieved 2012-01-10.
  5. ↑ V. Nos (2021). "Probnet: Geometric Extrapolation of Integer Sequences with error prediction". Retrieved 2023-03-14.
  6. ↑ J. Scott Armstrong; Fred Collopy; J. Thomas Yokum (2004). "Decomposition by Causal Forces: A Procedure for Forecasting Complex Time Series" (PDF).
  7. ↑ Shuangren Zhao; Kang Yang; Xintie Yang (2011). "Reconstruction from truncated projections using mixed extrapolations of exponential and quadratic functions" (PDF). Journal of X-Ray Science and Technology. 19 (2): 155–72. doi:10.3233/XST-2011-0284. PMID 21606580. Archived from the original (PDF) on 2017-09-29. Retrieved 2014-06-03.
  8. ↑ Steel, Daniel (2007). Across the Boundaries: Extrapolation in Biology and Social Science. Oxford: Oxford University Press. ISBN 9780195331448.
  9. ↑ Franklin, James (2013). "तर्क जिनकी ताकत निरंतर भिन्नता पर निर्भर करती है". Journal of Informal Logic. 33 (1): 33–56. doi:10.22329/il.v33i1.3610. Retrieved 29 June 2021.

संदर्भ

  • Extrapolation Methods. Theory and Practice by C. Brezinski and M. Redivo Zaglia, North-Holland, 1991.
  • Avram Sidi: "Practical Extrapolation Methods: Theory and Applications", Cambridge University Press, ISBN 0-521-66159-5 (2003).
  • Claude Brezinski and Michela Redivo-Zaglia : "Extrapolation and Rational Approximation", Springer Nature, Switzerland, ISBN 9783030584177, (2020).
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=बहिर्वेशन_(एक्सट्रपलेशन)&oldid=249641’