पुनरावर्ती न्यूनतम वर्ग फ़िल्टर: Difference between revisions
No edit summary |
|||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
'''पुनरावर्ती न्यूनतम वर्ग (आरएलएस)''' एक [[अनुकूली फ़िल्टर]] एल्गोरिथ्म है जो पुनरावर्ती रूप से उन गुणांकों को ढूंढता है जो इनपुट संकेत से संबंधित भारित रैखिक न्यूनतम वर्ग लागत | '''पुनरावर्ती न्यूनतम वर्ग (आरएलएस)''' एक [[अनुकूली फ़िल्टर]] एल्गोरिथ्म है जो पुनरावर्ती रूप से उन गुणांकों को ढूंढता है जो इनपुट संकेत से संबंधित भारित रैखिक न्यूनतम वर्ग लागत फलन को कम करते हैं। यह दृष्टिकोण अन्य एल्गोरिदम जैसे कि [[न्यूनतम माध्य वर्ग]] (एलएमएस) के विपरीत है जिसका लक्ष्य माध्य वर्ग त्रुटि को कम करना है। आरएलएस की व्युत्पत्ति में, इनपुट संकेतों को नियतात्मक माना जाता है, जबकि एलएमएस और इसी तरह के एल्गोरिदम के लिए उन्हें [[स्टोकेस्टिक]] माना जाता है। अपने अधिकांश प्रतिस्पर्धियों की तुलना में, आरएलएस अत्यंत तीव्र अभिसरण प्रदर्शित करता है। हालाँकि, यह लाभ उच्च कम्प्यूटेशनल सम्मिश्रता की कीमत पर मिलता है। | ||
==प्रेरणा== | ==प्रेरणा== | ||
आरएलएस की खोज गॉस ने की थी, लेकिन 1950 तक अप्रयुक्त या नजरअंदाज कर दिया गया था, जब प्लैकेट ने 1821 में गॉस के मूल कार्य को फिर से खोजा था। सामान्य तौर पर, आरएलएस का उपयोग किसी भी समस्या को हल करने के लिए किया जा सकता है जिसे अनुकूली फिल्टर द्वारा हल किया जा सकता है। उदाहरण के लिए, मान लीजिए कि | आरएलएस की खोज गॉस ने की थी, लेकिन 1950 तक अप्रयुक्त या नजरअंदाज कर दिया गया था, जब प्लैकेट ने 1821 में गॉस के मूल कार्य को फिर से खोजा था। सामान्य तौर पर, आरएलएस का उपयोग किसी भी समस्या को हल करने के लिए किया जा सकता है जिसे अनुकूली फिल्टर द्वारा हल किया जा सकता है। उदाहरण के लिए, मान लीजिए कि संकेत <math>d(n)</math> प्रतिध्वनि वाले, ध्वनि वाले चैनल पर प्रसारित होता है जिसके कारण इसे प्राप्त किया जाता है | ||
:<math>x(n)=\sum_{k=0}^q b_n(k) d(n-k)+v(n)</math> | :<math>x(n)=\sum_{k=0}^q b_n(k) d(n-k)+v(n)</math> | ||
| Line 8: | Line 8: | ||
:<math>d(n) \approx \sum_{k=0}^{p} w(k)x(n-k)=\mathbf{w}^\mathit{T} \mathbf{x}_n</math> | :<math>d(n) \approx \sum_{k=0}^{p} w(k)x(n-k)=\mathbf{w}^\mathit{T} \mathbf{x}_n</math> | ||
जहां <math>\mathbf{x}_n = [x(n)\quad x(n-1)\quad\ldots\quad x(n-p)]^T</math> कॉलम सदिश है जिसमें <math>x(n)</math> के सबसे हाल के नमूने <math>p+1</math> | जहां <math>\mathbf{x}_n = [x(n)\quad x(n-1)\quad\ldots\quad x(n-p)]^T</math> कॉलम सदिश है जिसमें <math>x(n)</math> के सबसे हाल के नमूने <math>p+1</math> सम्मिलित हैं। प्राप्त वांछित संकेत का अनुमान है | ||
:<math>\hat{d}(n) = \sum_{k=0}^{p} w_n(k)x(n-k)=\mathbf{w}_n^\mathit{T} \mathbf{x}_n</math> | :<math>\hat{d}(n) = \sum_{k=0}^{p} w_n(k)x(n-k)=\mathbf{w}_n^\mathit{T} \mathbf{x}_n</math> | ||
| Line 15: | Line 15: | ||
जैसे-जैसे समय बढ़ता है, <math>\mathbf{w}_{n+1}</math>के लिए नए अनुमान को खोजने के लिए न्यूनतम वर्ग एल्गोरिथ्म को पूरी तरह से दोबारा करने से बचना चाहिए, <math>\mathbf{w}_n</math> के संदर्भ में। | जैसे-जैसे समय बढ़ता है, <math>\mathbf{w}_{n+1}</math>के लिए नए अनुमान को खोजने के लिए न्यूनतम वर्ग एल्गोरिथ्म को पूरी तरह से दोबारा करने से बचना चाहिए, <math>\mathbf{w}_n</math> के संदर्भ में। | ||
आरएलएस एल्गोरिदम का लाभ यह है कि आव्यूह को उलटने की कोई आवश्यकता नहीं है, जिससे कम्प्यूटेशनल लागत बचती है। | आरएलएस एल्गोरिदम का लाभ यह है कि आव्यूह को उलटने की कोई आवश्यकता नहीं है, जिससे कम्प्यूटेशनल लागत बचती है। अन्य लाभ यह है कि यह [[कलमन फ़िल्टर]] जैसे परिणामों के पीछे अंतर्ज्ञान प्रदान करता है। | ||
==विचार-विमर्श== | ==विचार-विमर्श== | ||
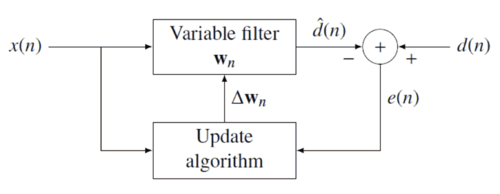
आरएलएस फ़िल्टर के पीछे का विचार फ़िल्टर गुणांक <math>\mathbf{w}_n</math> का उचित चयन करके और नए डेटा आने पर फ़िल्टर को अपडेट करके लागत | आरएलएस फ़िल्टर के पीछे का विचार फ़िल्टर गुणांक <math>\mathbf{w}_n</math> का उचित चयन करके और नए डेटा आने पर फ़िल्टर को अपडेट करके लागत फलन <math>C</math> को कम करना है। त्रुटि संकेत <math>e(n)</math> और वांछित सिग्नल <math>d(n)</math> को नीचे ऋणात्मक प्रतिक्रिया आरेख में परिभाषित किया गया है: | ||
[[File:AdaptiveFilter C.png|500px]] | [[File:AdaptiveFilter C.png|500px]] | ||
| Line 25: | Line 25: | ||
:<math>e(n)=d(n)-\hat{d}(n)</math> | :<math>e(n)=d(n)-\hat{d}(n)</math> | ||
भारित न्यूनतम वर्ग त्रुटि | भारित न्यूनतम वर्ग त्रुटि फलन <math>C</math>- जिस लागत फलन को हम कम करना चाहते हैं - वह फलन <math>e(n)</math> है इसलिए फ़िल्टर गुणांक पर भी निर्भर है: | ||
:<math>C(\mathbf{w}_n)=\sum_{i=0}^n\lambda^{n-i}e^2(i)</math> | :<math>C(\mathbf{w}_n)=\sum_{i=0}^n\lambda^{n-i}e^2(i)</math> | ||
जहाँ <math>0<\lambda\le 1</math> "विस्मृति कारक" है जो पुराने त्रुटि नमूनों को तेजी से कम महत्व देता है। | जहाँ <math>0<\lambda\le 1</math> "विस्मृति कारक" है जो पुराने त्रुटि नमूनों को तेजी से कम महत्व देता है। | ||
गुणांक | गुणांक सदिश <math>\mathbf{w}_{n}</math> की सभी प्रविष्टियों <math>k</math> के लिए आंशिक व्युत्पन्न लेकर और परिणामों को शून्य पर सेट करके लागत फलन को न्यूनतम किया जाता है। | ||
:<math>\frac{\partial C(\mathbf{w}_n)}{\partial w_n(k)}=\sum_{i=0}^n 2\lambda^{n-i}e(i)\cdot \frac{\partial e(i)}{\partial w_n(k)}=-\sum_{i=0}^n 2\lambda^{n-i}e(i)\,x(i-k)=0 \qquad k=0,1,\ldots,p</math> | :<math>\frac{\partial C(\mathbf{w}_n)}{\partial w_n(k)}=\sum_{i=0}^n 2\lambda^{n-i}e(i)\cdot \frac{\partial e(i)}{\partial w_n(k)}=-\sum_{i=0}^n 2\lambda^{n-i}e(i)\,x(i-k)=0 \qquad k=0,1,\ldots,p</math> | ||
अगला, प्रतिस्थापित करें <math>e(n)</math> त्रुटि संकेत की परिभाषा के साथ | अगला, प्रतिस्थापित करें <math>e(n)</math> त्रुटि संकेत की परिभाषा के साथ | ||
| Line 37: | Line 37: | ||
इस रूप को आव्यूह के संदर्भ में व्यक्त किया जा सकता है। | इस रूप को आव्यूह के संदर्भ में व्यक्त किया जा सकता है। | ||
:<math>\mathbf{R}_{x}(n)\,\mathbf{w}_{n}=\mathbf{r}_{dx}(n)</math> | :<math>\mathbf{R}_{x}(n)\,\mathbf{w}_{n}=\mathbf{r}_{dx}(n)</math> | ||
जहाँ <math>\mathbf{R}_{x}(n)</math> के लिए भारित [[नमूना माध्य और नमूना सहप्रसरण]] <math>x(n)</math>आव्यूह है, और <math>\mathbf{r}_{dx}(n)</math> के बीच [[ क्रॉस-सहप्रसरण |परस्पर सहप्रसरण]] के लिए समतुल्य अनुमान <math>d(n)</math> और <math>x(n)</math> है इस अभिव्यक्ति के आधार पर हम ऐसे गुणांक पाते हैं जो लागत | जहाँ <math>\mathbf{R}_{x}(n)</math> के लिए भारित [[नमूना माध्य और नमूना सहप्रसरण]] <math>x(n)</math>आव्यूह है, और <math>\mathbf{r}_{dx}(n)</math> के बीच [[ क्रॉस-सहप्रसरण |परस्पर सहप्रसरण]] के लिए समतुल्य अनुमान <math>d(n)</math> और <math>x(n)</math> है इस अभिव्यक्ति के आधार पर हम ऐसे गुणांक पाते हैं जो लागत फलन को कम करते हैं। | ||
:<math>\mathbf{w}_{n}=\mathbf{R}_{x}^{-1}(n)\,\mathbf{r}_{dx}(n)</math> | :<math>\mathbf{w}_{n}=\mathbf{R}_{x}^{-1}(n)\,\mathbf{r}_{dx}(n)</math> | ||
यह विचार-विमर्श का मुख्य परिणाम है। | यह विचार-विमर्श का मुख्य परिणाम है। | ||
== λ का चयन करना == | == λ का चयन करना == | ||
<math>\lambda</math> जितना छोटा होगा, सहसंयोजक आव्यूह में पिछले नमूनों का योगदान उतना ही छोटा होगा। यह फ़िल्टर को हाल के नमूनों के प्रति अधिक संवेदनशील बनाता है, जिसका अर्थ है कि फ़िल्टर गुणांक में अधिक उतार-चढ़ाव। <math>\lambda=1</math> केस को ग्रोइंग विंडो आरएलएस एल्गोरिथम के रूप में जाना जाता है। व्यवहार में, <math>\lambda</math> को | <math>\lambda</math> जितना छोटा होगा, सहसंयोजक आव्यूह में पिछले नमूनों का योगदान उतना ही छोटा होगा। यह फ़िल्टर को हाल के नमूनों के प्रति अधिक संवेदनशील बनाता है, जिसका अर्थ है कि फ़िल्टर गुणांक में अधिक उतार-चढ़ाव। <math>\lambda=1</math> केस को ग्रोइंग विंडो आरएलएस एल्गोरिथम के रूप में जाना जाता है। व्यवहार में, <math>\lambda</math> को सामान्यतः 0.98 और 1 के बीच चुना जाता है।<ref>Emannual C. Ifeacor, Barrie W. Jervis. Digital signal processing: a practical approach, second edition. Indianapolis: Pearson Education Limited, 2002, p. 718</ref> प्रकार-II अधिकतम संभावना अनुमान का उपयोग करके डेटा के एक सेट से इष्टतम <math>\lambda</math> का अनुमान लगाया जा सकता है।<ref>Steven Van Vaerenbergh, Ignacio Santamaría, Miguel Lázaro-Gredilla [http://gtas.unican.es/files/pub/stkrls_mlsp2012.pdf "Estimation of the forgetting factor in kernel recursive least squares"], 2012 IEEE International Workshop on Machine Learning for Signal Processing, 2012, accessed June 23, 2016.</ref> | ||
<!-- someone might like to include a diagram to show said fluctuations --> | <!-- someone might like to include a diagram to show said fluctuations --> | ||
==पुनरावर्ती एल्गोरिथ्म== | ==पुनरावर्ती एल्गोरिथ्म== | ||
विचार-विमर्श के परिणामस्वरूप गुणांक सदिश निर्धारित करने के लिए एक एकल समीकरण तैयार हुआ जो लागत | विचार-विमर्श के परिणामस्वरूप गुणांक सदिश निर्धारित करने के लिए एक एकल समीकरण तैयार हुआ जो लागत फलन को न्यूनतम करता है। इस अनुभाग में हम प्रपत्र का पुनरावर्ती समाधान प्राप्त करना चाहते हैं। | ||
:<math>\mathbf{w}_{n}=\mathbf{w}_{n-1}+\Delta\mathbf{w}_{n-1}</math> | :<math>\mathbf{w}_{n}=\mathbf{w}_{n-1}+\Delta\mathbf{w}_{n-1}</math> | ||
जहाँ <math>\Delta\mathbf{w}_{n-1}</math> समय पर एक सुधार कारक <math>{n-1}</math> है। हम क्रॉस सहप्रसरण को व्यक्त करके पुनरावर्ती एल्गोरिदम की व्युत्पत्ति | जहाँ <math>\Delta\mathbf{w}_{n-1}</math> समय पर एक सुधार कारक <math>{n-1}</math> है। हम क्रॉस सहप्रसरण को व्यक्त करके पुनरावर्ती एल्गोरिदम की व्युत्पत्ति प्रारम्भ करते हैं <math>\mathbf{r}_{dx}(n)</math> के अनुसार <math>\mathbf{r}_{dx}(n-1)</math> | ||
:{| | :{| | ||
|- | |- | ||
| Line 151: | Line 151: | ||
|<math>=\lambda\mathbf{P}(n)\,\mathbf{r}_{dx}(n-1)+d(n)\mathbf{P}(n)\,\mathbf{x}(n)</math> | |<math>=\lambda\mathbf{P}(n)\,\mathbf{r}_{dx}(n-1)+d(n)\mathbf{P}(n)\,\mathbf{x}(n)</math> | ||
|} | |} | ||
दूसरा चरण की पुनरावर्ती परिभाषा से अनुसरण करता है <math>\mathbf{r}_{dx}(n )</math>. आगे हम की पुनरावर्ती परिभाषा को | दूसरा चरण की पुनरावर्ती परिभाषा से अनुसरण करता है <math>\mathbf{r}_{dx}(n )</math>. आगे हम की पुनरावर्ती परिभाषा को सम्मिलित करते हैं <math>\mathbf{P}(n)</math> के वैकल्पिक रूप के साथ <math>\mathbf{g}(n)</math> और प्राप्त | ||
:{| | :{| | ||
|- | |- | ||
| Line 181: | Line 181: | ||
यह सहज रूप से संतोषजनक परिणाम इंगित करता है कि सुधार कारक त्रुटि और लाभ सदिश दोनों के लिए सीधे आनुपातिक है, जो भार कारक <math>\lambda</math> के माध्यम से नियंत्रित करता है कि कितनी संवेदनशीलता वांछित है. | यह सहज रूप से संतोषजनक परिणाम इंगित करता है कि सुधार कारक त्रुटि और लाभ सदिश दोनों के लिए सीधे आनुपातिक है, जो भार कारक <math>\lambda</math> के माध्यम से नियंत्रित करता है कि कितनी संवेदनशीलता वांछित है. | ||
== | ==आरएलएस एल्गोरिदम सारांश== | ||
पी-वें | पी-वें क्रम आरएलएस फ़िल्टर के लिए आरएलएस एल्गोरिदम को संक्षेप में प्रस्तुत किया जा सकता है | ||
{| | {| | ||
|- | |- | ||
| | | पैरामीटर: || <math>p=</math> फ़िल्टर क्रम | ||
|- | |- | ||
| || <math>\lambda=</math> | | || <math>\lambda=</math> विस्मृति कारक | ||
|- | |- | ||
| || <math>\delta=</math> | | || <math>\delta=</math> आरंभ करने के लिए मूल्य <math>\mathbf{P}(0)</math> | ||
|- | |- | ||
| | |आरंभीकरण: || <math>\mathbf{w}(0)=0</math>, | ||
|- | |- | ||
| ||<math>x(k)=0, k=-p,\dots,-1</math>, | | ||<math>x(k)=0, k=-p,\dots,-1</math>, | ||
| Line 197: | Line 197: | ||
| ||<math>d(k)=0, k=-p,\dots,-1</math> | | ||<math>d(k)=0, k=-p,\dots,-1</math> | ||
|- | |- | ||
| ||<math>\mathbf{P}(0)=\delta I</math> | | ||<math>\mathbf{P}(0)=\delta I</math> जहाँ <math>I</math> रैंक की सर्वसमिका आव्यूह <math>p+1</math> है | ||
|- | |- | ||
| | |गणना: || For <math>n=1,2,\dots </math> | ||
|- | |- | ||
||| | ||| | ||
| Line 222: | Line 222: | ||
|} | |} | ||
के लिए प्रत्यावर्तन <math>P</math> बीजगणितीय रिकाटी समीकरण का अनुसरण करता है और इस प्रकार कलमन फिल्टर के समानांतर खींचता है।<ref>Welch, Greg and Bishop, Gary [http://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf "An Introduction to the Kalman Filter"], Department of Computer Science, University of North Carolina at Chapel Hill, September 17, 1997, accessed July 19, 2011.</ref> | के लिए प्रत्यावर्तन <math>P</math> बीजगणितीय रिकाटी समीकरण का अनुसरण करता है और इस प्रकार कलमन फिल्टर के समानांतर खींचता है।<ref>Welch, Greg and Bishop, Gary [http://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf "An Introduction to the Kalman Filter"], Department of Computer Science, University of North Carolina at Chapel Hill, September 17, 1997, accessed July 19, 2011.</ref> | ||
==लैटिस पुनरावर्ती न्यूनतम वर्ग फ़िल्टर (LRLS)== | |||
'''लैटिस पुनरावर्ती न्यूनतम वर्ग''' अनुकूली फ़िल्टर मानक आरएलएस से संबंधित है, सिवाय इसके कि इसके लिए कम अंकगणितीय संचालन (आदेश ''एन'') की आवश्यकता होती है।<ref>Diniz, Paulo S.R., "Adaptive Filtering: Algorithms and Practical Implementation", Springer Nature Switzerland AG 2020, Chapter 7: Adaptive Lattice-Based RLS Algorithms. https://doi.org/10.1007/978-3-030-29057-3_7</ref> यह पारंपरिक एलएमएस एल्गोरिदम पर अतिरिक्त लाभ प्रदान करता है जैसे कि तेज अभिसरण दर, मॉड्यूलर संरचना, और इनपुट सहसंबंध आव्यूह के ईजेनवैल्यू प्रसार में भिन्नता के प्रति असंवेदनशीलता। वर्णित LRLS एल्गोरिदम पिछली त्रुटियों पर आधारित है और इसमें सामान्यीकृत फॉर्म सम्मिलित है। व्युत्पत्ति मानक आरएलएस एल्गोरिथ्म के समान है और की परिभाषा पर आधारित है <math>d(k)\,\!</math> आगे की पूर्वानुमान के स्थिति में, हमारे पास है <math>d(k) = x(k)\,\!</math> इनपुट संकेत के साथ <math>x(k-1)\,\!</math> सबसे अद्यतित नमूने के रूप में। पिछड़े पूर्वानुमान <math>d(k) = x(k-i-1)\,\!</math>की स्थिति है, जहां i भूतपूर्व में नमूने का सूचकांक है जिसकी हम पूर्वानुमान करना चाहते हैं, और इनपुट संकेत <math>x(k)\,\!</math> सबसे नवीन नमूना है।<ref>Albu, Kadlec, Softley, Matousek, Hermanek, Coleman, Fagan [http://wwwdsp.ucd.ie/dspfiles/main_files/pdf_files/hsla_fpl2001.pdf "Implementation of (Normalised) RLS Lattice on Virtex"], Digital Signal Processing, 2001, accessed December 24, 2011.</ref> | |||
== | |||
===पैरामीटर सारांश=== | ===पैरामीटर सारांश=== | ||
| Line 233: | Line 230: | ||
:<math>\kappa_b(k,i)\,\!</math> पश्चगामी परावर्तन गुणांक है | :<math>\kappa_b(k,i)\,\!</math> पश्चगामी परावर्तन गुणांक है | ||
:<math>e_f(k,i)\,\!</math> तात्कालिक पूर्ववर्ती अग्रगामी | :<math>e_f(k,i)\,\!</math> तात्कालिक पूर्ववर्ती अग्रगामी पूर्वानुमान त्रुटि का प्रतिनिधित्व करता है | ||
:<math>e_b(k,i)\,\!</math> तात्कालिक पश्चगामी पूर्वानुमान त्रुटि का प्रतिनिधित्व करता है | :<math>e_b(k,i)\,\!</math> तात्कालिक पश्चगामी पूर्वानुमान त्रुटि का प्रतिनिधित्व करता है | ||
| Line 247: | Line 244: | ||
:<math>\varepsilon\,\!</math> एक छोटा धनात्मक स्थिरांक है जो 0.01 हो सकता है | :<math>\varepsilon\,\!</math> एक छोटा धनात्मक स्थिरांक है जो 0.01 हो सकता है | ||
=== | ===LRLS एल्गोरिदम सारांश=== | ||
LRLS फ़िल्टर के लिए एल्गोरिदम को संक्षेप में प्रस्तुत किया जा सकता है | |||
{| | {| | ||
|- | |- | ||
| | | आरंभीकरण: | ||
|- | |- | ||
||| For <math display=inline>i = 0,1,\ldots,N</math> | ||| For <math display=inline>i = 0,1,\ldots,N</math> | ||
| Line 265: | Line 262: | ||
||| End | ||| End | ||
|- | |- | ||
| | | गणना: | ||
|- | |- | ||
||| For <math display=inline>k \ge 0</math> | ||| For <math display=inline>k \ge 0</math> | ||
| Line 309: | Line 306: | ||
||| | ||| | ||
|} | |} | ||
==सामान्यीकृत लैटिस पुनरावर्ती न्यूनतम वर्ग फ़िल्टर (NLRLS)== | |||
LRLS के सामान्यीकृत रूप में कम पुनरावर्तन और चर हैं। इसकी गणना एल्गोरिदम के आंतरिक चर के लिए सामान्यीकरण लागू करके की जा सकती है जो उनके परिमाण को एक से सीमित रखेगा। इसका उपयोग आमतौर पर वास्तविक समय के अनुप्रयोगों में नहीं किया जाता है क्योंकि विभाजन और वर्ग-रूट संचालन की संख्या उच्च कम्प्यूटेशनल भार के साथ आती है। | |||
===NLRLS एल्गोरिदम सारांश=== | |||
NLRLS फ़िल्टर के लिए एल्गोरिदम को संक्षेप में प्रस्तुत किया जा सकता है | |||
=== | |||
{| | {| | ||
|- | |- | ||
| | | आरंभीकरण: | ||
|- | |- | ||
||| For <math display=inline>i = 0,1,\ldots,N.</math> | ||| For <math display=inline>i = 0,1,\ldots,N.</math> | ||
| Line 332: | Line 327: | ||
||| {{pad|2em}}<math>\sigma_x^2(-1) = \lambda\sigma_d^2(-1) = \varepsilon\,\!</math> | ||| {{pad|2em}}<math>\sigma_x^2(-1) = \lambda\sigma_d^2(-1) = \varepsilon\,\!</math> | ||
|- | |- | ||
| | | गणना: | ||
|- | |- | ||
||| For <math display=inline>k \ge 0</math> | ||| For <math display=inline>k \ge 0</math> | ||
| Line 364: | Line 359: | ||
||| | ||| | ||
|} | |} | ||
==यह भी देखें== | ==यह भी देखें== | ||
*अनुकूली फ़िल्टर | *अनुकूली फ़िल्टर | ||
*[[कर्नेल अनुकूली फ़िल्टर]] | *[[कर्नेल अनुकूली फ़िल्टर]] | ||
*[[न्यूनतम माध्य वर्ग फ़िल्टर]] | *[[न्यूनतम माध्य वर्ग फ़िल्टर]] | ||
*[[शून्य-बल तुल्यकारक]] | *[[शून्य-बल तुल्यकारक|जीरो-फोर्सिंग इक्वलाइज़र]] | ||
==संदर्भ== | ==संदर्भ== | ||
| Line 379: | Line 372: | ||
* R.L.Plackett, ''Some Theorems in Least Squares'', Biometrika, 1950, 37, 149–157, {{ISSN|0006-3444}} | * R.L.Plackett, ''Some Theorems in Least Squares'', Biometrika, 1950, 37, 149–157, {{ISSN|0006-3444}} | ||
* C.F.Gauss, ''Theoria combinationis observationum erroribus minimis obnoxiae'', 1821, Werke, 4. Gottinge | * C.F.Gauss, ''Theoria combinationis observationum erroribus minimis obnoxiae'', 1821, Werke, 4. Gottinge | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
{{Reflist}} | {{Reflist}} | ||
{{DEFAULTSORT:Recursive Least Squares Filter}} | {{DEFAULTSORT:Recursive Least Squares Filter}} [Category:Statistical signal processi | ||
[[Category: Machine Translated Page]] | [[Category:Created On 25/07/2023|Recursive Least Squares Filter]] | ||
[[Category: | [[Category:Machine Translated Page|Recursive Least Squares Filter]] | ||
[[Category:Pages with script errors|Recursive Least Squares Filter]] | |||
[[Category:Templates Vigyan Ready|Recursive Least Squares Filter]] | |||
[[Category:अंकीय संकेत प्रक्रिया|Recursive Least Squares Filter]] | |||
[[Category:फ़िल्टर सिद्धांत|Recursive Least Squares Filter]] | |||
[[Category:सांख्यिकीय संकेत प्रक्रिया|Recursive Least Squares Filter]] | |||
Latest revision as of 16:55, 21 August 2023
पुनरावर्ती न्यूनतम वर्ग (आरएलएस) एक अनुकूली फ़िल्टर एल्गोरिथ्म है जो पुनरावर्ती रूप से उन गुणांकों को ढूंढता है जो इनपुट संकेत से संबंधित भारित रैखिक न्यूनतम वर्ग लागत फलन को कम करते हैं। यह दृष्टिकोण अन्य एल्गोरिदम जैसे कि न्यूनतम माध्य वर्ग (एलएमएस) के विपरीत है जिसका लक्ष्य माध्य वर्ग त्रुटि को कम करना है। आरएलएस की व्युत्पत्ति में, इनपुट संकेतों को नियतात्मक माना जाता है, जबकि एलएमएस और इसी तरह के एल्गोरिदम के लिए उन्हें स्टोकेस्टिक माना जाता है। अपने अधिकांश प्रतिस्पर्धियों की तुलना में, आरएलएस अत्यंत तीव्र अभिसरण प्रदर्शित करता है। हालाँकि, यह लाभ उच्च कम्प्यूटेशनल सम्मिश्रता की कीमत पर मिलता है।
प्रेरणा
आरएलएस की खोज गॉस ने की थी, लेकिन 1950 तक अप्रयुक्त या नजरअंदाज कर दिया गया था, जब प्लैकेट ने 1821 में गॉस के मूल कार्य को फिर से खोजा था। सामान्य तौर पर, आरएलएस का उपयोग किसी भी समस्या को हल करने के लिए किया जा सकता है जिसे अनुकूली फिल्टर द्वारा हल किया जा सकता है। उदाहरण के लिए, मान लीजिए कि संकेत प्रतिध्वनि वाले, ध्वनि वाले चैनल पर प्रसारित होता है जिसके कारण इसे प्राप्त किया जाता है
जहां योगात्मक शोर का प्रतिनिधित्व करता है। आरएलएस फ़िल्टर का उद्देश्य -टैप FIR फ़िल्टर के उपयोग से वांछित संकेत को पुनर्प्राप्त करना है, :
जहां कॉलम सदिश है जिसमें के सबसे हाल के नमूने सम्मिलित हैं। प्राप्त वांछित संकेत का अनुमान है
फ़िल्टर के मापदंडों का अनुमान लगाना है, और प्रत्येक समय पर हम वर्तमान अनुमान को और अनुकूलित न्यूनतम-वर्ग अनुमान को के रूप में संदर्भित करते हैं। जैसा कि नीचे दिखाया गया है, भी एक कॉलम सदिश है, और ट्रांसपोज़, एक पंक्ति सदिश है। आव्यूह गुणनफल (जो कि डॉट गुणनफल है और , एक अदिश राशि है। अनुमान "अच्छा" है यदि कुछ न्यूनतम वर्ग अर्थों में परिमाण में छोटा है।
जैसे-जैसे समय बढ़ता है, के लिए नए अनुमान को खोजने के लिए न्यूनतम वर्ग एल्गोरिथ्म को पूरी तरह से दोबारा करने से बचना चाहिए, के संदर्भ में।
आरएलएस एल्गोरिदम का लाभ यह है कि आव्यूह को उलटने की कोई आवश्यकता नहीं है, जिससे कम्प्यूटेशनल लागत बचती है। अन्य लाभ यह है कि यह कलमन फ़िल्टर जैसे परिणामों के पीछे अंतर्ज्ञान प्रदान करता है।
विचार-विमर्श
आरएलएस फ़िल्टर के पीछे का विचार फ़िल्टर गुणांक का उचित चयन करके और नए डेटा आने पर फ़िल्टर को अपडेट करके लागत फलन को कम करना है। त्रुटि संकेत और वांछित सिग्नल को नीचे ऋणात्मक प्रतिक्रिया आरेख में परिभाषित किया गया है:
त्रुटि अनुमान के माध्यम से फ़िल्टर गुणांक पर परोक्ष रूप से निर्भर करती है:
भारित न्यूनतम वर्ग त्रुटि फलन - जिस लागत फलन को हम कम करना चाहते हैं - वह फलन है इसलिए फ़िल्टर गुणांक पर भी निर्भर है:
जहाँ "विस्मृति कारक" है जो पुराने त्रुटि नमूनों को तेजी से कम महत्व देता है।
गुणांक सदिश की सभी प्रविष्टियों के लिए आंशिक व्युत्पन्न लेकर और परिणामों को शून्य पर सेट करके लागत फलन को न्यूनतम किया जाता है।
अगला, प्रतिस्थापित करें त्रुटि संकेत की परिभाषा के साथ
समीकरण को पुनर्व्यवस्थित करने से परिणाम प्राप्त होते हैं।
इस रूप को आव्यूह के संदर्भ में व्यक्त किया जा सकता है।
जहाँ के लिए भारित नमूना माध्य और नमूना सहप्रसरण आव्यूह है, और के बीच परस्पर सहप्रसरण के लिए समतुल्य अनुमान और है इस अभिव्यक्ति के आधार पर हम ऐसे गुणांक पाते हैं जो लागत फलन को कम करते हैं।
यह विचार-विमर्श का मुख्य परिणाम है।
λ का चयन करना
जितना छोटा होगा, सहसंयोजक आव्यूह में पिछले नमूनों का योगदान उतना ही छोटा होगा। यह फ़िल्टर को हाल के नमूनों के प्रति अधिक संवेदनशील बनाता है, जिसका अर्थ है कि फ़िल्टर गुणांक में अधिक उतार-चढ़ाव। केस को ग्रोइंग विंडो आरएलएस एल्गोरिथम के रूप में जाना जाता है। व्यवहार में, को सामान्यतः 0.98 और 1 के बीच चुना जाता है।[1] प्रकार-II अधिकतम संभावना अनुमान का उपयोग करके डेटा के एक सेट से इष्टतम का अनुमान लगाया जा सकता है।[2]
पुनरावर्ती एल्गोरिथ्म
विचार-विमर्श के परिणामस्वरूप गुणांक सदिश निर्धारित करने के लिए एक एकल समीकरण तैयार हुआ जो लागत फलन को न्यूनतम करता है। इस अनुभाग में हम प्रपत्र का पुनरावर्ती समाधान प्राप्त करना चाहते हैं।
जहाँ समय पर एक सुधार कारक है। हम क्रॉस सहप्रसरण को व्यक्त करके पुनरावर्ती एल्गोरिदम की व्युत्पत्ति प्रारम्भ करते हैं के अनुसार
जहाँ है आयामी डेटा सदिश
वैसे ही हम व्यक्त करते हैं के अनुसार द्वारा
गुणांक सदिश उत्पन्न करने के लिए हम नियतात्मक ऑटो-सहप्रसरण आव्यूह के व्युत्क्रम में रुचि रखते हैं। उस कार्य के लिए वुडबरी आव्यूह सर्वसमिका काम आती है।
is -by- is -by-1 (column vector) is 1-by- (row vector) is the 1-by-1 identity matrix
वुडबरी आव्यूह सर्वसमिका इस प्रकार है
मानक साहित्य के अनुरूप आने के लिए, हम परिभाषित करते हैं
जहां लाभ सदिश है
आगे बढ़ने से पहले ये लाना जरूरी है दूसरे रूप में
बायीं ओर का दूसरा पद घटाने पर प्राप्त होता है
की पुनरावर्ती परिभाषा के साथ वांछित प्रपत्र इस प्रकार है
अब हम रिकर्सन पूरा करने के लिए तैयार हैं। विचार-विमर्श के अनुसार
दूसरा चरण की पुनरावर्ती परिभाषा से अनुसरण करता है . आगे हम की पुनरावर्ती परिभाषा को सम्मिलित करते हैं के वैकल्पिक रूप के साथ और प्राप्त
साथ हम अद्यतन समीकरण पर पहुँचते हैं
जहाँ
एक प्राथमिकता और एक पश्चवर्ती त्रुटि है। इसकी तुलना पिछली त्रुटि से करें; फ़िल्टर अद्यतन होने के बाद गणना की गई त्रुटि:
इसका अर्थ है कि हमें सुधार कारक मिल गया है
यह सहज रूप से संतोषजनक परिणाम इंगित करता है कि सुधार कारक त्रुटि और लाभ सदिश दोनों के लिए सीधे आनुपातिक है, जो भार कारक के माध्यम से नियंत्रित करता है कि कितनी संवेदनशीलता वांछित है.
आरएलएस एल्गोरिदम सारांश
पी-वें क्रम आरएलएस फ़िल्टर के लिए आरएलएस एल्गोरिदम को संक्षेप में प्रस्तुत किया जा सकता है
| पैरामीटर: | फ़िल्टर क्रम |
| विस्मृति कारक | |
| आरंभ करने के लिए मूल्य | |
| आरंभीकरण: | , |
| , | |
| जहाँ रैंक की सर्वसमिका आव्यूह है | |
| गणना: | For |
|
| |
| . |
के लिए प्रत्यावर्तन बीजगणितीय रिकाटी समीकरण का अनुसरण करता है और इस प्रकार कलमन फिल्टर के समानांतर खींचता है।[3]
लैटिस पुनरावर्ती न्यूनतम वर्ग फ़िल्टर (LRLS)
लैटिस पुनरावर्ती न्यूनतम वर्ग अनुकूली फ़िल्टर मानक आरएलएस से संबंधित है, सिवाय इसके कि इसके लिए कम अंकगणितीय संचालन (आदेश एन) की आवश्यकता होती है।[4] यह पारंपरिक एलएमएस एल्गोरिदम पर अतिरिक्त लाभ प्रदान करता है जैसे कि तेज अभिसरण दर, मॉड्यूलर संरचना, और इनपुट सहसंबंध आव्यूह के ईजेनवैल्यू प्रसार में भिन्नता के प्रति असंवेदनशीलता। वर्णित LRLS एल्गोरिदम पिछली त्रुटियों पर आधारित है और इसमें सामान्यीकृत फॉर्म सम्मिलित है। व्युत्पत्ति मानक आरएलएस एल्गोरिथ्म के समान है और की परिभाषा पर आधारित है आगे की पूर्वानुमान के स्थिति में, हमारे पास है इनपुट संकेत के साथ सबसे अद्यतित नमूने के रूप में। पिछड़े पूर्वानुमान की स्थिति है, जहां i भूतपूर्व में नमूने का सूचकांक है जिसकी हम पूर्वानुमान करना चाहते हैं, और इनपुट संकेत सबसे नवीन नमूना है।[5]
पैरामीटर सारांश
- अग्र परावर्तन गुणांक है
- पश्चगामी परावर्तन गुणांक है
- तात्कालिक पूर्ववर्ती अग्रगामी पूर्वानुमान त्रुटि का प्रतिनिधित्व करता है
- तात्कालिक पश्चगामी पूर्वानुमान त्रुटि का प्रतिनिधित्व करता है
- न्यूनतम न्यूनतम-वर्ग पिछड़ा पूर्वानुमान त्रुटि है
- न्यूनतम न्यूनतम-वर्ग अग्रेषित पूर्वानुमान त्रुटि है
- प्राथमिक और पश्चवर्ती त्रुटियों के बीच एक रूपांतरण कारक है
- फीडफॉरवर्ड गुणक गुणांक हैं।
- एक छोटा धनात्मक स्थिरांक है जो 0.01 हो सकता है
LRLS एल्गोरिदम सारांश
LRLS फ़िल्टर के लिए एल्गोरिदम को संक्षेप में प्रस्तुत किया जा सकता है
| आरंभीकरण: | |
| For | |
| (if for ) | |
| End | |
| गणना: | |
| For | |
| For | |
| Feedforward filtering | |
| End | |
| End | |
सामान्यीकृत लैटिस पुनरावर्ती न्यूनतम वर्ग फ़िल्टर (NLRLS)
LRLS के सामान्यीकृत रूप में कम पुनरावर्तन और चर हैं। इसकी गणना एल्गोरिदम के आंतरिक चर के लिए सामान्यीकरण लागू करके की जा सकती है जो उनके परिमाण को एक से सीमित रखेगा। इसका उपयोग आमतौर पर वास्तविक समय के अनुप्रयोगों में नहीं किया जाता है क्योंकि विभाजन और वर्ग-रूट संचालन की संख्या उच्च कम्प्यूटेशनल भार के साथ आती है।
NLRLS एल्गोरिदम सारांश
NLRLS फ़िल्टर के लिए एल्गोरिदम को संक्षेप में प्रस्तुत किया जा सकता है
| आरंभीकरण: | |
| For | |
| (if for ) | |
| End | |
| गणना: | |
| For | |
| (Input signal energy) | |
| (Reference signal energy) | |
| For | |
| Feedforward filter | |
| End | |
| End | |
यह भी देखें
- अनुकूली फ़िल्टर
- कर्नेल अनुकूली फ़िल्टर
- न्यूनतम माध्य वर्ग फ़िल्टर
- जीरो-फोर्सिंग इक्वलाइज़र
संदर्भ
- Hayes, Monson H. (1996). "9.4: Recursive Least Squares". Statistical Digital Signal Processing and Modeling. Wiley. p. 541. ISBN 0-471-59431-8.
- Simon Haykin, Adaptive Filter Theory, Prentice Hall, 2002, ISBN 0-13-048434-2
- M.H.A Davis, R.B. Vinter, Stochastic Modelling and Control, Springer, 1985, ISBN 0-412-16200-8
- Weifeng Liu, Jose Principe and Simon Haykin, Kernel Adaptive Filtering: A Comprehensive Introduction, John Wiley, 2010, ISBN 0-470-44753-2
- R.L.Plackett, Some Theorems in Least Squares, Biometrika, 1950, 37, 149–157, ISSN 0006-3444
- C.F.Gauss, Theoria combinationis observationum erroribus minimis obnoxiae, 1821, Werke, 4. Gottinge
टिप्पणियाँ
- ↑ Emannual C. Ifeacor, Barrie W. Jervis. Digital signal processing: a practical approach, second edition. Indianapolis: Pearson Education Limited, 2002, p. 718
- ↑ Steven Van Vaerenbergh, Ignacio Santamaría, Miguel Lázaro-Gredilla "Estimation of the forgetting factor in kernel recursive least squares", 2012 IEEE International Workshop on Machine Learning for Signal Processing, 2012, accessed June 23, 2016.
- ↑ Welch, Greg and Bishop, Gary "An Introduction to the Kalman Filter", Department of Computer Science, University of North Carolina at Chapel Hill, September 17, 1997, accessed July 19, 2011.
- ↑ Diniz, Paulo S.R., "Adaptive Filtering: Algorithms and Practical Implementation", Springer Nature Switzerland AG 2020, Chapter 7: Adaptive Lattice-Based RLS Algorithms. https://doi.org/10.1007/978-3-030-29057-3_7
- ↑ Albu, Kadlec, Softley, Matousek, Hermanek, Coleman, Fagan "Implementation of (Normalised) RLS Lattice on Virtex", Digital Signal Processing, 2001, accessed December 24, 2011.
[Category:Statistical signal processi