रोटरडायनामिक्स: Difference between revisions

From Vigyanwiki
No edit summary
 
(9 intermediate revisions by 5 users not shown)
Line 1: Line 1:
{{Short description|Branch of applied mechanics dealing with rotating structures}}
{{Short description|Branch of applied mechanics dealing with rotating structures}}
{{lead extra info|date=January 2022}}
'''रोटरडायनामिक्स''' जिसे रोटर डायनेमिक्स के रूप में भी जाना जाता है घूर्णन संरचनाओं के व्यवहार और निदान से संबंधित अनुप्रयुक्त यांत्रिकी की एक विशेष शाखा है। यह सामान्यतः [[जेट इंजन]] और [[वाष्प टरबाइन]] से लेकर ऑटो इंजन और कंप्यूटर [[डिस्क भंडारण]] तक की संरचनाओं के व्यवहार का विश्लेषण करने के लिए उपयोग किया जाता है। अपने सबसे बुनियादी स्तर पर रोटर डायनेमिक्स एक या एक से अधिक यांत्रिक संरचनाओं से संबंधित है जो बेयरिंग द्वारा समर्थित हैं  और आंतरिक घटनाओं से प्रभावित हैं जो निश्चित अक्ष के चारों ओर घूमते हैं। सहायक संरचना को [[स्टेटर (टरबाइन)|स्टेटर "टरबाइन]]" कहा जाता है। जैसे-जैसे घूर्णन की गति बढ़ती है कंपन का आयाम प्रायः अधिकतम सीमा से गुजरता है जिसे क्रांतिक गति कहा जाता है। यह आयाम सामान्यतः घूर्णन संरचना के असंतुलन से उत्तेजित होता हैI दैनिक उदाहरण स्वरुप [[इंजन संतुलन]] और [[टायर संतुलन]] सम्मिलित हैं। यदि इन [[महत्वपूर्ण गति]]यों पर कंपन का आयाम अत्यधिक है तो विपत्तिपूर्ण विफलता होती है। इसके अलावा [[टर्बोमशीनरी]] प्रायः अस्थिरता विकसित करती है जो टर्बोमशीनरी के आंतरिक स्थिति से संबंधित होती है और जिसे ठीक किया जाना चाहिए। यह बड़े रोटर डिजाइन करने वाले इंजीनियरों की मुख्य चिंता है।
रोटरडायनामिक्स जिसे रोटर डायनेमिक्स के रूप में भी जाना जाता है घूर्णन संरचनाओं के व्यवहार और निदान से संबंधित अनुप्रयुक्त यांत्रिकी की एक विशेष शाखा है। यह आमतौर पर [[जेट इंजन]] और [[वाष्प टरबाइन]] से लेकर ऑटो इंजन और कंप्यूटर [[डिस्क भंडारण]] तक की संरचनाओं के व्यवहार का विश्लेषण करने के लिए उपयोग किया जाता है। अपने सबसे बुनियादी स्तर पर रोटर डायनेमिक्स एक या एक से अधिक यांत्रिक संरचनाओं से संबंधित है जो बेयरिंग द्वारा समर्थित हैं  और आंतरिक घटनाओं से प्रभावित हैं जो निश्चित अक्ष के चारों ओर घूमते हैं। सहायक संरचना को [[स्टेटर (टरबाइन)|स्टेटर "टरबाइन]]" कहा जाता है। जैसे-जैसे घूर्णन की गति बढ़ती है कंपन का आयाम अक्सर अधिकतम सीमा से गुजरता है जिसे क्रांतिक गति कहा जाता है। यह आयाम आमतौर पर घूर्णन संरचना के असंतुलन से उत्तेजित होता हैI दैनिक उदाहरण स्वरुप  


[[इंजन संतुलन]] और [[टायर संतुलन]] शामिल हैं। यदि इन [[महत्वपूर्ण गति]]यों पर कंपन का आयाम अत्यधिक है तो विपत्तिपूर्ण विफलता होती है। इसके अलावा [[टर्बोमशीनरी]] अक्सर अस्थिरता विकसित करती है जो टर्बोमशीनरी के आंतरिक स्थिति से संबंधित होती है और जिसे ठीक किया जाना चाहिए। यह बड़े रोटर डिजाइन करने वाले इंजीनियरों की मुख्य चिंता है।
घूमने वाली मशीनरी प्रक्रिया में सम्मिलित तंत्र की संरचना के आधार पर कंपन पैदा करती है। मशीन में कोई भी कंपन के संकेत को बढ़ा सकता है। असंतुलन के कारण मशीन का कंपन घूर्णक मशीनरी के मुख्य पहलुओं में से एक है जिसका विस्तार से अध्ययन किया जाना चाहिए और डिजाइन करते समय विचार किया जाना चाहिए। घूर्णक मशीन सहित सभी वस्तुएँ वस्तु की संरचना के आधार पर [[प्राकृतिक आवृत्ति]] प्रदर्शित करती हैं। घूर्णन मशीन की महत्वपूर्ण गति तब होती है जब घूर्णन गति इसकी प्राकृतिक आवृत्ति से मेल खाती है। पहली बार जिस सबसे कम गति से संबंधित प्राकृतिक आवृत्ति का सामना करना पड़ता है उसे पहली महत्वपूर्ण गति कहा जाता हैI लेकिन जैसे-जैसे गति बढ़ती है उसमें अतिरिक्त गति का संचार होता है होते दिखाई देता है जो प्राकृतिक आवृत्ति के गुणक होते हैं। इसलिए प्रतिध्वनि शुरू करने वाली अतिरिक्त बल को कम करने के लिए  घूर्णी असंतुलन और अनावश्यक बाहरी बल या शक्ति को कम करना बहुत महत्वपूर्ण है। जब कंपन प्रतिध्वनि के रूप में होता है तो यह विध्वंसक ऊर्जा उत्सर्जित करता है जो घूर्णन मशीन को डिजाइन करते समय मुख्य विचारणीय तथ्य है I इसका मुख्य उद्देश्य गतिवर्धन और गतिविराम के समय संचालन में होने वाली जटिलताओं से सुरक्षित रखना है I यदि इस यदि इस व्यवस्था पर ध्यान केंद्रित नहीं किया गया तो तो इसका परिणाम उपकरण की हानि, मशीनरी पर अत्यधिक टूट-फूट जैसी गतिविधियां हो सकती हैं।


घूमने वाली मशीनरी प्रक्रिया में शामिल तंत्र की संरचना के आधार पर कंपन पैदा करती है। मशीन में कोई भी कंपन के संकेत को बढ़ा सकता है। असंतुलन के कारण मशीन का कंपन घूर्णक मशीनरी के मुख्य पहलुओं में से एक है जिसका विस्तार से अध्ययन किया जाना चाहिए और डिजाइन करते समय विचार किया जाना चाहिए। घूर्णक मशीन सहित सभी वस्तुएँ वस्तु की संरचना के आधार पर [[प्राकृतिक आवृत्ति]] प्रदर्शित करती हैं। घूर्णन मशीन की महत्वपूर्ण गति तब होती है जब घूर्णन गति इसकी प्राकृतिक आवृत्ति से मेल खाती है। पहली बार जिस सबसे कम गति से संबंधित प्राकृतिक आवृत्ति का सामना करना पड़ता है उसे पहली महत्वपूर्ण गति कहा जाता हैI लेकिन जैसे-जैसे गति बढ़ती है उसमें अतिरिक्त गति का संचार होता है होते दिखाई देता है जो प्राकृतिक आवृत्ति के गुणक होते हैं। इसलिए प्रतिध्वनि शुरू करने वाली अतिरिक्त बल को कम करने के लिए घूर्णी असंतुलन और अनावश्यक बाहरी बल या शक्ति को कम करना बहुत महत्वपूर्ण है। जब कंपन प्रतिध्वनि के रूप में होता है तो यह विध्वंसक ऊर्जा उत्सर्जित करता है जो घूर्णन मशीन को डिजाइन करते समय मुख्य विचारणीय तथ्य है I इसका मुख्य उद्देश्य गतिवर्धन और गतिविराम के समय संचालन में होने वाली जटिलताओं से सुरक्षित रखना है I यदि इस यदि इस व्यवस्था को नजरअंदाज किया जाता है तो तो इसका परिणाम उपकरण की हानि, मशीनरी पर अत्यधिक टूट-फूट जैसी चीजे हो सकती हैं।
मशीन की वास्तविक गतिशीलता को सैद्धांतिक रूप से पहचानना मुश्किल है I यह गणना सैद्धांतिक तौर पर सरलीकृत मॉडलों पर आधारित होती है जो विभिन्न संरचनात्मक घटकों से मिलती-जुलती होती हैI रोटरोडाइनेमिक्स की कुछ विश्लेषणात्मक विधियाँ भी हैं जैसे वितरित स्थानांतरण फ़ंक्शन विधि<ref>{{Cite journal|last1=Liu|first1=Shibing|last2=Yang|first2=Bingen|date=2017-02-22|title=Vibrations of Flexible Multistage Rotor Systems Supported by Water-Lubricated Rubber Bearings|journal=Journal of Vibration and Acoustics|volume=139|issue=2|pages=021016–021016–12|doi=10.1115/1.4035136|issn=1048-9002}}</ref> जो परिचालन में विश्लेषणात्मक और प्राकृतिक आवृत्तियों, विवेचनात्म्क गति और असंतुलित द्रव्यमान आवृत्ति का स्थानांतरण करती हैI  कोई भी आदिप्ररूप क्रमादेशिक मशीन प्रतिध्वनि की सटीक आवृत्तियों की पुष्टि करने के लिए परीक्षण करती हैं जिसमें पुनः डिजाइन करके ये सुनिश्चित किया जाता है कोई प्रतिध्वनि नहीं होती I


मशीन की वास्तविक गतिशीलता सैद्धांतिक रूप से पहचानना मुश्किल है I यह गणना सैद्धांतिक तौर पर सरलीकृत मॉडलों पर आधारित होती है जो विभिन्न संरचनात्मक घटकों से मिलती-जुलती होती हैI रोटरोडाइनेमिक्स की कुछ विश्लेषणात्मक विधियाँ भी हैं जैसे वितरित स्थानांतरण फ़ंक्शन विधि<ref>{{Cite journal|last1=Liu|first1=Shibing|last2=Yang|first2=Bingen|date=2017-02-22|title=Vibrations of Flexible Multistage Rotor Systems Supported by Water-Lubricated Rubber Bearings|journal=Journal of Vibration and Acoustics|volume=139|issue=2|pages=021016–021016–12|doi=10.1115/1.4035136|issn=1048-9002}}</ref> जो परिचालन में विश्लेषणात्मक और प्राकृतिक आवृत्तियों, विवेचनात्म्क गति और असंतुलित द्रव्यमान आवृत्ति का स्थानांतरण करती हैI  कोई भी आदिप्ररूप क्रमादेशिक मशीन प्रतिध्वनि की सटीक आवृत्तियों की पुष्टि करने के लिए परीक्षण करती हैं जिसमें पुनः डिजाइन करके ये सुनिश्चित किया जाता है कोई प्रतिध्वनि नहीं होती I  
== मूल सिद्धांत ==
[[गति का समीकरण]], सामान्यीकृत [[मैट्रिक्स (गणित)]] रूप में अक्षीय रूप से सममित रोटर के लिए स्थिर स्पिन गति पर घूमता है I


== मूल सिद्धांत ==
<math>
[[गति का समीकरण]], सामान्यीकृत [[मैट्रिक्स (गणित)]] रूप में, अक्षीय रूप से सममित रोटर के लिए स्थिर स्पिन गति पर घूमता है Ω है
:<math>
\begin{matrix}
\begin{matrix}
\mathbf {M}\ddot{\mathbf{q}}(t)+(\mathbf{C}+\mathbf{G})\dot{\mathbf{q}}(t)+(\mathbf{K}+\mathbf{N}){\mathbf{q}}(t)&=&\mathbf{f}(t)\\
\mathbf {M}\ddot{\mathbf{q}}(t)+(\mathbf{C}+\mathbf{G})\dot{\mathbf{q}}(t)+(\mathbf{K}+\mathbf{N}){\mathbf{q}}(t)&=&\mathbf{f}(t)\\
\end{matrix}
\end{matrix}
</math>
</math>
कहाँ पे:


:M सममित आव्यूह द्रव्यमान आव्यूह है
जहाँ :
: सी सममित [[भिगोना मैट्रिक्स]] है
 
: G तिरछा-[[सममित मैट्रिक्स]] है | तिरछा-सममित जाइरोस्कोपिक मैट्रिक्स
:'''M''' सममित आव्यूह द्रव्यमान आव्यूह है
: के सममित असर या सील कठोरता मैट्रिक्स है
: '''C''' सममित [[भिगोना मैट्रिक्स]] है
:N उदाहरण के लिए, केन्द्रापसारक तत्वों को शामिल करने के लिए विक्षेपण का जाइरोस्कोपिक मैट्रिक्स है।
: '''G''' तिरछा-[[सममित मैट्रिक्स]] है | तिरछा-सममित जाइरोस्कोपिक मैट्रिक्स के सममित असर या सील स्टिफनेस मैट्रिक्स है
जिसमें q जड़त्वीय निर्देशांक में रोटर का सामान्यीकृत निर्देशांक है और f एक मजबूर कार्य है, आमतौर पर असंतुलित सहित।
:'''N''' उदाहरण के लिए केन्द्रापसारक तत्वों को सम्मिलित करने के लिए विक्षेपण का जाइरोस्कोपिक मैट्रिक्स है।
जिसमें '''q''' जड़त्वीय निर्देशांक में रोटर का सामान्यीकृत निर्देशांक है और '''f'''  प्रेरक फलन हैI
 
जाइरोस्कोपिक मैट्रिक्स '''G'''  स्पिन गति Ω के समानुपाती है।


जाइरोस्कोपिक मैट्रिक्स जी स्पिन गति Ω के समानुपाती है।
उपरोक्त समीकरण के सामान्य समाधान में [[जटिल संख्या]] सम्मिलित हैं जो स्पिन गति पर निर्भर हैं। इस क्षेत्र के इंजीनियरिंग विशेषज्ञ इन समाधानों का पता लगाने के लिए [[कैंपबेल आरेख]] पर निर्भर होते हैं I
उपरोक्त समीकरण के सामान्य समाधान में [[जटिल संख्या]] [[egenvectors]] शामिल हैं जो स्पिन गति पर निर्भर हैं।
इस क्षेत्र के इंजीनियरिंग विशेषज्ञ इन समाधानों का पता लगाने के लिए [[कैंपबेल आरेख]] पर भरोसा करते हैं।


समीकरणों की रोटरडाइनैमिक प्रणाली की एक दिलचस्प विशेषता कठोरता, अवमंदन और द्रव्यमान के ऑफ-डायगोनल शब्द हैं। इन शब्दों को क्रॉस-युग्मित कठोरता, क्रॉस-युग्मित भिगोना और क्रॉस-युग्मित द्रव्यमान कहा जाता है। जब एक सकारात्मक क्रॉस-युग्मित कठोरता होती है, तो एक विक्षेपण प्रतिक्रिया बल को विक्षेपण की दिशा के विपरीत लोड पर प्रतिक्रिया करने के लिए और सकारात्मक भंवर की दिशा में प्रतिक्रिया बल का कारण बनता है। यदि यह बल उपलब्ध प्रत्यक्ष नमी और कठोरता की तुलना में काफी बड़ा है, तो रोटर अस्थिर होगा। जब एक रोटर अस्थिर होता है, तो विनाशकारी विफलता से बचने के लिए आमतौर पर मशीन को तत्काल बंद करने की आवश्यकता होती है।
समीकरणों की रोटरडाइनैमिक प्रणाली में कठोर, अवमंदन और द्रव्यमान के ऑफ-डायगोनल शब्दों की रोचक प्रक्रिया या तथ्य है I इन शब्दों को क्रॉस-युग्मित कठोरत, क्रॉस-युग्मित अवसंदन और क्रॉस-युग्मित द्रव्यमान कहा जाता है। जब समीकरणों में सकारात्मक क्रॉस-युग्मित कठोरता होती है तो यह विक्षेपण प्रतिक्रिया बल को विक्षेपण की दिशा के विपरीत बल पर प्रतिक्रिया करने के लिए और सकारात्मक दिशा में ले जाने के लिए प्रतिक्रिया बल का कारण बनता है। यदि यह बल उपलब्ध प्रत्यक्ष नमी और कठोरता की तुलना में काफी विस्तृत है तो ऐसे में घूर्णन अस्थिर होगा। जब एक रोटर अस्थिर होता है तो विध्वंसक विफलता से बचने के लिए सामान्यतः मशीन को तत्काल बंद करने की आवश्यकता होती है।


== कैंपबेल आरेख ==
== कैंपबेल आरेख ==


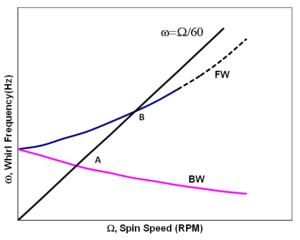
[[File:Campbelldiagram.png|thumb|300px|एक साधारण रोटर के लिए कैंपबेल आरेख]]कैंपबेल डायग्राम, जिसे व्हर्ल स्पीड मैप या फ्रीक्वेंसी इंटरफेरेंस के नाम से भी जाना जाता है
[[File:Campbelldiagram.png|thumb|300px|एक साधारण रोटर के लिए कैंपबेल आरेख]]कैंपबेल डायग्राम, जिसे "व्हर्ल स्पीड मैप" या "फ्रीक्वेंसी इंटरफेरेंस" के नाम से भी जाना जाता हैI साधारण रोटर सिस्टम का आरेख दाईं ओर दिखाया गया है। गुलाबी और नीले रंग के कर्व्स क्रमशः बैकवर्ड व्हर्ल (बीडब्ल्यू) और फॉरवर्ड व्हर्ल (एफडब्ल्यू) मोड दिखाते हैं जो स्पिन की गति बढ़ने पर अलग हो जाते हैं। जब बैकवर्ड व्हर्लफ्रीक्वेंसी या फॉरवर्ड व्हर्ल फ्रीक्वेंसी स्पिन स्पीड Ω के बराबर होती है जो सिंक्रोनस स्पिन स्पीड लाइन के साथ इंटरसेक्शन '''ए''' और '''बी''' द्वारा इंगित की जाती है तो रोटर की प्रतिक्रिया एक चोटी दिखा सकती है इसे क्रांतिक गति कहते हैं।
एक साधारण रोटर सिस्टम का आरेख दाईं ओर दिखाया गया है। गुलाबी और नीले रंग के कर्व्स क्रमशः बैकवर्ड व्हर्ल (BW) और फॉरवर्ड व्हर्ल (FW) मोड दिखाते हैं, जो स्पिन की गति बढ़ने पर अलग हो जाते हैं। जब BW फ्रीक्वेंसी या FW फ्रीक्वेंसी स्पिन स्पीड Ω के बराबर होती है, जो सिंक्रोनस स्पिन स्पीड लाइन के साथ इंटरसेक्शन ए और बी द्वारा इंगित की जाती है, तो रोटर की प्रतिक्रिया एक चोटी दिखा सकती है। इसे क्रांतिक गति कहते हैं।
 
== जेफकॉट रोटर ==
== जेफकॉट रोटर ==


जेफकोट रोटर (हेनरी होमन जेफकोट के नाम पर), जिसे यूरोप में [[गुस्ताफ डी लवल]] रोटर के नाम से भी जाना जाता है, इन समीकरणों को हल करने के लिए इस्तेमाल किया जाने वाला एक सरलीकृत गांठ वाला पैरामीटर मॉडल है। जेफकॉट रोटर एक गणितीय [[आदर्शीकरण (विज्ञान दर्शन)]] है जो वास्तविक रोटर यांत्रिकी को प्रतिबिंबित नहीं कर सकता है।
जेफकोट रोटर जिसे यूरोप में [[गुस्ताफ डी लवल|गुस्ताफ डी लावल]] घूर्णन के नाम से भी जाना जाता है वह इन समीकरणों को हल करने के लिए इस्तेमाल किया जाने वाला सरलीकृत पैरामीटर मॉडल है। जेफकॉट रोटर एक गणितीय [[आदर्शीकरण (विज्ञान दर्शन)|आदर्शीकरण विज्ञान]] है जो वास्तविक रोटर यांत्रिकी को प्रतिबिंबित नहीं कर सकता है।


== इतिहास ==
== इतिहास ==


रोटरडायनामिक्स का इतिहास सिद्धांत और व्यवहार के परस्पर क्रिया से भरा पड़ा है। विलियम जॉन मैक्कॉर्न रैनकिन | डब्ल्यू। जेएम रैंकिन ने पहली बार 1869 में कताई शाफ्ट का विश्लेषण किया, लेकिन उनका मॉडल पर्याप्त नहीं था और उन्होंने भविष्यवाणी की कि सुपरक्रिटिकल गति प्राप्त नहीं की जा सकती। 1895 में, डंकर्ले ने सुपरक्रिटिकल गति का वर्णन करते हुए एक प्रायोगिक पेपर प्रकाशित किया। एक स्वीडिश इंजीनियर, गुस्ताफ डी लावल ने 1889 में सुपरक्रिटिकल गति के लिए एक भाप टरबाइन चलाया, और केर ने 1916 में एक दूसरी महत्वपूर्ण गति के प्रायोगिक साक्ष्य दिखाते हुए एक पेपर प्रकाशित किया।
रोटरडायनामिक्स का इतिहास सिद्धांत और व्यवहार के परस्पर क्रिया से भरा पड़ा है। विलियम जॉन मैक्कॉर्न रैनकिन, डब्ल्यू जेएम रैंकिन ने पहली बार 1869 में कताई शाफ्ट का विश्लेषण किया लेकिन उनका मॉडल पर्याप्त नहीं था और उन्होंने भविष्यवाणी की कि सुपरक्रिटिकल गति प्राप्त नहीं की जा सकती। 1895 में डंकर्ले ने सुपरक्रिटिकल गति का वर्णन करते हुए प्रायोगिक पेपर प्रकाशित किया। एक स्वीडिश इंजीनियर, गुस्ताफ डी लावल ने 1889 में सुपरक्रिटिकल गति के लिए भाप टरबाइन चलाया और केर ने 1916 में एक दूसरी महत्वपूर्ण गति के प्रायोगिक साक्ष्य दिखाते हुए पेपर प्रकाशित किया।


सिद्धांत और व्यवहार के बीच संघर्ष को हल करने के लिए लंदन की रॉयल सोसाइटी द्वारा हेनरी जेफकॉट को नियुक्त किया गया था। उन्होंने 1919 में फिलोसोफिकल मैगज़ीन में एक पेपर प्रकाशित किया जिसे अब क्लासिक माना जाता है जिसमें उन्होंने स्थिर सुपरक्रिटिकल गति के अस्तित्व की पुष्टि की। अगस्त Föppl ने 1895 में समान निष्कर्ष प्रकाशित किए, लेकिन इतिहास ने बड़े पैमाने पर उनके काम को नजरअंदाज कर दिया।
सिद्धांत और व्यवहार के बीच संघर्ष को हल करने के लिए लंदन की रॉयल सोसाइटी द्वारा हेनरी जेफकॉट को नियुक्त किया गया था। उन्होंने 1919 में फिलोसोफिकल मैगज़ीन में पेपर प्रकाशित किया जिसे अब क्लासिक माना जाता है जिसमें उन्होंने स्थिर सुपरक्रिटिकल गति के अस्तित्व की पुष्टि की। अगस्त 1895 में समान निष्कर्ष प्रकाशित किए लेकिन इतिहास ने बड़े पैमाने पर उनके काम को नजरअंदाज कर दिया।


जेफकॉट के काम और द्वितीय विश्व युद्ध की शुरुआत के बीच अस्थिरता और मॉडलिंग तकनीकों के क्षेत्र में बहुत काम किया गया था, जिसकी परिणति [[निल्स ओटो मायक्लेस्टैड]] के काम में हुई।<ref>{{Cite journal
जेफकॉट के काम और द्वितीय विश्व युद्ध की शुरुआत के बीच अस्थिरता और मॉडलिंग तकनीकों के क्षेत्र में बहुत काम किया गया था जिसकी परिणति [[निल्स ओटो मायक्लेस्टैड]] के काम में हुई।<ref>{{Cite journal
  | last = Myklestad
  | last = Myklestad
  | first = Nils
  | first = Nils
Line 55: Line 51:
  | pages = 153–162
  | pages = 153–162
  | date = April 1944
  | date = April 1944
  | doi = 10.2514/8.11116}}</ref> और एमए प्रोहल<ref>{{Citation
  | doi = 10.2514/8.11116}}</ref> एमए प्रोहल<ref>{{Citation
  | last = Prohl
  | last = Prohl
  | first = M. A.
  | first = M. A.
Line 63: Line 59:
  | pages = A–142
  | pages = A–142
  | year = 1945
  | year = 1945
  }}</ref> जिसके कारण रोटर्स के विश्लेषण के लिए ट्रांसफर मैट्रिक्स मेथड (TMM) का मार्ग प्रशस्त हुआ। रोटरडायनामिक्स विश्लेषण के लिए आज उपयोग की जाने वाली सबसे प्रचलित विधि परिमित तत्व विधि है।
  }}</ref> जिसके कारण रोटर्स के विश्लेषण के लिए ट्रांसफर मैट्रिक्स मेथड का मार्ग प्रशस्त हुआ। रोटरडायनामिक्स विश्लेषण के लिए आज उपयोग की जाने वाली सबसे प्रचलित विधि परिमित तत्व विधि है।


आधुनिक कंप्यूटर मॉडल पर दारा चिल्ड्स के हवाले से एक उद्धरण में टिप्पणी की गई है, कंप्यूटर कोड से भविष्यवाणियों की गुणवत्ता का मूल मॉडल की सुदृढ़ता और [[सिस्टम विश्लेषक]] की भौतिक अंतर्दृष्टि से अधिक लेना-देना है। ... सुपीरियर एल्गोरिदम या कंप्यूटर कोड खराब मॉडल या इंजीनियरिंग निर्णय की कमी को ठीक नहीं करेंगे।
आधुनिक कंप्यूटर मॉडल पर दारा चिल्ड्स के हवाले से एक उद्धरण में टिप्पणी की गई हैI कंप्यूटर कोड से भविष्यवाणियों की गुणवत्ता का मूल मॉडल की सुदृढ़ता और [[सिस्टम विश्लेषक]] की भौतिक अंतर्दृष्टि से अधिक लेना-देना है। सुपीरियर एल्गोरिदम या कंप्यूटर कोड खराब मॉडल या इंजीनियरिंग की कमी को ठीक नहीं करेंगे।


प्रो. फ्रेडरिक नेल्सन|एफ. नेल्सन ने रोटरडायनामिक्स के इतिहास पर व्यापक रूप से लिखा है और इस खंड का अधिकांश भाग उनके काम पर आधारित है।
प्रो. फ्रेडरिक नेल्सन,एफ. नेल्सन ने रोटरडायनामिक्स के इतिहास पर व्यापक रूप से लिखा है और इस खंड का अधिकांश भाग उनके काम पर आधारित है।


== सॉफ्टवेयर ==
== सॉफ्टवेयर ==
{{multiple issues|section=yes|
ऐसे कई सॉफ्टवेयर पैकेज हैं जो समीकरणों के रोटर डायनेमिक सिस्टम को हल करने में सक्षम हैं। रोटर गतिशील विशिष्ट कोड डिजाइन उद्देश्यों के लिए अधिक बहुमुखी हैं। ये कोड असर गुणांक, साइड लोड और कई अन्य वस्तुओं को जोड़ना आसान बनाते हैं, जिनकी आवश्यकता केवल एक रोटरडायनामिकिस्ट को होती है। गैर-रोटर डायनेमिक विशिष्ट कोड पूर्ण विशेषताओं वाले सॉल्वर हैंऔर उनके समाधान तकनीकों में कई वर्षों का विकास है। गैर-रोटर डायनेमिक विशिष्ट कोड का उपयोग रोटर डायनेमिक्स के लिए डिज़ाइन किए गए कोड को कैलिब्रेट करने के लिए भी किया जा सकता है।
{{primary sources section|date=January 2022}}
{{cleanup list|section|date=January 2022}}
}}
ऐसे कई सॉफ्टवेयर पैकेज हैं जो समीकरणों के रोटर डायनेमिक सिस्टम को हल करने में सक्षम हैं। रोटर गतिशील विशिष्ट कोड डिजाइन उद्देश्यों के लिए अधिक बहुमुखी हैं। ये कोड असर गुणांक, साइड लोड और कई अन्य वस्तुओं को जोड़ना आसान बनाते हैं, जिनकी आवश्यकता केवल एक रोटरडायनामिकिस्ट को होती है। गैर-रोटर डायनेमिक विशिष्ट कोड पूर्ण विशेषताओं वाले FEA सॉल्वर हैं, और उनके समाधान तकनीकों में कई वर्षों का विकास है। गैर-रोटर डायनेमिक विशिष्ट कोड का उपयोग रोटर डायनेमिक्स के लिए डिज़ाइन किए गए कोड को कैलिब्रेट करने के लिए भी किया जा सकता है।


रोटरडायनामिक विशिष्ट कोड:
रोटरडायनामिक विशिष्ट कोड:
* डायनेमिक्स R4 (Alfa-Tranzit Co. Ltd)<ref>{{Cite web|title=ROTORDYNAMICS OF TURBOMACHINERY, Software and Engineering services, Alfa-Tranzit Co.|url=http://www.alfatran.com/|access-date=2022-01-11|website=www.alfatran.com}}</ref> - स्थानिक प्रणालियों के डिजाइन और विश्लेषण के लिए वाणिज्यिक सॉफ्टवेयर विकसित किया गया
* डायनेमिक्स R4 (Alfa-Tranzit Co. Ltd)<ref>{{Cite web|title=ROTORDYNAMICS OF TURBOMACHINERY, Software and Engineering services, Alfa-Tranzit Co.|url=http://www.alfatran.com/|access-date=2022-01-11|website=www.alfatran.com}}</ref> - स्थानिक प्रणालियों के डिजाइन और विश्लेषण के लिए वाणिज्यिक सॉफ्टवेयर विकसित किया गयाI
* एक्सस्ट्रीम रोटरडायनामिक्स, (सॉफ्टइनवे)<ref>{{Cite web|date=2016-07-27|title=AxSTREAM - Rotordynamics {{!}} Turbomachinery Design Software|url=https://www.softinway.com/software-applications/rotor-dynamics/|access-date=2022-01-11|website=www.softinway.com|language=en-US}}</ref> - रोटर डायनेमिक्स के लिए एकीकृत सॉफ्टवेयर प्लेटफॉर्म, बीम या 2डी-एक्सिसिमेट्रिक तत्वों पर परिमित तत्व विधि का उपयोग करके सभी व्यापक रूप से उपयोग किए जाने वाले रोटर प्रकारों के लिए पार्श्व, मरोड़ और अक्षीय रोटर गतिशीलता में सक्षम है, और स्वचालित होने में सक्षम है।
* एक्सस्ट्रीम रोटरडायनामिक्स, (सॉफ्टइनवे)<ref>{{Cite web|date=2016-07-27|title=AxSTREAM - Rotordynamics {{!}} Turbomachinery Design Software|url=https://www.softinway.com/software-applications/rotor-dynamics/|access-date=2022-01-11|website=www.softinway.com|language=en-US}}</ref> - रोटर डायनेमिक्स के लिए एकीकृत सॉफ्टवेयर प्लेटफॉर्म, बीम या 2डी-एक्सिसिमेट्रिक तत्वों पर परिमित तत्व विधि का उपयोग करके सभी व्यापक रूप से उपयोग किए जाने वाले रोटर प्रकारों के लिए पार्श्व, मरोड़ और अक्षीय रोटर गतिशीलता में सक्षम है, और स्वचालित होने में सक्षम है।
* रोटोर्टेस्ट, (लैमर - [[कैंपिनास विश्वविद्यालय]])<ref>{{Cite web|title=घर|url=https://www.fem.unicamp.br|url-status=live|access-date=2022-01-11|website=www.fem.unicamp.br}}</ref> - परिमित तत्व विधि आधारित सॉफ्टवेयर, जिसमें विभिन्न प्रकार के बियरिंग सॉल्वर शामिल हैं। लैमर (रोटेटिंग मशीनरी की प्रयोगशाला) - यूनिकैम्प (कैम्पिनास विश्वविद्यालय) द्वारा विकसित।
* रोटोर्टेस्ट, (लैमर - [[कैंपिनास विश्वविद्यालय]])<ref>{{Cite web|title=घर|url=https://www.fem.unicamp.br|url-status=live|access-date=2022-01-11|website=www.fem.unicamp.br}}</ref> - परिमित तत्व विधि आधारित सॉफ्टवेयर, जिसमें विभिन्न प्रकार के बियरिंग सॉल्वर सम्मिलित हैं। लैमर (रोटेटिंग मशीनरी की प्रयोगशाला) - यूनिकैम्प (कैम्पिनास विश्वविद्यालय) द्वारा विकसित।
* [[सैमसेफ]] रोटर<ref>{{cite web|url=http://www.lmsintl.com/rotor-dynamics|url-status=dead|title=Rotor dynamics analysis: SAMCEF Rotors is up to the challenge|access-date=2013-06-04|archive-date=2012-09-29|archive-url=https://web.archive.org/web/20120929073823/http://www.lmsintl.com/rotor-dynamics}}</ref> - रोटर्स सिमुलेशन के लिए सॉफ्टवेयर प्लेटफॉर्म (LMS Samtech,A Siemens Business)
* [[सैमसेफ]] रोटर<ref>{{cite web|url=http://www.lmsintl.com/rotor-dynamics|url-status=dead|title=Rotor dynamics analysis: SAMCEF Rotors is up to the challenge|access-date=2013-06-04|archive-date=2012-09-29|archive-url=https://web.archive.org/web/20120929073823/http://www.lmsintl.com/rotor-dynamics}}</ref> - रोटर्स सिमुलेशन के लिए सॉफ्टवेयर प्लेटफॉर्म (LMS Samtech,A Siemens Business)
* MADYN (परामर्श इंजीनियर क्लेमेंट)<ref>{{Cite web|title=घर|url=http://www.madyn.com|url-status=live|access-date=2022-01-11|website=www.madyn.de}}</ref> - नींव और आवास सहित कई रोटार और गियर के लिए वाणिज्यिक संयुक्त परिमित तत्व पार्श्व, मरोड़, अक्षीय और युग्मित सॉल्वर।
* MADYN (परामर्श इंजीनियर क्लेमेंट)<ref>{{Cite web|title=घर|url=http://www.madyn.com|url-status=live|access-date=2022-01-11|website=www.madyn.de}}</ref> - नींव और आवास सहित कई रोटार और गियर के लिए वाणिज्यिक संयुक्त परिमित तत्व पार्श्व, मरोड़, अक्षीय और युग्मित सॉल्वर।
Line 85: Line 77:
* iSTRDYN (डायनाटेक सॉफ्टवेयर एलएलसी)<ref>{{Cite web |url=http://www.istrdyn.com/ |title=Archived copy |access-date=2022-01-11 |archive-date=2021-05-07 |archive-url=https://web.archive.org/web/20210507094217/http://istrdyn.com/ |url-status=dead }}</ref> - वाणिज्यिक 2-डी अक्ष-सममित परिमित तत्व सॉल्वर
* iSTRDYN (डायनाटेक सॉफ्टवेयर एलएलसी)<ref>{{Cite web |url=http://www.istrdyn.com/ |title=Archived copy |access-date=2022-01-11 |archive-date=2021-05-07 |archive-url=https://web.archive.org/web/20210507094217/http://istrdyn.com/ |url-status=dead }}</ref> - वाणिज्यिक 2-डी अक्ष-सममित परिमित तत्व सॉल्वर
* FEMRDYN (डायनाटेक इंजीनियरिंग, इंक।)<ref>{{Cite web|title=FEMRDYN|url=http://dynatechengr.com/femrdyn.htm|access-date=2022-01-11|website=dynatechengr.com}}</ref> - वाणिज्यिक 1-डी अक्ष-सममित परिमित तत्व सॉल्वर
* FEMRDYN (डायनाटेक इंजीनियरिंग, इंक।)<ref>{{Cite web|title=FEMRDYN|url=http://dynatechengr.com/femrdyn.htm|access-date=2022-01-11|website=dynatechengr.com}}</ref> - वाणिज्यिक 1-डी अक्ष-सममित परिमित तत्व सॉल्वर
* DyRoBeS (Eigen Technologies, Inc.)<ref>{{Cite web|title=Dyrobes – A Revolution in Rotor Dynamics Software|url=https://dyrobes.com/|access-date=2022-01-11|language=en-US}}</ref> - वाणिज्यिक 1-डी बीम तत्व सॉल्वर
* रिमैप राइटेक<ref>{{Cite web |url=http://ritec-eg.com/Products/RITEC/RIMAP_Rotordynamic_Analysis_Software_Package.html |title=RITEC - RIMAP (Rotordynamic Analysis Software Package) |access-date=2013-10-01 |archive-date=2013-10-04 |archive-url=https://web.archive.org/web/20131004212801/http://ritec-eg.com/Products/RITEC/RIMAP_Rotordynamic_Analysis_Software_Package.html |url-status=dead }}</ref> - वाणिज्यिक 1-डी बीम तत्व सॉल्वर
* रिमैप (राइटेक)<ref>{{Cite web |url=http://ritec-eg.com/Products/RITEC/RIMAP_Rotordynamic_Analysis_Software_Package.html |title=RITEC - RIMAP (Rotordynamic Analysis Software Package) |access-date=2013-10-01 |archive-date=2013-10-04 |archive-url=https://web.archive.org/web/20131004212801/http://ritec-eg.com/Products/RITEC/RIMAP_Rotordynamic_Analysis_Software_Package.html |url-status=dead }}</ref> - वाणिज्यिक 1-डी बीम तत्व सॉल्वर
* रोटेटिंग मशीनरी एनालिसिस<ref>{{Cite web|title=घर|url=https://www.xlrotor.com/|access-date=2022-01-11|website=XLRotor|language=en-US}}</ref> - वाणिज्यिक 1-डी बीम तत्व सॉल्वर, चुंबकीय असर नियंत्रण प्रणाली और युग्मित पार्श्व-मरोड़ विश्लेषण सहित। एक्सेल स्प्रेडशीट का उपयोग करके रोटर डायनेमिक मॉडलिंग और विश्लेषण के लिए एक शक्तिशाली, तेज और उपयोग में आसान टूल। VBA मैक्रोज़ के साथ आसानी से स्वचालित, साथ ही 3D CAD सॉफ़्टवेयर के लिए एक प्लगइन।
* XLRotor (रोटेटिंग मशीनरी एनालिसिस, इंक।)<ref>{{Cite web|title=घर|url=https://www.xlrotor.com/|access-date=2022-01-11|website=XLRotor|language=en-US}}</ref> - वाणिज्यिक 1-डी बीम तत्व सॉल्वर, चुंबकीय असर नियंत्रण प्रणाली और युग्मित पार्श्व-मरोड़ विश्लेषण सहित। एक्सेल स्प्रेडशीट का उपयोग करके रोटर डायनेमिक मॉडलिंग और विश्लेषण के लिए एक शक्तिशाली, तेज और उपयोग में आसान टूल। VBA मैक्रोज़ के साथ आसानी से स्वचालित, साथ ही 3D CAD सॉफ़्टवेयर के लिए एक प्लगइन।
* एआरएमडी ([https://www.rbts.com रोटर बेयरिंग टेक्नोलॉजी एंड सॉफ्टवेयर, इंक])<ref>{{Cite web |title=ARMD Rotor Dynamics |url=https://www.rbts.com/ARMDRotorDynamics.html |url-status=live |archive-date= |access-date=2022-01-01}}</ref> - रोटरडायनामिक्स, मल्टी-ब्रांच टॉर्सनल वाइब्रेशन, फ्लुइड-फिल्म बियरिंग, अनुकूलन और प्रदर्शन मूल्यांकन के लिए वाणिज्यिक FEA-आधारित सॉफ़्टवेयर, जिसका उपयोग दुनिया भर में सभी उद्योगों के शोधकर्ताओं, ओईएम और अंतिम-उपयोगकर्ताओं द्वारा किया जाता है। .
* एआरएमडी ([https://www.rbts.com रोटर बेयरिंग टेक्नोलॉजी एंड सॉफ्टवेयर, इंक.])<ref>{{Cite web |title=ARMD Rotor Dynamics |url=https://www.rbts.com/ARMDRotorDynamics.html |url-status=live |archive-date= |access-date=2022-01-01}}</ref> - रोटरडायनामिक्स, मल्टी-ब्रांच टॉर्सनल वाइब्रेशन, फ्लुइड-फिल्म बियरिंग (हाइड्रोडायनामिक, हाइड्रोस्टैटिक, और हाइब्रिड) डिज़ाइन, अनुकूलन और प्रदर्शन मूल्यांकन के लिए वाणिज्यिक FEA-आधारित सॉफ़्टवेयर, जिसका उपयोग दुनिया भर में सभी उद्योगों के शोधकर्ताओं, ओईएम और अंतिम-उपयोगकर्ताओं द्वारा किया जाता है। .
* टेक्सास ए एंड एम यूनिवर्सिटी, टेक्सास ए एंड एम<ref>{{Cite web|title=Turbomachinery Laboratory|url=https://turbolab.tamu.edu/|access-date=2022-01-11|website=turbolab.tamu.edu}}</ref> - अकादमिक 1-डी बीम तत्व सॉल्वर
* XLTRC2 (टेक्सास ए एंड एम यूनिवर्सिटी | टेक्सास ए एंड एम)<ref>{{Cite web|title=Turbomachinery Laboratory|url=https://turbolab.tamu.edu/|access-date=2022-01-11|website=turbolab.tamu.edu}}</ref> - अकादमिक 1-डी बीम तत्व सॉल्वर
* कॉम्बोरोटर,[[वर्जीनिया विश्वविद्यालय]]<ref>{{cite web|url=http://www.virginia.edu/romac/ |title=Rotating Machinery and Controls Laboratory}}</ref> औद्योगिक उपयोग द्वारा बड़े पैमाने पर सत्यापित महत्वपूर्ण गति, स्थिरता और असंतुलित प्रतिक्रिया का मूल्यांकन करने वाले कई रोटार के लिए संयुक्त परिमित तत्व पार्श्व, मरोड़, अक्षीय सॉल्वर
* कॉम्बोरोटर ([[वर्जीनिया विश्वविद्यालय]])<ref>{{cite web|url=http://www.virginia.edu/romac/ |title=Rotating Machinery and Controls Laboratory}}</ref> - औद्योगिक उपयोग द्वारा बड़े पैमाने पर सत्यापित महत्वपूर्ण गति, स्थिरता और असंतुलित प्रतिक्रिया का मूल्यांकन करने वाले कई रोटार के लिए संयुक्त परिमित तत्व पार्श्व, मरोड़, अक्षीय सॉल्वर
*द्रव-प्रवाह मशीनरी संस्थान, [[पोलिश विज्ञान अकादमी]]<ref>{{cite web |url=http://www.imp.gda.pl/index_a.html |title=the Szewalski Institute of Fluid-flow Machinery |archiveurl=https://web.archive.org/web/20081215043824/http://www.imp.gda.pl/index_a.html |archivedate=2008-12-15 }}</ref> लीनियर और नॉन-लीनियर रेंज के भीतर रोटर-बियरिंग सिस्टम के विश्लेषण के लिए अकादमिक कंप्यूटर कोड पैकेज
* MESWIR (द्रव-प्रवाह मशीनरी संस्थान, [[पोलिश विज्ञान अकादमी]])<ref>{{cite web |url=http://www.imp.gda.pl/index_a.html |title=the Szewalski Institute of Fluid-flow Machinery |archiveurl=https://web.archive.org/web/20081215043824/http://www.imp.gda.pl/index_a.html |archivedate=2008-12-15 }}</ref> - लीनियर और नॉन-लीनियर रेंज के भीतर रोटर-बियरिंग सिस्टम के विश्लेषण के लिए अकादमिक कंप्यूटर कोड पैकेज
* डी एंड एम टेक्नोलॉजी)<ref>{{cite web |url=http://www.dnmco.com/ |archiveurl=https://web.archive.org/web/20210506005709/http://dnmco.com/ |title=D&M; Technology Co., Ltd |archivedate=2021-05-06 }}</ref> कई रोटार, गियर और लचीली डिस्क (HDD) के लिए वाणिज्यिक पार्श्व, मरोड़, अक्षीय और युग्मित सॉल्वर
* RoDAP (डी एंड एम टेक्नोलॉजी)<ref>{{cite web |url=http://www.dnmco.com/ |archiveurl=https://web.archive.org/web/20210506005709/http://dnmco.com/ |title=D&M; Technology Co., Ltd |archivedate=2021-05-06 }}</ref> - कई रोटार, गियर और लचीली डिस्क (HDD) के लिए वाणिज्यिक पार्श्व, मरोड़, अक्षीय और युग्मित सॉल्वर
* रोटोरिन्सा)<ref>{{Cite web|title=लामकोएस|url=http://lamcos.insa-lyon.fr/logiciels_rotorinsa.php?L=1index.php|access-date=2022-01-11|website=lamcos.insa-lyon.fr}}</ref> झुकने में रोटर्स के स्थिर-राज्य गतिशील व्यवहार के विश्लेषण के लिए एक फ्रांसीसी इंजीनियरिंग स्कूल द्वारा विकसित वाणिज्यिक परिमित तत्व सॉफ्टवेयर।
* रोटोरिन्सा (रोटोरिन्सा)<ref>{{Cite web|title=लामकोएस|url=http://lamcos.insa-lyon.fr/logiciels_rotorinsa.php?L=1index.php|access-date=2022-01-11|website=lamcos.insa-lyon.fr}}</ref> झुकने में रोटर्स के स्थिर-राज्य गतिशील व्यवहार के विश्लेषण के लिए एक फ्रांसीसी इंजीनियरिंग स्कूल (INSA-Lyon) द्वारा विकसित वाणिज्यिक परिमित तत्व सॉफ्टवेयर।
* [[COMSOL मल्टीफ़िज़िक्स|कंसोल मल्टीफ़िज़िक्स]], रोटरडायनामिक्स मॉड्यूल ऐड-ऑन रोटरडायनामिक्स मॉड्यूल<ref>{{Cite web|title=Rotordynamics Software for Predictive Analyses of Rotating Machines|url=https://www.comsol.com/rotordynamics-module|access-date=2022-01-11|website=www.comsol.com}}</ref>
* [[COMSOL मल्टीफ़िज़िक्स]], रोटरडायनामिक्स मॉड्यूल ऐड-ऑन (रोटरडायनामिक्स मॉड्यूल)<ref>{{Cite web|title=Rotordynamics Software for Predictive Analyses of Rotating Machines|url=https://www.comsol.com/rotordynamics-module|access-date=2022-01-11|website=www.comsol.com}}</ref>
* रैपिड-रोटोर्डाइनैमिक्स-सील रिसर्च<ref>{{Cite web|title=Rotordynamics-Seal Research - RSR|url=http://rotordynamics.net/|url-status=live|access-date=2022-01-11|website=rda.guru}}</ref> वाणिज्यिक परिमित तत्व आधारित सॉफ़्टवेयर लाइब्रेरी 3डी ठोस और बीम तत्व जिसमें रोटरडायनामिक गुणांक सॉल्वर सम्मिलित हैं
* रैपिड - (रोटोर्डाइनैमिक्स-सील रिसर्च)<ref>{{Cite web|title=Rotordynamics-Seal Research - RSR|url=http://rotordynamics.net/|url-status=live|access-date=2022-01-11|website=rda.guru}}</ref> वाणिज्यिक परिमित तत्व आधारित सॉफ़्टवेयर लाइब्रेरी (3डी ठोस और बीम तत्व) जिसमें रोटरडायनामिक गुणांक सॉल्वर शामिल हैं


== यह भी देखें ==
== यह भी देखें ==
Line 107: Line 98:


==संदर्भ==
==संदर्भ==
{{More footnotes needed|date=January 2022}}
{{Refbegin}}
{{Refbegin}}
* {{cite book|author=Chen, W. J., Gunter, E. J.|title=Introduction to Dynamics of Rotor-Bearing Systems|year=2005|isbn=978-1-4120-5190-3|publisher=Trafford|location=Victoria, BC}} uses DyRoBeS
* {{cite book|author=Chen, W. J., Gunter, E. J.|title=Introduction to Dynamics of Rotor-Bearing Systems|year=2005|isbn=978-1-4120-5190-3|publisher=Trafford|location=Victoria, BC}} uses DyRoBeS
Line 128: Line 118:
* Ganeriwala, S., Mohsen N (2008). ''Rotordynamic Analysis using XLRotor.'' [http://spectraquest.com/technote_display/?technote_id=29 SQI03-02800-0811]
* Ganeriwala, S., Mohsen N (2008). ''Rotordynamic Analysis using XLRotor.'' [http://spectraquest.com/technote_display/?technote_id=29 SQI03-02800-0811]
{{Refend}}
{{Refend}}


=== टिप्पणियाँ ===
=== टिप्पणियाँ ===
{{reflist}}
{{reflist}}
== बाहरी कड़ियाँ ==
== बाहरी कड़ियाँ ==
* [http://spectraquest.com/technote_display/?technote_id=29# Rotordynamic Analysis using XLRotor]
* [http://spectraquest.com/technote_display/?technote_id=29# Rotordynamic Analysis using XLRotor]
* [http://www.rotordynamics.org/ Gateway to technical literature on Rotordynamics]
* [http://www.rotordynamics.org/ Gateway to technical literature on Rotordynamics]
[[Category: गतिकी (यांत्रिकी)]]


[[Category: Machine Translated Page]]
[[Category:CS1]]
[[Category:CS1 English-language sources (en)]]
[[Category:CS1 errors]]
[[Category:CS1 maint]]
[[Category:Created On 25/01/2023]]
[[Category:Created On 25/01/2023]]
[[Category:Lua-based templates]]
[[Category:Machine Translated Page]]
[[Category:Pages with script errors]]
[[Category:Short description with empty Wikidata description]]
[[Category:Templates Vigyan Ready]]
[[Category:Templates that add a tracking category]]
[[Category:Templates that generate short descriptions]]
[[Category:Templates using TemplateData]]
[[Category:गतिकी (यांत्रिकी)]]

Latest revision as of 10:08, 25 August 2023

रोटरडायनामिक्स जिसे रोटर डायनेमिक्स के रूप में भी जाना जाता है घूर्णन संरचनाओं के व्यवहार और निदान से संबंधित अनुप्रयुक्त यांत्रिकी की एक विशेष शाखा है। यह सामान्यतः जेट इंजन और वाष्प टरबाइन से लेकर ऑटो इंजन और कंप्यूटर डिस्क भंडारण तक की संरचनाओं के व्यवहार का विश्लेषण करने के लिए उपयोग किया जाता है। अपने सबसे बुनियादी स्तर पर रोटर डायनेमिक्स एक या एक से अधिक यांत्रिक संरचनाओं से संबंधित है जो बेयरिंग द्वारा समर्थित हैं और आंतरिक घटनाओं से प्रभावित हैं जो निश्चित अक्ष के चारों ओर घूमते हैं। सहायक संरचना को स्टेटर "टरबाइन" कहा जाता है। जैसे-जैसे घूर्णन की गति बढ़ती है कंपन का आयाम प्रायः अधिकतम सीमा से गुजरता है जिसे क्रांतिक गति कहा जाता है। यह आयाम सामान्यतः घूर्णन संरचना के असंतुलन से उत्तेजित होता हैI दैनिक उदाहरण स्वरुप इंजन संतुलन और टायर संतुलन सम्मिलित हैं। यदि इन महत्वपूर्ण गतियों पर कंपन का आयाम अत्यधिक है तो विपत्तिपूर्ण विफलता होती है। इसके अलावा टर्बोमशीनरी प्रायः अस्थिरता विकसित करती है जो टर्बोमशीनरी के आंतरिक स्थिति से संबंधित होती है और जिसे ठीक किया जाना चाहिए। यह बड़े रोटर डिजाइन करने वाले इंजीनियरों की मुख्य चिंता है।

घूमने वाली मशीनरी प्रक्रिया में सम्मिलित तंत्र की संरचना के आधार पर कंपन पैदा करती है। मशीन में कोई भी कंपन के संकेत को बढ़ा सकता है। असंतुलन के कारण मशीन का कंपन घूर्णक मशीनरी के मुख्य पहलुओं में से एक है जिसका विस्तार से अध्ययन किया जाना चाहिए और डिजाइन करते समय विचार किया जाना चाहिए। घूर्णक मशीन सहित सभी वस्तुएँ वस्तु की संरचना के आधार पर प्राकृतिक आवृत्ति प्रदर्शित करती हैं। घूर्णन मशीन की महत्वपूर्ण गति तब होती है जब घूर्णन गति इसकी प्राकृतिक आवृत्ति से मेल खाती है। पहली बार जिस सबसे कम गति से संबंधित प्राकृतिक आवृत्ति का सामना करना पड़ता है उसे पहली महत्वपूर्ण गति कहा जाता हैI लेकिन जैसे-जैसे गति बढ़ती है उसमें अतिरिक्त गति का संचार होता है होते दिखाई देता है जो प्राकृतिक आवृत्ति के गुणक होते हैं। इसलिए प्रतिध्वनि शुरू करने वाली अतिरिक्त बल को कम करने के लिए घूर्णी असंतुलन और अनावश्यक बाहरी बल या शक्ति को कम करना बहुत महत्वपूर्ण है। जब कंपन प्रतिध्वनि के रूप में होता है तो यह विध्वंसक ऊर्जा उत्सर्जित करता है जो घूर्णन मशीन को डिजाइन करते समय मुख्य विचारणीय तथ्य है I इसका मुख्य उद्देश्य गतिवर्धन और गतिविराम के समय संचालन में होने वाली जटिलताओं से सुरक्षित रखना है I यदि इस यदि इस व्यवस्था पर ध्यान केंद्रित नहीं किया गया तो तो इसका परिणाम उपकरण की हानि, मशीनरी पर अत्यधिक टूट-फूट जैसी गतिविधियां हो सकती हैं।

मशीन की वास्तविक गतिशीलता को सैद्धांतिक रूप से पहचानना मुश्किल है I यह गणना सैद्धांतिक तौर पर सरलीकृत मॉडलों पर आधारित होती है जो विभिन्न संरचनात्मक घटकों से मिलती-जुलती होती हैI रोटरोडाइनेमिक्स की कुछ विश्लेषणात्मक विधियाँ भी हैं जैसे वितरित स्थानांतरण फ़ंक्शन विधि[1] जो परिचालन में विश्लेषणात्मक और प्राकृतिक आवृत्तियों, विवेचनात्म्क गति और असंतुलित द्रव्यमान आवृत्ति का स्थानांतरण करती हैI कोई भी आदिप्ररूप क्रमादेशिक मशीन प्रतिध्वनि की सटीक आवृत्तियों की पुष्टि करने के लिए परीक्षण करती हैं जिसमें पुनः डिजाइन करके ये सुनिश्चित किया जाता है कोई प्रतिध्वनि नहीं होती I

मूल सिद्धांत

गति का समीकरण, सामान्यीकृत मैट्रिक्स (गणित) रूप में अक्षीय रूप से सममित रोटर के लिए स्थिर स्पिन गति पर घूमता है I

जहाँ :

M सममित आव्यूह द्रव्यमान आव्यूह है
C सममित भिगोना मैट्रिक्स है
G तिरछा-सममित मैट्रिक्स है | तिरछा-सममित जाइरोस्कोपिक मैट्रिक्स के सममित असर या सील स्टिफनेस मैट्रिक्स है
N उदाहरण के लिए केन्द्रापसारक तत्वों को सम्मिलित करने के लिए विक्षेपण का जाइरोस्कोपिक मैट्रिक्स है।

जिसमें q जड़त्वीय निर्देशांक में रोटर का सामान्यीकृत निर्देशांक है और f प्रेरक फलन हैI

जाइरोस्कोपिक मैट्रिक्स G स्पिन गति Ω के समानुपाती है।

उपरोक्त समीकरण के सामान्य समाधान में जटिल संख्या सम्मिलित हैं जो स्पिन गति पर निर्भर हैं। इस क्षेत्र के इंजीनियरिंग विशेषज्ञ इन समाधानों का पता लगाने के लिए कैंपबेल आरेख पर निर्भर होते हैं I

समीकरणों की रोटरडाइनैमिक प्रणाली में कठोर, अवमंदन और द्रव्यमान के ऑफ-डायगोनल शब्दों की रोचक प्रक्रिया या तथ्य है I इन शब्दों को क्रॉस-युग्मित कठोरत, क्रॉस-युग्मित अवसंदन और क्रॉस-युग्मित द्रव्यमान कहा जाता है। जब समीकरणों में सकारात्मक क्रॉस-युग्मित कठोरता होती है तो यह विक्षेपण प्रतिक्रिया बल को विक्षेपण की दिशा के विपरीत बल पर प्रतिक्रिया करने के लिए और सकारात्मक दिशा में ले जाने के लिए प्रतिक्रिया बल का कारण बनता है। यदि यह बल उपलब्ध प्रत्यक्ष नमी और कठोरता की तुलना में काफी विस्तृत है तो ऐसे में घूर्णन अस्थिर होगा। जब एक रोटर अस्थिर होता है तो विध्वंसक विफलता से बचने के लिए सामान्यतः मशीन को तत्काल बंद करने की आवश्यकता होती है।

कैंपबेल आरेख

एक साधारण रोटर के लिए कैंपबेल आरेख

कैंपबेल डायग्राम, जिसे "व्हर्ल स्पीड मैप" या "फ्रीक्वेंसी इंटरफेरेंस" के नाम से भी जाना जाता हैI साधारण रोटर सिस्टम का आरेख दाईं ओर दिखाया गया है। गुलाबी और नीले रंग के कर्व्स क्रमशः बैकवर्ड व्हर्ल (बीडब्ल्यू) और फॉरवर्ड व्हर्ल (एफडब्ल्यू) मोड दिखाते हैं जो स्पिन की गति बढ़ने पर अलग हो जाते हैं। जब बैकवर्ड व्हर्लफ्रीक्वेंसी या फॉरवर्ड व्हर्ल फ्रीक्वेंसी स्पिन स्पीड Ω के बराबर होती है जो सिंक्रोनस स्पिन स्पीड लाइन के साथ इंटरसेक्शन ए और बी द्वारा इंगित की जाती है तो रोटर की प्रतिक्रिया एक चोटी दिखा सकती है इसे क्रांतिक गति कहते हैं।

जेफकॉट रोटर

जेफकोट रोटर जिसे यूरोप में गुस्ताफ डी लावल घूर्णन के नाम से भी जाना जाता है वह इन समीकरणों को हल करने के लिए इस्तेमाल किया जाने वाला सरलीकृत पैरामीटर मॉडल है। जेफकॉट रोटर एक गणितीय आदर्शीकरण विज्ञान है जो वास्तविक रोटर यांत्रिकी को प्रतिबिंबित नहीं कर सकता है।

इतिहास

रोटरडायनामिक्स का इतिहास सिद्धांत और व्यवहार के परस्पर क्रिया से भरा पड़ा है। विलियम जॉन मैक्कॉर्न रैनकिन, डब्ल्यू जेएम रैंकिन ने पहली बार 1869 में कताई शाफ्ट का विश्लेषण किया लेकिन उनका मॉडल पर्याप्त नहीं था और उन्होंने भविष्यवाणी की कि सुपरक्रिटिकल गति प्राप्त नहीं की जा सकती। 1895 में डंकर्ले ने सुपरक्रिटिकल गति का वर्णन करते हुए प्रायोगिक पेपर प्रकाशित किया। एक स्वीडिश इंजीनियर, गुस्ताफ डी लावल ने 1889 में सुपरक्रिटिकल गति के लिए भाप टरबाइन चलाया और केर ने 1916 में एक दूसरी महत्वपूर्ण गति के प्रायोगिक साक्ष्य दिखाते हुए पेपर प्रकाशित किया।

सिद्धांत और व्यवहार के बीच संघर्ष को हल करने के लिए लंदन की रॉयल सोसाइटी द्वारा हेनरी जेफकॉट को नियुक्त किया गया था। उन्होंने 1919 में फिलोसोफिकल मैगज़ीन में पेपर प्रकाशित किया जिसे अब क्लासिक माना जाता है जिसमें उन्होंने स्थिर सुपरक्रिटिकल गति के अस्तित्व की पुष्टि की। अगस्त 1895 में समान निष्कर्ष प्रकाशित किए लेकिन इतिहास ने बड़े पैमाने पर उनके काम को नजरअंदाज कर दिया।

जेफकॉट के काम और द्वितीय विश्व युद्ध की शुरुआत के बीच अस्थिरता और मॉडलिंग तकनीकों के क्षेत्र में बहुत काम किया गया था जिसकी परिणति निल्स ओटो मायक्लेस्टैड के काम में हुई।[2] एमए प्रोहल[3] जिसके कारण रोटर्स के विश्लेषण के लिए ट्रांसफर मैट्रिक्स मेथड का मार्ग प्रशस्त हुआ। रोटरडायनामिक्स विश्लेषण के लिए आज उपयोग की जाने वाली सबसे प्रचलित विधि परिमित तत्व विधि है।

आधुनिक कंप्यूटर मॉडल पर दारा चिल्ड्स के हवाले से एक उद्धरण में टिप्पणी की गई हैI कंप्यूटर कोड से भविष्यवाणियों की गुणवत्ता का मूल मॉडल की सुदृढ़ता और सिस्टम विश्लेषक की भौतिक अंतर्दृष्टि से अधिक लेना-देना है। सुपीरियर एल्गोरिदम या कंप्यूटर कोड खराब मॉडल या इंजीनियरिंग की कमी को ठीक नहीं करेंगे।

प्रो. फ्रेडरिक नेल्सन,एफ. नेल्सन ने रोटरडायनामिक्स के इतिहास पर व्यापक रूप से लिखा है और इस खंड का अधिकांश भाग उनके काम पर आधारित है।

सॉफ्टवेयर

ऐसे कई सॉफ्टवेयर पैकेज हैं जो समीकरणों के रोटर डायनेमिक सिस्टम को हल करने में सक्षम हैं। रोटर गतिशील विशिष्ट कोड डिजाइन उद्देश्यों के लिए अधिक बहुमुखी हैं। ये कोड असर गुणांक, साइड लोड और कई अन्य वस्तुओं को जोड़ना आसान बनाते हैं, जिनकी आवश्यकता केवल एक रोटरडायनामिकिस्ट को होती है। गैर-रोटर डायनेमिक विशिष्ट कोड पूर्ण विशेषताओं वाले सॉल्वर हैंऔर उनके समाधान तकनीकों में कई वर्षों का विकास है। गैर-रोटर डायनेमिक विशिष्ट कोड का उपयोग रोटर डायनेमिक्स के लिए डिज़ाइन किए गए कोड को कैलिब्रेट करने के लिए भी किया जा सकता है।

रोटरडायनामिक विशिष्ट कोड:

  • डायनेमिक्स R4 (Alfa-Tranzit Co. Ltd)[4] - स्थानिक प्रणालियों के डिजाइन और विश्लेषण के लिए वाणिज्यिक सॉफ्टवेयर विकसित किया गयाI
  • एक्सस्ट्रीम रोटरडायनामिक्स, (सॉफ्टइनवे)[5] - रोटर डायनेमिक्स के लिए एकीकृत सॉफ्टवेयर प्लेटफॉर्म, बीम या 2डी-एक्सिसिमेट्रिक तत्वों पर परिमित तत्व विधि का उपयोग करके सभी व्यापक रूप से उपयोग किए जाने वाले रोटर प्रकारों के लिए पार्श्व, मरोड़ और अक्षीय रोटर गतिशीलता में सक्षम है, और स्वचालित होने में सक्षम है।
  • रोटोर्टेस्ट, (लैमर - कैंपिनास विश्वविद्यालय)[6] - परिमित तत्व विधि आधारित सॉफ्टवेयर, जिसमें विभिन्न प्रकार के बियरिंग सॉल्वर सम्मिलित हैं। लैमर (रोटेटिंग मशीनरी की प्रयोगशाला) - यूनिकैम्प (कैम्पिनास विश्वविद्यालय) द्वारा विकसित।
  • सैमसेफ रोटर[7] - रोटर्स सिमुलेशन के लिए सॉफ्टवेयर प्लेटफॉर्म (LMS Samtech,A Siemens Business)
  • MADYN (परामर्श इंजीनियर क्लेमेंट)[8] - नींव और आवास सहित कई रोटार और गियर के लिए वाणिज्यिक संयुक्त परिमित तत्व पार्श्व, मरोड़, अक्षीय और युग्मित सॉल्वर।
  • मैडिन 2000 (डेल्टा जेएस इंक।)[9] - वाणिज्यिक संयुक्त परिमित तत्व (3डी टिमोचेंको बीम) पार्श्व, मरोड़, अक्षीय और युग्मित सॉल्वर कई रोटार और गियर, नींव और आवरण (अन्य स्रोतों से हस्तांतरण कार्यों और राज्य अंतरिक्ष मैट्रिक्स आयात करने की क्षमता), विभिन्न बीयरिंग (द्रव फिल्म, वसंत स्पंज) , चुंबकीय, रोलिंग तत्व)
  • iSTRDYN (डायनाटेक सॉफ्टवेयर एलएलसी)[10] - वाणिज्यिक 2-डी अक्ष-सममित परिमित तत्व सॉल्वर
  • FEMRDYN (डायनाटेक इंजीनियरिंग, इंक।)[11] - वाणिज्यिक 1-डी अक्ष-सममित परिमित तत्व सॉल्वर
  • रिमैप राइटेक[12] - वाणिज्यिक 1-डी बीम तत्व सॉल्वर
  • रोटेटिंग मशीनरी एनालिसिस[13] - वाणिज्यिक 1-डी बीम तत्व सॉल्वर, चुंबकीय असर नियंत्रण प्रणाली और युग्मित पार्श्व-मरोड़ विश्लेषण सहित। एक्सेल स्प्रेडशीट का उपयोग करके रोटर डायनेमिक मॉडलिंग और विश्लेषण के लिए एक शक्तिशाली, तेज और उपयोग में आसान टूल। VBA मैक्रोज़ के साथ आसानी से स्वचालित, साथ ही 3D CAD सॉफ़्टवेयर के लिए एक प्लगइन।
  • एआरएमडी (रोटर बेयरिंग टेक्नोलॉजी एंड सॉफ्टवेयर, इंक)[14] - रोटरडायनामिक्स, मल्टी-ब्रांच टॉर्सनल वाइब्रेशन, फ्लुइड-फिल्म बियरिंग, अनुकूलन और प्रदर्शन मूल्यांकन के लिए वाणिज्यिक FEA-आधारित सॉफ़्टवेयर, जिसका उपयोग दुनिया भर में सभी उद्योगों के शोधकर्ताओं, ओईएम और अंतिम-उपयोगकर्ताओं द्वारा किया जाता है। .
  • टेक्सास ए एंड एम यूनिवर्सिटी, टेक्सास ए एंड एम[15] - अकादमिक 1-डी बीम तत्व सॉल्वर
  • कॉम्बोरोटर,वर्जीनिया विश्वविद्यालय[16] औद्योगिक उपयोग द्वारा बड़े पैमाने पर सत्यापित महत्वपूर्ण गति, स्थिरता और असंतुलित प्रतिक्रिया का मूल्यांकन करने वाले कई रोटार के लिए संयुक्त परिमित तत्व पार्श्व, मरोड़, अक्षीय सॉल्वर
  • द्रव-प्रवाह मशीनरी संस्थान, पोलिश विज्ञान अकादमी[17] लीनियर और नॉन-लीनियर रेंज के भीतर रोटर-बियरिंग सिस्टम के विश्लेषण के लिए अकादमिक कंप्यूटर कोड पैकेज
  • डी एंड एम टेक्नोलॉजी)[18] कई रोटार, गियर और लचीली डिस्क (HDD) के लिए वाणिज्यिक पार्श्व, मरोड़, अक्षीय और युग्मित सॉल्वर
  • रोटोरिन्सा)[19] झुकने में रोटर्स के स्थिर-राज्य गतिशील व्यवहार के विश्लेषण के लिए एक फ्रांसीसी इंजीनियरिंग स्कूल द्वारा विकसित वाणिज्यिक परिमित तत्व सॉफ्टवेयर।
  • कंसोल मल्टीफ़िज़िक्स, रोटरडायनामिक्स मॉड्यूल ऐड-ऑन रोटरडायनामिक्स मॉड्यूल[20]
  • रैपिड-रोटोर्डाइनैमिक्स-सील रिसर्च[21] वाणिज्यिक परिमित तत्व आधारित सॉफ़्टवेयर लाइब्रेरी 3डी ठोस और बीम तत्व जिसमें रोटरडायनामिक गुणांक सॉल्वर सम्मिलित हैं

यह भी देखें

संदर्भ

  • Chen, W. J., Gunter, E. J. (2005). Introduction to Dynamics of Rotor-Bearing Systems. Victoria, BC: Trafford. ISBN 978-1-4120-5190-3.{{cite book}}: CS1 maint: multiple names: authors list (link) uses DyRoBeS
  • Childs, D. (1993). Turbomachinery Rotordynamics Phenomena, Modeling, & Analysis. Wiley. ISBN 978-0-471-53840-0.
  • Fredric F. Ehrich, ed. (1992). Handbook of Rotordynamics. McGraw-Hill. ISBN 978-0-07-019330-7.
  • Genta, G. (2005). Dynamics of Rotating Systems. Springer. ISBN 978-0-387-20936-4.
  • Jeffcott, H. H. (1919). "The Lateral Vibration Loaded Shafts in the Neighborhood of a Whirling Speed. - The Effect of Want of Balance". Philosophical Magazine. 6. 37.
  • Krämer, E. (1993). Dynamics of Rotors and Foundations. Springer-Verlag. ISBN 978-0-387-55725-0.
  • Lalanne, M., Ferraris, G. (1998). Rotordynamics Prediction in Engineering, Second Edition. Wiley. ISBN 978-0-471-97288-4.{{cite book}}: CS1 maint: multiple names: authors list (link)
  • Muszyńska, Agnieszka (2005). Rotordynamics. CRC Press. ISBN 978-0-8247-2399-6.
  • Nelson, F. (June 2003). "A Brief History of Early Rotor Dynamics". Sound and Vibration.
  • Nelson, F. (July 2007). "Rotordynamics without Equations". International Journal of COMADEM. 3. 10. ISSN 1363-7681.
  • Nelson, F. (2011). An Introduction to Rotordynamics. Vol. SVM-19 [1]. {{cite book}}: External link in |volume= (help)
  • Lalanne, M., Ferraris, G. (1998). Rotordynamics Prediction in Engineering, Second Edition. Wiley. ISBN 978-0-471-97288-4.{{cite book}}: CS1 maint: multiple names: authors list (link)
  • Vance, John M. (1988). Rotordynamics of Turbomachinery. Wiley. ISBN 978-0-471-80258-7.
  • Tiwari, Rajiv (2017). Rotor Systems: Analysis and Identification. CRC Press. ISBN 9781138036284.
  • Vance, John M., Murphy, B., Zeidan, F. (2010). Machinery Vibration and Rotordynamics. Wiley. ISBN 978-0-471-46213-2.{{cite book}}: CS1 maint: multiple names: authors list (link)
  • Vollan, A., Komzsik, L. (2012). Computational Techniques of Rotor Dynamics with the Finite Element Method. CRC Press. ISBN 978-1-4398-4770-1.{{cite book}}: CS1 maint: multiple names: authors list (link)
  • Yamamoto, T., Ishida, Y. (2001). Linear and Nonlinear Rotordynamics. Wiley. ISBN 978-0-471-18175-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
  • Ganeriwala, S., Mohsen N (2008). Rotordynamic Analysis using XLRotor. SQI03-02800-0811

टिप्पणियाँ

  1. ↑ Liu, Shibing; Yang, Bingen (2017-02-22). "Vibrations of Flexible Multistage Rotor Systems Supported by Water-Lubricated Rubber Bearings". Journal of Vibration and Acoustics. 139 (2): 021016–021016–12. doi:10.1115/1.4035136. ISSN 1048-9002.
  2. ↑ Myklestad, Nils (April 1944). "A New Method of Calculating Natural Modes of Uncoupled Bending Vibration of Airplane Wings and Other Types of Beams". Journal of the Aeronautical Sciences (Institute of the Aeronautical Sciences). 11 (2): 153–162. doi:10.2514/8.11116.
  3. ↑ Prohl, M. A. (1945), "A General Method for Calculating Critical Speeds of Flexible Rotors", Trans ASME, 66: A–142
  4. ↑ "ROTORDYNAMICS OF TURBOMACHINERY, Software and Engineering services, Alfa-Tranzit Co". www.alfatran.com. Retrieved 2022-01-11.
  5. ↑ "AxSTREAM - Rotordynamics | Turbomachinery Design Software". www.softinway.com (in English). 2016-07-27. Retrieved 2022-01-11.
  6. ↑ "घर". www.fem.unicamp.br. Retrieved 2022-01-11.{{cite web}}: CS1 maint: url-status (link)
  7. ↑ "Rotor dynamics analysis: SAMCEF Rotors is up to the challenge". Archived from the original on 2012-09-29. Retrieved 2013-06-04.
  8. ↑ "घर". www.madyn.de. Retrieved 2022-01-11.{{cite web}}: CS1 maint: url-status (link)
  9. ↑ "MADYN 2000 for Rotordynamics". www.delta-js.ch. Retrieved 2022-01-11.
  10. ↑ "Archived copy". Archived from the original on 2021-05-07. Retrieved 2022-01-11.{{cite web}}: CS1 maint: archived copy as title (link)
  11. ↑ "FEMRDYN". dynatechengr.com. Retrieved 2022-01-11.
  12. ↑ "RITEC - RIMAP (Rotordynamic Analysis Software Package)". Archived from the original on 2013-10-04. Retrieved 2013-10-01.
  13. ↑ "घर". XLRotor (in English). Retrieved 2022-01-11.
  14. ↑ "ARMD Rotor Dynamics". Retrieved 2022-01-01.{{cite web}}: CS1 maint: url-status (link)
  15. ↑ "Turbomachinery Laboratory". turbolab.tamu.edu. Retrieved 2022-01-11.
  16. ↑ "Rotating Machinery and Controls Laboratory".
  17. ↑ "the Szewalski Institute of Fluid-flow Machinery". Archived from the original on 2008-12-15.
  18. ↑ "D&M; Technology Co., Ltd". Archived from the original on 2021-05-06.
  19. ↑ "लामकोएस". lamcos.insa-lyon.fr. Retrieved 2022-01-11.
  20. ↑ "Rotordynamics Software for Predictive Analyses of Rotating Machines". www.comsol.com. Retrieved 2022-01-11.
  21. ↑ "Rotordynamics-Seal Research - RSR". rda.guru. Retrieved 2022-01-11.{{cite web}}: CS1 maint: url-status (link)

बाहरी कड़ियाँ

Retrieved from ‘https://www.vigyanwiki.in/index.php?title=रोटरडायनामिक्स&oldid=253511’