खंडित प्रतिगमन: Difference between revisions

From Vigyanwiki
(Created page with "{{Regression bar}} खंडित प्रतिगमन, जिसे टुकड़े-टुकड़े प्रतिगमन या टूटी-छड़ी प...")
 
No edit summary
 
(5 intermediate revisions by 4 users not shown)
Line 1: Line 1:
{{Regression bar}}
{{Regression bar}}
खंडित प्रतिगमन, जिसे टुकड़े-टुकड़े प्रतिगमन या टूटी-छड़ी प्रतिगमन के रूप में भी जाना जाता है, [[प्रतिगमन विश्लेषण]] में एक विधि है जिसमें [[स्वतंत्र चर]] को अंतराल में विभाजित किया जाता है और प्रत्येक अंतराल में एक अलग रेखा खंड फिट किया जाता है। विभिन्न स्वतंत्र चरों को विभाजित करके बहुभिन्नरूपी डेटा पर खंडित प्रतिगमन विश्लेषण भी किया जा सकता है। खंडित प्रतिगमन तब उपयोगी होता है जब स्वतंत्र चर, विभिन्न समूहों में क्लस्टर किए जाते हैं, इन क्षेत्रों में चर के बीच अलग-अलग संबंध प्रदर्शित करते हैं। खंडों के बीच की सीमाएँ ''ब्रेकप्वाइंट'' हैं।
'''खंडित प्रतिगमन (सेगमेंटेड रिग्रेशन)''', जिसे खंडशः प्रतिगमन या खंडित-स्टिक प्रतिगमन के रूप में भी जाना जाता है, [[प्रतिगमन विश्लेषण]] में एक विधि है जिसमें स्वतंत्र चर को अंतराल में विभाजित किया जाता है और प्रत्येक अंतराल में एक अलग रेखा खंड फिट किया जाता है। विभिन्न स्वतंत्र चरों को विभाजित करके बहुभिन्नरूपी डेटा पर सेगमेंटेड रिग्रेशन विश्लेषण भी किया जा सकता है। सेगमेंटेड रिग्रेशन तब उपयोगी होता है जब स्वतंत्र चर, विभिन्न समूहों में क्लस्टर किए जाते हैं, इन क्षेत्रों में चर के बीच अलग-अलग संबंध प्रदर्शित करते हैं। खंडों के बीच की सीमाएँ ''ब्रेकप्वाइंट'' हैं।


खंडित रैखिक प्रतिगमन खंडित प्रतिगमन है जिससे अंतराल में संबंध रैखिक प्रतिगमन द्वारा प्राप्त किए जाते हैं।
खंडित रैखिक प्रतिगमन सेगमेंटेड रिग्रेशन है जिससे अंतराल में संबंध रैखिक प्रतिगमन द्वारा प्राप्त किए जाते हैं।


==खंडित रैखिक प्रतिगमन, दो खंड==
==खंडित रैखिक प्रतिगमन, दो खंड==
[[File:SegReg3.gif|thumb|300px|पहला अंग क्षैतिज]]
[[File:SegReg3.gif|thumb|300px|पहला लिंब क्षैतिज]]
[[File:SegReg1.gif|thumb|300px|पहला अंग ऊपर की ओर झुका हुआ]]
[[File:SegReg1.gif|thumb|300px|पहला लिंब ऊपर की ओर झुका हुआ]]
[[File:SegReg2.gif|thumb|300px|पहला अंग नीचे झुका हुआ]]ब्रेकप्वाइंट द्वारा अलग किए गए दो खंडों के साथ खंडित रैखिक प्रतिगमन एक अलग प्रभावशाली कारक ('x') के प्रतिक्रिया फ़ंक्शन (Yr) के अचानक परिवर्तन को निर्धारित करने के लिए उपयोगी हो सकता है। ब्रेकप्वाइंट की व्याख्या एक महत्वपूर्ण, सुरक्षित या थ्रेशोल्ड मान के रूप में की जा सकती है जिसके परे या नीचे (अवांछित) प्रभाव होते हैं। निर्णय लेने में ब्रेकप्वाइंट महत्वपूर्ण हो सकता है <ref>''Frequency and Regression Analysis''. Chapter 6 in: H.P.Ritzema (ed., 1994), ''Drainage Principles and Applications'', Publ. 16, pp. 175-224, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. {{ISBN|90-70754-33-9}} . Free download from the webpage [http://www.waterlog.info/articles.htm] , under nr. 20, or directly as PDF : [http://www.waterlog.info/pdf/regtxt.pdf]</ref>
[[File:SegReg2.gif|thumb|300px|पहला लिंब नीचे झुका हुआ]]ब्रेकप्वाइंट द्वारा अलग किए गए दो खंडों के साथ खंडित रैखिक प्रतिगमन एक अलग प्रभावशाली कारक (x) के प्रतिक्रिया फ़ंक्शन (Yr) के अचानक परिवर्तन को निर्धारित करने के लिए उपयोगी हो सकता है। ब्रेकप्वाइंट की व्याख्या एक महत्वपूर्ण, सुरक्षित या थ्रेशोल्ड मान के रूप में की जा सकती है जिसके सीमा के बाहर या नीचे (अवांछित) प्रभाव होते हैं। निर्णय लेने में ब्रेकप्वाइंट महत्वपूर्ण हो सकता है।<ref>''Frequency and Regression Analysis''. Chapter 6 in: H.P.Ritzema (ed., 1994), ''Drainage Principles and Applications'', Publ. 16, pp. 175-224, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. {{ISBN|90-70754-33-9}} . Free download from the webpage [http://www.waterlog.info/articles.htm] , under nr. 20, or directly as PDF : [http://www.waterlog.info/pdf/regtxt.pdf]</ref>
आंकड़े कुछ परिणामों और प्रतिगमन प्रकारों को दर्शाते हैं।
आंकड़े कुछ परिणामों और प्रतिगमन प्रकारों को दर्शाते हैं।


एक खंडित प्रतिगमन विश्लेषण (y, x) डेटा के एक सेट की उपस्थिति पर आधारित है, जिसमें y आश्रित चर है और x स्वतंत्र चर है।
एक सेगमेंटेड रिग्रेशन विश्लेषण (y, x) डेटा के एक सेट की उपस्थिति पर आधारित है, जिसमें y आश्रित चर है और x स्वतंत्र चर है।


न्यूनतम वर्ग विधि को प्रत्येक खंड पर अलग से लागू किया जाता है, जिसके द्वारा दो प्रतिगमन रेखाओं को डेटा सेट को यथासंभव निकट से फिट करने के लिए बनाया जाता है, जबकि प्रेक्षित (y) और गणना के बीच ''अंतरों के वर्गों के योग'' (SSD) को कम किया जाता है। आश्रित चर के (वर्ष) मानों के परिणामस्वरूप निम्नलिखित दो समीकरण बनते हैं:
न्यूनतम वर्ग विधि को प्रत्येक खंड पर अलग से लागू किया जाता है, जिसके द्वारा दो प्रतिगमन रेखाओं को डेटा सेट को यथासंभव निकट से फिट करने के लिए बनाया जाता है, जबकि देखे गए ('''y''') और परिकलित (Yr) ''मानों के बीच अंतर'' (SSD) ''के वर्गों के योग'' को कम किया जाता है। आश्रित चर के परिणामस्वरूप निम्नलिखित दो समीकरण बनते हैं:


* वर्ष = ए<sub>1</sub>.एक्स + के<sub>1</sub> x <बीपी (ब्रेकप्वाइंट) के लिए
* Yr = A<sub>1</sub>.'''x''' + K<sub>1</sub>   '''x''' < BP (ब्रेकप्वाइंट) के लिए
* वर्ष = ए<sub>2</sub>.एक्स + के<sub>2</sub> x > BP (ब्रेकप्वाइंट) के लिए
* Yr = A<sub>2</sub>.'''x''' + K<sub>2</sub>    '''x''' > BP (ब्रेकप्वाइंट) के लिए
कहां:<br>
जहाँ:<br>
:Yr, x के एक निश्चित मान के लिए y का अपेक्षित (अनुमानित) मान है;
:Yr, x के एक निश्चित मान के लिए y का अपेक्षित (अनुमानित) मान है;
:ए<sub>1</sub> और ए<sub>2</sub> [[प्रतिगमन गुणांक]] हैं (रेखा खंडों की ढलान का संकेत);
:A<sub>1</sub> और A<sub>2</sub> प्रतिगमन गुणांक हैं (रेखा खंडों की गिरावट का संकेत);
:क<sub>1</sub> और के<sub>2</sub> प्रतिगमन स्थिरांक हैं ('y'-अक्ष पर अवरोधन को इंगित करते हुए)।
:K<sub>1</sub> और K<sub>2</sub> ''प्रतिगमन स्थिरांक'' हैं ('y'-अक्ष पर अवरोधन को इंगित करते हुए)।


डेटा कई प्रकार या रुझान दिखा सकता है,<ref>'' Drainage research in farmers' fields: analysis of data''. Part of project "Liquid Gold" of the International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Download as PDF : [http://www.waterlog.info/pdf/analysis.pdf]</ref> आंकड़े देखें.
डेटा कई प्रकार या रुझान दिखा सकता है,<ref>'' Drainage research in farmers' fields: analysis of data''. Part of project "Liquid Gold" of the International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Download as PDF : [http://www.waterlog.info/pdf/analysis.pdf]</ref> आंकड़े देखें.


विधि से दो [[पियर्सन उत्पाद-क्षण सहसंबंध गुणांक]] (R) भी प्राप्त होते हैं:
विधि से दो पियर्सन उत्पाद-क्षण सहसंबंध गुणांक (R) भी प्राप्त होते हैं:
*<math>R_1 ^ 2 = 1 - \frac{\sum (y - Y_r) ^ 2 }{ \sum (y - Y_{a1})^2}</math> x <बीपी (ब्रेकप्वाइंट) के लिए
*<math>R_1 ^ 2 = 1 - \frac{\sum (y - Y_r) ^ 2 }{ \sum (y - Y_{a1})^2}</math> x <BP (ब्रेकप्वाइंट) के लिए
और
और
*<math>R_2 ^ 2 = 1 - \frac{\sum (y - Y_r) ^ 2 }{ \sum (y - Y_{a2})^2}</math> x > BP (ब्रेकप्वाइंट) के लिए
*<math>R_2 ^ 2 = 1 - \frac{\sum (y - Y_r) ^ 2 }{ \sum (y - Y_{a2})^2}</math> x > BP (ब्रेकप्वाइंट) के लिए
कहां:<br>
जहाँ:<br>
: <math> \sum (y - Y_r) ^2 </math> प्रति खंड न्यूनतम SSD है
: <math> \sum (y - Y_r) ^2 </math> प्रति खंड न्यूनतम SSD है
और
और
:<बड़ा>य<sub>a1</sub></बड़ा> और <बड़ा>वाई<sub>a2</sub></big>संबंधित खंडों में y के औसत मान हैं।
:Y<sub>a1</sub> और Y<sub>a2</sub> संबंधित खंडों में '''y''' </big>के औसत मान हैं।


सबसे उपयुक्त प्रवृत्ति के निर्धारण में, यह सुनिश्चित करने के लिए [[सांख्यिकीय परीक्षण]] किए जाने चाहिए कि यह प्रवृत्ति विश्वसनीय (महत्वपूर्ण) है।
सबसे उपयुक्त प्रवृत्ति का निर्धारण करने में, यह सुनिश्चित करने के लिए सांख्यिकीय परीक्षण आयोजित किए जाने चाहिए कि प्रवृत्ति विश्वसनीय (महत्वपूर्ण) है।


जब कोई महत्वपूर्ण ब्रेकपॉइंट का पता नहीं लगाया जा सकता है, तो किसी को ब्रेकपॉइंट के बिना प्रतिगमन पर वापस आना चाहिए।
जब किसी महत्वपूर्ण ब्रेकप्वाइंट का पता नहीं लगाया जा सकता है, तो व्यक्ति को बिना ब्रेकप्वाइंट के प्रतिगमन पर वापस आना चाहिए।


==उदाहरण==
==उदाहरण==
[[File:Mustard_segm_regr_least_squares.png|thumb|350px| खंडित रैखिक प्रतिगमन, प्रकार 3बी]]दाईं ओर की नीली आकृति के लिए जो सरसों की उपज (Yr = Ym, t/ha) और [[मिट्टी की लवणता]] (x = Ss, मिट्टी के घोल EC की विद्युत चालकता dS/m में व्यक्त की जाती है) के बीच संबंध बताती है, यह पाया गया है कि :<ref>R.J.Oosterbaan, D.P.Sharma, K.N.Singh and K.V.G.K.Rao, 1990, ''Crop production and soil salinity: evaluation of field data from India by segmented linear regression''. In: Proceedings of the Symposium on Land Drainage for Salinity Control in Arid and Semi-Arid Regions, February 25th to March 2nd, 1990, Cairo, Egypt, Vol. 3, Session V, p. 373 - 383.</ref>
[[File:Mustard_segm_regr_least_squares.png|thumb|350px| खंडित रैखिक प्रतिगमन, प्रकार 3बी]]दाईं ओर की नीली आकृति के लिए जो सरसों की उपज (Yr = Ym, t/ha) और मिट्टी की लवणता ('''x''' = Ss, मिट्टी के घोल EC की विद्युत चालकता dS/m में व्यक्त की जाती है) के बीच संबंध बताती है, यह पाया गया है कि:<ref>R.J.Oosterbaan, D.P.Sharma, K.N.Singh and K.V.G.K.Rao, 1990, ''Crop production and soil salinity: evaluation of field data from India by segmented linear regression''. In: Proceedings of the Symposium on Land Drainage for Salinity Control in Arid and Semi-Arid Regions, February 25th to March 2nd, 1990, Cairo, Egypt, Vol. 3, Session V, p. 373 - 383.</ref>
बीपी = 4.93, ए<sub>1</sub> = 0, के<sub>1</sub> = 1.74, ए<sub>2</sub> = −0.129, के<sub>2</sub> = 2.38, आर<sub>1</sub><sup>2</sup> = 0.0035 (महत्वहीन), आर<sub>2</sub><sup>2</sup> = 0.395 (महत्वपूर्ण) और:
BP = 4.93, A<sub>1</sub> = 0, K<sub>1</sub> = 1.74, A<sub>2</sub> = −0.129, K<sub>2</sub> = 2.38, R<sub>1</sub><sup>2</sup> = 0.0035 (महत्वहीन), R<sub>2</sub><sup>2</sup> = 0.395 (महत्वपूर्ण) और:
* Ym = 1.74 टन/हेक्टेयर ‍
* Ym = 1.74 t/ha                        के लिए Ss < 4.93
* Ym = −0.129 Ss + 2.38 t/ha     Ss > 4.93 (ब्रेकप्वाइंट) के लिए
* Ym = −0.129 Ss + 2.38 t/ha     के लिए Ss > 4.93 (ब्रेकप्वाइंट)  
यह दर्शाता है कि मिट्टी की लवणता <4.93 dS/m सुरक्षित है और मिट्टी की लवणता > 4.93 dS/m मिट्टी की लवणता की प्रति इकाई वृद्धि से 0.129 टन/हेक्टेयर की दर से उपज कम हो जाती है।
यह दर्शाता है कि मिट्टी की लवणता <4.93 dS/m सुरक्षित है और मिट्टी की लवणता > 4.93 dS/m मिट्टी की लवणता की प्रति इकाई वृद्धि से 0.129 टन/हेक्टेयर की दर से उपज कम हो जाती है।


Line 48: Line 48:
[[File:CHAO.png|thumb|350px|उदाहरण समय श्रृंखला, प्रकार 5]]
[[File:CHAO.png|thumb|350px|उदाहरण समय श्रृंखला, प्रकार 5]]
[[File:SegReg_Anova_Table.png|thumb|350px|एनोवा तालिका का उदाहरण: इस मामले में ब्रेक पॉइंट का परिचय अत्यधिक महत्वपूर्ण है।]]प्रवृत्ति के प्रकार को निर्धारित करने के लिए निम्नलिखित सांख्यिकीय परीक्षणों का उपयोग किया जाता है:
[[File:SegReg_Anova_Table.png|thumb|350px|एनोवा तालिका का उदाहरण: इस मामले में ब्रेक पॉइंट का परिचय अत्यधिक महत्वपूर्ण है।]]प्रवृत्ति के प्रकार को निर्धारित करने के लिए निम्नलिखित सांख्यिकीय परीक्षणों का उपयोग किया जाता है:
# बीपी को प्रतिगमन गुणांक ए के एक फ़ंक्शन के रूप में व्यक्त करके ब्रेकपॉइंट (बीपी) का महत्व<sub>1</sub> और ए<sub>2</sub> और साधन Y<sub>1</sub> और वाई<sub>2</sub> y-डेटा और साधन X का<sub>1</sub> और एक्स<sub>2</sub> एक्स डेटा (बीपी के बाएं और दाएं), बीपी की [[मानक त्रुटि]] (एसई) की गणना करने के लिए जोड़ और गुणन में अनिश्चितता के प्रसार के नियमों का उपयोग करना, और छात्र के टी-टेस्ट को लागू करना
# प्रतिगमन गुणांक A<sub>1</sub> और A<sub>2</sub> और '''y-'''डेटा के माध्य Y<sub>1</sub> और Y<sub>2</sub> और '''x-''' डेटा (BP के बाएं और दाएं) के माध्य X<sub>1</sub> और X<sub>2</sub> के रूप में '''BP''' को व्यक्त करके ब्रेकप्वाइंट ('''BP''') का महत्व, का उपयोग करके '''BP''' की मानक त्रुटि (SE) की गणना करने और छात्र के t-टेस्ट को लागू करने के लिए जोड़ और गुणन में त्रुटियों के प्रसार के नियम
#ए का महत्व<sub>1</sub> और ए<sub>2</sub> विद्यार्थी के टी-वितरण और ए की मानक त्रुटि एसई को लागू करना<sub>1</sub> और ए<sub>2</sub>
#A<sub>1</sub> का महत्व और A<sub>2</sub> विद्यार्थी के टी-वितरण और मानक त्रुटि SE को लागू करने वाले A<sub>1</sub> और A<sub>2</sub> है।
#ए के अंतर का महत्व<sub>1</sub> और ए<sub>2</sub> उनके अंतर के एसई का उपयोग करके छात्र के टी-वितरण को लागू करना।
#A<sub>1</sub> के अंतर का महत्व और A<sub>2</sub> उनके अंतर के SE का उपयोग करके छात्र के टी-वितरण को लागू करना है।
#Y के अंतर का महत्व<sub>1</sub> और वाई<sub>2</sub> उनके अंतर के एसई का उपयोग करके छात्र के टी-वितरण को लागू करना।
#Y के अंतर का महत्व<sub>1</sub> और वाई<sub>2</sub> उनके अंतर के SE का उपयोग करके छात्र के टी-वितरण को लागू करना है।
#ब्रेकप्वाइंट के अस्तित्व के परीक्षण के लिए एक अधिक औपचारिक सांख्यिकीय दृष्टिकोण, छद्म स्कोर परीक्षण के माध्यम से होता है जिसमें खंडित रेखा के अनुमान की आवश्यकता नहीं होती है।<ref>{{Cite journal|last=Muggeo|first=VMR|date=2016|title=Testing with a nuisance parameter present only under the alternative: a score-based approach with application to segmented modelling|journal=Journal of Statistical Computation and Simulation|volume=86|issue=15|pages=3059–3067|doi=10.1080/00949655.2016.1149855|s2cid=124914264 |url=https://figshare.com/articles/journal_contribution/2747764/files/4428298.pdf}}</ref>
#ब्रेकप्वाइंट के अस्तित्व के परीक्षण के लिए एक अधिक औपचारिक सांख्यिकीय दृष्टिकोण, छद्म स्कोर परीक्षण के माध्यम से होता है जिसमें खंडित रेखा के अनुमान की आवश्यकता नहीं होती है।<ref>{{Cite journal|last=Muggeo|first=VMR|date=2016|title=Testing with a nuisance parameter present only under the alternative: a score-based approach with application to segmented modelling|journal=Journal of Statistical Computation and Simulation|volume=86|issue=15|pages=3059–3067|doi=10.1080/00949655.2016.1149855|s2cid=124914264 |url=https://figshare.com/articles/journal_contribution/2747764/files/4428298.pdf}}</ref>
इसके अलावा, सभी डेटा (आरए) के पियर्सन उत्पाद-क्षण सहसंबंध गुणांक, निर्धारण के गुणांक या स्पष्टीकरण के गुणांक, प्रतिगमन कार्यों के आत्म[[विश्वास अंतराल]] और विचरण विश्लेषण के विश्लेषण का उपयोग किया जाता है।<ref>''Statistical significance of segmented linear regression with break-point using variance analysis and F-tests''. Download from [http://www.waterlog.info/faqs.htm] under nr. 13, or directly as PDF : [http://www.waterlog.info/pdf/anova.pdf]</ref>
इसके अलावा, उपयोग सभी डेटा (Ra) के सहसंबंध गुणांक, निर्धारण के गुणांक या स्पष्टीकरण के गुणांक, प्रतिगमन कार्यों के विश्वास अंतराल और एनोवा (ANOVA) विश्लेषण से किया जाता है।<ref>''Statistical significance of segmented linear regression with break-point using variance analysis and F-tests''. Download from [http://www.waterlog.info/faqs.htm] under nr. 13, or directly as PDF : [http://www.waterlog.info/pdf/anova.pdf]</ref>
 
सभी डेटा (सीडी) के लिए निर्धारण का गुणांक, जिसे महत्व परीक्षणों द्वारा निर्धारित शर्तों के तहत अधिकतम किया जाना है, से पाया जाता है:
सभी डेटा (सीडी) के लिए निर्धारण का गुणांक, जिसे महत्व परीक्षणों द्वारा निर्धारित शर्तों के तहत अधिकतम किया जाना है, से पाया जाता है:
*<math>C_d=1-{\sum (y-Y_r)^2\over\sum (y-Y_a)^2}</math>
*<math>C_d=1-{\sum (y-Y_r)^2\over\sum (y-Y_a)^2}</math>
जहां Yr पूर्व प्रतिगमन समीकरणों के अनुसार y का अपेक्षित (अनुमानित) मान है और Ya सभी y मानों का औसत है।
जहां Yr पूर्व प्रतिगमन समीकरणों के अनुसार y का अपेक्षित (अनुमानित) मान है और Ya सभी y मानों का औसत है।


सीडी गुणांक 0 (बिल्कुल कोई स्पष्टीकरण नहीं) से 1 (पूर्ण स्पष्टीकरण, पूर्ण मिलान) के बीच होता है। <br>
सीडी गुणांक 0 (बिल्कुल कोई स्पष्टीकरण नहीं) से 1 (पूर्ण स्पष्टीकरण, पूर्ण मिलान) के बीच होता है। <br>शुद्ध, अखण्डित, रैखिक प्रतिगमन में, Cd और Ra<sub>2</sub> के मान बराबर होते हैं। खंडित प्रतिगमन में, विभाजन को उचित ठहराने के लिए Cd को Ra<sub>2</sub> से काफी बड़ा होना आवश्यक है।
शुद्ध, अखण्डित, रैखिक प्रतिगमन में, Cd और Ra के मान<sup>2</sup>बराबर हैं. खंडित प्रतिगमन में, सीडी को रा से काफी बड़ा होना चाहिए<sup>2</sup>विभाजन को उचित ठहराने के लिए।


ब्रेकप्वाइंट का [[अनुकूलन (गणित)]] मान ऐसे पाया जा सकता है कि सीडी गुणांक [[मैक्सिमा और मिनिमा]] है।
ब्रेकप्वाइंट का [[अनुकूलन (गणित)]] मान ऐसे पाया जा सकता है कि सीडी गुणांक [[मैक्सिमा और मिनिमा]] है।
Line 65: Line 65:
==अप्रभावी सीमा==
==अप्रभावी सीमा==


[[File:Mustard_segm_regr_no_effect.png|thumb|right|350px| X=0 से X=7.85 तक की सीमा का चित्रण जिस पर कोई प्रभाव नहीं है।]]खंडित प्रतिगमन का उपयोग अक्सर यह पता लगाने के लिए किया जाता है कि किस सीमा पर एक व्याख्यात्मक चर (एक्स) का आश्रित चर (वाई) पर कोई प्रभाव नहीं पड़ता है, जबकि पहुंच से परे एक स्पष्ट प्रतिक्रिया होती है, चाहे वह सकारात्मक हो या नकारात्मक।
[[File:Mustard_segm_regr_no_effect.png|thumb|right|350px| X=0 से X=7.85 तक की सीमा का चित्रण जिस पर कोई प्रभाव नहीं है।]]खंडित प्रतिगमन का उपयोग प्रायः उस सीमा को खोजने के लिए किया जाता है जिस पर एक व्याख्यात्मक चर (X) का आश्रित चर (Y) पर कोई प्रभाव नहीं पड़ता है, जबकि पहुंच से परे एक स्पष्ट प्रतिक्रिया होती है, चाहे वह सकारात्मक हो या नकारात्मक हो। बिना किसी प्रभाव की पहुंच X डोमेन के प्रारंभिक भाग में या इसके विपरीत इसके अंतिम भाग में पाई जा सकती है। "कोई प्रभाव नहीं" विश्लेषण के लिए, खंडित प्रतिगमन विश्लेषण के लिए न्यूनतम वर्ग विधि का अनुप्रयोग है।<ref>Segmented regression analysis, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Free download from the webpage [http://www.waterlog.info/segreg.htm]</ref> सबसे उपयुक्त तकनीक नहीं हो सकता है क्योंकि उद्देश्य सबसे लंबे खंड को ढूंढना है जिस पर Y-X संबंध को शून्य ढलान माना जा सकता है जबकि पहुंच से परे ढलान शून्य से काफी अलग है लेकिन इस ढलान के सर्वोत्तम मूल्य के बारे में ज्ञान भौतिक नहीं है। नो-इफ़ेक्ट रेंज खोजने की विधि रेंज पर प्रगतिशील आंशिक प्रतिगमन<ref>Partial Regression Analysis, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Free download from the webpage [http://www.waterlog.info/partreg.htm]</ref> है, छोटे चरणों के साथ सीमा का विस्तार करना जब तक कि प्रतिगमन गुणांक शून्य से काफी भिन्न न हो जाए।
बिना किसी प्रभाव की पहुंच एक्स डोमेन के प्रारंभिक भाग में या इसके विपरीत इसके अंतिम भाग में पाई जा सकती है। बिना प्रभाव वाले विश्लेषण के लिए, खंडित प्रतिगमन विश्लेषण के लिए न्यूनतम वर्ग विधि का अनुप्रयोग <ref>Segmented regression analysis, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Free download from the webpage [http://www.waterlog.info/segreg.htm]</ref> यह सबसे उपयुक्त तकनीक नहीं हो सकती है क्योंकि उद्देश्य सबसे लंबे खिंचाव को ढूंढना है जिस पर Y-X संबंध को शून्य ढलान वाला माना जा सकता है जबकि पहुंच से परे ढलान शून्य से काफी अलग है लेकिन इस ढलान के सर्वोत्तम मूल्य के बारे में ज्ञान है भौतिक नहीं. नो-इफ़ेक्ट रेंज खोजने की विधि प्रगतिशील आंशिक प्रतिगमन है <ref>Partial Regression Analysis, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Free download from the webpage [http://www.waterlog.info/partreg.htm]</ref> सीमा पर, छोटे चरणों के साथ सीमा का विस्तार तब तक करें जब तक कि प्रतिगमन गुणांक शून्य से काफी भिन्न न हो जाए।


अगले चित्र में ब्रेक पॉइंट X=7.9 पर पाया जाता है, जबकि उसी डेटा के लिए (सरसों की उपज के लिए ऊपर नीला चित्र देखें), न्यूनतम वर्ग विधि केवल X=4.9 पर ब्रेक पॉइंट प्राप्त करती है। बाद वाला मान कम है, लेकिन ब्रेक पॉइंट से परे डेटा का फिट बेहतर है। इसलिए, यह विश्लेषण के उद्देश्य पर निर्भर करेगा कि किस विधि को नियोजित करने की आवश्यकता है।
अगले चित्र में ब्रेक पॉइंट X=7.9 पर पाया जाता है, जबकि उसी डेटा के लिए (सरसों की उपज के लिए ऊपर नीला चित्र देखें), न्यूनतम वर्ग विधि केवल X=4.9 पर ब्रेक पॉइंट प्राप्त करती है। बाद वाला मान कम है, लेकिन ब्रेक पॉइंट से सीमा के बाहर डेटा का फिट बेहतर है। इसलिए, यह विश्लेषण के उद्देश्य पर निर्भर करेगा कि किस विधि को नियोजित करने की आवश्यकता है।


==यह भी देखें==
==यह भी देखें==
Line 79: Line 78:
* प्रतिगमन असंततता डिजाइन
* प्रतिगमन असंततता डिजाइन
* [[चरणबद्ध प्रतिगमन]]
* [[चरणबद्ध प्रतिगमन]]
* खंडित प्रतिगमन के लिए [[SegReg]]|SegReg (सॉफ्टवेयर)।
* खंडित प्रतिगमन के लिए SegReg (सॉफ़्टवेयर)


==संदर्भ==
==संदर्भ==
<references />
<references />


{{DEFAULTSORT:Segmented Regression}}[[Category: प्रतिगमन मॉडल]]
{{DEFAULTSORT:Segmented Regression}}
 
 


[[Category: Machine Translated Page]]
[[Category:Created On 07/07/2023|Segmented Regression]]
[[Category:Created On 07/07/2023]]
[[Category:Machine Translated Page|Segmented Regression]]
[[Category:Pages with empty portal template|Segmented Regression]]
[[Category:Portal-inline template with redlinked portals|Segmented Regression]]
[[Category:Templates Vigyan Ready|Segmented Regression]]
[[Category:प्रतिगमन मॉडल|Segmented Regression]]

Latest revision as of 10:11, 28 August 2023

एक श्रृंखला का हिस्सा
प्रतिगमन विश्लेषण
मॉडल
अनुमान
पार्श्वभूमि

खंडित प्रतिगमन (सेगमेंटेड रिग्रेशन), जिसे खंडशः प्रतिगमन या खंडित-स्टिक प्रतिगमन के रूप में भी जाना जाता है, प्रतिगमन विश्लेषण में एक विधि है जिसमें स्वतंत्र चर को अंतराल में विभाजित किया जाता है और प्रत्येक अंतराल में एक अलग रेखा खंड फिट किया जाता है। विभिन्न स्वतंत्र चरों को विभाजित करके बहुभिन्नरूपी डेटा पर सेगमेंटेड रिग्रेशन विश्लेषण भी किया जा सकता है। सेगमेंटेड रिग्रेशन तब उपयोगी होता है जब स्वतंत्र चर, विभिन्न समूहों में क्लस्टर किए जाते हैं, इन क्षेत्रों में चर के बीच अलग-अलग संबंध प्रदर्शित करते हैं। खंडों के बीच की सीमाएँ ब्रेकप्वाइंट हैं।

खंडित रैखिक प्रतिगमन सेगमेंटेड रिग्रेशन है जिससे अंतराल में संबंध रैखिक प्रतिगमन द्वारा प्राप्त किए जाते हैं।

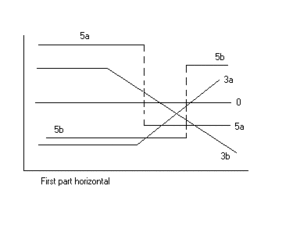
खंडित रैखिक प्रतिगमन, दो खंड

पहला लिंब क्षैतिज
पहला लिंब ऊपर की ओर झुका हुआ
पहला लिंब नीचे झुका हुआ

ब्रेकप्वाइंट द्वारा अलग किए गए दो खंडों के साथ खंडित रैखिक प्रतिगमन एक अलग प्रभावशाली कारक (x) के प्रतिक्रिया फ़ंक्शन (Yr) के अचानक परिवर्तन को निर्धारित करने के लिए उपयोगी हो सकता है। ब्रेकप्वाइंट की व्याख्या एक महत्वपूर्ण, सुरक्षित या थ्रेशोल्ड मान के रूप में की जा सकती है जिसके सीमा के बाहर या नीचे (अवांछित) प्रभाव होते हैं। निर्णय लेने में ब्रेकप्वाइंट महत्वपूर्ण हो सकता है।[1]

आंकड़े कुछ परिणामों और प्रतिगमन प्रकारों को दर्शाते हैं।

एक सेगमेंटेड रिग्रेशन विश्लेषण (y, x) डेटा के एक सेट की उपस्थिति पर आधारित है, जिसमें y आश्रित चर है और x स्वतंत्र चर है।

न्यूनतम वर्ग विधि को प्रत्येक खंड पर अलग से लागू किया जाता है, जिसके द्वारा दो प्रतिगमन रेखाओं को डेटा सेट को यथासंभव निकट से फिट करने के लिए बनाया जाता है, जबकि देखे गए (y) और परिकलित (Yr) मानों के बीच अंतर (SSD) के वर्गों के योग को कम किया जाता है। आश्रित चर के परिणामस्वरूप निम्नलिखित दो समीकरण बनते हैं:

  • Yr = A1.x + K1 x < BP (ब्रेकप्वाइंट) के लिए
  • Yr = A2.x + K2   x > BP (ब्रेकप्वाइंट) के लिए

जहाँ:

Yr, x के एक निश्चित मान के लिए y का अपेक्षित (अनुमानित) मान है;
A1 और A2 प्रतिगमन गुणांक हैं (रेखा खंडों की गिरावट का संकेत);
K1 और K2 प्रतिगमन स्थिरांक हैं ('y'-अक्ष पर अवरोधन को इंगित करते हुए)।

डेटा कई प्रकार या रुझान दिखा सकता है,[2] आंकड़े देखें.

विधि से दो पियर्सन उत्पाद-क्षण सहसंबंध गुणांक (R) भी प्राप्त होते हैं:

  • x <BP (ब्रेकप्वाइंट) के लिए

और

  • x > BP (ब्रेकप्वाइंट) के लिए

जहाँ:

प्रति खंड न्यूनतम SSD है

और

Ya1 और Ya2 संबंधित खंडों में y के औसत मान हैं।

सबसे उपयुक्त प्रवृत्ति का निर्धारण करने में, यह सुनिश्चित करने के लिए सांख्यिकीय परीक्षण आयोजित किए जाने चाहिए कि प्रवृत्ति विश्वसनीय (महत्वपूर्ण) है।

जब किसी महत्वपूर्ण ब्रेकप्वाइंट का पता नहीं लगाया जा सकता है, तो व्यक्ति को बिना ब्रेकप्वाइंट के प्रतिगमन पर वापस आना चाहिए।

उदाहरण

खंडित रैखिक प्रतिगमन, प्रकार 3बी

दाईं ओर की नीली आकृति के लिए जो सरसों की उपज (Yr = Ym, t/ha) और मिट्टी की लवणता (x = Ss, मिट्टी के घोल EC की विद्युत चालकता dS/m में व्यक्त की जाती है) के बीच संबंध बताती है, यह पाया गया है कि:[3]

BP = 4.93, A1 = 0, K1 = 1.74, A2 = −0.129, K2 = 2.38, R12 = 0.0035 (महत्वहीन), R22 = 0.395 (महत्वपूर्ण) और:

  • Ym = 1.74 t/ha                        के लिए Ss < 4.93
  • Ym = −0.129 Ss + 2.38 t/ha     के लिए Ss > 4.93 (ब्रेकप्वाइंट)

यह दर्शाता है कि मिट्टी की लवणता <4.93 dS/m सुरक्षित है और मिट्टी की लवणता > 4.93 dS/m मिट्टी की लवणता की प्रति इकाई वृद्धि से 0.129 टन/हेक्टेयर की दर से उपज कम हो जाती है।

जैसा कि नीचे विस्तार से बताया गया है, यह आंकड़ा आत्मविश्वास अंतराल और अनिश्चितता को भी दर्शाता है।

परीक्षण प्रक्रियाएं

उदाहरण समय श्रृंखला, प्रकार 5
एनोवा तालिका का उदाहरण: इस मामले में ब्रेक पॉइंट का परिचय अत्यधिक महत्वपूर्ण है।

प्रवृत्ति के प्रकार को निर्धारित करने के लिए निम्नलिखित सांख्यिकीय परीक्षणों का उपयोग किया जाता है:

  1. प्रतिगमन गुणांक A1 और A2 और y-डेटा के माध्य Y1 और Y2 और x- डेटा (BP के बाएं और दाएं) के माध्य X1 और X2 के रूप में BP को व्यक्त करके ब्रेकप्वाइंट (BP) का महत्व, का उपयोग करके BP की मानक त्रुटि (SE) की गणना करने और छात्र के t-टेस्ट को लागू करने के लिए जोड़ और गुणन में त्रुटियों के प्रसार के नियम
  2. A1 का महत्व और A2 विद्यार्थी के टी-वितरण और मानक त्रुटि SE को लागू करने वाले A1 और A2 है।
  3. A1 के अंतर का महत्व और A2 उनके अंतर के SE का उपयोग करके छात्र के टी-वितरण को लागू करना है।
  4. Y के अंतर का महत्व1 और वाई2 उनके अंतर के SE का उपयोग करके छात्र के टी-वितरण को लागू करना है।
  5. ब्रेकप्वाइंट के अस्तित्व के परीक्षण के लिए एक अधिक औपचारिक सांख्यिकीय दृष्टिकोण, छद्म स्कोर परीक्षण के माध्यम से होता है जिसमें खंडित रेखा के अनुमान की आवश्यकता नहीं होती है।[4]

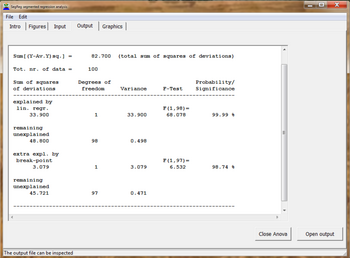
इसके अलावा, उपयोग सभी डेटा (Ra) के सहसंबंध गुणांक, निर्धारण के गुणांक या स्पष्टीकरण के गुणांक, प्रतिगमन कार्यों के विश्वास अंतराल और एनोवा (ANOVA) विश्लेषण से किया जाता है।[5]

सभी डेटा (सीडी) के लिए निर्धारण का गुणांक, जिसे महत्व परीक्षणों द्वारा निर्धारित शर्तों के तहत अधिकतम किया जाना है, से पाया जाता है:

जहां Yr पूर्व प्रतिगमन समीकरणों के अनुसार y का अपेक्षित (अनुमानित) मान है और Ya सभी y मानों का औसत है।

सीडी गुणांक 0 (बिल्कुल कोई स्पष्टीकरण नहीं) से 1 (पूर्ण स्पष्टीकरण, पूर्ण मिलान) के बीच होता है।
शुद्ध, अखण्डित, रैखिक प्रतिगमन में, Cd और Ra2 के मान बराबर होते हैं। खंडित प्रतिगमन में, विभाजन को उचित ठहराने के लिए Cd को Ra2 से काफी बड़ा होना आवश्यक है।

ब्रेकप्वाइंट का अनुकूलन (गणित) मान ऐसे पाया जा सकता है कि सीडी गुणांक मैक्सिमा और मिनिमा है।

अप्रभावी सीमा

X=0 से X=7.85 तक की सीमा का चित्रण जिस पर कोई प्रभाव नहीं है।

खंडित प्रतिगमन का उपयोग प्रायः उस सीमा को खोजने के लिए किया जाता है जिस पर एक व्याख्यात्मक चर (X) का आश्रित चर (Y) पर कोई प्रभाव नहीं पड़ता है, जबकि पहुंच से परे एक स्पष्ट प्रतिक्रिया होती है, चाहे वह सकारात्मक हो या नकारात्मक हो। बिना किसी प्रभाव की पहुंच X डोमेन के प्रारंभिक भाग में या इसके विपरीत इसके अंतिम भाग में पाई जा सकती है। "कोई प्रभाव नहीं" विश्लेषण के लिए, खंडित प्रतिगमन विश्लेषण के लिए न्यूनतम वर्ग विधि का अनुप्रयोग है।[6] सबसे उपयुक्त तकनीक नहीं हो सकता है क्योंकि उद्देश्य सबसे लंबे खंड को ढूंढना है जिस पर Y-X संबंध को शून्य ढलान माना जा सकता है जबकि पहुंच से परे ढलान शून्य से काफी अलग है लेकिन इस ढलान के सर्वोत्तम मूल्य के बारे में ज्ञान भौतिक नहीं है। नो-इफ़ेक्ट रेंज खोजने की विधि रेंज पर प्रगतिशील आंशिक प्रतिगमन[7] है, छोटे चरणों के साथ सीमा का विस्तार करना जब तक कि प्रतिगमन गुणांक शून्य से काफी भिन्न न हो जाए।

अगले चित्र में ब्रेक पॉइंट X=7.9 पर पाया जाता है, जबकि उसी डेटा के लिए (सरसों की उपज के लिए ऊपर नीला चित्र देखें), न्यूनतम वर्ग विधि केवल X=4.9 पर ब्रेक पॉइंट प्राप्त करती है। बाद वाला मान कम है, लेकिन ब्रेक पॉइंट से सीमा के बाहर डेटा का फिट बेहतर है। इसलिए, यह विश्लेषण के उद्देश्य पर निर्भर करेगा कि किस विधि को नियोजित करने की आवश्यकता है।

यह भी देखें

संदर्भ

  1. ↑ Frequency and Regression Analysis. Chapter 6 in: H.P.Ritzema (ed., 1994), Drainage Principles and Applications, Publ. 16, pp. 175-224, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. ISBN 90-70754-33-9 . Free download from the webpage [1] , under nr. 20, or directly as PDF : [2]
  2. ↑ Drainage research in farmers' fields: analysis of data. Part of project "Liquid Gold" of the International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Download as PDF : [3]
  3. ↑ R.J.Oosterbaan, D.P.Sharma, K.N.Singh and K.V.G.K.Rao, 1990, Crop production and soil salinity: evaluation of field data from India by segmented linear regression. In: Proceedings of the Symposium on Land Drainage for Salinity Control in Arid and Semi-Arid Regions, February 25th to March 2nd, 1990, Cairo, Egypt, Vol. 3, Session V, p. 373 - 383.
  4. ↑ Muggeo, VMR (2016). "Testing with a nuisance parameter present only under the alternative: a score-based approach with application to segmented modelling" (PDF). Journal of Statistical Computation and Simulation. 86 (15): 3059–3067. doi:10.1080/00949655.2016.1149855. S2CID 124914264.
  5. ↑ Statistical significance of segmented linear regression with break-point using variance analysis and F-tests. Download from [4] under nr. 13, or directly as PDF : [5]
  6. ↑ Segmented regression analysis, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Free download from the webpage [6]
  7. ↑ Partial Regression Analysis, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. Free download from the webpage [7]
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=खंडित_प्रतिगमन&oldid=253784’