शुल्ज़-ज़िम्म वितरण: Difference between revisions
From Vigyanwiki
(Created page with "{{Short description|Conventional name of the gamma distribution when applied to macromolecular polydispersity}} {{Infobox probability distribution | name = Schulz–Zi...") |
No edit summary |
||
| (4 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Conventional name of the gamma distribution when applied to macromolecular polydispersity}} | {{Short description|Conventional name of the gamma distribution when applied to macromolecular polydispersity}} | ||
{{Infobox probability distribution | {{Infobox probability distribution | ||
| name = | | name = शुल्ज़-ज़िम्म | ||
| type = continuous | | type = continuous | ||
| pdf_image = SchulzZimmPDF.pdf | | pdf_image = SchulzZimmPDF.pdf | ||
| Line 10: | Line 10: | ||
| variance = <math>\frac{1}{k}</math> | | variance = <math>\frac{1}{k}</math> | ||
}} | }} | ||
शुल्ज़-ज़िम्म वितरण [[गामा वितरण]] का एक विशेष | '''शुल्ज़-ज़िम्म वितरण''' [[गामा वितरण]] का एक विशेष कारक है। [[ पॉलीमर |पॉलीमर]] की बहुविक्षेपणता को मॉडल करने के लिए इसका व्यापक रूप से उपयोग किया जाता है। इस संदर्भ में, इसे वर्ष1939 में गुंटर विक्टर शुल्ज़ द्वारा<ref>G V Schulz (1939), Z. Phys. Chem. 43B, 25-46. - Eq (27a) with -ln(''a''), ''k''+1 in place of our ''x,k''.</ref> और वर्ष 1948 में ब्रूनो एच. ज़िम द्वारा पेश किया गया था।<ref>B H Zimm (1948), J. Chem. Phys. 16, 1099. - Proposes a two-parameter variant of Eq (13) without derivation and without reference to Schulz or whomsoever. One of the two parameters can be eliminated by the requirement <n>=1.</ref> | ||
इस वितरण में केवल एक आकार पैरामीटर k है, स्केल θ=1/k पर तय किया गया है। तदनुसार, संभाव्यता घनत्व | |||
इस वितरण में केवल एक आकार पैरामीटर ''k'' है, स्केल θ=1/k पर तय किया गया है। तदनुसार, संभाव्यता घनत्व फलन है | |||
<math display="block">f(x)=\frac{k^k x^{k - 1} e^{-kx}}{\Gamma(k)}.</math> | <math display="block">f(x)=\frac{k^k x^{k - 1} e^{-kx}}{\Gamma(k)}.</math> | ||
जब पॉलिमर पर लागू किया जाता है, तो चर x सापेक्ष द्रव्यमान या श्रृंखला की लंबाई होती है <math>x=M/M_n</math>. तदनुसार, | जब पॉलिमर पर लागू किया जाता है, तो चर x सापेक्ष द्रव्यमान या श्रृंखला की लंबाई होती है <math>x=M/M_n</math>. तदनुसार, वृहत पैमाने पर वितरण <math>f(M)</math> स्केल पैरामीटर के साथ सिर्फ एक गामा वितरण है <math>\theta=M_n/k</math>. यह बताता है कि क्यों शुल्ज़-ज़िम्म वितरण अपने पारंपरिक अनुप्रयोग डोमेन के बाहर असाधारण है। | ||
वितरण का माध्य 1 और विचरण 1/k है। पॉलिमर | वितरण का माध्य 1 और विचरण 1/k है। पॉलिमर प्रसार है <math>\langle x^2\rangle / \langle x\rangle = 1+1/k</math>. | ||
वृहत k के लिए शुल्ज़-ज़िम्म वितरण गाऊसी वितरण के निकट पहुंचता है। एल्गोरिदम में जहां किसी को नमूने वर्णन करने की आवश्यकता होती है <math>x\ge 0</math>, शुल्ज़-ज़िम वितरण को गॉसियन की तुलना में प्राथमिकता दी जानी चाहिए क्योंकि बाद वाले को ऋणात्मक x को रोकने के लिए स्वेच्छा से कट-ऑफ की आवश्यकता होती है। | |||
==संदर्भ== | ==संदर्भ== | ||
{{Reflist}} | {{Reflist}} | ||
[[Category:Created On 08/07/2023]] | [[Category:Created On 08/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:निरंतर वितरण]] | |||
Latest revision as of 10:16, 28 August 2023
|
Probability density function 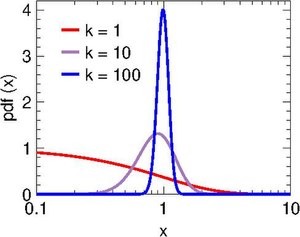 | |||
| Parameters | (shape parameter) | ||
|---|---|---|---|
| Support | |||
| Mean | |||
| Variance | |||
शुल्ज़-ज़िम्म वितरण गामा वितरण का एक विशेष कारक है। पॉलीमर की बहुविक्षेपणता को मॉडल करने के लिए इसका व्यापक रूप से उपयोग किया जाता है। इस संदर्भ में, इसे वर्ष1939 में गुंटर विक्टर शुल्ज़ द्वारा[1] और वर्ष 1948 में ब्रूनो एच. ज़िम द्वारा पेश किया गया था।[2]
इस वितरण में केवल एक आकार पैरामीटर k है, स्केल θ=1/k पर तय किया गया है। तदनुसार, संभाव्यता घनत्व फलन है
जब पॉलिमर पर लागू किया जाता है, तो चर x सापेक्ष द्रव्यमान या श्रृंखला की लंबाई होती है . तदनुसार, वृहत पैमाने पर वितरण स्केल पैरामीटर के साथ सिर्फ एक गामा वितरण है . यह बताता है कि क्यों शुल्ज़-ज़िम्म वितरण अपने पारंपरिक अनुप्रयोग डोमेन के बाहर असाधारण है।
वितरण का माध्य 1 और विचरण 1/k है। पॉलिमर प्रसार है .
वृहत k के लिए शुल्ज़-ज़िम्म वितरण गाऊसी वितरण के निकट पहुंचता है। एल्गोरिदम में जहां किसी को नमूने वर्णन करने की आवश्यकता होती है , शुल्ज़-ज़िम वितरण को गॉसियन की तुलना में प्राथमिकता दी जानी चाहिए क्योंकि बाद वाले को ऋणात्मक x को रोकने के लिए स्वेच्छा से कट-ऑफ की आवश्यकता होती है।
संदर्भ
- ↑ G V Schulz (1939), Z. Phys. Chem. 43B, 25-46. - Eq (27a) with -ln(a), k+1 in place of our x,k.
- ↑ B H Zimm (1948), J. Chem. Phys. 16, 1099. - Proposes a two-parameter variant of Eq (13) without derivation and without reference to Schulz or whomsoever. One of the two parameters can be eliminated by the requirement <n>=1.