संयोजन (साहचर्य): Difference between revisions

Latest revision as of 15:44, 28 August 2023

गणित में, पूर्णांक n का संयोजन धनात्मक पूर्णांक के अनुक्रम के योग के रूप में n लिखने की विधि है। इस प्रकार दो अनुक्रम जो अपने पदों के क्रम में भिन्न होते हैं, उनके योग की विभिन्न रचनाओं को परिभाषित करते हैं, जबकि उन्हें उस संख्या के समान विभाजन (संख्या सिद्धांत) को परिभाषित करने के लिए माना जाता है। इस प्रकार प्रत्येक पूर्णांक में परिमित रूप से अनेक विशिष्ट रचनाएँ होती हैं। इस प्रकार ऋणात्मक संख्याओं का कोई संघटन नहीं होता है, किन्तु 0 का संघटन होता है, प्रत्येक धनात्मक पूर्णांक n में 2ⁿ⁻¹ विशिष्ट रचनाएँ होती है।

3 बिट बाइनरी अंक प्रणाली और 4 की रचनाओं के मध्य विक्षेप

पूर्णांक n की अशक्त रचना n की रचना के समान है, किन्तु अनुक्रम की नियमो को शून्य होने की अनुमति देती है: इस प्रकार यह अनुक्रम के योग के रूप में n लिखने का विधि है गैर-ऋणात्मक पूर्णांकों का परिणामस्वरूप प्रत्येक धनात्मक पूर्णांक असीम रूप से कई अशक्त रचनाओं को स्वीकार करता है (यदि उनकी लंबाई सीमित नहीं है)। इस प्रकार किसी अशक्त रचना के अंत में कई पद 0 जोड़ने को सामान्यतः अलग अशक्त रचना को परिभाषित करने के लिए नहीं माना जाता है; इस प्रकार दूसरे शब्दों में, अशक्त रचनाओं को नियमो 0 द्वारा अनिश्चित काल तक विस्तारित माना जाता है।

सामान्यीकरण करने के लिए, (गैर-ऋणात्मक या धनात्मक) पूर्णांकों के उपसमुच्चय a के लिए पूर्णांक n की a-प्रतिबंधित रचना, 'में या अधिक तत्वों का क्रमबद्ध संग्रह है। इस प्रकार 'a जिसका योग n है |^[1]

उदाहरण

6

1 + 1 + 1 + 1 + 1 + 1
2 + 1 + 1 + 1 + 1
1 + 2 + 1 + 1 + 1
की 32 रचनाएँ। . .
1 + 5
6

6

1 + 1 + 1 + 1 + 1 + 1
2 + 1 + 1 + 1 + 1
3 + 1 + 1 + 1
के 11 विभाजन। . .
3 + 3
6

5 की सोलह रचनाएँ हैं:

5
4+1
3+2
3 + 1 + 1
2+3
2 + 2 + 1
2 + 1 + 2
2 + 1 + 1 + 1
1+4
1 + 3 + 1
1+2+2
1 + 2 + 1 + 1
1 + 1 + 3
1 + 1 + 2 + 1
1 + 1 + 1 + 2
1 + 1 + 1 + 1 + 1.

इसकी तुलना 5 के सात विभाजनों से करें:

5
4+1
3+2
3 + 1 + 1
2 + 2 + 1
2 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1.

रचनाओं के अंशों पर अंकुश लगाना संभव है। उदाहरण के लिए 5 की पाँच रचनाएँ अलग-अलग शब्दों में हैं:

5
4+1
3+2
2+3
1+4.

इसकी तुलना 5 के तीन विभाजनों के साथ अलग-अलग शब्दों में करें:

5
4+1
3+2.

रचनाओं की संख्या

n +1 से k +1 क्रमित विभाजनों की रचनाओं की संख्या पास्कल के त्रिकोण का निर्माण करती है

n की {1,2}-प्रतिबंधित रचनाओं को गिनने के लिए फाइबोनैचि अनुक्रम का उपयोग करना, उदाहरण के लिए, समय में या दो कदम उठाते हुए, लंबाई n की सीढ़ी पर चढ़ने के विधि की संख्या

परंपरागत रूप से संवृत्त रचना को 0 की एकमात्र रचना के रूप में गिना जाता है, और ऋणात्मक पूर्णांकों की कोई रचना नहीं होती है।

वहाँ 2ⁿ⁻¹ n ≥ 1 की रचनाएँ है; यहाँ प्रमाण है:

सरणी के प्रत्येक n − 1 बॉक्स में या तो प्लस चिह्न या अल्पविराम लगता है

{\big (}\,\overbrace {1\,\square \,1\,\square \,\ldots \,\square \,1\,\square \,1} ^{n}\,{\big )}

इस प्रकार n की अद्वितीय रचना तैयार करता है। इसके विपरीत, n की प्रत्येक रचना धन और अल्पविराम का निर्धारण निर्धारित करती है। चूँकि n − 1 बाइनरी विकल्प हैं, परिणाम इस प्रकार है। इसी तर्क से पता चलता है कि पुर्णतः k भागों (एक 'k-रचना') में n की रचनाओं की संख्या द्विपद गुणांक ${n-1 \choose k-1}$ द्वारा दी गई है . ध्यान दें कि भागों की सभी संभावित संख्याओं का योग करने पर हमें 2^n-1 प्राप्त होता है n की रचनाओं की कुल संख्या के रूप में:

\sum _{k=1}^{n}{n-1 \choose k-1}=2^{n-1}.

अशक्त रचनाओं के लिए, संख्या ${n+k-1 \choose k-1}={n+k-1 \choose n}$ है, क्योंकि n + k की प्रत्येक k-संरचना नियम के अनुसार n की अशक्त संरचना से मेल खाती है

a_{1}+a_{2}+\ldots +a_{k}=n+k\quad \mapsto \quad (a_{1}-1)+(a_{2}-1)+\ldots +(a_{k}-1)=n

इस सूत्र से यह पता चलता है कि पुर्णतः k भागों में n की अशक्त रचनाओं की संख्या k - 1 की पुर्णतः n + 1 भागों में अशक्त रचनाओं की संख्या के समान है।

a-प्रतिबंधित रचनाओं के लिए पुर्णतः k भागों में n की रचनाओं की संख्या विस्तारित द्विपद (या बहुपद) गुणांक द्वारा दी गई है ${\binom {k}{n}}_{(1)_{a\in A}}=[x^{n}]\left(\sum _{a\in A}x^{a}\right)^{k}$ ,

जहां वर्गाकार कोष्ठक $x^{n}$ के गुणांक के निष्कर्षण को दर्शाते हैं इसके बाद आने वाले बहुपद में उपयोग किया जाता है।^[2]

सजातीय बहुपद

सदिश समष्टि का आयाम $K[x_{1},\ldots ,x_{n}]_{d}$ क्षेत्र K पर n चरों में घात d के सजातीय बहुपद का n भागों में d की अशक्त रचनाओं की संख्या है। इस प्रकार वास्तव में, समिष्ट का आधार एकपदी के समुच्चय $x_{1}^{d_{1}}\cdots x_{n}^{d_{n}}$ द्वारा दिया जाता है ऐसा है कि $d_{1}+\ldots +d_{n}=d$ . प्रतिपादकों के बाद से $d_{i}$ शून्य होने की अनुमति है, इस प्रकार ऐसे एकपदी की संख्या d की अशक्त रचनाओं की संख्या के समान है।

यह भी देखें

स्टार्स और बार (संयोजक)

संदर्भ

↑ Heubach, Silvia; Mansour, Toufik (2004). "Compositions of n with parts in a set". Congressus Numerantium. 168: 33–51. CiteSeerX 10.1.1.484.5148.
↑ Eger, Steffen (2013). "Restricted weighted integer compositions and extended binomial coefficients" (PDF). Journal of Integer Sequences. 16.

Heubach, Silvia; Mansour, Toufik (2009). Combinatorics of Compositions and Words. Discrete Mathematics and its Applications. Boca Raton, Florida: CRC Press. ISBN 978-1-4200-7267-9. Zbl 1184.68373.

बाहरी संबंध

Partition and composition calculator

[1] Heubach, Silvia; Mansour, Toufik (2004). "Compositions of n with parts in a set". Congressus Numerantium. 168: 33–51. CiteSeerX 10.1.1.484.5148.

[2] Eger, Steffen (2013). "Restricted weighted integer compositions and extended binomial coefficients" (PDF). Journal of Integer Sequences. 16.

[1]

[2]

@@ Line 1: / Line 1: @@
-{{Other uses of|Composition}}
+{{Other uses of|संयोजन}}
-गणित में, एक [[पूर्णांक]] ''n'' का संयोजन (सख्ती से) [[सकारात्मक पूर्णांक]]ों के अनुक्रम के [[योग]] के रूप में ''n'' लिखने का एक तरीका है। दो अनुक्रम जो अपने पदों के क्रम में भिन्न होते हैं, उनके योग की विभिन्न रचनाओं को परिभाषित करते हैं, जबकि उन्हें उस संख्या के समान [[विभाजन (संख्या सिद्धांत)]] को परिभाषित करने के लिए माना जाता है। प्रत्येक पूर्णांक में परिमित रूप से अनेक विशिष्ट रचनाएँ होती हैं। ऋणात्मक संख्याओं का कोई संघटन नहीं होता, लेकिन 0 का एक संघटन होता है, खाली क्रम। प्रत्येक धनात्मक पूर्णांक ''n'' में <span style=white-space:nowrap >2 होता है<sup>n−1</sup></span> विशिष्ट रचनाएँ।
+गणित में, [[पूर्णांक]] ''n'' का संयोजन [[सकारात्मक पूर्णांक|धनात्मक पूर्णांक]] के अनुक्रम के [[योग]] के रूप में ''n'' लिखने की विधि है। इस प्रकार दो अनुक्रम जो अपने पदों के क्रम में भिन्न होते हैं, उनके योग की विभिन्न रचनाओं को परिभाषित करते हैं, जबकि उन्हें उस संख्या के समान [[विभाजन (संख्या सिद्धांत)]] को परिभाषित करने के लिए माना जाता है। इस प्रकार प्रत्येक पूर्णांक में परिमित रूप से अनेक विशिष्ट रचनाएँ होती हैं। इस प्रकार ऋणात्मक संख्याओं का कोई संघटन नहीं होता है, किन्तु 0 का संघटन होता है, प्रत्येक धनात्मक पूर्णांक ''n'' में <span style=white-space:nowrap >2<sup>n−1</sup> विशिष्ट रचनाएँ होती है</span>।
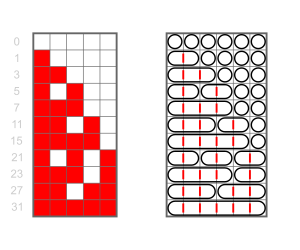
-[[File:Binary and compositions 4.svg|thumb|center|600px|3 बिट बाइनरी अंक प्रणाली और 4 की रचनाओं के बीच विक्षेप]]पूर्णांक ''n'' की एक कमजोर रचना ''n'' की रचना के समान है, लेकिन अनुक्रम की शर्तों को शून्य होने की अनुमति देती है: यह अनुक्रम के योग के रूप में ''n'' लिखने का एक तरीका है गैर-ऋणात्मक पूर्णांकों का. परिणामस्वरूप प्रत्येक धनात्मक पूर्णांक असीम रूप से कई कमजोर रचनाओं को स्वीकार करता है (यदि उनकी लंबाई सीमित नहीं है)। किसी कमजोर रचना के ''अंत'' में कई पद 0 जोड़ने को आम तौर पर एक अलग कमजोर रचना को परिभाषित करने के लिए नहीं माना जाता है; दूसरे शब्दों में, कमजोर रचनाओं को शर्तों 0 द्वारा अनिश्चित काल तक विस्तारित माना जाता है।
+[[File:Binary and compositions 4.svg|thumb|center|600px|3 बिट बाइनरी अंक प्रणाली और 4 की रचनाओं के मध्य विक्षेप]]पूर्णांक ''n'' की अशक्त रचना ''n'' की रचना के समान है, किन्तु अनुक्रम की नियमो को शून्य होने की अनुमति देती है: इस प्रकार यह अनुक्रम के योग के रूप में ''n'' लिखने का विधि है गैर-ऋणात्मक पूर्णांकों का परिणामस्वरूप प्रत्येक धनात्मक पूर्णांक असीम रूप से कई अशक्त रचनाओं को स्वीकार करता है (यदि उनकी लंबाई सीमित नहीं है)। इस प्रकार किसी अशक्त रचना के ''अंत'' में कई पद 0 जोड़ने को सामान्यतः अलग अशक्त रचना को परिभाषित करने के लिए नहीं माना जाता है; इस प्रकार दूसरे शब्दों में, अशक्त रचनाओं को नियमो 0 द्वारा अनिश्चित काल तक विस्तारित माना जाता है।
-आगे सामान्यीकरण करने के लिए, (गैर-नकारात्मक या सकारात्मक) पूर्णांकों के उपसमुच्चय ''ए'' के लिए एक पूर्णांक ''एन'' की ''ए''-प्रतिबंधित रचना, 'में एक या अधिक तत्वों का एक क्रमबद्ध संग्रह है। 'ए'' जिसका योग ''एन'' है।<ref>
+सामान्यीकरण करने के लिए, (गैर-ऋणात्मक या धनात्मक) पूर्णांकों के उपसमुच्चय ''a'' के लिए पूर्णांक n की ''a''-प्रतिबंधित रचना, 'में या अधिक तत्वों का क्रमबद्ध संग्रह है। इस प्रकार 'a'' जिसका योग ''n ''है |<ref>
 {{cite journal
   | last1=Heubach | first1=Silvia | author1-link = Silvia Heubach
@@ Line 11: / Line 11: @@
   | title=Compositions of n with parts in a set
   | journal=[[Congressus Numerantium]] | volume=168 | pages=33–51
-  | citeseerx=10.1.1.484.5148 }}</ref>
+  | citeseerx=10.1.1.484.5148 }}</ref>''
+==उदाहरण ==
-==उदाहरण==
 [[File:Compositions of 6.svg|thumb|6<br><br>1 + 1 + 1 + 1 + 1 + 1<br>2 + 1 + 1 + 1 + 1<br>1 + 2 + 1 + 1 + 1<br> की 32 रचनाएँ। . .<br>1 + 5<br>6]]
 [[File:Partitions of 6.svg|thumb|6<br><br>1 + 1 + 1 + 1 + 1 + 1<br>2 + 1 + 1 + 1 + 1<br>3 + 1 + 1 + 1<br> के 11 विभाजन। . .<br>3 + 3<br>6]]5 की सोलह रचनाएँ हैं:
 *5
 *4+1
 *3+2
 *3 + 1 + 1
 *2+3
 *2 + 2 + 1
 *2 + 1 + 2
 *2 + 1 + 1 + 1
 *1+4
 *1 + 3 + 1
 *1+2+2
 *1 + 2 + 1 + 1
 *1 + 1 + 3
 *1 + 1 + 2 + 1
 *1 + 1 + 1 + 2
 *1 + 1 + 1 + 1 + 1.
 इसकी तुलना 5 के सात विभाजनों से करें:
 *5
 *4+1
 *3+2
 *3 + 1 + 1
 *2 + 2 + 1
 *2 + 1 + 1 + 1
 *1 + 1 + 1 + 1 + 1.
 रचनाओं के अंशों पर अंकुश लगाना संभव है। उदाहरण के लिए 5 की पाँच रचनाएँ अलग-अलग शब्दों में हैं:
 *5
 *4+1
 *3+2
 *2+3
 *1+4.
 इसकी तुलना 5 के तीन विभाजनों के साथ अलग-अलग शब्दों में करें:
 *5
 *4+1
 *3+2.
-==रचनाओं की संख्या==
+==रचनाओं की संख्या ==
 [[File:pascal_triangle_compositions.svg|thumb|n&hairsp;+1 से k&hairsp;+1 क्रमित विभाजनों की रचनाओं की संख्या पास्कल के त्रिकोण का निर्माण करती है]]
-[[File:Fibonacci_climbing_stairs.svg|thumb|n की {1,2}-प्रतिबंधित रचनाओं को गिनने के लिए फाइबोनैचि अनुक्रम का उपयोग करना, {{nowrap|for example,}} एक समय में एक या दो कदम उठाते हुए, लंबाई n की सीढ़ी पर चढ़ने के तरीकों की संख्या]]परंपरागत रूप से खाली रचना को 0 की एकमात्र रचना के रूप में गिना जाता है, और नकारात्मक पूर्णांकों की कोई रचना नहीं होती है।
+[[File:Fibonacci_climbing_stairs.svg|thumb|n की {1,2}-प्रतिबंधित रचनाओं को गिनने के लिए फाइबोनैचि अनुक्रम का उपयोग करना, {{nowrap|उदाहरण के लिए,}} समय में या दो कदम उठाते हुए, लंबाई n की सीढ़ी पर चढ़ने के विधि की संख्या]]परंपरागत रूप से संवृत्त रचना को 0 की एकमात्र रचना के रूप में गिना जाता है, और ऋणात्मक पूर्णांकों की कोई रचना नहीं होती है।
-वहाँ 2 है<sup>n−1</sup> n ≥ 1 की रचनाएँ; यहाँ एक प्रमाण है:
+वहाँ 2<sup>n−1</sup> n ≥ 1 की रचनाएँ है; यहाँ प्रमाण है:
-सरणी के प्रत्येक n − 1 बॉक्स में या तो प्लस चिह्न या अल्पविराम लगाना
+सरणी के प्रत्येक n − 1 बॉक्स में या तो प्लस चिह्न या अल्पविराम लगता है
 :<math>
      \big(\,
@@ Line 66: / Line 64: @@
        \square\, 1}^n\,
      \big)
 </math>
-n की एक अनूठी रचना तैयार करता है। इसके विपरीत, n की प्रत्येक रचना धन और अल्पविराम का निर्धारण निर्धारित करती है। चूँकि n − 1 बाइनरी विकल्प हैं, परिणाम इस प्रकार है। इसी तर्क से पता चलता है कि बिल्कुल k भागों (एक 'k-रचना') में n की रचनाओं की संख्या [[द्विपद गुणांक]] द्वारा दी गई है <math>{n-1\choose k-1}</math>. ध्यान दें कि भागों की सभी संभावित संख्याओं का योग करने पर हमें 2 प्राप्त होता है<sup>n-1</sup> n की रचनाओं की कुल संख्या के रूप में:
+इस प्रकार n की अद्वितीय रचना तैयार करता है। इसके विपरीत, n की प्रत्येक रचना धन और अल्पविराम का निर्धारण निर्धारित करती है। चूँकि n − 1 बाइनरी विकल्प हैं, परिणाम इस प्रकार है। इसी तर्क से पता चलता है कि पुर्णतः k भागों (एक 'k-रचना') में n की रचनाओं की संख्या [[द्विपद गुणांक]] <math>{n-1\choose k-1}</math> द्वारा दी गई है . ध्यान दें कि भागों की सभी संभावित संख्याओं का योग करने पर हमें 2<sup>n-1</sup> प्राप्त होता है n की रचनाओं की कुल संख्या के रूप में:
 : <math> \sum_{k=1}^n {n-1 \choose k-1} = 2^{n-1}.</math>
-कमजोर रचनाओं के लिए, संख्या है <math>{n+k-1\choose k-1} = {n+k-1 \choose n}</math>, क्योंकि n + k की प्रत्येक k-संरचना नियम के अनुसार n की एक कमजोर संरचना से मेल खाती है
+अशक्त रचनाओं के लिए, संख्या <math>{n+k-1\choose k-1} = {n+k-1 \choose n}</math> है, क्योंकि n + k की प्रत्येक k-संरचना नियम के अनुसार n की अशक्त संरचना से मेल खाती है
 :<math>
    a_1+a_2+ \ldots + a_k = n +k \quad \mapsto \quad (a_1 -1) + (a_2-1) + \ldots + (a_k - 1) = n
 </math>
-इस सूत्र से यह पता चलता है कि बिल्कुल k भागों में n की कमजोर रचनाओं की संख्या k - 1 की बिल्कुल n + 1 भागों में कमजोर रचनाओं की संख्या के बराबर है।
+इस सूत्र से यह पता चलता है कि पुर्णतः k भागों में n की अशक्त रचनाओं की संख्या k - 1 की पुर्णतः n + 1 भागों में अशक्त रचनाओं की संख्या के समान है।
-ए-प्रतिबंधित रचनाओं के लिए, बिल्कुल k भागों में n की रचनाओं की संख्या विस्तारित द्विपद (या बहुपद) गुणांक द्वारा दी गई है <math>\binom{k}{n}_{(1)_{a\in A}}=[x^n]\left(\sum_{a\in A} x^a\right)^k</math>, जहां वर्गाकार कोष्ठक के गुणांक के निष्कर्षण को दर्शाते हैं <math>x^n</math> इसके बाद आने वाले बहुपद में।<ref>
+a-प्रतिबंधित रचनाओं के लिए पुर्णतः k भागों में n की रचनाओं की संख्या विस्तारित द्विपद (या बहुपद) गुणांक द्वारा दी गई है <math>\binom{k}{n}_{(1)_{a\in A}}=[x^n]\left(\sum_{a\in A} x^a\right)^k</math>,
+जहां वर्गाकार कोष्ठक <math>x^n</math> के गुणांक के निष्कर्षण को दर्शाते हैं इसके बाद आने वाले बहुपद में उपयोग किया जाता है।<ref>
 {{cite journal
   | last1=Eger | first1=Steffen
@@ Line 85: / Line 85: @@
   | url=https://cs.uwaterloo.ca/journals/JIS/VOL16/Eger/eger6.pdf
 }}</ref>
+==सजातीय बहुपद                                                                                                                    ==
+सदिश समष्टि का आयाम <math>K[x_1, \ldots, x_n]_d</math> क्षेत्र K पर n चरों में घात d के [[सजातीय बहुपद]] का n भागों में d की अशक्त रचनाओं की संख्या है। इस प्रकार वास्तव में, समिष्ट का आधार एकपदी के समुच्चय <math>x_1^{d_1}\cdots x_n^{d_n}</math> द्वारा दिया जाता है ऐसा है कि <math>d_1 + \ldots + d_n = d</math>. प्रतिपादकों के बाद से <math>d_i</math> शून्य होने की अनुमति है, इस प्रकार ऐसे एकपदी की संख्या d की अशक्त रचनाओं की संख्या के समान है।
+==यह भी देखें                                                                                                              ==
+*[[सितारे और बार (कॉम्बिनेटरिक्स)|स्टार्स और बार (संयोजक)]]
-==सजातीय बहुपद==
+==संदर्भ                                                                                                                       ==
-सदिश समष्टि का आयाम <math>K[x_1, \ldots, x_n]_d</math> क्षेत्र K पर n चरों में घात d के [[सजातीय बहुपद]] का n भागों में d की कमजोर रचनाओं की संख्या है। वास्तव में, स्थान का आधार एकपदी के समुच्चय द्वारा दिया जाता है <math>x_1^{d_1}\cdots x_n^{d_n}</math> ऐसा है कि <math>d_1 + \ldots + d_n = d</math>. प्रतिपादकों के बाद से <math>d_i</math> शून्य होने की अनुमति है, तो ऐसे एकपदी की संख्या d की कमजोर रचनाओं की संख्या के बराबर है।
-==यह भी देखें==
-*[[सितारे और बार (कॉम्बिनेटरिक्स)]]
-==संदर्भ==
 {{reflist}}
 *{{cite book |last1=Heubach |first1=Silvia |last2=Mansour |first2=Toufik |year=2009 |title=Combinatorics of Compositions and Words |series=Discrete Mathematics and its Applications |publisher=CRC Press |location=Boca Raton, Florida |isbn=978-1-4200-7267-9 |zbl=1184.68373}}
 ==बाहरी संबंध==
 *[http://www.se16.info/js/partitions.htm Partition and composition calculator]
-[[Category: संख्या सिद्धांत]] [[Category: साहचर्य]]
-[[Category: Machine Translated Page]]
+[[Category:Articles with hatnote templates targeting a nonexistent page]]
 [[Category:Created On 07/07/2023]]
+[[Category:Machine Translated Page]]
+[[Category:Pages with script errors]]
+[[Category:Templates Vigyan Ready]]
+[[Category:संख्या सिद्धांत]]
+[[Category:साहचर्य]]

Anonymous

Search

संयोजन (साहचर्य): Difference between revisions

Namespaces

More

Page actions

Latest revision as of 15:44, 28 August 2023

Contents

उदाहरण

रचनाओं की संख्या

सजातीय बहुपद

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

संयोजन (साहचर्य): Difference between revisions

Latest revision as of 15:44, 28 August 2023

उदाहरण

रचनाओं की संख्या

सजातीय बहुपद

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories