कोकर्नेल: Difference between revisions
(Created page with "{{Short description|Quotient space of a codomain of a linear map by the map's image}} {{Redirect|Coker (mathematics)|other uses|Coker (disambiguation)}} {{no footnotes|date=Fe...") |
No edit summary |
||
| (7 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Quotient space of a codomain of a linear map by the map's image}} | {{Short description|Quotient space of a codomain of a linear map by the map's image}}[[वेक्टर रिक्त स्थान|सदिश रिक्त स्थान]] के एक रेखीय मानचित्रण का '''कोकर्नेल''' {{math|''f'' : ''X'' → ''Y''}} भागफल स्थान है (रैखिक बीजगणित) {{math|''Y'' / im(''f'')}} के [[कोडोमेन]] का {{mvar|f}} की छवि द्वारा {{mvar|f}}. कोकरनेल के आयाम को कोरैंक कहा जाता है {{mvar|f}}. | ||
{{ | |||
{{ | |||
कोकर्नेल कर्नेल (श्रेणी सिद्धांत) के लिए दोहरे (श्रेणी सिद्धांत) हैं, इसलिए नाम: कर्नेल डोमेन का एक सबोबिज है (यह डोमेन के लिए मैप करता है), जबकि कोकर्नेल कोडोमेन का एक अंश पिंड है (यह मानचित्र से मैप करता है) कोडोमेन)। | |||
सहज रूप से, एक समीकरण दिया {{math|1=''f''(''x'') = ''y''}} जिसे कोई हल करना चाह रहा है, कोकरनेल उन बाधाओं को मापता है जो {{mvar|y}} इस समीकरण के समाधान के लिए संतुष्ट होना चाहिए - समाधान के लिए बाधाएं - जबकि कर्नेल समाधान में स्वतंत्रता की डिग्री को मापता है, यदि कोई उपलब्ध है। यह नीचे #अंतर्ज्ञान में विस्तृत है। | |||
सामान्यतः आकारिकी का कोकर्नेल {{math|''f'' : ''X'' → ''Y''}} कुछ [[श्रेणी सिद्धांत]] में (उदाहरण के लिए [[समूह (गणित)]] के बीच एक [[समूह समरूपता]] या हिल्बर्ट रिक्त स्थान के बीच एक [[परिबद्ध रैखिक संचालिका]]) एक पिंड है {{mvar|Q}} और एक रूपवाद {{math|''q'' : ''Y'' → ''Q''}} ऐसा है कि रचना {{math|''q f''}} श्रेणी का [[शून्य रूपवाद]] है, और इसके अलावा {{mvar|q}} इस संपत्ति के संबंध में सार्वभौमिक मानचित्रण संपत्ति है। प्रायः मैप {{mvar|q}} समझा जाता है, और {{mvar|Q}} का ही कोकर्नेल कहा जाता है {{mvar|f}}. | |||
[[सार बीजगणित]] में कई स्थितियों में, जैसे [[एबेलियन समूह]], सदिश रिक्त स्थान या [[मॉड्यूल (गणित)]] के लिए, [[समरूपता]] का कोकर्नेल {{math|''f'' : ''X'' → ''Y''}} का भागफल समुच्चय है {{mvar|Y}} की [[छवि (गणित)]] द्वारा {{mvar|f}}. [[टोपोलॉजी]] सेटिंग्स में, जैसे कि हिल्बर्ट रिक्त स्थान के बीच बंधे रैखिक ऑपरेटरों के साथ, सामान्यतः भागफल में जाने से पहले छवि को बंद करना (गणित) लेना पड़ता है। | |||
[[सार बीजगणित]] में कई स्थितियों में, जैसे [[एबेलियन समूह]] | |||
== औपचारिक परिभाषा == | == औपचारिक परिभाषा == | ||
कोकर्नेल को श्रेणी सिद्धांत के सामान्य ढांचे में परिभाषित किया जा सकता है। परिभाषा को समझने के लिए विचाराधीन श्रेणी में शून्य आकारिकी होनी चाहिए। आकारिकी का कोकरनेल {{math|''f'' : ''X'' → ''Y''}} के बराबर के रूप में परिभाषित किया गया है {{mvar|f}} और शून्य रूपवाद {{math|0<sub>''XY''</sub> : ''X'' → ''Y''}}. | कोकर्नेल को श्रेणी सिद्धांत के सामान्य ढांचे में परिभाषित किया जा सकता है। परिभाषा को समझने के लिए विचाराधीन श्रेणी में शून्य आकारिकी होनी चाहिए। आकारिकी का कोकरनेल {{math|''f'' : ''X'' → ''Y''}} के बराबर के रूप में परिभाषित किया गया है {{mvar|f}} और शून्य रूपवाद {{math|0<sub>''XY''</sub> : ''X'' → ''Y''}}. | ||
स्पष्ट रूप से, इसका अर्थ निम्नलिखित | स्पष्ट रूप से, इसका अर्थ निम्नलिखित है: कोकरनेल का {{math|''f'' : ''X'' → ''Y''}} एक पिंड है {{mvar|Q}} साथ एक मोर्फिज्म के साथ {{math|''q'' : ''Y'' → ''Q''}} जैसे कि आरेख | ||
<div शैली = पाठ-संरेखण: केंद्र; >[[Image:Cokernel-01.svg]]</div> | <div शैली = पाठ-संरेखण: केंद्र; >[[Image:Cokernel-01.svg]]</div> | ||
[[क्रमविनिमेय आरेख]]। इसके अलावा, रूपवाद {{mvar|q}} इस आरेख के लिए [[सार्वभौमिक संपत्ति]] होनी चाहिए, अर्थात ऐसा कोई अन्य {{math|''q''′ : ''Y'' → ''Q''′}} कंपोज करके प्राप्त किया जा सकता है {{mvar|q}} एक अद्वितीय | [[क्रमविनिमेय आरेख]]। इसके अलावा, रूपवाद {{mvar|q}} इस आरेख के लिए [[सार्वभौमिक संपत्ति]] होनी चाहिए, अर्थात ऐसा कोई अन्य {{math|''q''′ : ''Y'' → ''Q''′}} कंपोज करके प्राप्त किया जा सकता है {{mvar|q}} एक अद्वितीय मोर्फिज्म के साथ {{math|''u'' : ''Q'' → ''Q''′}}: | ||
<div शैली = पाठ-संरेखण: केंद्र; >[[Image:Cokernel-02.png]]</div> | <div शैली = पाठ-संरेखण: केंद्र; >[[Image:Cokernel-02.png]]</div> | ||
जैसा कि सभी सार्वभौमिक निर्माणों के साथ होता है, कोकरनेल, यदि यह | जैसा कि सभी सार्वभौमिक निर्माणों के साथ होता है, कोकरनेल, यदि यह उपलब्ध है, एक अद्वितीय समरूपता के लिए अद्वितीय है, या अधिक सटीक रूप से: यदि {{math|''q'' : ''Y'' → ''Q''}} और {{math|''q''′ : ''Y'' → ''Q''′}} के दो कोकर्नेल हैं {{math|''f'' : ''X'' → ''Y''}}, तो वहाँ अद्वितीय समरूपता उपलब्ध है {{math|''u'' : ''Q'' → ''Q''′}} साथ {{math|1=''q''' = ''u'' ''q''}}. | ||
सभी समकक्षों की तरह, कोकरनेल {{math|''q'' : ''Y'' → ''Q''}} अनिवार्य रूप से एक एपिमोर्फिज्म है। इसके विपरीत | सभी समकक्षों की तरह, कोकरनेल {{math|''q'' : ''Y'' → ''Q''}} अनिवार्य रूप से एक एपिमोर्फिज्म है। इसके विपरीत एपिमोर्फिज्म को [[सामान्य रूपवाद]] (या सामान्य) कहा जाता है यदि यह कुछ आकारिकी का कोकर्नेल है। एक श्रेणी को सामान्य कहा जाता है यदि प्रत्येक [[अधिरूपता]] सामान्य है (उदाहरण के लिए [[समूहों की श्रेणी]] असामान्य है)। | ||
=== उदाहरण === | === उदाहरण === | ||
समूहों की श्रेणी में, एक समूह समरूपता का कोकर्नेल {{math|''f'' : ''G'' → ''H''}} का [[भागफल समूह]] है {{mvar|H}} की छवि के सामान्य समापन (समूह सिद्धांत) द्वारा {{mvar|f}}. एबेलियन समूहों के मामले में, चूंकि प्रत्येक [[उपसमूह]] सामान्य है, कोकर्नेल न्यायपूर्ण है {{mvar|H}} आदर्श (रिंग थ्योरी) की छवि {{mvar|f}}: | समूहों की श्रेणी में, एक समूह समरूपता का कोकर्नेल {{math|''f'' : ''G'' → ''H''}} का [[भागफल समूह]] है {{mvar|H}} की छवि के सामान्य समापन (समूह सिद्धांत) द्वारा {{mvar|f}}. एबेलियन समूहों के मामले में, चूंकि प्रत्येक [[उपसमूह]] सामान्य है, कोकर्नेल न्यायपूर्ण है {{mvar|H}} आदर्श (रिंग थ्योरी) की छवि {{mvar|f}}: | ||
:<math>\operatorname{coker}(f) = H / \operatorname{im}(f).</math> | :<math>\operatorname{coker}(f) = H / \operatorname{im}(f).</math> | ||
=== विशेष स्थितियां === | |||
पूर्ववर्ती श्रेणी में, आकारिकी को जोड़ना और घटाना समझ में आता है। ऐसी श्रेणी में, दो आकारिकी का समतुल्य {{mvar|f}} और {{mvar|g}} (यदि यह उपलब्ध है) उनके अंतर का सिर्फ कोकर्नेल है: | |||
=== विशेष | |||
: <math>\operatorname{coeq}(f, g) = \operatorname{coker}(g - f).</math> | : <math>\operatorname{coeq}(f, g) = \operatorname{coker}(g - f).</math> | ||
[[एबेलियन श्रेणी]] में (एक विशेष प्रकार की पूर्ववर्ती श्रेणी) [[छवि (श्रेणी सिद्धांत)]] और आकारिकी की सह-छवि {{mvar|f}} द्वारा दिया गया है | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\operatorname{im}(f) &= \ker(\operatorname{coker} f), \\ | \operatorname{im}(f) &= \ker(\operatorname{coker} f), \\ | ||
| Line 44: | Line 38: | ||
विशेष रूप से, प्रत्येक एबेलियन श्रेणी सामान्य (और सामान्य भी) है। यानी हर [[एकरूपता]] {{mvar|m}} को कुछ रूपवाद के कर्नेल के रूप में लिखा जा सकता है। विशेष रूप से, {{mvar|m}} अपने स्वयं के कोकर्नेल का कर्नेल है: | विशेष रूप से, प्रत्येक एबेलियन श्रेणी सामान्य (और सामान्य भी) है। यानी हर [[एकरूपता]] {{mvar|m}} को कुछ रूपवाद के कर्नेल के रूप में लिखा जा सकता है। विशेष रूप से, {{mvar|m}} अपने स्वयं के कोकर्नेल का कर्नेल है: | ||
:<math>m = \ker(\operatorname{coker}(m))</math> | :<math>m = \ker(\operatorname{coker}(m))</math> | ||
== अंतर्ज्ञान == | == अंतर्ज्ञान == | ||
कोकर्नेल को अवरोधों के स्थान के रूप में सोचा जा सकता है जो एक समीकरण को संतुष्ट करना चाहिए, अवरोधों के स्थान के रूप में, जैसे कि [[कर्नेल (बीजगणित)]] समाधानों का स्थान है। | कोकर्नेल को अवरोधों के स्थान के रूप में सोचा जा सकता है जो एक समीकरण को संतुष्ट करना चाहिए, अवरोधों के स्थान के रूप में, जैसे कि [[कर्नेल (बीजगणित)]] समाधानों का स्थान है। | ||
| Line 53: | Line 45: | ||
:<math>0 \to \ker T \to V \overset T \longrightarrow W \to \operatorname{coker} T \to 0.</math> | :<math>0 \to \ker T \to V \overset T \longrightarrow W \to \operatorname{coker} T \to 0.</math> | ||
इनकी व्याख्या इस प्रकार की जा सकती है: एक रैखिक समीकरण दिया गया है {{math|1=''T''(''v'') = ''w''}} समाधान करना, | इनकी व्याख्या इस प्रकार की जा सकती है: एक रैखिक समीकरण दिया गया है {{math|1=''T''(''v'') = ''w''}} समाधान करना, | ||
* कर्नेल सजातीय समीकरण के समाधान का स्थान है {{math|1=''T''(''v'') = 0}}, और इसका आयाम समाधान में स्वतंत्रता की डिग्री की संख्या है {{math|1=''T''(''v'') = ''w''}}, अगर वे | * कर्नेल सजातीय समीकरण के समाधान का स्थान है {{math|1=''T''(''v'') = 0}}, और इसका आयाम समाधान में स्वतंत्रता की डिग्री की संख्या है {{math|1=''T''(''v'') = ''w''}}, अगर वे उपलब्ध हैं; | ||
* कोकर्नेल डब्ल्यू पर बाधाओं का स्थान है जो समीकरण को हल करने के लिए संतुष्ट होना चाहिए, और इसका आयाम स्वतंत्र बाधाओं की संख्या है जो समाधान के लिए समीकरण के लिए संतुष्ट होना चाहिए। | * कोकर्नेल डब्ल्यू पर बाधाओं का स्थान है जो समीकरण को हल करने के लिए संतुष्ट होना चाहिए, और इसका आयाम स्वतंत्र बाधाओं की संख्या है जो समाधान के लिए समीकरण के लिए संतुष्ट होना चाहिए। | ||
कोकरनेल का आयाम और छवि का आयाम (रैंक) भागफल स्थान के आयाम के रूप में लक्ष्य स्थान के आयाम तक जुड़ते हैं {{math|''W'' / ''T''(''V'')}} बस अंतरिक्ष का आयाम घटा छवि का आयाम है। | कोकरनेल का आयाम और छवि का आयाम (रैंक) भागफल स्थान के आयाम के रूप में लक्ष्य स्थान के आयाम तक जुड़ते हैं {{math|''W'' / ''T''(''V'')}} बस अंतरिक्ष का आयाम घटा छवि का आयाम है। | ||
एक साधारण उदाहरण के रूप में, मानचित्र पर विचार करें {{math|''T'': '''R'''<sup>2</sup> → '''R'''<sup>2</sup>}}, द्वारा दिए गए {{math|1=''T''(''x'', ''y'') = (0, ''y'')}}. फिर एक समीकरण के लिए {{math|1=''T''(''x'', ''y'') = (''a'', ''b'')}} समाधान करने के लिए, हमारे पास होना चाहिए {{math|1=''a'' = 0}} (एक बाधा), और उस स्थिति में समाधान स्थान है {{math|(''x'', ''b'')}}, या समकक्ष, {{math|1=(0, ''b'') + (''x'', 0)}}, (स्वतंत्रता की एक डिग्री)। कर्नेल को उप-स्थान के रूप में व्यक्त किया जा सकता है {{math|(''x'', 0) ⊆ ''V''}}: का मान है {{mvar|x}} एक समाधान में स्वतंत्रता है। कोकरनेल को वास्तविक मूल्यवान मानचित्र के माध्यम से व्यक्त किया जा सकता है {{math|''W'': (''a'', ''b'') → (''a'')}}: एक | एक साधारण उदाहरण के रूप में, मानचित्र पर विचार करें {{math|''T'': '''R'''<sup>2</sup> → '''R'''<sup>2</sup>}}, द्वारा दिए गए {{math|1=''T''(''x'', ''y'') = (0, ''y'')}}. फिर एक समीकरण के लिए {{math|1=''T''(''x'', ''y'') = (''a'', ''b'')}} समाधान करने के लिए, हमारे पास होना चाहिए {{math|1=''a'' = 0}} (एक बाधा), और उस स्थिति में समाधान स्थान है {{math|(''x'', ''b'')}}, या समकक्ष, {{math|1=(0, ''b'') + (''x'', 0)}}, (स्वतंत्रता की एक डिग्री)। कर्नेल को उप-स्थान के रूप में व्यक्त किया जा सकता है {{math|(''x'', 0) ⊆ ''V''}}: का मान है {{mvar|x}} एक समाधान में स्वतंत्रता है। कोकरनेल को वास्तविक मूल्यवान मानचित्र के माध्यम से व्यक्त किया जा सकता है {{math|''W'': (''a'', ''b'') → (''a'')}}: एक सदिश दिया गया {{math|(''a'', ''b'')}}, का मान है {{mvar|a}} समाधान होने में बाधा है। | ||
इसके अतिरिक्त, कोकरनेल को कुछ ऐसा माना जा सकता है जो कि कर्नेल [[इंजेक्शन (गणित)]] का पता लगाता है उसी तरह प्रक्षेपण का पता लगाता है। एक | इसके अतिरिक्त, कोकरनेल को कुछ ऐसा माना जा सकता है जो कि कर्नेल [[इंजेक्शन (गणित)]] का पता लगाता है उसी तरह प्रक्षेपण का पता लगाता है। एक मैप इंजेक्शन है अगर और केवल अगर इसका कर्नेल साधारण है, और एक मैप विशेषण है अगर और केवल अगर इसका कोकर्नेल साधारण है, या दूसरे शब्दों में, यदि {{math|1=''W'' = im(''T'')}}. | ||
== संदर्भ == | == संदर्भ == | ||
*[[Saunders Mac Lane]]: ''[[Categories for the Working Mathematician]]'', Second Edition, 1978, p. 64 | *[[Saunders Mac Lane]]: ''[[Categories for the Working Mathematician]]'', Second Edition, 1978, p. 64 | ||
*[[Emily Riehl]]: [http://www.math.jhu.edu/~eriehl/context.pdf#page=100 Category Theory in Context], [https://store.doverpublications.com/048680903x.html Aurora Modern Math Originals], 2014, p. 82, p. 139 footnote 8. | *[[Emily Riehl]]: [http://www.math.jhu.edu/~eriehl/context.pdf#page=100 Category Theory in Context], [https://store.doverpublications.com/048680903x.html Aurora Modern Math Originals], 2014, p. 82, p. 139 footnote 8. | ||
[[de:Kern (Algebra)#Kokern]] | [[de:Kern (Algebra)#Kokern]] | ||
[[Category:Created On 08/05/2023]] | [[Category:Created On 08/05/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:श्रेणी सिद्धांत]] | |||
[[Category:समरूपता प्रमेय]] | |||
[[Category:सार बीजगणित]] | |||
Latest revision as of 15:24, 29 August 2023
सदिश रिक्त स्थान के एक रेखीय मानचित्रण का कोकर्नेल f : X → Y भागफल स्थान है (रैखिक बीजगणित) Y / im(f) के कोडोमेन का f की छवि द्वारा f. कोकरनेल के आयाम को कोरैंक कहा जाता है f.
कोकर्नेल कर्नेल (श्रेणी सिद्धांत) के लिए दोहरे (श्रेणी सिद्धांत) हैं, इसलिए नाम: कर्नेल डोमेन का एक सबोबिज है (यह डोमेन के लिए मैप करता है), जबकि कोकर्नेल कोडोमेन का एक अंश पिंड है (यह मानचित्र से मैप करता है) कोडोमेन)।
सहज रूप से, एक समीकरण दिया f(x) = y जिसे कोई हल करना चाह रहा है, कोकरनेल उन बाधाओं को मापता है जो y इस समीकरण के समाधान के लिए संतुष्ट होना चाहिए - समाधान के लिए बाधाएं - जबकि कर्नेल समाधान में स्वतंत्रता की डिग्री को मापता है, यदि कोई उपलब्ध है। यह नीचे #अंतर्ज्ञान में विस्तृत है।
सामान्यतः आकारिकी का कोकर्नेल f : X → Y कुछ श्रेणी सिद्धांत में (उदाहरण के लिए समूह (गणित) के बीच एक समूह समरूपता या हिल्बर्ट रिक्त स्थान के बीच एक परिबद्ध रैखिक संचालिका) एक पिंड है Q और एक रूपवाद q : Y → Q ऐसा है कि रचना q f श्रेणी का शून्य रूपवाद है, और इसके अलावा q इस संपत्ति के संबंध में सार्वभौमिक मानचित्रण संपत्ति है। प्रायः मैप q समझा जाता है, और Q का ही कोकर्नेल कहा जाता है f.
सार बीजगणित में कई स्थितियों में, जैसे एबेलियन समूह, सदिश रिक्त स्थान या मॉड्यूल (गणित) के लिए, समरूपता का कोकर्नेल f : X → Y का भागफल समुच्चय है Y की छवि (गणित) द्वारा f. टोपोलॉजी सेटिंग्स में, जैसे कि हिल्बर्ट रिक्त स्थान के बीच बंधे रैखिक ऑपरेटरों के साथ, सामान्यतः भागफल में जाने से पहले छवि को बंद करना (गणित) लेना पड़ता है।
औपचारिक परिभाषा
कोकर्नेल को श्रेणी सिद्धांत के सामान्य ढांचे में परिभाषित किया जा सकता है। परिभाषा को समझने के लिए विचाराधीन श्रेणी में शून्य आकारिकी होनी चाहिए। आकारिकी का कोकरनेल f : X → Y के बराबर के रूप में परिभाषित किया गया है f और शून्य रूपवाद 0XY : X → Y.
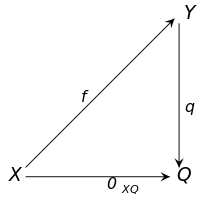
स्पष्ट रूप से, इसका अर्थ निम्नलिखित है: कोकरनेल का f : X → Y एक पिंड है Q साथ एक मोर्फिज्म के साथ q : Y → Q जैसे कि आरेख
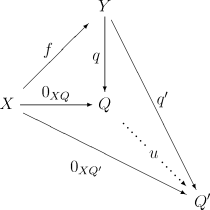
क्रमविनिमेय आरेख। इसके अलावा, रूपवाद q इस आरेख के लिए सार्वभौमिक संपत्ति होनी चाहिए, अर्थात ऐसा कोई अन्य q′ : Y → Q′ कंपोज करके प्राप्त किया जा सकता है q एक अद्वितीय मोर्फिज्म के साथ u : Q → Q′:
जैसा कि सभी सार्वभौमिक निर्माणों के साथ होता है, कोकरनेल, यदि यह उपलब्ध है, एक अद्वितीय समरूपता के लिए अद्वितीय है, या अधिक सटीक रूप से: यदि q : Y → Q और q′ : Y → Q′ के दो कोकर्नेल हैं f : X → Y, तो वहाँ अद्वितीय समरूपता उपलब्ध है u : Q → Q′ साथ q' = u q.
सभी समकक्षों की तरह, कोकरनेल q : Y → Q अनिवार्य रूप से एक एपिमोर्फिज्म है। इसके विपरीत एपिमोर्फिज्म को सामान्य रूपवाद (या सामान्य) कहा जाता है यदि यह कुछ आकारिकी का कोकर्नेल है। एक श्रेणी को सामान्य कहा जाता है यदि प्रत्येक अधिरूपता सामान्य है (उदाहरण के लिए समूहों की श्रेणी असामान्य है)।
उदाहरण
समूहों की श्रेणी में, एक समूह समरूपता का कोकर्नेल f : G → H का भागफल समूह है H की छवि के सामान्य समापन (समूह सिद्धांत) द्वारा f. एबेलियन समूहों के मामले में, चूंकि प्रत्येक उपसमूह सामान्य है, कोकर्नेल न्यायपूर्ण है H आदर्श (रिंग थ्योरी) की छवि f:
विशेष स्थितियां
पूर्ववर्ती श्रेणी में, आकारिकी को जोड़ना और घटाना समझ में आता है। ऐसी श्रेणी में, दो आकारिकी का समतुल्य f और g (यदि यह उपलब्ध है) उनके अंतर का सिर्फ कोकर्नेल है:
एबेलियन श्रेणी में (एक विशेष प्रकार की पूर्ववर्ती श्रेणी) छवि (श्रेणी सिद्धांत) और आकारिकी की सह-छवि f द्वारा दिया गया है
विशेष रूप से, प्रत्येक एबेलियन श्रेणी सामान्य (और सामान्य भी) है। यानी हर एकरूपता m को कुछ रूपवाद के कर्नेल के रूप में लिखा जा सकता है। विशेष रूप से, m अपने स्वयं के कोकर्नेल का कर्नेल है:
अंतर्ज्ञान
कोकर्नेल को अवरोधों के स्थान के रूप में सोचा जा सकता है जो एक समीकरण को संतुष्ट करना चाहिए, अवरोधों के स्थान के रूप में, जैसे कि कर्नेल (बीजगणित) समाधानों का स्थान है।
औपचारिक रूप से, कोई मानचित्र के कर्नेल और कोकर्नेल को जोड़ सकता है T: V → W सटीक क्रम से
इनकी व्याख्या इस प्रकार की जा सकती है: एक रैखिक समीकरण दिया गया है T(v) = w समाधान करना,
- कर्नेल सजातीय समीकरण के समाधान का स्थान है T(v) = 0, और इसका आयाम समाधान में स्वतंत्रता की डिग्री की संख्या है T(v) = w, अगर वे उपलब्ध हैं;
- कोकर्नेल डब्ल्यू पर बाधाओं का स्थान है जो समीकरण को हल करने के लिए संतुष्ट होना चाहिए, और इसका आयाम स्वतंत्र बाधाओं की संख्या है जो समाधान के लिए समीकरण के लिए संतुष्ट होना चाहिए।
कोकरनेल का आयाम और छवि का आयाम (रैंक) भागफल स्थान के आयाम के रूप में लक्ष्य स्थान के आयाम तक जुड़ते हैं W / T(V) बस अंतरिक्ष का आयाम घटा छवि का आयाम है।
एक साधारण उदाहरण के रूप में, मानचित्र पर विचार करें T: R2 → R2, द्वारा दिए गए T(x, y) = (0, y). फिर एक समीकरण के लिए T(x, y) = (a, b) समाधान करने के लिए, हमारे पास होना चाहिए a = 0 (एक बाधा), और उस स्थिति में समाधान स्थान है (x, b), या समकक्ष, (0, b) + (x, 0), (स्वतंत्रता की एक डिग्री)। कर्नेल को उप-स्थान के रूप में व्यक्त किया जा सकता है (x, 0) ⊆ V: का मान है x एक समाधान में स्वतंत्रता है। कोकरनेल को वास्तविक मूल्यवान मानचित्र के माध्यम से व्यक्त किया जा सकता है W: (a, b) → (a): एक सदिश दिया गया (a, b), का मान है a समाधान होने में बाधा है।
इसके अतिरिक्त, कोकरनेल को कुछ ऐसा माना जा सकता है जो कि कर्नेल इंजेक्शन (गणित) का पता लगाता है उसी तरह प्रक्षेपण का पता लगाता है। एक मैप इंजेक्शन है अगर और केवल अगर इसका कर्नेल साधारण है, और एक मैप विशेषण है अगर और केवल अगर इसका कोकर्नेल साधारण है, या दूसरे शब्दों में, यदि W = im(T).
संदर्भ
- Saunders Mac Lane: Categories for the Working Mathematician, Second Edition, 1978, p. 64
- Emily Riehl: Category Theory in Context, Aurora Modern Math Originals, 2014, p. 82, p. 139 footnote 8.