पैटर्न ब्लॉक: Difference between revisions
(Created page with "thumb|प्लास्टिक पैटर्न ब्लॉकपैटर्न ब्लॉक 1960 के दशक में व...") |
No edit summary |
||
| (19 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:Plastic pattern blocks.JPG|thumb|प्लास्टिक पैटर्न ब्लॉक]]पैटर्न ब्लॉक 1960 के दशक में विकसित [[गणितीय जोड़तोड़]] का एक | [[File:Plastic pattern blocks.JPG|thumb|प्लास्टिक पैटर्न ब्लॉक]]'''पैटर्न ब्लॉक''' '''1960''' के दशक में विकसित [[गणितीय जोड़तोड़|मैथमैटिकल मनीप्यूलेटिव]] का एक समुच्चय है। छह आकार का गणित सीखने के लिए एक खेल संसाधन और उपकरण दोनों होता है , यह स्थानिक तर्क कौशल विकसित करने के लिए काम करते हैं, जो गणित सीखने के लिए वास्तविक है। सभी बातों के अलावा, वे बच्चों को यह देखने की अनुमति देते हैं कि आकृतियों को कैसे बनाया जा सकता है और अन्य आकृतियों में कैसे विघटित किया जा सकता है, बच्चों को संख्याओं,आकृतियों,रंगो आदि की दोहराव वाली व्यवस्था के बारे में परिचित कराते हैं। पैटर्न ब्लॉक समुच्चय के सिर्फ छह आकृतियों की कई प्रजातियां है: | ||
*समबाहु त्रिभुज (हरा) | *समबाहु त्रिभुज (हरा) | ||
*60° सम[[चतुर्भुज]] (2 त्रिभुज) (नीला) | *60° सम[[चतुर्भुज]] (2 त्रिभुज) (नीला) जिसे दो हरे त्रिभुजों के साथ मिलाया जा सकता है | ||
*30° संकरा समचतुर्भुज (बेज) जिसका पार्श्व-लंबाई हरे त्रिभुज के समान | *30° संकरा समचतुर्भुज (बेज) जिसका पार्श्व-लंबाई हरे त्रिभुज के समान होता है | ||
* ट्रेपेज़ॉइड (आधा [[षट्भुज]] या 3 त्रिकोण) (लाल) जिसे तीन हरे त्रिकोणों के साथ मिलाया जा सकता है | * समलम्ब चतुर्भुज (ट्रेपेज़ॉइड) (आधा [[षट्भुज]] या 3 त्रिकोण) (लाल) जिसे तीन हरे त्रिकोणों के साथ मिलाया जा सकता है | ||
*नियमित षट्कोण (6 त्रिकोण) (पीला) जिसे हरे त्रिकोणों में से छह के साथ मिलान किया जा सकता है | *नियमित षट्कोण (6 त्रिकोण) (पीला) जिसे हरे त्रिकोणों में से छह के साथ मिलान किया जा सकता है | ||
* | *वर्गाकार (नारंगी) हरे त्रिकोण के समान पार्श्व-लंबाई के साथ मिलाया जा सकता हैं | ||
सभी कोण 30° (एक वृत्त का 1/12) के गुणक | सभी कोण 30° (एक वृत्त का 1/12) के गुणक है: 30° (1×), 60° (2×), 90° (3×), 120° (4×), और 150° (5×). | ||
== उपयोग == | == उपयोग == | ||
ब्लॉक को गणित और खेल दोनों को ध्यान में रखकर बनाया गया है। 1968 ईडीसी टीचर्स गाइड | पैटर्न ब्लॉक को गणित और खेल दोनों को ध्यान में रखकर बनाया गया है। 1968 में ईडीसी टीचर्स गाइड के द्वारा दी गयी सुझाव है: ब्लॉकों को बाहर निकालें, और स्वयं उनके साथ खेलें। अपने कुछ विचारों का प्रयोग करें । फिर, जब आप बच्चों को ब्लॉक दें, तो आराम से बैठें और देखें कि वे क्या करते हैं।<ref name="Teacherguide">{{cite book |last1=Elementary Science Study |title=Teacher's guide for pattern blocks |date=1970 |url=https://books.google.com/books?id=m1oQAQAAMAAJ |access-date=28 November 2018}}</ref> ब्लॉक गणितीय रूप से संचारित होता है, बच्चों के स्व-निर्देशित खेल से विभिन्न प्रकार के गणितीय अनुभव हो सकते हैं।<ref name="PatternBlocksATM">{{cite book |last1=Gregg |first1=Simon |title=Pattern Blocks |date=2020 |publisher=Association of Teachers of Mathematics |location=Derby, England |isbn=978-1912185207 |url=https://www.atm.org.uk/Shop/Pattern-Blocks-book-and-slides/ACT123pk |access-date=1 November 2020}}</ref> '''बिली''' '''हारग्रोव''' और जे जे मेबैंक्स ने नाटक की कई लगातार विशेषताओं की पहचान की है, जो घटित होती हैं:<ref>From the accompanying booklet to his Twenty-First Century Pattern Blocks</ref> | ||
* रचना और विघटन | * रचना और विघटन | ||
* समरूपता | * समरूपता | ||
| Line 17: | Line 17: | ||
* नकारात्मक अंतरिक्ष | * नकारात्मक अंतरिक्ष | ||
* प्रतिनिधि | * प्रतिनिधि | ||
[[File:A symmetrical pattern block design created by eight year olds.jpg|thumb|आठ साल के बच्चों द्वारा बनाया गया एक सममित पैटर्न ब्लॉक डिज़ाइन]] | [[File:A symmetrical pattern block design created by eight year olds.jpg|thumb|आठ साल के बच्चों द्वारा बनाया गया एक सममित पैटर्न ब्लॉक डिज़ाइन]]'''ईडीसी टीचर्स गाइड''' जारी है: कई बच्चे निराकार आकृति बनाकर प्रारम्भ करते हैं - सममित और असममित दोनों तरीकों से । जैसे-जैसे खेल जारी रहता है, ये आकृति अधिक से अधिक सुरुचिपूर्ण और जटिल हो सकता है, या सरल हो जाता है , क्योंकि बच्चें अपने विचारों में संशोधन करतें हैंI उपयोग का एक उदाहरण मेहा अग्रवाल द्वारा दिया गया है: '''केंद्र''' से प्रारम्भ करते हुए, मैं अपना पैटर्न बनाने के लिए ब्लॉक के बाद स्तर को जोड़ूंगा - यह पुनरावृत्त(दुबारा घटित होने की ) प्रक्रिया थी, क्योंकि अगर कुछ सौंदर्यपूर्ण रूप से आकर्षक या सही ढंग से नहीं दिखता है , तो परत को छीलने और इसे फिर से ठीक करने की आवश्यकता होती है। सबसे अच्छी बात संतुष्टि थी, जो मुझे तब मिली, जब मेरी रचना पूरी हुई। हालांकि व्यक्तिगत रूप से थका देने वाला, सामूहिक रूप से इन ब्लॉकों ने एक जटिल कृति का निर्माण किया जो कला और गणित, बड़ी तस्वीर का विवरण, सादगी और जटिलता को एक साथ लाया था ।<ref>{{cite news|last=McFarland|first=Matt|title=The childhood toys that inspired female engineers and scientists|url=https://www.washingtonpost.com/blogs/innovations/wp/2013/12/09/the-childhood-toys-that-inspired-female-engineers-and-scientists/|access-date=10 December 2013|newspaper=The Washington Post|date=9 December 2013}}</ref> | ||
== इतिहास == | == इतिहास == | ||
प्राथमिक अध्ययन विज्ञान (ईएसएस) परियोजना के हिस्से के रूप में न्यूटन, मैसाचुसेट्स [[शिक्षा विकास केंद्र]] में थें। उपयोग करने के लिए शिक्षक विकसित किये गए थे <ref>[http://www.picciotto.org/math-ed/angles/index.html Picciotto Math Education]</ref> शिक्षक मार्गदर्शिका का पहला परीक्षण संस्करण में कहा गया है: 1963 में एडवर्ड प्रेनोवित्ज़ '''के''' द्वारा पैटर्न ब्लॉक पर काम प्रारम्भ किया गया था। उन्होंने ब्लॉक के उपयोग के लिए अधिकांश विचारों को विकसित किया था और पहले कक्षा परीक्षणों की व्यवस्था की थी। कई ईएसएस सदस्यों ने समझने की कोशिश की और इसके गतिविधियों पर अपना सुझाव दिया।<ref name="MT157">{{cite journal |last1=Walter |first1=Marion |journal=Mathematics Teaching |date=December 1996 |issue=157 |page=3 |title=पत्र|url=https://www.atm.org.uk/Mathematics-Teaching-Journal-Archive/3856 |access-date=3 May 2020}}</ref> [[मैरियन वाल्टर]] 1960 के दशक में परियोजना का हिस्सा थे, 1996 में उन्होंने प्रेनोवित्ज़ से बात की, तो उन्होंने एक विशेष आकार के सभी ब्लॉकों के लिए एक रंग के वितरण करने पर विचार किया था , Cuisenaire(गणित सीखने के लिए सहायक उपकरण ) छड़ों की तरह, जिसने उन्हें यह विचार दिया था , ब्लॉकों के नए गुण में से एक होना। उनकी पसंद में यह भी महत्वपूर्ण था कि कुछ ब्लॉक थे, जो विशेष तरीकों से संयुक्त (जुड़े हुए ) थे।<ref name="MT157" /> | |||
== विकास == | == विकास == | ||
संगत आकार जो पैटर्न ब्लॉकों का विस्तार करते हैं, व्यावसायिक रूप से उपलब्ध हैं। भिन्नात्मक पैटर्न ब्लॉक के दो समुच्चय सम्मिलित हैं: दोनों दो ब्लॉक के साथ।<ref>{{cite web|title=Spark: Math Manipulatives|url=http://www.ucds.org/spark/manipulatives.html|website=www.ucds.org}}</ref> पहले में एक गुलाबी दोहरा षट्भुज और चार त्रिभुजों के बराबर एक काला शेवरॉन है। दूसरे में एक भूरे रंग का आधा- समलम्ब चतुर्भुज(ट्रेपजॉइड ) और एक गुलाबी आधा-त्रिकोण है। एक और समुच्चय डेसी-ब्लॉक, छह आकृतियों से बना है, क्रमशः चार, पांच, सात, आठ, नौ और दस त्रिकोणों के बराबर है । | |||
क्रिस्टोफर डेनियलसन ने ब्लॉक का एक नया | क्रिस्टोफर डेनियलसन ने ब्लॉक का एक नया समुच्चय विकसित किया, जिसे इक्कीसवीं सदी का पैटर्न ब्लॉक कहा जाता है।<ref name="21stC">{{cite web |last1=Danielson |first1=Christopher |title=Twenty-First Century Pattern Blocks |url=https://talkingmathwithkids.com/shop/21st-century-pattern-blocks/ |website=Talking Math With Your Kids |archive-url=https://web.archive.org/web/20181209184106/http://talkingmathwithkids.squarespace.com:80/store/21st-century-pattern-blocks |archive-date=2018-12-09 |url-status=dead |access-date=28 November 2018}}</ref> इस सेट में समचतुर्भुज का आकार पारंपरिक सेट में नीले समचतुर्भुज के समान है। काइट (ज्यामिति) और विशेष समकोण त्रिभुज 30°–60°–90° त्रिभुज 30°–60°–90° त्रिभुज का क्षेत्रफल के समान होता है, जबकि काइट (ज्यामिति) और षट्भुज का क्षेत्रफल उससे दोगुना होता है। पारंपरिक सेट की तरह, सभी कोण 30° के गुणक हैं। | ||
<gallery> | <gallery> | ||
Fraction pattern blocks 1.jpg| | Fraction pattern blocks 1.jpg|काला शेवरॉन और गुलाबी डबल हेक्सागोन अंश पैटर्न ब्लॉकों का एक सेट है | ||
Fraction pattern blocks 2.jpg| | Fraction pattern blocks 2.jpg|बैंगनी त्रिकोण और भूरा चतुर्भुज अंश पैटर्न ब्लॉकों की एक और जोड़ी है। | ||
Pattern Blocks and Deci-Blocks.jpg| | Pattern Blocks and Deci-Blocks.jpg|पैटर्न ब्लॉक और डेसी-ब्लॉक | ||
21st-century-pattern-blocks.jpg| | 21st-century-pattern-blocks.jpg|इक्कीसवीं सदी के पैटर्न ब्लॉक | ||
</gallery> | </gallery> | ||
== उदाहरण == | == उदाहरण == | ||
{| class=wikitable | {| class=wikitable | ||
|+ | |+ इग्जैम्पल कंस्ट्रक्शन (उदहारण निर्माण ) | ||
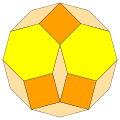
!colspan=4| | !colspan=4|रेगुलर डोडेकागन | ||
! | !आइसोटाक्सल आक्टगन(अष्टकोना) | ||
|- | |- | ||
|[[File:Wooden pattern blocks dodecagon.JPG|120px]] | |[[File:Wooden pattern blocks dodecagon.JPG|120px]] | ||
| Line 67: | Line 72: | ||
*[http://www.mathedpage.org/manipulatives/pattern-blocks/: Secondary school activities using pattern blocks] | *[http://www.mathedpage.org/manipulatives/pattern-blocks/: Secondary school activities using pattern blocks] | ||
* [https://arxiv.org/abs/2102.06046 A Quasiperiodic Tiling With 12-Fold Rotational Symmetry and Inflation Factor 1 + Sqrt(3)] Theo P. Schaad, Peter Stampfli, 10 Feb 2021 | * [https://arxiv.org/abs/2102.06046 A Quasiperiodic Tiling With 12-Fold Rotational Symmetry and Inflation Factor 1 + Sqrt(3)] Theo P. Schaad, Peter Stampfli, 10 Feb 2021 | ||
[[Category:Created On 03/02/2023]] | [[Category:Created On 03/02/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:आकृतियों की सूची|पैटर्न ब्लॉक]] | |||
[[Category:गणितीय जोड़तोड़]] | |||
[[Category:बचपन शिक्षा सामग्री]] | |||
Latest revision as of 16:51, 29 August 2023
पैटर्न ब्लॉक 1960 के दशक में विकसित मैथमैटिकल मनीप्यूलेटिव का एक समुच्चय है। छह आकार का गणित सीखने के लिए एक खेल संसाधन और उपकरण दोनों होता है , यह स्थानिक तर्क कौशल विकसित करने के लिए काम करते हैं, जो गणित सीखने के लिए वास्तविक है। सभी बातों के अलावा, वे बच्चों को यह देखने की अनुमति देते हैं कि आकृतियों को कैसे बनाया जा सकता है और अन्य आकृतियों में कैसे विघटित किया जा सकता है, बच्चों को संख्याओं,आकृतियों,रंगो आदि की दोहराव वाली व्यवस्था के बारे में परिचित कराते हैं। पैटर्न ब्लॉक समुच्चय के सिर्फ छह आकृतियों की कई प्रजातियां है:
- समबाहु त्रिभुज (हरा)
- 60° समचतुर्भुज (2 त्रिभुज) (नीला) जिसे दो हरे त्रिभुजों के साथ मिलाया जा सकता है
- 30° संकरा समचतुर्भुज (बेज) जिसका पार्श्व-लंबाई हरे त्रिभुज के समान होता है
- समलम्ब चतुर्भुज (ट्रेपेज़ॉइड) (आधा षट्भुज या 3 त्रिकोण) (लाल) जिसे तीन हरे त्रिकोणों के साथ मिलाया जा सकता है
- नियमित षट्कोण (6 त्रिकोण) (पीला) जिसे हरे त्रिकोणों में से छह के साथ मिलान किया जा सकता है
- वर्गाकार (नारंगी) हरे त्रिकोण के समान पार्श्व-लंबाई के साथ मिलाया जा सकता हैं
सभी कोण 30° (एक वृत्त का 1/12) के गुणक है: 30° (1×), 60° (2×), 90° (3×), 120° (4×), और 150° (5×).
उपयोग
पैटर्न ब्लॉक को गणित और खेल दोनों को ध्यान में रखकर बनाया गया है। 1968 में ईडीसी टीचर्स गाइड के द्वारा दी गयी सुझाव है: ब्लॉकों को बाहर निकालें, और स्वयं उनके साथ खेलें। अपने कुछ विचारों का प्रयोग करें । फिर, जब आप बच्चों को ब्लॉक दें, तो आराम से बैठें और देखें कि वे क्या करते हैं।[1] ब्लॉक गणितीय रूप से संचारित होता है, बच्चों के स्व-निर्देशित खेल से विभिन्न प्रकार के गणितीय अनुभव हो सकते हैं।[2] बिली हारग्रोव और जे जे मेबैंक्स ने नाटक की कई लगातार विशेषताओं की पहचान की है, जो घटित होती हैं:[3]
- रचना और विघटन
- समरूपता
- पैटर्न
- तीन आयाम
- नकारात्मक अंतरिक्ष
- प्रतिनिधि
ईडीसी टीचर्स गाइड जारी है: कई बच्चे निराकार आकृति बनाकर प्रारम्भ करते हैं - सममित और असममित दोनों तरीकों से । जैसे-जैसे खेल जारी रहता है, ये आकृति अधिक से अधिक सुरुचिपूर्ण और जटिल हो सकता है, या सरल हो जाता है , क्योंकि बच्चें अपने विचारों में संशोधन करतें हैंI उपयोग का एक उदाहरण मेहा अग्रवाल द्वारा दिया गया है: केंद्र से प्रारम्भ करते हुए, मैं अपना पैटर्न बनाने के लिए ब्लॉक के बाद स्तर को जोड़ूंगा - यह पुनरावृत्त(दुबारा घटित होने की ) प्रक्रिया थी, क्योंकि अगर कुछ सौंदर्यपूर्ण रूप से आकर्षक या सही ढंग से नहीं दिखता है , तो परत को छीलने और इसे फिर से ठीक करने की आवश्यकता होती है। सबसे अच्छी बात संतुष्टि थी, जो मुझे तब मिली, जब मेरी रचना पूरी हुई। हालांकि व्यक्तिगत रूप से थका देने वाला, सामूहिक रूप से इन ब्लॉकों ने एक जटिल कृति का निर्माण किया जो कला और गणित, बड़ी तस्वीर का विवरण, सादगी और जटिलता को एक साथ लाया था ।[4]
इतिहास
प्राथमिक अध्ययन विज्ञान (ईएसएस) परियोजना के हिस्से के रूप में न्यूटन, मैसाचुसेट्स शिक्षा विकास केंद्र में थें। उपयोग करने के लिए शिक्षक विकसित किये गए थे [5] शिक्षक मार्गदर्शिका का पहला परीक्षण संस्करण में कहा गया है: 1963 में एडवर्ड प्रेनोवित्ज़ के द्वारा पैटर्न ब्लॉक पर काम प्रारम्भ किया गया था। उन्होंने ब्लॉक के उपयोग के लिए अधिकांश विचारों को विकसित किया था और पहले कक्षा परीक्षणों की व्यवस्था की थी। कई ईएसएस सदस्यों ने समझने की कोशिश की और इसके गतिविधियों पर अपना सुझाव दिया।[6] मैरियन वाल्टर 1960 के दशक में परियोजना का हिस्सा थे, 1996 में उन्होंने प्रेनोवित्ज़ से बात की, तो उन्होंने एक विशेष आकार के सभी ब्लॉकों के लिए एक रंग के वितरण करने पर विचार किया था , Cuisenaire(गणित सीखने के लिए सहायक उपकरण ) छड़ों की तरह, जिसने उन्हें यह विचार दिया था , ब्लॉकों के नए गुण में से एक होना। उनकी पसंद में यह भी महत्वपूर्ण था कि कुछ ब्लॉक थे, जो विशेष तरीकों से संयुक्त (जुड़े हुए ) थे।[6]
विकास
संगत आकार जो पैटर्न ब्लॉकों का विस्तार करते हैं, व्यावसायिक रूप से उपलब्ध हैं। भिन्नात्मक पैटर्न ब्लॉक के दो समुच्चय सम्मिलित हैं: दोनों दो ब्लॉक के साथ।[7] पहले में एक गुलाबी दोहरा षट्भुज और चार त्रिभुजों के बराबर एक काला शेवरॉन है। दूसरे में एक भूरे रंग का आधा- समलम्ब चतुर्भुज(ट्रेपजॉइड ) और एक गुलाबी आधा-त्रिकोण है। एक और समुच्चय डेसी-ब्लॉक, छह आकृतियों से बना है, क्रमशः चार, पांच, सात, आठ, नौ और दस त्रिकोणों के बराबर है ।
क्रिस्टोफर डेनियलसन ने ब्लॉक का एक नया समुच्चय विकसित किया, जिसे इक्कीसवीं सदी का पैटर्न ब्लॉक कहा जाता है।[8] इस सेट में समचतुर्भुज का आकार पारंपरिक सेट में नीले समचतुर्भुज के समान है। काइट (ज्यामिति) और विशेष समकोण त्रिभुज 30°–60°–90° त्रिभुज 30°–60°–90° त्रिभुज का क्षेत्रफल के समान होता है, जबकि काइट (ज्यामिति) और षट्भुज का क्षेत्रफल उससे दोगुना होता है। पारंपरिक सेट की तरह, सभी कोण 30° के गुणक हैं।
उदाहरण
| रेगुलर डोडेकागन | आइसोटाक्सल आक्टगन(अष्टकोना) | |||
|---|---|---|---|---|

|

|

|
|

|
यह भी देखें
- सोकोलर टाइलिंग - एपेरियोडिक टाइलिंग जो पैटर्न के 3 ब्लॉक कनेक्शन के विशिष्ट नियमों के साथ आकार लेते हैं।
संदर्भ
- ↑ Elementary Science Study (1970). Teacher's guide for pattern blocks. Retrieved 28 November 2018.
- ↑ Gregg, Simon (2020). Pattern Blocks. Derby, England: Association of Teachers of Mathematics. ISBN 978-1912185207. Retrieved 1 November 2020.
- ↑ From the accompanying booklet to his Twenty-First Century Pattern Blocks
- ↑ McFarland, Matt (9 December 2013). "The childhood toys that inspired female engineers and scientists". The Washington Post. Retrieved 10 December 2013.
- ↑ Picciotto Math Education
- ↑ 6.0 6.1 Walter, Marion (December 1996). "पत्र". Mathematics Teaching (157): 3. Retrieved 3 May 2020.
- ↑ "Spark: Math Manipulatives". www.ucds.org.
- ↑ Danielson, Christopher. "Twenty-First Century Pattern Blocks". Talking Math With Your Kids. Archived from the original on 2018-12-09. Retrieved 28 November 2018.
बाहरी संबंध
- Pattern Block Templates: Printable Worksheets for Pattern Blocks
- Flash Pattern Blocks for web and Mandalar for mobile devices (iOS/Android).
- ETA/Cuisenaire: Educational manipulatives & supplemental materials for grades PreK-12.
- Background on the Elementary Science Study
- Educational and supplemental materials for K-12
- Secondary school activities using pattern blocks
- A Quasiperiodic Tiling With 12-Fold Rotational Symmetry and Inflation Factor 1 + Sqrt(3) Theo P. Schaad, Peter Stampfli, 10 Feb 2021





